由于电力系统中的非线性负荷、变频调速装置、风电场和光伏电站等均为间谐波源,因此,系统中不仅存在大量的整数次谐波,而且存在着非整数次谐波(次谐波、间谐波)。间谐波对电力系统及设备的危害很大,会引起灯光闪烁、低频继电器异常运行、无源滤波器过流跳闸、感应电动机噪声和振动等问题。因此,必须对间谐波进行治理,而治理的前提在于对间谐波的精确测量[1]。
快速傅立叶变换(FFT)是最常用的电力系统谐波分析方法[2],但其频率分辨率不高,且易受噪声尤其是时变噪声的影响。为了提高频率分辨率,实际工程中通常采用较长的数据窗,但噪声的影响依然很难克服。现代谱估计算法具有较高的频率分辨率,如自回归模型算法和特征值法[3, 4, 5, 6, 7, 8, 9, 10],但当信号中含有噪声,尤其是时变噪声时,所得谱估计结果会含有大量伪峰,可能无法区分真实的谐波和间谐波成分。小波变换[11]和时频分析[12]也被用于分析电力系统间谐波,虽然这些方法对噪声不敏感,但频率分辨率和估计精度较低,运算量也较大。
最小方差(MVDR)谱估计最初是由Capon在1969年研究地震波的空间谱时提出的[13]。之后,Lacoss于1971年将该方法用于单一时间序列谱估计[14],并证明了由该方法得出的估计是信号谱分量的最小方差无偏估计。文献[15]将最小方差方法应用于电力系统间谐波谱估计中,然而,由于需要进行矩阵求逆运算,导致该算法计算量较大。Musicus于1985年给出了最小方差递推算法[16],通过使用Gohberg-Semencul公式和Levinson递推算法使运算变得更为快捷。
本文采用Musicus提出的最小方差递推算法,将其用于电力系统间谐波谱估计。其优点是稳健性较好,对噪声不敏感,计算速度快。仿真结果验证了该方法的有效性。
1 基于最小方差谱估计的间谐波分析原理
设含M个谐波和间谐波的周期信号为:
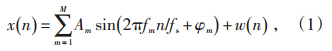
n—采样点;
fs—采样频率;
w(n)—噪声序列。
将信号x(n)输入到1个FIR滤波器中,则输出响应为:
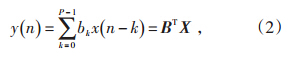
P—滤波器阶数;
B—滤波器系数矢量,B=(b0,b1,…,bP-1);
X—信号数据矢量,X=[x(n),x(n-1),…,x(n-P)]T。
则滤波器输出的平均功率(即输出序列的方差)为:
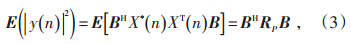
选择滤波器的原则是在频率点f处,FIR滤波器的频率响应归一化为1,即:
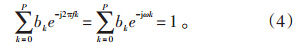
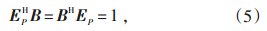
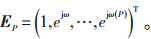
在满足式(5)约束的情况下,使滤波器输出平均功率最小化,可得到1个系数经过优化的滤波器。由于谐波和间谐波的能量主要集中在所对应的频率点上,因此当某次谐波成分无失真地通过该滤波器时,其他次谐波和噪声严重衰减,从而达到检测谐波和抑制噪声的目的。
对滤波器系数矢量B的求解是1个有约束的极值问题,令目标函数T(B)为:
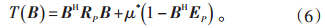
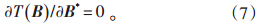
由式(7),可得:

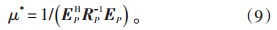
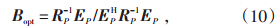
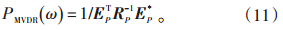
由式(11)可以看出,在作最小方差谱估计时,涉及相关矩阵RP的逆矩阵运算,计算量较大。而采用以下算法[16]可以使整个运算更为快捷。
令RP-1为自相关矩阵的逆矩阵,其中的元素为Rl,k-1 ,可将式(11)写为下列形式:
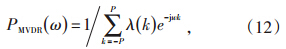

由于RP是Toeplitz矩阵,则可根据Gohberg-Se-mencul公式[17]来推导Rl,k-1,即:
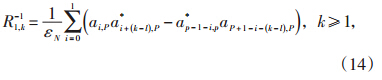
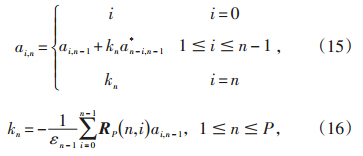
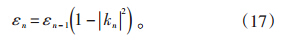
现有阶数预测法则(如最终预测误差准则,Akaike信息准则等)所预估的结果都不理想。因此,通常采用经验法则进行阶数预估,阶数的取值范围为N/3~N/2(其中,N为信号采样点数),这样得到的谱估计效果较好[18]。
Levinson递推算法提供了一种阶数逐渐增高的参数估计方法,每一阶的系数和误差均可由前一阶的结果递推获得,从而提高了计算效率。
将所求得的系数ai,n和误差εn代入式(14),求得Rl,k-1 ,再将Rl,k-1 代入式(13),则:
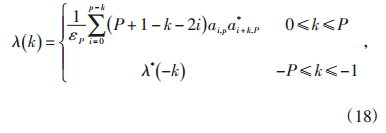
将λ(k)代入式(12)中,则可求得PMVDR(ω)。在谱估计曲线上搜索,对应各峰值位置处即为各次谐波和间谐波的角频率估计结果。3 仿真算例
为验证最小方差递推算法的可靠性,本文将该算法与MUSIC算法、Burg算法、FFT算法进行了比较,采用Matlab软件进行仿真。
设信号除基波(频率为50Hz,相位为π/3)外还含有1.7,3,3.5,7,7.3次谐波分量;幅值分别为基波的12%,7%,10%,8%,6%,相位分别为π/6,π/3,0,π/4,π/5。信号的采样频率为1000Hz,采样点数为256,根据经验法则和采样点数,设定阶数为120。3.1 算例1
在信号中加入方差σ=1.5的时变白噪声,该噪声在0.15s时开始出现,持续时间为1/4个周波(5ms)。仿真结果如图 1所示。
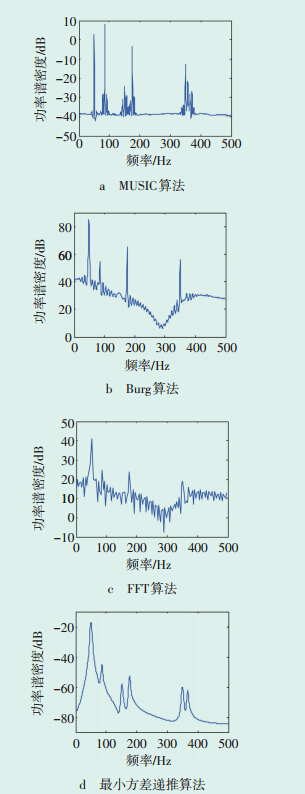 |
图1 时变白噪声下的功率谱估计结果 |
从图 1可以看出,受到时变噪声的影响,MUSIC算法、Burg算法和FFT算法谱估计结果均出现大量伪峰。其中,MUSIC算法谱估计结果在85Hz附近、140~190Hz及340~380Hz均出现由噪声引起的幅值较大的伪峰,无法将其与信号中的谐波和间谐波成分区分开来;Burg算法中的伪峰幅值较小,但信号中的3次和7.3次谐波同样由于幅值较小,因此被淹没在伪峰中,无法检测出来;FFT算法无法检测到3次和7.3次谐波,也无法将信号中的谐波和间谐波与噪声区分开来。
最小方差递推算法可以检测到频率为50Hz、86Hz、151Hz、176Hz、350Hz、367Hz的6个谱峰,平均频率误差为0.83Hz,图中未含伪峰,检测结果虽然有一定的误差,但是仍能够反映实际的谐波情况,检测精度满足工程要求。说明采用最小方差递推算法可有效抑制噪声,从而得到稳定、准确的频率估计结果,说明该算法具有较好的稳健性。3.2 算例2
在信号中加入30dB高斯白噪声,该噪声持续时间与信号相同,试验结果如图 2所示。
 |
图 2 高斯白噪声下的功率谱估计结果 |
从图 2可以看出,在高斯白噪声的影响下,MU-SIC算法和Burg算法谱估计结果均出现大量伪峰,无法将其与信号中的谐波和间谐波成分区分开。FFT算法谱估计结果虽然也存在一些伪峰,但伪峰幅值较小,可将其与谐波和间谐波成分区分开,检测到的6个谱峰的频率分别为50.78Hz,85.94Hz,148.44Hz,175.78Hz,351.56Hz,367.19Hz,平均频率误差为1.3Hz。最小方差递推算法谱估计结果基本不含伪峰,可以检测到所有的谐波和间谐波成分,检测到的6个谱峰的频率分别为50Hz,86Hz,151Hz,176Hz,350Hz,367Hz,平均频率误差为0.83Hz。3.3 结论
通过以上分析可以看出,相对MUSIC算法、Burg算法及FFT算法,最小方差递推算法谱估计结果受伪峰影响最小,同时该算法的平均频率误差也较低。4 结束语
本文将最小方差递推算法用于电力系统间谐波谱估计,通过仿真试验对该算法的谱估计性能进行检验。结果表明:该算法具有良好的噪声抑制性能,在信号含噪声的情况下,可以精确检测出信号所含的各次谐波和间谐波的频率。由于算法利用了Levinson递推法,计算效率高。同时,该方法无需同步采样,为硬件电路的简化创造了条件。
| [1] | 林海雪.电力系统中的间谐波问题[J].供用电,2001,18 (13):6-9. |
| [2] | 张伏生,耿中行,葛耀中.电力系统谐波分析的高精度 FFT算法[J].中国电机工程学报,1999,19(3):63-66. |
| [3] | 蔡忠法,陈隆道.基于AR谱估计和Adaline神经元的间谐波分析[J].电力系统自动化,2007,31(17):78-82. |
| [4] | 马秉伟,刘会金,周莉,等.一种基于自回归模型的间谐波谱估计的改进算法[J].中国电机工程学报,2005,25(15): 79-83. |
| [5] | 丁屹峰,程浩忠,吕干云,等.基于Prony算法的谐波和间谐波频谱估计[J].电工技术 学报,2005,20(10):94-97. |
| [6] | 欧阳华,吴正国,尹为民.dq 变换和MUSIC算法在间谐波检测中的应用[J].电力系统及其自动化学报,2012,24 (5):83-87. |
| [7] | 李新,程纯东,张淮清.基于实值Root-MUSIC和Prony算法的间谐波参数估计[J].电力自动化设备,2012,32(11): 56-59. |
| [8] | 高培生,谷湘文,吴为麟.基于空间谱和支持向量回归机的间谐波分析[J].电力系统自动化,2007,31(24):67-70. |
| [9] | 田伟,王洪希,白晶.基于互高阶谱MUSIC法的间谐波检测[J].继电器,2007,35(22):49-52. |
| [10] | 张滨生,喻乐,和敬涵,等.基于快速TLS-ESPRIT的间谐波检测算法[J].电力自动化设备,2011,31(2):26-31. |
| [11] | 曹健,林涛,强晓刚,等.采用改进支持向量机和复小波变换的谐波和间谐波测量方法[J].高电压技术,2011,37 (6):1384-1390. |
| [12] | 曹健,林涛,徐遐龄,等.基于最小二乘和时频原子变换的谐波/间谐波测量算法[J].电工技术学报,2011,26 (10):1-7. |
| [13] | J Capon. High-resolution frequency-wavenumber spectrum analysis[J]. IEEE,1969, 57(8): 1408-1418. |
| [14] | R T Lacoss. Data adaptive spectral analysis methods[J]. Geophysics,1971,36(4):661-675. |
| [15] | 朱天敬,王晨曦.基于SVD-MMVDR和Prony算法的间谐波参数估计[J].电力科学与工程,2013,29(11):5-10. |
| [16] | Bruce R Musicus.Fast MLM power spectrum estimation from uniformly spaced correlations[J].IEEE Transactions on Acoustics,Speech,and Signal Processing,1985,33(4): 1333-1335. |
| [17] | T Kailath, A Vieira, M Morf. Inverses of Toeplitz operators, innovations,and orthogonal polynomials[J].SIAM Rev, 1978(20):106-119. |
| [18] | G Proakis J. 统计信号处理算法[M].汤俊,译.北京:清华大学出版社,2006:455-462. |
 2015, Vol. 33
2015, Vol. 33 
