2. 内蒙古上都发电有限责任公司, 内蒙古锡林浩特 027200
2. Inner Mongolia Shangdu Thermal Power Co., Ltd., Inner Mongolia Xilinhot 027200
科学技术的进步,特别是计算机技术的迅速发展为电厂控制技术水平的不断提高创造了条件,现代控制理论与技术在电厂得到了越来越广泛的应用。工程实际应用中,准确建立被控对象的数学模型是获得理想控制效果的必要条件。通常情况下,被控对象往往很复杂且具有时变性,准确建立其相应的数学模型较为困难,即使是电厂技术人员有时也无法准确描述其数学模型。另外,工艺系统实际运行中数学模型的参数也会有所变化,使已建立的模型难以取得理想的控制效果,甚至会失控。准确建立被控对象的数学描述是所有控制理论得以成功实施的基本条件,建立控制对象的精确数学模型也是进行系统辨识的基础。具体地说,系统辨识就是在系统已经进行了必要的数据处理和数据计算的基础上,从1组给定的模型中,确定1个与所测系统等价的模型,即辨识是利用数学方法从输入、输出数据序列中提取对象数学模型的1种方法[1]。1 循环流化床锅炉燃烧控制系统主要任务与对象 1.1 工艺过程
循环流化床燃烧技术是由最早的火床燃烧技术发展形成的,通过提高火床底部的送风量,将固体颗粒吹起并使其处于悬浮状态,从而使固体颗粒具有流体的性质。这种方式不仅易于床料的均匀混合,而且流动性也得到了很大的提高,进而优化了燃烧效果和传热效果。随着空气量的不断增加,这些固体颗粒也会被气流带走,这时利用安装在炉膛出口的分离器将未完全燃烧的颗粒从大量固体颗粒中分离、收集并再次送回炉膛,从而形成固体颗粒的循环利用,故称之为循环流化床燃烧。 1.2 控制系统任务
使燃料提供的热量适应锅炉负荷的要求是循环流化床锅炉燃烧控制系统的基本任务,同时还要保证锅炉运行的安全性和经济性。循环流化床锅炉控制系统的主要任务有:
(1)保持锅炉主蒸汽压力在正常范围内;
(2)锅炉的安全稳定与经济运行;
(3)引风量与送风量的协调配合;
(4)确保锅炉床温稳定,并处于最佳温度范围内;
(5)床层高度控制在合理范围内;
(6)控制二级返料回灰量,保证系统能量平衡,返料回灰量的控制水平直接影响循环流化床锅炉的床温、循环倍率。 1.3 主要控制对象
床温是循环流化床锅炉运行最重要的控制参数之一,直接影响着炉内脱硫和脱硝过程,主要根据煤质的结焦温度和能否最大限度地发挥脱硫剂的脱硫能力进行选择。如床温过高,则炉膛内部容易结焦,破坏了循环流化床的正常运行状态,安全性变差;床温过低,则易引起炉膛灭火、停炉,影响正常的生产运行。床温变化也会对汽水系统造成直接影响,引起主蒸汽压力和温度等参数的波动。维持床温在正常范围内,保证锅炉出口蒸汽参数合格是循环流化床锅炉安全稳定与经济运行的关键。实际运行中绝大多数燃烧控制和调节任务也都是围绕这一目标进行的[2]。目前应用最广泛的控制床温办法是调节给煤量,但采用传统控制给煤量的方法难以取得理想的控制效果,而采用神经网络方法进行系统建模和辨识,并在此基础上引入现代控制理论,可取得较好的控制效果[3]。因此,建立床温控制对象模型是目前循环流化床床温控制系统开发工作的重要一环,已成为研制和完善此类控制系统的迫切需要和首要任务。本文拟通过神经网络辨识技术来测试控制对象模型的准确性。2 人工神经网络及系统辨识方法介绍 2.1 人工神经网络特点
人工神经网络是在对人脑组织结构、活动机制初步认识的基础上提出的1种新型计算模型,该模型具有分布式存储、并行协同处理等特点[4]。人工神经网络因其良好的非线性映射能力和柔软的拓扑结构,现已被广泛应用于模式识别、信号处理、数据预测、最优化问题计算、系统辨认、信息的智能化处理、图像处理、复杂控制、语音理解以及函数拟合等方面[4,5,6]。 2.2 建模方法
从过程控制的角度考虑,神经网络建模的优势在于其“黑箱”理论(即可以把过程看作是1个“黑箱”,而不用考虑过程是如何进行的,只需研究对象的主要控制变量和输出变量之间的相互关系)[4, 5]。人工神经网络在处理未知模型和多变量非线性系统方面具有其他系统无法比拟的优势,同时神经网络可以任意逼近非线性函数(在选择合适的BP网络的隐层数和输出层激活函数的情况下,算法具有很强的逼近性能),克服了许多机理建模存在的难题,并且可以用于实时学习、预测和仿真[6]。建模过程不需要机理方面的细节知识,只需要根据神经网络数学模型输出的被控对象信息修改网络参数,即可实现从输入到输出的非线性映射关系。2.3 算法
神经网络的算法多种多样,需要针对不同的控制对象,在分析其特性和要求的基础上选择相应的神经网络结构。对循环流化床锅炉的系统辨识,主要从辨识的快速性和泛化性2个方面进行选择。神经网络辨识的快速性是指建立1个符合标准的较快网络速度,神经网络的算法是影响辨识速度的主要因素。对于循环流化床锅炉来说,辨识速度快可以在非常短的时间内完成对锅炉燃烧系统的床温控制。神经网络辨识的泛化是指对于不在训练样本集中的非训练样本,神经网络仍能给出正确的输入、输出关系[2]。如果神经网络的泛化能力强,在锅炉燃烧参数发生变化时,炉膛内的床温可以保持不变。单神经元自适应PID控制算法见公式(1)[7]。
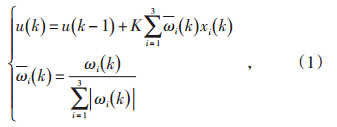
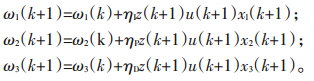
燃料量s与床温G的传递函数见公式(2)[8],系统逻辑结构如图 1所示。
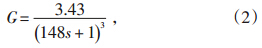
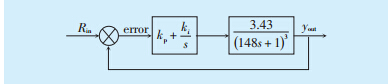 | 图 1 燃料量控制床温系统逻辑结构 |
首先根据经验公式计算出在PI控制下的控制器参数TAT=4.116,实际取值4;积分时间Ti=188,取正弦信号序列值作为给定信号值,在PI控制器作用下得到系统输出值。然后把输入和输出序列的前1000个点作为训练样本对BP神经网络进行训练,输入、输出序列的后1000个点作为测试样本,对训练好的神经网络进行测试[9]。设计神经网络为3层网络结构:输入层为2个神经元节点,隐层为10个神经元节点,输出层为1个神经元节点。在MAT⁃LAB下对系统进行辨识,仿真系统阶跃响应曲线如图 2、图 3所示。
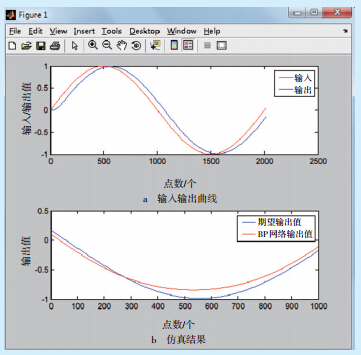 | 图 2 BP网络输出值与模拟期望输出值的比较图 |
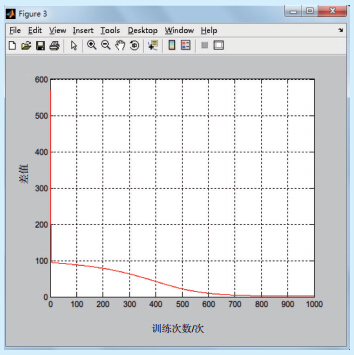 | 图 3 网络的计算输出值与训练样本期望输出值之间的差值变化过程 |
图 2中,上半部分为PI控制下的系统输入、输出曲线,其中的前1000个点用于训练BP神经网络,后1000个点用于测试;下半部分的仿真结果表明,经过训练的BP网络输出值能够比较好地模拟期望输出值,说明经过训练的BP网络能够较好地模拟系统的闭环响应。
由图 3可见,随着训练次数的增加,网络的权值变化可以使输出值与期望值之差逐渐减小,直到满足精度要求。3.2 试验结果
通过对神经网络闭环控制系统自适应PID控制进行仿真试验,说明BP网络能够较好地模拟系统的闭环响应,验证了神经网络PID控制中微分学习速率、比例学习速率、积分学习速率等参数在控制中所起的作用。
(1)在积分学习速率、比例学习速率不变的情况下,微分学习速率对单神经元PID控制器的控制效果影响不大。
(2)在微分学习速率、积分学习速率不变的情况下,比例系数学习速率越大则超调量越小,响应速度也会越慢。
(3)在比例学习速率、微分学习速率不变的情况下,积分系数学习速率越大则响应会越快,超调量也会越大。4 结束语
将神经网络应用到闭环系统辨识中,通过MAT⁃LAB仿真,系统的阶跃响应说明经过训练的BP网络能够较准确地模拟系统的闭环响应,验证了应用神经网络进行系统辨识的有效性和可行性。
| [1] | Di Maggio T, Bursi J M,Lafanechere L,et a1. Circulating fluidized bed boiler numerical modeling:Part I A steady state model for CFB power plants and its application to the 250 MW Provence unit,A modular software to assess and forecast the operation of the largest CFB boiler in the world[C]//Science Press,5th International Conference on Circulating Fluidized Beds.Beijing: Science Press,1996:466-470. |
| [2] | 付萍,姚丽欣,李小珂,等.循环流化床锅炉床温系统控制特性分析及参数优化[J].华北电力大学学报,2005,32 (5):89-91. |
| [3] | 边立秀,周俊霞,付松.循环流化床锅炉床温控制建模与仿真[J].华北电力大学学报,2003,30(1):53-56. |
| [4] | 叶海文,倪维斗,李政.燃煤循环流化床锅炉模型化的人工神经网络方法[J].清华大学学报(自然科学版),l997, 37(2):19-23. |
| [5] | 马宝萍.模糊建模与神经网络控制的研究及其在循环流化床锅炉中的应用[D].南京:东南大学,2000:1-20. |
| [6] | 焦李成.神经网络系统理论[M].西安:西安电子科技大学出版社,1996:1-66. |
| [7] | 王晓天.基于神经网络辨识的循环流化床锅炉的床温控制研究[D].昆明:昆明理工大学,2005:39-41. |
| [8] | 赵伟杰,张文震,冯晓露.循环流化床锅炉床温的控制特性[J].动力工程,2007,27(4):545-550. |
| [9] | 康支霞,张宪,马永光,等.循环流化床锅炉床温控制神经网络动态建模[J].锅炉技术,2006,37(S1):32-35. |
| [10] | 刘晴,张正刚,丁维明.神经网络预测PID控制在气化炉中的应用[J].自动化仪表,2014(5):60-62. |
| [11] | 徐继松.基于CFB热电联产系统的自动控制研究[D].沈阳:沈阳建筑大学,2013:19-26. |
 2014, Vol. 32
2014, Vol. 32 
