0 引言
水电机组在内蒙古电网中主要承担着调峰任 务,开展水轮机组及其调节系统性能参数测试与仿 真建模工作对内蒙古电网动态稳定性仿真计算有 重要意义。正确建立符合设备实际运行状态的数 学模型及合理设定其参数,是确保电力系统稳定性 分析结果准确、可靠的基础。早期电力系统仿真计 算采用的水轮机—原动机模型较为简单,常采用水 轮机理想模型,这种模型对于使用线性分析技术来 调节的控制系统是可行的,但对涉及功率输出和频 率变化大的研究对象是不合适的[1]。因此,依据水 轮机及其引水系统工作机理,开展更合理、更接近 于真实系统的非线性原动机模型构建与仿真校核 的研究工作是十分必要的。 1 水轮机及引水系统建模优化 1.1 混流式水轮机数学模型
水轮机实际工作过程中,流量q 和水轮机主动 力矩mt等特性参数会随工况的变化而改变。水轮 机过渡过程中的瞬时力矩由稳态力矩和动态附加 力矩组成,稳态力矩可从水轮机稳态试验的综合特 性曲线换算得到,动态附加力矩主要由水流惯性产 生。当水轮机处于小扰动后的暂态过程时,可以只 考虑水轮机的稳态特性,近似采用能量试验得到的 综合特性曲线计算,其计算精度在允许范围内[1,2]。
对于水轮机某个工作点,水轮机力矩方程和流 量方程可用传递系数进行描述[2]:
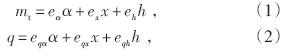
ex、eα、eh—分别为力矩对水轮机转速、导叶 开度、水头的传递系数;
eqx、eqα、eqh—分别为流量对水轮机转速、导叶 开度、水头的传递系数。
实际应用中,由于导叶接力器行程测取方便, 且导叶接力器行程y(标幺值)与导叶开度α的关系 可以近似为线性对应关系,因此常使用y来代替α。
当机组转速变化不大时,可以认为x≈0,则上 述表达式可写为:

eqy—流量对导叶行程的传递系数,eqy = ∂q/∂y 。
根据公式(3)、(4)推导搭建的混流式水轮机模 型结构框图见图 1所示。
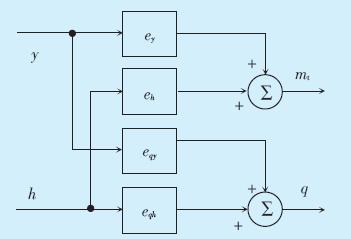 |
图 1 混流式水轮机模型结构 |
实际工程中水轮机引水系统的类型和结构十 分复杂,要精确描述引水系统的动态过程,必须采用复杂的非线性系统数学模型(如基于特征线法和 基于二端网络的数学模型等),这种数学模型对于 研究水轮机控制系统过渡过程是必要的,但对于电 力系统稳定计算则略显复杂。
因水流惯性引起的水击现象会引起管道内压 力波动,进而影响水轮机的出力及其调节系统的动 态特性,因此在电力系统稳定性计算中主要考虑水 流惯性的水锤效应对水轮机引水系统、调节系统动 特性的影响[1,2]。一般在小扰动情况下,且管道长度 小于600 m时,可以忽略引水系统的弹性水锤,那么 刚性引水系统管道水锤效应的数学表达式为:

Hr—额定水头,m;
Qr—额定流量,m3/h;
L—引水系统管道长度,m;
F—引水系统管道截面积,m2;
g—重力加速度,m/s2。
根据公式(5)、(6)建立的引水系统的传递函数 框图如图 2所示。
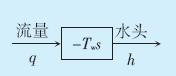 |
图 2 考虑刚性水锤效应的引水系统传递函数框图 |
早先采用的理想水轮机的模型是经过一系列 简化和假设确定的,从PGV(导叶指令)到PE (输出功 率)的数学模型可整理成图 3所示的Tw卡形式[3]。
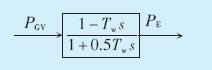 |
图 3 理想混流式水轮机及引水系统的传递函数框图 |
考虑刚性水锤效应后,从PGV到PE间的混流式 水轮机及引水系统的数学模型如图 4所示。
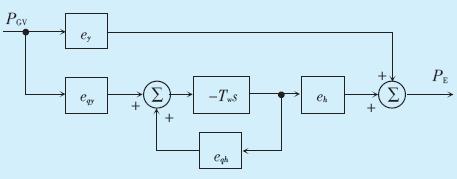 |
图 4 混流式水轮机及引水系统的传递函数框图 |
若对图 4所示模型进行简化,令ey=1,ex=-1,eh= 1.5,eqy=1,eqx=0,eqh=0.5,即与图 3所示的理想模型一 致。 2 应用实例 2.1 机组简介
某水电站1号机组水轮机为天津阿尔斯通水电 设备有限公司生产的混流式水轮机,型号为HL (220)-LJ-580,额定功率180 MW,额定转速100 r/ min,设计水头66.15 m,额定流量290.7 m3/s,水轮机 飞轮矩(GD2)为60 000 tm2。调速系统配备天津阿尔 斯通水电设备有限公司的TSLG型调速器,发电机 为哈尔滨电机有限责任公司生产的SF180-60/ 12800型发电机。 2.2 水轮机模型及参数辨识
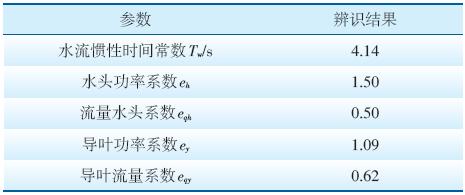
导叶开度给定5%阶跃试验记录曲线见图 5所 示。根据图 3所示的水轮机模型,以导叶接力器行 程为输入量、机组机械功率为输出量进行模型参数 辨识,结果如表 1所示;辨识模型在同样导叶开度扰 动下的仿真曲线和实测曲线对比如图 6所示。
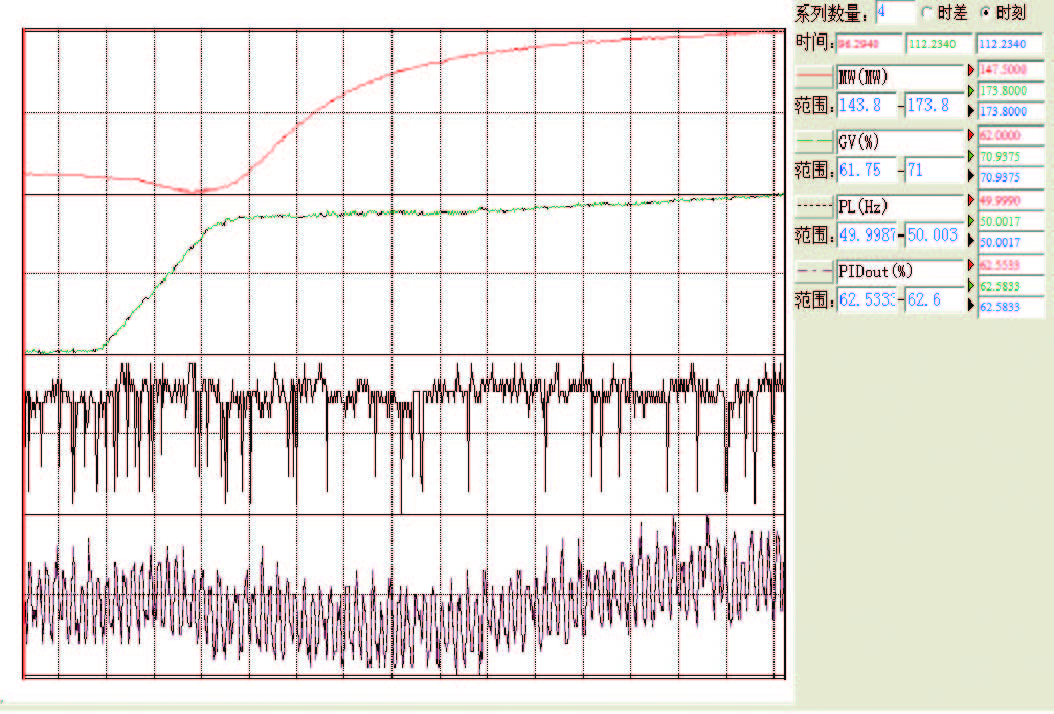 |
图 5 导叶开度给定5%阶跃试验记录 |
| 表 1 水轮机模型辨识结果 |
从图 5可以看出,机组功率仿真结果与实测功 率相当吻合。根据甩负荷试验中转子转速飞升曲 线,可辨识得出该水轮机的转子时间常数Ta= 8.1937 s。
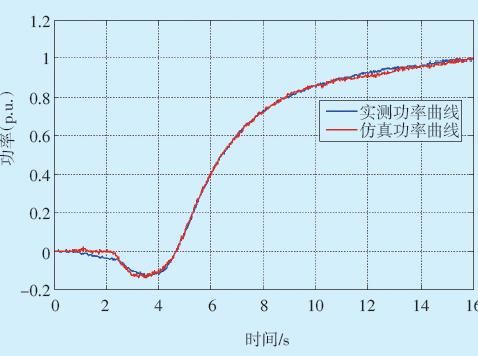 |
图 6 水轮机模型参数辨识结果仿真与实测数据的对比 |
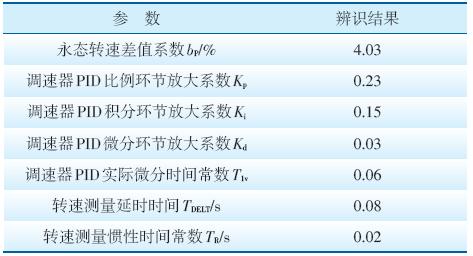
水轮机调速系统建模技术发展迅速,目前大多 采用matlab软件进行调速系统参数的拟合辨识。依 据调速器模型GM、GM+卡[3,4],以频差信号为输入 量、导叶指令为输出量,对该机组调速器模型参数 进行辨识。辨识过程采用基于遗传算法的参数辨 识方法[5],获取的主要参数见表 2所示。
| 表 2 机组调速器模型辨识结果 |
根据机组执行机构的模型GA卡[3,4],以导叶指 令为输入量、导叶开度为输出量,对执行机构模型 参数进行辨识。辨识过程采用基于遗传算法的参 数辨识方法[5,6,7,8],主要参数辨识结果见表 3所示。
| 表 3 机组调速系统执行机构模型辨识结果 |
将通过辨识获取的水轮机及引水系统模型、调 速器模型、执行机构模型的参数代入仿真软件中建 立的水轮机稳定计算使用的模型中,将给定频率扰 动试验数据作为输入量进行仿真计算,仿真结果与 实测结果的对比曲线如图 7所示。图 7中输出功率 的变化规律,以及仿真功率和实际功率的吻合度均 表明所建立的模型和辨识得到的参数都能较好地 反映系统的动态特性。
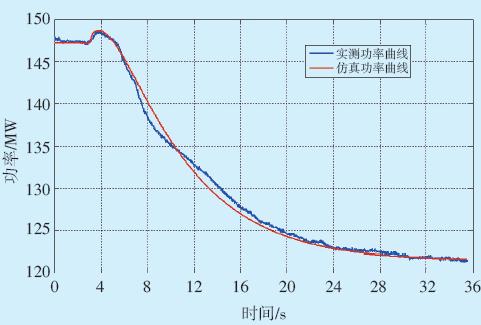 |
图 7 频率扰动下机组模型仿真校核 |
构建了更能反映水轮机及引水系统真实工作 过程的多参数模型,将其应用到某台180 MW混流 式水轮机调速系统参数测试工作后,成功辨识了水 轮机及引水系统模型、调速器模型、执行机构模型 的各项参数;通过进行给定频率扰动仿真计算,验 证了所确定的水轮机及调节系统模型及参数的准 确性和可靠性。混流式水轮机模型研究工作的开 展,有利于提高电力系统稳定性分析及调度分析计 算的准确性,研究成果可供类似机组的建模辨识工 作参考。
| [1] | 龚强,吴道平.水轮机调速系统参数辨识与系统建模测试简介[J].江西电力,2011,35(3):36-39. |
| [2] | 沈祖诒.水轮机调节系统分析[M].北京:中国水利电力出版社,1991:23-36. |
| [3] | 中国电力科学研究院.PSD-BPA暂态稳定程序用户手册[R].北京:中国电力科学研究院,2005:3-5. |
| [4] | 全国电网运行与控制标准化技术委员会.DL/T 1235— 2013 同步发电机原动机及其调节系统参数实测与建模导则[S].北京:中国电力出版社,2013:3-6. |
| [5] | 戴义平,邓仁刚,刘炯,等.基于遗传算法的汽轮机数学电液调节系统的参数辨识研究[J].中国电机工程学报, 2002,22(7):101-104. |
| [6] | 李悝,张靖,孙海顺,等.水轮机及其调速系统建模与参数辨识方法[J].水电能源科学,2006,24(4):79-82. |
| [7] | 董彦同,万天虎,石峯,等.基于CFD的混流式水轮机减压、管数值分析[J].陕西电力,2008,36(1):68-71. |
| [8] | 万天虎,何常胜,李华.水轮发电机组一次调频仿真与参数辨识[J].陕西电力,2009,37(3):55-58. |
 2014, Vol. 32
2014, Vol. 32