由于全球性的大自然气候变化,极端天气时有发生,而电力系统又是现代经济社会中的重要基础设施,对于人类社会和国民经济的顺利运转具有重要意义。因此如果由于自然灾害而造成电力系统出现大面积中断或崩溃,将会对国民经济造成巨大影响。
近年来随着储能设备的技术不断成熟,储能电池的成本持续降低,储能设备在配电网中的占比不断增大。储能设备具有容量配置灵活、响应速度快、输出功率稳定等优点,常规条件下,主要应用于调峰、调频、缓解阻塞、电压支撑与无功控制等[1];当发生极端自然灾害时,储能设备亦可用作紧急电源,为重要的负荷节点提供供电保障。目前,有研究者对如何增强系统韧性展开了研究。在台风灾害下的配电网故障发生率建模方面,文献[2]全面考虑事故发生频次、中断供电时长和缺供电量等因素,对配电网不同的风险等级进行了分类,并结合系统气候影响因素做了相关研究,但没有涉及增强韧性的具体措施。文献[3]采用5种机器学习算法构建了配电网的杆塔损伤空间分布预计建模,做到了对分析结果可视化,但未涉及杆塔内部联系的关联性。文献[4]构建了数据-机理共同推动的台风配电网故障率建模,同时涉及台风和暴雨两种自然灾害,但没有对韧性与经济性方面的主次进行分析。文献[5]给出了兼顾韧性强度的城市配电网络的储能装置规划方法,提出的二阶段鲁棒性优化建模,可有效保障重要负荷节点的不间断安全供电。文献[6]主张运用移动式储能的空间便捷性,并利用负荷形成故障微电网来提升其系统弹性,但未涉及台风气候的时间维度和空间维度,且较依赖城市的交通路况。尽管国内外对储能设备的选址与定容的规划方法已经有不少探索,但对于增强系统韧性方面尚有欠缺。
储能设备作为分布式电源的一种,在提升电网韧性的同时,也能够在日常工作中降低配电网的网络损耗,因供电网络的网络损耗不但和负载大小直接相关,而且与储能设备的优化选择有着必然联系。储能设备合理的选址和定容,可以确保系统安全平稳运转,同时能够减少运营成本,因此研究如何合理选择储能设备的位置和容量意义重大[7-10]。文献[11]针对分布式电源规划问题改进了原有的遗传计算流程,创建了一种多目标优化建模,使用权重系数法把多目标函数转化成单目标函数加以计算,不过该方法需要重新统一量纲,由于经验不足可能会使目标函数难以转换。文献[12]对灰狼计算算法加以完善,引入了混沌序列来产生初始种群,以减少系统网损、降低分布式电源投资运营费用、减少电压偏移为多目标函数,进行了优化配置建模。
本文所构建的目标函数在考虑韧性提升基础上,兼顾对系统网损和设备成本的影响,同时考虑配电网的韧性指标,对各项指标进行无量纲化和归一化处理,从而确定各个目标函数的权重,得到综合目标函数。在此基础上,根据储能的选址、定容问题对多目标粒子群计算做出改进,并将之运用于储能装置的设计问题中。
1 分布式电源优化配置模型以最小化有功网损、最小化年投资运行费用和最大化韧性指标来建立目标函数,以功率平衡、节点电压平衡和储能设备的装置容量为约束条件,规划合理的优化选配方案。
1.1 目标函数(1)有功网络损耗f1。f1计算公式见式(1):
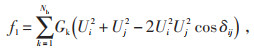
|
(1) |
式中:Nb为支路数量;Gk为节点i和节点j之间支路的电流输出电导;Ui和Uj为节点i和节点j的电压幅值;δij为节点i和节点j的电压相角差。
(2)储能设备投资成本。储能系统成本包括储能建设成本和运行成本,其中储能建设成本包括储能容量成本Ce和储能功率成本Cp,储能设备投资成本函数f2见式(2):

|
(2) |
式中:Cop, i为节点i的储能运行成本,S1, 2, 3为储能设备参与一次调频补偿收益、调峰补偿收益和峰谷套利收益的总和。
(3)韧性指标。本文主要通过系统功能在极端气候下的缺失面积来反映配电网韧性,利用故障场景的发生概率和相应的负荷曲线缺失面积来估算配电网的弹性能力,即韧性指标,其目标函数f3见式(3),极端气候下的电网配电功能曲线如图 1所示。
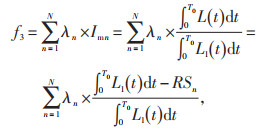
|
(3) |

|
| 图 1 极端气候下配电网系统功能曲线 Figure 1 Function curve of distribution network system under extreme climate |
式中:λn为场景n的发生概率;N为选择的故障发生场景个数;Imn为场景n的供电量不足程度;T0表明城市供电网络受到极端气候影响的持续时间,包含台风风灾穿越该配电网所用的时间以及配电网恢复供电的持续时间,由于各个场景下的故障恢复所需时间不同,T0应远大于各场景中相应的t4(见图>1);L(t)表示极端气候造成重大故障发生时的真实负荷曲线;L1(t)表示系统无故障运作时的目标负荷曲线;Sn为图 1中真实曲线与目标曲线所包裹的区域,代表负荷曲线的缺失面积。
本文以f1、f2最小,f3最大,设置储能优化模型的综合优化目标:
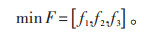
|
(4) |
(1)节点电压Vi(t) 约束条件如下:

|
(5) |
式中:Vmax、Vmin为节点电压的上下限。
(2)功率平衡约束条件如下:

|
(6) |
式中:PG(t) 为电源有功出力;nnew为分布式储能的安装数量;Pnew, i(t) 为第i个分布式储能在t时刻的有功出力;Pload(t) 为t时刻系统的总负荷。
(3)储能容量和功率约束条件如下:

|
(7) |
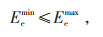
|
(8) |
式中:Pemax和Pemin分别为储能功率上、下限,Eemax和Eemin和分别为储能容量上、下限。
(4)储能数量约束条件如下:
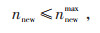
|
(9) |
式中:nnew为储能设备安装数量,nnewmax为最大安装数量。
2 多目标权重系数的确定 2.1 函数的标准化函数的标准化又称为无量纲化,本文综合考虑网损费用、投资效益和韧性提升这三个目标函数,由于存在量纲差异的情况,相互之间会存在矛盾,从而无法使各个子目标共同达到最优化。因此需要对各个子目标实行无量纲化,本文采用直线型无量纲法当中的极差标准法,如式(10)所示:
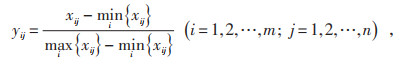
|
(10) |
式中:yij为目标极差化后的数据;xij为评价策略i中指标j的具体数据;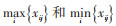
层次分析法(Analytic Hierarchy Process,AHP)是由美国运筹学家Saaty发明的一种主观判断分析方法[13]。AHP将一个复杂的多目标决策划分为多指标的不同层级,利用定性指标来模糊定量计算阶段的单顺序和总顺序,进而确定多目标的策略方法。
(1)构造判断矩阵A:
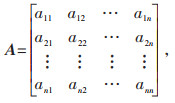
|
(11) |
式中:aij表示指标i和指标j的相对重要关系,(i=1,2,…,n;j=1,2,…,n),矩阵中所有要素的取值都可通过AHP准则来判断。
(2)求特征值。计算判断矩阵A的最大特征根λmax及特征向量ω = {ω1, ω2, …, ωn},结果中的特征向量为权重向量,即可得出多目标函数的权重系数。
(3)一致性检查。
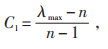
|
(12) |
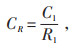
|
(13) |
式中:C1为判断不相同情形时的一致性指标;R1为AHP给定的随机一致性指标;当一致性因子CR < 0.1时,则表明该权重系数为可以选择。
2.3 多目标函数的归一化各个子目标由式(10)无量纲化后,通过层次分析法对不同的目标函数进行主观赋权,进而决定子目标的相对权重,最终把各个子目标函数统一为:
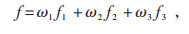
|
(14) |
式中:f为无量纲化后的总目标函数;ω1、ω2、ω3为通过层次分析法确定的权重系数。
3 改进粒子群算法 3.1 标准粒子群算法粒子群算法是一种依靠随机性求解的遗传算法。首先在解空间中随机产生大量粒子,粒子均匀分布在解空间中。粒子根据自己的当前位置、历史位置和种群的总体情况来进行迭代进化,从而寻求最优解。粒子速度νid(k)及其位置xid(k)的更新公式如下:
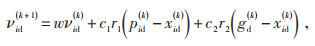
|
(15) |
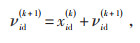
|
(16) |
式中:w为惯性权重;c1、c2为加速因子;r1、r2为(0,1)之间的随机数;pid(k)为第i个粒子的历史最优解;gd(k)为种群全局最优解。
粒子群算法在解决单目标优化的问题中表现优异,但是多目标优化问题的解,是几组连续解的集合,无法通过粒子群算法直接求解。多目标粒子解算法将求出的互不支配的解保存在Pareto解集中,求解出一系列非劣解。在这些非劣解中选取全局最优和历史最优解,指导粒子的进化。
利用多目标粒子解算法进行储能系统的优化配置时,存在以下问题:
(1)粒子维度过高,迭代过程中易陷入维度陷阱;增加种群数量可解决该问题,但采用该方法,又会导致计算量和耗时大大增加;
(2)在优化求解储能实际问题时,未充分利用信息指导粒子进化进程。
3.2 基于主仆模式(master⁃slave)的算法改进根据本文建立的模型,为了提高算法的利用率,添加基于主仆模式的改进方法。首先,可以将问题分解为诸多的主粒子(master)和仆粒子(slave),根据适应值的不同,挑选master粒子。每个master粒子下有不同数量的slave粒子,master粒子1所在区域的位置A1为master和slave所有粒子的历史最优位置。同理,可以得到对应的A2和A3等粒子的最优位置,对比不同最优位置的数值,得出全局最优位置B。这种算法的优点是,如果master粒子1所属粒子陷入局部最优或者无法找寻到最优解的情况,master粒子2、master粒子3及其他master粒子所在区域仍继续搜寻,一定程度上保证了解的最优性。master社区粒子的位置A为master社区和slave社区所有粒子的最优过去位置。而slave社区粒子的位置A仅为该slave社区所有粒子的最优过去位置。这样,当划分出多个slave社区时,即使有一个slave社区粒子收敛陷入局部最优,仍能保证master社区粒子有较大的概率跳出这个局部最优位置。
master⁃slave算法的优点是实现单线程程序的多线程计算,通过将一个任务分成多个子任务的方式,显著提升了计算性能、计算的可靠性和精准程度。
3.3 算法流程提升改进多目标粒子群算法流程如图 2所示。

|
| 图 2 改进多目标粒子群计算流程图 Figure 2 Flow chart of improved multi⁃objective particle swarm calculation |
本文以改进的IEEE33节点配电控制系统为例,对利用Matlab软件进行计算分析。IEEE33节点配电系统见图 3。该系统总共包含33个节点、32条支路和1个变压器,系统的基准电压为12.66 kV,节点电压允许范围为0.9~1.1(p.u.),初始网架的有功负荷为5500 kW,故障期间电网负荷为0.5~0.8(p.u.)。算例中,最多连接3个储能设备,储能设备可以连接的位置节点为{2,3,…,33}。储能设备的最大额定功率和额定容量分别为350 kW和1000 kW时,与之相对应的成本系数分别为7000元/kW和35元/kWh,单位功率年运行维护成本为63元/kW·a。储能设备的放电效率为0.9,荷电状态范围为0.1~0.9。配电网中的重要负荷默认已接入一条转供线路。根据城市的土地成本不同,将储能的站址分为3个区域,每个站点的成本分别为910 000元(节点1—9,19—22),700 000元(节点23—25,26—33)和490 000元(节点10—18),储能设备收益以广东某地区为例,峰平谷比为1.7∶1∶0.38,平时电价0.528 3元/kWh;储能设备算作负的PQ节点处理,功率因数为0.9。计算的参数设置为:种群数量为200;最大迭代次数d=250;主要控制因数C1=2;次要随机因数C2为[0,0.5]的随机数。通过AHP法确定各个目标函数的权重,分别为ω1=0.352、ω2=0.220、ω3=0.428,其中韧性指标占比最大。

|
| 图 3 IEEE33节点配电网系统 Figure 3 IEEE33 node distribution network system |
为验证本文方法的有效性,设置如下两个场景:
(1)不添加任何韧性防护措施;
(2)添加储能设备进行韧性防护。
以配电网加权负荷损失作为系统功能损失的直观表现,非重要负荷的单位失负荷成本为70元/kWh,重要负荷单位失负荷成本为7000元/kWh;台风过境时间选择15 min。
表 1为IEEE33节点算例台风灾害下不同场景的技术经济对比,场景1重要负荷损失为35.7%,而场景2重要负荷损失为0;场景1非重要负荷损失为58.17,场景2的非重要负荷损失比场景1少7.28%,同时加权负荷损失大大减少,仅为场景1的8.54%,韧性指标得到大幅提升。除此之外,场景2的网络损耗也比场景1的网络损耗降低了36.6%,可见达到了降低网络损耗的效果。表 2为程序运行速度对比,可以明显看到,使用本文改进的粒子群算法可使程序运行速度得到大幅提升,提升比例达到260%。
| 表 1 IEEE33节点算例台风灾害下不同场景的技术经济对比 Table 1 Technical and economic comparison of IEEE33 node cases under typhoon disaster |
| 表 2 程序运行速度对比 Table 2 Comparison of program running speed |
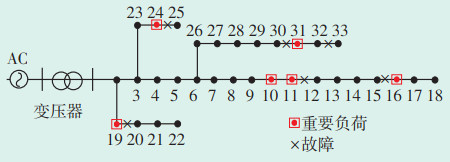
图 4为IEEE33节点算例场景1的规划结果,从图中可知,重要负荷节点16、31的供电线路都遭到了破坏,非重要节点12—18、20—22、25、26—33也受到了破坏,损失了大量的负荷,造成了巨大的经济损失。
|
| 图 4 IEEE33节点算例场景1的规划结果 Figure 4 Planning of IEEE33 node example Scenario 1 |
图 5为IEEE33节点算例场景2的规划结果,从图中可知,在保证故障位置不变的情况下,增加3个储能设备之后(储能设备配置参数如表 3所示),所有的重要节点负荷都得到了供电保障,而非重要负荷节点17、18、32也得到了供电保障。根据表 3,本算例的储能设备在理想情况下可以在7~8年收回成本。

|
| 图 5 IEEE33节点算例场景2的规划结果 Figure 5 Planning of IEEE33 node example Scenario 2 |
| 表 3 IEEE33节点算例储能配置的参数结果 Table 3 Parameter of energy storage configuration of IEEE33 nodes |
本文针对配电网的韧性提升问题,提出了一种基于主仆模式(master⁃slave)的多目标粒子群算法,可有效针对储能设备进行选址、定容,通过该方法能够显著提升计算的性能、可靠性和精准程度。结果表明,本文研究的方法能在保证重要负荷节点在台风灾害下有稳定的供电保障,同时还兼顾了配电网的有功网损和储能设备的经济性。
同时对配置储能构建韧性配电网规划方法进行了研究,提出了基于相关理论的模型,对配置分布式可再生能源构建韧性电网的规划具有一定的现实意义。
本文研究仅针对与一种固定灾害场景的计算,并未涉及随机故障灾害场景的生成与筛选,并且在多目标粒子群算法的优化上还稍有欠缺,接下来将针对上述问题进行研究。
| [1] |
陈大宇. 含电储能系统的新型辅助服务市场研究[D]. 北京: 华北电力大学, 2016.
(  0) 0)
|
| [2] |
冯喜春, 张松岩, 朱天曈, 等. 基于区间二型模糊多属性决策方法的大规模储能选型分析[J].
高电压技术, 2021, 47(11): 4123-4136 (  0) 0)
|
| [3] |
张稳, 盛万兴, 刘科研, 等. 计及天气因素相关性的配电网故障风险等级预测方法[J].
电网技术, 2018, 42(8): 2391-2398 ZHANG Wen, SHENG Wanxing, LIU Keyan, et al. Distribution network failure risk level prediction methodconsidering the correlation of weather factors[J]. Power System Technology, 2018, 42(8): 2391-2398 (  0) 0)
|
| [4] |
HOU Hui, YU Shiwen, WANG Hongbin, et al. Risk assessment and its visualization of power tower under typhoon disaster based on machine learning algorithms[J].
Energies, 2019, 12(2): 1-23 (  0) 0)
|
| [5] |
张海波, 马伸铜, 程鑫, 等. 保证重要负荷不间断供电的配电网储能规划方法[J].
电网技术, 2021, 45(1): 259-268 ZHANG Haibo, MA Shentong, CHENG Xin, et al. Energy stor-age planning method of distribution network to ensure uninter-rupted power supply of important loads[J]. Power System Technology, 2021, 45(1): 259-268 (  0) 0)
|
| [6] |
Kim J, Dvorkin Y. Enhancing distribution system resilience with mobile energy storage and microgrids[J].
IEEE Trans on Smart Grid, 2019, 10(5): 4996-5006 DOI:10.1109/TSG.2018.2872521 (  0) 0)
|
| [7] |
张勇军, 张锶恒, 刘斯亮, 等. 考虑分布式光伏与储能接入的配变双层规划[J].
电力系统保护与控制, 2020, 48(24): 9-15 ZHANG Yongjun, ZHANG Siheng, LIU Siliang, et al. Distribution transformer bi-level planning considering distributed photo-voltaic and energy storage integration[J]. Power System Protection and Control, 2020, 48(24): 9-15 (  0) 0)
|
| [8] |
李旭斌, 朱永洁, 喻琢舟, 等. 主动配电网"源-荷-储"协调优化控制方法研究[J].
机电工程技术, 2020, 49(5): 61-64 LI Xubin, ZHU Yongjie, YU Zhuozhou, et al. Reserch on "DG-Load-ESS" Coordinated Control in Active Distribution Network[J]. Mechanical & Electrical Engineering Technology, 2020, 49(5): 61-64 (  0) 0)
|
| [9] |
张帆, 杨翾, 商佳宜, 等. 考虑负荷损失最小的配网孤岛划分策略研究[J].
高压电器, 2021, 57(4): 181-188 ZHANG Fan, YANG Xuan, SHANG Jiayi, et al. Study on island partition strategy of distribution network considering minimum load loss[J]. High Voltage Apparatus, 2021, 57(4): 181-188 (  0) 0)
|
| [10] |
段建东, 孙茜, 陈鲁鹏, 等. 基于改进和声搜索算法的有源配电网优化调度[J].
高压电器, 2021, 57(11): 1-9 DUAN Jiandong, SUN Qian, CHEN Lupeng, et al. Optimal dispatching of active distribution network based on improved harmony search algorithms[J]. High Voltage Apparatus, 2021, 57(11): 1-9 (  0) 0)
|
| [11] |
王振浩, 李文文, 陈继开, 等. 基于改进自适应遗传算法的分布式电源优化配置[J].
电测与仪表, 2015, 52(5): 30-34 WANG Zhenhao, LI Wenwen, CHEN Jikai, et al. Optimal configuration of distributed power sources based on improved adaptive genetic algorithm[J]. Electrical Measurement & Instrumentation, 2015, 52(5): 30-34 (  0) 0)
|
| [12] |
张涛, 张东方, 王凌云. 基于灰狼算法的分布式电源优化配置[J].
水电能源科学, 2018, 36(4)204-207, 212 ZHANG Tao, ZHANG Dongfang, WANG Lingyun. Optimal allocation of distributed generation based on Gray Wolf algorithm[J]. Water Resources and Power, 2018, 36(4)204-207, 212 (  0) 0)
|
| [13] |
吴勇军, 薛禹胜, 谢云云, 等. 台风及暴雨对电网故障率的时空影响[J].
电力系统自动化, 2016, 40(2): 20-29 WU Yongjun, XUE Yusheng, XIE Yunyun, et al. Spatial andtemporal effects of typhoons and rainstorms on power network-failure rate[J]. Automation of Electric Power Systems, 2016, 40(2): 20-29 (  0) 0)
|
 2023, Vol. 41
2023, Vol. 41