大量光伏和风力等分布式电源(Distributed Generation,DG)接入使得传统配电网逐步转变为多能源多路径系统,提高了配电网供电的可靠性[1-2],但其灵活的接入特点以及出力的不确定性与波动性,会对配电网可靠性产生不利影响[3-4]。
低压配电网中三相不平衡问题普遍存在[5-8],其主要原因是负荷分配不均以及单相DG的接入。配电网重构(Distribution Network Reconfiguration,DNR)是指通过对分段开关和联络开关的断开与闭合来改变网络拓扑结构,从而减小网损、提高电能质量、均衡网络有功和无功以及提高对DG的接纳能力[9-11],进而缓解三相不平衡问题的方法。
国内外学者对DNR进行了广泛而深入的研究,文献[12]分析了重构过程中DG出力不确定性的解决方法和各种重构模型的优缺点。文献[13]提出一种可以改进现有直角坐标的线性潮流计算无法处理PV节点三相不平衡线性潮流的计算方法,此方法无须迭代可直接计算配电网辐射状、弱环状和含PV节点3种情况的三相不平衡潮流。文献[14]针对含不确定性的三相不平衡运行配电网重构问题,以有功网损最小为优化目标函数,考虑DG和负荷注入功率的不确定性进行建模,对一天内的时段进行合理划分,采用基于三相Distflow潮流方程建立含不确定性预算的配电网两阶段鲁棒动态重构模型,但鲁棒性是考虑了模型最差情况下的安全运行,结果相对保守,经济性较差。文献[15]建立了考虑系统有功损耗、节点最低电压幅值及开关操作次数的配电网重构多目标优化模型,结合粒子群算法和Pareto支配方法来求解,即多目标粒子群算法。虽然粒子群算法实现简单、收敛速度快,但很容易陷入局部最优从而导致早熟收敛。文献[16]提出了一种含分布式电源的主动配电网重构策略,以最小化网损为目标函数,将改进的教与学优化算法应用于配电网供电路径的快速优化。该方法收敛速度快、寻优时间短、运行稳定,但没有考虑配电网三相不平衡运行情况。大M法是运筹优化建模中常用到的方法,目的是将非线性问题转化成线性问题,使得问题能够使用运筹经典模型来求解。文献[17]从数学优化的角度研究了含分布式电源配电网重构的二阶锥规划模型。首先建立以配电网有功损耗最小化为目标的优化模型,其次采用凸松弛的Distflow模型描述配电网的潮流方程,并基于生成树的配电网连通性约束,将Distflow中的节点电压用大M约束进行松弛,但没有考虑分布式电源的波动性和负荷的时变性对配电网的影响。
本文在大M法松弛模型约束的前提下,提出以降低有功损耗和三相不平衡度为目标,基于三相电流注入法(Three⁃Phase Current Injection Emethod,TCIM)[18]的配电网重构方法。该方法使用单相节点导纳矩阵描述三相网络,充分考虑大量单相分布式电源的波动性和单相负荷的时变性对网络的影响;使用多边形内近似法将所提模型转为混合整数化线性规划(Mixed ⁃ Integer Linear Programming,MILP);加入各相充放电功率可以单独控制[19]的三相储能设备(Energy Storage,ES),提高单相资源的时空调用能力;加入单相静止无功发生器(Static Var Generator,SVG)补偿无功,缓解网络无功不足和光伏逆变器牺牲部分有功出力来提高无功出力而造成的有功不足,提高网络单相的调节能力,配合重构改变供电路径,降低网络有功损耗,提高三相平衡度。最后,通过改进IEEE 33节点配电系统的计算与分析,验证本文方法的有效性。
1 优化模型 1.1 目标函数配电网运行时,由于单相负荷和单相分布式电源的时空分布不均,三相不平衡会导致相电压偏移变大,线路损耗增加[20],影响电网的运行及用户用电。因此,本文以全天有功损耗最小和三相不平衡度最小为目标函数,其中三相不平衡度可用式(1)表示:
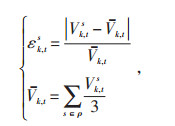
|
(1) |
式中:ρ—集合{L1,L2,L3,U,V,W},s ∈ρ;
Vk, t—t时刻节点k三相电压平均值;
Vk, ts—t时刻节点k的s相电压幅值;
εk, ts—t时刻节点k的s相三相不平衡度。
对于整个系统,三相不平衡度可用式(2)表示:
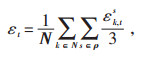
|
(2) |
式中:εt—t时刻网络三相不平衡度;
N—网络节点集合。
网络的有功损耗Ploss, t计算见式(3):
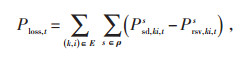
|
(3) |
式中:E—网络的线路集合;
Psd, ki, ts—t时刻线路ki上s相的送端功率;
Prsv, ki, ts—t时刻线路ki上s相的受端功率,
其中:
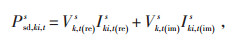
|
(4) |
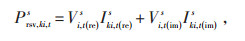
|
(5) |
式中:Iki, t(re)s—t时刻线路ki上s相电流的实部;
Iki, t(im)s—t时刻线路ki上s相电流的虚部;
Vk, t(re)s—t时刻节点k上s相电压实部;
Vk, t(im)s—t时刻节点k上s相电压虚部;
Vi, t(re)s—t时刻节点i上s相电压实部;
Vi, t(im)s—t时刻节点i上s相电压虚部。
本文考虑有功损耗和三相不平衡度的目标函数(F)如式(6)所示:
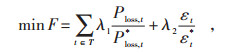
|
(6) |
式中:T—t的集合;
λ1、λ2—有功损耗和三相不平衡度的权重系数,且λ1+λ2=1;
Ploss, t*—未优化前t时刻有功损耗;
εt*—未优化前t时刻网络三相不平衡度。
1.2 约束条件决策变量在满足目标函数的同时,还需要满足潮流约束、电流注入约束、线路连接状态约束、网络辐射状态运行约束、开关动作次数约束、电压和电流幅值约束、DG出力约束、ES和SVG运行约束。
1.2.1 潮流约束在三相网络中,各相之间存在耦合,由于相间耦合关系的非线性会造成模型非凸,给求解各相的物理量带来很大困难,本文使用相间互导纳来近似地表示三相之间的耦合关系,相间互导纳为常量,可将相间非线性耦合线性化,并基于电路理论分别求解三相网络中各相的物理量。相间互导纳如式(7)所示:
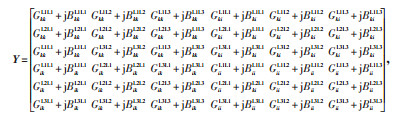
|
(7) |
式中:Y—线路kk、ki、ii和sq相之间构成的6×6导纳矩阵;Y = G + jB, q ∈ ρ,s ∈ ρ,G为导纳Y的实部,B为导纳Y的虚部。
网络的节点电压方程如式(8)所示,对于三相不含中性线的潮流模型,可根据式(8)推导出余下潮流约束:
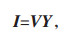
|
(8) |
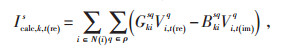
|
(9) |
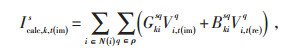
|
(10) |
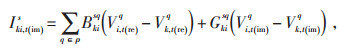
|
(11) |
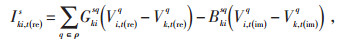
|
(12) |
式中:N(i)—与节点k相关联的节点集合,规定k节点到i节点为正方向;
I—网络节点电流向量;
V—网络节点电压向量;
Icalc, k, t(re)s—t时刻节点k上s相电流实部;
Icalc, k, t(im)s—t时刻节点k上s相电流虚部;
Vi, t(re)q—t时刻节点i上q相电压实部;
Vi, t(im)q—t时刻节点i上q相电压虚部;
Vk, t(re)q—t时刻节点k上q相电压实部;
Vk, t(im)q—t时刻节点k上q相电压虚部;
Gkisq—线路ki的电导;
Bkisq—线路ki上sq相的电纳。
1.2.2 电流注入约束如式(13)所示,节点的注入电流大小由注入功率确定,各节点注入有功功率(Pinj, k, ts) 和无功功率(Qinj, k, ts) 大小如式(14)和(15)所示,将式(14)和(15)带入式(13)即可得出三相不含中性线模型,模型中各节点各相电流注入方程如式(16)和(17)所示。
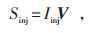
|
(13) |
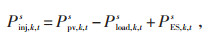
|
(14) |
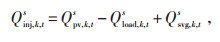
|
(15) |
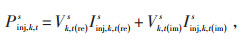
|
(16) |
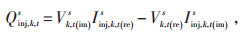
|
(17) |
式中:Sinj—网络的总注入功率;
Iinj—网络的总注入电流;
Qpv, k, ts—t时刻节点k上s相光伏的无功功率;
Qload, k, ts—t时刻节点k上s相负荷的无功功率;
Qsvg, k, ts—t时刻节点k上s相SVG的无功功率;
Ppv, k, ts—t时刻节点k上s相光伏的有功功率;
Pload, k, ts—t时刻节点k上s相负荷的有功功率;
PES, k, ts—t时刻节点k上s相ES的有功功率;
Iinj, k, t(re)s—t时刻节点k上s相注入电流的实部;
Iinj, k, t(im)s—t时刻节点k上s相注入电流的虚部。根据欧姆定律,其他节点流入该节点的电流大
小等于该节点自身注入电流大小,据此可以得到基于注入电流不平衡量的潮流方程见式(18)和(19)。
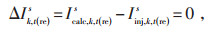
|
(18) |
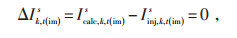
|
(19) |
式中:ΔIk, t(re)s—t时刻节点k上s相注入电流实部的不平衡量;
ΔIk, t(im)s—t时刻节点k上s相注入电流虚部的不平衡量。
1.2.3 线路连接状态约束
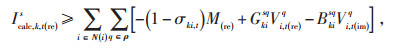
|
(20) |
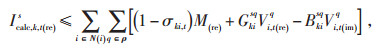
|
(21) |
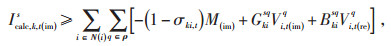
|
(22) |
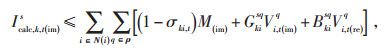
|
(23) |
式中:M(re)、M(im)—正实数;
σki, t—t时刻线路ki的连接状态。σki, t= 1表示在t时刻线路ki闭合,式(20)—(23)分别等价于式(9)和式(10),此时线路两端电压幅值存在相关性;σki, t = 0表示在t时刻线路断开,由于较大正数M(re)和M(im)的存在,导致式(20)—(23)中的约束不起作用,线路两端电压幅值不存在相关性,但断开线路ki两端电压幅值与网络其他节点存在相关性,因此断开线路两端电压幅值由其他节点的约束关系决定。
1.2.4 网络辐射状态运行约束
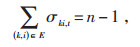
|
(24) |
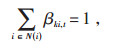
|
(25) |
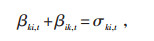
|
(26) |
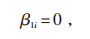
|
(27) |
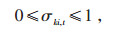
|
(28) |
式中:βki, t—t时刻节点k与节点i之间的关系变量。
式(24)表明线路与节点之间须满足的数量关系,否则会出现孤立的节点;βki, t = 1时,节点k是节点i的父节点,反之节点k不是节点i的父节点;式(25)和(26)表明线路ki连接时,有且只有一个父节点;式(27)表示平衡节点一定不是父节点。
1.2.5 开关动作次数约束
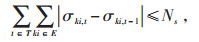
|
(29) |
式中:Ns—最大动作开关次数。
1.2.6 电压幅值约束
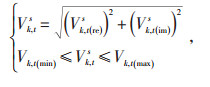
|
(30) |
式中:Vk, t(min)—t时刻节点k上电压幅值的下限;
Vk, t(max)—t时刻节点k上电压幅值的上限。
1.2.7 电流幅值约束
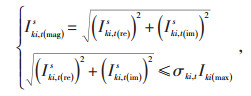
|
(31) |
式中:Ik, t(mag)s—t时刻线路ki上s相电流幅值大小;
Iki(max)—线路ki流经电流幅值的上限。
1.2.8 DG出力约束在约束式(14)和(15)中,光伏的有功和无功分别用节点注入的有功和无功表示,并将配电网出口母线认为是平衡节点,其他节点为PQ节点。光伏逆变器发出的无功功率不是无限的,而是受到多方面因素制约,本文考虑以可控的光伏逆变器为模型建模,其约束见式(32)—(34)。
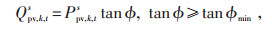
|
(32) |
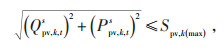
|
(33) |
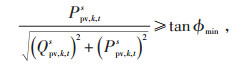
|
(34) |
式中:Qpv, k, ts—t时刻节点k上s相光伏逆变器发出的无功;
Spv, k(max)—节点k上光伏的最大容量;
tan ϕ—光伏逆变器的功率因数;
tan ϕmin—光伏逆变器的最小功率因数。
1.2.9 ES运行约束
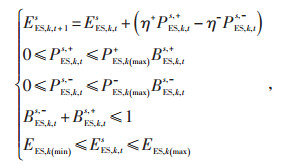
|
(35) |
式中:PES, k, ts, +—t时刻节点k上s相ES的充电功率;
PES, k, ts, -—t时刻节点k上s相ES的放电功率;
BES, k, ts, +—t时刻节点k上s相充电功率的0~1变量;
BES, k, ts, -—t时刻节点k上s相放电功率的0~1变量;
EES, k, ts—t时刻节点k上s相ES的电量;
η+—充电效率;
η-—放电效率;
EES, k(min)—ES电量上限;
EES, k(max)—ES电量下限;
PES, k(max)+—节点k的ES充电功率上限;
PES, k(max)-—节点k的ES放电功率上限。
1.2.10 SVG运行约束
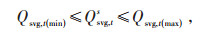
|
(36) |
式中:Qsvg, t(min)—SVG补偿无功的上限;
Qsvg, t(max)—SVG补偿无功的下限。
2 模型处理与求解根据优化模型,式(30)、(31)、(33)、(34)都为混合整数非线性问题,尽管现有的求解器能对其求解,但难以保证其全局最优性。本文将上述非线性约束线性化处理,从而将模型转化成线性问题,以便快速求解,并保证其最优性。
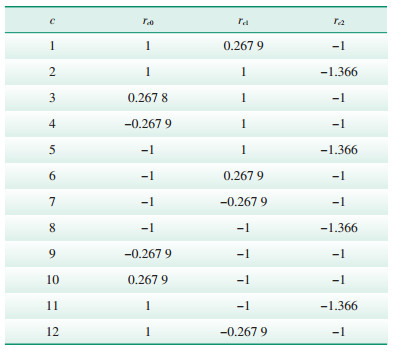
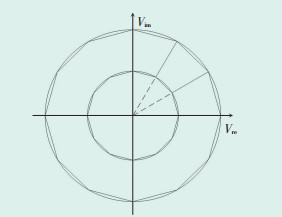
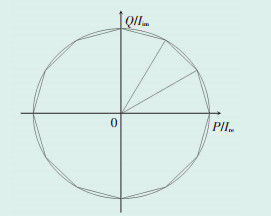
2.1 圆形约束线性化式(30)电压约束的可行域为小圆之外、大圆之内,见图 1;式(31)和(33)电流和功率约束的可行域为圆的内部,见图 2,可采用多边形内近似法对圆形约束进行线性化[21]。为了考虑转化后的精度,采用圆内接正12边形来近似表示上述圆形约束,多边形内近似法系数见表 1。式(30)、(31)和(33)可以分别线性化表示为:
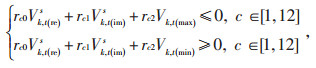
|
(37) |
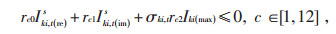
|
(38) |
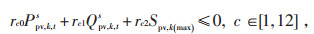
|
(39) |
|
| 图 1 电压约束的多边形内近似法示意图 Figure 1 Schematic diagram of the polygon inner approximation for voltage constraints 图中:Vim、Vre—电压的虚部和实部。 |
|
| 图 2 电流和功率约束的多边形内近似法示意图 Figure 2 Schematic diagram of the polygon inner approximation for current and power constraints 图中:Q—无功功率;P—有功功率;Iim、Ire—电流的虚部和实部。 |
| 表 1 多边形内近似法系数 Table 1 Coefficient of the polygon inner approximation method |
式中:rc0、rc1、rc2—线性化约束对应的系数;
c—多边形的边数,且c ∈ N。
2.2 功率因数线性化式(34)为功率因数取值范围约束,将功率因数的取值设置在滞后0.85与超前0.85之间,即tan ϕmin = 0.85。当功率因数为定值时,可使用不等式的变化方法,将式(35)转化为DG输出的无功功率约束。
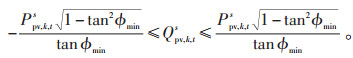
|
(40) |
采用改进IEEE 33节点配电测试系统验证方法的有效性,任何网络连接关系都可以用节点导纳矩阵表示。本算例使用Opendss软件建立改进IEEE 33导纳矩阵,使用基于python平台的pyomo建模语言建模,采用IPOPT求解器进行求解。计算机配置英特尔Core-i5-10600KF,主频4.10 GHz,内存16 GB。
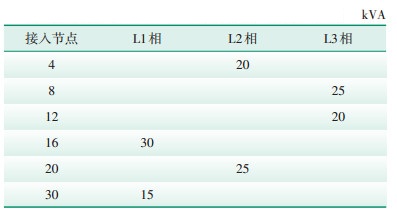
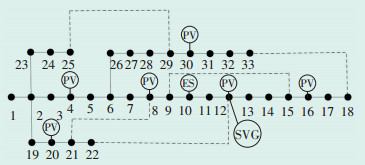
改进IEEE 33节点测试系统见图 3,选择容量为500 kVA的10 kV/400 V配电变压器,电压上下限为±5%,在节点8-21、9-15、12-22、18-33、25-29设置了联络开关,初始状态均为断开,并在节点4、8、12、16、20、30接入单相光伏,光伏的接入情况以及额定容量设置如表 2所示。节点10接入三相ES,三相容量均为30 kVA,最大充放电功率为15 kW,节点12接入单相SVG,补偿区间为0~25 kvar。
|
| 图 3 IEEE 33节点网络图 Figure 3 IEEE 33 node network diagram |
| 表 2 光伏接入节点额定容量 Table 2 Rated capacity of photovoltaic access |
单次潮流的优化只可以决定某一个时刻优化结果,为了直观地对同一时间不同条件下的算例进行分析评估,算例中以1天24 h为优化时长,步长为60 min,对配电网运行进行优化重构。本文采用文献[22]中提供的100个住宅的负荷使用情况,所提供的负荷数据以恒阻抗、恒电流、恒功率表示,即时变的ZIP负荷模型。为了充分体现网络的三相不平衡情况,在各节点各相中随机分配负荷。
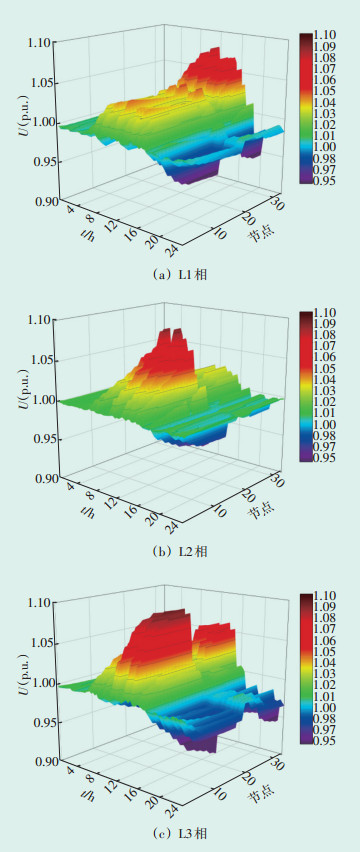
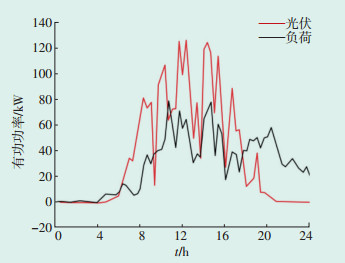
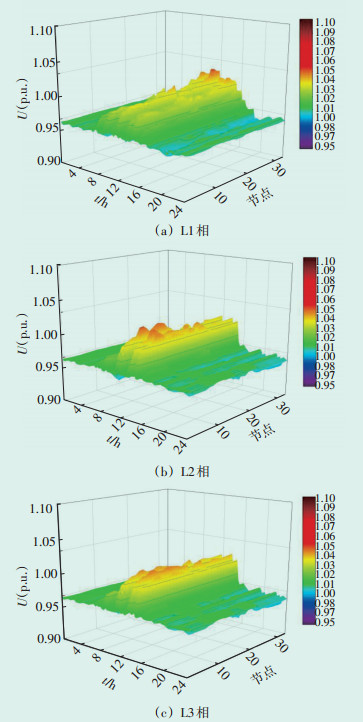
3.1 原始网络分析为了表现本文所提方案对配电网的积极影响,先对原始系统进行分析,原始系统1天24 h内三相电压变化以及光伏出力和负荷有功功率变化见图 4和图 5。通过图 4和图 5可以看出,00:00—06:00,光伏出力和负荷消耗功率基本保持一致,系统各相电压波动很小。在09:00—17:00时,光伏出力大于负荷功率需求,但由于光伏的容量以及并网位置不同,三相电压的波动情况也不同。线路L1相光伏并网位置靠近线路末端,因此L1相末端节点电压提升幅度较大;线路L2相光伏并网位置靠近线路前端,因此L2相前端节点电压提升幅度较大;线路L3相的光伏并网位置靠近线路中端,因此L3相前端和末端电压提升幅度都较大。19:00—24:00,三相负荷功率需求大于光伏出力,各相电压均下降。光伏并网位置不同以及其出力的波动性和负荷的时变性,导致各节点出现电压波动大、电能质量差等情况。
|
| 图 4 重构前三相电压变化 Figure 4 Change of three⁃phase voltage before reconstruction |
|
| 图 5 光伏和负荷有功功率曲线 Figure 5 PV output and load active power curve |
表 3为考虑ES和SVG配电网的33节点动态重构结果,图 6为重构后网络三相电压情况,与重构前的电压情况对比,电压质量得到明显改善,各相电压均衡,没有出现电压越限的情况。
| 表 3 33节点动态重构结果 Table 3 Dynamic reconstruction results of 33 nodes |
|
| 图 6 重构后三相电压变化 Figure 6 Change of three⁃phase voltage after reconstruction |
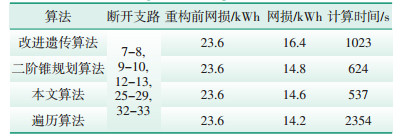
为了对比本文所提方法与其他算法结果的差异,选取了改进遗传算法[23]和二阶锥规划算法[24]与本文算法以及遍历算法结果对比,本文仅选取了波动较大的11:00—12:00进行对比,优化结果见表 4。
| 表 4 算法对比结果 Table 4 Algorithm comparison results |
根据对比结果可知,二阶锥规划算法和本文的算法可以获得正确的重构策略,即遍历算法得到的结果;而改进遗传算法虽然能够降低网络有功损耗,但是陷入了局部最优解。从计算的精度来看,改进遗传算法编码不能全面将优化问题的约束表示出来,因此需要考虑对不可行解采用阈值,进而增加了工作量和求解时间,而二阶锥规划算法属于二次规划范畴,求解效率还是低于本文模型。
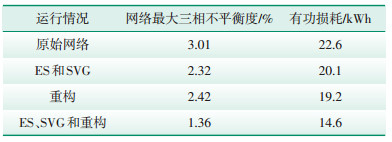
3.3 ES和SVG运行分析ES不平衡输入、输出和SVG的无功补偿可以控制三相网络某相的电压波动,从而有效提高网络三相平衡度。本文选取了11:00—12:00,此时网络不平衡度以及有功损耗对比情况见表 5。
| 表 5 不同方案结果对比 Table 5 Comparison of results of different schemes |
由表 5可以看出,ES和SVG对网络三相不平衡有一定的改善,同时也能够降低有功损耗,但由于ES和SVG的出力有限以及供电路径的限制,对网络的调节能力有限;重构可以改变网络供电路径,从而减小网络有功损耗。因有功损耗主要取决于线路两端的电压差,各节点电压越接近平衡节点电压(电压额定值),则有功损耗越小,所以网络三相不平衡度也会随之减小,但联络开关的开、断是针对三相线路,不能仅断开三相中某一相,对单相调节能力有限。在考虑ES和SVG的配电网重构中,在改变供电路径的同时能够根据实际情况合理分配单相资源,进一步改善三相不平衡情况和减小有功损耗。
4 结束语分布式电源灵活的接入特点以及出力的不确定性和负荷的时变性给配电网带来诸多挑战,同时在实际运行中,配电网多为三相不平衡状态,为了解决三相不平衡问题,本文提出以有功最小和三相不平衡度最小为目标函数的三相不平衡配电网重构模型。结果表明,三相电流注入法使用单相节点导纳矩阵描述三相网络,充分考虑了大量单相分布式电源的波动性和单相负荷的时变性对网络的影响,因此在计及三相不平衡的有源配电网重构模型中,本文算法的求解精度要高于其他算法。本文使用大M法对断开线路约束的松弛,避免了断开线路的约束对模型的影响,使用圆内接正12边形来近似表示上述圆形约束,将非线性约束线性化,提高了算法的求解效率;同时配电网动态重构缓解了配电网的三相不平衡情况,减少了配电网的有功损耗,并随着SVG和ES的并网,重构对配电网的优化效果将得到进一步提高。
| [1] |
于达, 张玮, 王辉. 布式电源并网控制研究综述[J].
齐鲁工业大学学报, 2022, 36(1): 59-65 YU Da, ZHANG Wei, WANG Hui. Survey on grid-connected control of distributed generation[J]. Journal of Shandong Institute of Light Industry, 2022, 36(1): 59-65 (  0) 0)
|
| [2] |
肖永江, 于永进, 张桂林. 基于改进乌燕鸥算法的分布式电源优化配置[J].
电力系统保护与控制, 2022, 50(3): 148-155 XIAO Yongjiang, YU Yongjin, ZHANG Guilin. Optimal configuration of distributed power generation based on an improved sooty tern optimization algorithm[J]. Power System Protection and Control, 2022, 50(3): 148-155 (  0) 0)
|
| [3] |
赵永生, 王吉文, 凌松, 等. 分布式电源接入对配电网供电可靠性影响分析[J].
电气自动化, 2020, 42(6)32-34, 111 ZHAO Yongsheng, WANG Jiwen, LING Song, et al. Analysis on the influence of distributed power supply accessupon power supply reliability of distribution networks[J]. Electrical Automation, 2020, 42(6)32-34, 111 DOI:10.3969/j.issn.1000-3886.2020.06.011 (  0) 0)
|
| [4] |
吴斌, 单来支, 王庆, 等. 基于三相不平衡的分布式光伏接入配电网的优化配置研究[J].
电力系统保护与控制, 2019, 47(24): 108-114 WU Bin, SHAN Laizhi, WANG Qing, et al. Research on optimal configuration of distributed photovoltaic access distribution network based on three - phase unbalance[J]. Power System Protection and Control, 2019, 47(24): 108-114 (  0) 0)
|
| [5] |
冯亚明. 低压配电网三相不平衡问题及处理对策探究[J].
科技创新与应用, 2021, 11(25): 116-118 (  0) 0)
|
| [6] |
高永键. 低压配电网三相不平衡问题及对策[J].
通信电源技术, 2018, 35(10): 251-252 GAO Yongjian. Analysis of Three-phase Unbalance of Low-voltage Distribution Network and Countermeasures[J]. Telecom Power Technologies, 2018, 35(10): 251-252 (  0) 0)
|
| [7] |
杨超. 三相不平衡对低压配电网的安全经济性评估[D]. 济南: 济南大学, 2019.
(  0) 0)
|
| [8] |
张铧文, 马莹. 低压配电网三相负荷不平衡优化问题分析[J].
现代工业经济和信息化, 2020, 10(9): 22-23 ZHANG Huawen, MA Ying. Analysis of Three - phase Load Imbalance Optimization in Low-voltage Distribution Network[J]. Modern Industrial Economy and Informationization, 2020, 10(9): 22-23 (  0) 0)
|
| [9] |
秦昕, 李修华, 要航, 等. 含有分布式电源配电网重构的研究现状及发展趋势[J].
电气开关, 2015, 53(4): 74-78 QIN Xin, LI Xiuhua, YAO Hang, et al. The Status Quo of the Current Research on Distribution Network Reconstruction of Distributed Power Supply and Its Tendency of Future Development[J]. Electric Switcher, 2015, 53(4): 74-78 (  0) 0)
|
| [10] |
邓桂秀, 江修波, 蔡金锭. 浅析配电网网络重构研究现状和发展[J].
机电技术, 2013, 36(4): 84-87 (  0) 0)
|
| [11] |
刘路宁, 彭春华, 温泽之, 等. 基于配电网动态重构的分布式光伏消纳策略[J].
电力自动化设备, 2019, 39(12): 56-62 LIU Luning, PENG Chunhua, WEN Zezhi, et al. Distributed photovoltaic consumption strategy based on dynamic reconfiguration of distribution network[J]. Electric Power Automation Equipment, 2019, 39(12): 56-62 (  0) 0)
|
| [12] |
林清源, 薛毓强, 曾乙宸. 配电网重构研究综述[J].
电气开关, 2021, 59(1): 3-8 LIN Qingyuan, XUE Yuqiang, ZENG Yichen. Overview of Research on Distribution Network Reconfiguration[J]. Electric Switcher, 2021, 59(1): 3-8 (  0) 0)
|
| [13] |
李红伟, 潘力, 韩璐, 等. 基于电压幅值对数变换的配电网三相不平衡线性潮流计算[J].
中国电力, 2022, 55(5): 143-148 LI Hongwei, PAN Li, HAN Lu, et al. Three-Phase Unbalanced Linear Power Flow Calculation Based on Voltage Magnitude Logarithmic Transformation[J]. Electric Power, 2022, 55(5): 143-148 (  0) 0)
|
| [14] |
吴在军, 成晟, 朱承治, 等. 三相不平衡有源配电网鲁棒动态重构[J].
电力系统自动化, 2019, 43(5): 66-74 WU Zaijun, CHENG Sheng, ZHU Chengzhi, et al. Robust Dynamic Reconfiguration of Three - phase Unbalanced Active Distribution Network[J]. Automation of Electric Power Systems, 2019, 43(5): 66-74 (  0) 0)
|
| [15] |
陈萍, 毛弋, 童伟, 等. 基于多目标粒子群算法的配电网多目标优化重构[J].
电力系统及其自动化学报, 2016, 28(7): 68-72 CHEN Ping, MAO Yi, TONG Wei, et al. Multi - objective Distribution Network Reconfiguration Based on Multi-objective Particle Swarm Optimization[J]. Proceedings of the CSU-EPSA, 2016, 28(7): 68-72 (  0) 0)
|
| [16] |
潘本仁, 王和春, 张妍, 等. 含分布式电源的主动配电网重构策略研究[J].
电力系统保护与控制, 2020, 48(15): 102-107 PAN Benren, WANG Hechun, ZHANG Yan, et al. Study on an active distribution network reconstruction strategy with distributed power supply[J]. Power System Protection and Control, 2020, 48(15): 102-107 (  0) 0)
|
| [17] |
姚艳, 许家玉, 崔勤越. 基于DistFlow的含分布式电源配电网优化重构模型[J].
能源工程, 2020(1): 12-16 YAO Yan, XU Jiayu, CUI Qinyue. Study on optimization reconfiguration modelling for distribution networkwith distributed generators based on DistFlow equations[J]. Energy Engineering, 2020(1): 12-16 (  0) 0)
|
| [18] |
Garcia P A N, Pereira J L R, Carneiro S, et al. Three-phase power flow calculations using the current injection method[J].
IEEE Trans. Power Syst, 2000, 15(2): 508-514 (  0) 0)
|
| [19] |
陈家超, 李钦豪, 唐渊, 等. 考虑光伏选相投切的低压配电网三相平衡优化[J].
电力自动化设备, 2022, 42(4): 71-78 CHEN Jiachao, LI Qinhao, TANG Yuan, et al. Three-phase balance optimization of low-voltage distribution network considering photovoltaic phase selection and switching[J]. Electric Power Automation Equipment, 2022, 42(4): 71-78 (  0) 0)
|
| [20] |
何月军, 郝思鹏, 刘思亦, 等. 基于序分量和量测值的三相不平衡度量研究[J].
电力系统保护与控制, 2020, 48(24): 44-51 HE Yuejun, HAO Sipeng, LIU Siyi, et al. Research on three phase unbalanced ratio measurement based on sequence components and measured values[J]. Power System Protection and Control, 2020, 48(24): 44-51 (  0) 0)
|
| [21] |
WANG Shouxiang, CHEN Sijia, GE Leijiao, et al. Distributed generation hosting capacity evaluation for distribution systems considering the robust optimal operation of OLTC and SVC[J].
IEEE Transactions on Sustainable Energy, 2016, 7(3): 1111-1123 (  0) 0)
|
| [22] |
Mckenna K, Keane A. Residential Load Modeling of Price-Based Demand Response for Network Impact Studies[J].
IEEE Transactions on Smart Grid, 2016, 7(5): 2285-2294 (  0) 0)
|
| [23] |
王联智, 冯建伟, 谢敏, 等. 基于遗传算法的低压配电网三相不平衡负载控制方法[J].
自动化技术与应用, 2022, 41(5)8-10, 22 WANG Lianzhi, FENG Jianwei, XIE Min, et al. Three-phase Unbalanced Load Control Method for Low-voltage Distribution Network Based on Genetic Algorithm[J]. Techniques of Automation and Applications, 2022, 41(5)8-10, 22 (  0) 0)
|
| [24] |
TIAN Zhuang, WU Wenchuan, ZHANG Boming, et al. Mixedinteger second - order cone programing model for VAR optimisation and network reconfiguration in active distribution networks[J].
IET Generation, Transmission & Distribution, 2016, 10(8): 1106-1115 (  0) 0)
|
 2023, Vol. 41
2023, Vol. 41