资源利用方式粗放、利用效率相对较低是中国工业经济发展中面临的一个突出问题,而这一问题在工业用地利用方面表现得尤为明显。相关研究表明,与发达工业化国家相比,中国城市工业用地在建设用地中所占比例明显偏高,而容积率、产出强度等指标则明显偏低[1-3]。在供给侧结构性改革的背景下,提升工业用地利用效率对于推动工业转型升级,促进工业经济由规模速度型向质量效益型转变具有重要意义。虽然厂商和企业是工业用地的使用主体,但其行为和决策时刻受到政府的市场规制、产业政策、财税金融政策等因素的影响,因而制度因素必然是工业用地利用行为和利用效率的重要影响因素。
政治集权下的经济分权是转型期中国的基本制度特征,而财政分权是经济分权的重要组成部分[4-5]。财政分权体制下,地方政府主要通过辖区内的经济扩张来增加财政收入[6],因而该体制强化了地方财政收入与本地经济发展的联系[4-6]。在经济发展初中级阶段,为实现经济增长和财政增收,地方政府往往采用压低工业用地价格的方式招商引资[7-9]。低廉的地价使得厂商和企业缺乏集约利用土地的激励,引发了工业用地低效利用现象的大量产生[10]。由于财政分权程度越高,地方政府发展本地经济的财政激励越强,地区间为争夺流动性税基而开展的“土地引资竞争”就越激烈,工业地价扭曲、工业用地利用效率损失也越严重,因而有学者认为财政分权会对工业用地利用效率产生负面影响[11]。上述分析虽然较好地把握了财政分权对工业用地利用效率影响的阶段性特征,但忽略了经济发展不同阶段地方政府行为逻辑的动态变化,以及制度环境变迁对地方政府行为的影响,因而充分理解财政分权对工业用地利用效率的影响机理尚待更加深入的考察。
已有大量研究致力于考察财政分权对经济活动的影响,具体涉及财政分权对经济增长[12]、地方公共物品供给[13]、地方政府规模[14]的影响等。近年来,学者们开始关注财政分权对技术效率和包括工业用地在内的要素利用效率的影响。陶然等[6]和张兰等[11]指出,在经济发展初中级阶段,财政分权可能导致地方政府间为争夺流动性税基而开展“竞次”式低水平竞争(如压低生产要素价格、降低环保管制要求等),进而阻碍技术进步、降低要素利用效率。赵文哲[15]则指出,提高财政分权程度有助于充分发挥地方政府在获取地方性信息方面的比较优势(相较于中央政府),确保其能因地制宜地制定和实施有利于促进本地技术进步和技术效率提高的财政政策,这种影响在技术进步成为经济增长主要动力的阶段表现得尤为明显。然而,系统分析不同经济发展阶段地方政府财政激励响应、行为逻辑变化的研究较少,也很少有学者针对不同发展阶段财政分权对工业用地利用效率影响的差异进行实证检验。有鉴于此,本文首先分析不同经济发展阶段地方政府的财政激励响应及其对工业用地利用效率的影响。继而利用2000—2015年间中国大陆的省级面板数据,通过构建和估计面板门槛模型分析检验财政分权对工业用地利用效率的影响是否存在非线性特征,以期为深化财税体制改革,促进工业用地利用效率的提升提供有益的启示。
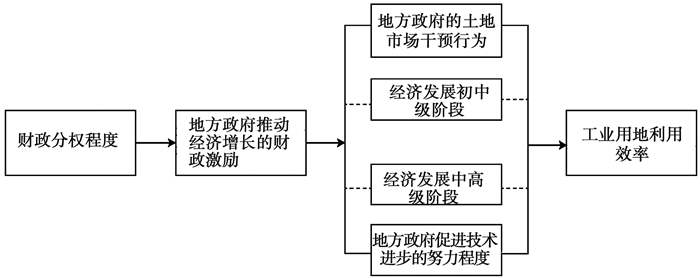
二、理论分析财政分权指中央政府向地方政府下放部分财政管理与决策权的财政制度,一定程度的财政分权则对应于某一级政府实际拥有的财政自主度[4-5]。财政分权体制下,地方政府主要通过推动本地经济发展来增加财政收入[6]。财政分权程度越高,地方政府支出对其自有收入的依赖度就越高,地方政府发展本地经济的财政激励也就越强,或者说,为实现财政增收而推动本地经济发展的努力程度也就越高[4]。财政分权程度的提高使得地方政府在支出方向上具有更大的自主性,从而更有可能按激励方向改变财政支出结构[15]。虽然财政分权程度越高,地方政府推动本地经济增长的财政激励就越强,但在不同发展阶段,地方政府推动经济增长的策略和手段有所不同,财政分权对工业用地利用效率的影响机制也因此有所差异(图 1)。在经济发展初中级阶段,要素积累是经济增长的主要源泉,地方政府主要通过压低生产要素(包括土地)价格来推动经济增长[6]。该阶段财政分权主要通过影响地方政府的土地市场干预行为而对工业用地利用效率产生影响。在经济发展中高级阶段,由于技术进步逐渐取代要素积累成为经济增长的主要源泉[16],要素市场体系不断发育完善,因而地方政府主要通过促进前沿技术进步和技术效率的提高来推动经济增长。该阶段财政分权主要通过影响地方政府促进技术进步的努力程度而对工业用地利用效率产生影响。
|
图 1 财政分权对工业用地利用效率的影响机制 |
在以要素驱动型为特征的初中级发展阶段,地方政府主要通过大规模提供廉价工业用地(以协议出让方式为主)的方式招商引资①,进而推动本地经济增长和财政增收。这种做法虽然使地方政府在短期内损失了一定的土地出让收入,但一旦制造业企业形成生产能力,就会带来一个相对稳定的、以增值税和企业所得税为主的持续收入流[6]。此外,制造业发展能够促进人口集聚,进而带动服务业部门营业税收入的增长,并推动商业用地和住宅用地需求及相关出让金收入的增长[7]。然而,从土地利用的角度看,由于低廉的地价不能充分反映工业用地资源的稀缺程度,企业倾向于使用相对廉价的土地替代其他生产要素,而缺乏集约利用土地的激励,从而造成工业用地利用效率的损失[8]。该阶段财政分权程度越高,地方政府为实现财政增收而开展的“土地引资竞争”越激烈,工业地价扭曲、工业用地利用效率损失也就越严重。因而可以预期在该阶段财政分权会对工业用地利用效率产生负向影响。
① 地方政府吸引投资的方式还包括提供补贴性配套基础设施,降低劳工、环保管制要求等。
随着经济发展方式由规模速度型向质量效益型转变,前沿技术进步和技术效率提高对经济增长的贡献作用日益凸显。地方政府通常通过直接或间接两种方式促进前沿技术进步和技术效率的提高。直接方式指地方政府增加用于基础研究、应用研究、技术研发、科技条件与服务、科技交流与合作等方面的公共支出,以及通过增加教育支出促进人力资本积累、为技术进步创造基础条件;间接方式指地方政府通过制定和实施各种财税激励政策促进企业开展研发活动和技术改造。地方政府的上述做法在提升企业技术水平的同时,无疑也会促进包括工业用地在内的各类生产要素利用效率的提高。在经济发展中高级阶段、经济增长动力转换的背景下,财政分权程度越高,地方政府为实现财政增收而促进前沿技术进步、技术效率提高的努力程度就越高,工业用地利用效率也会随之提高。由于在获取地方性信息方面具有比较优势,地方政府往往更能因地制宜地制定有利于本地发展的财政政策[13, 15],因而财政分权程度的提高也有利于提高政府的科技支出绩效。此外,随着经济发展水平的提高和土地市场体系的发育、完善,地方政府开展“土地引资竞争”所依赖的外部条件也在逐渐瓦解。2006年印发的《国务院关于加强土地调控有关问题的通知》明确要求“工业用地必须采用招标拍卖挂牌方式出让”。自该文件发布实施以来,工业用地出让市场的竞争性和透明度不断提高,划拨和协议出让主导工业用地资源配置的局面得到了扭转。赵爱栋等采用经出让方式加权修正的工业用地出让价格溢价率测度了工业用地市场化水平,发现2007—2013年间全国工业用地市场化水平呈逐年上升趋势,6年间提高了221.45%[8]。因而,由于中高级发展阶段经济增长动力和制度环境的变化,可以预期在该阶段财政分权会对工业用地利用效率产生正向影响。
综合上述分析,提出本文的研究假说:财政分权对工业用地利用效率的影响在不同经济发展阶段有所差异,存在非线性特征。在经济发展初中级阶段,财政分权对工业用地利用效率产生负向影响;在经济发展中高级阶段,财政分权则对工业用地利用效率产生正向影响。
三、研究方法与数据说明 (一) 研究方法1.财政分权程度的测度
既有研究主要采用“收入型指标”“支出型指标”和“财政自主度型指标”等3种方法衡量财政分权程度[4]。
陈硕和高琳分析了各类指标的适用性,指出“收入型指标”和“支出型指标”虽能反映出中央地方财政关系的跨时期变化,却不能很好地反映出这种关系的地区间差异[4]。具体来说,在利用收入型指标和支出型指标测算同一年份不同省份的财政分权程度时,由于所有省份均面临一个共同的中央政府,因而计算公式的分母没有任何差异。财政分权程度的截面差异将完全来自分子,即各省份财政收入(或支出)规模的相对大小。然而,地方政府的财政收入(或支出)规模与其所拥有的财政自主度显然是两个不同的概念。与“收入型指标”和“支出型指标”相比,“财政自主度型指标”公式的分子和分母均存在跨时期和跨地区变化,因而更适用于截面或面板数据,在近年来的实证研究中也得到了广泛应用。该指标的构建方法如下:

|
(1) |
该指标的数值越大,表示地方政府支出对其自有收入的依赖度越高,也即财政自主性越强。
2.工业用地利用效率的测度
既有研究主要采用2种方法测度工业用地利用效率:一是基于数据包络分析(Data Employment Analysis,DEA)的非参数方法;二是基于随机前沿分析(Stochastic Frontier Analysis, SFA)的参数方法。非参数方法的问题在于,许多研究只是在传统的全要素框架下加入了土地投入,而并未分解出土地投入在产出增长中的单独效率贡献[17-18]。因而测度出的效率值实质上是“考虑工业用地投入的工业生产效率”,而非真正意义上的工业用地利用效率。参数方法的优点在于,通过对随机前沿生产函数的推导和估计,便于度量具有明确经济含义的单要素利用效率。此外,随机前沿分析在构造生产前沿面时可以有效分离随机因素的影响,进而减少由测量误差及其他随机性误差造成的估计偏误[19]。
本研究借鉴Reinhard等提出的单要素利用效率定义及随机前沿分析框架下的测算方法[20],来界定工业用地利用效率的内涵并分析其测度方法。工业用地利用效率最高的生产者具有这样的特征,即在维持产出水平和其他要素投入量不变的情况下,工业用地投入量最小。因而,工业用地利用效率可以定义为,在给定的产出水平和其他要素投入水平下,生产单元可能达到的最小工业用地投入量(也称为目标工业用地投入量)与实际工业用地投入量的比值:
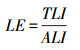
|
(2) |
式(2)中LE表示工业用地利用效率,TLI和ALI分别表示目标工业用地投入量和实际工业用地投入量。由于ALI总是大于或等于TLI,因而LE的取值在0~1之间。实际工业用地投入量与目标工业用地投入量越接近,工业用地利用效率越高。
在随机前沿分析框架下测度工业用地利用效率,首先需要确定随机前沿生产函数的函数形式。本研究采用超越对数生产函数,其原因主要包括两个方面:一方面,与Cobb-Douglas生产函数和常替代弹性(Constant Elasticity of Substitution, CES)生产函数相比,超越对数函数能够更好地反映投入要素之间、投入要素与技术进步之间的相互作用关系[21];另一方面,由于Cobb-Douglas生产函数所有投入要素的产出弹性都是不变的,因而测算出的工业用地利用效率排名将与工业生产效率排名完全一致,仍然无法将工业用地利用效率从全要素框架下分离出来。采用投入要素产出弹性可变的超越对数函数,则可克服这一缺陷。超越对数随机前沿生产函数的具体形式为:
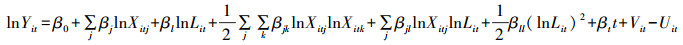
|
(3) |
式(3)中下标i和t分别表示省份和年份;Yit表示工业产出水平;X表示除土地外的其他要素投入量,下标j和k是要素标志(j=1, 2;k=1, 2;βjk=βkj),Xit1和Xit2分别代表劳动力投入和资本投入;Lit表示工业用地面积;t为时间趋势变量,反映技术变化的影响;Vit为随机误差项,表示生产中不可控因素(如突发事件、自然灾害等)和测量误差的影响,Vit服从N(0, σv2);Uit为非负随机变量,表示由技术非效率造成的实际生产点偏离生产前沿面的情况,Uit服从N+(μ, σμ2)。
保持式(3)中产出水平和其他要素的投入水平不变,当不存在技术非效率(Uit=0)时,工业用地投入量达到不存在冗余的最优水平:
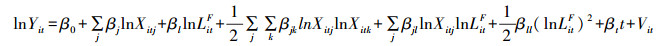
|
(4) |
式(4)中LitF即为在给定的产出水平和其他要素投入水平下,可能达到的最小工业用地投入量。通过将式(3)和式(4)联立,可以推导出工业用地利用效率的参数表达式:
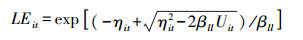
|
(5) |
其中: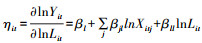
3.面板门槛模型的构建和估计
根据前文的分析,财政分权对工业用地利用效率的影响在经济发展的不同阶段有所不同,可以采用门槛模型检验二者之间的这种非线性关系。本文根据Hansen的方法构建如下面板门槛模型:
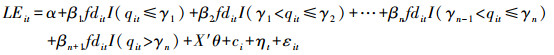
|
(6) |
式(6)中下标i和t分别表示省份和年份;LEit表示工业用地利用效率;fdit表示财政分权程度(受门槛变量影响的解释变量);qit为门槛变量,即用来划分样本的分组变量;γ为待估计的门槛值;I(·)为示性函数(括号内条件满足时取1,否则取0);β为不同区段解释变量fdit的影响系数;X表示一组影响工业用地利用效率的控制变量;ci和ηt分别表示不随时间变化的地区效应和不随地区变化的时间效应;εit表示误差项。为提高分析结果的稳健性,本文选取了2个划分不同经济发展阶段的门槛变量:一是人均地区生产总值(pcgdp);二是高技术产业占比(htratio)。值得注意的是,门槛变量也可以作为控制变量出现在模型中[22]。
根据Hansen提出的面板门槛模型估计方法,首先将任意qit作为初始值赋给γ,并对式(6)进行OLS估计,得到相应的残差平方和。然后根据残差平方和最小化原则确定最优的门槛值,进而得到各斜率系数的估计值[22]。除进行参数估计外,还需进行两方面的检验:一是门槛效应是否显著;二是所估计的门槛值是否等于其真实值,并构建门槛值γ的置信区间。实证分析中,若单门槛效应显著,应接着检验是否存在双门槛效应,以此类推,直至门槛效应不显著为止。
(二) 变量选择和数据来源1.工业投入产出指标选择和数据来源
本文以2000—2015年为研究期,以中国大陆除西藏外的30个省级行政区作为数据观测单元。采用工业总产值度量工业产出水平(indusgdp),分别利用工业行业城镇单位从业人员和工业用地面积衡量劳动力投入水平(labor)和土地投入水平(indusland)。参考张海洋[23]和姚志毅等[24]的方法,采用工业部门固定资产净值度量资本投入水平(即工业行业资本存量,capital)。分别采用分地区工业生产者出厂价格指数和固定资产投资价格指数将工业总产值和工业部门固定资产净值折算为2000年不变价。工业总产值、工业行业城镇单位从业人员和工业部门固定资产净值数据来源于历年的《中国城市统计年鉴》,工业用地面积数据来源于历年的《中国城市建设统计年鉴》,分地区工业生产者出厂价格指数和固定资产投资价格指数来源于历年的《中国统计年鉴》。
2.面板门槛模型的控制变量选择和数据来源
根据前文的分析,门槛变量也可以作为控制变量出现在模型中,因而,本文选取的影响工业用地利用效率的控制变量首先包括人均地区生产总值(pcgdp)和高技术产业占比(htratio)。以人均GDP表征的地区经济发展水平越高,各类生产要素的利用效率通常也越高。高技术企业具有产品附加值高、单位面积土地产出高的特征,因而高技术产业占比的提升有助于提高区域整体的工业用地利用效率。除此之外,参考既有研究[2, 8, 25],本文还选取了如下控制变量:(1)外资(含港澳台资)企业产值占比(fratio)。外资企业通常具有较高的技术和管理水平,其工业用地利用效率往往也较高。(2)土地市场规范程度(llegal)。土地市场规范程度越高,市场秩序越好,越有利于通过市场机制提高土地资源的配置和利用效率。(3)以人均耕地面积表征的土地资源禀赋(pccland)。土地资源禀赋条件越好,工业用地后备资源越充裕,工业用地集约利用的激励程度可能反而越低[8]。高技术产业占比用高技术产业主营业务收入占地区工业企业主营业务收入的比重来表示。外资企业产值占比用外资企业工业总产值占地区工业总产值的比重来表示。参考赵爱栋等的研究,采用土地违法案件涉及土地面积占行政辖区面积的比重来逆向反映土地市场规范程度[8]。该数值越小,表明目标地区土地违法现象越少,土地市场规范程度越高。相关数据来源于历年的《中国统计年鉴》《中国城市统计年鉴》《中国高技术产业统计年鉴》和《中国国土资源统计年鉴》。人均GDP为根据地区生产总值指数折算的2000年不变价。实证分析中对人均GDP和人均耕地面积进行了对数化处理,这样做既可以缓解异方差性和偏态性,也可以缩小变量的取值范围、减少极端观测值对估计结果的影响。各变量的定义和描述性统计参见表 1。
| 变量 | 定义 | 平均值 | 标准差 | 最小值 | 最大值 |
| indusgdp | 工业总产值/亿元 | 7819.763 | 10910.26 | 36.095 | 68909.27 |
| labor | 工业行业城镇单位从业人员数/万人 | 94.851 | 73.602 | 3.05 | 469.63 |
| capital | 工业部门固定资产净值/亿元 | 2446.847 | 2279.967 | 38.13 | 14176.42 |
| indusland | 工业用地面积/公里2 | 206.742 | 170.579 | 0.47 | 829.70 |
| pcgdp | 人均地区生产总值/(万元/人) | 1.977 | 1.417 | 0.148 | 0.951 |
| htratio | 高技术产业占比 | 0.086 | 0.077 | 0.002 | 0.407 |
| fratio | 外资(含港澳台资)企业产值占比 | 0.216 | 0.174 | 0.004 | 0.677 |
| llegal | 土地市场规范程度 | 0.0001355 | 0.0002367 | 0.000001 | 0.002029 |
| pccland | 人均耕地面积/(亩/人) | 1.644 | 1.183 | 0.116 | 6.239 |
本文采用Stata14.0软件估计随机前沿生产函数,估计结果如表 2所示。γ表示技术非效率的方差占总方差的比例(γ=σμ2/(σv2+σμ2)),其值为0.900,并且在1%的统计水平上显著,表明工业生产过程中存在着显著的效率损失,因而采用随机前沿模型是合适的。利用随机前沿生产函数参数估计结果和要素投入量的观测值,基于式(5)测算出各省级行政区各年份的工业用地利用效率,全国及各省级行政区的工业用地利用效率均值如表 3所示。从空间维度看,工业用地利用效率存在着显著的地区差异,东部省份的效率水平明显高于中西部省份。全国及各省级行政区的财政分权程度均值如表 4所示。从中可以看出,财政分权程度也存在着显著的地区差异。
| 待估参数 | 估计值 | 标准误 |
| β1 | 0.210 | 0.620 |
| β2 | 2.482*** | 0.681 |
| βl | -1.819*** | 0.646 |
| β11 | -0.055 | 0.086 |
| β22 | -0.160*** | 0.056 |
| γ | 0.900*** | 0.040 |
| βll | -0.021 | 0.043 |
| β12 | 0.028 | 0.099 |
| β1l | 0.031 | 0.064 |
| β2l | 0.119*** | 0.048 |
| σv2 | 0.021*** | 0.001 |
| σμ2 | 0.188** | 0.083 |
| 注:下标1、2、l分别对应于劳动力、资本和土地投入;***、**、*分别表示在1%、5%、10%的统计水平上显著。 | ||
| 省份 | 工业用地利用效率均值 | 省份 | 工业用地利用效率均值 | 省份 | 工业用地利用效率均值 | ||
| 北京 | 0.858 | 浙江 | 0.956 | 海南 | 0.655 | ||
| 天津 | 0.983 | 安徽 | 0.730 | 重庆 | 0.815 | ||
| 河北 | 0.723 | 福建 | 0.893 | 四川 | 0.786 | ||
| 山西 | 0.539 | 江西 | 0.707 | 贵州 | 0.585 | ||
| 内蒙古 | 0.687 | 山东 | 0.872 | 云南 | 0.770 | ||
| 辽宁 | 0.769 | 河南 | 0.682 | 陕西 | 0.665 | ||
| 吉林 | 0.803 | 湖北 | 0.741 | 甘肃 | 0.621 | ||
| 黑龙江 | 0.588 | 湖南 | 0.773 | 青海 | 0.444 | ||
| 上海 | 0.894 | 广东 | 0.971 | 宁夏 | 0.510 | ||
| 江苏 | 0.927 | 广西 | 0.729 | 新疆 | 0.606 | ||
| 全国 | 0.743 |
| 省份 | 财政分权程度均值 | 省份 | 财政分权程度均值 | 省份 | 财政分权程度均值 | ||
| 北京 | 0.863 | 浙江 | 0.815 | 海南 | 0.474 | ||
| 天津 | 0.755 | 安徽 | 0.458 | 重庆 | 0.526 | ||
| 河北 | 0.515 | 福建 | 0.699 | 四川 | 0.433 | ||
| 山西 | 0.525 | 江西 | 0.443 | 贵州 | 0.361 | ||
| 内蒙古 | 0.412 | 山东 | 0.708 | 云南 | 0.396 | ||
| 辽宁 | 0.598 | 河南 | 0.456 | 陕西 | 0.438 | ||
| 吉林 | 0.370 | 湖北 | 0.475 | 甘肃 | 0.272 | ||
| 黑龙江 | 0.389 | 湖南 | 0.441 | 青海 | 0.187 | ||
| 上海 | 0.870 | 广东 | 0.828 | 宁夏 | 0.303 | ||
| 江苏 | 0.809 | 广西 | 0.433 | 新疆 | 0.345 | ||
| 全国 | 0.520 |
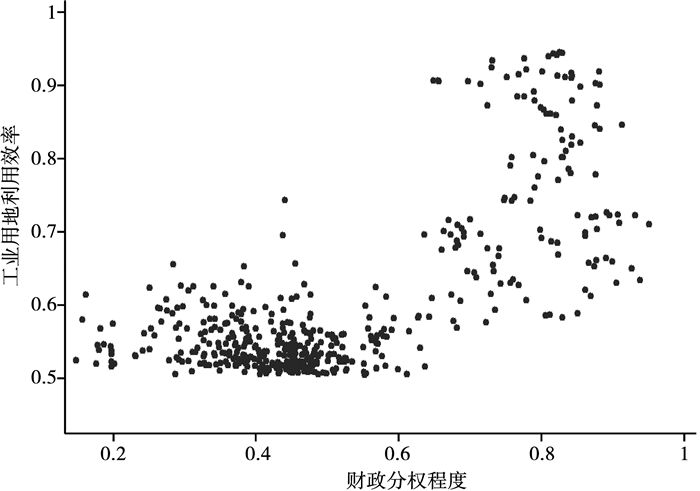
通过散点图(图 2)描述了财政分权程度与工业用地利用效率的相关关系。从图 2可以看出,二者之间存在非线性关系:当经济发展水平、财政分权程度较低时,财政分权程度与工业用地利用效率呈一定程度的负相关;而当经济发展水平、财政分权程度较高时,财政分权程度与工业用地利用效率则呈一定程度的正相关。值得注意的是,散点图分析忽略了工业用地利用效率的其他影响因素。为得出关于财政分权对工业用地利用效率影响的更为稳健的结论,需要进行进一步的计量分析。
|
图 2 财政分权与工业用地利用效率散点图 |
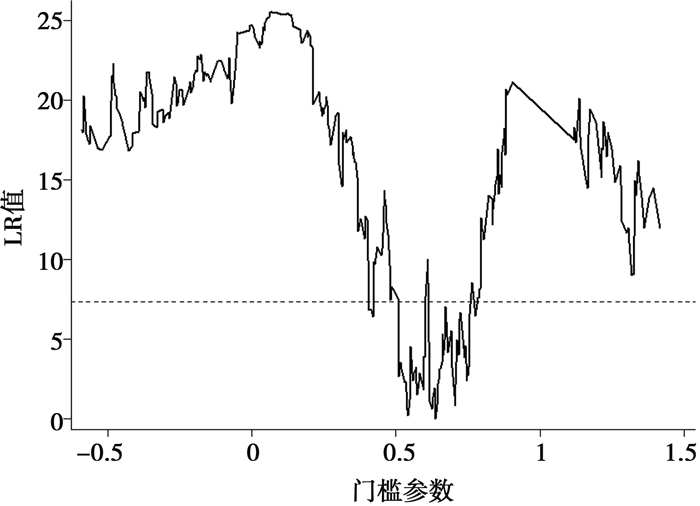
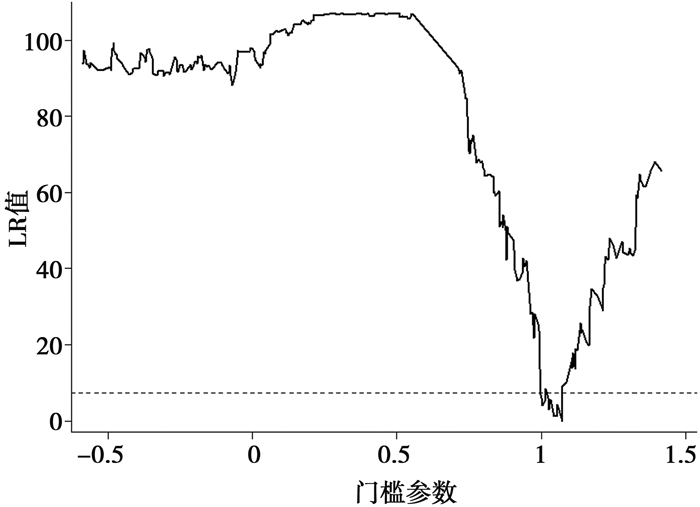
首先采用人均地区生产总值(对数形式,lnpcgdp)作为门槛变量。估计门槛模型的第一步是确定门槛的个数。依次在无门槛效应、单门槛效应、双重门槛效应和三重门槛效应的设定下对模型(6)进行估计,得到的F统计量和采用自抽样法(bootstrap tests)得出的P值如表 5所示。单门槛效应和双重门槛效应均非常显著,而三重门槛效应不显著,因此,应基于双重门槛模型进行分析。两个门槛的估计值及相应的95%置信区间如表 6所示,而借助于图 3和图 4的似然比(likelihood ratio)函数图,可以更为清晰地理解门槛值的估计和置信区间的构造。门槛估计值为似然比检验统计量LR等于0时所对应的γ值(图 3和图 4中分别为0.637和1.071),而各门槛估计值的95%置信区间是由LR值小于5%显著水平下临界值(图中虚线)时所对应γ值构成的区间。面板门槛模型的估计结果如表 7所示。注意到门槛变量为人均地区生产总值的对数,两个门槛值所对应的人均GDP分别为1.891万元和2.918万元(2000年不变价)①。财政分权对工业用地利用效率的影响在不同经济发展阶段有所差异,体现出显著的非线性特征。当人均GDP小于1.891万元和介于1.891万元与2.918万元之间时,财政分权对工业用地利用效率具有显著的负向影响(影响系数分别为-0.051和-0.012)。当人均GDP大于2.918万元时,财政分权的影响显著为正(影响系数为0.048),表明经济发展达到一定水平之后,地方政府财政自主度的增强有助于促进工业用地利用效率的提升。控制变量中,人均地区生产总值变量和高技术产业占比变量的系数均显著为正,表明经济发展水平的提高和产业结构升级均促进了工业用地利用效率的提升。与理论预期一致,以人均耕地面积表征的土地资源禀赋与工业用地利用效率显著负相关,表明土地资源禀赋状况越好,工业用地集约利用的激励程度反而越低。
| 门槛检验 | 临界值 | ||||
| F值 | P值 | 1% | 5% | 10% | |
| 单门槛检验 | 135.800*** | 0.000 | 31.025 | 36.900 | 51.110 |
| 双重门槛检验 | 31.230** | 0.017 | 20.044 | 23.828 | 36.585 |
| 三重门槛检验 | 21.260 | 0.530 | 47.801 | 62.022 | 80.458 |
| 注:P值和临界值均为采用自抽样法重复抽样300次得到的结果;***、**、*分别表示在1%、5%、10%的统计水平上显著。 | |||||
| 门槛值 | 估计值 | 95%置信区间 |
| 门槛值γ′1 | 0.637 | [0.624, 0.645] |
| 门槛值γ′2 | 1.071 | [1.036, 1.073] |
|
图 3 第一个门槛的估计值和置信区间(lnpcgdp为门槛变量) |
|
图 4 第二个门槛的估计值和置信区间(lnpcgdp为门槛变量) |
| 变量 | 系数估计值 | 标准误 | t值 | P值 |
| lnpcgdp | 0.035 | 0.003 | 11.060*** | 0.000 |
| htratio | 0.164 | 0.047 | 3.470*** | 0.001 |
| fratio | -0.012 | 0.028 | -0.430 | 0.668 |
| llegal | -1.913 | 6.082 | -0.310 | 0.753 |
| lnpccland | -0.052 | 0.011 | -4.530*** | 0.000 |
| fditI(lnpcgdpit≤0.637) | -0.051 | 0.027 | -1.840* | 0.067 |
| fditI(0.637<lnpcgdpit≤1.071) | -0.012 | 0.004 | -3.060*** | 0.002 |
| fditI(lnpcgdpit>1.071) | 0.048 | 0.027 | 1.780* | 0.076 |
| 观测数 | 480 | |||
| F统计量 | 128.240 | |||
| withinR2 | 0.714 | |||
| 注:***、**、*分别表示在1%、5%、10%的统计水平上显著。 | ||||
① 分别相当于2015年的2.681万元和4.138万元。根据世界银行2015年发布的世界各国经济发展水平分组标准,人均国民生产总值低于1045美元(约合6509元人民币)为低收入国家,介于1045美元和4125美元(约合25692元人民币)之间为中等偏下收入国家,介于4126美元和12735美元(79319元人民币)之间为中等偏上收入国家,高于12736美元为高收入国家。本文估计的第一门槛值与中等偏下收入国家和中等偏上收入国家的临界值基本吻合,第二门槛值则处于中等偏上收入国家的区间内。
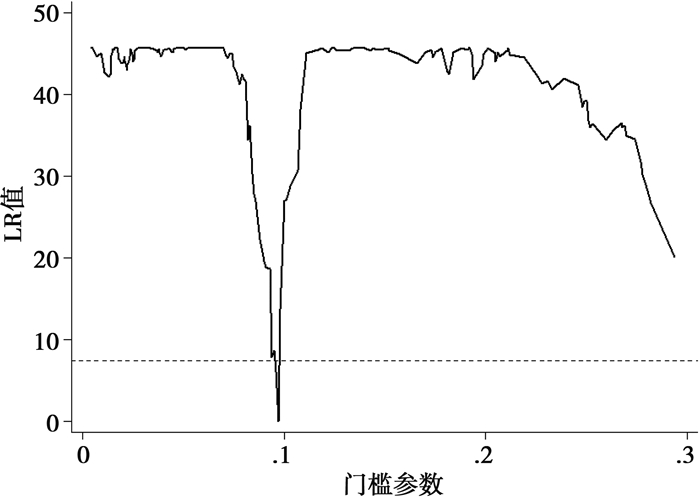
为提高分析结果的稳健性,继而采用高技术产业占比(htratio)作为门槛变量,依次在无门槛效应、单门槛效应、双重门槛效应和三重门槛效应的设定下重新对模型(6)进行估计,得到的F统计量和采用自抽样法(bootstrap tests)得出的P值如表 8所示。单门槛效应在统计上显著,而双重门槛效应和三重门槛效应均不显著。因而应基于单门槛模型进行分析。门槛估计值及相应的95%置信区间如表 9所示,似然比函数图如图 5所示。面板门槛模型的估计结果(表 10)依然表明,财政分权对工业用地利用效率的影响具有显著的非线性特征。当高技术产业占比小于0.097时,财政分权对工业用地利用效率具有显著的负向影响(影响系数为-0.064);而当高技术产业占比大于0.097时,财政分权的影响则由负转正(影响系数为0.030),表明随着产业结构趋于高级化,财政分权程度的提高能够促进工业用地利用效率的提升。
| 门槛检验 | 临界值 | ||||
| F值 | P值 | 1% | 5% | 10% | |
| 单门槛检验 | 48.600 | 0.023 | 33.782 | 39.552 | 59.348 |
| 双重门槛检验 | 31.650 | 0.120 | 32.823 | 37.445 | 47.010 |
| 三重门槛检验 | 18.960 | 0.380 | 34.836 | 53.105 | 73.243 |
| 注:P值和临界值均为采用自抽样法重复抽样300次得到的结果;***、**、*分别表示在1%、5%、10%的统计水平上显著。 | |||||
|
图 5 门槛的估计值和置信区间(htratio为门槛变量) |
| 变量 | 系数估计值 | 标准误 | t值 | P值 |
| lnpcgdp | 0.111 | 0.021 | 5.230 | 0.000*** |
| htratio | 0.123 | 0.061 | 2.040 | 0.042** |
| fratio | -0.023 | 0.034 | -0.670 | 0.502 |
| llegal | 2.112 | 7.143 | 0.300 | 0.768 |
| lnpccland | -0.102 | 0.019 | -5.450 | 0.000*** |
| fditI(lnpcgdpit≤0.097) | -0.064 | 0.038 | -1.680 | 0.094* |
| fditI(lnpcgdpit>0.097) | 0.030 | 0.013 | 2.230 | 0.026** |
| 观测数 | 480 | |||
| F统计量 | 37.190 | |||
| withinR2 | 0.662 | |||
| 注:***、**、*分别表示在1%、5%、10%的统计水平上显著。 | ||||
本文在分析不同经济发展阶段地方政府的财政激励响应及其对工业用地利用效率影响的基础上,利用2000—2015年间中国大陆的省级面板数据,通过构建和估计面板门槛模型分析检验了财政分权对工业用地利用效率影响的门槛效应。研究结果表明,财政分权对工业用地利用效率的影响在不同经济发展阶段有所差异,体现出显著的非线性特征。采用人均地区生产总值作为门槛变量的估计结果显示,当人均GDP小于1.718万元和介于1.718万元与2.713万元之间时,财政分权对工业用地利用效率具有显著的负向影响;当人均GDP大于2.713万元时,财政分权的影响显著为正。采用高技术产业占比作为门槛变量的估计结果显示,当高技术产业占比小于0.097时,财政分权对工业用地利用效率具有显著的负向影响;当高技术产业占比大于0.097时,财政分权的影响显著为正。总体来说,当经济发展达到一定水平之后,财政分权对工业用地利用效率的影响由负转正。
在经济发展的不同阶段,地方政府对财政激励的响应有所差异。应当充分关注不同阶段地方政府行为逻辑的变化,通过合理调整中央与地方财政关系引导地方政府行为,促进经济增长质量与效率的提高。考虑到中国幅员辽阔,同一时期内各地区可能处于不同的发展阶段,更应注重差异化的政策设计。在处于初中级发展阶段的地区,提高地方政府的财政自主度虽然可以调动其发展本地经济的积极性,但也可能导致地方政府在财政激励的作用下采用压低生产要素价格等不当手段推动经济增长,进而造成包括工业用地在内的要素利用效率的损失,降低了经济增长质量。因而,中央政府可以考虑加强对这些地区的转移支付力度,以减少因过度财政激励而产生的“竞次”式低水平竞争,同时应注重加强包括要素市场体系在内的市场规制建设。对于已处于中高级发展阶段的地区,由于经济增长动力已在发生转换、市场体系较为完善,可以考虑赋予地方政府更大的财政自主权,使其充分发挥在获取地方性信息方面的比较优势,因地制宜地制定和实施有利于本地发展的财政政策。此外,也应注重完善地方官员的政绩考核体制,改变过分强调经济增长速度的做法,引导地方政府更加注重经济增长的质量与效率。
| [1] | 唐健, 谭永忠, 徐小峰. 中国商住用地价格倒挂及其产生机理[J]. 中国土地科学, 2011(1): 22–29. |
| [2] | 陈伟, 彭建超, 吴群. 中国省域工业用地利用效率时空差异及影响因素研究[J]. 资源科学, 2014(10): 2046–2056. |
| [3] | 陈伟, 彭建超, 吴群. 城市工业用地利用损失与效率测度[J]. 中国人口·资源与环境, 2015(2): 15–22. DOI: 10.3969/j.issn.1002-2104.2015.02.003 |
| [4] | 陈硕, 高琳. 央地关系:财政分权度量及作用机制再评估[J]. 管理世界, 2012(6): 43–59. |
| [5] | 徐国祥, 龙硕, 李波. 中国财政分权度指数的编制及其与增长、均等的关系研究[J]. 统计研究, 2016, 33(9): 36–46. |
| [6] | 陶然, 陆曦, 苏福兵, 等. 地区竞争格局演变下的中国转轨:财政激励和发展模式反思[J]. 经济研究, 2009(7): 21–33. |
| [7] | Tao R, Su F, Liu M, et al. Land Leasing and Local Public Finance in China's Regional Development:Evidence from Prefecture-level Cities[J]. Urban Studies, 2010, 47(10): 2217–2236. DOI: 10.1177/0042098009357961 |
| [8] | 赵爱栋, 马贤磊, 曲福田. 市场化改革能提高中国工业用地利用效率吗[J]. 中国人口·资源与环境, 2016, 26(3): 118–126. DOI: 10.3969/j.issn.1002-2104.2016.03.015 |
| [9] | 黄金升, 陈利根, 张耀宇, 等. 产业结构差异下地方政府经济行为与工业地价研究[J]. 产业经济研究, 2017(3): 81–90. |
| [10] | 陶然, 袁飞, 曹广忠. 区域竞争、土地出让与地方财政效应:基于1999-2003年中国地级城市面板数据的分析[J]. 世界经济, 2007(10): 15–27. |
| [11] | 张兰, 汪应宏, 徐春鹏, 等. 财政分权、地方政府竞争与工业用地利用效率——基于广东省地级市层面的实证研究[J]. 现代城市研究, 2017(3): 103–111. DOI: 10.3969/j.issn.1009-6000.2017.03.016 |
| [12] | 谢贞发, 张玮. 中国财政分权与经济增长——一个荟萃回归分析[J]. 经济学(季刊), 2015(2): 435–452. |
| [13] | 傅勇. 财政分权、政府治理与非经济性公共物品供给[J]. 经济研究, 2010(8): 4–15. |
| [14] | 吴木銮, 林谧. 政府规模扩张:成因及启示[J]. 公共管理学报, 2010(4): 1–11. |
| [15] | 赵文哲. 财政分权与前沿技术进步、技术效率关系研究[J]. 管理世界, 2008(7): 34–44. |
| [16] | 姜海, 曲福田. 不同发展阶段建设用地扩张对经济增长的贡献与响应[J]. 中国人口·资源与环境, 2009(1): 70–75. DOI: 10.3969/j.issn.1002-2104.2009.01.013 |
| [17] | 周亚虹, 宗庆庆, 陈曦明. 财政分权体制下地市级政府教育支出的标尺竞争[J]. 经济研究, 2013(11): 127–139. |
| [18] | 张少华, 蒋伟杰. 基于ISP指数的中国能源生产率再测度与分解研究[J]. 数量经济技术经济研究, 2014(6): 55–73. |
| [19] | 张少华, 蒋伟杰. 能源效率测度方法:演变、争议与未来[J]. 数量经济技术经济研究, 2016(7): 3–24. |
| [20] | Reinhard S, Lovell C A K, Thijssen G. Econometric Estimation of Technical and Environmental Efficiency:an Application to Dutch Dairy Farms[J]. American Journal of Agricultural Economics, 1999, 81(1): 44–60. DOI: 10.2307/1244449 |
| [21] | 郑照宁, 刘德顺. 考虑资本-能源-劳动投入的中国超越对数生产函数[J]. 系统工程理论与实践, 2004(5): 51–54. DOI: 10.3321/j.issn:1000-6788.2004.05.008 |
| [22] | Hansen B E. Threshold Effects in Non-dynamic Panels:Estimation, Testing, and Inference[J]. Journal of Econometrics, 1999, 93(2): 345–368. DOI: 10.1016/S0304-4076(99)00025-1 |
| [23] | 张海洋. R&D两面性、外资活动与中国工业生产率增长[J]. 经济研究, 2005(5): 107–117. |
| [24] | 姚志毅, 张亚斌, 李德阳. 参与国际分工对中国技术进步和技术效率的长期均衡效应[J]. 数量经济技术经济研究, 2010(6): 72–83. |
| [25] | 郭贯成, 丁晨曦, 王雨蓉. 新型城镇化对工业用地利用效率的影响:理论框架与实证检验[J]. 中国土地科学, 2016(8): 81–89. |
 2019, Vol. 19
2019, Vol. 19

