文章信息
- 许秀川, 温涛, 张卫国.
- 耕地面积、劳动供给、工资水平与城镇化的非线性关系——一个理论模型及其门槛面板数据的实证
- 南京农业大学学报(社会科学版), 2016, 16(3): 101-110
-
文章历史
- 收稿日期: 2015-08-20
随着中国经济总量不断上升,基数越来越大,经济增长速率趋于下降。根据国家统计局最新数据,2014年中国GDP为636463亿元人民币,增长率7.4%,按汇率算已超过10万亿美元。国际货币基金组织对中国2015年经济增长率的预测为6.8%,略低于世界银行的7.2%。中国经济下行压力不断扩大,这一现象被学界和政府称为经济的“新常态”。有学者认为中国的城镇化和美国的高科技是21世纪全球经济增长的“两大引擎”,城镇化作为“促增长”和“调结构”的重要手段被寄予厚望。2014年3月国务院印发了《国家新型城镇化规划(2014—2020年)》,认为城镇化是现代化的必由之路,是破除城乡二元结构的重要依托,是解决农业农村农民问题的重要途径。陆铭等[1]认为劳动力由农村向城市转移是城镇化的唯一定义,陆铭等[2, 3]的研究均以非农就业的比重反映城镇化的水平,本文也沿用这一观点。虽然研究城镇化的文献已浩如烟海,但作者发现,在城乡一体化的框架下,以城乡经济均衡为基础,并体现中国小农经济与大量农民工外出就业等因素对城镇化影响的理论模型及相应的实证研究并不多见。本文试图从体现小农经济的城乡经济均衡入手,构建相应的城镇化理论模型,并对模型进行实证检验,以期获得新的结论及启示。
在已有的相关外文文献中,Yao[4]研究指出,农村劳动力就地转移主要受制于城镇部门提供工作机会能力,即主要受乡镇企业发展约束的影响。Wu和Yao[5]实证研究了中国农村劳动力流动的过程,认为城镇化过程基本符合农民收益最大化均衡的原则。Hertel et,al[6]分析了劳动力的流动性以及城乡资源的分布结构对城镇化与农民收入的影响。Chen et,al[7]认为中国农村劳动力转移将持续至2050年,城市化率达75%以后,农村耕地利用将保持稳定水平,农地利用模式将由现在的粗放耕作变为集约生产模式。Cervini-Plá、Ramos和Silva[8]研究发现,非工资性因素(主要包括解雇成本、工资税等)最终仍通过对工资的间接影响从而影响劳动的决策。Song、Thiss和Zhu [9]比较了农民的三种就业选择模式:在农业部门务农,在工业部门创业,转移到城市部门就业,其研究结果表明,无论哪种模式,劳动力从农村向城镇部门转移总能提高农民的福利水平。Brauw和Rozelle[10]发现中国农村劳动力转移后获得的收入主要被用于房屋和其他耐用消费品的消费,基本上不用于农业的生产性投资,因而对农业生产没有促进作用。
国内文献利用城乡二元结构模型对中国城镇化及相关影响因素已进行了丰富的理论与实证研究,如顾海英等[11],顾骅珊[12],陈宗胜、黎德福[13],郭涛、宋德勇[14]等。现有关于中国二元结构与城镇化的模型关注重点主要在城乡关系、城镇对农村剩余劳动力的吸收,而对农民的资源禀赋及其微观生产决策、城镇就业与工资水平的影响关注较少,城镇化模型的微观基础较弱。伍山林[15]认为,城乡关系满足刘易斯模型的基本假设是人多地少,人均耕地面积较小,剩余劳动力大量存在。但目前很少有学者直接研究人均耕地面积对城镇化的影响,大多数关于人均耕地面积的研究是其对农业生产的不利影响:包括阻碍了农业规模效益的提高[16];提高了机械物质费用,降低了劳动和土地生产率,给农业生产带来不便[17];提高了灌溉系统投资成本、土地产权的保护成本、农户信息成本等[18]。但也有研究发现了人均耕地面积较小的好处,例如促进了劳动力的充分利用,增加了农民种植的收入[19],有利于缩小农民收入的不平等[20]。吕晓等[21]认为目前关于人均耕地面积的研究主要集中在其成因及对农业生产的影响,而对城镇化直接影响的研究相对较少。
关于劳动力供给、城镇工资水平对农村劳动力转移与城镇化影响的研究,蔡昉[22]认为中国已经进入刘易斯第2转折点,劳动力已不再无限供给,沿海地区出现民工荒的现象体现了劳动力供给变化的影响。秦立建[23]认为劳动力非农转移使农户减少了农业生产投入工作量,减少了粮食产量。徐清[24]认为中国高收入城市的工资对农村劳动力转移的拉力已过了峰值呈递减的倒U形状态,而低收入的城市还处于递增阶段。
已有研究在农业生产要素的作用机理、劳动力流动的决策、工资水平的影响机制等方面为本文的研究奠定了理论与实证的基础,但存在以下方面的不足:(1)现有文献没有研究劳均耕地面积对城镇化的直接影响机制,这使得现有城镇化模型对小农经济这一微观基础研究不够深入。(2)没有考虑劳均耕地面积、城镇工资水平以及人口总量等关键变量的异质性对城镇化的影响,虽然徐清[24]的研究意识到了不同地区工资收入水平对劳动力转移的拉力存在不同阶段的特征,但作者囿于模型与方法的限制,没有对这种异质性本身进行理论与实证研究。本文试图从理论与实证上弥补已有研究的不足:首先,试图构建一个有微观基础的、体现中国小农经济特征的城镇化模型,在完全竞争与农民收益最大化的框架下,以农户微观决策为起点,推导农业与非农就业劳动力均衡的比例。其次,由于中国幅员辽阔,地区差异较大,劳均耕地面积、人口、城镇工资水平等存在较大的异质性,本文试图在农户微观决策模型中分析这种异质性的影响。最后,通过公开数据对理论模型进行实证研究。作者发现,近年来发展起来的“门槛效应”方法特别适合本文关于城镇化各因素异质性影响的研究。基于“体制转换”的门槛面板数据方法可以很好地考察模型中主要变量对城镇化可能存在的异质性影响及其非线性效应。本文结构安排为:第一部分为引言及文献综述,第二部分为劳动就业均衡比例决定的理论模理,第三部分为关于理论模型的门槛面板数据的实证,第四部分为结论与政策建议。
二、理论模型 (一)均衡条件下城乡就业的比例假设农村由近似同质的n个家庭组成,每个家庭i有li单位的劳动力,ki单位的土地,生产函数为科布—道格拉斯型,家庭的年务农增加值为yi,假设家庭生产满足Solow模型的基本条件,技术水平Ai保持不变,生产函数规模报酬不变,则有①:
①由于家庭联产承包制,以农户为生产单位的主体很少拥有大量机械或其他的资本投入,农户的非农所得也基本上不增加农业的生产性投资[10],本文关于农户的生产函数只考虑土地和劳动力的投入,并未考虑资本的投入,这也是相关研究的普遍做法,例如陈宗胜、黎德福(2004)[13],郭涛、宋德勇(2006)[14]等均在农户生产函数中只考虑了劳动力和土地,未考虑资本。

由规模报酬不变性易得对所有c≥0:

假设每个农民家庭除了务农,还可以到城市打工,假设农民在城市打工的年工资收入为w,则农民面临的选择可表示为在打工和务农之间进行选择:
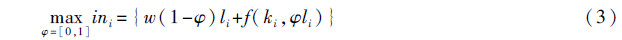
即农民家庭可以把li单位的劳动力的φ比例(对个体农户指务农劳动时间比例,对整体经济也代表务农劳动力在总劳动力中的比重)用于务农,1-φ比例用于进入城镇打工,获取收入ini。由生产函数规模报酬不变性质可知耕地和劳动是可分的,即把i=1,2,…n个家庭合并成一个家庭,生产要素按同比例增加,则:

因此,对全社会的农民家庭收入进行加总,则有:
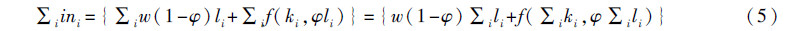
令全社会的总收入为IN=∑iini,总耕地数量为K=∑iki,总劳动力为L=∑ili,则社会收入最大化模型为:
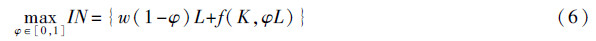
根据式(6)求最优的φ,一阶条件为əIN/əφ=0,由此可得-wL+AKa(1-α)φ-αL1-α=0,即wL=AKα(1-α)φ-αL1-α,等式的含义为农户在城镇部门务工的边际收入等于其在农村部门务农的边际收入,整理可得:

即务农的时间比例φ与务工工资(w)的α次方根成反比,与劳均耕地面积(K/L)成正比:φ∝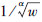 ,φ∝K/L。(7)式的推导条件过于苛刻,假设所有农户为相同的家庭,拥有相同的要素及要素比例。如果放宽这一假设,但仍保留技术不变及生产规模报酬不变。根据舒尔茨[25]的理论,与常识的直觉相反,传统农业国家的农民实质上已经非常充分地利用了已有的知识、经验及生产要素,在传统农业的技术水平上生产是十分有效率的,因此规模报酬不变的假设是相对合理的。由规模报酬不变性仍可得生产函数的可加性,但不必假设每个农户为同质。本文假设农户拥有的耕地面积(ki)及劳动力数量(li)服从正态分布:ki~N(k,σk),li~N(l,σl),K,l为农户平均耕地面积和劳动力数量,σK,σl分别为相应的标准差。由K=nk,L=nl,则生产函数的可加性及正态分布的可加性,可得解φ服从正态分布,其期望值为:
,φ∝K/L。(7)式的推导条件过于苛刻,假设所有农户为相同的家庭,拥有相同的要素及要素比例。如果放宽这一假设,但仍保留技术不变及生产规模报酬不变。根据舒尔茨[25]的理论,与常识的直觉相反,传统农业国家的农民实质上已经非常充分地利用了已有的知识、经验及生产要素,在传统农业的技术水平上生产是十分有效率的,因此规模报酬不变的假设是相对合理的。由规模报酬不变性仍可得生产函数的可加性,但不必假设每个农户为同质。本文假设农户拥有的耕地面积(ki)及劳动力数量(li)服从正态分布:ki~N(k,σk),li~N(l,σl),K,l为农户平均耕地面积和劳动力数量,σK,σl分别为相应的标准差。由K=nk,L=nl,则生产函数的可加性及正态分布的可加性,可得解φ服从正态分布,其期望值为:

(7)式和(8)式分别在确定和随机条件下得到的收入最大化时,社会劳动力在农村就业务农的比例为φ,在城镇就业务工的比例为1-φ,即城镇化率为1-φ。
(二)角点均衡与门槛效应前文分析假设均衡点发生在生产函数的光滑内点,但农业生产具有特殊性:生产分为农忙与农闲时期,在农忙时期农业生产的边际报酬是较高的,但到了农闲时期生产的边际报酬迅速下降,近似于零。对某个农户i,其最优化决策可用图 1表示:
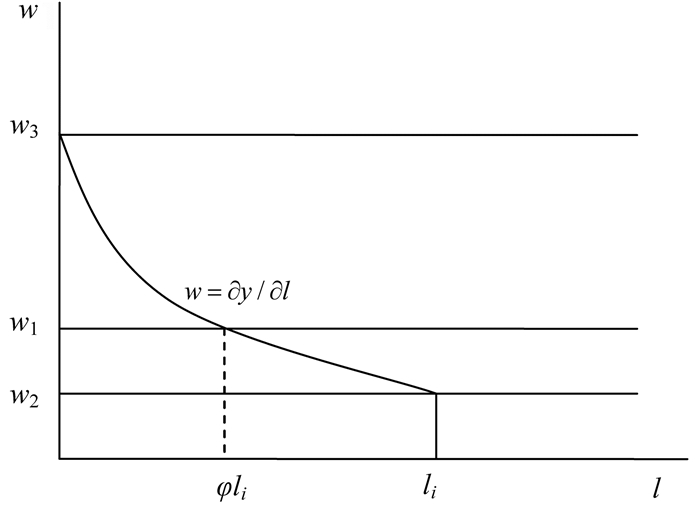 | 图 1 内点解与角点解 |
根据图 1,对农户i在其耕地面积确定的条件下,在农忙时,农业生产随着劳动投入的增加,务农收入服从边际报酬递减规律,但在农闲时,务农的边际收入迅速降为0。当工资为w1时,最优的务农比例如前所述为φ;当工资下降至w2的临界值时,农户将所有的劳动投入到农业生产中;当工资上升至w3的临界值时,农户将所有的劳动投入到城镇务工,不再务农。可见,只有当工资水平在区间[w2,w3]时,最优的务农比例才随着工资的变化而变化,超出这一区间,较高或较低的工资,务农或务工的劳动比例为0或1,不再随工资变化而变化。
由于角点解的存在,不同的农户拥有的耕地、劳动力的数量不同,不同地区的城镇工资水平也有所差异,这些因素共同作用都会影响均衡点的位置。对所有农户进行加总时,(7)式或(8)式不一定是光滑的函数,而是随着务农边际报酬曲线的不同,是分段光滑的。即随着耕地面积、劳动力数量、工资水平等因素的变化,这些因素对最优务农比例φ的影响也随之发生变化:可以设想根据图 1对农户i水平加总得到总期望边际报酬曲线,角点解的存在使加总曲线为分段光滑的,甚至存在跳跃间断点的可能。这种要素自身数量的变化导致其影响的结构性变化,称为内生的“体制转换”(Regime Switches),也即门槛效应,当要素数量跨过一些“门槛值”后,其影响会产生跳跃式的非线性效果。
三、门槛面板数据的实证分析 (一)计量模型设定由于理论模型的微观基础是农户的最优决策,而本文要考察的主要目标是耕作面积、工资水平及劳动力供给等因素对劳动力转移与城镇化等宏观现象的影响。因此,可利用微观加总法得到的宏观变量之间关系,推导出相关的计量模型,使用省际面板数据对模型进行实证研究。
结合式(7)和式(8)取对数变换,可得:
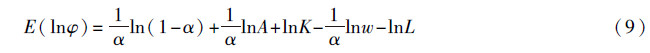
由图 1可知,φ的比例由水平的工资线和向下倾斜的农业边际报酬曲线相交决定。不同家庭面对的是同样的城镇工资水平,随着家庭耕地面积的不同,劳动投入的边际报酬下降的速度将不同,因此本文重点关注家庭拥有耕地面积对劳动力比例φ的影响。
将(9)式由总体期望模型转化为样本模型,由于农户家庭耕地面积的变化将影响务农的边际报酬,将K还原为nk,为考察社会劳动力供给对劳动力转移的影响,L不作还原,采用省际面板数据,可得实证模型为:
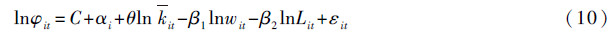
其中:i为省级行政单位,t为年份;φit为第一产业劳动力占三次产业劳动力总数的比重,wit为城镇工资水平,kit为劳均耕地面积①,Lit为三次产业劳动力总数;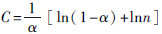 ,
,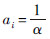 =lnAi,
=lnAi,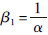 ,β2≈1,C为公共常数项,ai为固定效应。θ为重点关注的系数,即劳均耕地面积对劳动力比例φ的弹性。根据前文门槛效应的分析,假设其大小随劳均耕地面积(k)、城镇工资水平(w)和劳动总供给(L)的变化而可能存在体制转换效应。
,β2≈1,C为公共常数项,ai为固定效应。θ为重点关注的系数,即劳均耕地面积对劳动力比例φ的弹性。根据前文门槛效应的分析,假设其大小随劳均耕地面积(k)、城镇工资水平(w)和劳动总供给(L)的变化而可能存在体制转换效应。
①此处用“劳均耕地面积”替代理论模型中的“农户平均耕地面积”,“劳均耕地面积”由各省的总耕地面积除以相应的农业劳动力总量得到,而“农户平均耕地面积”理论上应该等于各省的总耕地面积除以相应的农户总户数,由数据的可得性,我们用“劳均耕地面积”作为“农户平均耕地面积”的代理变量,理论上二者应该是高度相关的,特别是在中国实行家庭联产承包制,大量青壮年农民工外出打工的条件下,“劳均耕地面积”可能是比“农户平均耕地面积”更能反映农业生产实际情况的变量,即使如此,由于耕地撂荒的存在,“劳均耕地面积”与“农民实际耕作的面积”仍然是有差异的,由于统计数据可能无法及时更新,本文无法获得准确的各省实质被耕作的耕地面积数据,这种差异只能归入计量模型的随机误差当中。
Hansen[26]的门槛回归模型的基本思想是以某个变量q为分组变量(即门槛变量),如果对分组变量的某临界值γ可以使分组子样本的残差平方和之和达到最小值,则该临界值称为门槛值。门槛值可能不止一个,在找到第1个门槛值后,可以在此基础上继续寻找第2个门槛值,直到检验不显著或样本数不允许为止。对式(10)含有1个和2个门槛值的门槛面板模型为:
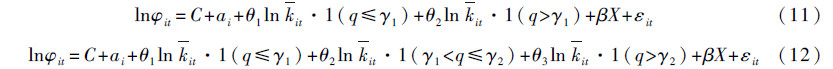
其中:q为门槛变量,γ1和γ2为第1个和第2个门槛值,1(·)为示性函数,括号内条件满足取值1,否则取0。对式(11),Gregorya和Hansen[27]提出门槛检验方法为:在无门槛效应假设θ1=θ2下,可构造LM统计量检验残差平方和与有门槛条件下的差异是否显著,进而决定是否拒绝原假设,由于F统计量并非标准分布,可采用自助法进行检验。对于门槛值的具体确定及其置信区间,Hansen[28]提出LR检验法,可根据LR趋势图来划分门槛区间。在找到第1个门槛的基础上,可增加门槛个数,继续检验式(12)。理论上只要检验的统计量显著,就可以继续增加门槛个数。但随着门槛数的增加,总样本被不断划分成更小的区间,剩余区间的样本数会不断减少,使得统计检验的功效(power)下降,因此,本文根据门槛临界值的统计检验显著性,同时结合门槛区间的样本数,以及不同门槛个数下解释变量估计系数大小及其显著性的变化,来确定最优的门槛个数,并对门槛估计的结果进行比较和解释。
(二)数据与实证结果由于2007、2011—2013年的《中国统计年鉴》均无全国各省按三次产业划分的劳动力数据,根据数据的可得性,采用1997—2010年全国31个省、直辖市和自治区的面板数据为分析区间,其中2006年各省的分产业劳动力数据为按线性插值法获得的估计值。原始数据及对数变换数据的描述性统计见表 1。
| 变量 | 单位 | 均值 | 中位数 | 标准差 | 最小值 | 最大值 | 样本数 |
| φ | - | 45.9% | 48.6% | 15.5% | 3.93% | 76.3% | 434 |
| k | 亩/人 | 2.27 | 1.49 | 2.13 | 0.27 | 11.73 | 434 |
| w | 元/年 | 17792.08 | 14434.4 | 11341.62 | 4742.95 | 71873.92 | 434 |
| L | 万人 | 2173.54 | 1883.8 | 1506.39 | 118.4 | 6041.56 | 434 |
| lnφ | - | 3.7268 | 3.8836 | 0.5319 | 1.3686 | 4.3347 | 434 |
| lnk | - | 0.5335 | 0.3988 | 0.7054 | -1.3093 | 2.4622 | 434 |
| lnw | - | 9.6004 | 9.5774 | 0.612 | 8.4644 | 11.1827 | 434 |
| lnL | - | 7.3494 | 7.5410 | 0.9377 | 4.7741 | 8.7064 | 434 |
表 1中φ为1997—2010年各省(下同)第一产业劳动力数量占三次产业劳动力总数的比重,k为劳均耕地面积拥有量,w为按可比价指数进行平减后城镇单位在岗职工年平均工资,L为第一、第二和第三产业劳动力人数总和。由表中数据可知,1997—2010年第一产业劳动力占总劳动力比重平均为45.9%,最小值为3.93%,最大值达76.3%,可见在实证时间区间内,不同省份务农劳动力比重差异较大。各省劳均耕地面积平均只有2.27亩,中位数为1.49亩,最小值只有0.27亩,最大值为11.73亩,省际农业生产要素差异较大,有利于门槛效应的估计。利用Hansen[26]的固定效应门槛面板数据模型,一方面以固定效应控制各省固有差异的影响,另一方面对估计系数的检验采用异方差稳健统计量作为检验标准,以消除异方差的影响。
首先,对无门槛面板数据模型进行固定效应与随机效应估计,Hausman检验统计量为274.12,在1%显著水平上拒绝了随机效应模型,表明固定效应模型适用。其次,对门槛面板模型进行LM检验和LR检验,结果见表 2和图 2-4。由表 2可知,以k和w为门槛变量时,LM检验均拒绝了无门槛模型及单门槛模型,但超过第2个门槛的样本数分别只有18个和23个,第三个结构区间内样本数较少。LR统计量的临界值为7.3523,图 2和图 3虚线为临界值线,LR趋势图越过临界值击破零点只有一次,故认为以k和w为门槛变量时只取单门槛估计结果较可靠。以L为门槛变量有3个门槛值显著,图 4印证了区间划分的合理性,但3门槛与2门槛估计系数变化不大,故本文只给出无门槛、单门槛及双门槛的估计结果,见表 3和表 4。当以k和w为门槛变量时,主要以单门槛结果为准,而以L为门槛变量时,主要以双门槛结果为准,最终以无门槛、单门槛及双门槛的结果比较进行稳健性检验。
| 门槛 变量 | 门槛数 | 门槛值 | LM检验 | 自举法 p值 | 区间样本数 | 样本合计 | ||||
| q≤γ1 | γ1<q≤γ2 | γ2<q≤γ3 | q>γ3 | |||||||
| k | 1 | 1.57 | 47.64 | 0.000 | 244 | 190 | 434 | |||
| 2 | 8.23 | 14.91 | 0.000 | 244 | 172 | 18 | 434 | |||
| w | 1 | 8825.49 | 48.30 | 0.000 | 104 | 330 | 434 | |||
| 2 | 36393.41 | 15.20 | 0.000 | 104 | 307 | 23 | 434 | |||
| L | 1 | 379.07 | 26.95 | 0.000 | 51 | 383 | 434 | |||
| 2 | 952.80 | 27.77 | 0.000 | 51 | 56 | 327 | 434 | |||
| 3 | 4012.90 | 22.155 | 0.000 | 51 | 56 | 272 | 55 | 434 | ||
| 变量 | 无门槛模型 | 门槛变量 | ||
| 固定效应 | k | w | L | |
| 门槛值(γ1) | - | 1.57 | 8825.49 | 379.07 |
| lnk | 0.2451*** (0.0279) | - | - | - |
| lnk(q<γ1) | - | 0.3430*** (0.0481) | 0.1575*** (0.0458) | -0.2641*** (0.0793) |
| lnk(q>γ1) | - | 0.1124*** (0.0342) | 0.2327*** (0.0451) | 0.2752*** (0.0459) |
| lnw | -0.0954*** (0.0096) | -0.0852*** (0.0100) | -0.1391*** (0.0120) | -0.0980*** (0.0111) |
| ln L | -0.9828*** (0.0606) | -0.9512*** (0.0693) | -0.8524*** (0.0705) | -0.9855** (0.0721) |
| 残差平方和 | 2.0604 | 1.8406 | 1.8379 | 1.9300 |
| 样本数 | 434 | 434 | 434 | 434 |
| 注:括号内为稳健标准差;**、***分别表示5%和1%显著,下同。 | ||||
| 变量 | 无门槛模型 | 门槛变量 | |||
| 固定效应 | k | w | L | ||
| 门槛值(γ1, γ2) | - | γ1=1.57 γ2=8.23 | γ1=8825.49 γ2=36391.41 | γ1=379.07 γ2=952.80 | |
| lnk | 0.2451*** (0.0279) | - | - | - | |
| lnk(q<γ1) | - | 0.3311*** (0.0490) | 0.0978** (0.0430) | -0.2701*** (0.0805) | |
| lnk(γ1<q<γ2) | - | 0.0897*** (0.0344) | 0.1748*** (0.0420) | 0.3668*** (0.0512) | |
| lnk(q>γ2) | - | 0.1436*** (0.0351) | 0.2667*** (0.0487) | 0.1101** (0.0482) | |
| lnw | -0.0954*** (0.0096) | -0.093*** (0.0100) | -0.1406*** (0.0117) | -0.0792*** (0.0111) | |
| lnL | -0.9828*** (0.0606) | -0.9255*** (0.0673) | -0.8442*** (0.0707) | -1.1084*** (0.0677) | |
| 残差平方和 | 2.0604 | 1.7741 | 1.7702 | 1.8041 | |
| 样本数 | 434 | 434 | 434 | 434 | |
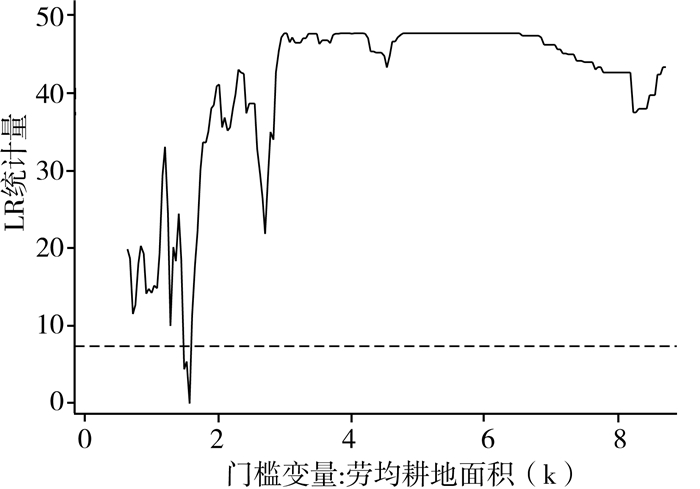 | 图 2 以劳均耕地面积为门槛变量的LR趋势图 |
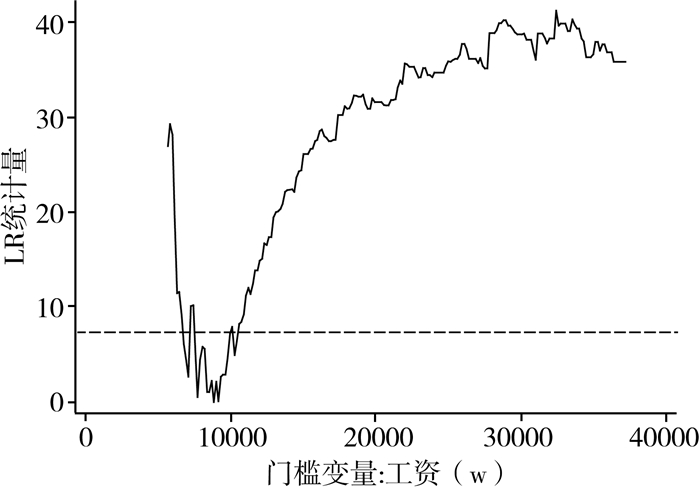 | 图 3 以工资为门槛变量的LR趋势图 |
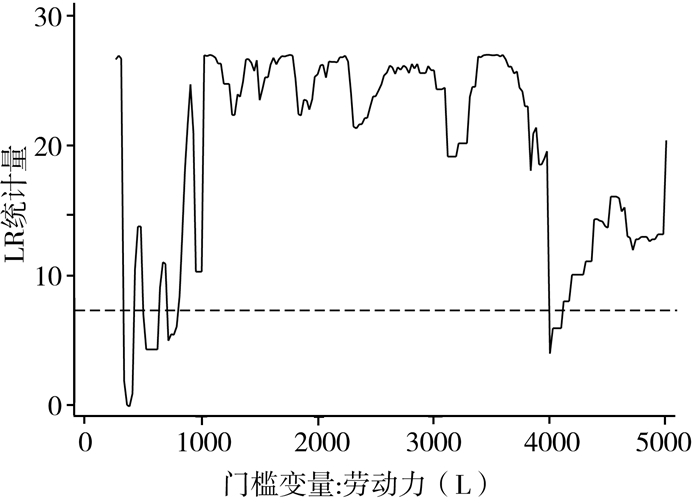 | 图 4 以劳动力总量为门槛变量的LR趋势图 |
对模型各种估计结果进行比较可知,系数估计的符号方向与大小基本与理论相符,不同估计方法得出的系数估计也具有稳定性,估计结果可信。综合分析各种结果,可得出以下结论:
第一,以劳均耕地面积为门槛变量,无门槛时劳均耕地面积对农业劳动力比重的弹性为0.2451,在第1个门槛值(劳均耕地1.57亩)以下,耕地面积对农业劳动力的弹性为0.3430,在第1个门槛值以上,弹性下降为0.1124,在第2个门槛值以上,弹性为0.1436。总之,虽然劳均耕地面积对务农人口比重均为正影响,即在劳动力数量一定的条件下,耕地总面积的增加会带来劳均耕地面积的增加,同时也会增加农业劳动力比重,这是符合经济学原理和直觉的。但劳均耕地面积对务农人口比重的弹性系数在第1个门槛值以下比在第1个门槛值以上大3倍多,比在第2个门槛值以上大2倍多,由表 1可知各省的劳均耕地面积为2.27亩,但中位数只有1.49亩,第1个门槛值(1.57亩)只比中位数略大,小于平均数,劳均耕地面积没跨过第1个门槛值的样本数为244个,占总样本数的56.22%。因此,由于人口增长、城镇化和工业用地需求的扩张,未来我国耕地面积总量上升的可能性不大,只有通过转移农村劳动力,增加农地要素集聚水平和劳均耕地面积水平,才能降低耕地对农业均衡就业比重的弹性系数,促进城镇化的推进。
第二,以工资为门槛变量,当工资水平未跨过8825.49元的门槛值时(占总样本数的23.96%),耕地面积对农业劳动力的弹性为0.1575,而当工资跨过门槛值后,弹性上升至0.2327。这似乎与传统的“推—拉”理论的直觉不符:工资较低时耕地吸收农业劳动力的弹性较小,工资较高反而耕地吸收农业劳动力弹性变大。“推—拉”理论假设全社会为单一的城乡二元结构经济,农村收入低的推力与城镇工资高的拉力使劳动力从农村流向城市。对于中国这样拥有31个省、直辖市、自治区的大国,每一个省内部都近似一个小的城乡二元结构经济体,同时农村劳动力可以跨省流动,因此,使用省际面板数据得出的实证结果可以得到很好的解释:工资高的地区经济较为发达,农业生产力也较高,同时政府对农业的财政支持及工业对农业的反哺能力也较强,因此农业就业比重较高,而在经济较落后的地区,工资较低,政府对农业的支持能力有限,工业对农业的反哺能力较弱,农业生产力较低,大量农业劳动力外流,因而耕地对农业劳动力的吸收能力较弱。
第三,以劳动力总供给量为门槛变量,当劳动力数量低于第1个门槛值(379.07万人)处于第1区间(占总样本数的11.75%)时,耕地吸纳农村劳动力的弹性为-0.2701;当劳动力数量跨过第1个门槛,并小于第2个门槛(952.80万人)处于第2区间(占总样本数的12.90%)时,耕地吸纳劳动力的弹性上升为0.3668;当劳动力数量再跨越过第2个门槛处于第3区间(占总样本数62.67)后,弹性为下降为0.1101,跨过第3个门槛(4012.90万人)进入第4区间(占样本数12.67%)后,耕地吸纳农业劳动力弹性将继续下降(为节省篇幅3门槛模型从略)。劳动力总供给的变化对耕地吸纳农业劳动力有明显的非线性特征:当总劳动力供给较少时,耕地对农村劳动力吸纳的弹性为负,随着劳动力供给增加,跨过门槛值后弹性变大,然后逐渐减小。
第四,工资水平对农村劳动力转移的弹性在各种估计结果中变化不大,约为-0.1,该弹性衡量了城镇工资水平上升对劳动力转移的拉力,即城镇工资上升1%,非农就业比重将上升0.1%;劳动力总供给水平对农业就业比重的弹性在各种估计结果中也较稳定,约为-1.0的单位弹性,即劳动力总量增长1%,城镇化率随之上升1%,可见,劳动力供给的增长有利于城镇化水平的提高,从而人口老龄化与劳动力供给的减少将不利于城镇化水平的上升。
四、结论与政策建议在以农民最大化务农与打工收益的微观机制下,本文推导了城乡均衡就业比重决定的模型,根据农户资源禀赋差异及农业生产的特殊性,论证了城乡就业均衡可能存在的门槛效应,结合门槛面板数据方法,利用省际面板数据对模型进行了实证检验,结果表明门槛效应的确存在,根据理论与实证结果,本文提出以下政策建议:(1)加快促进适度规模经营,提高农业生产要素的集聚水平,释放农业劳动力。对生产要素禀赋与经济发展水平不同的地区,可因地制宜,制定相应的政策措施,例如,在耕地资源匮乏的地区,主要采用财政支农、加大对农村劳动力转移的支持等扶持性政策;而对耕地资源较丰富的地区,可支持家庭农场及农业产业化经营,促进农地流转与集中,提高规模效率。在经济较发达的地区,加强工业对农业的反哺能力,提高对农业投资的补贴、贷款优惠等;在经济较落后的地区,加强农业劳动力转移后农村扶贫开发、耕地保护与退耕还林建设等。(2)应促进城乡居民收入稳步增长,及时制定与提升农民工最低工资标准,保持经济的长期增长,逐步实现低收入的省份向中等发达水平行列的迈进,从而提高工业反哺农业的能力。(3)促进东部成熟产业向中西部梯度转移,支持落后地区农村劳动力就近转移,逐步缩小各地区的工资差异水平,实现城镇化均衡发展,避免人口与劳动力向发达地区、发达城市过度集中。(4)由于人口老龄化加速和生育率下降,劳动力总供给趋于下降,不利于城镇化水平的提高,应加快生育政策的改革,维持劳动力供给的平稳,促进城镇化水平的稳步提升。
| [1] | 陆铭,蒋仕卿,陈钊,等.摆脱城市化的低水平均衡——制度推动、社会互动与劳动力流动[J].复旦学报:社会科学版,2013(3):48-64. |
| [2] | 陆铭,陈钊.城市化、城市倾向的经济政策与城乡收入差距[J].经济研究,2004(4):50-58. |
| [3] | 陆铭,向宽虎,陈钊.中国城市化和城市体系调整:基于文献的评论[J].世界经济,2011(6):3-25. |
| [4] | Yao S. Chinas Rural Economy in the First Decade of the 21st Century: Problems and Growth Constraints [J]. China Economic Review, 2002,13(12): 354-360. |
| [5] | Wu Z, Yao S. Intermigration and Intramigration in China:A Theoretical and Empirical Analysis[J]. China Economic Review,2003,14(8):371-385. |
| [6] | Hertel T, Zhan F, Wang Z. Implicationof WTO Accession for Poverty in China[C]// Bhattasali D, Li S,Martin W. China and the WTO: Accession, Policy Reform and Poverty Strategies. World Band and Oxford University, Washington D C,2004. |
| [7] | Chen R, Ye C, Cai Y, Xing X, Chen Q. The Impact of Rural Out-migration on Land Use Transition in China: Past, Present and Trend [J]. Land Use Policy,2014,40(9):101-110. |
| [8] | Cervini-Plá M, Ramos X, Silva J. Wage Effects of Non-wage Labor Costs[J].European Economic Review, 2014,72 (11):113-137. |
| [9] | Song H, Thisse J, Zhu X. Urbanization and/or Rural Industrialization in China[J]. Regional Science and Urban Economics,2012, 42(1):126-134. |
| [10] | Brauw A, Rozelle S. Migration and Household Investment in Rural China [J]. China Economic Review, 2008,19(1):320-335. |
| [11] | 顾海英,史清华,程英,等.现阶段"新二元结构"问题缓解的制度与政策——基于上海外来农民工的调研[J]. 管理世界,2011(11):55-65. |
| [12] | 顾骅珊.破解城乡"双二元结构":基于浙江嘉兴的经验研究[J].农业经济问题,2013(2):99-105. |
| [13] | 陈宗胜,黎德福.内生农业技术进步的二元经济增长模型——对"东亚奇迹"和中国经济的再解释[J]. 经济研究,2004(11):16-27. |
| [14] | 郭涛,宋德勇.农村劳动力转移的二元经济内生增长模型[J].南方经济,2006(8):77-84. |
| [15] | 伍山林.刘易斯模型适用性考察[J].财经研究,2008(8):4-16. |
| [16] | 叶春辉,许庆,徐志刚.农地细碎化的缘由与效应[J].农业经济问题,2008(9):9-15. |
| [17] | 王秀清,苏旭霞.农用地细碎化对农业生产的影响——以山东省莱西市为例[J].农业技术经济,2002(2):2-7. |
| [18] | 连雪君,毛雁冰.土地细碎化必然导致土地生产效率降低?——对土地细碎化与土地生产效率研究的批判性分析[J].华中农业大学学报:社会科学版,2013(6):109-115. |
| [19] | 李功奎,钟甫宁.农地细碎化、劳动力利用与农民收入——基于江苏省经济欠发达地区的实证研究[J].中国农村经济,2006(4):42-18. |
| [20] | 许庆,田士超,徐志刚,等.农地制度、土地细碎化与农民收入不平等[J].经济研究,2008(2):83-92. |
| [21] | 吕晓,黄贤金,钟太洋,等.中国农地细碎化问题研究进展[J].自然资源学报,2011(3):530-540. |
| [22] | 蔡昉.刘易斯转折点后的农业发展政策选择[J].中国农村经济,2008(8):4-15. |
| [23] | 秦立建,张妮妮,蒋中一.土地细碎化、劳动力转移与中国农户粮食生产——基于安徽省的调查[J]. 农业技术经济,2011(11):16-23. |
| [24] | 徐清.工资"拉力"与城市劳动力流入峰值——基于"推拉"理论的中国经济实证[J].财经科学,2012(10):37-45. |
| [25] | 西奥多 舒尔茨.改造传统农业[M].梁小民,译.北京:商务印书馆,1987:24-29. |
| [26] | Hansen B.Sample Splitting and Threshold Estimation[J]. Econometrica, 2000,68(3):575-603. |
| [27] | Gregorya A, Hansen B. Residual-based Tests for Cointegration in Models with Regime Shifts[J]. Journal of Econometrics, 1996,70(1):99-126. |
| [28] | Hansen B. Threshold Effects in Non-dynamic Panels: Estimation, Testing and Inference [J]. Journal of Econometrics, 1997,93(2):345-368. |
 2016, Vol. 16
2016, Vol. 16

