文章信息
- 马佳富, 张海军, 朱思洪, 贺亮, 袁加奇, 邓晓亭
- MA Jiafu, ZHANG Haijun, ZHU Sihong, HE Liang, YUAN Jiaqi, DENG Xiaoting
- 带附加气室空气弹簧等效刚度和等效阻尼高斯模型
- Gaussian model of the equivalent stiffness and damping for air spring with auxiliary chamber
- 南京农业大学学报, 2016, 39(5): 880-886
- Journal of Nanjing Agricultural University, 2016, 39(5): 880-886.
- http://dx.doi.org/10.7685/jnau.201511017
-
文章历史
- 收稿日期: 2015-11-06
带附加气室的空气弹簧具有刚度低、振动固有频率小等优点。车辆振动过程中, 在不需要外界输入能量的情况下, 可通过调节节流孔面积改变悬架的振动特性参数, 以达到减振目的[1]。带附加气室的空气弹簧因其刚度的非线性特性而广泛应用于车辆悬架及精密仪器隔振等领域[2-5]。
带附加气室空气弹簧振动特性参数与气室初始气压、节流孔面积、激振频率、振幅及附加气室容积等因素相关, 呈非线性关系, 是其设计及应用的重要性能参数[6-10]。目前, 主要通过理论分析和试验测定两种途径确定振动特性参数。Toyofuku等[11]将理论计算与试验研究相结合分析带附加气室空气弹簧连接管径、振动频率、振幅对空气弹簧刚度的影响; Liu等[12-13]通过理论分析建立带附加气室空气弹簧数学模型, 并通过试验得到带附加气室空气弹簧振动特性参数与孔口直径、激振频率及附加气室容积的关系, 验证数学模型的正确性。孙丽琴等[14-15]分析连接管路管径、管长、附加气室容积及初始气压对空气弹簧刚度随频率变化的影响规律。但到目前为止, 对建立的带附加气室空气弹簧理论模型的误差分析还尚未见有研究报道。
本文采用自由衰减法测试带附加气室空气弹簧振动特性参数, 研究初始气压及节流孔面积对振动特性参数的影响规律。通过试验结果修正和验证弹簧理论计算模型, 并对试验结果进行高斯拟合; 将试验数据分别和理论计算模型、高斯模型进行对比分析, 以期为实现弹簧出力连续精确可调及后续车辆空气悬架系统的主动控制提供理论依据。
1 振动特性参数测量试验与分析带附加气室空气弹簧自由衰减振动时, 其刚度随振幅及频率的减小略有变化[16], 为简化起见, 假设弹簧在振动过程中刚度不变, 研究弹簧气室初始压力和节流孔面积对其振动特性参数的影响规律。
1.1 试验系统的设计带附加气室空气弹簧振动特性参数采用自由衰减法测试, 示意图如图 1所示。试验台为自行研制的机械式振动试验台; 弹簧选择美国Firestone公司生产的1T15M-2型膜式空气弹簧; 附加气室是容积为22 L的刚性圆筒(约为空气弹簧主气室容积的2倍), 附加气室与主气室通过带有球阀的金属软管连接, 通过步进电机改变球阀阀芯的转动角度获得不同节流孔面积。根据弹簧刚度和阻尼随孔口直径变化的规律[17]及球阀节流孔面积和步进电机步进数的对应关系, 节流孔面积分别取0、11、21、34、45、57、67、78、89、112、187、263、336、415和491 mm2; 带附加气室空气弹簧上端的质量共计1 254 kg(某客车1/4车辆模型的簧载质量); 改变空气弹簧的初始气压(分别为0.225、0.250和0.275 MPa, 其中0.250 MPa为空气弹簧推荐的正常工作气压, 工作高度为240 mm); 试验过程中, 通过外力使质量块向下移动42 mm, 空气弹簧被压缩, 然后撤除外力, 使其在直线导轨的作用下, 做垂向自由衰减振动, 研究不同初始气压下节流孔面积对弹簧等效刚度、等效阻尼及阻尼比的影响规律。

|
图 1 自由衰减法系统测试示意图 Figure 1 System testing schematic of free attenuation |
图 2所示为3种初始气压下带附加气室空气弹簧等效刚度、等效阻尼及等效阻尼比随节流孔面积变化曲线。图 2-a表明:对应3种初始气压, 带附加气室空气弹簧垂向刚度随节流孔面积变化的规律基本一致, 面积越大, 弹簧刚度越小。当面积小于21 mm2或大于112 mm2时, 弹簧分别保持较大刚度或较小刚度基本不变, 而面积在21~112 mm2变化时对弹簧刚度的影响较为明显。以空气弹簧推荐的工作气压为例, 节流孔面积从21 mm2增大至112 mm2, 其刚度值从111 kN·m-1减小到67 kN·m-1, 刚度减小了约40%。对应相同节流孔面积, 随弹簧初始气压的增大, 弹簧刚度逐渐增加。

|
图 2 弹簧振动特性参数随节流孔面积变化的关系曲线 Figure 2 The curve of spring vibration parameters change with orifice area |
图 2-b表明:对应3种初始气体压力, 带附加气室空气弹簧等效阻尼随节流孔面积变化的规律基本一致, 弹簧阻尼随节流孔面积先增大后减小, 当面积在0~56 mm2时, 其阻尼随节流孔面积的增大而增大; 面积在57~187 mm2时, 阻尼随节流孔面积的增大而减小; 当面积大于187 mm2时, 主、附气室完全相通, 阻尼与节流孔面积无关; 当孔口关闭或者很大(节流孔面积大于187 mm2)时, 阻尼不为0, 证明空气弹簧自身存在阻尼。以空气弹簧推荐的工作气压为例, 节流孔面积从0增大至57 mm2, 其阻尼从1.3 kN·s·m-1增大至6.0 kN·s·m-1; 面积从57 mm2增大至187 mm2时, 阻尼从6.0 kN·s·m-1减小至1.6 kN·s·m-1; 节流孔大开, 阻尼为1.3 kN·s·m-1。对应相同节流孔面积, 弹簧初始压力越大阻尼越小。
图 2-c所示为带附加气室空气弹簧阻尼比随节流孔面积变化的试验曲线, 其变化趋势与阻尼随节流孔面积的变化趋势相同, 呈单峰形式; 节流孔面积在0~187 mm2时对系统阻尼比的影响较为明显。
2 理论模型的试验验证 2.1 理论模型由于带附加气室空气弹簧垂向动态特性具有明显的非线性, 故在一定精度范围内, 利用小偏差线性化方法对系统非线性模型进行线性化处理, 得到其等效物理模型如图 3所示。将此复杂系统等效为刚度、阻尼并联的振动系统, 建立系统等效刚度和等效阻尼的计算模型如式(1)与式(2)[18-20]。

|
图 3 带附加气室空气弹簧等效模型 Figure 3 The equivalent model of air spring with auxiliary chamber |

|
(1) |

|
(2) |
式中: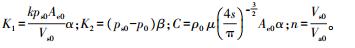
参照文献[18, 21], 试验构建带附加气室空气弹簧系统的工作参数如表 1所示。
| Vs0/m3 | Va0/m3 | Ae0/m2 | ρ0/(kg·m-3) | α | β | k | ω | μ |
| 0.010 6 | 0.022 0 | 0.048 5 | 4.66 | 0.05 | -0.01 | 1.4 | 9.71 | 0.4 |
理论模型计算结果与试验结果的比较如图 4、图 5所示。比较发现, 对应3种气压, 等效刚度与等效阻尼计算结果与试验结果较一致, 验证了模型的正确性。对比图中数据, 得到0.225、0.250和0.275 MPa 3种气压下等效刚度最大误差分别为15.43%、7.80%和13.53%, 等效阻尼最大误差分别为35.33%、65.40%和110.73%, 表明试验值与理论值存在一定误差。这是因为修正系数μ与节流孔的流通能力相关, 由流体力学理论可知, 在压力差下, 节流孔的流通能力影响因素较为复杂; 容积变化率α、面积变化率β与空气弹簧气囊材质和活塞形状等因素相关。针对本试验系统, 参照文献[22-23]中的研究方法改变参数, 将多次试验所得结果与计算结果进行比较来确定各值, 所以理论模型的确定是建立在试验基础之上。对空气悬架进行半主动控制时, 虽然理论模型能够描述带附加气室空气弹簧节流孔面积对振动特性参数的影响规律, 但用理论值代替实际值, 导致误差偏大, 不能实现对悬架振动特性参数的精确控制。

|
图 4 弹簧刚度的理论曲线与试验曲线 Figure 4 The theoretical and experimental curve of spring stiffness |

|
图 5 弹簧阻尼的理论曲线与试验曲线 Figure 5 The theoretical and experimental curve of spring damping |
对图 4、图 5的分析可知, 用理论模型计算带附加气室空气弹簧的垂向刚度、阻尼值与试验值误差较大; 式(1)和(2)表明, 理论模型是建立在试验的基础上, 且公式繁琐复杂。
图 2所示的试验曲线说明带附加气室空气弹簧等效刚度、等效阻尼与节流孔面积呈非线性关系, 且曲线表现出明显的突起和抬肩。由于高斯函数具有非线性特性, 且其参数具有明确的物理意义[24], 为推断弹簧在设计的工作载荷下, 不同初始气压P对弹簧的刚度—节流孔面积、阻尼—节流孔面积关系模型, 本文采用高斯拟合法对试验数据进行分析。高斯拟合使用式(3)的高斯函数对数据点集进行函数逼近的拟合方法, 为确保分析的准确性, 分别对试验数据进行二至五项高斯拟合, 并对拟合结果进行比较。

|
(3) |
式中:x为弹簧特性参数; s为节流孔面积; i为高斯函数最高项数; ai、bi、ci为实常数, 且ai > 0。
3.1 等效刚度高斯模型的建立图 6为初始气压分别为0.225、0.250和0.275 MPa时带附加气室空气弹簧等效刚度随节流孔面积变化的试验曲线和二项高斯拟合曲线, 图中等效刚度高斯模型曲线与试验曲线较一致。将其数据进行比较, 得到0.225、0.250和0.275 MPa对应的等效刚度最大误差分别为13.91%、4.15%和7.87%, 表明试验值与拟合值之间存在的误差较小, 且仅用二项高斯函数就能非常精确地拟合试验曲线。

|
图 6 弹簧刚度的试验曲线与二项高斯拟合曲线 Figure 6 The fitting and experimental curve of spring stiffness |
式(4)~(6)为0.225、0.250和0.275 MPa对应的带附加气室空气弹簧等效刚度的高斯模型。根据高斯函数的特性可知, 各气压下的节流孔面积s与第一项指数函数中b1相等时, 得到弹簧的最大刚度, 且刚度值为高斯模型中各项系数之和。表明高斯模型能够准确地预测节流孔面积与弹簧刚度的关系。

|
(4) |

|
(5) |

|
(6) |
图 7显示, 初始气压分别为0.225、0.250和0.275 MPa时带附加气室空气弹簧等效阻尼随节流孔面积变化的试验曲线和三项高斯拟合曲线。表明等效阻尼高斯模型曲线与试验曲线较一致, 将其数据进行比较, 得到对应3种气体压力, 等效阻尼最大误差分别为15.30%、11.50%和19.62%。由于选择二项高斯拟合相关度不够, 所以采用三项高斯拟合以达到所需的拟合精度。

|
图 7 弹簧阻尼的试验曲线与三项高斯拟合曲线 Figure 7 The fitting and experimental curve of spring damping |
式(7)~(9)为0.225、0.250和0.275 MPa对应的带附加气室空气弹簧等效阻尼的高斯模型。根据高斯函数的特性可知, 各气压下的节流孔面积s与第一项指数函数中b1相等时, 得到弹簧的最大阻尼, 且阻尼值为高斯模型中各项系数之和。表明高斯模型能够准确快速地预测节流孔面积与弹簧阻尼的关系。

|
(7) |

|
(8) |

|
(9) |
通过式(4)~(9)建立的3种气压下弹簧等效刚度、等效阻尼随节流孔面积变化的高斯模型, 根据式(10)求出对应的等效阻尼比。

|
(10) |
式中:m为簧载质量。
图 8所示为3种不同气压下弹簧阻尼比试验值与高斯模型计算出预测值的残差图, 图中残差点比较均匀地分布在水平带状区域中, 表明高斯模型假设满足试验结果。根据式(11)得出0.225、0.250和0.275 MPa 3种气压下阻尼比的确定系数R2分别为0.96、0.97、0.97, 进一步说明高斯函数的拟合效果较好。

|
图 8 试验值与预测值残差图 Figure 8 Experimental and predicted values of the residual plots |

|
(11) |
式中:Yi为拟合值; y为试验数据平均值; yi为试验值。
4 结论1)自由衰减法测试节流孔面积及初始气压对带附加气室空气弹簧垂向刚度、阻尼及阻尼比的影响规律。结果表明:节流孔开度的大小可以显著改变带附加气室空气弹簧的刚度和阻尼。当节流孔面积由21 mm2增至112 mm2时, 空气弹簧的刚度减小约40%;当节流孔面积由0 mm2增至187 mm2时, 空气弹簧的阻尼呈单峰式变化, 面积在57 mm2处阻尼达到最大值。综合节流孔面积对空气弹簧振动特性参数的影响规律, 节流孔面积的调节范围可取为21~112 mm2。带附加气室空气弹簧初始气压对其刚度和阻尼有较明显的影响, 初始气压越大, 空气弹簧的刚度越大, 阻尼越小。
2)根据试验结果及带附加气室空气弹簧理论计算模型, 确定其振动特性参数的理论曲线。将试验值与理论计算值进行比较, 得到等效刚度的最大误差分别为15.43%、7.80%和13.53%, 等效阻尼最大误差分别为35.33%、65.40%和110.73%(对应初始气压为0.225、0.250和0.275 MPa)。表明该模型能够描述带附加气室空气弹簧节流孔面积对振动特性参数的影响规律, 但在对空气悬架进行半主动控制时, 用理论值代替实际值误差较大, 不能实现对悬架振动特性参数的精确控制。
3)对试验测得刚度—节流孔面积数据点集进行二项高斯拟合, 得到拟合值与试验值的最大误差分别为13.91%、4.15%和7.87%;对测得阻尼—节流孔面积数据点集进行三项高斯拟合, 得到拟合值与试验值的最大误差分别为15.30%、11.50%和19.62%(对应初始气压为0.225、0.250和0.275 MPa)。对等效阻尼比计算精度的分析表明, 高斯模型假设满足试验结果, 且模型的计算精度高、结构简单, 为实现所设计的工况下带附加气室空气弹簧出力连续精确可调及后续车辆空气悬架的主动控制提供理论依据。
| [1] | 刘增华, 李芾, 傅茂海, 等. 半主动空气弹簧悬挂系统控制策略及仿真分析[J]. 系统仿真学报, 2007, 19(3): 3022–3025. Liu Z H, Li F, Fu M H, et al. Analysis of control tactics and simulation about semi-active air spring suspension system[J]. Journal of System Simulation, 2007,19(3): 3022–3025. (in Chinese) |
| [2] | 戚壮, 李芾, 黄运华, 等. 高速动车组空气弹簧垂向动态特性研究[J]. 机械工程学报, 2015, 51(10): 129–136. Qi Z, Li F, Huang Y H, et al. Study on the vertical dynamic characteristics of air spring used in high-speed EMU[J]. Journal of Mechanical Engineering, 2015,51(10): 129–136. DOI: 10.3901/JME.2015.10.129 (in Chinese) |
| [3] | 戚壮, 李芾, 孙树磊, 等. 动车组转向架空气弹簧支撑模式研究[J]. 机车电传动, 2013(5): 9–12. Qi Z, Li F, Sun S L, et al. A study on the air spring suspension morphologies of EMUs bogie[J]. Electric Drive for Locomotives, 2013(5): 9–12. (in Chinese) |
| [4] | 赵建文.空气弹簧在光学平台隔振系统中的应用研究[D].西安:西安电子科技大学, 2006. Zhao J W. Research on the application of air spring for the vibration isolation system of an optics platform[D]. Xi'an:Xi'an University of Electronic Science and Technology, 2006(in Chinese with English abstract). http://cdmd.cnki.com.cn/article/cdmd-10701-2006055558.htm |
| [5] | Kawashima K, Kato T, Sawamoto K, et al. Realization of virtual sub chamber on active controlled pneumatic isolation table with pressure differentiator[J]. Precision Engineering, 2007,31: 139–145. DOI: 10.1016/j.precisioneng.2006.05.002 |
| [6] | Zargar B, Fahim A, Jnifene A. Development, validation, and parameter sensitivity analyses of a nonlinear mathematical model of air springs[J]. Journal of Vibration and Control, 2012,18(12): 1777–1787. DOI: 10.1177/1077546311426250 |
| [7] | Lee S J. Development and analysis of an air spring model[J]. International Journal of Automotive Technology, 2010,11(4): 471–479. DOI: 10.1007/s12239-010-0058-5 |
| [8] | Facchinetti A, Mazzola L, Alfi S, et al. Mathmatical modelling of the secondary air spring suspension in railway vehicles and its effect on safety and ride comfort[J]. Vehicle System Dynamics, 2010,48(Supple): 429–449. |
| [9] | Sayyaadi H, Shokouhi N. Effects of air reservoir volume and connecting pipe's length and diameter on the air spring behavior in rail-vehicles[J]. Iranian Journal of Science and Technology, 2010,34(B5): 499–508. |
| [10] | Nieto A J, Morales A L, Gonzalez A, et al. An analytical model of pneumatic suspensions based on an experimental characterization[J]. Journal of Sound and Vibration, 2008,313: 290–307. DOI: 10.1016/j.jsv.2007.11.027 |
| [11] | Toyofuku K, Yamada C, Kagawa T, et al. Study on dynamic characteristic analysis of air spring with auxiliary chamber[J]. JSAE Review, 1999,20: 349–355. DOI: 10.1016/S0389-4304(99)00032-6 |
| [12] | Liu H, Lee J C. Model development and experimental research on an air spring with auxiliary reservoir[J]. International Journal of Automotive Technology, 2011,12(6): 839–847. DOI: 10.1007/s12239-011-0096-7 |
| [13] | Liu H, Lee J C. Model development of automotive air spring based on experimental research[C]//IEEE 3rd International Conference. Measuring Technology and Mechatronics Automation, 2011:585-590. http://dl.acm.org/citation.cfm?id=1954710 |
| [14] | 孙丽琴, 李仲兴, 沈旭峰. 带附加气室空气弹簧动态特性仿真与试验研究[J]. 机械设计与制造, 2013(9): 158–161. Sun L Q, Li Z X, Shen X F. Characteristics simulation and experimental research of air spring with auxiliary chamber[J]. Machinery Design and Manufacture, 2013(9): 158–161. (in Chinese) |
| [15] | 孙丽琴, 李仲兴, 郭继伟. 连接管路对附加气室空气弹簧刚度特性影响的试验研究[J]. 机械设计与制造, 2013(10): 51–57. Sun L Q, Li Z X, Guo J W. Test study of the effect of connecting pipe on dynamic characteristics of air spring with auxiliary chamber[J]. Machinery Design and Manufacture, 2013(10): 51–57. (in Chinese) |
| [16] | 王家胜, 朱思洪. 带附加气室空气弹簧动刚度影响因素试验研究[J]. 振动与冲击, 2010, 29(6): 1–3. Wang J S, Zhu S H. Experimental study on influential factors on dynamic stiffness of air spring with auxiliary chamber[J]. Journal of Vibration and Shock, 2010,29(6): 1–3. (in Chinese) |
| [17] | 贺亮, 朱思洪. 带附加空气室空气弹簧垂直刚度和阻尼实验研究[J]. 机械强度, 2006, 28(Supple): 33–36. He L, Zhu S H. Research on the vertical stiffness and damping of the air spring with auxiliary chamber by test[J]. Journal of Mechanical Strength, 2006,28(Supple): 33–36. (in Chinese) |
| [18] | 王家胜, 朱思洪, 贺亮. 基于复刚度带附加气室空气弹簧振动特性研究[J]. 中国机械工程, 2009, 20(12): 1418–1422. Wang J S, Zhu S H, He L. Research on vibration characteristics of air spring with auxiliary chamber based on complex stiffness[J]. Chinese Mechanical Engineering, 2009,20(12): 1418–1422. (in Chinese) |
| [19] | 王家胜.带附加气室空气弹簧动力学特性研究[D].南京:南京农业大学, 2009. Wang J S. Research on dynamic characteristics of air spring with auxiliary chamber[D]. Nanjing:Nanjing Agricultural University, 2009(in Chinese with English abstract). http://cdmd.cnki.com.cn/article/cdmd-10307-2010173951.htm |
| [20] | Zhu S H, Wang J S, Zhang Y. Research on theoretical calculation model for dynamic stiffness of air spring with auxiliary chamber[C]//IEEE Vehicle Power and Propulsion Conference(VPPC). Harbin, China, 2008. |
| [21] | 贺亮.带附加空气室空气弹簧垂向刚度及阻尼特性实验研究[D].南京:南京农业大学, 2006. He L. Research on the vertical stiffness and damping of the air spring with auxiliary chamber by test[D]. Nanjing:Nanjing Agricultural University, 2006(in Chinese with English abstract). http://cdmd.cnki.com.cn/article/cdmd-10307-2007010362.htm |
| [22] | 李滨, 陈无畏. 汽车膜式空气弹簧的分析与计算[J]. 合肥工业大学学报(自然科学版), 2004, 27(10): 1191–1195. Li B, Chen W W. Analysis and calculation of diaphragm air spring of an automobile[J]. Journal of Hefei University of Technology(Natural Science Edition), 2004,27(10): 1191–1195. (in Chinese) |
| [23] | 张俊玲, 王浩宇. 重型汽车用空气弹簧刚度特性及帘线参数的影响[J]. 长安大学学报(自然科学版), 2013, 33(6): 115–119. Zhang J L, Wang H Y. Influence of cord parameters on stiffness characteristics of air spring for heavy vehicles[J]. Journal of Chang'an University(Natural Science Edition), 2013,33(6): 115–119. (in Chinese) |
| [24] | 李睿, 金保昇, 仲兆平, 等. 高斯多峰拟合用于生物质热解三组分模型的研究[J]. 太阳能学报, 2010, 31(7): 806–810. Li R, Jin B S, Zhong Z P, et al. Research on biomass pyrolysis three-pseudocomponent model by Gaussian multi-peaks fitting[J]. Acta Energiae Solaris Sinica, 2010,31(7): 806–810. (in Chinese) |




