文章信息
- 吐尔逊·买买提, 丁为民, 谢建华
- Tursun MAMAT, DING Weimin, XIE Jianhua
- 时间序列组合预测模型研究:以农业机械总动力为例
- Research of combination prediction model for time series:a case study in total power of agricultural machinery
- 南京农业大学学报, 2016, 39(4): 688-695
- Journal of Nanjing Agricultural University, 2016, 39(4): 688-695.
- http://dx.doi.org/10.7685/jnau.201510042
-
文章历史
- 收稿日期:2015-10-27
2. 新疆农业大学机械交通学院, 新疆 乌鲁木齐 830052
2. School of Mechanical and Traffic Engineering, Xinjiang Agricultural University, Urumqi 830052, China
农业机械总动力是内含双向多重因果反馈关系,线性和非线性特征相互作用,以及存在众多不确定因素的复杂时间序列。该序列在其变化当中与农业机械化政策、社会经济环境、人民收入水平等因素之间存在离散的双向影响,其发展规律的复杂性超出了一般的非线性系统。此类非线性系统的一个显著特点是系统各部分之间的相互作用会产生出复杂的、难以预测的行为,包括平衡态的失稳和多平衡态、分岔突变以及混沌和湍流[1]。
应用数据挖掘技术对农业机械总动力等时间序列的发展趋势进行研究,挖掘其中隐含的知识并对其进行分析,在此基础上设计相应预测及决策服务模型,为促进农业机械化、提高生产效率、提高决策水平、健全调控和基层服务能力、促进农业机械化进入信息化领域的步伐有很大的推进作用。
目前,建立农业机械总动力或类似的时间序列预测模型常用的方法有两类,一类是单一预测模型,另一类是组合预测模型。单一预测模型有曲线回归分析法、自回归积分滑动平均模型(autoregressive integrated moving average model,ARIMA)、指数平滑法、灰色系统预测法、人工神经网络法、模糊分析法和时间序列法等。单一预测模型虽然具有构造和应用简单等特性,但其具有一定局限性。
曲线回归模型有线性、二次项、复合、增长、对数、立方、S、指数分布、逆、幂和Logistic等形式,此类方法适合于预测时间短、总体变化趋势比较平稳的序列,可以很好地反映事物的总体发展趋势,但对于逼近复杂的非线性函数其有误差波动大等缺点[2, 3]。ARIMA模型在预测相对非平稳序列时具有较大优势,模型被识别后就可以从时间序列的过去值及现在值来预测未来趋势,并常用于时间序列预测中,对数据量无特别的要求[4]。指数平滑模型用于数据需要消除波动的领域,是使用较广泛的用于预测时间序列变化趋势的预测方法,将预测对象随着时间(或空间)推移而形成的数据序列视为一个随机序列,然后用一定的数学模型近似描述这个序列。3次指数平滑预测法能排除特征数据所受的外部偶然干扰,从而能够平稳地反映数据序列的变化趋势,可以适用多数的预测分析[5]。灰色预测模型用于时间短、数据量不大、波动小的问题[6]。BP神经网络有自组织、自学习、自适应、容错能力强、可以任意逼近非线性函数。对时间序列一般采用滑动预测方法,但需要的数据量较大,有时逼近局部最小,从而影响泛化能力[7]。
组合预测模型建立方法有基于粗糙集(Rough sets)、Shapley、熵权法(entropy-right method,ERM)、小波分析等。粗糙集是一个刻画不完整、不确定、不精确、不一致的信息,并从中发现隐含的知识和规律的数据分析方法。基于粗糙集的权重计算方法中通过测度依赖度、重要度,求出属性的权重[8]。熵权法的基本原理是通过度量评价指标体系中指标数据所蕴含的信息量来计算各指标的权重。当评价对象在某项指标上的值相差较大时,熵值较小,说明该指标提供的有效信息量较大,从而量化指标权重[9]。Shapley值法是用于解决多人合作对策问题的一种数学方法,它主要集中应用在合作收益在各合作方之间的分配,Shapley值实现的是每个合作成员对该合作联盟的贡献大小,突出反映了各个成员在合作中的重要性,从而可以确定各成员在合作联盟中所得权重[10]。虽然这些方法为建立组合预测模型提供了精度较高的权重计算方法,但仍然在精度、有效信息抽取能力、构造难度和实用性等方面有改进余地。
为此,笔者综合上述各种方法的优缺点,提出一种时间序列组合预测模型,并和其他几种组合预测模型进行对比,为预测时间序列提供新的途径。
1 组合预测模型思想对于一些复杂的非线性预测系统,采用单一模型的预测方法,难以获得满意的结果。根据近年的理论和实践研究,采用组合预测方法是提高预测精度的有效途径[11, 12]。
组合预测方法是由Bates和Granger于1969年首次提出的实用预测方法[13]。它是对同一个预测对象采用不同的单项预测模型,以适当的加权平均形式,在某个准则下求得最优加权系数,从而可以充分利用各种单项预测方法所提供的信息,达到提高预测精度的目的。组合预测模型方法能增强预测的稳定性,具有较高的预测时间序列发展趋势的能力。对时间序列进行预测分析时,可以应用不同函数对系统进行拟合,而不同算法或函数往往有不同的特点。能否将各种不同的模型组合在一起达到更好的预测效果是组合预测思想的出发点。因组合预测方法是通过求个体预测值的加权算术平均而得到它们的组合预测值,因此,建立组合预测模型的关键是,根据预测对象特征,正确选择构建组合模型的每个单一模型和恰当地确定各单一预测模型在组合模型中的权重[14, 15, 16]。组合预测方法的最大特点是从各种模型中提取有效的预测信息,使m种预测模型(m>1)并行工作,根据预测对象的时间序列生成相应的函数。假设m种预测模型对同一序列进行预测,则由这m种单一预测模型构成的组合模型为:


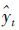 为t时刻组合预测模型的预测值;
为t时刻组合预测模型的预测值;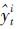 为t时刻第i种预测模型的预测值;ki为第i种预测模型的权重系数(i=1,2,…,m),用式(2)求得。组合预测模型中权重的确定是构造模型的关键因素。笔者提出基于百分误差的单一模型权重计算方法并建立组合预测模型,并对该方法与基于粗糙集、Shapley、熵权法等方法进行对照分析。
2 构造单一模型
为t时刻第i种预测模型的预测值;ki为第i种预测模型的权重系数(i=1,2,…,m),用式(2)求得。组合预测模型中权重的确定是构造模型的关键因素。笔者提出基于百分误差的单一模型权重计算方法并建立组合预测模型,并对该方法与基于粗糙集、Shapley、熵权法等方法进行对照分析。
2 构造单一模型
当把时间作为影响农业机械总动力的各种因素的综合时,可以建立总动力随时间变化的预测模型。不同的单一预测模型、预测函数或算法对预测对象特征的依赖度不同。如:同一个预测对象的历史数据作为数据源,用不同的方法建立预测模型时,因不同预测模型所使用的算法对数据源分布特征的依赖程度有明显差异,导致各模型所获得的预测精度、拟合优度的波动幅度差异较大。因此,建立组合预测模型时,根据单一模型在目标序列的预测精度、预测值的波动幅度作为依据正确选取构建组合模型的单一模型是关键的一步。
经分析可知,农业机械总动力数据具有数据量较少、总体上波动幅度不大等特征,并呈现出逐年递增的趋势。根据以上分析,本文中考虑以曲线回归模型、ARIMA模型、3次指数平滑和灰色模型GM(1,1)为组合模型中的单一模型。
2.1 建立曲线回归模型本文中应用SPSS(statistical product and service solutions)软件的线性函数等11种函数对农业机械总动力进行曲线拟合[2, 3],对得到的模型进行显著性检验,利用方差分析所提供的F统计量,检验预测模型的总体线性关系的显著性,在F检验通过的情况下选取拟合优度最大的模型为候选模型。拟合优度可以用以下公式计算:

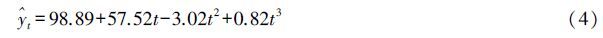
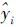 、yi和y分别代表预测值、源序列和平均值。实践中R2>0.8,则可以认为拟合度较高,在拟合度满足条件情况下,计算每个预测项的平均绝对百分误差(mean absolute percent error,MAPE),从候选模型中选取MAPE小于10%模型为正式的组合预测模型构成元素。依据上述方法,从新疆农机总动力历史数据为源序列的11种曲线模型中筛选3次曲线回归模型,并建立相应的预测模型,见式(4)。式中:
、yi和y分别代表预测值、源序列和平均值。实践中R2>0.8,则可以认为拟合度较高,在拟合度满足条件情况下,计算每个预测项的平均绝对百分误差(mean absolute percent error,MAPE),从候选模型中选取MAPE小于10%模型为正式的组合预测模型构成元素。依据上述方法,从新疆农机总动力历史数据为源序列的11种曲线模型中筛选3次曲线回归模型,并建立相应的预测模型,见式(4)。式中: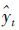 为模型在t时刻(t=1,2,…,n)的预测值。
2.2 构造ARIMA模型
为模型在t时刻(t=1,2,…,n)的预测值。
2.2 构造ARIMA模型
ARIMA是由博克思和詹金斯于20世纪70年代初提出的时间序列预测方法。其基本思想是:将预测对象随时间推移而形成的数据序列视为1个随机序列,用一定的数学模型来近似这个序列。具体而言,使用ARIMA模型对时间序列进行建模,主要包括平稳性检验、平稳化处理、模型结构确定、参数估计和模型检验等过程[4]。式(5)为ARIMA(p,d,q)模型的公式。
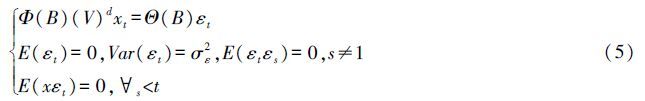
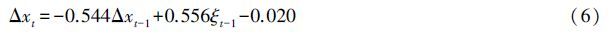
n次指数平滑值的计算公式为:



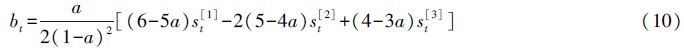

在Matlab 2014a环境中编程并计算模型参数at、bt和ct。因农业机械总动力趋势较为稳定,所以从a=0.02~0.30区间内,取不同值进行试验,结果显示,平滑因数a=0.15时MAPE和误差平方和(sum of the squared errors,SSE)取值分别为3.95%和28 252,拟合优度也接近1,模型指标满足要求,可得出预测模型为:

GM(1,1)模型是灰色系统理论中应用最广泛的一种灰色动态预测模型,该模型由一个单变量的一阶微分方程构成。它主要用于复杂系统某一主导因素特征值的拟合和预测,以揭示主导因素变化规律和未来发展变化态势。设定原时间序列X(0)有n个观测值:


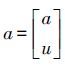 ,利用最小二乘法求解可得
,利用最小二乘法求解可得

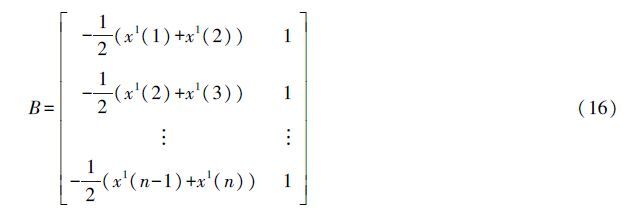
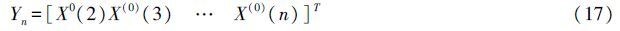
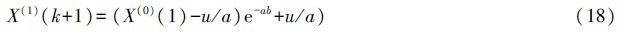
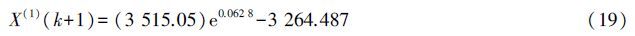
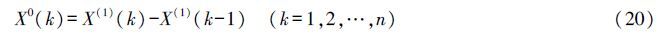
本研究中应用Matlab 2014a实现了GM(1,1)模型,并计算出后验差的比值c=0.116 25<0.35,小误差概率 P=1.00>0.95,模型指标说明建立的模型拟合精度较高,可用于序列未来趋势的预测。
2.5 单一模型预测应用2.1~2.4节建立的模型对新疆农业机械总动力进行检验性预测,各模型预测值见表 1。其中组合模型值为下一节建立的组合预测模型的预测值。
| 年份 Year | 实际动力 Actual value | 拟合值 Fitted values | ||||
| 曲线回归Cubic curves | ARIMA | 指数平滑Exponential smoothing | 灰色模型Grey model | 组合模型Combination model | ||
| 1978 | 250.20 | 153.46 | 250.20 | 250.20 | ||
| 1979 | 208.00 | 202.48 | 231.21 | 227.80 | ||
| 1980 | 248.50 | 246.44 | 170.47 | 236.14 | 242.57 | 225.27 |
| 1981 | 265.30 | 285.84 | 227.42 | 247.44 | 258.29 | 257.79 |
| 1982 | 278.20 | 321.17 | 279.40 | 261.34 | 275.03 | 287.41 |
| 1983 | 305.40 | 352.92 | 295.38 | 283.32 | 292.85 | 311.96 |
| 1984 | 345.20 | 381.59 | 321.22 | 316.41 | 311.83 | 343.59 |
| 1985 | 384.60 | 407.67 | 368.09 | 356.78 | 332.04 | 381.29 |
| 1986 | 396.00 | 431.66 | 419.57 | 389.20 | 353.56 | 410.93 |
| 1987 | 429.00 | 454.04 | 439.27 | 425.23 | 376.47 | 438.07 |
| 1988 | 459.90 | 475.31 | 458.97 | 462.47 | 400.87 | 464.61 |
| 1989 | 496.30 | 495.96 | 495.51 | 502.65 | 426.85 | 497.30 |
| 1990 | 523.10 | 516.49 | 533.68 | 540.18 | 454.51 | 527.42 |
| 1991 | 560.80 | 537.39 | 565.60 | 580.37 | 483.97 | 559.31 |
| 1992 | 594.00 | 559.16 | 599.94 | 620.08 | 515.33 | 590.85 |
| 1993 | 608.30 | 582.28 | 638.25 | 650.62 | 548.73 | 617.19 |
| 1994 | 624.90 | 607.26 | 654.27 | 675.48 | 584.29 | 637.74 |
| 1995 | 653.80 | 634.57 | 660.97 | 701.77 | 622.16 | 659.93 |
| 1996 | 688.90 | 664.73 | 684.94 | 731.82 | 662.48 | 689.71 |
| 1997 | 732.70 | 698.21 | 724.19 | 768.38 | 705.42 | 727.89 |
| 1998 | 770.70 | 735.52 | 773.63 | 806.79 | 751.13 | 768.72 |
| 1999 | 814.40 | 777.15 | 820.73 | 848.89 | 799.81 | 812.38 |
| 2000 | 858.50 | 823.58 | 866.09 | 893.56 | 851.65 | 857.59 |
| 2001 | 883.10 | 875.33 | 914.79 | 931.02 | 906.84 | 898.83 |
| 2002 | 924.20 | 932.86 | 943.94 | 970.63 | 965.61 | 941.27 |
| 2003 | 973.90 | 996.69 | 975.39 | 1015.50 | 1028.19 | 989.34 |
| 2004 | 1047.90 | 1067.31 | 1028.95 | 1074.86 | 1094.82 | 1054.11 |
| 2005 | 1121.00 | 1145.20 | 1108.80 | 1143.75 | 1165.78 | 1129.46 |
| 2006 | 1190.00 | 1230.87 | 1200.25 | 1217.08 | 1241.33 | 1209.92 |
| 2007 | 1275.50 | 1324.79 | 1279.88 | 1300.44 | 1321.78 | 1295.89 |
| 2008 | 1375.60 | 1427.48 | 1368.27 | 1396.87 | 1407.44 | 1392.97 |
| 2009 | 1503.27 | 1539.42 | 1479.34 | 1514.21 | 1498.65 | 1509.73 |
| 2010 | 1642.93 | 1661.10 | 1620.73 | 1650.82 | 1595.78 | 1644.04 |
| 2011 | 1795.94 | 1793.02 | 1784.75 | 1805.89 | 1699.20 | 1794.25 |
| 2012 | 1968.27 | 1935.67 | 1958.63 | 1981.36 | 1809.32 | 1959.09 |
| 2013 | 2165.87 | 2089.55 | 2150.26 | 2181.07 | 1926.58 | 2143.02 |
| 注:数据来源,《新中国农业60年统计资料》(中国农业出版社)和《新疆统计年鉴》(新疆统计局)。 Note:Data source,60 Years of New Chinese Agriculture Statistics (China Agricultural Press), Xinjiang Statistical Yearbook (Xinjiang Bureau of Statistics). | ||||||
组合预测模型中可以结合不同预测方法的优点,综合利用各种算法提供的信息,从而提高预测精度。构造组合预测模型的关键因素是,除了正确选取单一模型外,还要采取正确的方法和步骤,确定各单一模型对组合模型预测精度的贡献率,即权重[19]。
3.1 计算各模型的重要度和权重单一模型对组合模型的预测值的影响程度依赖其预测值和权重,单一模型权重又取决于各单一模型预测值对预测对象的重要度,如重要度高,则权重较大,反之亦然。基于百分误差的权重计算步骤为:
1) 计算预测周期内各时段拟合值的误差。
2) 根据误差的结果计算百分误差。
3) 计算某个预测模型在某个时段的拟合百分误差在该时段所有模型拟合百分误差之和中所占的比例,确定每个时段的某个模型的重要度。
4) 根据某个预测模型在某个时段的重要度在该时段所有模型重要度之和中所占比例确定每个时段的某个模型的权重。计算公式为:
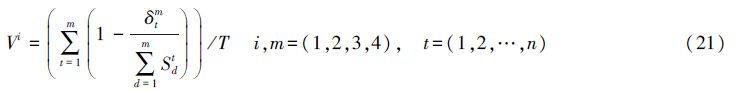

| 曲线回归 Cubic curves | ARIMA | 指数平滑 Exponential smoothing | 灰色模型 Grey model | |
| 重要度 Importance degree | 0.751 4 | 0.862 1 | 0.773 1 | 0.613 4 |
| 权重Weight | 0.250 5 | 0.287 4 | 0.257 7 | 0.204 5 |
基于百分误差的权重确定方法,根据单一模型预测结果的精度和真实度对预测模型的重要度和权重进行计算和分配,从而在组合模型建立过程中为单一模型的权重确定提供了依据。
3.2 组合预测模型构造应用表 2中各模型的权重系数即可建立基于百分误差的新疆农业机械总动力组合预测模型。组合预测模型为:
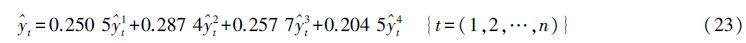
式中: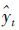 为组合预测模型在t时刻的预测值。
为组合预测模型在t时刻的预测值。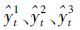 和
和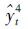 是各单一模型的预测值。应用该组合模型预测出的农业机械总动力预测值见表 1。同时应用该模型对新疆农业机械总动力2014至2018年发展趋势做出预测。预测结果(表 3)表明:到2018年新疆农业机械总动力仍然保持快速增长的趋势,但从实践和理论分析可知,时间序列在发展过程中难以长期保持其增长趋势;从时间序列的预测模型角度来看,基于有限的少量样本序列建立的预测模型难以发掘目标序列发展曲线的全部形状。但短期预测可以较为精确地预测其发展趋势。
是各单一模型的预测值。应用该组合模型预测出的农业机械总动力预测值见表 1。同时应用该模型对新疆农业机械总动力2014至2018年发展趋势做出预测。预测结果(表 3)表明:到2018年新疆农业机械总动力仍然保持快速增长的趋势,但从实践和理论分析可知,时间序列在发展过程中难以长期保持其增长趋势;从时间序列的预测模型角度来看,基于有限的少量样本序列建立的预测模型难以发掘目标序列发展曲线的全部形状。但短期预测可以较为精确地预测其发展趋势。
| 104 kW | |||||
| 年份 Year | |||||
| 2014 | 2015 | 2016 | 2017 | 2018 | |
| 总动力Total power | 2 261.56 | 2 435.26 | 2 620.32 | 2 819.40 | 3 032.30 |
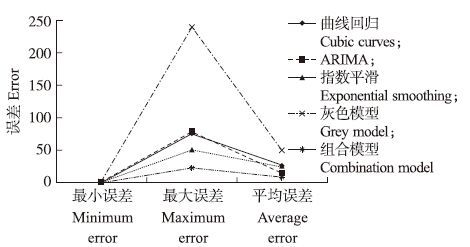
建立组合预测模型后,检验组合预测模型是否可行及有效时,常用的检验指标有误差、拟合优度、MAPE和SSE[20]。依据表 1预测值,计算各单一模型和本文建立的组合模型的误差。由表 4可见:组合模型的最大误差、平均误差及SSE等指标和单一模型相比明显下降。图 1也说明,组合模型的最小、最大和平均误差的波动幅度与单一模型相比缩小。同时该结果也反映出组合模型最小误差大于2个单一模型,但其值接近0,是处在可接受的范围内。应用式(3)计算拟合优度,并计算4个单一模型及组合模型的MAPE。由表 5可知:组合模型和单一模型拟合优度接近1,但组合预测模型MAPE和各单一模型相比明显下降。这也说明组合预测模型预测结果和单一模型相比趋向于更加稳定。
| 曲线回归Cubic curves | ARIMA | 指数平滑Exponential smoothing | 灰色模型Grey model | 组合模型Combination model | |
| 最小误差Minimum error | 0.34 | 0.79 | 2.57 | 3.17 | 0.81 |
| 最大误差Maximum error | 96.74 | 78.03 | 50.58 | 239.29 | 23.23 |
| 平均误差Average error | 28.78 | 14.97 | 24.97 | 49.29 | 8.54 |
| 误差平方和SSE | 43 636 | 14 921 | 28 252 | 151 819 | 4 065 |
|
图 1 模型误差波动 Fig. 1 Model error fluctuation |
| 曲线回归Cubic curves | ARIMA | 指数平滑Exponential smoothing | 灰色模型Grey model | 组合模型Combination model | |
| 拟合优度 Goodness of fit | 0.995 3 | 0.996 8 | 1.029 0 | 0.944 3 | 0.998 8 |
| MAPE/% | 5.18 | 2.86 | 3.95 | 6.28 | 1.298 4 |
时间序列组合预测模型领域中,研究者提出了多种预测模型的建立方法,这些方法的最大不同点就是单一模型的权重计算所采用的算法不同。为了进行不同组合预测模型之间的对照分析,本文中分别应用基于粗糙集理论、熵权法和Shapley法的特征权重计算方法建立组合预测模型。利用自组织映射(self-organization mapping,SOM)无监督聚类,对由各单一模型预测值和实际总动力组成的时间序列进行聚类,生成离散化的决策表,计算属性依赖度和重要度,在此基础上计算各单一模型的权重,从而构建基于粗糙集的组合预测模型[8]。同时应用文献[9, 10]提出的基于熵权法和Shapley法,计算本文筛选的4种单一模型的权重,并建立组合预测模型。用这3种组合预测模型对新疆农业机械总动力进行预测,并计算3种组合预测模型预测值的MAPE、拟合优度和SSE,并和本文提出的组合预测模型对应指标进行比较。结果表明:基于百分误差的组合预测模型的拟合优度与基于粗糙集、Shapley和熵权法的组合预测模型拟合优度相比,分别提高了2.40%、5.10%和2.27%,预测值的MAPE分别和上述3种方法相比减少了0.37、2.43和1.40(表 6)。
| 粗糙集Rough sets | Shapley | 熵权法Entropy weight method | 组合模型Combination model | |
| 拟合优度Goodnees of fit | 0.974 9 | 0.947 9 | 0.976 2 | 0.998 8 |
| MAPE/% | 1.673 0 | 3.726 1 | 2.702 4 | 1.298 4 |
| SSE | 5 927.29 | 19 761.40 | 8 725.29 | 4 064.53 |
以新疆农业机械总动力数据为研究对象,建立了基于百分误差的时间序列组合预测模型,进行了模型检验,并与4种单一模型的预测精度进行比较,结果表明,预测周期内组合模型的最大和平均误差与各单一模型最优值相比,分别降低了27.35和6.43,SSE减少了73%,MAPE降低了1.56%,减少了预测误差的波动幅度。
以模型拟合优度和MAPE作为评价指标,对本文提出的组合预测模型的拟合优度与基于粗糙集、Shapley和熵权法的组合预测模型进行比较,结果表明:基于百分误差的组合预测模型的拟合优度与基于粗糙集、Shapley和熵权法的组合预测模型拟合优度相比,分别提高了2.40%、5.10%和2.27%,预测值的MAPE分别和上述3种方法相比减少了0.37、 2.43 和 1.40。本文提出的时间序列组合预测方法,在有效预测农业机械总动力,从时间序列中提取有效信息,提高预测精度和减少预测值的波动方面有一定的参考价值。
| [1] | 黄玉祥,郭康权,朱瑞祥.大中型拖拉机需求量混沌特征分析及预测时效研究[J]. 西北农林科技大学学报,2007,23(8):135-139. Huang Y X,Guo K Q,Zhu R X. Analysis of chaos characteristics and forecasting time-scale of the demand for big-medium-sized tractors[J]. Northwest Agriculture and Forestry University,2007,23(8):135-139(in Chinese with English abstract). |
| [2] | Aranildo R L,Alex J C,William W H. Nonlinear regression in environmental sciences using extreme learning machines:a comparative[J]. Evaluation Environmental Modelling and Software,2015,73(5):175-188. |
| [3] | Andreas F.How to determine the unique contributions of input-variables to the nonlinear regression function of a multilayer perceptron[J]. Ecological Modelling,2015,309/310:60-63. |
| [4] | 朱立学,罗锡文,臧英,等.基于3次指数平滑的水稻生产综合机械化发展水平预测[J]. 农机化研究,2007,29(7):51-57. Zhu L X,Luo X W,Zang Y,et al. 3-exponential flatting method based on rice mechanization forecast[J]. Journal of Agricultural Mechanization Research,2007,29(7):51-57(in Chinese with English abstract). |
| [5] | 王国权,王森,刘华勇,等.基于自适应的动态三次指数平滑法的风电场风速预测[J]. 电力系统保护与控制,2014,42(15):117-122. Wang G Q,Wang S,Liu H Y,et al. Self-adaptive and dynamic cubic ES method for wind speed forecasting[J]. Power System Protection and Control,2014,42(15):117-122(in Chinese with English abstract). |
| [6] | Thananchai L. Grey prediction on indoor comfort temperature for HVAC systems[J]. Expert Systems with Applications,2008,34:2284-2289. |
| [7] | 鞠金艳,王金武,王金峰.基于BP神经网络的农机总动力组合预测方法[J]. 农业机械学报,2011,41(6):87-92. Ju J Y,Wang J W,Wang J F. Combined prediction method of total power of agricultural machinery based on BP neural network[J]. Transactions of the Chinese Society for Agricultural Machinery,2011,41(6):87-92(in Chinese with English abstract). |
| [8] | 郑文钟,何勇.基于粗糙集的粮食产量组合预测模型[J]. 农业机械学报,2005,36(11):75-78. Zheng W Z,He Y. Study on evaluation methods for agricultural mechanization developing level based on rough set theory and fuzzy aggregation[J]. Transactions of the Chinese Society for Agricultural Machinery,2005,36(11):75-78(in Chinese with English abstract). |
| [9] | Pan G B,Xu Y P,Yu Z H,et al. Analysis of river health variation under the background of urbanization based on entropy weight and matter-element model:a case study in Huzhou City in the Yangtze River Delta,China[J]. Environmental Research,2015,139(5):31-35. |
| [10] | 李书金,张强.一种基于Shapley值的联盟结构分配方法[J]. 北京理工大学学报,2007,27(8):745-749. Li S J,Zhang Q. A method of allocation among players in coalition structure based on the shapley value[J]. Transactions of Beijing Institute of Technology,2007,27(8):745-749(in Chinese with English abstract). |
| [11] | 江志华,朱国宝.灰色预测模型GM(1,1)及在交通运量预测中的应用[J]. 武汉理工大学学报(交通科学与工程版),2004,28(2):305-307. Jiang Z H,Zhu G B. Grey model-GM(1,1)and its application to predicting transportation volume[J]. Journal of Wuhan University of Technology(Traffic Science and Engineering Edition),2004,28(2):305-307(in Chinese with English abstract). |
| [12] | 邱洪臣,朱瑞祥,李卫,等.基于离散灰色模型的中国农机总动力预测[J]. 农机化研究,2014,36(1):80-83. Qiu H C,Zhu R X,Li W,et al. A forecast for agricultural machinery total power of China using discrete gray model[J]. Journal of Agricultural Mechanization Research,2014,36(1):80-83(in Chinese with English abstract). |
| [13] | Bates J M,Granger C W J.The combination of forecasts[J]. Operational Research Quarterly,1969,20(4):451-468. |
| [14] | 鹿应荣,杨印生,刘洪霞.基于BP神经网络的非线性组合预测模型在粮食物流需求预测中的应用[J]. 吉林大学学报,2008,38(2):61-64. Lu Y R,Yang Y S,Liu H X. Application of nonlinear combination forecasting based on neural networks in grain logistic demand[J]. Journal of Jilin University,2008,38(2):61-64(in Chinese with English abstract). |
| [15] | Ma L,Lin B,Zhen B Y,et al. A new combination prediction model for short-term wind farm output power based on meteorological data collected by WSN[J]. International Journal of Control and Automation,2014,7(1):171-180. |
| [16] | Hong J,Koo H,Kim T. Easy,reliable method for mid-term demand forecasting based on the bass model:a hybrid approach of NLS and OLS[J]. European Journal of Operational Research,2016,248:681-690. |
| [17] | Pektas A O,Cigizoglu H K. ANN hybrid model versus ARIMA and ARIMAX models of runoff coefficient[J]. Journal of Hydrology,2013,500:21-36. |
| [18] | Shi H Y,Zhang X,Su X M,et al. Trend prediction of FDI based on the intervention model and ARIMA-GARCH-M model[J]. AASRI Procedia,2012,3:387-393. |
| [19] | Wang J Z,Hu J M. A robust combination approach for short-term wind speed forecasting and analysis:combination of the ARIMA(Autoregressive Integrated Moving Average),ELM(Extreme Learning Machine),SVM(Support Vector Machine)and LSSVM(Least Square SVM)forecasts using a GPR(Gaussian Process Regression)model[J]. Energy,2015,93:41-56. |
| [20] | Sermpinis G,Stasinakis C,Theofilatos K,et al. Modeling,forecasting and trading the EUR exchange rates with hybrid rolling genetic algorithms:support vector regression forecast combinations[J]. European Journal of Operational Research,2015,247:831-846. |




