文章信息
- 郭军, 王克华, 曲亮, 沈曼曼, 马猛, 窦套存, 胡玉萍.
- GUO Jun, WANG Kehua, QU Liang, SHEN Manman, MA Meng, DOU Taocun, HU Yuping.
- 应用随机回归模型分析蛋鸡蛋黄质量遗传参数
- Genetic parameters for yolk weight in resource population with random regression model
- 南京农业大学学报, 2016, 39(01): 145-149
- Journal of Nanjing Agricultural University, 2016, 39(01): 145-149.
- http://dx.doi.org/10.7685/jnau.201503053
-
文章历史
- 收稿日期:2015-03-26
市场对鸡蛋品质选育提出了新要求,越来越多的消费者偏爱蛋黄比例高的餐桌蛋。为了培育适应市场需求的蛋鸡品种,亟需开展蛋黄质量遗传规律研究,以获取蛋黄相关性状的遗传参数。蛋黄质量随周龄增加呈规律性变化,属于动态性状,也称经向性状(longitudinal trait)。应用随机回归模型分析动态性状是当前流行趋势,该模型容错能力强、柔韧性好,同一个体不同时期数据互为参照[1]。随机回归模型最初用于奶牛育种[2, 3],由赵福平[4]、张健[5]引入我国用于分析产奶量遗传参数。近年来,随机回归模型已经扩展到家禽遗传评估,主要用于产蛋数和体质量遗传力估计,尚未见应用随机回归模型评估蛋黄质量遗传参数的报道[1]。国内外学者针对蛋鸡蛋黄质量性状已经做了许多遗传评估工作,所用遗传模型不尽相同:有的采用半同胞家系或全同胞家系估计遗传方差,如Hill等[6]、Rodda等[7];有的采用单性状统计模型,如Zhang等[8]、Wolc等[9];有的采用多性状统计模型,如Hartmann等[10]。综合国内外现有蛋黄质量遗传评估研究进展,尚存以下不足:试验材料仅采集一个时间点,不能呈示蛋黄质量动态变化规律;单性状或多性状动物模型虽能满足遗传参数评估需要,但其EBV估算精度不如随机回归模型[3, 11, 12]。本试验以绿壳蛋鸡——白来航资源群体为素材,收集40~60周蛋黄质量数据,以Legendre多项式嵌入加性遗传效应、永久环境效应,旨在以随机回归模型分析蛋黄质量遗传规律及遗传参数。
1 材料与方法 1.1 试验鸡以绿壳蛋鸡与白来航鸡组建F2分离群体。F1群体由513只鸡组成,F2群体由1 744只鸡组成。试验鸡以三段式饲养,0~7周为育雏阶段,8~18周为育成阶段,18周之后为产蛋阶段。试验鸡只单独戴翅号、单笼饲养,笼具为3层阶梯式,饲喂常规饲料。育成期每日光照8 h。机械化喂料、清粪。蛋黄质量测定期为40~60周,每4周测量1次。根据SAS软件分析结果,将年效应列入固定效应。
1.2 统计分析系谱数据及蛋黄质量数据经初步筛选,去除明显错误或重复数据,整理成Excel格式,然后,对蛋黄质量数据再次整理,除去3倍标准差之外数值。应用SAS ANOVA校正环境方差,确定进入固定效应的因素,并获得蛋黄质量平均数,然后,用WOMBAT软件的AIREML方法分析蛋黄质量(协)方差组分以及遗传力[13]。模型公式如下:
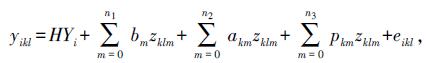
式中,yikl是第i批次第l周龄第k只鸡蛋黄质量;HYi是批次固定效应;bm是第m个固定回归系数;akm是加性效应第m个随机回归系数;pkm是永久环境效应第m个随机回归系数;zklm是嵌入的勒让德多项式协变量;eikl是残差效应;n1、n2、n3是嵌入固定效应、加性遗传以及永久环境效应勒让德多项式阶数。个体k周龄1与周龄2之间的协方差公式如下:
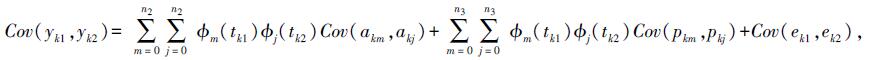
式中:Cov(yk1,yk2)是k个体1周龄与2周龄的蛋黄质量协方差;Cov(akm,akj)是k个体mth随机回归阶数与jth随机回归阶数加性遗传协方差;Cov(pkm,pkj)是k个体mth随机回归阶数与jth随机回归阶数永久环境协方差;Cov(ek1,ek2)是k个体1周龄与2周龄间蛋黄质量残差;Φm(tk1)是k个体1周龄的m阶勒让德多项式。运行WOMBAT软件获得协方差矩阵,将时间函数和勒让德多项式代入后,得到加性遗传(协)方差和永久环境效应(协)方差。各周龄蛋黄质量遗传力(h2)、重复力(r)以及遗传相关系数(rA)分别以下面的公式求得:
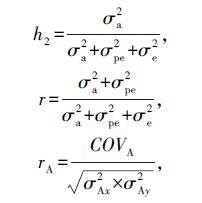
式中:σ2a为加性遗传方差;σ2pe为永久环境方差;σ2e为残差;COVA为协方差;σ2Ax/Ay分别为x/y节点加性遗传方差。
本研究采用的AIC准则、BIC准则选择最适合描述蛋黄质量的统计模型并进行比较,以期提高数据分析的准确度。AIC准则由日本学者赤池弘次(Akaike)首次提出,该准则针对当前模型与真模型之间存在的K—L距离给出无偏估计量,其公式为:[14]
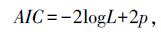
BIC准则,即贝叶斯信息准则,是统计模型选择中广泛采用的标准。如果真模型存在于分析模型之列,BIC值最小的即为真模型。计算BIC值公式为:
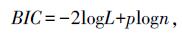
两式中:L是模型的极大似然函数;p为模型的独立参数总数;n为观察值总数。
2 结果与分析 2.1 蛋黄质量数据描述2011—2014年,连续统计3个世代资源群体蛋黄质量,基本信息见图1。蛋黄质量中位数随周龄增加而增加,上、下四分位数也是同样趋势。经SAS ANOVA分析,蛋黄质量平均值存在极显著差异(P<0.000 1)。本研究中各周龄蛋黄质量平均值存在显著差异(α=0.05)。40、44、48、52、56和60周龄样本数依次为2 120、1 894、1 829、1 900、2 019和1 997,蛋黄质量平均值分别为15.16、15.68、15.82、16.13、16.43和16.69 g。
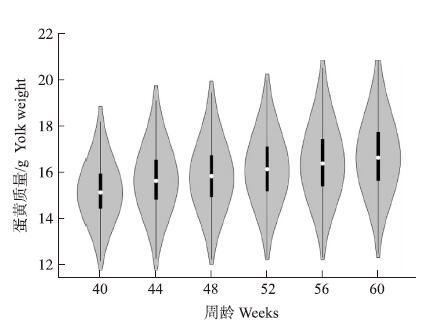 |
图 1 资源群体40~60周蛋黄质量 Fig. 1 Yolk weight between 40 weeks and 60 weeks in resource population提琴图主要包括3个节点,即上四分位数、中位数、下四分位数。提琴边界由密度值生成。 Violinplot was composed of 3 key points,i.e.upper quartile,median,lower quartile.Borders of violin plot were generated by the density vlaues. |
表1列出几个模型对应的AIC值和BIC值。蛋鸡分离群体蛋黄质量加性遗传效应适于嵌入3阶勒让德多项式随机回归模型,永久环境效应适于嵌入2阶勒让德多项式随机回归模型,更高阶数多项式无法完成数据收敛。应用随机回归模型计算的各方差组分见表2。40周龄蛋黄质量残差比率较低,按时间顺序依次为:25%、34%、33%、30%、33%、31%。加性遗传方差趋势与永久环境方差的基本一致,随周龄增加而增加。60周龄临近产蛋末期,蛋鸡自身生理调节机能降低,受外界环境影响较大,永久环境方差增大。用3阶Legendre多项式拟合的加性遗传协方差见图2。
| 模型 Models | AIC | BIC | 最大对数似然值 LogL | 参数量/个 p | 多项式阶数 Polynomials orders | |
| 加性遗传效应 Genetic effect | 永久环境效应 Permanent environmental effect | |||||
| 1 | 12 925.58 | 12 984.56 | -6 454.79 | 8 | 1 | 1 |
| 2 | 12 760.97 | 12 834.69 | -6 370.49 | 10 | 1 | 2 |
| 3 | 12 745.84 | 12 841.68 | -6 359.92 | 13 | 1 | 3 |
| 4 | 12 736.49 | 12 810.21 | -6 358.25 | 10 | 2 | 1 |
| 5 | 12 774.49 | 12 862.95 | -6 375.25 | 12 | 2 | 2 |
| 6 | 12 720.45 | 12 831.03 | -6 345.23 | 15 | 2 | 3 |
| 7 | 12 722.19 | 12 818.30 | -6 349.10 | 12 | 3 | 1 |
| 8 | 12 707.72 | 12 810.66 | -6 338.86 | 15 | 3 | 2 |
| 周龄 Weeks | 加性遗传方差 Genetic variance | 永久环境方差 Permanent environmental variance | 残差 Residual | 表型方差 Phenotypic variance | 遗传力 Heritability | 重复力 Repeatability |
| 40 | 0.75 | 0.33 | 0.44 | 1.52 | 0.49 | 0.71 |
| 44 | 0.79 | 0.33 | 0.71 | 1.83 | 0.43 | 0.61 |
| 48 | 0.85 | 0.34 | 0.72 | 1.91 | 0.45 | 0.62 |
| 52 | 0.93 | 0.38 | 0.68 | 1.99 | 0.47 | 0.66 |
| 56 | 0.99 | 0.45 | 0.80 | 2.24 | 0.44 | 0.64 |
| 60 | 1.07 | 0.54 | 0.77 | 2.38 | 0.45 | 0.68 |
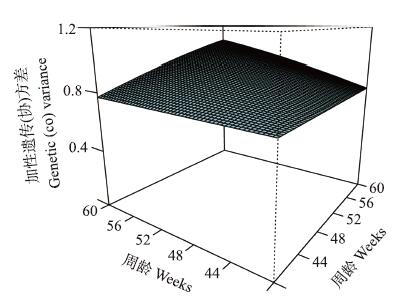 | 图 2 各周龄蛋黄质量遗传(协)方差估计值 Fig. 2 Estimated genetic(co)variances between yolk weights at different weeks |
蛋鸡资源群体蛋黄质量遗传力为0.43~0.49,40周龄蛋黄质量遗传力较高,44周龄遗传力最低,之后蛋黄质量遗传力逐渐升高,至56、60周龄遗传力回落(表2)。遗传力变化受加性遗传方差影响,同时也与残差有关。40周龄加性遗传方差最小,但是由于同时期残差、永久环境方差也是最小,导致40周龄蛋黄质量遗传力最高。
2.3 蛋黄质量遗传相关遗传相关系数是制定育种规划、实施指数选择所必需的。本研究结果表明,不同周龄蛋黄质量遗传相关系数为0.86~0.99,相邻周龄之间遗传相关系数较高(表3)。不同周龄之间蛋黄质量表型相关系数为0.54~0.62,最小表型相关系数发生在44周龄与60周龄之间。各个表型相关系数检验结果达到极显著水平(P<0.000 1)。
| 周龄 Weeks | 周龄 Weeks | |||||
| 40 | 44 | 48 | 52 | 56 | 60 | |
| 40 | 0.64 | 0.61 | 0.58 | 0.56 | 0.57 | |
| 44 | 0.98 | 0.60 | 0.58 | 0.55 | 0.54 | |
| 48 | 0.95 | 0.99 | 0.63 | 0.59 | 0.60 | |
| 52 | 0.91 | 0.97 | 0.99 | 0.65 | 0.62 | |
| 56 | 0.89 | 0.95 | 0.98 | 0.99 | 0.64 | |
| 60 | 0.86 | 0.92 | 0.95 | 0.97 | 0.99 | |
3.1 蛋黄质量是中等遗传力性状
蛋黄质量是蛋品质选育重要指标之一,现有蛋黄质量遗传评估研究多集中在国外商品蛋鸡。本研究以中国地方鸡种与白来航鸡组建分离群体,虽然分析对象为杂交群体,但50%遗传物质来源于绿壳蛋鸡,对于中国地方鸡种选育工作具有一定参考意义。本研究结果表明蛋黄质量属于中等遗传力性状,与前人研究结果基本一致。Jaffe[15]研究发现,白来航鸡的32周龄蛋黄质量遗传力为0.43,蛋黄质量与蛋质量遗传相关系数为0.82,表型相关系数为0.53。Hill等[6]研究结果表明,白来航鸡蛋黄质量遗传力为0.32±0.19,重复力0.65。Rodda等[7]以大样本评估加拿大来航型蛋鸡遗传参数,结果表明65周龄蛋黄质量遗传力为0.5±0.1。Hartmann等[10]以白来航鸡为素材评估蛋黄相关性状遗传参数,结果表明,29周龄蛋黄质量遗传力为0.22±0.04,重复力为0.37±0.02。Zhang等[8]发现,矮小型褐壳蛋鸡的40周龄蛋黄质量遗传力为0.45±0.10。Wolc等分析发现,褐壳蛋鸡的26~28周龄蛋黄质量遗传力为0.47±0.02。本研究使用个体动物模型估计遗传力、重复力以及遗传相关,Wolc等[9]、Zhang等[8]也是应用个体动物模型计算遗传参数,3个研究的对象不同,但是估计的蛋黄质量遗传力相差不大,表明个体动物模型稳定性好、适用范围广。
3.2 随机回归模型适用于蛋黄质量遗传评估本研究中,有的动物个体只有2~3条记录,多元方差分析或者单性状重复检测模型需要舍弃这些记录不全的个体,而随机回归模型可以获得稳定而可靠的结果。随机回归模型多用在奶牛泌乳性状、畜禽生长性状,近年来已用于分析蛋鸡产蛋性状[16, 17, 18, 19],但尚未见其应用于分析蛋黄质量遗传参数的研究报告,因此需要从头优化多项式最适拟合阶次。据Pool等[20]分析,拟合多项式时并非阶次越高越好,高阶次多项式意味着计算量增加,同时估计值容易产生偏差。为了减少多项式拟合阶数,本研究做了两方面工作:差异化随机误差,也就是不同周龄对应不同的随机误差;删除只有1条蛋黄质量记录的个体,保证完整记录达到90%以上。以3阶Legendre多项式嵌入加性遗传效应,以2阶Legendre多项式嵌入永久环境效应,同时以2阶Legendre多项式嵌入固定效应,经过如此优化处理的模型得到的AIC值、BIC值最小,以此为最适模型。
3.3 遗传相关随测定间隔增加而降低遗传相关系数是衡量性状受间接选择影响程度的指标,系数越高表明主效基因之间连锁程度越紧密,或者存在一因多效。资源群体不同周龄蛋黄质量遗传相关系数较高,表明任一周龄蛋黄质量列入选育指标都将影响其他周龄蛋黄质量。与遗传相关系数相比,表型相关系数较低。据王富德等[21]结果,表型相关系数与遗传力的平方根有关。本研究中,不同周龄蛋黄质量遗传力为0.43~0.49,由此推知表型相关系数主要取决于环境相关系数。
遗传参数包括遗传力、重复力等,对于育种值估计以及选择方案评估具有重要意义。本研究应用随机回归模型分析了蛋黄质量遗传力和重复力,结果表明蛋黄质量加性遗传方差应嵌入3阶Legendre多项式,永久环境方差应嵌入2阶Legendre多项式,加性遗传方差随周龄增加而增加。本试验结果还表明随机回归模型柔韧性较好,适用于蛋黄质量遗传参数估算。
| [1] | Schaeffer L R. Application of random regression models in animal breeding[J]. Livestock Production Science,2004,86(1):35-45. |
| [2] | Jamrozik J,Schaeffer L R,Dekkers J C. Genetic evaluation of dairy cattle using test day yields and random regression model[J]. Journal of Dairy Science,1997,80(6):1217-1226. |
| [3] | Kirkpatrick M,Heckman N. A quantitative genetic model for growth,shape,reaction norms,and other infinite-dimensional characters[J]. Journal of Mathematical Biology,1989,27(4):429-450. |
| [4] | 赵福平,陈斌,彭慧珍,等. 用随机回归模型对湖南荷斯坦奶牛日产奶量进行协方差函数估计[J]. 畜牧兽医学报,2007,38(2):139-143. Zhao F P,Chen B,Peng H Z,et al. Estimating covariance functions for daily milk yields of holstein dairy cows in hunan using a random regression model[J]. Acta Veterinaria et Zootechnica Sinica,2007,38(2):139-143(in Chinese with English abstract). |
| [5] | 张健,卢金,杨润清. 基于随机回归模型估计奶牛产奶量的遗传参数[J]. 东北农业大学学报,2007,38(6):805-808. Zhang J,Lu J,Yang R Q. Estimation of genetic parameters for milk yield of cattle by random regression model[J]. Journal of Northeast Agricultural University,2007,38(6):805-808(in Chinese with English abstract). |
| [6] | Hill A T,Krueger W F,Quisenberry J H. A biometrical evaluation of component parts of eggs and their relationship to other economically important traits in a strain of White Leghorns[J]. Poultry Science,1966,45(6):1162-1185. |
| [7] | Rodda D D,Friars G W,Gavora J S,et al. Genetic parameter estimates and strain comparisons of egg compositional traits[J]. British Poultry Science,1977,18(4):459-473. |
| [8] | Zhang L C,Ning Z H,Xu G Y,et al. Heritabilities and genetic and phenotypic correlations of egg quality traits in brown-egg dwarf layers[J]. Poultry Science,2005,84(8):1209-1213. |
| [9] | Wolc A,Arango J,Settar P,et al. Genetic parameters of egg defects and egg quality in layer chickens[J]. Poultry Science,2012,91(6):1292-1298. |
| [10] | Hartmann C,Johansson K,Strandberg E,et al. One-generation divergent selection on large and small yolk proportions in a White Leghorn line[J]. British Poultry Science,2000,41(3):280-286. |
| [11] | Albuquerque L G,Meyer K. Estimates of covariance functions for growth from birth to 630 days of age in Nelore cattle[J]. Journal of Animal Science,2001,79(11):2776-2789. |
| [12] | Huisman A,Veerkamp R,van Arendonk J. Genetic parameters for various random regression models to describe the weight data of pigs[J]. Journal of Animal Science,2002,80(3):575-582. |
| [13] | Meyer K. WOMBAT:A tool for mixed model analyses in quantitative genetics by restricted maximum likelihood(REML)[J]. Journal of Zhejiang University Science B,2007,8(11):815-821. |
| [14] | Akaike H. A new look at the statistical model identification[C]//IEEE Transactions on Automatic Control,1974:716-723. |
| [15] | Jaffe W P. The relationships between egg weight and yolk weight[J]. British Poultry Science,1964,5(3):295-298. |
| [16] | Anang A,Mielenz N,Sch ler L. Monthly model for genetic evaluation of laying hens:Ⅱ. Random regression[J]. British Poultry Science,2002,43(3):384-390. |
| [17] | Wolc A,Arango J,Settar P,et al. Evaluation of egg production in layers using random regression models[J]. Poultry Science,2011,90(1):30-34. |
| [18] | Luo P T,Yang R Q,Yang N. Estimation of genetic parameters for cumulative egg numbers in a broiler dam line by using a random regression model[J]. Poultry Science,2007,86(1):30-36. |
| [19] | Farzin N,Torshizi R V,gerami A,et al. Estimates of genetic parameters for monthly egg production in a commercial female broiler line using random regression models[J]. Livestock Science,2013,153(1):33-38. |
| [20] | Pool M H,Janss L L G,Meuwissen T H E. Genetic parameters of Legendre polynomials for first parity lactation curves[J]. Journal of Dairy Science,2000,83(11):2640-2649. |
| [21] | 王富德,张世苹. 表型相关系数和遗传相关系数的计算和应用[J]. 辽宁农业科学,1982(1):20-25. Wang F D,Zhang S P. Estimation and application on phenotypic and genetic correlation coefficients[J]. Liaoning Agricultural Sciences,1982(1):20-25(in Chinese). |




