文章信息
- 姜春霞, 鲁植雄, 徐浩, 周晶, Willen B. Hoogmoed. 2015.
- JIANG Chunxia, LU Zhixiong, XU Hao, ZHOU Jing, Willen B.Hoogmoed. 2015.
- 农业土壤表面不平度分形维数计算方法的对比与分析
- Comparison of calculation methods of fractal dimension on agricultural soil surface roughness
- 南京农业大学学报, 38(1): 161-167
- Journal of Nanjing Agricultural University, 38(1): 161-167.
- http://dx.doi.org/10.7685/j.issn.1000-2030.2015.01.024
-
文章历史
- 收稿日期:2014-06-10
2. Farm Technology Group, Wageningen University and Research Centre, Wageningen 6700, The Netherlands
2. Farm Technology Group, Wageningen University and Research Centre, Wageningen 6700, The Netherlands
20世纪70年代,法国数学家Mandelbrot提出了分形理论(fractal theory)[1, 2, 3, 4, 5],用于研究不可求微分、形状不规则、具有粗糙表面的几何形体,而且一般用于研究非线性系统。分形理论被广泛应用于土壤科学研究中[6, 7],表征土壤中不规则、不稳定和具有高度复杂结构的特性,起到很好的效果。
土壤表面表征的结果是否有效与选择的分形维数计算方法是否合适有很大关系[8, 9]。目前,变差法、结构函数法、轮廓均方根法、R/S法和功率谱法等是计算土壤表面分形维数的主要方法,每种计算方法的应用特点与区域都不相同。如果所选的分形维数计算方法与实际分形集的类型不相符合,就会使所得到的分形维数计算值误差较大[10]。因此,选择合适的分形维数计算方法很重要。
本研究采用变差法、结构函数法和轮廓均方根法对4种常规耕作土壤地表进行分形维数的计算,以找出适合用来表征土壤表面不平度分形特性的方法。
1 材料与方法 1.1 测试土壤
为了得到真实有效的土壤表面不平度的数据,荷兰瓦赫宁根大学的土壤技术组成员在试验地进行了相关土壤表面不平度数据测量试验(鲁植雄教授当时在荷兰进修,参与此试验)。试验时间为2011年10月26日。所测量土壤属于壤质土。
1.2 测试方法
利用非接触式激光不平度测量仪测量土壤表面不平度,该仪器由荷兰瓦赫宁根大学制造。给测量仪一个测量基准,在不接触地面的情况下,可以测量激光头和地面的相对高度,从而得到土壤表面的粗糙程度。激光头扫描范围为1 m,每隔5 mm采样1次。试验测量了播种后地表(垂直于播种方向)、播种后地表(平行于播种方向)、犁地后地表(垂直于犁地方向)和整地后地表(平行于整地方向)4种常规耕作土壤的地面不平度。
1.3 测试仪器
非接触式地面不平度测量仪主要由激光传感器、电源、电机、水平尺、坦克链、控制箱、撑脚组成。用于测量各种路面和地面的不平度数据,其精度为5 mm,测量平面为1 m×50 cm。图 1为现场测量地表不平度。
 | 图 1 测量地表不平度 Fig. 1 Measuring the roughness of soil surface sowed |
非接触式地面不平度测量仪主要利用激光三角位移法来测量两点之间的距离(图 2),试验中就是基准和地面间的距离,把N个基准与地面的距离汇成图线就能得到地面的不平度曲线。
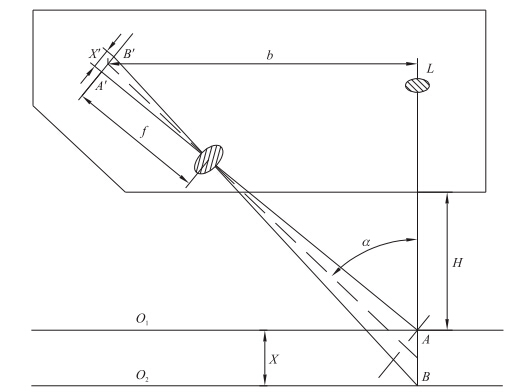 | 图 2 激光三角法测量位移系统原理图 Fig. 2 The measurement principle of the laser profilerL:光源Light source;O1:最高测量物体表面Highest measurement surfaces;O2:最低测量物体表面Minimum measurement surfaces;A:光束投射到最高测量物体表面的点Point where the light beam hits the surface of the measured object;A′:光束投射到O1面,通过透镜反射到探测器上的点Point where the scattered light reflection of surface O1 is focussed through the lens on the detector;B:光束投射到最低测量物体表面的点Point where light beam hits the guage probe;B′:光束投射到O2面,通过透镜反射到探测器上的点Point where the scattered light reflection of surface O2 is focussed through the lens on the detector; f:透镜到探测器之间的距离Focal distance of a lens in front of the detector;H:探针的最低点到测量中心点的距离Standoff distance from lower edge of the gauge probe to the middle of the measurement range;X:A点到B点的距离Distance from A to B;X′:A′点到B′点的距离Distance from A′to B′;α:光束和探测器光轴间的夹角Angle between the light beam and the optical axis of the detector;B:光束到探测器间的距离Distance between light source and detector |
从光源L发出一束光束到达测量物体O1表面,光束与被测物体相交于A点,再通过透镜反射到探测器上,与探测器交于A′点。如果被测物体下降距离X,光束将到达O2表面,交于B点,通过透镜反射到探测器上,与探测器交于B′点,A′与B′之间的距离为X′。X和X′之间的关系是由光源和探测器之间的布置决定的。如果透镜和探测器之间是机械连接,那么X和X′之间的关系已知,可以用于线性测量[11, 12, 13]。 1.4 分形维数的计算方法
目前,变差法、结构函数法、轮廓均方根法、R/S法和功率谱法等是计算土壤表面分形维数的主要方法。其中:R/S法虽然在双对数坐标上的标度律直线关系较好,但其计算的分形维数值小于1,因此不能用于路面分形维数的计算[14];功率谱法在计算工程表面粗糙曲线的分形维数时,其线性关系不明显,计算精度较低[15]。所以选用变差法、结构函数法、轮廓均方根法作为本文分形维数的计算方法。 1.4.1 变差法
变差法[16]的主要计算原理是:假设把宽为R的矩形(盒子)覆盖到曲线上,矩形的高等于框内曲线的峰值减去谷值,逐步平移矩形直到分形图线全部被矩形遍及,将每次矩形的宽乘以高就得到每个矩形的面积S,再将所有的矩形面积相加就能得到总的矩形面积S(R),改变矩形宽度R的大小并重复以上操作,得到一系列S(R)。操作时应该注意保证矩形经过的范围要远远大于R,将S(R)和R2相除可以得到R区间内曲线的斜率(N):

变差法在D<1.4时有较高精度,变差法适合于分析维数小于1.4的轮廓曲线。 1.4.2 结构函数法
结构函数法[17]将表面粗糙程度形成的曲线当作时间序列Z(x),那么具有分形特性的时间序列能使其采样数据的结构函数满足:
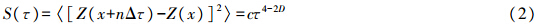
t和S(τ)一一对应,改变t,S(τ)也相应改变。对于分形曲线,t与S(τ)的关系可表示为:

分形维数(D)与斜率(W)存在如下关系:

在计算表面轮廓分形维数时,相比于其他方法,结构函数法计算的分形维数偏差最小,是目前进行表面轮廓分形维数计算的一种可行方法[18]。在计算磨损表面的轮廓曲线分形维数时也可以使用结构函数法[19]。 1.4.3 均方根法
选取一个取样长度,对于所要分形的曲线,它的曲线高度均方根为:

对上式进行对数运算,便有如下直线方程形式,即

从式(6)中不难看出,如果曲线合适,那么曲线在双对数坐标上呈现了测度与尺度的线性关系,这时可以得到分形维数同直线斜率(k)的关系为D=2-k。
若用于机加工粗糙表面,均方根法[20, 21, 22]具有较强的适应能力、宽而稳定的无标度区间,以及较好的表征效果。另外,均方根法在分形维数时,它有着明确的物理意义,而且计算方法比其他几种计算方法简单直观。此外,均方根法计算分形维数时还能表征地面不平度纵断面表面的复杂程度以及地面的复杂程度。
2 结果与分析 2.1 土壤表面不平度测试结果
图 3为4种常规耕作方式的地表不平度,每种地表的测量长度为20 m,每隔5 mm采样1次,可以得到4 000个数据。
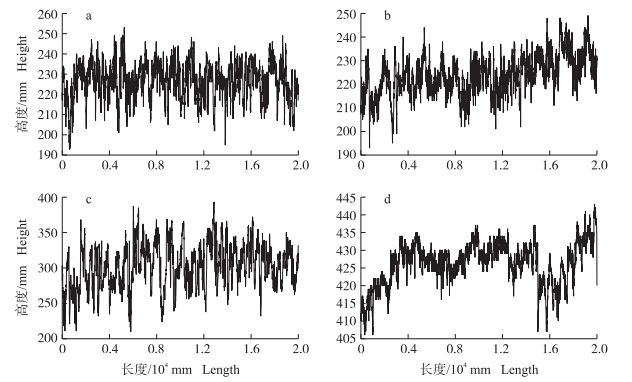 | 图 3 4种耕作方式的土壤表面不平度曲线 Fig. 3 Soil surface roughness of 4 kinds of tillagesa.播种后地表(垂直于播种方向)Sowed surface(perpendicular to the sowed direction);b.播种后地表(平行于播种方向)Sowed surface(along with the sowed direction);c.犁地后地表(垂直于犁地方向)Ploughed surface(perpendicular to the ploughed direction);d.整地后地表(平行于整地方向)Rolled surface(along with the rolled direction) |
传统参数在描述表面不平度时具有一定的局限性,很难用这些传统参数建立的各种模型来反映土壤的实际情况,而分形维数[23]可以用来表征物体表面的不规则和复杂的程度,通过计算土壤表面的分形维数可以得到该种土壤的表面结构,表征土壤的实际表面。通过Matlab编程,利用变差法、结构函数法和均方根法对播种后地表(垂直于播种方向)、播种后地表(平行于播种方向)、犁地后地表(垂直于犁地方向)和整地后地表(平行于整地方向)进行了分形维数的计算。
从图 4可以得出:变差法、结构函数法和均方根法计算4种常规耕作地面所得到的分形维数D在1~2之间,符合分形维数的合理数值区间。平行于耕作方向的地表分形维数大于垂直于耕作方向的地表的分形维数,说明平行于耕作方向的地表起伏小,有着微小而又复杂的表面结构。理论上犁地后地表土块比播种后地表及整地后地表土块大,从图 4中可以看出,犁地后地表的分形维数最小,正好说明了这个问题。
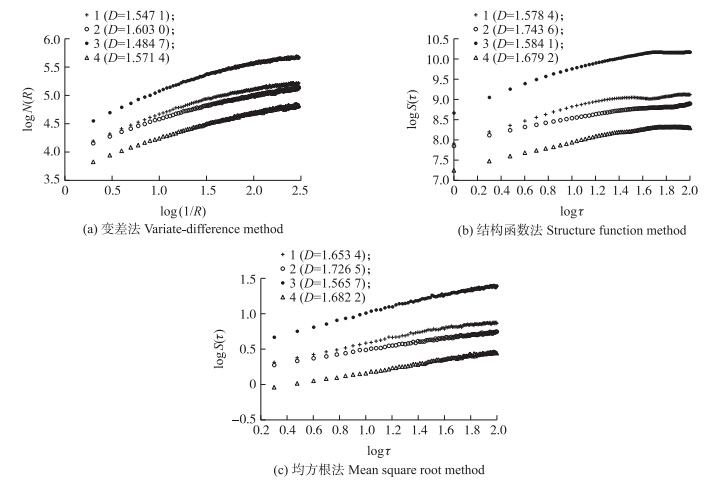 | 图 4 4种土壤在不同计算方法下的表面分形维数 Fig. 4 Surface fractal dimension in different calculation methods for 4 kind of soil roughness1.播种后地表(垂直于播种方向)Sowed surface(perpendicular to the sowed direction);2.播种后地表(平行于播种方向)Sowed surface(along with the sowed direction);3.犁地后地表(垂直于犁地方向)Ploughed surface(perpendicular to the ploughed direction);4.整地后地表(平行于整地方向)Rolled surface(along with the rolled direction) |
此外,由图 4可知:在双对数坐标图中,某一区间内为直线,当横坐标增大时,直线的线性关系变差,最后不再满足线性关系。可以得出土壤表面不平度曲线并不是规则分形,而存在无标度区间。因此,对于土壤表面进行分形研究前,应首先确定无标度区间。在双对数坐标图中,均方根法的直线区间大,也就是无标度区间宽,能很好地适应土壤表面的分形特性,同时在以后的工作中,获得同样结果的条件下能够减少工作量和工作时间。
2.3 无标度区间计算结果
地面是属于自然界大量存在的随机分形系统的一种,不像数学上的分形,具有在无穷尺度上的自相似或自仿射性,而是近似地或统计意义上存在自相似,这种自相似仅存在于一定的尺度变化范围,一旦超出了这个尺度变化范围,其自相似性就不复存在,这个尺度变化范围就是分形的无标度区。无标度区间是分形的一个重要限定,在计算分形维数时,确定土壤的无标度区间是精确计算分形维数的重要保证。本文利用相关系数检验法计算无标度区间,计算中相关系数都大于95%(表 1),这样能确保计算得到的无标度区间有效且精确。
| 计算方法 Calculation method | 播种(垂直) Sowed surface (vertical) | 播种(平行) Sowed surface (parallel) | 犁地(垂直) Ploughed surface (vertical) | 整地(平行) Rolled surface (parallel) | |
| 变差法 Variate-difference method | 无标度区间 Non-scale range | [1,131] | [1,185] | [1,123] | [1,178] |
| 相关系数 Correlation coefficient | 0.984 8 | 0.987 0 | 0.987 4 | 0.990 1 | |
| 结构函数法 Structure function method | 无标度区间 Non-scale range | [1,99] | [1,45] | [1,38] | [1,48] |
| 相关系数 Correlation coefficient | 0.996 8 | 0.986 1 | 0.986 3 | 0.991 8 | |
| 均方根法 Mean square root method | 无标度区间 Non-scale range | [1,68] | [1,68] | [1,68] | [1,68] |
| 相关系数 Correlation coefficient | 0.993 5 | 0.996 2 | 0.995 6 | 0.998 9 | |
由表 1可知:3种方法进行线性回归的相关系数都大于0.98,变差法和结构函数法的无标度区间在4种不同耕作方式下很不相同,而且变化大,所以很不稳定;而均方根法的无标度区间在4种耕作方式下均没变,比较稳定,均方根法线性回归的相关系数较大。
3 结论
常规耕作土壤表面不平度的分形维数的合理数值为1~2,文中采用的变差法、结构函数法以及均方根法计算得到的分形维数都在此区间内,但每一种方法计算的数值及精度却不一样。综合而言,均方根法在计算耕作土壤表面的分形维数时有着较高的精度,而且不同的耕作方式下,计算得到的无标度区间较稳定。
播种后地表(平行于播种方向)的分形维数大于播种后地表(垂直于播种方向)的分形维数。这表明前者起伏小,但复杂程度高;后者起伏大,但复杂程度低。形成这种结果的原因是为了利于种子成长,平行于播种方向的土壤相对平坦,但是土壤细碎;而对于两个播种行的间隔处的土壤要求相对较低,间隔处土壤颗粒大而又有着相对大的起伏。从图表也可以看出,犁地后地表的分形维数相对较小,因为犁地的主要作用是松土,对于土壤颗粒大小及起伏程度没有要求;播种后地表的分形维数较大,因为种子的成长需要土壤松软平坦。
| [1] | Mandelbrot B B. The Fractal Geometry of Nature[M]. San Francisco:Freeman,1982:150-154 |
| [2] | Michael F B. Fractals Everywhere[M]. 2nd ed. Boston:Academic Press,1993:254-270 |
| [3] | 孙洪泉. 分形几何与分形插值[M]. 北京:科学出版社,2011:10-13 [Sun H Q. Fractal Geometry and Fractal Interpolation[M]. Beijing:Science Press,2011:10-13(in Chinese)] |
| [4] | Huang Y M,Chen C J. 3D Fractal reconstruction of terrain profile data based on digital elevation model[J]. Chaos,Solitons and Fractals,2009,40(4):1741-1749 |
| [5] | 丁俊,孙洪泉. 优化分形维数计算方法[J]. 四川建筑科学研究,2011,37(5):54-56,69 [Ding J,Sun H Q. The optimum analysis on determination methods of fractal dimension[J]. Sichuan Building Science,2011,37(5):54-56,69(in Chinese with English abstract)] |
| [6] | 蔡新民,丁新新,潘健,等. 分形理论在土壤科学研究中的应用[J]. 防护林科技,2011(6):8-13 [Cai X M,Ding X X,Pan J,et al. Application of fractal theory in soil science[J]. Protection Forest Science and Technology,2011(6):8-13(in Chinese with English abstract)] |
| [7] | Cheng Z H,Zhang J B,Zhu A N. Introducing fractal dimension to estimation of soil sensitivity to preferential flow[J]. Pedosphere,2002,12(3):201-206 |
| [8] | 母少东,蒋光华,李浩,等. 不同植烟区土壤对烟叶碳氮代谢品质相关指标的影响[J]. 南京农业大学学报,2014,37(4):109-116. doi:10.7685/j.issn.1000-2030.2014.04.016 [Mu S D,Jiang G H,Li H,et al. Effects of different planting tobacco soils on carbon and nitrogen metabolism indexes related to quality of tobacco leaves[J]. Journal of Nanjing Agricultural University,2014,37(4):109-116(in Chinese with English abstract)] |
| [9] | 南江宽,陈效民,王晓洋,等. 石膏与肥料配施对滨海盐土降盐抑碱的效果研究[J]. 南京农业大学学报,2014,37(4):103-108. doi:10.7685/j.issn.1000-2030.2014.04.015 [Nan J K,Chen X M,Wang X Y,et al. Effects of gypsum and fertilizers amendment on reducing salinity and preventing alkalization of coastal saline soil[J]. Journal of Nanjing Agricultural University,2014,37(4):103-108(in Chinese with English abstract)] |
| [10] | 朱华,葛世荣. 结构函数与均方根分形表征效果的比较[J]. 中国矿业大学学报,2004,33(4):396-399 [Zhu H,Ge S R. Comparison of fractal characterization effects of structure function and mean square root[J]. Journal of China University of Mining Technology,2004,33(4):396-399(in Chinese with English abstract)] |
| [11] | Lu Z X,Nan C,Perdok U D,et al. Characterisation of soil profile roughness[J]. Biosystems Engineering,2005,91(3):369-377 |
| [12] | 蔡祥,孙宇瑞,林剑辉,等. 基于激光反射的土壤表面粗糙度测量装置设计与试验[J]. 农业机械学报,2010,41(1):68-71 [Cai X,Sun Y R,Lin J H,et al. Design of a laser scanner for characterizing soil surface roughness[J]. Transactions of the Chinese Society for Agricultural Machinery,2010,41(1):68-71(in Chinese with English abstract)] |
| [13] | 黄战华,罗曾,李莎,等. 激光三角法大量程小夹角位移测量系统的标定方法研究[J]. 光电工程,2012,39(7):26-30 [Huang Z H,Luo Z,Li S,et al. Calibration method of large-arrange small-angle laser triangulation measuring system[J]. Opto-Electronic Engineering,2012,39(7):26-30(in Chinese with English abstract)] |
| [14] | 赵兰英. 基于分形理论的路面不平度分级与模拟研究[D]. 南京:南京农业大学,2009 [Zhao L Y. Study of road surface roughness grade and simulation based on fractal theory[D]. Nanjing:Nanjing Agricultural University,2009(in Chinese with English abstract)] |
| [15] | 李志强,马吉胜,李伟. 频谱法计算路面不平度分形维数的方法[J]. 军械工程学院学报,2009,21(2):41-44 [Li Z Q,Ma J S,Li W. The method of computing road roughness fractal dimension by frequency-spectrum method[J]. Journal of Ordnance Engineering College,2009,21(2):41-44(in Chinese with English abstract)] |
| [16] | Zallen R. The Physics of Amorphous Solids[M]. New York:John Wiley & Sons,1983:80-85 |
| [17] | He L,Zhu J. The fractal character of processed metal surfaces[J]. Wear,1997,208(1/2):17-24 |
| [18] | 王建军,魏宗信. 粗糙表面轮廓分形维数的计算方法[J]. 工具技术,2006,40(8):73-75 [Wang J J,Wei Z X. Computation method for fractal dimension of rough surface profile[J]. Tool Engineering,2006,40(8):73-75(in Chinese with English abstract)] |
| [19] | 周新聪,萧汉梁,严新平,等. 磨损表面轮廓曲线分形维数的计算方法[J]. 武汉理工大学学报:交通科学与工程版,2001,25(4):419-421 [Zhou X C,Xiao H L,Yan X P,et al. Calculation of the fractal dimension of wear surface profiles[J]. Journal of Wuhan University of Technology:Transportation Science & Engineering Edition,2001,25(4):419-421(in Chinese with English abstract)] |
| [20] | 侯占峰,李林,陈智,等. 土壤表面分形表征效果对比[J]. 农业机械学报,2011,42(4):39-42 [Hou Z F,Li L,Chen Z,et al. Effects comparison on fractal characterization for soil surface roughness[J]. Transactions of the Chinese Society for Agricultural Machinery,2011,42(4):39-42(in Chinese with English abstract)] |
| [21] | Gadelmawla E S,Koura M M,Maksoud T M A,et al. Roughness parameters[J]. Journal of Materials Processing Technology,2002,123(1):133-145 |
| [22] | 梁俊,蒋金龙,赵雪莲,等. 随机中点位移法在三维地形插值显示的适用性分析[J]. 测绘科学,2007,32(3):44-46 [Liang J,Jiang J L,Zhao X L,et al. The applicability analysis of MPD method in 3D terrain interpolation[J]. Science of Surveying and Mapping,2007,32(3):44-46(in Chinese with English abstract)] |
| [23] | 鲁涛,赵雁,欧阳的华. 含能材料表面分形维数计算及其对摩擦感度影响[J]. 计算机与应用化学,2014,31(2):226-230 [Lu T,Zhao Y,Ouyang D H. Estimation of surface fractal dimension of energetic materials and influence on friction sensitivity[J]. Computers and Applied Chemistry,2014,31(2):226-230(in Chinese with English abstract)] |




