2.深海载人装备国家重点实验室, 江苏无锡 214082;
3.船舶振动噪声重点实验室, 江苏无锡 214082
2.State Key Laboratory of Deep-sea Manned Vehicles, Wuxi 214082, Jiangsu, China;
3.National Key Laboratory on Ship Vibration and Noise, Wuxi 214082, Jiangsu, China
结构与水介质的耦合动力学理论将结构与周围流场作为一个统一的系统, 分析两者的动力学行为, 又可称为“水弹性力学”. Heller和Abramson (1959)给出了水弹性力学的一般定义: “水弹性力学是研究惯性力、水动力和弹性力之间相互作用现象的学科. ”它与刚体流固耦合作用分析的根本区别在于结构内力参与了惯性力与水动力的相互作用.船舶水弹性力学(hydroelasticity of ships) 是它的一个重要分支.
按激励源进行分类, 船舶结构与水介质耦合动力学, 亦即船舶水弹性力学的第一个主要研究范畴是流场环境因素(波浪、砰击、甲板上浪、液体晃荡、涡流扰动、水下爆炸及声波等) 引起的航行船舶、驻留浮体或其他类型海洋结构物的稳态、瞬态和随机动响应(包括刚体运动、结构强迫动变形、振动与噪声等) 以及波浪绕射或目标声散射; 第二个主要研究范畴是在非流场环境因素(如机械设备与推进器) 激励下, 由船舶或海洋结构物运动与动变形引起的周边水体的运动与波浪, 或水中声辐射.
这两个研究范畴所包涵的内容非常丰富.按问题所涉及的流场波动特性的不同, 在分析中可把水介质处理成不可压缩流场和可压缩声介质两大类.如重点关注的研究对象是重力波(水面波或水下内波) 的稳态激励(即波浪激励) 或瞬态激励(如砰击、甲板上浪、液体晃荡、涡流扰动激励等) 引起的船舶与局部结构动响应, 因与波浪频率相应的水中声波的波长远大于船舶及其运动的特征尺度, 只要没有产生激波或相变, 流场介质的密度变化甚小, 可忽略水的可压缩性对船体结构所受水动力的影响.如关注的重点不是重力波效应, 而是强压缩波(如水下爆炸冲击波) 或弱压缩波(声波) 与船舶结构的相互作用, 或者关注伴有空泡生成和演化的流场与结构相互作用问题, 则必须考虑水的可压缩性.针对强压缩波、弱压缩波以及是否产生空泡的不同情况, 相应流场的理论表述方法不同.本文不讨论水下爆炸冲击波或空泡与结构物相互作用的理论与分析方法, 讨论的内容限于声波, 即弱压缩波的范畴.这就涉及结构与水介质耦合动力学的两个主要研究分支--分析不可压缩流场中波浪激励下结构动响应的船舶水弹性力学和分析可压缩流场中结构声学效应的船舶水弹性力学.后者又称为船舶声弹性力学.
如果下一个定义, 船舶声弹性力学是“研究惯性力、水中声压和结构弹性力之间相互作用现象的学科”.水中船舶声弹性力学问题的激励源可以是声波激励、船舶机械激励、推进器激励及流场激励等, 研究频率范围的跨度从几赫兹到几万赫兹.在声弹性问题中, 频率较高时, 船体振动的特征长度将接近或者小于水中声波波长, 此时水的可压缩性将对船体振动产生影响, 必须将水看成可压缩声介质; 在几赫兹或者十几赫兹的低频域, 虽然水的可压缩性对船体振动的影响较小, 但船体振动引起水介质的微幅振动将以声波的形式传递到远处, 此时也需要考虑水介质的可压缩性.
近年, Zou等(2010)与邹明松(2014)以Wu (1984)建立的带航速三维水弹性力学理论为基础, 继承了经典三维水弹性力学流固耦合边界条件及数值计算处理方法, 建立了可压缩声介质中的流固耦合运动方程, 形成了一套与波浪中船舶耐波性理论与水弹性力学理论一脉相承、可用于解决复杂船舶结构低中频段振动、声辐射与声散射问题的船舶三维声弹性理论.
船舶水弹性、声弹性力学是相互影响、协同发展的.本文从不同的工程应用背景出发, 从理论、工程应用等方面对不可压缩流场中的三维船舶水弹性力学和可压缩流场中的船舶声弹性力学的发展进行系统综述.关于船舶力学更广泛研究领域的综述可参见《世纪之交的船舶力学》 (吴有生1999) 和《船舶结构耦合动力学问题》 (吴有生等2007).
2 不可压缩流场中波激动响应分析的船舶三维水弹性力学研究 2.1 船舶三维线性水弹性力学研究线性水弹性力学理论假定流体为均质、无黏、无旋的不可压理想流体, 结构是线弹性的, 流场的扰动及结构相对平衡位置的非定常运动与动变形是微幅的.
20世纪70年代, 首先诞生了船舶二维线性水弹性力学理论(Bishop & Price 1979), 其核心是将船体结构简化为非均匀Euler梁或Timoshenko梁, 将从耐波性理论中发展起来的二维切片理论(Salvesen et al. 1970) 引入流体与结构耦合动响应分析中, 亦即将船舶周围流场的运动简化为与船体纵轴垂直的平面内的二维流动, 忽略沿船体纵向分布的水动力之间的相互干扰.此后, 船舶二维线性与非线性水弹性力学理论获得了迅速而广泛的发展(Bishop et al. 1980, Belik et al. 1980, Temarel 1980, Che et al. 1992, 夏锦祝1994).由于二维线性水弹性理论具有建模简便、计算效率高的特点, 能基本满足细长型船舶运动与受力特性的分析需求, 从20世纪70年代末至21世纪初, 得到了广泛的应用(Bishop et al. 1991, 董艳秋等1989, 王振鸿等1999).
2.1.1 频域分析方法二维线性水弹性力学理论仅适用于细长型船体, 不能计及船体端部的三维效应, 也不能用于任意形状的非细长船舶与浮式海洋工程结构物. 20世纪80年代, Wu (1984)、Price和Wu (1984)及Bishop等(1986)将三维船舶运动势流理论(Newman 1978) 与三维弹性结构动力学理论相结合, 建立了适用于波浪中任意形状三维弹性浮体承受内、外激励时动响应分析的三维线性水弹性力学理论, 给出了可变形弹性结构周边流场的附加质量、附加阻尼、流体恢复力系数及波浪激励力的广义表达形式, 并严格地证明了在水中可变形体湿表面流场法向速度应满足的广义流固界面条件(Price-Wu边界条件, 见式(1)).该广义流固界面条件决定了船体湿表面的流场非定常速度势与弹性船体结构动位移和角位移(包括刚体运动与结构动变形) 及船舶恒速航行时物面的定常流动速度分量之间的关系; 当物体为仅有六个运动自由度的刚体时, 即简化为Newman界面条件(Newman 1978). 夏锦祝和吴有生(1993)进一步给出了计及弹性体表面应变张量影响的流固耦合界面条件的一般形式.当弹性体表面无切向外力(亦即不计流体的黏性效应) 时, 该条件即为Price-Wu边界条件
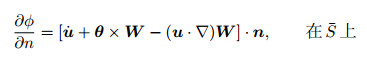
|
(1) |
式中, ϕ为船体的流场激励及由各类激励引起的非定常速度势; n={nx, ny, nz}为船体湿表面上指向流场的单位法向矢量; u={u, v, w}和θ={θx, θy, θz}分别为船体动响应(包括刚体运动与动变形) 引起的线位移矢量和角位移矢量, 它们是位置与时间的函数; W为初始静止的水域中, 以恒定速度U随物体做直线运动的平衡坐标系内物体表面的非均匀定常流场速度矢量; S表示船体平均湿表面.当物体为仅有六个运动自由度的刚体时, 该式即简化为与Newman界面条件相同的形式(Newman 1978).
Price和Wu (1989)进一步引入了Morison近似修正, 在用三维水弹性力学理论分析船舶横摇运动与结构动响应时, 能近似考虑流体黏性带来的附加水动力阻尼的影响. 杜双兴(1990)发展了零航速三维脉动源Green函数快速计算方法, 提高了三维水弹性力学计算分析方法的实用性.为提高三维水弹性力学方法与软件在大型与极大型浮体分析中的实用性, 针对诸多浮体结构具有前后及左右舷对称性的特点, Wu等(1991)提出了水弹性数值计算的双重复合奇点分布方法, 极大地减少了计算量, 成为海上极大型浮动结构物概念设计(Wu et al. 1993, Riggs & Ertekin 1991, Wang et al. 1991, Du & Ertekin 1991, 王志军2001) 的有效工具.
在三维水弹性计算分析中, 针对零航速浮体及低速细长船体, 可引入细长体、扁体或薄体假设, 采用不计航速的脉动源格林函数, 并不计船体航行引起的定常流场对流固耦合动响应的影响, 简化计算方法, 提高计算效率.但这一简化算法不适用于波浪中航行的非细长与非扁薄的船舶与海洋浮体, 也不适用于中高航速的情况.为此, 杜双兴(1996)发展了Bessho型移动脉动源Green函数(Bessho 1977) 的快速算法(杜双兴和吴有生1998) 及由航速引起的非均匀定常流场在船体湿表面上速度分布的计算方法, 从而将广义水弹性力学理论(Wu 1984) 中所有与航速有关的项保留在数值计算分析中, 建立了较为完善的三维航行船体线性水弹性力学频域分析理论的数值计算方法.在理论上, 可不受浮体细长比的限制, 扩大航速范围, 更合理地进行频域内排水型航行船体的水弹性响应分析.应用与试验比较表明, 在船舶结构外载荷与动变形分析所关注的频率范围内, 该方法给出的结果合理可用; 但由于Green函数在水线附近的奇异性, 在有些频率上的计算结果需要进一步修正与校验.
为验证船舶三维水弹性力学理论及数值计算方法, 1989年以来, 中国船舶科学研究中心(CSSRC) 在吴有生院士的倡导和主持下, 开展了除水动力外形、船体质量惯量分布与总体结构弯扭刚度分布相似以外, 船体关键部位结构刚度也相似的“整体弹性材料缩比船模”的制造及波浪中动响应的试验技术研究. 林吉如等(1992)对有机玻璃、聚乙烯及ABS等的物理特性进行了各种试验, 证实了精心选择的ABS在弹性模量、泊松比、线弹性范围、蠕变性能、反复加载与温度变化情况下机械性能的稳定性及加温成形性能等方面能够满足制作缩比薄壁结构船模所必需的“刚度相似”的基本要求.继而在CSSRC完成了S175船、驱逐舰与小水线面双体船等多艘缩比弹性材料船模的水池试验研究(图 1), 获得了缩比薄壁船体船模在规则与非规则波中运动与结构动应变的数据, 验证了理论与数值计算方法的合理性与适用性(Wu et al. 2003).

|
| 图 1 整体弹性材料船模的水池试验照片(CSSRC). (a) S175船型的船模试验, (b) 一艘驱逐舰的船模试验 |
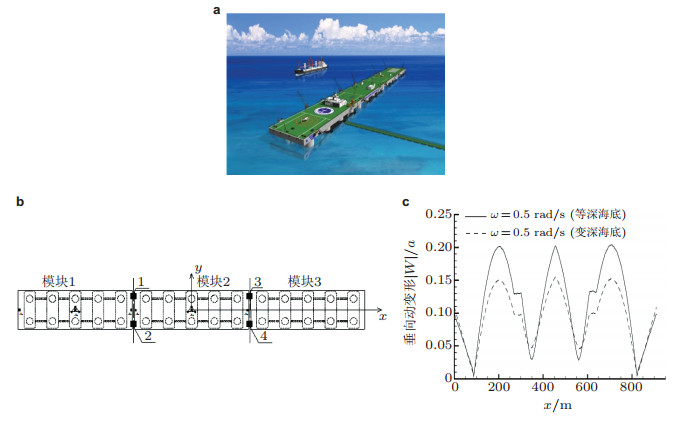
三维频域线性水弹性力学理论及计算方法能对任意形状弹性浮体的载荷、运动、变形和内力作统一的分析, 近三十年来不断发展, 并获得了广泛的应用. Lundgren等(1988)、杜双兴等(1993)分析了浮船坞在波浪中拖航时的动响应及发生海损事故的原因. Price和Wu (1985)、Wu (1984)、Kean等(1991)、叶永林等(2010)分析了在波浪中航行的小水线面双体船的动应力. 谢永和等(2006)、Xie和Li (2006)开发了有限水深环境中的三维频域线性水弹性力学计算方法及计算程序, 对一艘300000 DWT FPSO在特定水深海况下的运动与波浪载荷响应进行评估, 发现浅水效应对载荷的预报结果具有明显影响. Yang等(2015)分析了尺度为3 ×300m的多模块柔性连接超大型浮动平台在波浪激励下的结构动响应, 比较了平坦海底及近岸海底地形变化的不同环境对结构动响应的影响, 如图 2所示.
|
| 图 2 (a) 典型超大型浮动平台三维效果图, (b) 3个300m长半潜式模块柔性连接的超大型浮动平台示意图, (c) 等深海底与变深海底环境中0度浪向规则波作用下平台垂向动变形幅值沿全长分布的比较(Yang et al. 2015) |
王大云(1996)、Wang和Wu (1998)采用三维线性时域Green函数, 结合Price-Wu流固交界面条件, 给出了围绕弹性浮体的三维势流时域积分方程, 导出了弹性浮体的广义时域水动力系数表达式, 建立了船舶结构在波浪中受力、运动和变形的三维线性水弹性力学时域分析理论.在数值计算中引入了时变问题的Hamilton精细积分算法, 提高了计算的效率和精度.
Kim等(2012)采用有限元方法处理三维浮体结构, 用B样条Rankine湿面元方法处理浮体周围流场的运动, 通过隐式迭代实现时域内的流固耦合求解, 通过数值算例和试验结果验证了计算方法的正确性, 并计算分析了一艘大型集装箱船在顶浪状态下的结构动应力.
2.2 船舶三维非线性水弹性力学研究概况线性水弹性理论仅适用于小波陡以及船体作微幅运动和变形的情况.在实船与模型试验中经常会发现, 高海情环境中船舶的波浪载荷与运动存在较明显的非线性现象.对此, 线性理论不能给出准确的结果.
在应用需求牵引下, 二维与三维非线性水弹性力学理论应运而生. Yamamoto等(1978)较早地基于切片理论, 在计算流体外力时计及瞬时湿表面的影响, 开展了二维非线性水弹性理论的研究.此后, 不同程度地考虑水动力与结构的非线性因素, 先后出现了多种二维非线性水弹性力学理论, 并开展了具体的应用研究(顾懋祥等1987, Gu et al. 1989, 吴有生等1994, 夏锦祝1994, 宋竞正等1995, 徐向东1996, Wu & Moan 1996, Xia et al. 1998, 朱克强等2005).
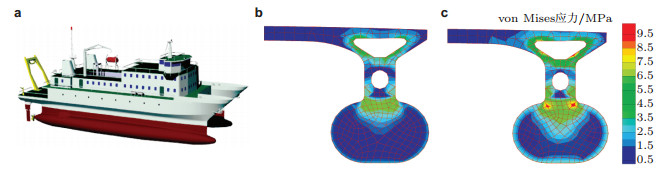
与二维线性水弹性力学理论相似, 二维非线性水弹性力学理论也仅适用于细长型船体. Wu等(1997)提出了三维二阶船舶非线性水弹性力学理论.该理论计及一阶速度势及一阶运动与变形响应对二阶流场作用力与二阶结构响应的贡献, 考虑了高海情条件下船体大幅运动、大角度刚体转动和瞬时湿表面变化对航行船舶的流体作用力与结构动响应的影响. 陈徐均(2001)、Chen等(2003)基于该理论, 建立了零航速系泊浮体的三维二阶水弹性力学计算方法和计算程序, 对系泊浮式箱梁的二阶波浪载荷与非线性结构动响应进行了数值分析, 并讨论了二阶力对总响应的贡献以及和频与差频响应对总响应的影响.田超(2007) 建立了带有该非线性理论中全部航速项的数值计算方法, 与计及航速影响与非均匀定常兴波流场影响、较为严格的一阶速度势及一阶运动与变形响应的线性水弹性力学分析方法结合起来, 给出了较为完整的航行浮体三维二阶非线性水弹性力学数值分析方法和计算程序. Tian和Wu (2006)应用该程序分析比较了不规则波中迎浪航行的小水线面双体船的三维线性与非线性水弹性响应, 结果表明, 非线性应力和变形的预报结果较线性预报结果大20%~30%;与其他各种非线性水动力相比, 瞬时湿表面变化引起的非线性作用力的贡献相对较大. Wu等(2007)应用该程序成功预报了一艘以设计航速(12节) 在生存海况中航行的1 500 t级小水线面双体船的运动、结构载荷与应力(见图 3), 并与船模试验结果相互印证, 为该船的结构设计提供了依据. Tian等(2009)分析了以15 km/h航速在规则与非规则波中迎浪航行的一艘1.8 × 105 t散货船的线性与非线性波激振动. Hu等(2012)则用上述三维二阶非线性水弹性力学方法进行了一艘5.0×105 t矿砂船由波浪和波激振动引起的载荷的短期与长期预报, 与模型试验结果进行了比较, 并分析了在三条航线上该船结构的疲劳累计损伤特性.
|
| 图 3 船舶以12节航速迎浪航行, 不规则波海况为H1/3=3.25 m, T01=7.53 s (田超2007). (a) 1 500 t SWATH海洋调查船, (b) 横舱壁上von Mises应力分布的线性解, (c) 横舱壁上von Mises应力分布的考虑瞬时湿表面变化的非线性解 |
船舶结构声弹性力学的主要应用领域是弹性浮体与水介质的耦合振动及由此引起的声辐射、声散射和声传播问题.声辐射问题主要是研究船舶结构受激振动向水中辐射声波, 声波在水域环境中传播的现象.声散射问题主要是研究主动声波作用到船体上引起散射声波, 散射声波在水域中传播的现象.这两类声弹性问题都具有明确的工程应用背景, 近几十年来国内外在该领域的研究异常活跃.为便于表述、阐明相互之间的关系与发展过程, 下面从规则结构声弹性问题的解析方法、任意结构声弹性问题的数值分析方法、海洋环境中的浮体结构声弹性研究以及计算与试验技术四个方面, 对声弹性力学的相关研究进展做简要的回顾.实际上这四个方面是相互联系、相互交叉的.
3.1 规则结构声弹性问题的解析方法采用解析方法研究规则结构的声弹性问题发展于20世纪50年代, 主要涉及到平板、加筋平板、球壳、圆柱壳、加筋单双层圆柱壳等多类结构形式, 相关研究由简到繁逐步发展.由于解析方法计算效率高、物理概念清晰, 便于揭示基本规律和机理, 解析计算结果又可用作为各种数值算法的考核基准, 半个世纪以来受到了国内外学者的关注, 出现了大量论文著作.
3.1.1 与声辐射相关的研究Junger和Feit (1986)论述了多种规则弹性结构(包括无限大平板、矩形平板、薄球壳、无限长圆柱壳、两端简支圆柱壳、两端自由圆柱壳) 在均匀声介质中的耦合振动和声辐射问题, 并借助解析计算深入分析了相应的基本规律和机理. Skelton和James (1997)计算了单方向双周期加筋无限大平板的流固耦合振动及声辐射, 并与无限大光板的声辐射进行比对, 分析了加筋的影响; 还推导了无限大正交加筋平板、带有点接触附连物(如集中质量、弹簧、质量-弹簧) 的平板、多层球壳、多层平板、多层圆筒等模型的流固耦合振动与声辐射的解析解. Fahy和Gardonio (2007)对梁和平板弯曲波的频散现象进行了分析, 解释了吻合频率的概念; 在波数域内对矩形平板振动形态进行分解, 从声辐射角度说明了平板振动模态中边模态和角模态的物理意义; 并针对圆柱壳体, 详细分析了其振动形态、各阶模态声阻抗及对应的声辐射特征. 何祚镛(2001)收录了包括柔软弦、薄板、带周期栅的膜、周期支撑固定的薄板、周期加筋薄板、球壳、圆柱壳与加肋圆柱壳在内的规则结构的流固耦合振动和声辐射的解析计算模型.该专著中很多资料来源于20世纪80年代何祚镛教授的授课讲义, 反映了当时国内的研究成果.
在规则结构声弹性研究领域, 从用于机理分析的简单规则结构, 到反映潜艇结构主要特征的复杂圆柱壳结构, 先后发展了多种分析方法. Burroughs (1984)利用环形肋骨的空间周期性, 结合Possion求和公式, 建立了双周期环向加肋无限长圆柱壳的声辐射模型.陈越澎(1999) 建立了环形实肋板连接有限长双层圆柱壳的振动和声辐射解析计算方法.汤渭霖和何兵蓉(2001) 利用两端简支圆柱光壳的干模态振型函数作为基函数, 只考虑环肋骨的径向反作用力, 计算了水中两端简支加肋圆柱壳的振动和声辐射. 吴文伟等(2002)在Burroughs (1984)研究成果的基础上, 进一步建立了环形实肋板连接的无限长双层加肋圆柱壳受点机械力激励的声辐射模型(见图 4), 并采用稳相法开展了远场辐射噪声的计算分析.

|
| 图 4 环形实肋板连接的无限长双层加肋圆柱壳声辐射计算模型(吴文伟等2002) |
刘涛(2002)建立了实肋板连接有限长双层圆柱壳的振动和声辐射解析计算模型.通过算例分析指出:低频范围内壳间环形水层的耦合作用是主要的, 高频范围内实肋板的耦合作用居主要地位. 陈美霞等(2003)研究了流场中有限长加筋双层圆柱壳受径向点激励的振动和声辐射性能. 曾革委(2004)建立了一个无限长双层圆柱壳受径向集中力激励的辐射噪声解析计算模型, 考虑了环肋、舱壁和实肋板对内外圆柱壳的径向反作用力.通过算例, 研究了实肋板和舷间水对内外壳间振动传递和水下辐射噪声的影响.计算结果表明:在1kHz以内实肋板和舷间水都是重要的声传递通道. 姚熊亮等(2009)研究了不同壳间连接介质的加筋双层圆柱壳的振动声辐射特性, 通过内壳受径向激励力的算例分析得出结论:实肋板和舷间水介质都是重要的声传递通道, 水层的耦合作用随频率的增高而减弱, 实肋板的耦合作用随频率的增高而增强.
为进一步准确模拟工程对象(如水下船舶) 的结构特点, 国内外学者进一步采用解析方法研究了内部包含子结构的圆柱壳体声弹性问题. Bjarnason等(1994)、Choi等(1995)采用Lagrange运动方程建立了两端为半球壳、内部含圆形舱壁板的圆柱壳的流固耦合振动和声辐射计算模型, 并进行了求解. Guo (1996)建立了内部有轴向弹性平板的无限长圆柱壳声弹性模型, 计算了简谐激励力作用在弹性平板上时的辐射噪声. 骆东平等(2004)开展了具有内部浮动甲板的环肋圆柱壳结构在流体中振动、声辐射特性的研究, 采用四自由度弹簧技术模拟圆柱壳体和浮动甲板之间的弹性连接. 陈清坤等(2010)建立了流场中带压载及舱壁的有限长环肋圆柱壳在径向集中力激励下的振动和声辐射解析计算模型, 将舱壁等价为施加在柱壳上的线力, 压载作为附加质量平摊到壳板上, 通过算例分析得出结论:舱壁对声辐射的影响可忽略不计, 频率较高时压载可发挥有效的减振降噪作用.
为降低舰船壳体的振动和声辐射, 通常在船体上粘贴阻尼材料或声学覆盖层. Maidanik和Biancardi (1982)研究了在一个无限大平板表面粘贴柔性层或者在平板上方设置气-液混合层两种附加去耦层方案对平板声辐射的抑制效果. Laulagnet和Guyader (1991)将声学覆盖层等效为一个复刚度参数, 建立了敷设声学覆盖层的有限长圆柱壳的辐射声功率计算方法. Laulagnet和Guyader (1994)基于描述柔性层运动的Navier方程, 进一步建立了声学覆盖层的三维计算模型及其渐近展开求解方法.国内也有多位学者用Navier方程求解敷设声学覆盖层的圆柱壳声弹性问题(彭旭2004, 田宝晶2006). 殷学文(2001)采用多层均匀分布厚壁圆柱筒模型模拟声学覆盖层, 利用声学覆盖层的声阻抗建立了“圆柱壳-声学覆盖层-水介质”耦合的声振模型, 并结合稳相法计算了敷设消声瓦的双层加肋圆柱壳的水下辐射噪声. 邹明松(2012)建立了敷设声学覆盖层的双层加筋圆柱壳的水下声辐射计算模型, 分析了不同静水压下声学覆盖层的降噪效果.此外, 针对复合材料结构声辐射问题, 有的学者还开展了无限大双周期加筋叠层复合平板与无限长加筋叠层复合圆柱壳的声辐射问题的研究(Yin et al. 2007, Cao et al. 2012).
3.1.2 与声散射相关的研究基于解析解的规则弹性结构声散射问题与声辐射问题几乎有着相同的研究历史、类似的研究对象及丰富的成果, 下面仅给出若干例子.
早在20世纪50年代, James和Faran (1951)就研究了均质圆柱和球体的声散射问题, 同时考虑了弹性体内的压缩波和剪切波; Junger (1952)则研究了无限大理想声介质中弹性圆柱壳和弹性球壳的声散射问题. Junger和Feit (1986)在其专著中论述了无限大弹性平板的声反射, 弹性球壳和弹性圆柱壳的声散射问题. Skelton和James (1997)的专著论述了多层平板、多层球壳和多层圆柱的声反射和声散射问题.我国的刘国利和汤渭霖(1996)采用解析方法推导了平面声波斜入射时水中无限长圆柱壳体纯弹性共振散射函数的简明表达式; 汤渭霖和范军(1999)采用解析方法研究了水中双层同心弹性球壳的声散射; 范军等(2003)采用弹性薄壳理论和Fourier变换方法导出了水下双层无限长圆柱壳的散射声场的解析解; 郑国垠等(2009, 2010) 开展了充水有限长圆柱薄壳声散射的理论分析与实验验证.
3.2 任意结构声弹性问题的数值分析方法解析方法很难准确预报船舶类复杂结构的强迫振动及水中近、远场声辐射特征.随着计算机技术的进步, 各类水中结构声弹性数值计算方法及软件取得了长足的发展与应用.
结构水中声弹性问题研究的进展可针对不同的工程应用对象及不同的数值计算方法, 分成低频、中频和高频三个频段, 分别叙述.本文重点叙述其中的低频和中频段部分.实际上, 三个频段之间并无特别明确的界线, 存在不可避免的交叉, 随着计算方法的发展和改进, 一个频段的计算方法会向其他频段适当延伸, 在下面的分频段概述中也会有所体现.
3.2.1 结构低频段声弹性数值计算方法用于低频段声弹性问题研究的计算方法绝大多数基于离散单元概念, 例如有限元方法(finite element method, FEM)、无限元法(infinite element method, IEM) 和边界元法(boundary element method, BEM) 等.
目前已有多款功能较强、各具特色的有限元分析方法通用商业软件(如NASTRAN、ANSYS、ABAQUS等), 可用于解决水中结构的声弹性问题. Hunt等(1974, 1975) 采用有限元方法求解了弹性结构的声辐射和声散射问题. Kallivokas和Bielak (1993)采用有限元方法在时域中分析了弹性结构的瞬态声耦合问题, 在截断边界上给出了一个新的吸声边界条件.
采用有限元方法计算宽阔水域中的声辐射问题时, 计算量很大, 一般只能计算结构近处的声场.此时, 多用“有限元-边界元”方法(弹性结构用有限元处理, 流场用边界元处理, 缩写为FEM/BEM).边界元方法能够自动满足远场辐射条件, 只需在流固耦合边界面上划分单元实现离散求解, 计算空间较有限元法降低了一维, 而且用于描述流场中声传播的Green函数具有解析表达式, 计算精度高, 可有效处理无限大或半无限大流场中的声学问题, 克服了有限元法的不足, 成为求解低频段复杂结构水中声弹性问题最常用的方法. 20世纪60年代, Chen和Schweikert (1963)、Mocormick和Baron (1965)将FEM/BEM相结合解决了弹性结构的声辐射问题. Everstine和Henderson (1990)指出FEM/BEM相结合是高精度求解大尺度结构声弹性问题的最实用的方法.其将NASTRAN的有限元方法同自建的边界元数值方法相结合, 将流场处理成无限大理想声介质, 开发了结构流固耦合计算程序NASHUA.该程序可调用NASTRAN计算得到干结构的阻抗矩阵, 同时还可以应用NASTRAN的前/后处理图像显示系统, 已具备开展大尺度复杂结构流固耦合计算分析的能力. Giordano和Koopmann (1995)以角频率为变量进行流体声阻抗矩阵的多项式拟合展开, 并截取前面4项, 在状态空间内建立FEM/BEM耦合方程, 该方法可以消除系数矩阵对频率的依赖性, 并能实现广义模态解耦.当激励工况和计算频率改变时, 该方法无需重新计算基础矩阵, 有效地提升了工作效率. Peters等(2014)采用FEM/BEM结合的方法, 分析了一个内部布有质量与隔振系统的三个加肋船体舱段的水下声辐射特性.国内采用FEM/BEM相结合的方法求解水下结构的声弹性问题始于20世纪80年代(Zhu 1986, Zhang et al. 1987); 到20世纪90年代, 具备了采用FEM/BEM方法解决复杂结构声弹性问题的能力(张敬东和何祚镛1990, 崔宏武等1990, 沈顺根等1992, 谭林森等1999); 2000年以来, 有大量学者基于多种商业软件, 利用该方法解决低频段复杂结构的水中声弹性问题. 商德江(2000)和邹春平等(2004)采用ANSYS和SYSNOISE软件, 分别预报了简单和复杂结构以及水面舰船的水下声辐射. 邹元杰(2004)将板-块体组合有限元模型与声学边界元模型结合, 建立了阻尼复合壳体结构在集中力激励下和内场声激励下的声振耦合数值计算模型, 分析了阻尼黏弹性层的减振降噪和隔声效果. 王旌生(2007)采用结构有限元法和声学边界元法, 研究了水中复合材料泵喷推进器导管结构的振动和声学特性.
边界元是边界积分方法的数值离散, 在水弹性或者声学领域应用最广泛的边界积分方法是Helmholtz边界积分方法(势方法) 和简单源方法(源汇分布法).这两种方法在理论上均是严密的, 简单源方法可由Helmholtz边界积分方法导出, 但两者的积分方程形式和待求量不同(Schenck 1968, Wu 1984). Helmholtz边界积分方程中包含了Green函数与Green函数的一阶偏导数, 待求量为声压和速度; 简单源边界积分方程中只含有Green函数, 待求量为源强.
上述两种边界元方法均存在奇异积分和不规则频率(某些特征频率处解不唯一或无解) 问题, 还存在非对称满系数矩阵方程的求解问题.针对这三个问题, 国内外开展了大量的研究工作.已经发展并应用的奇异积分处理方法主要有:退化单元法(Seybert et al. 1984, 嵇醒等1997, 黎胜和赵德有2000)、利用脉动球源解析解的间接处理方法(李小瑜和傅志方1989)、极坐标变换法(赵健等1989)、三角斜坐标系方法(Hui et al.1999) 等.在Helmholtz积分边界元方法中, 处理特征频率处解不唯一性问题的方法主要有: CHIEF (combined helmholtz integral equation formulation) 方法(Schenck 1968)、Burton-Miller方法(Burton & Miller 1971)、非边界配置方法(Achenbach et al. 1988) 和波叠加方法(Koopmann et al. 1989).其中, CHIEF方法和Burton-Miller方法是最具代表性、应用最广的两种方法. Burton-Miller方法的理论基础比CHIEF方法更严格, 但Burton-Miller方法存在超奇异积分的问题, 计算精度和计算速度较低. CHIEF方法需要设定内点(CHIEF点), 当选取的内点与相应的内部Dirichlet问题的振型节点重合时, 计算会失效.针对该问题, 赵键等(1989)提出了增加以内点积分方程的导数式为补充方程的改进CHIEF方法. Wu和Seybert (1991)提出了CHIEF块法(CHIEFblock). 胡宗军等(2010)提出了将三维声学边界元半解析算法与CHIEF点法相结合的方法, 有效克服了特征频率处解的不唯一性问题. Jang等(2013)还将CHIEF方法引入时域声学边界元计算中, 增强了计算结果的稳定性.基于源强积分方程的声学简单源方法, 在物体湿表面分布单极子点声源, 通过边界条件确定这些点声源的源强, 然后线性叠加求解整个声场.在20世纪六七十年代曾有学者用该方法求解声弹耦合问题(Chen & Schweikert 1963).简单源方法同样存在不规则频率的问题(在特征频率上无解, Schenck 1968), 往往成为要解决的一个难点.此后在声弹性领域的边界元计算中较多采用Helmholtz积分方法.边界元方法中要求解一个非对称满系数矩阵方程, 其存储量与全部节点的总自由度数的平方成正比; 采用直接法求解时, 其运算量与总自由度数的立方成正比, 这限制了边界元法在大规模工程问题中的应用.针对该问题, 国内外研究发展了快速多极子算法(Epton & Dembart 1995, Wang & Ji 2008, Gumerov & Duraiswami 2009, 李善德等2011)、并行计算技术(张健飞和姜弘道2003, Takahashi & Hamada 2009) 等应对方法.
国内外还发展和初步应用了“有限元-有限元-无限元”方法, 用于解决低频段复杂结构的水中声弹性问题(Astley & Macaulay 1994, Burnett & Holford 1998).该方法的主要思想是:弹性结构采用结构有限元离散, 近场声介质采用流体有限元处理, 远场声辐射则采用无限元处理.理论上, 采用无限元处理后, 远场声辐射条件能较好满足, 且能给近场声提供一个较准确的边界条件.但该方法的研究尚不完善, 到目前为止在工程中尚未广泛应用.此外, 求解声学问题的其他方法, 例如边界无网格方法(Chen et al. 2002, Young et al. 2006, Lin et al. 2014) 等也在研究之中.
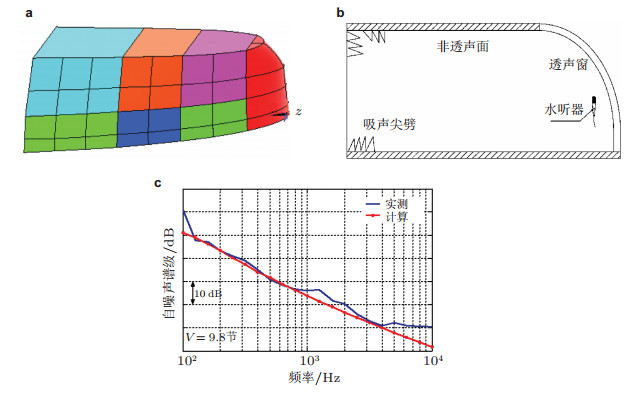
3.2.2 任意结构高频段声弹性数值计算方法进入高频段后, 结构振动模态非常密集, 不存在明显的共振和反共振特点, 且结构本身的不确定性(如尺寸、材料属性或者制造公差等的小量变化) 往往对该频段内的响应有显著的影响.这些特点不仅使确定性数值计算方法计算量大, 而且也未必有精度优势.因此, 具有统计特性、能在平均意义上给出分析结果的统计能量法(statistical energy analysis, SEA) 便成为解决高频段任意结构声弹性问题的最常用方法.国内外在该方法的发展和应用上取得了非常丰富的研究成果, 并且已应用到船舶结构振动和噪声分析中(Hynna et al. 1995, 俞孟萨2007, 丁宏和陈美霞2011). 俞孟萨(2007)采用集成统计能量法(ISEA) 预报了某实船在航行状态下艏部声呐自噪声的水动力噪声分量, 并与实测结果进行了比对, 如图 5所示.
|
| 图 5 某实船9.8节航速下, 艏部声呐自噪声计算与实测比对(俞孟萨2007). (a) 艏部声呐罩外形, (b) 艏部声呐罩自噪声测量示意图, (c) 艏部声呐自噪声谱级计算与实测结果比对 |
在高频段, 除统计能量法以外, 还有渐近模态法(asymptotic modal analysis) (Dowell & Kubota 1985), 目前该方法仅适用于简单连接结构的分析, 能够在结构和边界条件比较简单的情况下弥补统计能量法的一些缺陷.此外还有功率流方法(power flow method) (Lase et al. 1996)、解析模型计算与试验修正结合的方法(吴文伟等2004) 等, 在此不详细展开.
3.2.3 结构中频段声弹性数值计算方法中频段的结构动力学问题往往会出现两种情况:
(1) 部分子结构的特征尺寸小于或相当于其振动波波长, 振动模态稀疏, 对该类子结构可采用有限元等低频数值方法较好地处理; 其他部分子结构的特征尺寸远大于振动波波长, 振动模态密集, 结构建模的不确定性会对动响应产生较大的影响, 如用有限元等低频数值方法, 计算效率和计算精度都存在问题, 但满足统计能量分析方法的使用条件.
(2) 结构内的振动波波长介于短波长和长波长之间, 振动模态已较密集, 但尚未充分满足统计能量法的使用条件; 与此同时, 如采用传统的有限元等低频数值方法, 计算量将很大, 且计算精度也得不到保证.
针对第一种中频段情况, Langley和Bremne (1999)提出了有限元-统计能量混合方法(FE-SEA) 的基本理论, 其主要思想是在应用模态叠加法的同时, 将振型及相应的主坐标分解为整体模态集和局部模态集, 并对与这两个模态集相关的子系统分别用有限元法和统计能量法建立运动方程. Shorter和Langley (2005)在上述基于模态的FE-SEA混合法的基础上, 应用扩散场互易原理(diffuse field reciprocity relationship) 实现FE子结构与SEA子结构之间的耦合, 提出了基于波动理论的FE-SEA混合方法.该方法克服了其他混合方法只能考虑能量单向传递的不足, 可应用于更为复杂的结构形式.同年, 法国ESI也以基于波动理论的FE-SEA混合方法为理论基础推出了PAM-VA One软件.国内也有多位学者采用FE-SEA混合方法处理空气中或者水中的结构振动和声辐射问题(陈书明等2010, 姚熊亮等2011, 张瑾等2012).
针对第二种中频段情况, 有学者提出放宽统计能量法中的一些基本假设, 实现传统统计能量法由高频向中频扩展. Fredo (1997)提出了一种类似于统计能量分析的方法, 采用部分能量影响系数方程来求解不符合传统统计能量分析基本假设的部分. Choi等(1997)在多振子能量流关系中放弃了自然频率在被分析频段内均布, 以及连接点所有模型振型平方和为1的假设, 提出了参数化统计能量分析方法. Maxit和Guyader (2003)进一步考虑了多个子系统的能量流关系, 提出了更加通用的统计模态能量分析方法(SmEDA). Maxit等(2014)在SmEDA方法的基础上, 在传递损耗计算中计入了结构非共振模态的贡献.另外, 有学者提出了将传统有限元等低频数值方法由低频向高频扩展的思想, 建立了相应的计算方法, 如为提高计算效率、降低计算复杂度而建立的动态子结构方法(Hurty 1960, Gladwell 1964).通过大模型的子结构分割计算、自由度缩聚、再耦合集成, 动态子结构方法在一定程度上提高了低频传统数值方法的分析频率范围.现今, 动态子结构方法已较为成熟, 并在工程中获得了广泛的应用(殷学纲等1991, 丁渭平2002, 向树红等2004).有研究将结构振动能量控制方程与有限元方法相结合提出了用于解决中高频结构动力学问题的能量有限元法(energy finite element analysis, EFEA) (Wohlever & Bernhard 1990), 近些年来该方法不断发展(Bouthier & Bernhard 1995, Cabos & Jokat 1998, Borlase & Vlahopoulos 2000), 在船舶结构振动噪声领域展现出良好的应用前景(孙丽萍2004, 吴轶钢2008).
此外, Soize (1993)和Strasberg等(1996)提出的模糊子结构(structural fuzzy) 方法也有助于解决中频段问题.模糊子结构方法将具有统计特性的大量子结构作为模糊结构处理, 通过引入随机边界阻抗, 实现模糊子结构与确定性主体结构的耦合. 刘涛等(2003)提出了一种计算内部有支座结构的有限长圆柱壳体声辐射的解析/数值混合方法.该方法采用有限元方法处理内部支座结构, 计算出基座到壳体的动力传递, 将力引入壳体振动方程, 再采用解析法计算壳体结构水下辐射噪声, 结合解析解与数值解的优点, 对减少计算量, 扩展用于中频段计算有一定帮助. 姚熊亮等(2008)采用类似的解析/数值混合方法求解了内部含基座的加筋双层壳的振动声辐射问题. Kassem等(2009)提出了基于统计计算模型的能量密度场方法(energy-density field approach), 用于处理低中频段的振动与声学问题. 周海安等(2012)采用有限元与空间波数法相结合的解析/数值混合方法研究了表面粘贴周期加强块的无限大平板的振动响应和声辐射问题.
3.3 海洋环境中的浮体结构声弹性研究长期以来, 在研究海洋弹性浮体结构在水中的振动、声辐射和声散射问题时, 通常把海水介质处理成理想的声介质, 并常常忽略自由液面和海底边界的影响; 在研究海洋波导中的声波传播问题时, 往往更多地关注单极子点声源引起的声传播规律.实际上, 这两个领域的问题是交叉关联的.现有的相关理论及分析手段, 如船舶三维声弹性理论与简单源汇数值计算方法(邹明松等2010, Zou et al. 2010; 邹明松2014) 及海洋声传播理论与计算方法(布列霍夫斯基1983, 杨士莪1994, Jensen et al. 2011, Porter 2001), 已经为海洋弹性浮体结构流固耦合振动声辐射与海洋波导环境中的声传播预报分析的融合提供了良好的基础条件.近年来, 国内外已开展了海洋环境中浮体结构声弹性问题的理论和计算方法研究, 部分成果具备了一定的工程应用价值, 简述如下.
3.3.1 与声辐射相关的研究国内外对水中结构声弹性计算方法的研究多数将流场处理成无界理想声介质, 不考虑水底、水面的反射和吸收, 更不考虑海洋环境中的介质密度与声速分层等因素.实际上, 水面舰船或者水下船舶航行在各种海洋环境中, 其辐射声场必然与所处的海洋声学环境密切相关.
Seybert和Soenarko (1988)建立了半空间边界积分方程, 讨论了无限大刚性壁面对脉动球的近场声压的影响. Li等(1994)推导了具有阻抗型边界条件的半空间Green函数, 并建立了相应的声学边界积分方程. 黎胜(2001)研究了自由液面和刚性壁面对脉动球声辐射的影响.上述三篇文献尚未考虑声弹性耦合作用. 邹元杰和赵德有(2004)采用能计入压力释放水面和刚性水底边界条件的Green函数, 建立了浅水域声学边界元方程和相应的FEM/BEM流固耦合振动方程, 生成了用于浅水中结构声弹性求解的计算程序.方箱结构的数值算例表明, 浅水中水面和水底边界对结构声辐射特性存在较大的影响.这几项研究, 不再限于无界流场.但是, 压力释放水面或者刚性水底边界还不足于描写实际海洋水声波导环境(ocean hydro-acoustic waveguide environment).关于实际海洋波导环境中弹性体声辐射问题的研究, 目前还鲜见报道.
3.3.2 与声散射相关的研究与声辐射研究相比, 声散射研究更多地考虑了不均匀海洋声学环境的影响, 这与水声探测工程应用需求(如海底目标物的探测) 密切相关.
Schmidt (2004)将虚拟源方法(virtual source approach) 应用于求解弹性浮体在三维海洋波导中的声散射问题, Abawi (2011)采用虚拟源方法计算周期不平海面的声散射问题, 该方法在理论上具有较普遍的适用性, 但尚有三处需进一步改进: (1) Green函数矩阵计算量大, 文献(Jensen et al. 2011) 中有一小节专门介绍了缩减Green函数矩阵计算量的一些方法, 包括根据具体问题的特点, 简化波导Green函数, 目前已经实现的数值计算还主要针对少数几个较简单的海洋波导(Lucifredi & Schmidt 2006, Abawi & Porter 2007, Jensen et al. 2011); (2) 在流固耦合声弹性问题的建模求解中, Schmidt (2004)采用弹性浮体湿表面上自由度所对应的动刚度矩阵来建立流固耦合边界条件, 因动刚度矩阵依赖于弹性体在水中的湿谐振频率, 计算需足够细密; 目前已实现的一些数值算例仅集中于动刚度矩阵存在解析解的弹性球体、球壳等简单浮体, 对复杂浮体而言, 计算量巨大; (3) Schmidt (2004)应用虚拟源方法时, 未提及边界元方法中的不规则频率(某些特征频率处解不唯一或无解) 问题, 解决好该问题是提升计算方法普遍适用性的前提.
汤渭霖(1999)基于物理声学方法, 推导了存在界面时的修正Kirchhoff近似公式, 提供了一种计算浸没在海面下或躺在海底的水下目标的声回波计算方法. 范军(2001)将该方法与板块元数值方法相结合, 预报了界面附近沉底水雷型目标的目标强度, 发现界面的存在对于水雷回波特性有很大的影响. 王桂波和彭临慧(2005)直接利用Ingenito波导中的简正波解, 建立了浅海波导中刚性球的声散射计算模型和数值算法, 分析了海底、海面边界条件对目标声散射的影响. 尤云祥等(2007)研究了压力释放(声软) 和刚性(声硬) 边界条件下三维海洋波导中的声散射问题, 基于Galerkin变分原理和DtN映射方法, 发展了数值求解这类声散射问题的一种自然边界元与有限元耦合的求解方法. 姜琳和赵德有(2008)将水处理成理想声介质, 采用边界元方法研究了压力释放水面和刚性水底边界条件下刚性椭球声散射问题. Jiang和Hong (2009)基于Greenberg方法推导了含有阻抗边界条件的浅水Green函数, 利用边界元法研究了海底是阻抗边界的浅水环境中的刚性椭球体声散射问题. 陈燕等(2010)建立了一种基于虚源法和物理声学方法计算浅海波导中目标回声的射线声学方法, 并进行了浅海Pekeris波导中由圆锥、圆柱和半球头组成的复杂形状刚性体声散射的数值计算. 范威等(2012)采用边界元方法分析了在声速剖面随深度变化的浅海波导中软的或者刚性浮体的声散射现象.目前国内的这些研究, 基本集中在刚体或者是简单的阻抗性边界, 尚未发展到声弹性领域.
3.4 计算与试验技术 3.4.1 计算技术如前所述, 近二三十年来, 国内外针对典型水下船舶结构的声弹性问题, 开展了大量理论和计算方法的基础研究.美欧等国家开发了一些可用于水下船舶等复杂浮体流固耦合振动及水下辐射噪声评估的计算软件, 如法国Metravib RDS公司的GAP软件, 英国Frazer-Nash公司的FNV-Noise软件, 美国NCE公司的Designer Noise软件.俄罗斯经长期研究, 结合工程实践经验, 已形成一套实用的方案设计阶段和技术设计阶段使用的水下船舶声学性能评估方法.国内船舶结构声弹性问题的数值计算, 或者基于通用的商业软件, 或者基于自编软件, 呈现出多样化的特点.通用的商业软件并非专门为船舶声弹性计算服务, 当分析开阔水域内船舶结构声辐射问题, 且涉及与船内各系统(如机械与管路系统、隔振浮筏系统、桨-轴系统) 的耦合时, 计算效率受到限制.本文的第4节将结合作者所在团队的工作, 介绍基于船舶三维声弹性力学理论的计算技术的发展情况.
3.4.2 试验技术船舶声弹性问题与船舶噪声控制的需求密切相关.在工程需求推动下, 试验研究与理论研究同步开展, 受到各国的重视.美欧多国已形成了包括实验水池、湖泊试验场和海上固定试验场在内的系列性专业试验场所, 以及包括小尺度模型、大尺度缩比试验艇、全尺度试验艇和实船在内的多类试验对象(刘兴章2011, 刘兴章和陈涛2011).在潜艇推进器噪声、水动力噪声和机械噪声的预报与控制技术研究, 新技术验证, 及实船噪声检测与治理中发挥了重要作用.例如, 美国在本德奥瑞湖无人潜艇水下试验场中利用大尺度缩比试验艇(large scale vehicle, LSV) 进行潜艇减振降噪技术的系列研究; 在东南阿拉斯加潜艇水声试验场开展各型潜艇水下结构振动、自噪声与辐射噪声检测与弱点评估试验.俄罗斯也建设了装备精良的声学测量船与固定式水声试验场, 包括远东、北海与黑海海域的实艇声学性能测量基地, 建造了大尺度缩比试验艇及专用的常规动力试验潜艇(如1710型“白鲸”号).俄罗斯制定了潜艇水下辐射噪声的码头系泊试验、浮筒悬吊水下试验及航行试验的一整套测量方法与规范, 详细规定了测量参数、测量条件、测量装置位置、测量距离、潜艇机动方式、数据处理方法等内容和要求.我国及英、德、挪威等国也建有专门的船舶水下振动声辐射研究和检测的试验场, 开展了不同尺度的模型试验和实船试验.
4 作者所在课题组的研究进展尽管国内外在船舶结构流固耦合振动与声辐射研究领域已开展了广泛的研究, 但如何科学地反映流体与水中结构在振动与声辐射过程中的耦合作用, 分析一艘船舶在不同水深、不同潜深、不同方位和距离上形成辐射声场的分布特征和相互之间的差异, 说明机械与结构的振动、船体近旁自噪声和远场辐射噪声之间的传递和演变规律等, 仍是船舶振动噪声领域关注的问题.这要求进一步发展适用于具有任意形状、复杂内外结构的船舶, 能计及自由液面、海底及航速影响, 计算精度符合工程需求, 计算量可为船舶研究与设计部门的计算系统承受的船舶三维声弹性计算分析理论和方法.
针对该工程背景, 2008年吴有生院士提出在带航速浮体三维水弹性力学理论的基础上发展船舶三维声弹性理论及相应计算技术的设想.经过持续研究, 中国船舶科学研究中心已形成了一套较为完整、且具有不断扩充潜力的理论方法体系; 编制的计算软件, 经过数值算例、模型试验、实尺度舱段试验以及实船测试数据的多重考核验证, 不断改进完善, 已成为水面与水下船舶声学设计、声学性能定量评估与优化以及振动噪声机理探索与分析的有力工具; 在一系列工程问题上应用, 取得了丰富的结果.
作者所在课题组发展的船舶三维声弹性理论属于水弹性流固耦合振动研究与海洋水声学研究的交叉领域, 从整体理论方程与计算方法而言, 该理论更偏重于前者, 是与经典的三维水弹性力学理论一脉相承的.从工程应用而言, 船舶三维声弹性理论与本文第3节中所述的船舶结构声弹性力学具有相同的应用目标.整体而言, 船舶三维声弹性理论有其特有的内涵, 主要体现在三个方面: (1) 证明了Price-Wu广义流固界面条件在声弹性力学中的适用性; (2) 在理论与计算方法上实现了船舶流固耦合振动、声辐射与海洋声传播的融合集成, 具有较强的适用性; (3) 从理论方法, 到计算软件, 到工程应用, 到研究领域的开拓, 形成了一个紧密的体系.本节首次对这部分工作进行一个单独的整体性的介绍.
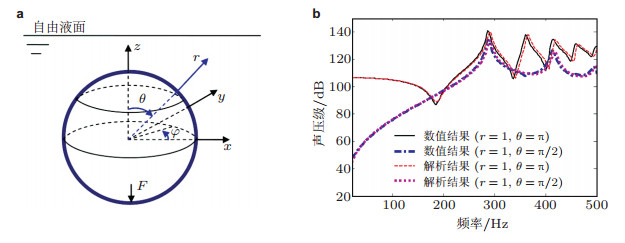
4.1 理论方法 4.1.1 考虑自由液面影响的均匀声介质中航行船舶的三维声弹性理论邹明松等(2010)通过引入计及自由液面效应的理想可压流体Green函数, 并基于Price-Wu广义流固界面条件, 建立了带航速和考虑自由液面影响的均匀声介质中的船舶三维声弹性理论.该理论既适用于声辐射问题, 也适用于声散射问题.由于在船舶声弹性理论中计入了航速的影响, 理论上更加完备.基于该理论方法, 编制成相应的计算程序, 通过与具有解析解的算例、模型试验及实船测试结果的比较验证了计算程序的正确性. 图 6为在一个径向集中力作用下的弹性薄球壳结构声辐射的数值计算结果与解析解比较的示例(Zou et al. 2010), 从图中可见, 两者吻合良好.假设该球壳以恒定航速沿x方向移动时, 计算分析了航速对辐射噪声声压的影响.量阶分析和数值计算表明, 航速对流固耦合振动及水下声辐射的影响主要限于低频域及近场区.
|
| 图 6 半径为0.5 m的单层弹性球壳水下声辐射考核算例(Zou et al. 2010). (a) 计算模型及坐标系示意图, (b) 无界流场环境中位于(r, θ) 处场点的声压级数值结果与解析解的比对 |
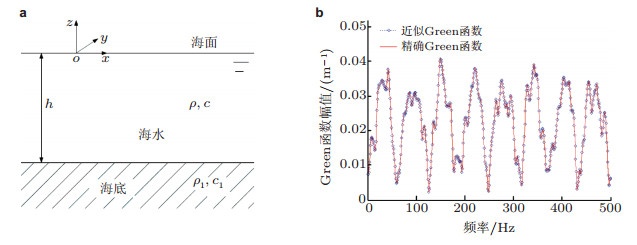
Zou等(2012)针对我国近海的实际情况, 重点考虑海底与水面的影响, 不计海水密度与声速等变化与分层, 引入Pekeris水声波导模型(见图 7(a)), 将均匀声介质中的船舶三维声弹性理论与水声信道理论相结合, 建立了有限水深声学环境中的船舶三维声弹性理论及分析方法; 给出了耦合求解三维结构声弹性响应的动力学方程和水声传播方程的方法与步骤; 针对常见浅海的特征, 引入了Pekeris波导Green函数的近似级数表达式, 有效降低了数值计算的复杂度、减少了计算量; 并通过算例验证了计算精度, 见图 7(b).
|
| 图 7 Pekeris波导模型及其Green函数的近似级数表达式的验证(Zou et al. 2012). (a) 海水和海底为参数不同的理想声介质的Pekeris波导模型, (b) 源点和场点相对位置满足要求时, 近似Green函数计算精度考核 |
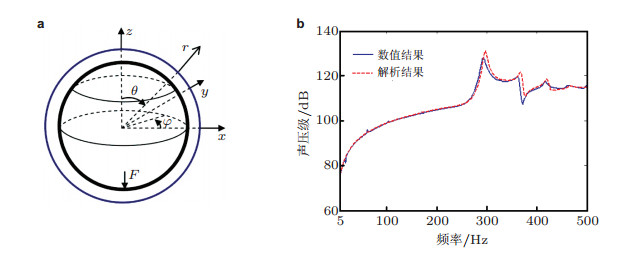
水下双层壳体船舶存在舷间水及其与结构的耦合振动声辐射问题.针对该类问题, 邹明松和吴有生(2012)进一步发展了双流域耦合的船舶三维声弹性计算方法, 扩展了工程应用范围.用舷间充水双层弹性薄球壳结构声辐射的解析结果(邹明松等2013) 对相应的计算方法和计算程序进行考核验证, 如图 8所示.
|
| 图 8 外壳半径为0.65 m内壳半径为0.5 m的双层弹性球壳水下声辐射考核算例(邹明松和吴有生2012). (a) 计算模型及坐标系示意图, (b) 无界流场中(r=100, θ=π) 处场点的声压换算的声源级数值结果与解析结果的比对 |
针对船舶表面敷设声学覆盖层降低声目标强度和水下辐射噪声重要工程需求, 邹明松(2014)建立了敷设声学覆盖层的船舶三维声弹性力学理论和计算方法.通过引入描述声学覆盖层内外表面间声振传递的四端参数法(邹明松等2013), 实现了“船体结构-声学覆盖层-水介质”的声振耦合求解.
4.1.4 船舶声弹性子结构分离及集成方法船体内部结构(如横舱壁、铺板、基座等) 的复杂性及设计过程中不可避免的局部结构调整使得应用三维声弹性方法进行船舶的定量声学设计与优化, 面临建模与计算的工作量过大的困境.为克服该障碍, 邹明松和吴有生(2014)建立了能有效提高计算效率, 特别适用于改变船体内部子结构, 进行振动噪声传递效果分析及局部结构声学设计优化的“船舶声弹性子结构分离与集成方法” (SSSI方法).其主要思想是:将主船体与船内子结构分离, 采用模态综合超单元方法形成子结构的输入输出自由度缩聚动刚度矩阵, 采用三维声弹性方法实现主船体与水介质的流固耦合求解, 通过边界连接条件完成主船体与子结构的综合集成.
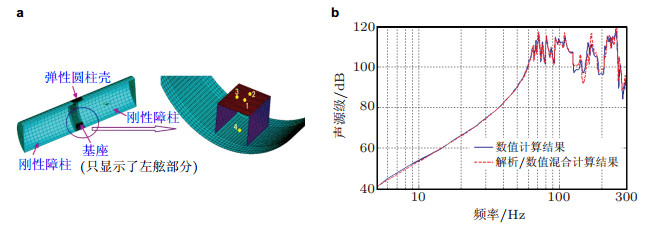
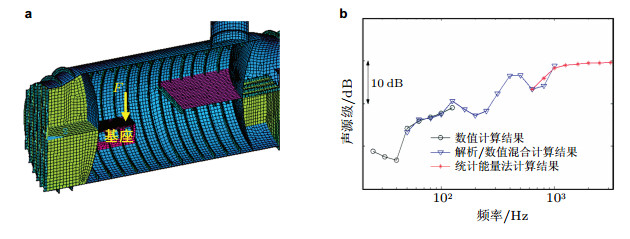
邹明松(2014)及Zou和Wu (2015)进而针对潜艇类水下船舶主体结构的特征, 采用两端简支单层加肋圆柱壳解析计算模型来描述主船体结构, 应用解析方法求解流固耦合作用, 建立了解析/数值混合的声弹性子结构方法(MANS方法), 该方法可有效提高计算效率和扩展计算频段范围.通过装有内部设备基座的圆柱壳结构声辐射计算模型, 验证了MANS方法及其计算程序的正确性, 见图 9.特别需要指出的是, 在预报类似于加筋圆柱壳结构的水中声辐射时, 基于声弹性理论的数值方法一般适用于数百赫兹以下的低频域, 而统计能量法(SEA) 通常适用于高频域. MANS方法则弥补了两者间中频段预报方法的空缺. 图 10(a)是一个半径2.5 m的加筋圆柱壳.在其基座上作用一个垂向单位变频激励力时, 用这三种方法预报的辐射噪声1/3倍频程声源级见图 10(b) (Zou & Wu 2015).显然, 从低频到高频, 三者接续良好. MANS方法为解决加筋圆柱壳类结构中频段水中声辐射预报问题提供了前所未有的高效手段.
|
| 图 9 用MANS方法预报总长为22 m的圆柱壳模型水下声辐射的比较结果(邹明松2014). (a) 计算模型, (b) 1号点施加垂向单位力激励时无界流场中辐射噪声声源级的比对结果 |
|
| 图 10 加筋圆柱壳模型水下声辐射全频域计算结果的比较(Zou & Wu 2015). (a) 半径为2.5m的加筋圆柱壳及激励点, (b) 用声弹性理论数值方法、MANS方法和SEA方法预报辐射噪声声源级的比对结果 |
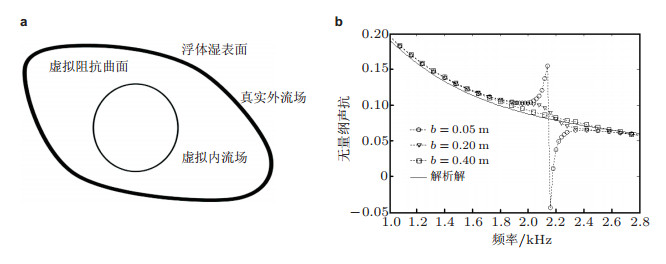
为解决简单源数值方法(源汇分布法) 中出现不规则频率影响计算精度与效果的问题, 邹明松等(2013)提出了虚拟阻抗封闭曲面法(CVIS方法), 在浮体内部的虚拟流场中引入一个虚拟的阻抗封闭曲面(见图 11(a)), 用于吸收内部虚拟流场的声振能量, 消除谐振, 从而抑制求解声学问题时出现的不规则频率.其有效性经过了多种水下浮体的计算验证. 图 11(b)为一个半径为0.5m的球形浮体的模态声阻抗计算结果.在2160Hz处存在不规则频率, 使模态声阻抗无定值.在浮体内部布设了边长为b的立方体虚拟阻抗面后, 当虚拟阻抗面的边长b > 0.2m时, 不规则频率的影响受到抑制.由大量算例归纳得出了虚拟阻抗封闭曲面关键参数的选取原则.此即, 其阻抗应等于流体的特征阻抗, 其面积应取为进行声弹性分析的浮体湿表面面积的0.1~0.4倍.此时, 消除不规则频率的效果较佳.
|
| 图 11 消除不规则频率的虚拟阻抗封闭曲面法. (a) 虚拟阻抗曲面及内外流场示意图, (b) 半径为0.5m的球体刚体平动对应的无量纲声抗(采用边长为b的立方体虚拟阻抗曲面, 其阻抗值取为流体特征阻抗) |
Zou等(2015)在船舶三维声弹性频域分析方法的基础上, 利用频域干模态附连水质量和附连水阻尼的卷积积分和Fourier变换, 给出时域中描述广义水动力的迟滞函数, 形成了船舶结构流固耦合振动的时域方程, 可在时域内处理瞬态振动噪声问题.通过算例验证了三维声弹性时域计算方法与软件的正确性.
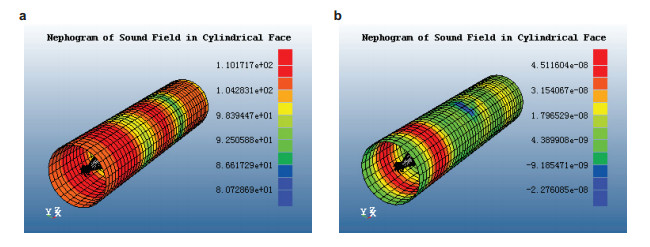
4.2 计算技术2014年, 中国船舶科学研究中心推出专业计算软件--船舶三维水弹性声学分析软件(THAFTS-Acoustic 1.0).该软件可进行水面、水下船舶流固耦合振动、声辐射以及声传播的统一分析, 具备大规模高效并行计算功能及用户体验良好的前、后处理功能. 图 12是可用于潜艇辐射噪声亮点定位的围绕艇体的流场中一个圆柱面上声压级云图与声强云图的显示功能.该软件的核心求解代码是基于船舶三维声弹性理论, 在三维水弹性分析软件(three-dimensional hydroelastic analyses of floating traveling structure, THAFTs) 的基础上开发而成. THAFTS软件的形成和发展是基于20世纪80年代初由Bishop、Price和吴有生等组成的研究团队提出与发展的船舶三维水弹性力学理论(Wu 1984, Bishop et al. 1986)、以及由中国船舶科学研究中心在吴有生院士带领下的研究队伍不断深化研究与开拓发展形成的多种理论方法和分析技术(Wu et al. 1991, 杜双兴1996, 王大云1996, Wu et al. 1997, 陈徐均2001, 田超2007), 并经过了多年的试验研究与验证(Wu et al. 2003, 2007; 林吉如等1992; Hu et al. 2012).同时, 在三十年的发展历程中, 不仅从具体应用中获取了经验, 也在广泛的交流中吸取了营养.
|
| 图 12 THAFTS-Acoustic 1.0软件后处理功能的示例. (a) 包络船体的圆柱面上的声压级云图, (b) 包络船体的圆柱面上的声强云图 |
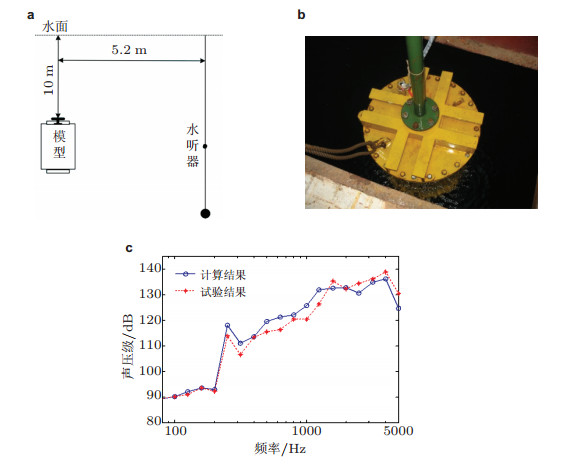
在THAFTS基础上开发的船舶三维水弹性声学分析软件THAFTS-Acoustic 1.0的计算精度与工程实用性已通过数值算例、模型试验、实尺度舱段试验以及实船测试数据的多重考核验证, 图 13与图 14给出了两项试验的概况.
|
| 图 13 电磁激振机激励的半径为0.36 m的加筋圆柱壳的水下声辐射考核试验(邹明松2014). (a) 新安江水库开阔水域中试验模型吊放及水听器布置示意图, (b) 模型吊放现场照片, (c) 水听器场点1/3Oct声压谱级比对结果 |
|
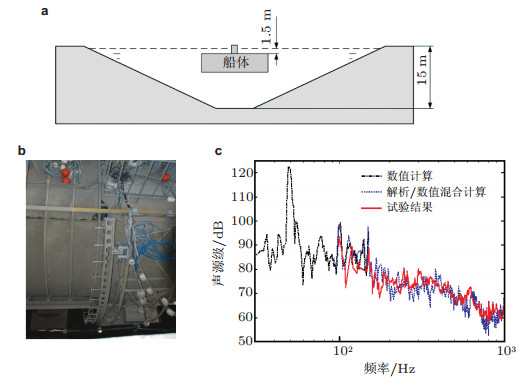
| 图 14 由两个舱室组成总长约19 m的实尺度船体水下声辐射考核试验(邹明松2014). (a) 船体在水池中的试验位置, (b) 移动扫描测量船体辐射声功率的由48对双水听器构成的环形声强传感器阵, (c) 在舱内机械设备激励下由船体辐射声功率换算的声源级比对结果(因水池环境限制, 有效测试频段在100 Hz以上) |
采用无限水深环境中的船舶三维声弹性计算方法, 叶永林等(2011)分析了流体压缩性对加肋圆柱壳结构的模态附连水质量及机械阻抗的影响; 叶永林(2012)还研究分析了图 3(a)所示的小水线面双体船在机械设备激励下的结构振动与水下声辐射问题; 谢基榕(2011)研究分析了基于梁-舱段组合模型的推进器激励下桨-轴-船体耦合水下辐射噪声问题; Qi和Zou (2013)分析了单层与双层加肋圆柱壳在不同部位、不同方向载荷激励下水下辐射噪声的差异及规律.
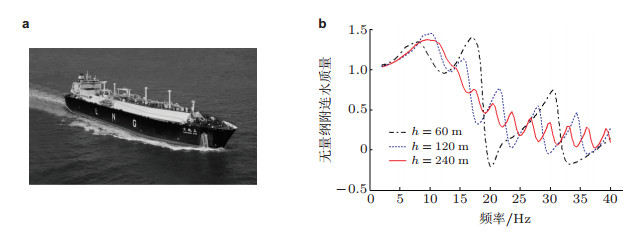
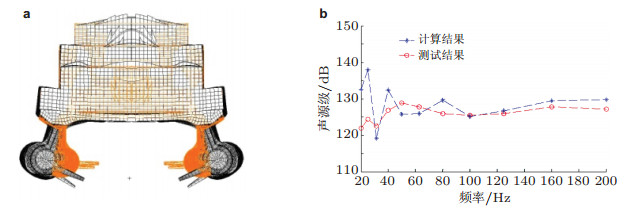
Zou等(2013)采用有限水深环境中的船舶三维声弹性计算方法, 分析了海底、海面边界对一艘LNG船(图 15(a)) 的广义水动力系数及水下声辐射的影响, 研究发现船体和水底之间声波来回反射形成的驻波现象会使广义水动力系数随频率变化而波动, 见图 15(b). Zou等(2014)采用有限水深环境中的船舶三维声弹性计算方法, 评估了30 m水深海域中图 3(a)所示的小水线面双体船在推进电机和主辅发电机激励下的水下辐射噪声, 并把声源级预报结果与小水线面双体船以6节航速航行时由正横方向距船65 m、水面下7.5 m处声压测点的测试结果换算的声源级进行了比较, 见图 16.预报时, 推进电机和主辅发电机的激励加速度取自码头试验测量结果, 而声压测试在开阔海域航行时进行, 机械负荷及激励特性不完全相同, 且还有其他次要的外激励, 导致40 Hz以下两者的声源级存在差异.
|
| 图 15 有限水深环境中一艘LNG船的低频声波驻波现象. (a) 计算对象, (b) 计算取不同水深h时, 船体一阶垂向弯曲振动对应的无量纲化附连水质量(Zou et al. 2013) |
|
| 图 16 一艘小水线面双体船在机械激励下的水下辐射噪声. (a) 典型模态(下潜体内外摆动) 振型示例, (b) 推进电机和主辅发电机激励下场点声压换算的声源级比对结果(Zou et al. 2014) |
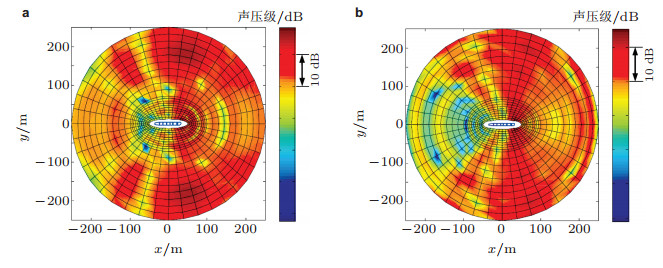
应用船舶三维声弹性理论及相应的计算方法, 邹明松(2014)首次较系统地探讨了船舶辐射声场信息不同的测量环境与观察方式(包括不同水深和潜深、不同测量距离和方位、不同采样时段) 对船舶噪声水平(声源级) 评定效果的影响, 获得了一些具有实际参考价值的定量规律.作为示例, 图 17给出了在两个不同水深和潜深环境中, 一个7舱段的单层壳船体结构受3个典型机械激励力作用时水平剖面内的声场分布云图, 可见两者之间存在明显的差异.
|
| 图 17 不同水深潜深环境下船体水平剖面内的声场分布云图(邹明松2014). (a) 水深65m, 潜深30m; (b) 水深500m, 潜深250m |
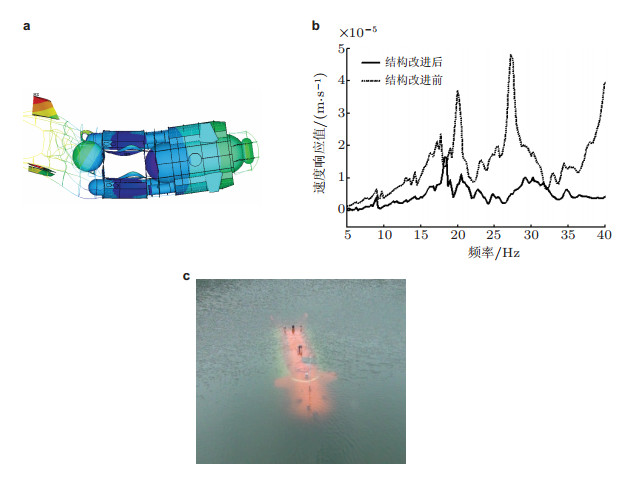
Sun和Zou (2015)采用船舶三维水弹性声学分析软件, 计算分析了一型潜水器水下航行时的流固耦合振动特性, 从减振的角度, 对安装推进电机的尾部框架结构进行了优化设计.仿真计算结果显示, 优化改进后的结构方案能显著降低尾部振动(图 18).
|
| 图 18 潜水器尾部结构减振优化(Sun & Zou 2015). (a) 潜水器尾部结构横向摇摆的典型模态振型, (b) 尾部框架结构改进前后振动速度响应比对, (c) 潜水器试验照片 |
祁立波和邹明松(2015)计算了在横向和纵向载荷激励下, 整船尺度的船体梁模型和三维壳模型的低频水下辐射噪声.重点分析了弯纵耦合现象对船体水下辐射噪声的影响规律, 分析了单个模态对辐射噪声总量的贡献大小, 并揭示出其中起重要贡献的优势模态. 祁立波(2015)提出利用船舶三维声弹性理论与计算方法, 用整船三维动力学计算模型评估水下航行体桨-轴-船体耦合振动声辐射的动力学建模规则; 创新提出了数值分析与实船测量相结合, 由结构响应确定螺旋桨非定常激励力的“间接定量识别方法”; 形成了水下航行体桨-轴-船体低频耦合振动声辐射预报方法并揭示了低频线谱的形成机理; 提出了控制桨-轴-船体低频耦合振动声辐射的主要技术途径及优化方案.
5 结束语本文阐述了船舶水弹性力学与声弹性力学的研究内涵、相互之间的联系、国内外的研究进展, 及近年来作者所在部门发展的船舶三维声弹性理论与计算技术, 及其工程应用情况.其中, 船舶三维声弹性理论、计算方法和开发的THAFTS-Acoustic软件已在工程需求的推动和应用与验证的过程中, 发展成船舶振动与声辐射分析的有效工具.
国内外对船舶振动噪声预报与控制技术及相关的流固耦合动力学的研究已有丰富的内涵、丰硕的成果和广泛的应用.尽管如此, 21世纪“绿色、安全与智能”船舶技术的发展方向, 新技术和新船型突飞猛进的发展, 对复杂海洋环境中船舶振动与声辐射及其声场效应的预报、控制和设计技术, 对异常噪声的形成机理和治理技术不断提出新的需求.下列问题将成为该领域中部分值得关注的研究内容:
(1) 各类典型的海洋声学环境中的船舶声弹性理论与计算方法;
(2) 与海洋环境相融合的船舶辐射与散射声场传播规律的定量预报技术;
(3) 描述机械操控引起的瞬态噪声及复杂系统自激振动声辐射的船舶声弹性时域分析技术;
(4) 基于船舶声弹性直接分析方法, 与子结构技术、参数化建模技术及数据库技术相结合的船舶定量声学设计及优化技术;
(5) 激励源在线监测与结构水中声弹性性能分析相结合的船舶声学状态自动监控技术.
在人类进一步开发利用海洋的历程中, 类型各异, 安全、快速、干净、舒适、经济的绿色海洋运载工具将以进化了的新面貌出现在海洋空间, 支撑经济与社会的安全、稳定与可持续发展.其技术需求推动着船舶力学的研究领域越来越多地从物理对象与周围介质力学与声学性能的孤立研究走向耦合和统一研究; 从稳态现象的研究延伸到瞬态现象的研究; 从线性问题的研究深入到非线性问题的研究; 从单一学科的研究拓展到交叉学科的研究.船舶流固耦合动力学与船舶声弹性力学的研究与应用正处在该发展趋势的前沿, 要求人们做出更多的努力, 开拓创新.
| 布列霍夫斯基.1983. 海洋声学. 北京: 科学出版社 . ( Brekhovskikh L M.1983. Ocean Acoustics. Beijing: Science Press ). |
| 陈美霞, 骆东平, 陈小宁, 蔡敏波, 周锋. 2003. 有限长双层壳体声辐射理论及数值分析. 中国造船, 44 :59–67. ( Chen M X, Luo D P, Chen X N, Cai M B, Zhou F. 2003. Theoretical and numerical analysis on sound radiation of a finite double shell. Shipbuilding of China, 44:59–67. ) |
| 陈清坤, 陈美霞, 和卫平, 高菊. 2010. 舱壁与压载对流场中有限长圆柱壳声辐射影响. 舰船科学技术, 32 :21–25. ( Chen Q K, Chen M X, He W P, Gao J. 2010. Impact of bulkhead and ballast on acoustic radiation of submerged finite cylindrical shell. Ship Science and Technology, 32:21–25. ) |
| 陈书明, 王登峰, 曹晓琳, 昝建明. 2010. 车内噪声FE-SEA混合建模及分析方法. 振动工程学报, 23 :140–144. ( Chen S M, Wang D F, Cao X L, Zan J M. 2010. Hybrid FE-SEA modeling and analysis method of car interior noise. Journal of Vibration Engineering, 23:140–144. ) |
| 陈徐均. 2001.浮体二阶非线性水弹性力学分析方法.[博士论文].无锡:中国船舶科学研究中心 Chen X J. 2001. Second order hydroelasticity analyses for marine structure.[PhD Thesis]. Wuxi: China Ship Scientific Research Center |
| 陈燕, 汤渭霖, 范军. 2010. 浅海波导中目标回声计算的射线声学方法. 声学学报, 35 :335–342. ( Chen Y, Tang W L, Fan J. 2010. The geometrical acoustic method for calculating the echo targets submerged in a shallow water waveguide. Acta Acustica, 35:335–342. ) |
| 陈越澎. 1999.加筋柱壳的声学设计方法研究.[博士论文].武汉:华中理工大学 Chen Y P. 1999. Research on acoustic design method of stiffened cylindricalshell.[PhD Thesis]. Wuhan: Huazhong University of Science and Technology |
| 崔宏武, 赵德有, 罗志雍, 宗智. 1990. 结构振动的水中声辐射计算. 中国造船, 3 :49–54. ( Cui H W, Zhao D Y, Luo J Y, Zong Z. 1990. Numerical calculation of underwater acoustic radiation by structure vibration. Shipbuilding of China, 3:49–54. ) |
| 丁宏, 陈美霞. 2011.基于统计能量法的双层圆柱壳振动与声性能分析//第十三届船舶水下噪声学术讨论会论文集, 鹰潭, 138-146 Ding H, Chen M X. 2011. Analysis of vibro-acoustic characteristics of double cylindrical shells by using statistical energy method//Proceedings of the 13th Conference on Underwater Noise of Ships, Yingtan, 138-146 |
| 丁渭平. 2002. 车身乘坐室声振耦合的动态子结构修改方法. 噪声与振动控制, 2 :17–19. ( Ding W P. 2002. A new dynamic substructure modification method for structure-acoustic coupling analysis of an automobile's passenger compartment. Noise and Vibration Control, 2:17–19. ) |
| 董艳秋, 林维学, 朱建国. 1989. 浅吃水肥大船波激振动研究. 中国造船, 1 :76–83. ( Dong Y Q, Lin W X, Zhu J G. 1989. A study on wave-excited vibration of shallow draft fullform ship. Shipbuilding of China, 1:76–83. ) |
| 杜双兴. 1990.海洋浮体结构的直接分析方法-三维线性水弹性随机分析理论及应用.[硕士论文].无锡:中国船舶科学研究中心 Du S X. 1990. Direct analysis method of the ocean floating bodies-the random analysis theory and application of linear three-dimensional hydroelasticity.[Master Thesis]. Wuxi: China Ship Scientific Research Center |
| 杜双兴. 1996.完善的三维航行船体线性水弹性力学频域分析方法.[博士论文].无锡:中国船舶科学研究中心 Du S X. 1996. Perfect frequency domain analysis method of linear three-dimensional hydroelasticity of ships with forward speed.[PhD Thesis]. Wuxi: China Ship Scientific Research Center |
| 杜双兴, 林吉如. 1993. 25000G/T浮动船坞拖航中运动和结构动应力的水弹性分析. 舰船性能研究, 4 :43–58. ( Du S X, Lin J R. 1993. Hydroelastic analysis of the movement and structure dynamic stress of a 25000G/T floating dock during towage. Research on Ship Performance, 4:43–58. ) |
| 杜双兴, 吴有生. 1998. Bessho型移动脉动源格林函数快速数值积分法. 中国造船, 2 :40–48. ( Du S X, Wu Y S. 1998. A fast evaluation method for the Bessho form translating-pulsating source Green's function. Shipbuilding of China, 2:40–48. ) |
| 范军. 2001.水中复杂目标回声特性研究.[博士论文].上海:上海交通大学 Fan J. 2001. Study on echo characteristics of underwater complex targets.[PhD Thesis]. Shanghai: Shanghai Jiao Tong University |
| 范军, 刘涛, 汤渭霖. 2003. 水中双层无限长圆柱壳体声散射. 声学学报, 28 :345–350. ( Fan J, Liu T, Tang W L. 2003. Acoustic scatter from double infinite concentric cylindrical shells in water. Acta Acustica, 28:345–350. ) |
| 范威, 范军, 陈燕. 2012. 浅海波导中目标散射的边界元方法. 声学学报, 37 :132–142. ( Fan W, Fan J, Chen Y. 2012. Boundary element method for target scattering in shallow water waveguide. Acta Acustica, 37:132–142. ) |
| 顾懋祥, 吴有生, 夏锦祝. 1987. 波浪中弹性船舶对称响应的时域分析. 舰船性能研究, 4 :31–44. ( Gu M X, Wu Y S, Xia J Z. 1987. Time domain analysis of symmetric response of elastic ships in waves. Research on ship performance, 4:31–44. ) |
| 何祚镛.2001. 结构振动与声辐射. 哈尔滨: 哈尔滨工程大学出版社 . ( He Z Y.2001. Vibration and Acoustic Radiation of Structures. Harbin: Harbin Engineering University Press ). |
| 胡宗军, 牛忠荣, 程长征, 周焕林. 2010. 三维Helmholtz积分方程外问题几乎奇异积分的半解析算法. 应用力学学报, 27 :532–537. ( Hu Z J, Niu Z R, Cheng C Z, Zhou H L. 2010. A semi-analytical algorithm for nearly singular integral of three dimensional exterior Helmholtz integral equation problem. Chinese Journal of Applied Mechanics, 27:532–537. ) |
| 嵇醒, 臧跃龙, 程玉民.1997. 边界元法进展及通用程序. 上海: 同济大学出版社 . ( Ji X, Zhang Y L, Cheng Y M.1997. Progress of Boundary Element Method and General Program. Shanghai: Tongji University Press ). |
| 姜琳, 赵德有. 2008. 浅海波导中椭球体声散射特性研究. 大连理工大学学报, 48 :528–532. ( Jiang L, Zhao D Y. 2008. Study of acoustic scattering from ellipsoids in shallow water wave-guide. Journal of Dalian University of Technology, 48:528–532. ) |
| 李善德, 黄其柏, 张潜. 2011. 快速多极边界元方法在大规模声学问题中的应用. 机械工程学报, 47 :82–89. ( Li S D, Huang Q B, Zhang Q. 2011. Application of fast multipole boundary element method for large-scale acoustic problems. Journal of Mechanical Engineering, 47:82–89. ) |
| 黎胜. 2001.水下结构声辐射和声传输的数值分析及主动控制模拟研究.[博士论文].大连:大连理工大学 Li S. 2001. Numerical analysis and active control simulation of underwater structural acoustic radiation and transmission.[PhD Thesis]. Dalian: Dalian University of Technology |
| 黎胜, 赵德有. 2000. 用边界元法计算结构振动辐射声场. 大连理工大学学报, 40 :391–394. ( Li S, Zhao D Y. 2000. Calculation of acoustic field radiated by vibrating structures using BEM. Journal of Dalian University of Technology, 40:391–394. ) |
| 李小瑜, 傅志方. 1989. 结构振动辐射声场的预估--边界积分方程中奇异积分的间接处理. 振动工程学报, 2 :59–65. ( Li X Y, Fu Z F. 1989. Pre-estimation of sound field radiated by a vibrating structure-singular integral processing method in boundary integral equation. Journal of Vibration Engineering, 2:59–65. ) |
| 林吉如, 郑苏龙, 孙勇, 章一军, 王雅洁. 1992. 整体弹性船模试验技术. 中国造船, 2 :63–71. ( Lin J R, Zheng S L, Sun Y, Zhang Y J, Wang Y J. 1992. Experimental techniques of the continued elastic model. Shipbuilding of China, 2:63–71. ) |
| 刘国利, 汤渭霖. 1996. 平面声波斜入射到水中无限圆柱的纯弹性共振散射. 声学学报, 21 :506–516. ( Liu G L, Tang W L. 1996. Pure elastic resonance scattering of an obliquely incident plane acoustic wave by a submerged infinite cylinder. Acta Acustica, 21:506–516. ) |
| 刘涛. 2002.水中复杂壳体的声-振特性研究.[博士论文].上海:上海交通大学 Liu T. Research on sound and vibration characteristics of complex cylindrical shell submerged in water.[PhD Thesis]. Shanghai: Shanghai Jiao Tong University |
| 刘涛, 汤渭霖, 何世平. 2003. 数值/解析混合方法计算含复杂结构的有限长圆柱壳体声辐射. 船舶力学, 7 :99–104. ( Liu T, Tang W L, He S P. 2003. Computation of sound radiation from complicated cylindrical shell by using numerical analytical matching method. Journal of Ship Mechanics, 7:99–104. ) |
| 刘兴章. 2011. 美国潜艇水声试验场现状及启示. 舰船科学技术, 33 :140–143. ( Liu X Z. 2011. Development prospect and revelation of submarine underwater noise test ground of US navy. Ship Science and Technology, 33:140–143. ) |
| 刘兴章, 陈涛. 2011. 挪威海格纳斯潜艇水声试验场测量设施分析. 噪声与振动控制, 5 :161–164. ( Liu X Z, Chen T. 2011. Analysis of facilities of Norwegian acoustic testing field in Heggernes. Noise and Vibration Control, 5:161–164. ) |
| 骆东平, 肖邵予, 曹钢, 郭华林. 2004. 甲板刚度和垂向位置对环肋圆柱壳声辐射性能的影响. 哈尔滨工程大学学报, 25 :605–609. ( Luo D P, Xiao S Y, Cao G, Guo H L. 2004. Vibroacoustic influence of the stiffness and location of the floating deck to cylindrical shell. Journal of Harbin Engineering University, 25:605–609. ) |
| 彭旭. 2004.敷设阻尼层潜艇舱段结构声辐射性能分析.[硕士论文].武汉:华中科技大学 Peng X. Analysis of structure-borne noise of submarine compartment coated with viscoelastic layer.[Master Thesis]. Wuhan: Huazhong University of Science and Technology |
| 祁立波. 2015.桨-轴-艇体耦合振动声辐射的三维声弹性分析方法.[博士论文].无锡:中国船舶科学研究中心 Qi L B. 2015. Three-dimensional sono-elastical analysis method of propeller-shaft-hull coupled vibration and acoustic radiation of a ship.[PhD Thesis]. Wuxi: China Ship Scientific Research Center |
| 祁立波, 邹明松. 2015. 加肋圆柱体水下低频辐射声特性研究. 船舶力学, 19 :874–883. ( Qi L B, Zou M S. 2015. Research on acoustic radiation of stiffened cylinder in low-frequency. Journal of Ship Mechanics, 19:874–883. ) |
| 商德江. 2000.复杂弹性壳体水下结构振动和声场特性研究.[博士论文].哈尔滨:哈尔滨工程大学 Shang D J. 2000. Research on sound and vibration characteristics of complex elastic shell submerged in water.[PhD Thesis]. Harbin: Harbin Engineering University |
| 沈顺根, 李琪华, 王大云, 程贯一. 1992. 加肋旋转壳结构噪声声辐射水弹性研究. 中国造船, 117 :53–62. ( Shen S G, Li Q H, Wang D Y, Cheng G Y. 1992. Hydroelastic analysis of sound radiation from a stiffened shell of revolution. Shipbuilding of China, 117:53–62. ) |
| 宋竞正, 任慧龙, 戴仰山. 1995. 船体非线性波浪载荷的水弹性分析. 中国造船, 2 :22–31. ( Song J Z, Ren H L, Dai Y S. 1995. Hydroelastic analysis of nonlinear wave-induced loads of ship hull. Shipbuilding of China, 2:22–31. ) |
| 孙丽萍. 2004.能量有限元法研究及其应用.[博士论文].哈尔滨:哈尔滨工程大学 Sun L P. 2004. Investigation and application of energy finite element method.[PhD Thesis]. Harbin: Harbin Engineering University |
| 谭林森, 骆东平, 吴崇健, 伏同先. 1999. 潜水器动力舱振动与声辐射. 华中理工大学学报, 27 :7–9. ( Tan L S, Luo D P, Wu C J, Fu T X. 1999. The vibration and sound radiation of submarine dynamic cabin. J. Huazhong Univ. of Sci. & Tech., 27:7–9. ) |
| 汤渭霖. 1999. 用物理声学方法计算界面附近目标的回波. 声学学报, 24 :1–5. |
| Tang W L. 2001. Calculation of acoustic scattering from object near an interface using physical acoustic method. Acta Acustica, 24:1–5. |
| 汤渭霖, 范军. 1999. 水中双层弹性球壳的回声特性. 声学学报, 24 :174–182. ( Tang W L, Fan J. 1999. Echoes from double elastic spherical shell in water. Acta Acustica, 24:174–182. ) |
| 汤渭霖, 何兵蓉. 2001. 水中有限长加肋圆柱壳体振动和声辐射近似解析解. 声学学报, 26 :1–5. ( Tang W L, He B R. 2001. Approximate analytic solution of vibration and sound radiation from stiffened finite cylindrical shells in water. Acta Acustica, 26:1–5. ) |
| 田宝晶. 2006.敷设阻尼层的加肋圆柱壳辐射性能及噪声特性分析.[博士论文].哈尔滨:哈尔滨工程大学 Tian B J. 2006. Cylindrical shells with viscoelastic layer and noise characteristics analysis.[PhD Thesis]. Harbin: Harbin Engineering University http://cdmd.cnki.com.cn/Article/CDMD-10217-2006133439.htm |
| 田超. 2007.航行船舶的非线性水弹性理论与应用研究.[博士论文].上海:上海交通大学 Tian C. 2007. Study on the theory and applications of nonlinear hydroelasticity of ships with forward speed. [PhD Thesis]. Shanghai: Shanghai Jiao Tong University |
| 王大云. 1996.三维船舶水弹性力学的时域分析方法.[博士论文].无锡:中国船舶科学研究中心 Wang D Y. 1996. Time domain analysis method of three-dimensional hydroelasticity of ships.[PhD Thesis]. Wuxi: China Ship Scientific Research Center http://d.wanfangdata.com.cn/Thesis_Y204979.aspx |
| 王桂波, 彭临慧. 2005. 浅海波导中刚性球声散射特性研究. 中国海洋大学学报, 35 :515–520. ( Wang G B, Peng L H. 2005. Studies on scattering from a rigid sphere in a shallow water wave-guide. Periodical of Ocean University of China, 35:515–520. ) |
| 王旌生. 2007.黏弹性复合材料结构水中振动和声辐射特性研究.[博士论文].上海:上海交通大学 Wang J S. 2007. Study on the vibration and acoustic properties of submerged composite material and composite structures.[PhD Thesis]. Shanghai: Shanghai Jiao Tong University |
| 王振鸿, 吴文伟, 徐敏, 席亦农. 1999. 船舶在波浪中的水平弯曲-扭转耦合响应水弹性分析. 中国造船, 40 :42–47. ( Wang Z H, Wu W W, Xu M, Xi Y N. 1999. Hydroelasticity analysis of horizontal bend-torsion coupled responses of ships in waves. Shipbuilding of China, 40:42–47. ) |
| 王志军. 2001.箱式超大型浮体结构的水弹性响应研究.[博士论文].上海:上海交通大学 Wang Z J. 2001. Study on hydroelastic response of box-type very large floating structure.[PhD Thesis]. Shanghai: Shanghai Jiao Tong University |
| 吴文伟, 沈荣瀛, 沈顺根. 2004. 设备基座输入机械阻抗工程估算方法. 振动工程学报, 17 :694–697. ( Wu W W, Shen R Y, Shen S G. 2004. An engineering approach to evaluate the input impedance of the machine foundation. Journal of Vibration Engineering, 17:694–697. ) |
| 吴文伟, 吴崇健, 沈顺根. 2002. 双层加肋圆柱壳振动和声辐射研究. 船舶力学, 6 :44–51. ( Wu W W, Wu C J, Shen S G. 2002. Study of the vibroacoustic radiation from the reinforced double cylindrical shells. Journal of Ship Mechanics, 6:44–51. ) |
| 吴轶钢. 2008.零阶能量有限元方法及其在船舶结构声辐射中的应用研究.[博士论文].武汉:武汉理工大学 Wu Y G. 2008. The research on zero-order energy flow analysis and its application in structural acoustic problems of ship structure.[PhD Thesis]. Wuhan: Wuhan University of Technology |
| 吴有生.1999. 世纪之交的船舶力学. 上海: 上海交通大学出版社 -399. ( Wu Y S.1999. Ship Mechanics at the Beginning of the 21st Century. Shanghai: Shanghai Jiao Tong University Press -399 ). |
| 吴有生, 司马灿, 刘建湖. 2007.船舶结构耦合动力学问题//第九届全国振动理论及应用学术会议论文集, 杭州, 25-31 Wu Y S, Sima C, Liu J H. 2007. Fluid-structure interaction problems of ships//Proceedings of the 9th National Conference on Vibration Theory and Application, Hangzhou, 25-31 |
| 吴有生, 夏锦祝, 王朝晖, 刘应中. 1994. 船舶波浪砰击的二维非线性水弹性力学分析. 中国船舶科学研究中心技术报告 . ( Wu Y S, Xia J Z, Wang C H, Liu Y Z. 1994. Two-dimensional nonlinear hydroelastic analysis of wave slamming of ships. China Ship Scientific Research Center Reports . ) |
| 夏锦祝. 1994.细长浮体的水弹性力学理论.[博士论文].无锡:中国船舶科学研究中心 Xia J Z. 1994. Hydroelasticity theories of slenser floating structures.[PhD Thesis]. Wuxi: China Ship Scientific Research Center |
| 夏锦祝, 吴有生. 1993. 流固耦合问题的一个一般交界面条件. 舰船性能研究, 3 :15–22. ( Xia J Z, Wu Y S. 1993. A general interface condition of the fluid-structure interaction problems. Research on Ship Performance, 3:15–22. ) |
| 向树红, 邱吉宝, 王大钧. 2004. 模态分析与动态子结构方法新进展. 力学进展, 34 :289–303. ( Xiang S H, Qiu J B, Wang D J. 2004. The resent progresses on modal analysis and dynamic sub-structure method. Advances in Mechanics, 34:289–303. ) |
| 谢基榕. 2011.推进器激励下的艇体声辐射及其控制技术研究.[博士论文].无锡:中国船舶科学研究中心 Xie J R. 2011. Propeller excitated noise radiation of ship hull structure.[PhD Thesis]. Wuxi: China Ship Scientific Research Center |
| 谢永和, 李润培, 杨建民. 2006. 水深对超大型FPSO水弹性响应的影响. 上海交通大学学报, 40 :993–996. ( Xie Y H, Li R P, Yang J M. 2006. The effects of water depth on hydroelastic response of a very large FPSO. Journal of Shanghai Jiaotong University, 40:993–996. ) |
| 徐向东. 1996.舰船结构冲击屈曲破损机理.[硕士论文].无锡:中国船舶科学研究中心 Xu X D. Damage mechanism of impact buckling of ship structures.[Master Thesis]. Wuxi: China Ship Scientific Research Center |
| 杨士莪.1994. 水声传播原理. 哈尔滨: 哈尔滨工程大学出版社 . ( Yang S E.1994. Principle of Underwater Acoustic Propagation. Harbin: Harbin Engineering University Press ). |
| 姚熊亮, 计方, 钱德进, 明磊. 2009. 壳间连接介质对双层壳声辐射性能的影响. 声学技术, 28 :312–317. ( Yao X L, Ji F, Qian D J, Ming L. 2009. The effect of linked materials on the sound radiation from double cylindrical shell. Technical Acoustics, 28:312–317. ) |
| 姚熊亮, 钱德进, 张爱国, 张阿漫. 2008. 内部含基座的加筋双层壳振动与声辐射计算. 中国舰船研究, 3 :31–36. ( Yao X L, Qian D J, Zhang A G, Zhang A M. 2008. Computation of vibration and sound radiation from double cylindrical shell coupled with frame. Chinese Journal of Ship Research, 3:31–36. ) |
| 姚熊亮, 王献忠, 孙龙泉, 庞福振. 2011. 复杂结构中频声振问题的方法研究. 振动工程学报, 24 :444–449. ( Yao X L, Wang X Z, Sun L Q, Pang F Z. 2011. The hybrid method for vibro-acoustic problem of the complex structure. Journal of Vibration Engineering, 24:444–449. ) |
| 叶永林. 2012.波浪中航行船体结构振动与噪声的水弹性分析.[博士论文].无锡:中国船舶科学研究中心 Ye Y L. 2012. Hydroelastic analysis of the structural vibration and noise radiation of a ship traveling in wave.[PhD Thesis]. Wuxi: China Ship Scientific Research Center |
| 叶永林, 吴有生, 尤国红. 2010.小水线面双体船波浪外载荷分析//北京造船工程学会学术交流论文集, 53-60 Ye Y L, Wu Y S, You G H. 2010. Analysis of SWATH ship wave loads//Proceeding of the Beijing Society of Naval Architects and Marine Engineers Conference, 53-60 |
| 叶永林, 邹明松, 周金华, 吴有生, 尤国红. 2011. 基于三维水弹性力学的浮体结构机械阻抗分析. 中国造船, 52 :53–60. ( Ye Y L, Zou M S, Zhou J H, Wu Y S, You G H. 2011. Mechanical impedance analysis by 3D hydroelasticity method. Shipbuilding of China, 52:53–60. ) |
| 殷学纲, 陈淮, 蹇开林.1991. 结构振动分析的子结构方法. 北京: 中国铁道出版社 . ( Yin X G, Chen H, Jian K L.1991. Substructure Method for Structure Vibration Analysis. Beijing: China Railway Publishing House ). |
| 殷学文. 2001.敷设消声瓦的双层加筋圆柱壳结构的振动和声辐射研究.[硕士论文].无锡:中国船舶科学研究中心 Yin X W. 2001. Research on vibration and acoustic radiation of stiffened double cylindrical shells coated with anechoic tile.[Master Thesis]. Wuxi: China Ship Scientific Research Center |
| 尤云祥, 潘文峰, 缪国平. 2007. 三维海洋波导中Helmholtz方程外问题的数值解. 上海交通大学学报, 41 :830–834. ( You Y X, Pan W F, Miao G P. 2007. The numerical solution for the exterior problem of the Helmholtz equation in 3D ocean waveguide. Journal of Shanghai Jiaotong University, 41:830–834. ) |
| 俞孟萨. 2007.舰船随机声弹性理论及声纳罩声学设计研究.[博士论文].无锡:中国船舶科学研究中心 Yu M S. 2007. Theory of random acoustoelasticity for ships and its application in acoustic design of sonar domes.[PhD Thesis]. Wuxi: China Ship Scientific Research Center |
| 曾革委. 2004. 无限长双层加肋圆柱壳水下声辐射解析计算. 振动工程学报, 17 :1010–1013. ( Zeng G W. 2004. Acoustic radiation from fluid-loaded infinite circular cylindrical double-shell. Journal of Vibration Engineering, 17:1010–1013. ) |
| 张健飞, 姜弘道. 2003. 大型边界元方程组的并行直接分块求解算法. 应用力学学报, 20 :129–133. ( Zhang J F, Jiang H D. 2003. A parallel direct block algorithm for large-scale BEM equation system. Chinese Journal of Applied Mechanics, 20:129–133. ) |
| 张敬东, 何祚镛. 1990. 有限元+边界元--修正的模态分解法预报水下旋转薄壳的振动和声辐射. 声学学报, 15 :12–19. ( Zhang J D, He Z Y. 1990. A finite element+boundary element-modified modal decomposition method for vibration and sound radiation from submerged revolutional shells. Acta Acustica, 15:12–19. ) |
| 张瑾, 马兴瑞, 韩增尧, 邹元杰. 2012. 中频力学环境预示的FE-SEA混合方法研究. 振动工程学报, 25 :206–214. ( Zhang J, Ma X R, Han Z Y, Zou Y J. 2012. FE-SEA hybrid method for the mid-frequency dynamic prediction. Journal of Vibration Engineering, 25:206–214. ) |
| 赵键, 汪鸿振, 朱物华. 1989. 边界元法计算已知振速封闭面的声辐射. 声学学报, 14 :250–257. ( Zhao J, Wang H Z, Zhu W H. 1989. Boundary element method for calculating acoustic radiation from closed surfaces with prescribed velocity distribution. Acta Acustica, 14:250–257. ) |
| 郑国垠, 范军, 汤渭霖. 2009. 充水有限长圆柱薄壳声散射: I. 理论.声学学报, 34 :490–497. ( Zheng G Y, Fan J, Tang W L. 2009. Acoustic scattering from fluid-filled finite cylindrical shell in water: I. theory. Acta Acustica, 34:490–497. ) |
| 郑国垠, 范军, 汤渭霖. 2010. 充水有限长圆柱薄壳声散射: Ⅱ. 实验.声学学报, 35 :31–37. ( Zheng G Y, Fan J, Tang W L. 2010. Acoustic scattering from fluid-filled finite cylindrical shell in water: Ⅱ. experiment. Acta Acustica, 35:31–37. ) |
| 朱克强, 郑道昌, 周江华, 刘桂云, 包雄关. 2005. 典型高速船的非线性水弹性响应. 宁波大学学报(理工版), 18 :458–462. ( Zhu K Q, Zheng D C, Zhou J H, Liu G Y, Bao X G. 2005. Nonlinear hydroelasticity response of representative high speed ship. Journal of Ningbo University (NSEE), 18:458–462. ) |
| 周海安, 王晓明, 梅玉林. 2012. 流固耦合的周期加强板的振动及声辐射研究. 力学学报, 44 :287–296. ( Zhou H A, Wang X M, Mei Y L. 2012. Theoretical analysis of the vibration and sound radiation from an infinite fluid-structure coupled plate stiffened by two-dimensional periodic structures. Chinese Journal of Theoretical and Applied Mechanics, 44:287–296. ) |
| 邹春平, 陈端石, 华宏星. 2004. 船舶水下辐射噪声特性研究. 船舶力学, 8 :113–124. ( Zou C P, Chen D S, Hua H X. 2004. Study on characteristics of ship underwater radiation noise. Journal of Ship Mechanics, 8:113–124. ) |
| 邹明松. 2012. 敷设声学覆盖层的双层加筋圆柱壳结构声辐射建模及声特性研究. 中国船舶科学研究中心技术报告 . ( Zou M S. 2012. Research on acoustic radiation of stiffened double cylindrical shells covered with acoustic layers. China Ship Scientific Research Center Reports . ) |
| 邹明松. 2014.船舶三维声弹性理论.[博士论文].无锡:中国船舶科学研究中心 Zou M S. 2014. Three-dimensional sono-elasticity of ships.[PhD Thesis]. Wuxi: China Ship Scientific Research Center |
| 邹明松, 刘艳敏, 祁立波. 2013. 舷间充水双层弹性薄球壳结构声辐射研究. 船舶力学, 17 :155–163. ( Zou M S, Liu Y M, Qi L B. 2013. Structural-acoustic radiation of elastic thin spheric double-shell with contained water. Journal of Ship Mechanics, 17:155–163. ) |
| 邹明松, 吴文伟, 余晓丽, 廖彬彬. 2013. 静水压下声学覆盖层声阻抗研究. 舰船科学技术, 35 :57–60. ( Zou M S, Wu W W, Yu X L, Liao B B. 2013. Calculation of acoustic coating's impedance under hydrostatic pressure. Ship Science and Technology, 35:57–60. ) |
| 邹明松, 吴有生. 2012. 多不连通流域耦合的声介质中三维结构水弹性力学研究. 中国造船, 53 :85–94. ( Zou M S, Wu Y S. 2012. Three dimensional hydroelasticity analysis of acoustic responses of structures coupled with multiply-disconnected fluid regions. Shipbuilding of China, 53:85–94. ) |
| 邹明松, 吴有生. 2014. 水弹性子结构分离及集成方法. 船舶力学, 18 :574–580. ( Zou M S, Wu Y S. 2014. A method used for separating and coupling substructure based on hydroelasticity theory and dynamic substructural theory. Journal of Ship Mechanics, 18:574–580. ) |
| 邹明松, 吴有生, 祁立波, 周金华. 2013. 声介质中水弹性力学消除不规则频率的方法. 船舶力学, 17 :1202–1208. ( Zou M S, Wu Y S, Qi L B, Zhou J H. 2013. Method to eliminate irregular frequencies in three-dimensional hydroelasticity in acoustic medium. Journal of Ship Mechanics, 17:1202–1208. ) |
| 邹明松, 吴有生, 沈顺根, 吴文伟. 2010. 考虑航速及自由液面影响的声介质中三维结构水弹性力学研究. 船舶力学, 14 :1304–1311. ( Zou M S, Wu Y S, Shen S G, Wu W W. 2010. Three-dimensional hydroelasticity with forward speed and free surface in acoustic medium. Journal of Ship Mechanics, 14:1304–1311. ) |
| 邹元杰. 2004.水中阻尼复合壳体结构声振特性的数值分析.[博士论文].大连:大连理工大学 Zou Y J. 2004. Numerical analysis of vibro-acoustic characteristics of underwater damped composite shells. [PhD Thesis]. Dalian: Dalian University of Technology |
| 邹元杰, 赵德有. 2004. 结构在浅水中的振动和声辐射特性研究. 振动工程学报, 17 :269–274. ( Zou Y J, ZhaoD Y. 2004. A vibro-acoustic study on structures in shallow water. Journal of Vibration Engineering, 17:269–274. ) |
| Abawi A T. 2011. The use of the virtual source technique in computing scattering from periodic ocean surface. J. Acoust. Soc. Am., 130:683–688. doi:10.1121/1.3613707 |
| Abawi A T, Porter M B. 2007. Propagation in an elastic wedge using the virtual source technique. J. Acoust. Soc. Am., 121:1374–1382. doi:10.1121/1.2431336 |
| Achenbach J D, Kechter J D, Xu Y L. 1988. Off boundary approach to the boundary element method. Comput. Mech. Appl. Mech. Engng., 70:191–201. doi:10.1016/0045-7825(88)90157-0 |
| Astley R J, Macaulay G J. 1994. Mapped wave envelope element for acoustic radiation and scattering. J. of Sound and Vibration, 170:97–117. doi:10.1006/jsvi.1994.1048 |
| Belik O, Bishop R E D, Price W D. 1980. On the slamming response of ships to regular head waves. Trans. RINA, 122:325–337. |
| Bessho M. 1977. On the fundamental singularity in the theory of ship motions in a seaway. Memoirs of the Defense Academy of Japan, 17:95–105. |
| Bishop R E D, Price W G. 1979. Hydroelasticity of Ships. Cambridge University Press . |
| Bishop R E D, Price W G, Temarel P. 1980. A unified dynamic analysis of antisymmetric ship response to waves, Suppl. Papers RINA, 122:349–365. |
| Bishop R E D, Price W G, Temarel P. 1991. A theory on the loss of the MV Derbyshire. Trans. RINA, 133:389–453. |
| Bishop R E D, Price W G, Wu Y S. 1986. A general linear hydroelasticity theory of floating structures moving in a seaway. Phil. Trans. Royal Soc. London., 316:375–426. doi:10.1098/rsta.1986.0016 |
| Bjarnason J, Igusa T, Choi S H, Achenbach J D. 1994. The effect of substructures on the acoustic radiation from axisymmetric shells of finite length. J. Acoust. Soc. Am., 96:246–255. doi:10.1121/1.410477 |
| Borlase G A, Vlahopoulos N. 2000. An energy finite element optimization process for reducing high-frequency vibration in large-scale structures. Finite Element in Analysis and Design, 36:51–67. doi:10.1016/S0168-874X(00)00007-X |
| Bouthier O M, Bernhard R J. 1995. Simple models of the energetics of transversely vibrating plates. Journal of Sound and Vibration, 182:149–1666. doi:10.1006/jsvi.1995.0187 |
| Burnett D S, Holford R L. 1998. Prolate and oblate spheroidal acoustic infinite element. Comput. Methods Appl. Mech. Eng., 158:117–141. doi:10.1016/S0045-7825(97)00251-X |
| Burroughs C B. 1984. Acoustics radiation from fluid loaded infinite circular cylinders with doubly periodic ring supports. J. Acoust. Soc. Am, 75:715–722. doi:10.1121/1.390582 |
| Burton A J, Miller G F. 1971. The application of the integral equation method to the numerical solution of some exterior boundary value problems. Proc. R. Soc. Lond. A., 323:201–210. doi:10.1098/rspa.1971.0097 |
| Cabos C, Jokat J. 1998. Computation of structure-borne noise propagation in ship structures using noiseFEM. In: Proceedings PRADS98, Osterveld and Tan eds. Elsevier :927–934. |
| Cao X T, Hua H X, Ma C. 2012. Acoustic radiation from shear deformable stiffened laminated cylindrical shells. Journal of Sound and Vibration, 331:651–670. doi:10.1016/j.jsv.2011.10.006 |
| Che X L, Riggs H R, Ertekin R C, Wu Y S, Wang M L. 1992. Two-dimensional analysis of prying response of twin-hull floating structures//Proceeding of Second International Offshore & Polar Engineering Conference, ISOPE'92. |
| Chen J T, Chang M H, Chen K H, Lin S R. 2002. The Boundary collocation method with meshless concept for acoustic eigenanalysis of two-dimensional cavities using radial basis function. Journal of Sound and Vibration, 257:667–711. doi:10.1006/jsvi.2002.5038 |
| Chen L H, Schweikert D G. 1963. Sound radiation from an arbitary body. J. Acoust. Soc. Am., 35:1626–1632. doi:10.1121/1.1918770 |
| Chen X J, Wu Y S, Cui W C, Tang X F. 2003. Nonlinear hydroelastic analysis of a moored floating body. Ocean Engineering, 30:965–1003. doi:10.1016/S0029-8018(02)00078-1 |
| Choi S B, Pierre C, Castanier M P. 1997. Statistical energy methods for mid-frequency vibration analysis//Proceeding 1997 SAE noise and Vibration Conference and Exposition, Traverse City, MI, USA. |
| Choi S H, Igusa T, Achenbach J D. 1995. Nonaxisymmetric vibration and acoustic radiation of submerged cylindrical shell of finite length containing internal substructures. J. Acoust. Soc. Am., 98:353–362. doi:10.1121/1.413689 |
| Dowell E H, Kubota Y. 1985. Asymptotic modal and statistical energy analysis of dynamical systems. J. Applied Mech., 52:949–957. doi:10.1115/1.3169174 |
| Du S X, Ertekin R C. 1991. Dynamic response analysis of a flexibly joined Multimodule very large floating structure//OCEANS'91, USA. |
| Epton M, Dembart B. 1995. Multipole translation theory for the three dimensional Laplace and Helmholtz equations. SIAM Journal scientific Computing, 16:865–897. doi:10.1137/0916051 |
| Everstine G C, Henderson F M. 1990. Coupled finite element/boundary element approach for fluid-structure interaction. J. Acoust. Soc. Am., 87:1938–1947. doi:10.1121/1.399320 |
| Fahy F, Gardonio P.2007. Sound and Structural Vibration-Radiation, Transmission and Response, Second Edition. Oxford: Academic Press in an imprint of Elsevier . |
| Fredo C R. 1997. A SEA-like approach for the derivation of energy flow coefficients with a finite element model. Journal of Sound and Vibration, 199:645–666. doi:10.1006/jsvi.1996.0634 |
| Giordano J A, Koopmann G H. 1995. State space boundary element-finite element coupling for fluidstructure interaction analysis. J. Acoust. Soc. Am., 98:363–372. doi:10.1121/1.413691 |
| Gladwell G M L. 1964. Branch mode analysis of vibrating systems. Journal of Sound and Vibration, 1:41–59. doi:10.1016/0022-460X(64)90006-9 |
| Gu M X, Wu Y S, Xia J Z. 1989. Time domain analysis of non-linear hydroelastic response of ships//Fourth PRADS, Varna, Bulgaria. |
| Gumerov N A, Duraiswami R. 2009. A broadband fast multipole accelerated boundary element method for the three dimensional Helmholtz equation. 125: 191-205. |
| Guo Y P. 1996. Acoustic radiation from cylindrical shells due to internal forcing. J. Acoust. Soc. Am., 99:1495–1505. doi:10.1121/1.414728 |
| Heller S R, Abramson H N. 1959. Hydroelasticity: A new naval science. J. Am. Soc. Naval Engns., 71:205–209. |
| Hu J J, Wu Y S, Tian C, Wang X L, Zhang F. 2012. Hydroelastic analysis and model test of structural responses and fatigue behaviors of an ultra large ore carrier in waves. J. of Eng. for the Maritime Environment, 226:135–155. |
| Hui C Y, Shia D. 1999. Evaluations of hypersingular integrals using Gaussian quadrature. Int. J. Num. Meth. Eng., 44:205–214. doi:10.1002/(ISSN)1097-0207 |
| Hunt J T, Knittel M R, Barach D. 1974. Finite element approach to acoustic radiation from elastic structures. J. Acoust. Soc. Am., 55:269–280. doi:10.1121/1.1914498 |
| Hunt J T, Knittel M R, Nichols C S, Barach D. 1975. Finite element approach to acoustic scattering from elastic structures. J. Acoust. Soc. Am., 57:287–299. doi:10.1121/1.380459 |
| Hurty W C. 1960. Vibration of structure systems by component mode synthesis. Jour. Engr. Mech. Div., ASCE, 86:51–59. |
| Hynna P, Klinge P, Vuoksinen J. 1995. Prediction of structure-borne sound transmission in large welded ship structures using statistical energy analysis. Journal of Sound and Vibration, 180:583–607. doi:10.1006/jsvi.1995.0101 |
| James J, Faran J R. 1951. Sound scattering by solid cylinders and spheres. J. Acoust. Soc. Am., 23:405–418. doi:10.1121/1.1906780 |
| Jang H W, Ih J G. 2013. Stabilization of time domain acoustic boundary element method for the exterior problem avoiding the nonuniqueness. J. Acoust. Soc. Am., 133:1237–1244. doi:10.1121/1.4774377 |
| Jensen F B, Kuperman W A, Porter M B, Schmidt H. 2011. Computational Ocean Acoustics, Second Edition. Springer . |
| Jiang L, Hong M. 2009. Studies on scattering from ellipsoids in a shallow water with sea bottom impedance. Journal of Ship Mechanics, 13:1013–1021. |
| Junger M C. 1952. Sound scattering by thin elastic shells. J. Acoust. Soc. Am., 24:366–373. doi:10.1121/1.1906905 |
| Junger M C, Feit D.1986. Sound, Structures, and Their Interaction, Second Edition. Massachusetts: The MIT Press . |
| Kallivokas L F, Bielak J. 1993. Time-domain analysis of transient structural acoustics problems based on the finite element method and a novel absorbing boundary element. J. Acoust. Soc. Am., 94:3480–3492. doi:10.1121/1.407202 |
| Kassem M, Soize C, Gagliardini L. 2009. Energy-density field approach for low-and medium-frequency vibroacoustic analysis of complex structure using a statistical computational model. Journal of Sound and Vibration, 323:849–863. doi:10.1016/j.jsv.2009.01.014 |
| Kean A J, Temarel P, Wu X J, Wu Y S. 1991. Hydroelasticity of non-beamlike ships in waves. The Dynamics of Ships, The Royal Soc. London, 153 . |
| Kim K H, Kim Y. 2012. Numerical analysis on ship hydroelasticity by using 3D rankine panel method and 3D finite element method//Proc. 6th International Conference on Hydroelasticity in Marine Technology, Tokyo, Japan, 63-74. |
| Koopmann G H, Song L, Fahnline J B. 1989. A method for computing acoustic fields based on the principle of wave superposition. J. Acoust. Soc. Am., 86:2433–2438. doi:10.1121/1.398450 |
| Langley R S, Bremner P. 1999. A hybrid method for the vibration analysis of complex structural-acoustic systems. J. Acoust. Soc. Am., 105:1657–1671. doi:10.1121/1.426705 |
| Laulagnet B, Guyader J L. 1991. Sound radiation from a finite cylindrical shell covered with a compliant layer. J. Vibration and Acoustics, 113:267–272. doi:10.1115/1.2930180 |
| Laulagnet B, Guyader J L. 1994. Sound radiation from finite cylindrical coated shells by means of asymptotic expansion of three-dimension equation for coating. J. Acoust. Soc. Am., 96:277–286. doi:10.1121/1.410480 |
| Lase Y, Ichchou M N, Jezequel L. 1996. Energy flow analysis of bars and beams: theoretical formulations. Journal of Sound and Vibration, 192:281–308. doi:10.1006/jsvi.1996.0188 |
| Li W L, Wu T W, Seybert A F. 1994. A half-space boundary element method for acoustic problems with a reflecting plane of arbitrary impedance. Journal of Sound and Vibration, 171:173–184. doi:10.1006/jsvi.1994.1112 |
| Lin J, Chen W, Chen C S. 2014. Numerical treatment of acoustic problems with boundary singularities by the singular boundary method. Journal of Sound and Vibration, 333:3177–3188. doi:10.1016/j.jsv.2014.02.032 |
| Lucifredi I, Schmidt H. 2006. Subcritical scattering from buried elastic shells. J. Acoust. Soc. Am., 120:3566–3583. doi:10.1121/1.2357711 |
| Lundgren J, Price W G, Wu Y S. 1988. A hydroelastic investigation into the behaviour of a floating 'dry' dock in waves//Spring Meeting, RINA, London. |
| Maidanik G, Biancardi R. 1982. Use decoupling to reduce the radiated noise generated by panels. J. Sound and Vibration, 81:165–185. doi:10.1016/0022-460X(82)90202-4 |
| Maxit L, Ege K, Totaro N, Guyader J L. 2014. Non resonant transmission modeling with statistical modal energy distribution analysis. Journal of Sound and Vibration, 333:499–519. doi:10.1016/j.jsv.2013.09.007 |
| Maxit L, Guyader J L. 2003. Extension of SEA model to subsystems with non-uniform modal energy distribution. Journal of Sound and Vibration, 265:337–358. doi:10.1016/S0022-460X(02)01459-1 |
| Mocormick J M, Baron M L. 1965. Sound radiation from submerged cylindrical shells of finite length. ASME Trns., Ser.B., 87:393–405. |
| Newman J N. 1978. The theory of ship motions. Advances in Applied Mechanics, 18:221–285. |
| Peters H, Kinns R, Kessissoglou N. 2014. Effects of internal mass distribution and its isolation on the acoustic characteristics of a submerged hull. Journal of Sound and Vibration, 333:1684–1697. doi:10.1016/j.jsv.2013.10.017 |
| Porter M B. 2001. The KRAKEN normal mode program. SACLANT Undersea Research Center. |
| Price W G, Wu Y S. 1984. Hydroelasticity of marine structure//Sectional Lecture S-10, the 16th In. Congress of Theoretical and Applied Mechanics (IUTAM), Lyngby, Denmark. |
| Price W G, Wu Y S. 1985. Structural responses of a SWATH of multi-hulled vessel travelling in waves//Int. Conf. On SWATH ships and Advanced Multi-hulled Vessels, RINA, London. |
| Price W G, Wu Y S. 1989. The influence of non-linear fluid forces in the time domain responses of flexible SWATH ships excited by a seaway//OMAE'89, 2: 125-135. |
| Qi L B, Zou M S. 2013. Acoustic radiation of stiffened cylinder with different shells. Journal of Ship Mechanics, 17:697–701. |
| Riggs H R, Ertekin R C. 1991. Approximate methods for dynamic response of multi-module floating structures//Proceedings of 1st International Workshop on Very Large Floating Structures, VLFS'91. |
| Salvesen N, Tuck E O, Faltinsen O. 1970. Ship motions and sealoads. Transaction of the Society of Naval Architecture and Marine Engineers, 78:250–287. |
| Schenck H A. 1968. Improved integral formulation for acoustic radiation problems. J. Acoust. Soc. Am., 44:41–58. doi:10.1121/1.1911085 |
| Schmidt H. 2004. Virtual source approach to scattering from partially buried elastic targets. In Porter M B, Siderius M and Kuperman W A, editors, American Institute of Physics Conference Series, 728:456–463. |
| Seybert A F, Soenarko B. 1988. Radiation and scattering of acoustic waves from bodies of arbitrary shape in a three-dimensional half space. ASME Transactions, J. Vib. Acoust. Stress Rel. Dsgn., 110:112–117. doi:10.1115/1.3269465 |
| Seybert A F, Soenarko B, Rizzo F J, Shippy D J. 1984. Application of the BIE method to sound radiation problems using an isoparametric element. ASME Transactions, J. Vib. Acoust. Stress Rel. Dsgn., 106:414–420. doi:10.1115/1.3269211 |
| Skelton E A, James J H.1997. Theoretical Acoustics of Underwater Structures. London: Imperial College Press . |
| Shorter P J, Langley R S. 2005. Vibro-acoustic analysis of complex systems. Journal of Sound and Vibration, 288:669–699. doi:10.1016/j.jsv.2005.07.010 |
| Soize C. 1993. A model and numerical method in the medium frequency range for vibroacoustic predicitions using the theory of structural fuzzy. J. Acoust. Soc. Am., 94:849–965. doi:10.1121/1.408186 |
| Strasberg M, Feit D. 1996. Vibration damping of large structures induced by attached small resonant structures. J. Acoust. Soc. Am., 99:335–344. doi:10.1121/1.414545 |
| Sun J G, Zou M S. 2015. Vibration response analysis of an underwater submersible. Journal of Ship Mechanics, 19:303–310. |
| Takahashi T, Hamada T. 2009. GPU-accelerated boundary element method for Helmholtz equation in three dimensions. Int. J. Numer. Meth. Engng., 80:1295–1321. doi:10.1002/nme.v80:10 |
| Temarel P. 1980. Unified dynamic analysis of antisymmetric response of ships to waves.[PhD Thesis]. London: University of London. |
| Tian C, Wu Y S. 2006. The second-order hydroelastic analysis of a SWATH ship moving in large-amplitude waves. Journal of Hydrodynamics, Ser. B., 18:631–639. doi:10.1016/S1001-6058(07)60001-8 |
| Tian C, Wu Y S, Chen Y Q. 2009. Numerical predictions on the hydroelastic responses of a large bulker in waves//Proceedings of the 5th International Conference on Hydroelasticity in Marine Technology, Southampton, UK. |
| Wang D Y, Wu Y S. 1998. Three dimensional hydroelastic analysis in time domain with application to an elastic ship model. Journal of Hydrodynamics, 10:54–61. |
| Wang M L, Du S X, Ertekin R C. 1991. Hydroelastic reponse and fatigue analysis of a multi-module very large floating structure//International Symposium on Fatigue and Fracture in Steel and Concrete Structures, Madras, India. |
| Wang X R, Ji Z L. 2008. Application of FMBEM to predict silencer acoustic performance. Journal of University of Science and Technology of China, 38:207–217. |
| Wohlever J C, Bernhard R J. 1990. Mechanical energy flow models of rods and beams. Journal of Sound and Vibration, 153:1–19. |
| Wu M K, Moan T. 1996. Linear and nonlinear hydroelastic analysis of high speed vessels. Journal of Ship Research, 40:149–163. |
| Wu T W., Seybert A F. 1991. A weighted residual formulation for the CHIEF method in acoustics. J. Acoust. Soc. Am., 90:1608–1614. doi:10.1121/1.401901 |
| Wu Y S. 1984. Hydroelasticity of floating bodies.[PhD Thesis]. London: Brunel University. |
| Wu Y S. 1991. A modified hydroelasticity theory and its application to long multi-body structures. China Ship Scientific Research Center Reports. |
| Wu Y S, Chen R Z, Lin J R. 2003. Experimental technique of hydroelastic ship model//Proceedings of the Third International Conference on Hydroelasticity in Marine Technology, Oxford, UK. |
| Wu Y S, Du S X, Riggs H R, Ertekin R C. 1993. Fluid-structure interaction analysis of very large floating structures// Aero-Hydroelasticity Developments and Applications. Beijing: Seismological Press. |
| Wu Y S, Maeda H, Kinoshita T. 1997. The second order hydrodynamic actions on a flexible body. SEISANKENKYU, Institute of Industrial Science of Univ. of Tokyo, 49:8–19. |
| Wu Y S, Ni Q J, Xie W, Zhou S Y, Tian C, Zhang Y, Wu Q. 2007. Hydrodynamic performance and structural design of a SWATH ship//Proceedings of International Conference on Practical Design of Ships and Other Floating Structures, Huston, USA. |
| Wu Y S, Wang D Y, Riggs H R, Ertekin R C. 1991. Composite singularity distribution method with application to hydroelasticity//Proceedings of the First International Workshop on Very Large Floating Structures, Honolulu, Hawaii, USA. Marine Structure, 6: 143-163. |
| Wu Y S, Xia J Z, Du S X. 1991. Two engineering approaches to hydroelastic analysis of slender ships//Dynamics of Marine Vehicles and Structures in Waves. Elsevier Science Publishers, 157-165. |
| Xia J Z, Wang Z H, Jensen J J. 1998. Non-linear wave loads and ship responses by a time-domain strip theory. Marine Structures, 11:101–123. doi:10.1016/S0951-8339(98)00008-2 |
| Xie Y H, Li R P. 2006. The effects of water depth on wave-induced loads of a very large FPSO by 3D hydroelastic theory//Proc. 4th International Conference on Hydroelasticity in Marine Technology, Wuxi, 35-40. |
| Yamamoto Y, Fujino M, Fukasawa T, Ohtsubo H. 1978. Slamming and whipping of ship among rough seas//Symp. Numerical Analysis of the Dynamics of Ship Structures, Association Technique Maritime at Aeronautique. |
| Yang P, Liu X L, Ding J, et al.. 2015. Hydroelastic responses of a VLFS in the waves influenced by complicated geographic environment//Proceedings of the 7th International Conference on Hydroelasticity in Marine Technology, Split, Croatia, 541-559. |
| Yin X W, Gu X J, Cui H F, Shen R Y. 2007. Acoustic radiation a laminated composite plate reinforced by doubly periodic parallel stiffeners. Journal of Sound and Vibration, 306:877–889. doi:10.1016/j.jsv.2007.06.047 |
| Young D L, Chen K H, Lee C W. 2006. Singular meshless method using double layer potentials for exterior acoustics. J. Acoust. Soc. Am., 119:96–107. doi:10.1121/1.2141130 |
| Zhang J T, He Z Y. 1987. Study of sound radiation of arbitrary revolution elastic shells dense medium excited by force//4th Int. cong. of Int. Maritime Association of East in Mediterrenean, Varna, Bulgarian. |
| Zhu X Q. 1986. Sound generation from a moving shell//Proc. and Int. Symp. on Shipboard Acoustic, Holland. |
| Zou M S, Wu Y S. 2015. A mixed analytical-numerical sono-elastic substructure method of submerged structures//Proceedings of the 8th International Conference on Navy and Shipbuilding Nowadays, St. Petersburg, Russia, 24-32. |
| Zou M S, Wu Y S, Liu Y M, Lin C G. 2013. A three-dimensional hydroelasticity theory for ship structures in acoustic field of shallow sea. Journal of Hydrodynamics, 25:929–937. doi:10.1016/S1001-6058(13)60442-4 |
| Zou M S, Wu Y S, Liu Y M. 2014. The application of three-dimensional hydroelastic analysis of ship structures in Pekeris hydro-acoustic waveguide environment. Acta Mechanica Sinica, 30:59–66. doi:10.1007/s10409-013-0096-0 |
| Zou M S, Wu Y S, Sima C. 2015. Time domain three-dimensional hydroelastic analysis of acoustic responses of a floating structure//Proceedings of the 7th International Conference on Hydroelasticity in Marine Technology, Split, Croatia, 729-738. |
| Zou M S, Wu Y S, Wu W W, Ye Y L, Tian C. 2012. The three-dimensional hydroelasticity theory of ship structures in acoustic fluid of shallow sea//Proceedings of the 6th International Conference on Hydroelasticity in Marine Technology, Tokyo, Japan, 125-134. |
| Zou M S, Wu Y S, Ye Y L. 2010. Three-dimensional hydroelasticity analysis of acoustic responses of ship structures//9th International Conference on Hydrodynamics, Shanghai, China, 844-851. |



