随着能源短缺、环境恶化问题的日益突出, 火力发电、石油、化工、核能、航空发动机等现代工业装备向着高温、高压和大型化趋势发展, 以提高装备的效益, 达到节约能源资源和保护环境的目的.随着装备向更高参数的发展, 其发生高温蠕变损伤断裂的风险加大, 因此保障高温装置和设备的安全可靠是现代工业文明面临的重大课题.
工业装置和设备中的高温部件在制造过程中不可避免地会产生缺陷, 在严苛的高温/高压/腐蚀环境及交变载荷下会产生缺陷和裂纹.随着部件使用时间的延长, 缺陷前蠕变损伤的累积将导致裂纹扩展.当蠕变裂纹扩展到由断裂力学所确定的临界长度时, 部件将发生失稳断裂失效.因此, 如何准确预测和评价蠕变裂纹扩展是高温结构寿命设计、完整性评定和运行维护中需要解决的核心问题.
目前, 蠕变裂纹扩展寿命的预测, 主要是基于宏观蠕变断裂力学的单参数理论, 通过宏观单参数C*实现材料的蠕变裂纹扩展(creep crack growth, CCG)速率数据向实际结构的移植.这一移植成立的理论前提是:实验室标准紧凑拉伸(compact tension, CT)试样和实际高温部件均处于高拘束裂尖状态, 当二者的C*相同时, 其裂尖前的应力、应变率场及CCG速率相同.然而实际情况是, 标准中规定的CT试样的几何、裂纹尺寸及弯曲加载方式使其裂尖处于高拘束状态; 而实际高温部件多为表面浅裂纹、且承受拉伸载荷, 其裂尖拘束较低.因此, 在同样的C*下, 实验室试样高拘束裂尖前的应力和应变率场强度将比实际部件高, 导致其CCG速率比实际部件大.显然, 按这种方法计算评价部件的蠕变裂纹扩展寿命, 将得到过于保守的结果, 因此迫切需要降低过大的保守性(Budden & Dean 2007).反之, 如果部件裂尖拘束高于试样, 将得到非保守的结果.产生这些问题的本质原因是实验室试样和实际结构裂尖拘束的不匹配, 即存在断裂拘束效应.而在现有的国内外高温缺陷评定的规范中, 还未考虑这种拘束效应对CCG速率的影响.因此, 为了提高蠕变裂纹扩展寿命评价的准确性(降低过大的保守性或消除非保守性), 迫切需要发展纳入裂尖拘束效应的高温部件蠕变裂纹扩展寿命的评价理论、技术和方法(Budden & Dean 2007).
在弹塑性断裂力学的框架内, 裂尖拘束效应已被广泛研究(Dodds et al. 1993), 已发展出了J-T (Betegeon & Hancock 1991), J-Q (O’Dowd & Shih 1991, 1992), J-A2 (Chao & Ji 1995), J-Tz (Guo 1993a, 1993b, 1995)等二参数断裂力学理论及J-Tz-QT (Guo 2000)等三参数断裂力学理论, 其中用T, Q, A2及QT定量化表征面内裂尖拘束, 用Tz表征面外拘束.此外, 基于细观损伤力学模型的裂纹起裂与扩展模拟的局部法, 通过裂尖断裂过程区应力、应变和损伤的计算亦可直接纳入裂尖拘束效应, 如基于GTN (Gurson-Tvergaard-Needleman)延性损伤力学的数值模拟方法已广泛用于不同拘束三维试样(Yang et al. 2014)及具有材料拘束效应的焊接接头试样(Fan et al. 2016)的延性裂纹扩展模拟.基于J-Q和J-T理论的拘束相关的缺陷评定方法也已纳入英国R6 (2006)、欧洲FITNET (2008)等先进规范中.由于本文主要综述作者对高温蠕变裂尖拘束的研究进展, 对这些弹塑性断裂拘束效应的研究状况未能展开全面介绍.
相比于弹塑性断裂拘束效应的研究和进展, 高温蠕变条件下的裂尖拘束效应的理论和应用研究还十分有限.目前主要在拘束对蠕变裂纹扩展速率影响的实验、蠕变裂尖拘束的定量化表征参数及影响因素、简化的理论预测模型等方面进行了一些研究.拘束效应主要由试样或结构几何、裂纹尺寸和加载方式所引起.许多实验和理论分析表明, 拘束影响CCG速率(Budden & Dean 2007; Nikbin et al. 1984, 1986; Webster & Ainsworth 1994; Nikbin 2004; Yatomi et al. 2004; Zhao et al. 2012, 2014; Tabuchi et al. 1991; Tan et al. 2012a, 2013; Yamamoto et al. 2009; Ozmat & Atgon 1991; Bettinson et al. 2000, 2002; Takahashi et al. 2005; Davies et al. 2006).在同一C*下, 平面应变下的CCG速率显著高于平面应力(Nikbin 1984, 1986; Webster & Ainsworth 1994; Nikbin et al. 2004; Yatomi et al. 2004); 深裂纹CT试样的CCG速率高于浅裂纹(Zhao et al. 2012); 随试样厚度的增大, CCG速率增大(Tan et al. 2012a, 2013; Zhao et al. 2014; Yamamoto et al. 2009), 厚试样的CCG速率比薄试样高3到5倍(Zhao et al. 2014, Yamamoto et al. 2009); CT试样的CCG速率比中心裂纹拉伸(centre-cracked tension, CCT)试样高3倍左右(Ozmat & Atgon 1991; Bettinson et al. 2000, 2002; Takahashi et al. 2005; Davies et al. 2006).由于不同研究者的试样拘束、C*水平和材料不同使裂尖前应力水平和分布不同, 从而引起材料微结构中(晶界、晶内和第二相)蠕变变形的机理不同, 如低应力水平下以晶界滑移与扩散蠕变为主; 高应力水平下以晶内/晶界位错运动的幂律蠕变为主(Asadi et al. 2012).裂尖应力及蠕变变形机理的不同进而引起蠕变断裂机理和材料蠕变延性的不同(Hales 1994, Kim et al. 2012).然而在不同裂尖拘束与C*偶合作用下, 材料中微孔洞与微裂纹的形核、长大和聚合的协同与竞争性蠕变损伤断裂的机理及其对CCG速率影响的规律还缺乏系统深入的研究和理解.
为建立纳入裂尖拘束效应的高温蠕变寿命工程评价方法, 首先需要从理论上研究定量化表征蠕变裂尖拘束的参数.在稳态蠕变条件下, 幂律蠕变类似于幂律塑性, C*参数类似于J积分.类比于弹塑性断裂条件下的J-Q二参数场, 蠕变裂尖应力和应变率场通常用C*-Q两参数描述, 用参数Q表征蠕变裂尖拘束(Shih et al. 1993, Budden & Ainsworth 1999, Bettinson et al. 2001), 并基于参数Q研究和预测拘束对CCG速率的影响(Nikbin 2004, Budden & Ainsworth 1999, Bettinson et al. 2001, Zhao et al. 2015).此外, 两参数C(t)-TZ (Xiang et al. 2011)和三参数C(t)-TZ-Q (Xiang et al. 2013)也被提出用于描述蠕变裂尖应力场, 用参数TZ表征面外蠕变拘束, 用Q表征面内蠕变拘束.在Q参数的定义中, 通常用HRR (Hutchinson-Rice-Rosengren)应力场作为参考场.
作者近年来的研究表明(Wang et al. 2010), 由于蠕变裂尖较大的变形钝化和损伤, HRR应力场也许不适合于作为定义拘束参数的参考场.从而提出基于标准平面应变高拘束CT试样的裂尖应力场作为参考场, 定义了一个新的蠕变拘束参数R (Wang et al. 2010).基于参数R的有限元方法(finite element method, FEM)计算, 研究了裂纹深度(Wang et al. 2010, Sun et al. 2011), 试样厚度(Sun et al. 2012)和加载方式(Wang et al. 2012)对蠕变裂尖拘束的影响.为便于工程应用和计算, 作者通过对参数R的修正, 定义了一个与载荷无关的拘束参数R* (Tan et al. 2014).基于参数R*及不同拘束试样的CCG速率实验结果, 研究建立了Cr-Mo-V钢拘束相关的CCG速率公式(Tan et al. 2014).为建立纳入裂尖拘束效应的CCG寿命评价的工程方法, 通过大量的FEM计算, 给出了高温承压管道的内表面半椭圆轴向裂纹(Liu et al. 2014)和环向裂纹(Liu et al. 2015a)的拘束参数R*的解, 并研究了材料蠕变性能对R*的影响及R*解的适用范围(Liu et al. 2016a).基于C*-R*两参数, 首次纳入拘束效应预测和评价了含内表面半椭圆轴向裂纹承压管道的蠕变裂纹扩展寿命(Liu et al. 2016b).基于参数R和R*, 分别对二维和三维高温承压管道的内表面裂纹的蠕变拘束进行了分析表征, 并研究了管道裂纹的裂尖拘束与不同几何试样裂尖拘束的关联(Liu et al. 2016b, Tan et al. 2015).作者在最近的工作中, 对面内/面外蠕变拘束进行了FEM分析(Liu et al. 2015b), 基于裂尖等效蠕变应变等值线所围面积定义了一个可以同时表征面内与面外蠕变拘束的统一拘束参数Ac (Ma et al. 2015), 基于Ac和CCG实验数据, 研究建立了统一拘束Ac与Cr-Mo-V钢(Ma et al. 2015, 2016a)和316H钢(Ma et al. 2106b) CCG速率的关联公式.对不同几何试样的Ac沿试样厚度的分布进行了3D FEM分析(Ma et al. 2016c).对宽范围C*区蠕变裂纹扩展速率及其拘束效应进行了数值预测研究(Zhang et al. 2014, 2015a, 2015b, 2015c).此外, 最近对非均质焊接接头中的材料拘束及其相关因素对蠕变裂纹扩展行为的影响及机理进行了研究(Chen et al. 2014, 2015a, 2015b).本文简要综述作者近年来在上述高温蠕变断裂拘束效应方面的研究工作(Tan et al. 2012b, 2013, 2014, 2015; Wang et al. 2010, 2012; Sun et al. 2011, 2012; Liu et al. 2014, 2015a, 2015b, 2016a, 2016b; Ma et al. 2015, 2016a, 2016b, 2016c; Zhang et al. 2014, 2015a, 2015b, 2015c; Chen et al. 2014, 2015a, 2015b)
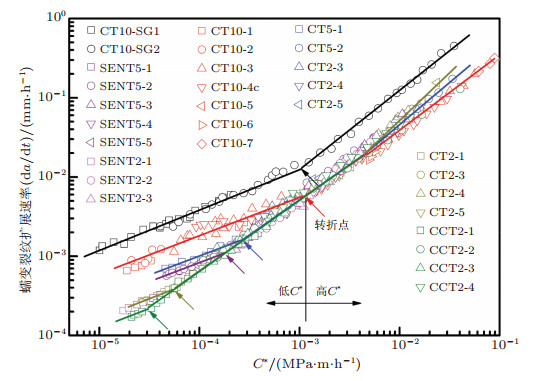
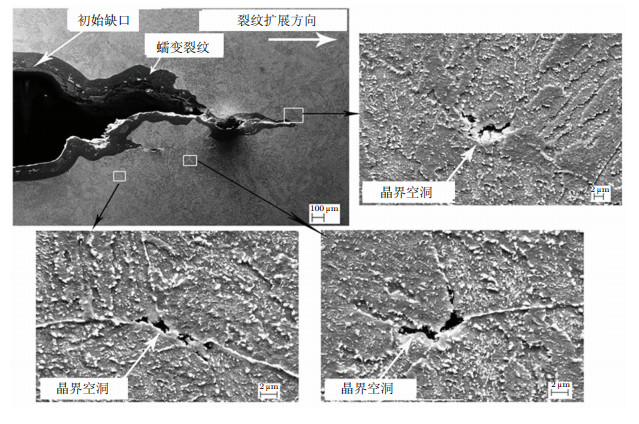
2 拘束对蠕变裂纹扩展行为的影响及机理许多实验结果表明:试样几何、裂纹尺寸、试样厚度、加载方式、载荷水平及材料蠕变性能等影响裂尖拘束, 从而影响蠕变裂纹扩展速率.如在同一C*水平下, 随试样厚度的增大, CCG速率增大(Tan et al. 2012, 2013; Zhao et al. 2014; Yamamoto et al. 2009); 随裂纹深度的增大, CCG速率增大(Zhao et al. 2012); CT试样的CCG速率高于CCT试样(Ozmat & Atgon 1991; Bettinson et al. 2000, 2002; Takahashi et al. 2005; Davies et al. 2006).为了探明拘束对蠕变裂纹扩展行为的影响规律及机理, 作者用不同厚度的CT试样对一种Cr-Mo-V钢在566℃下进行了蠕变裂纹扩展实验, 通过扫描电子显微镜研究了裂尖拘束对蠕变裂纹扩展影响的机理(Tan et al. 2013). CT试样的厚度从2 mm增大到10 mm以使试样面外拘束增大, 其中10 mm厚试样中心部位达到了平面应变的拘束水平(Sun et al. 2012), 其尺寸满足标准高拘束试样要求, 其测得的CCG速率数据一般可用于构件的蠕变寿命评价. 图 1的实验结果表明, 裂尖拘束对CCG速率的影响与C*水平相关.在低C*区随试样面外拘束的增大, CCG速率增大, 如图 1所示(图 1中CT试样的数据发表于文献(Tan et al. 2013), SENT (singleedge notched tension)和CCT试样数据发表于文献(Tan 2014)), 相应的断裂机理从延性晶间蠕变断裂(图 2)向脆性晶间蠕变断裂(图 3)发生了转变.在中等C*区, 拘束对CCG速率基本没有影响(图 1), 相应的延性晶间蠕变断裂机理不变.在高C*区, 随拘束增大, CCG速率略有下降(图 1), 相应的断裂机理为混合性晶间和穿晶延性断裂.如果用中-高C*区的CCG数据外推得到的低C*区数据用于高温构件的蠕变寿命预测将得到非保守结果.这些发现为建立裂尖拘束和C*水平相关的高温蠕变寿命预测模型和方法提供了物理基础.这些结果也表明, 在建立CCG速率与拘束参数的定量关联时, 需要考虑不同C*区蠕变断裂机理的不同, 在蠕变断裂机理不发生变化的C*区建立关联.
|
| 图 1 裂尖拘束对蠕变裂纹扩展速率的影响(Tan et al. 2013, Tan 2014) |
|
| 图 2 低拘束低C*试样(CT2-1)的蠕变延性晶间断裂(Tan et al. 2013) |

|
| 图 3 高拘束低C*试样(CT10-2)的蠕变脆性晶间断裂(Tan et al. 2013) |
在稳态蠕变条件下, 幂律蠕变类似于幂律塑性, C*参数类似于J积分.类比于弹塑性断裂条件下的J-Q二参数场, 蠕变裂尖应力和应变率场一般用式(1)中的C*-Q二参数描述(Shih et al. 1993, Budden & Ainsworth 1999)
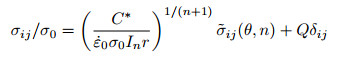
|
(1) |
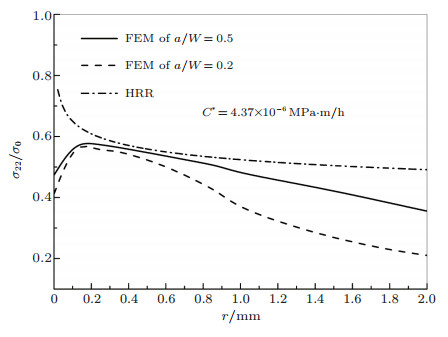
其中, σij为裂尖前正应力, σ0为标称应力(一般取为材料的屈服应力), 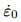
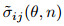
|
| 图 4 稳态蠕变条件下CT试样裂尖前的应力分布(Wang et al. 2010) |
图 4中裂尖区HRR应力奇异性不存在的原因是裂尖前的蠕变变形导致了裂尖钝化和损伤.裂尖的钝化和损伤将引起裂尖低应力, 使裂尖前的最大应力出现在距裂尖一定距离处, 而并不是HRR场预测的在裂尖处.由于HRR奇异场并不能描述蠕变条件下近裂尖区的应力分布, 且HRR解析场仅限于幂律蠕变材料和平面应力/应变状态.因此, 基于HRR参考场的Q参数不一定能准确地表征宽范围材料和应力状态下的蠕变裂尖拘束效应.由于平面应变状态下的深裂纹高拘束CT试样通常被用来测量材料的蠕变裂纹扩展速率, 由FEM计算的这一试样的裂尖应力场可以作为定义蠕变裂尖拘束参数的参考场.因此, 基于a/W=0.5的深裂纹高拘束CT试样的应力场, 本文作者按下式定义了一个新的拘束参数R (Wang et al. 2010)
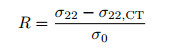
|
(2) |
R表征了相同C*下, 一定试样或结构蠕变裂尖应力σ22与a/W=0.5的深裂纹高拘束CT试样应力σ22, CT的差, σ0为标称应力, 一般取屈服应力. R ≥ 0意味着高拘束, R < 0为低拘束, 负R值的增大意味着裂尖拘束的降低.基于参数R, 作者进一步基于FEM分析, 表征了各种不同几何和加载方式试样的面内和面外拘束, 研究了试样几何、裂纹尺寸、加载方式、C*水平、蠕变时间和裂尖距离等因素对拘束参数R的影响规律及机理(Sun et al. 2011, 2012; Wang et al. 2012). 图 5和图 6所示为FEM计算的典型不同几何和加载方式试样的裂尖拘束参数R.随裂纹深度的增大, 拘束R增大(图 5(a)); 随载荷水平C*的增大, 拘束R降低(图 5(b)).弯曲主导加载的试样(CT, SENB, single-edge notched bend)的裂尖拘束高于拉伸主导加载的试样(SENT, CCT) (图 6(a)); 随试样厚度的增大, 拘束R增大, 试样中心区域(z/B=0.3~0.5, z为离试样表面的距离, B为试样厚度)的拘束高于表面部分(z/B=0~0.2) (图 6(b)).

|
| 图 5 (a)不同裂纹深度CT试样的裂尖拘束参数R的分布, (b) R随载荷水平C*的变化(Sun et al. 2011) |

|
| 图 6 (a)不同加载方式试样的裂尖拘束参数R随C*的变化, (b) R沿CT试样的厚度分布(Sun et al. 2012) |
实验室试样及实际高温构件的载荷水平一般不同, 从而使C*不同, 而上述蠕变拘束参数R与载荷水平C*相关, 这给拘束的表征、计算、拘束参数解的获得及应用带来不便.为了解决这一问题, 作者通过对R参数的修正提出了一个与载荷无关的蠕变拘束参数R* (Tan et al. 2014), 其定义如下

|
(3) |
其中, 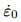

|
(4) |
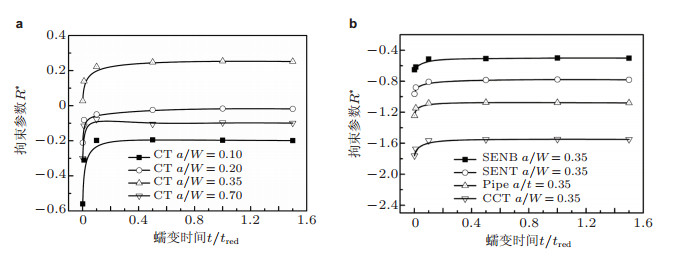
其中, A为蠕变系数, C1*为待评价拘束的试样或构件裂纹的C*, C2*为标准CT试样裂纹的C*.这样在R*的计算中无需保持待评价试样或构件的C*和CT试样的C*水平相同, 给R*的计算和应用带来方便. R*的载荷无关性通过大量试样和管道在不同载荷水平下的FEM计算已得到了验证. 图 7表明, 在稳态蠕变(t/tred=1)时, 不同载荷水平下各种加载方式试样和管道及不同厚度CT试样的拘束参数R*在裂尖前的分布不随载荷水平C*变化.参数R*与蠕变时间t/tred的关系曲线的FEM计算表明, 在蠕变早期(0 < t/tred < 0.1)阶段, R*随着蠕变时间而增大, 随后几乎不随t/tred改变(图 8).因而, 稳态蠕变条件下的参数R*可以略有保守地表征整个蠕变时间内构件和试样的拘束水平, 并可将其用于建立材料拘束相关的蠕变裂纹扩展性能. R*可用于纳入拘束效应的高温构件/试样的蠕变裂纹扩展寿命评价, 以降低目前评价方法过大的保守性或避免非保守性(Liu et al. 2016b).

|
| 图 7 稳态蠕变时(t/tred=1), 不同载荷水平下拘束参数R*在裂尖前的分布. (a)各种加载方式试样和管道, (b)不同厚度CT试样(Tan et al. 2014) |
|
| 图 8 拘束参数R*随蠕变时间t/tred的变化. (a)不同裂纹深度(a/W)的CT试样, (b)裂纹深度为a/W=0.35的不同加载方式的试样(Tan et al. 2014) |
承压管道是电力、石化等行业的主要高温部件, 其制造和运行中的缺陷主要是表面浅裂纹.为准确评定这些缺陷的蠕变裂纹扩展寿命, 需要基于C*-R*两参数评定以纳入裂尖拘束效应的影响.为此, 需要分析承压管道三维表面裂纹的拘束特征及影响因素, 并给出其工程计算解.为此, 作者通过大量三维FEM计算, 给出了不同几何管道的不同尺寸轴向和环向内表面半椭圆裂纹的拘束参数R*的插值计算表格及工程计算公式(Liu et al. 2014, 2015a).
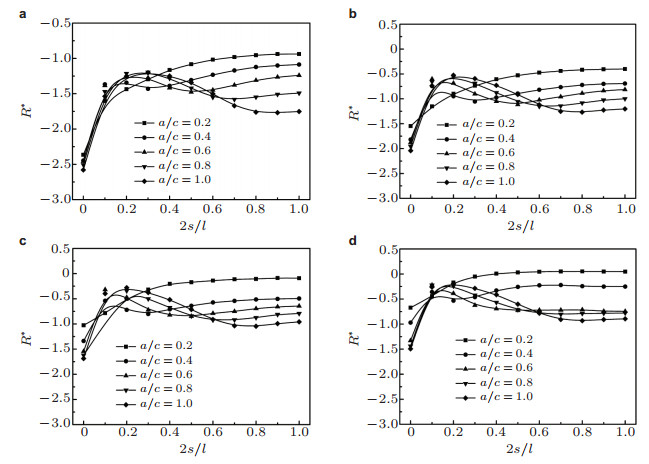
图 9为典型径厚比Ri/t=10 (Ri为管道内半径, t为壁厚)的管道轴向不同尺寸内表面半椭圆裂纹前沿的拘束参数R*的分布(Liu et al. 2014).随裂纹深度比a/t (a为裂纹深度, t为管道壁厚)和裂纹长度c的增大, 裂纹前沿的拘束增大; 随裂纹形状比a/c增大, R*最大值的位置从裂纹前沿的较深部分(2Φ/π ≈ 1, Φ为表征裂纹长度的角度)向自由表面部分(2Φ/π=0)移动. 图 10为典型径厚比Ri/t=10的管道环向不同尺寸内表面半椭圆裂纹前沿的拘束参数R*的分布(Liu et al. 2015a).在裂纹最深点(2s/l=1, s为距裂纹表面点的距离, l为裂纹弧长)处的拘束随裂纹长度c的增大而增大, 最大拘束的位置由裂纹前沿的自由表面部分(2s/l ≈=0.2)向较深部分(2s/l ≈ 1)改变; 裂尖拘束水平随裂纹深度a/t的增大而增大. 图 11表明随环向和轴向裂纹深度和长度的增大, 蠕变裂纹扩展速率比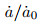

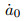
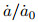

|
| 图 9 典型径厚比Ri/t=10的管道轴向不同尺寸内表面半椭圆裂纹前沿的拘束参数R*的分布(t/tred=1). (a) a/t=0.2, (b) a/t=0.4, (c) a/t=0.6, (d) a/t=0.8 (Liu et al. 2014) |
|
| 图 10 典型径厚比Ri/t=10的管道环向不同尺寸内表面半椭圆裂纹前沿的拘束参数R*的分布(t/tred=1). (a) a/t=0.2, (b) a/t=0.4, (c) a/t=0.6, (d) a/t=0.8 (Liu et al. 2015a) |

|
图 11 典型径厚比Ri/t=10的管道裂纹的拘束相关的蠕变裂纹扩展速率比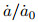 |
基于C*-R*两参数, 作者在国际上首次纳入拘束效应预测和评价了含内表面半椭圆轴向裂纹承压管道的蠕变裂纹扩展寿命(Liu et al. 2016b), 并给出了纳入拘束效应的CCG寿命评价的基本方法.并与基于传统单参数C*和FEM计算得到的结果进行了对比.结果表明:对于浅而短的管道裂纹, 基于单参数C*的寿命评价过于保守.为了降低过大的保守度, 强烈推荐在管道的蠕变裂纹扩展寿命评价中纳入拘束效应的影响.结果也表明, 随着初始裂纹尺寸的减小, 基于C*-R*两参数寿命评价得到的精度增益增大; 基于两参数法也可预测裂纹扩展过程中的形态变化.这些研究表明C*-R*两参数法具有良好的工程应用前景.
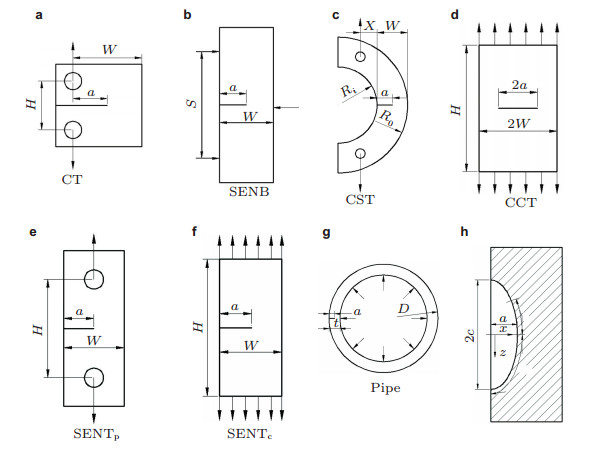
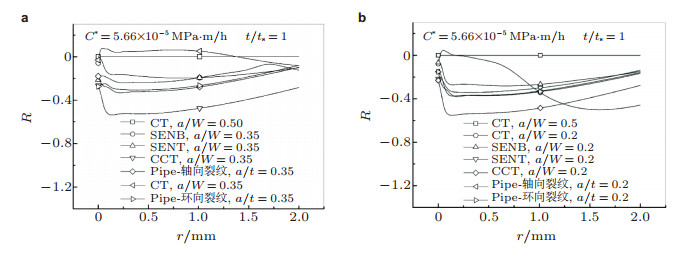
6 试样与管道轴向裂纹蠕变裂尖拘束的关联在结构完整性评定中, 纳入裂尖拘束效应的另一工程方法是基于两参数断裂力学理论和拘束分析, 找出与实际构件裂尖拘束最匹配的实验室试样, 用该试样测得的材料断裂性能数据评价结构的完整性.这一方法在弹塑性断裂力学领域已得到了一定的发展, 而在蠕变断裂力学领域还缺乏这方面的研究.作者基于蠕变拘束参数R和R*的FEM计算, 分别对二维和三维高温承压管道的内表面轴向裂纹的蠕变拘束进行了分析表征, 并研究了管道裂纹的裂尖拘束与不同几何和加载方式试样裂尖拘束的关联(Tan et al. 2012, 2015), 为在承压管道蠕变寿命评价中使用基于拘束设计的试样提供了技术支持. FEM计算分析的试样和管道的几何如图 12所示(Tan et al. 2015). 图 13和图 14中的计算结果表明:裂尖拘束由高到低的试样顺序为CT, CST, SENB, SENT和CCT; SENT试样的裂尖拘束与轴向管道裂纹的拘束最为接近; 试样和管道裂纹的裂尖拘束均随裂纹深度(a/W或a/t)的增大而增大(Tan et al. 2012, 2015).进一步的比较分析表明, 对于管道几何D/t=5, 10, 20和30 (D为管道外直径, t为管道壁厚)及裂纹深度为a/t < 0.35 (a为裂纹深度)的内/外表面轴向裂纹, 图 12所示的销式加载的SENTp试样(H/W=4, W=25 mm, B=12.5 mm, a/W=0.35)的裂尖拘束略高于管道裂纹.因此, 可以用该尺寸的SENTp试样测定的CCG速率数据略微保守地评定a/t < 0.35的管道内/外表面轴向裂纹的扩展寿命.对于a/t > 0.35的深裂纹管道, 可以用a/W=0.5的SENTp试样的CCG速率数据评定.
|
| 图 12 FEM计算裂尖拘束的试样和管道几何. (a) CT试样, (b) SENB试样, (c) CST (C-shaped tension)试样, (d) CCT试样, (e)销式加载的SENT试样(SENTp), (f)钳式加载的SENT试样(SENTc), (g)轴向裂纹管道, (h)管道裂纹尺寸表征(Tan et al. 2015) |
|
| 图 13 不同几何试样和轴向裂纹管道裂尖拘束的比较(Tan et al. 2012). (a) a/W=0.35, (b) a/W=0.2 |

|
| 图 14 B/W=0.5及W=25 mm的试样及t=25 mm的管道裂纹的平均拘束Ravg*值(Tan et al. 2015) |
拘束在本质上是结构对裂尖塑性变形的阻碍.拘束包括面内拘束和面外拘束, 面内拘束主要受裂纹深度及韧带尺寸的影响; 而面外拘束主要受平行于裂纹前沿的尺寸, 即试样厚度的影响.上述基于裂尖应力场的拘束参数Q, R和R*对面内拘束敏感, 主要用于表征面内拘束及较低的面外拘束.而在实际结构中面内与面外拘束一般同时存在, 为了描述二者的交互作用及结构的总体拘束水平, 需要发展可以同时有效地表征面内与面外拘束的统一拘束参数.近年来, 在弹塑性断裂力学领域基于裂尖塑性应变已提出了统一拘束参数ϕ (Mostafavi et al. 2009, 2010, 2011)和Ap (Yang et al. 2012, 2014a, 2014b; Mu et al. 2014), 而在蠕变断裂力学领域, 还未见任何研究.本文作者通过对不同试样面内/面外的蠕变拘束分析, 裂尖前等效蠕变应变分布的FEM计算, 并结合不同拘束试样的CCG试验和数值模拟, 研究提出了基于裂尖等效蠕变应变的面内与面外统一的拘束表征参数Ac, 其定义如下(Ma et al. 2015)
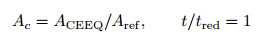
|
(5) |
ACEEQ是给定C*水平下待评定结构或试样在稳态蠕变(t/tred=1)时裂尖前等效蠕变应变εc等值线所围的面积, Aref是同样C*和t/tred=1时平面应变标准CT试样裂尖前等效蠕变应变εc等值线所围的面积, 该面积为参考面积. 图 15表明不同面内/面外拘束试样的蠕变裂纹扩展速率da/dt和不同εc下的拘束参数Ac可以形成一条统一的关联线, 说明Ac对面内和面外拘束同样敏感, 是一个面内与面外统一的蠕变拘束表征参数, 且与裂尖前等效蠕变应变εc的选取值无关.进一步的分析发现, 参数Ac是与载荷无关的, 即其值不随载荷水平C*变化(图 16(a)). 图 16(a)表明, 当蠕变时间t/tred > 0.7后, 对于大多数试样, Ac基本不随蠕变时间t/tred变化.因而, Ac可以在t/tred=1的稳态蠕变下定义和计算, 并可以用来表征面内与面外的复合拘束对CCG速率的影响. 图 16(a)中针对Cr-Mo-V钢建立的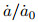
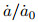

|
| 图 15 不同面内/面外拘束试样的蠕变裂纹扩展速率da/dt和拘束参数Ac的关联(Ma et al. 2015) |

|
图 16 (a)不同拘束试样的CCG速率比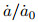 |
为了基于C*-R*或C*-Ac两参数蠕变断裂力学理论, 实现含缺陷高温部件的蠕变裂纹扩展寿命的准确评价, 需要建立材料的CCG速率与C*-R*或C*-Ac两个参数的关联(传统单参数评定中, 仅建立CCG速率与C*一个参数的关联), 即建立材料拘束相关的蠕变裂纹扩展速率.基于单参数C*的蠕变裂纹扩展速率通常表示为
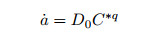
|
(6) |
其中, 

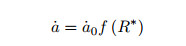
|
(7) |
其中, 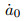
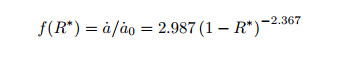
|
(8) |
其中, 标准CT试样的CCG速率公式为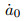
按同样方法研究得到的316H钢的CCG速率与C*和拘束参数R*的关系如下
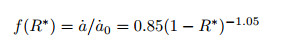
|
(9) |
其中, 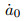
若采用参数Ac来表征蠕变拘束, 研究得到的Cr-Mo-V钢的CCG速率与C*和拘束参数Ac的关系如下(Ma et al. 2015)
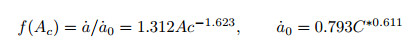
|
(10) |
按同样方法研究得到的316H钢的CCG速率与C*和拘束参数Ac的关系如下(Ma et al. 2016b)
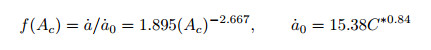
|
(11) |
上述这些材料拘束相关的蠕变裂纹扩展速率可用于纳入拘束效应的CCG寿命评价中, 用以预测不同拘束构件或试样的CCG速率(Liu et al. 2016b).
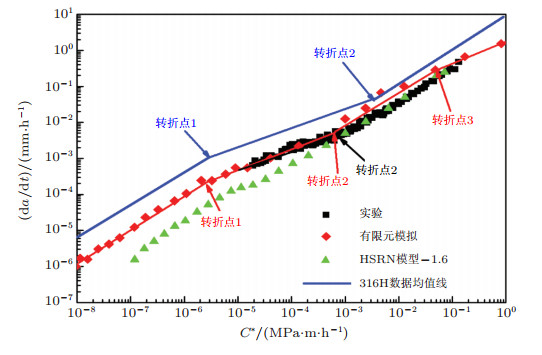
9 宽范围C*区蠕变裂纹扩展速率及其拘束效应的数值预测在目前的高温材料和结构的蠕变寿命预测、评价和设计中, 还未有效考虑材料蠕变本构和蠕变延性的应力相关性及裂尖拘束的影响, 因而存在非保守性(不安全)或过大的保守性(不经济).作者以Cr-Mo-V钢为研究对象, 将其应力区相关的蠕变本构和蠕变延性模型, 嵌入基于延性耗竭的蠕变损伤力学模型和ABAQUS有限元软件中, 开发了蠕变裂纹扩展模拟技术(Zhang et al. 2015a).通过模拟的CCG速率与现有文献中的试验数据的对比验证了模拟的可靠性(图 17), 并进一步数值研究了应力区相关的蠕变本构和蠕变延性及不同几何试样的裂尖拘束对宽范围C*区蠕变裂纹扩展速率的影响规律和力学机理(Zhang et al. 2014, 2015b, 2015c).
|
| 图 17 采用应力相关的蠕变本构和延性方法模拟得到的宽范围C*下的da/dt-C*曲线及与实验曲线的对比(Zhang et al. 2015a) |
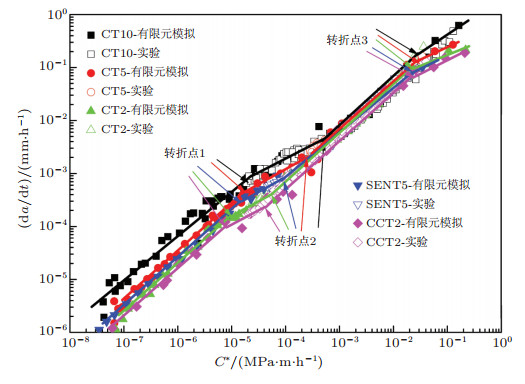
图 17为采用应力区相关的蠕变本构和延性方法模拟得到的宽范围C*下的da/dt-C*曲线(Zhang et al. 2015b), 发现曲线由4段不同斜率的直线段构成, 含有3个斜率转折点, 探明了斜率转变点产生的力学机理; 分析了da/dt-C*曲线的分段线性特征对高温结构蠕变寿命评价所产生的影响, 即用高C*区或中间过渡C*区的CCG数据外推评价低C*下高温结构的蠕变寿命将产生非保守或过于保守的结果. 图 18为不同拘束试样在宽范围C*下模拟的蠕变裂纹扩展速率da/dt-C*曲线及与实验的对比(Zhang et al. 2014), 结果表明, 模拟曲线与实验曲线吻合良好, 在低C*和过渡C*区, 裂尖拘束对蠕变裂纹扩展速率有显著影响, CCG速率随着试样拘束水平的提高而增大.分析表明:在宽范围C*区, 拘束对CCG行为的影响主要是由于裂尖应力状态与应力相关的蠕变延性在不同C*区交互作用的结果.用数值方法进一步研究了不同试样面内与面外拘束及其交互作用对宽范围C*区蠕变裂纹扩展速率的影响(Zhang et al. 2015c).结果表明:面内与面外拘束对CCG速率的影响存在交互作用, 即高的面内拘束强化了面外拘束对CCG速率的影响; 同样, 高的面外拘束强化了面内拘束对CCG速率的影响.提出在材料CCG速率的试验测定和高温部件蠕变寿命的准确预测中, 需要考虑面内、面外拘束及其交互作用的影响.这些数值模拟研究也为发展宽范围C*下材料拘束相关的蠕变裂纹扩展速率公式提供了方法.
|
| 图 18 不同拘束试样在宽范围C*下模拟的蠕变裂纹扩展速率da/dt-C*曲线及与实验的对比(Zhang et al. 2015b) |
材料拘束指裂尖前由于材料性能(强度、加工硬化及蠕变性能等)的不同或失配对裂尖应力状态的影响及进而对材料断裂行为的影响.作者对P92钢焊接接头CT试样建立了多材料FEM力学模型, 基于延性耗竭蠕变损伤模型的FEM, 系统地研究了与材料拘束相关的各因素对焊接接头蠕变裂纹扩展行为的影响规律.主要包括:焊接接头材料蠕变性能失配(Chen et al. 2014)及裂尖热影响区(heat-affected-zone, HAZ)宽度(Chen et al. 2015a)引起的不同材料拘束对接头CCG行为的影响; 接头中不同初始裂纹位置及载荷水平引起的不同材料拘束对接头蠕变CCG行为的影响(Chen et al. 2015).基于裂尖区及不同材料界面区的应力-应变分布、接头的蠕变裂纹起裂(creep crack initiation, CCI)时间、CCG路径、CCG速率及破断寿命的详细计算结果, 及与文献实验结果的对比分析, 研究了材料拘束相关的各因素对接头CCG行为影响的机理, 探讨了材料拘束对高温焊接接头安全评价和寿命设计的影响.
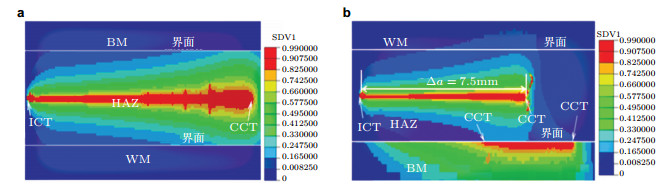
研究发现:当裂尖HAZ材料的蠕变强度至少比周围一种非裂尖材料低时, 接头中的裂纹沿原始裂纹面直线扩展(图 19(a)), 材料拘束效应使接头寿命降低.而当裂尖HAZ材料蠕变强度至少高于周围一种非裂尖材料时, 裂纹沿原始裂纹面直线扩展一段距离后, 在材料界面处的软材料中由于高的三轴应力而形成二次裂纹(second crack, SC) (图 19(b)), SC的快速扩展导致接头断裂, SC的形成时间主导整个焊接接头的破断寿命.对于裂尖HAZ为蠕变软材料的焊接接头, 随HAZ材料区宽度的增大, 材料拘束效应逐渐减小, 接头破断寿命增长(图 20).对于焊接接头中一些特定位置的裂纹, 由于各材料区蠕变本构方程的应力区相关性及材料拘束效应的不同, 导致其在不同载荷水平下的CCG行为不同(Chen et al. 2015b).在低载荷水平下, 各材料间较大的材料拘束效应使SC在材料界面处的软材料中形成, CCG速率较高; 而在较高载荷水平下, 所有裂纹均沿初始裂纹面直线扩展, CCG速率较低.如果用从高载荷下外推得到的低载荷下的CCG速率数据去评定或设计工作在低载荷下的焊接接头, 则可能出现非保守(不安全)的结果.在高温焊接接头的蠕变安全评价及寿命设计中, 需要充分和全面考虑材料拘束相关因素, 包括材料蠕变性能失配、不同材料区宽度、裂纹位置及载荷水平对裂纹扩展行为和寿命的影响.
|
| 图 19 焊接接头裂纹扩展损伤云图. (a)裂纹沿原始裂纹面直线扩展, (b)二次裂纹的形成(Chen et al. 2014) |

|
| 图 20 (a) HAZ为蠕变软材料时不同HAZ宽度的焊接接头的△a-t曲线, (b)破断寿命随HAZ宽度的变化曲线(Chen et al. 2015a) |
本文综述了作者近年来在高温蠕变断裂拘束效应方面的研究工作.主要内容包括:提出以标准平面应变高拘束CT试样的裂尖应力场作为参考场, 定义了一个新的蠕变拘束参数R.基于参数R, 研究得到了裂纹深度, 试样厚度和加载方式对蠕变裂尖拘束的影响规律.为便于工程应用和计算, 通过对参数R的修正, 定义了一个载荷无关的拘束参数R*.基于参数R和R*, 分别对二维和三维高温承压管道的内表面裂纹的蠕变拘束进行了分析表征, 并研究了管道裂纹的裂尖拘束与不同几何试样裂尖拘束的关联, 提出基于SENT试样的CCG数据可实现管道裂纹的拘束匹配评定.基于参数R*及不同拘束试样的CCG速率实验结果, 研究建立了Cr-Mo-V钢和316H钢拘束相关的CCG速率公式.通过大量的FEM计算, 给出了高温承压管道的内表面半椭圆轴向裂纹和环向裂纹的拘束参数R*的解, 并研究了材料蠕变性能对R*的影响及R*解的适用范围.基于C*-R*两参数, 对含裂纹管道的CCG寿命进行了纳入拘束的评价, 并给出拘束评价的基本方法.在最近的工作中, 对面内/面外蠕变拘束进行了研究, 基于裂尖等效蠕变应变等值线所围面积研究定义了一个可以同时表征面内与面外蠕变拘束的统一拘束参数Ac, 并建立了统一拘束参数Ac与Cr-Mo-V钢和316H钢CCG速率的关联公式.对宽范围C*区蠕变裂纹扩展速率及其拘束效应进行了数值预测研究; 对非均质焊接接头中的材料拘束相关因素对蠕变裂纹扩展行为的影响及机理也进行了研究.
上述研究为建立纳入拘束效应的高温构件的蠕变裂纹扩展寿命评价的方法奠定了理论和技术基础.在该领域可进一步开展的研究包括:基于拘束参数R*的高温蠕变裂纹扩展寿命评定的技术方法、评定案例及验证研究; 纳入拘束效应的评定方法与现有的先进国际高温缺陷评定规范(如BS7910, R 5等)相结合, 发展我国自主的先进高温缺陷评定规范; 为实现更高级别精度的高温缺陷的拘束评定, 进一步研究面内与面外统一的拘束参数Ac的应用技术和方法; 研究试验与数值模拟相结合的材料拘束相关的CCG速率的构建方法; 研究纳入几何与材料拘束效应的焊接接头CCG寿命评价的技术方法; 研究纳入拘束效应的蠕变-疲劳裂纹扩展寿命评价的理论和技术方法.
| Asadi M, Hegde S R, Sawatzky T, Guillot D, Koul A K, Saari H, Weck A. 2012. Constructing a validated deformation mechanisms map using low temperature creep strain accommodation processes for nickel-base alloy 718//Proceedings of the ASME 2012 Pressure Vessels and Piping Division Conference. Toronto, Ontario, Canada, PVP2012-78092. |
| Betegeon C, Hancock J W. 1991. Two parameter characterization of elastic plastic crack-tip fields. Journal of Applied Mechanics, 58:104–110. doi:10.1115/1.2897135 |
| Bettinson A D, Nikbin K M, O' Dowd N P, Webster G A. 2000. The influence of constraint on the creep crack growth of 316H stainless steel//Proceedings 5th International Conference Structural Integrity Assessment.Cambridge, UK. |
| Bettinson A D, O'Dowd N P, Nikbin K M, Webster G A. 2001. Two parameter characterization of crack tip fields under creep conditions//IUTAM Symposium on creep in structures. Netherlands, 95-104. |
| Bettinson A D, O'Dowd N P, Nikbin K M, Webster G A. 2002. Experimental investigation of constraint effects on creep crack growth//ASME 2002 Pressure Vessels and Piping Conference. Vancouver, BC, Canada. |
| Budden P J, Ainsworth R A. 1999. The effect of constraint on creep fracture assessments. International Journal of Fracture, 97:237–247. doi:10.1023/A:1018305919622 |
| Budden P J, Dean D W. 2007. Constraint effects on creep crack growth//Proceedings of eighth international conference on creep and fatigue at elevated temperatures. July 22-26, San Antonio, Texas. |
| Chao Y J, Ji W. 1995. Cleavage fracture quantified by J and A2//Constraint Effects in Fracture Theory and Applications, ASTM STP1244, vol. 2. Philadelphia, PA:American Society for Testing and Materials, 1-20. |
| Chen G, Wang G Z, Xuan F Z, Tu S T. 2014. Mismatch effect in creep properties on creep crack growth behavior in welded joints. Materials and Design, 63:600–608. doi:10.1016/j.matdes.2014.06.047 |
| Chen G, Wang G Z, Xuan F Z, Tu S T. 2015a. Effects of HAZ widths on creep crack growth properties of welded joints. Welding in the World, 59:851–860. doi:10.1007/s40194-015-0259-7 |
| Chen G, Wang G Z, Zhang J W, Xuan F Z, Tu S T. 2015b. Effects of initial crack positions and load levels on creep failure behavior in P92 steel welded joint. Engineering Failure Analysis, 47:56–66. doi:10.1016/j.engfailanal.2014.10.005 |
| Davies C M, Mueller F, Nikbin K M, O'Dowd N P, Webster G A. 2006. Analysis of creep crack initiation and growth in different geometries for 316H and carbon manganese steels. Journal of ASTM International, 3:1–20. |
| Dodds R H, Shih J C F, Anderson T L. 1993. Continuum and micromechanics treatment of constraint in fracture. International Journal of Fracture, 64:101–133. |
| Fan K, Wang G Z, Xuan F Z, Tu S T. 2016. Geometry and material constraint effects on fracture resistance behavior of bi-material interfaces. International Journal of Fracture :1–13. doi:10.1007/s10704-016-0112-z.1-13 |
| FITNET FFS Procedure. 2008. Final Draft MK8, Prepared by European fitness-for-service networkFITNET. |
| Guo W L. 1993a. Elastoplastic three dimensional crack border field-I. Singular structure of the field. Engineering Fracture Mechanics, 46:93–104. doi:10.1016/0013-7944(93)90306-D |
| Guo W L. 1993b. Elastoplastic three dimensional crack border field-II. Asymptotic solution for the field.Engineering Fracture Mechanics, 46:105–113. |
| Guo W L. 1995. Elasto-plastic three-dimensional crack border field-III.Fracture parameters. Engineering Fracture Mechanics, 51:51–71. doi:10.1016/0013-7944(94)00215-4 |
| Guo W L. 2000. Recent advances in three-dimensional fracture mechanics. Key Engineering Materials, 183:193–198. |
| Hales R. 1994. The role of cavity growth mechanisms in determining creep-rupture under multiaxial stresses. Fatigue & Fracture of Engineering Materials & Structures, 17:579–591. |
| Kim N H, Kim Y J, Davies C M, Nikbin K M, Dean D W. 2012. Creep failures simulations for 316H at 550°//Proceedings of the ASME 2012 Pressure Vessels and Piping Division Conference. Toronto, Ontario, Canada, PVP2012-78133. |
| Liu S, Wang G Z, Xuan F Z, Tu S T. 2014. Creep constraint analysis and constraint parameter solutions for axial semi-elliptical surface cracks in pressurized pipes. Engineering Fracture Mechanics, 132:1–15. doi:10.1016/j.engfracmech.2014.10.019 |
| Liu S, Wang G Z, Tu S T, Xuan F Z. 2015a. Creep constraint analysis and constraint parameter solutions for circumferential surface cracks in pressurized pipes. Engineering Fracture Mechanics, 148:1–14. doi:10.1016/j.engfracmech.2015.09.012 |
| Liu S, Wang G Z, Xuan F Z, Tu S T. 2015b. Three-dimensional finite element analyses of in-plane and outof-plane creep crack-tip constraints for different specimen geometries. Engineering Fracture Mechanics, 133:264–280. doi:10.1016/j.engfracmech.2015.10.009 |
| Liu S, Wang G Z, Xuan F Z, Tu S T. 2016a. Effects of creep properties of materials on creep crack-tip constraint parameter R*. Materials at High Temperatures, 33:208–217. doi:10.1080/09603409.2016.1145397 |
| Liu S, Wang G Z, Tu S T, Xuan F Z. 2016b. Creep crack growth prediction and assessment incorporating constraint effect for pressurized pipes with axial surface cracks. Engineering Fracture Mechanics, 154:92–110. doi:10.1016/j.engfracmech.2016.01.009 |
| Ma H S, Wang GZ, Xuan F Z, Tu S T. 2015. Unified characterization of in-plane and out-of-plane creep constraint based on crack-tip equivalent creep strain. Engineering Fracture Mechanics, 142:1–20. doi:10.1016/j.engfracmech.2015.05.044 |
| Ma H S, Wang G Z, Tu S T, Xuan F Z. 2016a. Unified correlation of in-plane and out-of-plane creep constraints with creep crack growth rate. International Journal of Pressure Vessels and Piping, 139-140:47–60. doi:10.1016/j.ijpvp.2016.03.003 |
| Ma H S, Wang G Z, Liu S, Tu S T, Xuan F Z. 2016b. In-plane and out-of-plane unified constraint-dependent creep crack growth rate of 316H steel. Engineering Fracture Mechanics, 155:88–101. doi:10.1016/j.engfracmech.2016.01.017 |
| Ma H S, Wang G Z, Liu S, Tu S T, Xuan F Z. 2016c. Three-dimensional analyses of unified characterization parameter of in-plane and out-of-plane creep constraint. Fatigue & Fracture of Engineering Materials and Structures, 39:251–263. |
| Mostafavi M, Smith D J, Pavier M J. 2011. Fracture of aluminum alloy 2024 under biaxial and triaxial loading. Engineering Fracture Mechanics, 78:1705–1716. doi:10.1016/j.engfracmech.2010.11.006 |
| Mostafavi M, Pavier M J, Smith D J. 2009. Unified measure of constraint//International Conference on Engineering Structural Integrity Assessment. Manchester, UK:ESIA10. |
| Mostafavi M, Smith D J, Pavier M J. 2010. Reduction of measured toughness due to out-of-plane constraint in ductile fracture of aluminium alloy specimens. Fatigue & Fracture of Engineering Materials & Structures, 33:724–739. |
| Mu M Y, Wang G Z, Xuan F Z, Tu S T. 2014. Unified parameter of in-plane and out-of-plane constraint effects and its correlation with brittle fracture toughness of steel. International Journal of Fracture, 190:87–98. doi:10.1007/s10704-014-9976-y |
| Nikbin K M, Smith D J, Webster G A. 1984. Prediction of creep crack growth from uniaxial creep data. Procceedings of the Royal Society of London, Series A, 396:183–197. doi:10.1098/rspa.1984.0116 |
| Nikbin K M, Smith D J, Webster G A. 1986. An engineering approach to the prediction of creep crack growth. Journal of Engineering Materials and Technology, 108:186–191. doi:10.1115/1.3225859 |
| Nikbin K M. 2004. Justification for meso-scale modelling in quantifying constraint during creep crack growth. Materials Science Engineering A, 365:107–113. doi:10.1016/j.msea.2003.09.014 |
| O'Dowd N P, Shih C F. 1991. Family of crack-tip fields characterized by a triaxiality parameter.I:Structure of fields. Journal of Mechanics and Physics of Solids, 39:989–1015. doi:10.1016/0022-5096(91)90049-T |
| O'Dowd N P, Shih C F. 1992. Family of crack-tip fields characterized by a triaxiality parameter.II:Fracture Applications.. Journal of Mechanics and Physics of Solids, 40:939–963. doi:10.1016/0022-5096(92)90057-9 |
| Ozmat B, Argon A S, Parks D M. 1991. Growth modes of cracks in creeping type 304 stainless steel. Mechanics of Materials, 11:1–17. doi:10.1016/0167-6636(91)90036-Y |
| R6 Revision 4, 2006. with amendments, Assessment of the integrity of structures containing defects, British Energy Genation Ltd., Gloucester, UK. |
| Shih C F, O'Dowd N P, Kirk M T. 1993. A framework for quantifying crack tip constraint//Constraint Effects in Fracture, American Society for Testing and Materials, Philadelphia, 2-20. |
| Sun P J, Wang G Z, Xuan F Z, Tu S T, Wang Z D. 2011. Quantitative characterization of creep constraint induced by crack depths in compact tension specimens. Engineering Fracture Mechanics, 78:653–665. doi:10.1016/j.engfracmech.2010.11.017 |
| Sun P J, Wang G Z, Xuan F Z, Tu S T, Wang ZD. 2012. Three-dimensional numerical analyses of out-ofplane creep crack-tip constraint in compact tension specimens. International Journal of Pressure Vessels and Piping, 96-97:78–89. doi:10.1016/j.ijpvp.2012.06.007 |
| Tabuchi M, Kubo K, Yagi K. 1991. Effect of specimen size on creep crack growth rate using ultra-large CT specimens for 1Cr-Mo-V steel. Engineering Fracture Mechanics, 40:311–321. doi:10.1016/0013-7944(91)90266-4 |
| Takahashi Y, Igari T, Kawashima F, Date S, Titoh N I, Noguchi Y, Kobayashi K, Tabuchi M. 2005. High temperature crack growth behavior of high-chromium steels//18th International conference on structural mechanics in reactor technology. Beijing, China, 1904-1915. |
| Tan J P, Wang G Z, Xuan F Z, Tu S T. 2012a. Experimental investigation of in-plane constraint and out-of-plane constraint effects on creep crack growth//Proceedings of the ASME 2012 Pressure Vessels and Piping Division Conference. Toronto, Ontario, Canada, PVP2012-78478. |
| Tan J P, Wang G Z, Xuan F Z, Tu S T. 2012b. Correlation of creep crack-tip constraint between axially cracked pipelines and test specimens. International Journal of Pressure Vessels and Piping, 98:16–25. doi:10.1016/j.ijpvp.2012.06.004 |
| Tan J P, Tu S T, Wang G Z, Xuan F Z. 2013. Effect and mechanism of out-of-plane constraint on creep crack growth behavior of a Cr-Mo-V steel. Engineering Fracture Mechanics, 99:324–34. doi:10.1016/j.engfracmech.2013.01.017 |
| Tan J P. 2014. Creep life assessment of structures containing crack incorporating constraint effect.[PhD Thesis]. Shanghai:East China University of Science and Technology. |
| Tan J P, Tu S T, Wang G Z, Tu S T. 2014. Load-independent creep constraint parameter and its application. Engineering Fracture Mechanics, 116:41–57. doi:10.1016/j.engfracmech.2013.12.015 |
| Tan J P, Tu S T, Wang G Z, Xuan F Z. 2015. Characterization and correlation of 3-D creep constraint between axially cracked pipelines and test specimens. Engineering Fracture Mechanics, 136:96–114. doi:10.1016/j.engfracmech.2015.01.018 |
| Wang G Z, Liu X L, Xuan F Z, Tu S T. 2010. Effect of constraint induced by crack depth on creep crack-tip stress field in CT specimens. International Journal of Solids and Structures, 47:51–57. doi:10.1016/j.ijsolstr.2009.09.015 |
| Wang G Z, Kui L B, Xuan F Z, Tu S T. 2012. Numerical investigation on the creep crack-tip constraint induced by loading configuration of specimens. Engineering Fracture Mechanics, 79:353–362. doi:10.1016/j.engfracmech.2011.11.014 |
| Webster G A, Ainsworth R A.1994. High Temperature Component Life Assessment. London: Chapman and Hall, Springer . |
| Xiang M J, Yu Z B, Guo W L. 2011. Characterization of three-dimensional crack border fields in creeping solids. International Journal of Solids and Structures, 48:2695–2705. doi:10.1016/j.ijsolstr.2011.05.013 |
| Xiang M J, Guo W L. 2013. Formulation of the stress fields in power law solids ahead of three-dimensional tensile cracks. International Journal of Solids and Structures, 50:3067–3088. doi:10.1016/j.ijsolstr.2013.05.011 |
| Yatomi M, O'Dowd N P, Nikbin K M, Webster G A. 2006. Theoretical and numerical modelling of creep crack growth in a carbon-manganese steel. Engineering Fracture Mechanics, 73:1158–1175. doi:10.1016/j.engfracmech.2005.12.012 |
| Yamamoto M, Miura N, Ogata T. 2009. Effect of constraint on creep crack propagation of mod. 9Cr-1Mo steel weld joint//ASME 2009 Pressure Vessels and Piping Conference:American Society of Mechanical Engineers, 1533-1539. |
| Yang J, Wang G Z, Xuan F Z, Tu S T. 2012. Unified characterization of in-plane and out-of-plane constraint based on crack-tip equivalent plastic strain. Fatigue & Fracture of Engineering Materials & Structures, 36:504–514. |
| Yang J, Wang G Z, Xuan F Z, Tu S T. 2014a. A Unified correlation of in-plane and out-of-plane constraint with fracture resistance of a dissimilar metal welded joint. Engineering Fracture Mechanics, 115:296–307. doi:10.1016/j.engfracmech.2013.11.018 |
| Yang J, Wang G Z, Xuan F Z, Tu S T. 2014b. Unified correlation of in-plane and out-of-plane constraint with fracture toughness. Fatigue & Fracture of Engineering Materials & Structures, 37:132–145. |
| Zhang J W, Wang G Z, Xuan F Z, Tu S T. 2014. Prediction of creep crack growth behavior in Cr-Mo-V steel specimens with different constraints for a wide range of C*. Engineering Fracture Mechanics, 132:70–84. doi:10.1016/j.engfracmech.2014.10.025 |
| Zhang J W, Wang G Z, Xuan F Z, Tu S T. 2015a. The influence of stress-regime dependent creep model and ductility in the prediction of creep crack growth rate in Cr-Mo-V steel. Materials and Design, 65:644–651. doi:10.1016/j.matdes.2014.09.070 |
| Zhang J W, Wang G Z, Xuan F Z, Tu S T. 2015b. Effect of stress dependent creep ductility on creep crack growth behavior of steels for wide range of C*. Materials at High Temperatures, 32:369–376. doi:10.1179/1878641314Y.0000000027 |
| Zhang J W, Wang G Z, Xuan F Z, Tu S T. 2015c. In-plane and out-of-plane constraint effects on creep crack growth rate in Cr-Mo-V steel for a wide range of C*. Materials at High Temperatures, 32:512–523. doi:10.1179/1878641314Y.0000000039 |
| Zhao L, Jing H, Xu L, Han Y, Xiu J. 2012. Evaluation of constraint effects on creep crack growth by experimental investigation and numerical simulation. Engineering Fracture Mechanics, 96:251–266. doi:10.1016/j.engfracmech.2012.08.009 |
| Zhao L, Jing H Y, Xiu J, Han Y D, Xu L Y. 2014. Experimental investigation of specimen size effect on creep crack growth behavior in P92 steel welded joint. Materials & Design, 57:736–743. |
| Zhao L, Xu L Y, Han Y D, Jing H Y. 2015. Quantifying the constraint effect induced by specimen geometry on creep crack growth behavior in P92 steel. International Journal of Mechanicals Science, 94-95:63–74. doi:10.1016/j.ijmecsci.2015.02.009 |



