2.中国科学院大学工程科学学院, 北京 100049
2.School of Engineering Science, University of Chinese Academy of Sciences, Beijing 100049, China
随着油气资源的开采向深海的进军, 当水深超过300 m后因海洋环境变得更加恶劣而且水深较大传统的固定式平台已经不能适应这种深水海洋工程的需求取而代之的是浮式生产系统, 包括以油轮为基础的浮式生产储油卸油船(floating production storage and offloading FPSO)、半潜式平台、张力腿平台和单立柱式(Spar)平台等(见图 1). 无论采用何种浮式平台方案, 都需要使用立管和管道/生产管线它们是海洋工程基础结构的关键组成部分, 其中立管是进行深水石油天然气开采必不可少的设备它连接了海底矿藏与海面的作业平台主要进行钻探、导液、导泥、传递信息等工作.

|
| 图 1 深水平台及其水下立管系统(http://oceanexplorer.noaa.gov/explorations/12lophelia/background/platforms/media/platform_types.html) |
开采竞争的激烈化要求石油公司以尽可能低的平台建造成本开采尽可能多的油气资源平台成本的降低, 很大程度上依赖于平台结构的合理、准确的设计.在深海平台系统的结构设计中除了要考虑上部浮体本身在作业和极端海况环境下的载荷、系统响应和运动稳定性问题还要考虑其水下小尺度结构例如立管、隔水管(以下统称为立管)等细长结构的疲劳和强度问题因为这些水下结构的外部需要承受复杂海洋环境载荷(如海流、波浪、内波等)和平台运动的影响内部有所输送的油或气(有时是高温高压的)通过这些载荷的长期周期作用以及它们之间的耦合效应会引起结构的周期往复运动从而降低结构的疲劳寿命甚至可能造成立管的大幅度运动直接导致结构破坏.
立管涡激振动即立管尾流涡脱落的频率与结构频率接近时发生的自激振动(vortex-induced vibration VIV)一直以来是立管结构疲劳破坏的一个主要因素也是长期以来海洋工程中颇具挑战性的问题之一因为涡激振动在本质上是非线性的、自激又自限制的多自由度共振响应涉及结构运动的非线性例如锁频响应、滞回、位移的跳跃以及分叉和混沌;又涉及流体力学的非定常剪切层、分离点移动、转捩、湍流等诸多复杂问题因此目前人们尚未能对VIV问题给出精确的理论解尤其对其中的一些非线性现象的认识和机理解释仍然存在诸多争议(Sarpkaya 1979, 2004; Vandiver et al. 2009; Williamson & Govardhan 2004, 2008; Chen et al. 2014; Wu et al. 2012a; Balasubramanian & Skop 1996; 王艺 2010; 郑仲钦 2012a).
而随着水深的增加, 柔性立管(flexible riser FR)的涡激振动问题变得更加严峻. 一方面因为水深的增加使立管的长度成倍地增加立管系统在设计、安装和运行方面的困难急剧上升其设计成本占总体系统的成本比例大幅度提高甚至一艘深海钻采平台立管系统的造价与平台结构和锚链系统的总造价相当.另一方面, 从海洋环境条件和结构本身的特性来看:
(1) 随着水深的增加深海洋流作用加强而且沿结构展向(水深方向)的分布不再是均匀的例如海流速度沿结构展向的剪切变化、海流方向沿结构变化以及海洋内波的作用等使得流场作用沿结构展向表现出幅值、方向、相位的非均匀性也就是说水下结构所承受的环境载荷变得更加复杂;
(2) 水深增加使立管的结构长度增大, 结构的柔度也增大而通常在很大的深度范围内这些水下结构在水中没有支撑设备保护;从深水立管展长与直径的比(长径比)很大(高达103量级)的柔性梁结构动力特性来看其结构的柔性大自然模态的频率低且模态密集(相邻模态的频率差值很小), 因此在同样的来流条件下大长径比柔性立管较一般的刚性圆柱易出现高阶-多阶模态参与的宽带振动而且除了横向振动, 还伴随有扭转、轴向振动从而造成立管响应和受力形式更加多样;
(3) 深水浮式平台运动幅度相对于潜水固定导管架平台明显增大上部浮体运动与水下结构的动力耦合作用增强而且诱发了一些新的耦合稳定性和动响应问题(例如参数激励、轴向/横向的双向耦合效应、非线性响应放大、新锁频区域等问题).
还有其他的一些因素例如立管的结构形式更加多样(诸如立管束、复合式立管等)以及不断增大的立管几何尺寸(半径)、轴向张力、阻力等等所有这些因素使得深水立管的VIV预测和控制变得更加困难. 因此深水平台的水下细长结构(立管、海底管线等)在海流、波浪、内波等环境载荷作用下的涡激振动问题一直以来成为国际上深水油气开采中的一个热点问题(Vandiver et al. 2009, Chen et al. 2014, Tognarelli et al. 2004, Marcollo et al. 2007, Xu et al. 2012, Wang et al. 2007, 张立武 2010, Chen et al. 2016, Fu et al. 2014; Yang & Xiao 2014, 唐友刚等 2013).
本文将对近几十年国内外在海洋立管的涡激振动的现象观察、机理认识、响应分析和预测等方面的研究进展进行论述.
展示涡激振动这种典型的非线性流固耦合现象所具有的特征例如自激、自限制、展向相关等;总结不同的结构响应预测方法和有关实验/数值模拟结果;讨论当前基础理论研究和实际工程中的热点问题和挑战并对今后的研究工作方向进行力所能及的展望.
2 海洋柔性立管VIV的基本特征 2.1 深水平台的立管系统根据Clausen和D'Souza(2001) 的统计世界上悬挂在各种浮式平台上的生产立管超过1 550根钻井立管则超过150根. 其中, 85%的生产立管为柔性. 在巴西Roncador Seillean FPSO上使用的生产立管所处的水深达到1 853 m是当时水深最大的生产立管. 钻井立管的最大水深则超过3 000 m例如我国首座自主设计、建造的第六代半潜式"海洋石油981"钻井平台于2012年5月首钻成功, 其最大设计作业水深为3 000 m最大设计钻井深度达10 000 m. 这些深海立管的长径比也非常大最大为2 000以上.
为适应深海平台的特殊要求, 目前立管有多种结构形式按照材料分可以分为刚性立管和柔性立管, 按照线型分可以分为顶张力立管(top tension riser, TTR)、钢悬链线立管(steel catenary riser SCR)、惰性S立管、陡峭型S立管、陡峭型波浪立管等, 如图 2(Narzul & Marion 1986). 目前, 国外运用最多的深水立管是TTR, SCR 以及FR. TTR一般用在水深不超过1 500 m的张力腿和Spar平台上主要进行油气的输送和油田的开采; 而SCRFR由于具有结构上和材料上的优点已经被国外用于深水以及超深水的半潜式和FPSO中进行油气的输送和流体的注入和输出.
|
| 图 2 几种典型海洋立管. (a) 顶张力立管, (b) 钢悬链线立管, (c) 惰性S立管, (d) 陡峭型S立管(e)惰性波浪立管, (f) 惰性型波浪立管 |
对深海浮式平台系统, 立管的长度比较长, 可以从几百米到几千米; 而且除了海底井口和平台底部外, 立管的其他地方通常没有固定支撑.在海洋立管设计中, 立管的强度和结构疲劳是主要的考虑因素之一.立管的结构疲劳和破坏主要来源于3个方面:(1) 海流流经立管等圆柱型结构其尾迹中的涡脱落的频率与结构的自振频率一致(或者接近)时引起结构的涡激振动;(2) 波浪力的周期作用而导致的立管往复运动;(3) 上部浮体在波浪、海流作用下的往复运动带动与其连接的水下立管周期性运动.随着水深的增加波浪作用和平台的往复运动造成的立管疲劳损伤在整个立管结构疲劳损伤中所占的比例不断减小而涡激振动所占的比例逐渐增大.
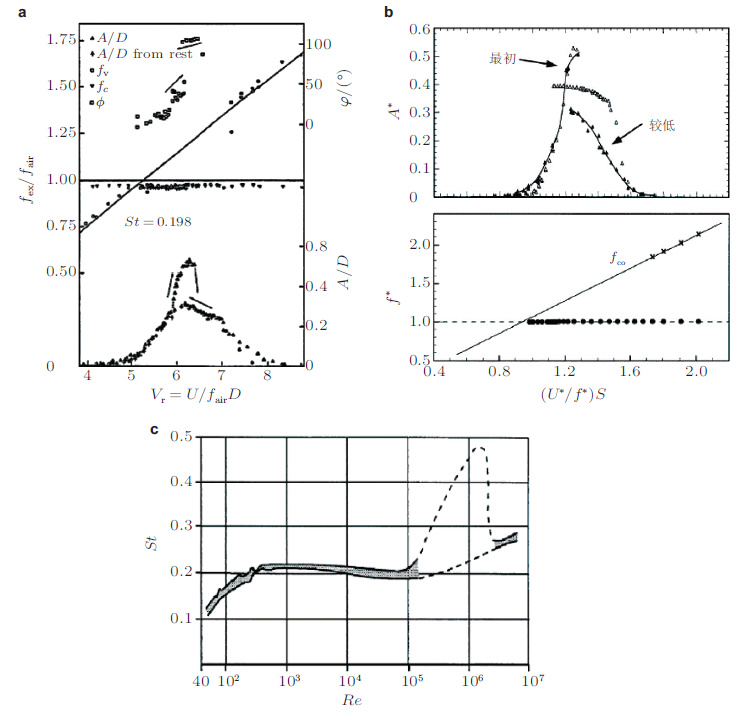
2.2 VIV的基本特征当流体以一定的速度流经圆柱体, 在一定的雷诺数范围内尾流中会形成稳定的交替脱落的旋涡即著名的卡门涡街.这种交替脱落的旋涡使柱体受到垂直于水流方向(cross flow CF)和顺水流方向(in line, IL)的脉动压力.如果该圆柱体是弹性支撑的或者结构本身是弹性的那么当泻涡频率与结构的自然频率接近时, 锁频(lock-in)就可能发生见图 3(a)和图 3(b). 有时, 为了与强迫振动(forced vibration在流体中通过对结构施加强迫外力而使结构发生周期共振)的情况加以区别, 把这种由于结构和周围流体的耦合而引发的锁频运动称为自激振动(self-excited vibration), 或者自由振动(free vibration).因为实验观察发现(Sarpkaya 2004; Williamson & Govardhan 2004, 2008), 强迫振动和自激振动的尾迹涡脱落模式和响应模式均有不同例如在低雷诺数的强迫振动中发现的P+S涡脱落模式并没有在自由振动中观察到.
|
| 图 3 涡激振动基本现象的实验观察. (a) 风洞中的弹性支持刚性圆柱的锁频共振 (Feng ,1968) , (b) 水中弹性支持刚性圆柱的锁频共振 (Williamson & Govardhan ,2004) (c) 静止圆柱的斯特鲁哈数与雷诺数的关系 (Blevins ,1987) |
静止圆柱体旋涡的脱落频率可以由Strouhal定律计算, fst = St(U/D), 式中, fst为静止圆柱的涡脱落频率U为来流速度, D为圆柱直径, St为斯特鲁哈尔数(Strouhal number). 因此, 旋涡脱落频率可用无因次的St表示, St数随雷诺数的变化如图 3(c)所示, 在工程应用中一般取为0.2.实验表明, 当来流速度U为4fnD~12fnD时结构就有可能发生锁频, 当结构为柔性且有多模态参与时锁频范围更窄一些, U范围取为更窄的5fnD~10fnD(fn为结构自然频率).
事实上, 涡激振动在自然界是经常发生的现象如风引起电缆、桥梁缆索甚至烟囱、楼宇等高大建筑物的振动;在许多工程结构中也常发生例如飞机机翼的控制升力面、核反应堆的热交换器、导流管、热井、发动机等的振动.该问题在海洋工程中的水下结构中显得尤为突出例如钻井隔水管、生产立管、水下拖缆、系泊系统缆线以及Spar平台、导管架平台、海上风机的支撑桩柱等细长圆柱结构.近几十年来研究人员最初通过小尺度风洞中刚性圆柱的实验观察、简单的唯象模型进行模拟后来结合计算流体动力学(computational fluid dynamics CFD)和有限元法(finite element method FEM)的大规模数值计算、大尺度的柔性缆索在剪切流中的现场实验、理论分析和物理机理解释希望达到深刻认识、合理预测、积极预防涡激振动的目的.尽管已经拥有了许多研究结果, 但是因为涡激振动问题本身的多学科性涉及流体力学、结构动力学、振动与波传播、CFD和FEM、声学、小波变换和统计学等学科到目前为止人们仍然未能对VIV问题给出完美的统一的预测模型尤其对其中的一些非线性现象的认识和机理解释仍然存在诸多争议很难达成共识.
经过多年的物理实验和数值模拟对涡激振动固有特性中的流固耦合机理的认识有了显著提高下面将分别从涡激振动的自激-自限制性、波传播特性、尾迹涡模式的多样性、流固耦合表征等几个方面展开论述.
2.2.1 自激-自限制随着流经圆柱的流体速度的提高涡脱落的频率与结构的自振频率越来越接近尾迹涡中的非定常动压就会激励起结构的运动; 当然结构的运动又反过来影响尾迹中的涡动力.当结构横向振动的振幅超过某一临界值(例如0.1D), (Mandini 1961, Sainsbury & King 1971, Dickens 1979, Okajima et al. 2002, Sugimoto et al. 2002)时, 结构的运动会增强尾迹涡的涡强度(Davies 1976, Atsavapranee et al. 1998).初始涡和脱落涡的涡通量比值从固定圆柱的0.51±0.08(Atsavapranee et al. 1998; Berger & Wille 1972)提高到处于锁频共振状态的圆柱的0.66±0.09.如果从能量的角度来看当周围的流体对结构所做的功(能量交换)在一个周期内为正值时就会导致结构的周期振荡;这个能量交换的数值的大小很大程度上受流体速度、结构运动和涡激升力的幅值与相位的影响Huerre(2002) 将这种奇妙的结构运动与其尾迹流场中涡脱落的反馈与自适应描述为一个整体的模态即一个在流场中能自维持的、时间上为周期性的特定的空间构架系统.也就是说, 自激振动的初始涡脱落模式和频率自动调整以达到一个合适的值而使得系统共振, Sarpkaya(2004) 对这种系统自我调整机理的解释是: 由于结构的运动它通过让流体的虚质量以及相应的频率和加速度改变而去适应涡脱落的变化, 就像流体和结构达到共同的频率结构在这个频率下发生较大幅度的振动也就是说涡尾迹动力和结构动力的两个频率互相适应.
然而, 涡激振动的运动幅度不会随着流体速度的增大而单调地增大而是达到一个最大值(通常为1.5 D~2.0D)后开始下降直至退出锁频区域.随着流体速度和结构运动振幅的提高, 对于流体而言结构的直径(或者结构两个剪切层之间的距离)看起来变大了(Di Silvio 1969), 因为该直径的增大伴随着流速的增大因此涡脱落频率可以基本保持不变, 但是与固定圆柱的涡脱落频率有偏差.换言之, 自激振动的初始, 实际涡脱落频率fvor是下降的与静水中的振荡实验频率略有不同. 但是如果速度进一步提高涡脱落频率与结构的固有频率偏差增大系统的调节涡脱落模式和频率以适应结构运动的能力不能满足自适应的需求从而使涡激升力减小, 结构运动幅度减小, 直至退出锁频区域;另一个原因可能是升力系数并不是随着来流速度增大而单调增大当达到某一特定来流雷诺数后开始减小, 而且结构大振幅时交错涡脱落的稳定性遭到破坏, 也会使升力下降从而导致振幅的增长受到限制. 也就是说结构不能无限制地从周围流体中吸收能量这一点与结构发散的机翼的气动弹性流固耦合颤振现象有根本的不同.
总之这种奇妙的涡尾迹动力和结构动力相互作用使整个系统保持在某一周期震荡的平衡态的振动赋予了涡激振动独有的与常规的结构共振、流致振动不同的一些特征例如振动的自激励、振幅的自限制. 了解涡激振动的这些基本特征有助于建立更合理、准确的预测模型它不仅要给出一个精度可以接受的响应而且能捕捉到涡激振动的基本特征. 甚至可以说衡量一个VIV预测模型的标准之一就是该模型是否能(或者在一定程度上)捕捉到涡激振动的自激、自限制等基本特征.
2.2.2 尾迹涡脱落的多模式钝体绕流最重要的固有特性是边界层从固壁表面分离以及涡交替脱落形成涡街它的机理涉及涡量的产生、集聚、耗散、涡层相互作用、底压作用、以及远场尾流的反馈影响等多种因素包含丰富的非定常涡动力学问题.固体相对于流体的剪切运动和无滑移条件使得固体表面产生涡量边界涡量通过黏性扩散传入流体内部使得固壁附近的流体层变成涡量较大的边界层.边界层在流体黏性阻力和逆压的作用下会产生与固体表面的分离现象即逆压区中的惯性力需要克服黏性力、逆压梯度产生的逆压强在一定条件下, 固体表面附近的流体质点速度下降到零甚至出现负值(向上游移动). 边界层从固壁表面分离形成向下游拖曳的剪切层剪切层的内层和外层流速的不均匀使得自由剪切层发生卷曲, 形成旋涡.在一定的雷诺数条件下, Kelvin-Helmholtz 不稳定性使得旋涡的前后位置发生错动, 或者从动力系统的不稳定性看由于圆柱绕流动力系统的Hopf分岔, 引起对称附着涡失稳而发生交替脱落.离固壁表面近的涡的诱导作用使底压降低另一侧位于压强较高区域的涡层则被拉入尾流.被拉入尾流的涡层由于拉伸、扩散和耗散而被拉断终止了对旋涡涡量的输送, 使得旋涡强度增长率达到最小值产生一个涡脱落. 脱落涡原来所在的剪切层强度变得最小形成了离固壁表面较近的涡. 接着又开始了第二个涡脱落过程如此周而复始, 形成旋涡的交替脱落.
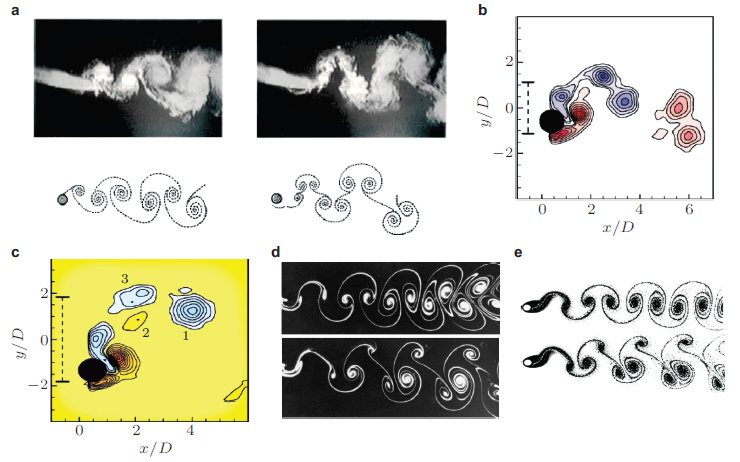
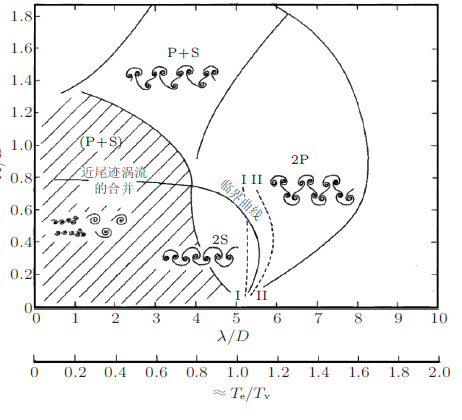
然而, 涡激振动中的圆柱尾迹涡脱落的模式不仅仅是经典的卡门涡街那样: 每一个周期中有两个单独的旋涡分别从圆柱的上部、下部交替脱落这种涡脱落模式被称为2S模式; 而且还存在2P, S+P, 2C, 2T等多种形形色色的尾迹涡. Brika和Laneville(1995) 用烟雾实验展示了不同响应分支对应2S和2P不同的涡脱落模式见图 4(a). 美国利海大学(Lehigh University)的Rockwell用PIV (particle visilizition velometer)方法测量了强迫振动圆柱的涡动力(Gu et al. 1994). Govardhan和Williamson(2004) 测量了自由振动的圆柱尾迹流场的涡动力. 美国康奈尔大学的流体力学教授Williamson对弹性支持的刚性圆柱、在低雷诺数下的强迫振动的尾迹流场进行了详细的实验研究相继观察到了多种涡脱落模式, 例如: 在铰支的圆柱实验中在高响应分支时观察到的2C模式, 即每半个周期中有两个同步旋转的旋涡脱落(Flemming & Williamson 2003)见图 4(b); 在XY双向振动, 质量比小于6的情况下观察到超高响应分支所对应的2T模式, 即每半个周期中有一组包括3个旋涡的涡脱落(Jauvtis & Williamson 2003)见图 4(c); Williamson和Roshko(1988)的实验结果与Meneghini和Bearman(1993)的数值模拟结果是一致的, 见图 4(d)和图 4(e). 这些不同涡模式对应不同的结构运动幅值(或者响应分支), 见图 5.
|
| 图 4 形态各异的圆柱尾迹涡脱落模式.(a) Brika和Laneville(1993) 首次实验展示了不同响应分支对应2S和2P不同的涡脱落模式;(b)铰支的圆柱实验中, 在高响应分支时观察到的2C模式(Flemming & Williamson, 2003);(c)在XY双向振动时观察到的的数值模拟超高响应分支所对应的2T模式(Jauvtis & Williamson, 2003);(d)Williamson和Govardhan(2004)实验结果(在层流中, Re<200);(e)Meneghini & Bearman(1993)的结果(Re<200) |
|
| 图 5 不同涡模式对应不同的结构运动幅值 (Wiliamson & Govardhan, 2004) |
需要指出的是, 也有学者(Sarpkaya 2004)表示尾迹模式的转换和跳跃依赖于很多因素如果仅仅只针对高相位区或者低相位区的某一个模式, 会有些片面; 而且系统的惯性会阻止当前条件的突然改变所以响应或者尾迹模式的变化应该是从一个周期到下一个周期的渐变过程即会沿着流向逐渐变化. 另外, 如果仔细观察相关的实验条件可以发现上述多种涡脱落模式多数是在低雷诺数情况下发生的, 甚至即使是在低雷诺数条件, 有的实验也观察不到2P模式(Re=500) (Blackburn & Henderson 1999); 所谓的初始分支(initial branch), 只在雷诺数低于5 000的实验中观察到而很少在雷诺数高于20 000的实验中观察到(Sarpkaya 2004).
2.2.3 系统的展向相关性对于细长的FR, 由于实际环境的扰动较大波和流速的大小/方向延结构展向是变化的而且结构本身的材料/几何特性沿展向也是非均匀分布的由于激励频率的带宽变宽以及协同不稳定性沿细长结构的不均匀传播沿着结构展向的不同位置系统的振动频率也不同这种多模态参与振动的现象使得VIV响应变得更加复杂正如VIV专家MIT的Vandiver教授指出的: "For long, rigid or flexible structures(e.g., a cable), the phenomenon is further complicated by the fact that the structure tends to respond at a variety of frequencies over its entire length. This, in turn, gives rise to additional and omni-directional fluid forces whose prediction is at best approximate"(Vandiver et al. 2009). 事实上现场测量观察到的深水FR的振动更多的是多模态振动(Alexander 1981, Vandiver 1998; Larsen & Halse 1997)而且系统的展向相关性不再是理想的即不再像刚性圆柱那样可以认为系统沿展向完全相关.
图 6(a)为三维CFD计算得到的柔性圆柱尾迹的涡量场可以清楚地看到, 在结构展向的不同位置例如振动的节点与波峰(或波谷)处, 其涡流场差别很大; 图 6(b)为结构的响应位移沿展向位置的时间演化, 从图 6(b)也可以看到, 结构振动不再是标准的驻波共振而是包含有行波和驻波等多种形式的一种复合运动.这些充分说明了细长柔性结构的涡激振动响应无论其尾迹的涡动力还是结构动力都因为三维效应的引入变得更加复杂也给其运动响应的预测、尤其是相关长度的观测和确定带来了更多的困难.
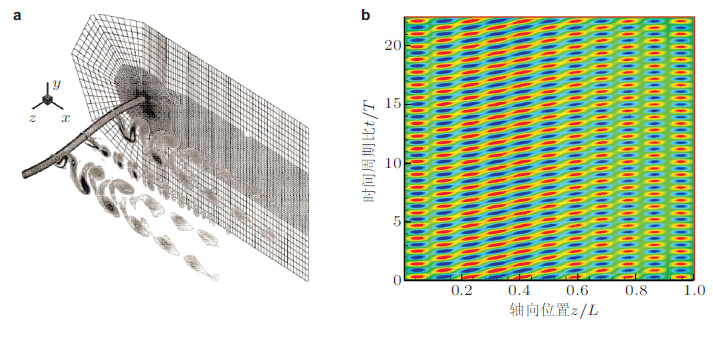
|
| 图 6 尾迹涡和结构运动的展向不均匀分布显示了涡激振动的展向相关性. (a) 三维CFD计算得到的柔性圆柱尾迹的涡量场(Wiliamson & Govardhan ,2004) , (b) 三维结构的响应位移沿展向位置的时间演化(张立武 ,2010) |
在水深较浅、立管展向长度较小时, 涡激振动通常为单模态锁频结构的振动通常表现为驻波共振, 因此已往的涡激振动预测模型包括尾流振子模型、模态叠加模型、相关模型等均是建立在驻波共振响应的假设下的.随着水深的增加, 立管长度增加而且几何结构更复杂其响应形式也多样化: 多模态振动、宽带随机振动以及涡致行波(vortex-induced wave, VIW)等. 当立管的长径比超过103时涡激振动经常呈现出行波效应. Vandiver等(2009) 曾基于无限长结构模型发展了针对大长径比结构的VIV计算程序(SHEARinf)但是目前处于研发阶段, 还没有实际应用;Facchinetti等(2004b)直接采用行波振动解的形式利用尾流振子模型研究了行波响应和结构动力与流体动力的相互作用.
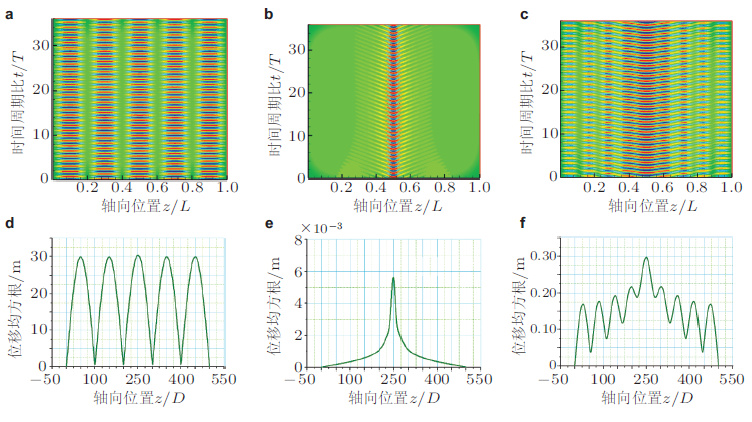
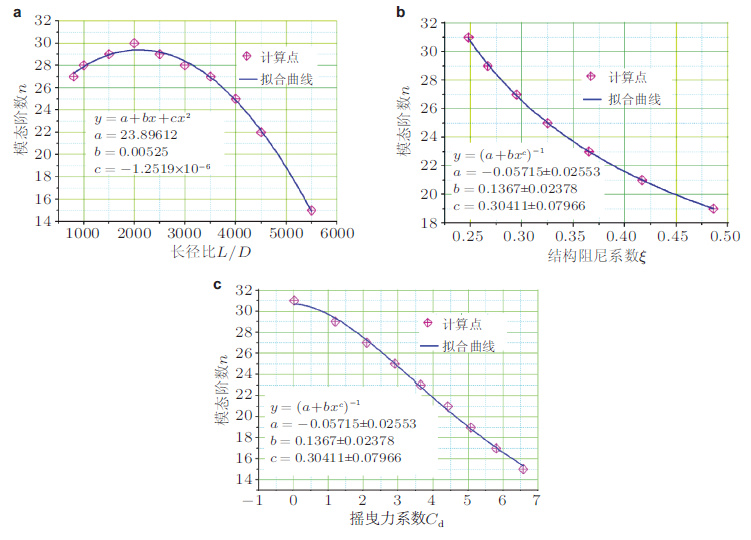
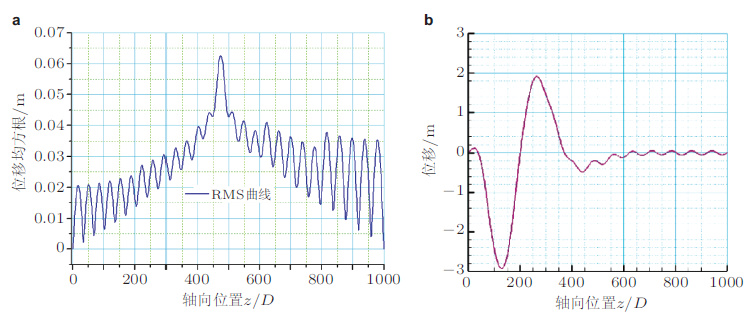
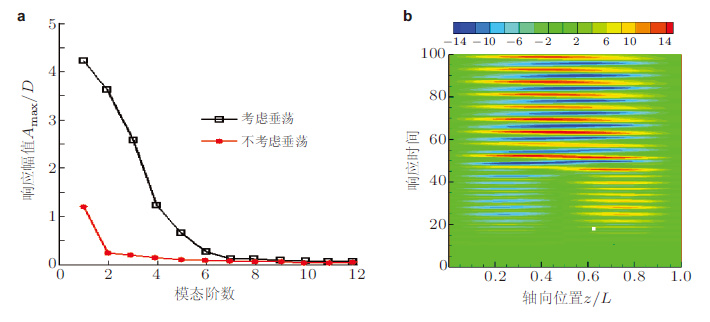
那么, 在什么条件下可以采用驻波预测模型又在什么条件下需要采用行波模型?张立武(2010) 通过量纲分析结合有限元数值模拟研究了细长FR的动响应(见图 7), 观察了出现行波的临界模态阶数ncri与长径比L/D、结构阻尼系数ζsn、拖曳力系数Cd的关系(见图 8). 结果表明:立管的响应形式可分为驻波、行波和中间状态3类(见图 7);控制响应形式的无量纲参数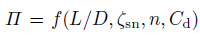
|
| 图 7 驻波、行波以及中间状态的位移响应. (a) 驻波位移时空云图;(b) 行波位移时空云图; (c) 中间位移状态时空云图; (d) 驻波均方根(root mean square, RMS)位移; (e) 行波RMS位移; (f) 中间状态RMS位移 |
|
| 图 8 出现行波的临界模态阶数ncri随系统参数的变化关系.(a)ncri随长径比L/D的变化(b)ncri随结构阻尼比ζsn的变化, (c)ncri随水动力阻力Cd的变化 |
从图 8可见, 由于随着结构模态阻尼比ζsn和水动力阻力系数Cd增加, 结构振幅衰减得很快因此结构的响应易于出现行波效应. 当立管结构承受高阶频率激励时振动衰减更快, 结构的响应也更容易出现行波. 当立管的长径比L/D增大时, 由于系统阻尼中结构和流体阻尼两部分交替主导的原因立管的响应先出现驻波或者中间状态, 然后更容易出现行波特征.
另外, 在实际工程中, 海洋立管结构并非理想均匀的.由于重力、浮力的作用, 张力沿轴向是变化的; 而且由于水深较大有的立管的截面几何尺寸、结构刚度也是沿轴向变化的由于结构参数沿轴向的变化细长FR响应中的波幅和波长在沿着结构展向传播过程中会发生变化.张立武(2010) 和Chen等(2012) 对具有轴向变化结构参数的立管固有动力特性进行了分析考察了变张力、变弯曲刚度的立管固有模态(见图 9).以理想Euler梁的振动为例, 假设解的形式为
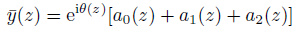
|
(1) |
其中, a1, a2为高阶小量. 使用WKB解法, 保留第一项得到张力梁的色散方程
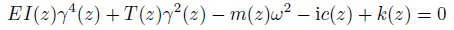
|
(2) |
其中, 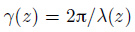
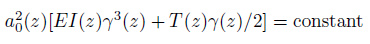
|
(3) |
|
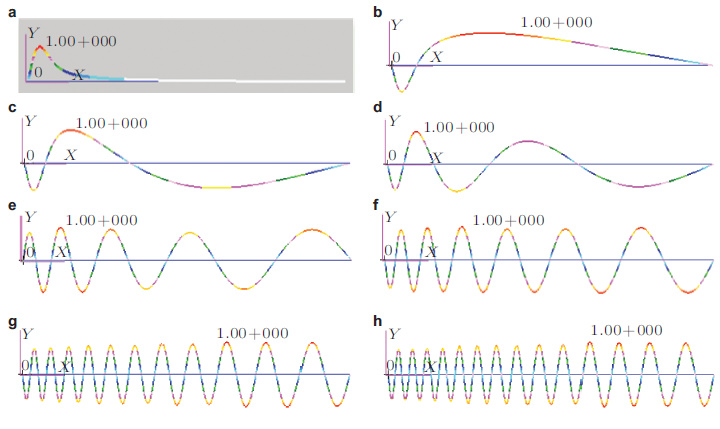
| 图 9 长度3 000 m变张力、变刚度立管的典型模态. (a)第1阶模态, (b) 第2阶模态, (c)第3阶模态, (d) 第5阶模态(e)第9阶模态, (f) 第13阶模态, (g)第23阶模态, (h) 第29阶模态 |
由式(3) 可以看出, 振幅a0(z)大小取决于中括号里各项的值.对于几何均匀而张力线性变化的梁, 由于EI(z)为常数且波数与波长成反比, 即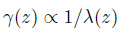
Chen等(2012) 对这种结构参数沿轴向变化的立管涡激振动响应的研究结果(见图 10)表明:张力和弯曲刚度都会影响弯曲模态幅值和波长, 张力越大, 波长越长, 弯曲刚度越大, 波长越小; 随着阶数的增加振幅最大点从立管底部向顶部移动, 波长较长的位置波速较大(见图 10(a)); 对于低张力立管某些模态响应会由于立管局部的轴向负压而出现大振幅运动(见图 10(b)), 这在实际工程中尤其需要注意.
|
| 图 10 变刚度立管的涡激振动响应. (a) 位移均方根, (b) 失稳响应 |
理论上说对流固耦合最直接的分析手段应该是将结构振动方程和结构周围绕流流场方程联立求解或是通过流场中的自激振动而不是强迫振动实验来观察.但是目前对海洋工程立管还不能彻底实现这两种理想研究方式这里借助简化模型来讨论结构动力和尾流水动力的流固耦合.在尾流振子法中描述尾流振子的运动时, 常用的van der Pol方程为
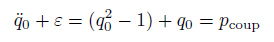
|
(4) |
其中, q0表示尾流升力系数, ε为van der Pol 参数方程右边项pcoup为结构对尾流的耦合作用力.目前对结构-流体动力的耦合形式还没有统一的确定描述, pcoup有多种表达形式, 被广泛采用的多为线性模型, 例如位移模型的pcoup=C0y0(C0为常系数)其他还有速度、加速度模型(Facchinetti et al. 2004a).
Facchinetti等(2004a)、郑仲钦和陈伟民(2012b)先后比较了3种线性耦合模型结果表明: 位移耦合模型所预测的结构振幅y0与速度和加速度线性耦合模型相比偏小, 甚至会比后两种模型低一个量级而且尾流升力系数q0在锁频阶段不仅没有放大反而减小(如图 11(a))这与实验观察到的当锁频发生时结构振幅与尾流升力均会增大的结果矛盾;速度耦合模型对锁频阶段简缩速度范围的预测在大质量比情况时较准确但是锁频区域只出现在简缩速度Ur > 1=St时得到的响应位移、升力和无量纲频率(结构与尾流频率比)表现出非对称的滞回与实验观测到的对称滞回不同(如图 11(b));加速度耦合模型在定性上能够较好地模拟涡激振动响应和升力放大及锁频区域对称性等特点但是在预测锁频区域宽度时, 仅适用于小质量比情况, 随着质量比增大对锁频区域的简缩速度范围的估计偏于保守(如图 11(c)). 总体来说相对于位移耦合模型, 速度、加速度耦合模型能准确地描述涡激振动系统它们所得耦合系统的动力特性与实验结果在定性上一致; 但是速度耦合和加速度耦合模型分别适用于不同的质量比二者对锁频区域范围的预测也不相同.
|
| 图 11 不同耦合模型给出的锁频阶段位移、升力系数、相位(加速度耦合模型)响应结果(Facchinetti et al. 2004a). (a) 位移耦合模型, (b) 速度耦合模型, (c) 加速度耦合模型 |
从结构振子与尾流振子耦合机理看, 对于位移耦合模型由于均匀流中结构横向静位移不会改变尾迹流场的动力特性也就是说结构与尾流的动力耦合不依赖于静态位移因此位移耦合不能很好地模拟二者间的动力耦合特性;速度耦合模型中结构横向速度会改变流体的攻角这主要影响了由拖曳力造成的水动力阻尼, 但是对升力影响较小;而结构运动加速度对尾流动力的影响, 相当于把近尾流看做系于运动结构上的van der Pol振子, 随结构运动, 能较好地描述结构对尾迹的动力作用从而模拟锁频阶段的主要动力特性, 如响应跳跃、滞回以及相位转变等. 另外由于位移耦合模型在理论上是隔热的, 系统无法与外界交换能量结构振幅的放大只能通过升力的减小来平衡因此位移模型无法描述锁频阶段的结构响应与升力均放大的现象(Facchinetti et al. 2004a); 而速度、加速度耦合模型与实验结果在定性上较为一致, 尤其是加速度模型对圆柱涡激振动大部分动力特性的模拟效果较好.
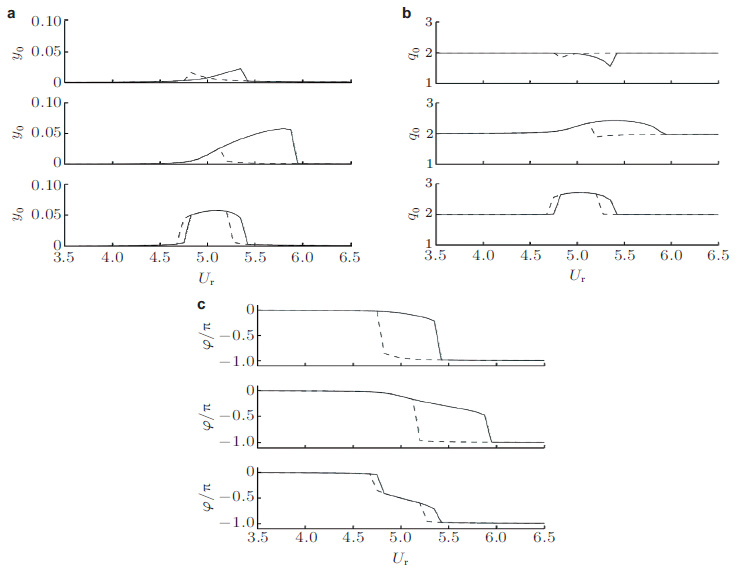
郑仲钦和陈伟民(2012b)提出了一种非线性耦合模型利用速度耦合与加速度耦合模型能够合理预测锁频振幅、升力并结合这两种耦合模型不同的质量比适用范围, 弥补二者预测锁频范围的不足从而合理地描述锁频区域的位置、锁频阶段结构响应及尾流升力. 图 12(a)为该模型预测的不同质量比系统的锁频范围, 作为对比, 图 12(b)~图 12(d)分别给出了线性模型的锁频简缩速度范围.可以看出位移模型给出的锁频简缩速度范围与实验差别最大(图 12(b);速度模型(图 12(c))在质量比μ > 3的情况下与实验数据吻合较好但是低质量比的结果小于实验值; 而加速度模型(图 12(d))与速度模型相反只在μ < 2时的效果较为理想, 当μ 继续增大计算的锁频范围窄于实验范围.图 12(a)表明新模型的锁频下限与实验数据基本吻合, 只在μ < 2时的锁频上限略宽于实验结果, 估算结果略偏于保守.
|
| 图 12 不同模型预测的锁频带宽简缩速度范围以及与实验结果的对比. (a) 非线性模型, (b) 位移耦合模型, (c) 速度耦合模型, (d) 加速度耦合模型 |
VIV现象并不是可以用少数几个定量参数就可以描述的因为当某一个参数的数值超过某一临界值则该参数可能会对整个系统的响应起关键作用而当其他参数达到其临界值后又会起主导作用. 例如在分离区、其周围的边界层、移动分离点上游的边界层中因为湍流会大大地改变结构尾迹的流场所以湍流(通常用4个积分长度尺度、涡耗散率表征)是影响VIV及其抑制设备周围流场的主要因素直接影响了VIV响应和具体抑制措施的效果. 关于VIV的影响参数问题重要的是面对某一特定的问题, 在众多的影响参数中, 确定出少数几个参数作为主要影响参数通过寻找在大量实验中都呈现出较大分散性的参数, 可以将这些参数作为主要影响参数.
总体来说, 控制和影响柔性立管 VIV的参数包括流体参数:流体密度、动力黏性系数、来流速度、湍流度;结构参数:立管外径、长度、轴向位置、材料密度、杨氏模量、结构阻尼比以及时间、流场和结构的边界条件、温度、摩擦、立管表面粗糙度等等.经无量纲化并保留主要影响参数, 可以得到以下几个关键无量纲参数:雷诺数、简缩速度、频率参数、长径比、质量比、阻尼比、时间比、舍韦数等(暂不考虑温度、摩擦、粗糙度等的影响).下面分别举例说明其中的几个主要无量纲参数.
(1) 简缩速度. 通常认为简缩速度给出了锁频范围(4<Ur<10或12) 简缩速度的变化直接导致结构涡激振动的位移、频率和相位等响应的幅值发生变化而且简缩速度的变化步长、大小不同, 振幅曲线也会有所不同, 参见图 13; 另外, 简缩速度给出了锁频区域沿结构展向的分布也就是说它的展向导数给出了流速的剪切度实际上影响了系统的展向相关性和结构响应的多模态参与程度.对于非均匀流情况, 将速度的导数D/U (dU=dz)作为影响VIV的独立无量纲参数来考虑.关于简缩速度的影响已经有大量文献讨论(Brika & Laneville 1993, 王艺 2010, Sarpkaya 2004; Williamson & Govardhan 2008, Chen et al. 2015), 这里不再赘述.
|
| 图 13 简缩速度的变化对涡激振动响应影响的实验结果 (Brika, 1995) . (a) 相位响应, (b) 涡脱落频率, (c) 振幅响应 |
(2) 雷诺数. 雷诺数Re的影响直观地体现在速度变化对响应的影响上实质上, 雷诺数影响了边界层的形态, 当Re达到某一值(2.0×104) 时自由剪切层中的转捩涡(transition vortex)消失;再达到某一值时(2.0×106) , 涡脱落参数的St会开始变大从定常流中的0.20增大到0.24而且尾迹宽度从D降到0.7D并伴随拖曳力系数的减小.
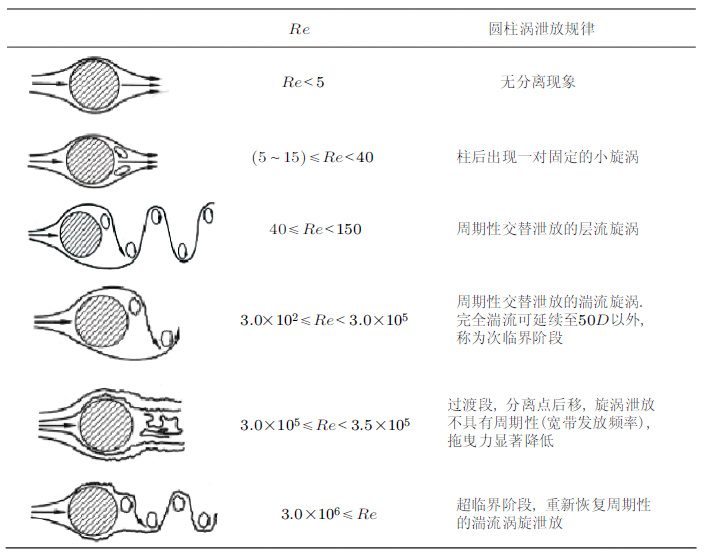
圆柱涡泄放规律与雷诺数(Re)直接相关, 在雷诺数很低时Re < 5流体不发生分离. Re增大至5~40时在物体后面出现一对固定旋涡. Re再增大, 这对旋涡就生长至其中一个旋涡破坏, 从而形成一个周期性的尾流, 出现交替发放的涡街(vortex street). Re在150以下涡街是层流; 150 < Re < 300是层流涡旋转为湍流的过渡段; 3.0×102 ≤ Re < 3.0×105, 称为亚临界段, 此时涡街完全是紊乱的并按一定的频率周期性地发放旋涡; 3.0×105 ≤ Re < 3.5×106称为过渡阶段, 此时分离点向后移, 阻力减小涡旋的发放是不规则的, 发放频率是宽频带随机的; Re ≥ 3.0×106称为超临界段, 此时重新建立起较规则的准周期性的涡街.具体总结见表 1.
对于雷诺数的影响, 有关文献的讨论也比较多(Brika & Laneville 1993, 王艺 2010, Sarpkaya 2004)下面将介绍另一个重要的影响参数-质量比并对其影响效果和机理进行讨论.
(3) 质量阻尼比. 对于确定的结构和流体系统, 系统的质量比μ 、阻尼比ζ和频率比是确定的, 从相似条件来看只有当两个系统的这3个参数外加长径比L/D、简缩速度Ur值都一致时, 两个系统的雷诺数Re才相同也就是说结构表面的边界层状态(层流或者湍流边界层)才相同, 这时两个系统的响应位移-简缩速度的变化关系才一致. 3个参数中质量比尤为重要, 起初, 质量比并没有作为单独的涡激振动的影响参数而是以质量比与阻尼比的乘积形式出现(Skop & Griffin 1973 Griffin et al. 1975; Khalak & Williamson 1999)关于组合参数μζ 对涡激振动横向振幅峰值Amax*的影响, 存在不同的研究成果以及看法.
Skop和Griffin(1973) 和Griffin等(1975) 首先提出了一个以质量比与阻尼比的乘积μζ 作为影响参数(当时被称为Skop-Griffin参数SG), 并且绘制了Griffin图. 如图 14, Griffin描述了SG对响应峰值的影响规律, 从图 14可以看到, Skop-Griffin参数SG影响振幅峰值, 无论是在水中或是在空气中, 振幅峰值随着μζ (SG)的增大而减小. Griffin和Hall(1991)的两组实验(SG均为0.5~0.6, 一组在水中μ = 3.8, 另一组在空气中μ = 34) 表明:(1) 质量比小, 锁频区域宽;(2) 相同的SG下的振幅峰值大致相等.
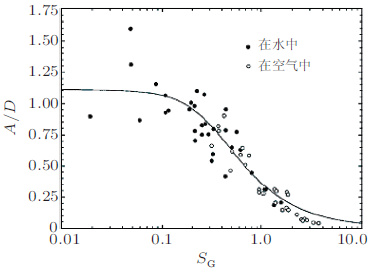
|
| 图 14 SG数对振幅峰值的影响 |
Sarpkaya(1978, 1979)也较早关注了这一问题他认为振动系统的动力方程直接表明了对于系统的振幅质量比和阻尼比的影响是相互独立的. 通过3组实验, 他发现每组的SG都相近而μ 不同且响应幅值很低, 通过分析这3组数据(1978)他认为质量比对振幅的影响不可忽略, 甚至对于SG≈2:0的情况, 质量比对振幅峰值的影响仍然能达到50%~100%并且认为只在SG ≥ 1.0的时候才适合用质量比和阻尼比的乘积来做为振幅的影响参数. Zdravkovich(1997) 也认为在海洋和海岸工程应用中质量比和阻尼比理应当作两个独立的参数.观察图 14, 可以看到Griffin图中的SG数范围为0.01~10, 且对于SG < 1.0的部分, 给出了很多数据结果也就是说Sarpkaya认为的SG ≥ 1.0的适用范围显得苛刻了.
SG参数对响应幅值的影响, 可以通过一个弹性支持的刚性圆柱的响应来说明其无量纲位移幅值为(Khalak & Williamson 1999)
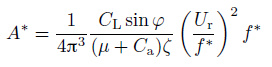
|
(5) |
其中,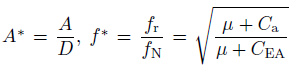
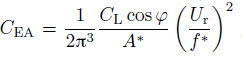
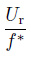
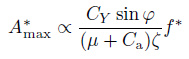
|
(6) |
因为升力是振幅的函数, f*随质量比的增大而减小所以对于小阻尼结构有Amax*∝(1/μζ).
|
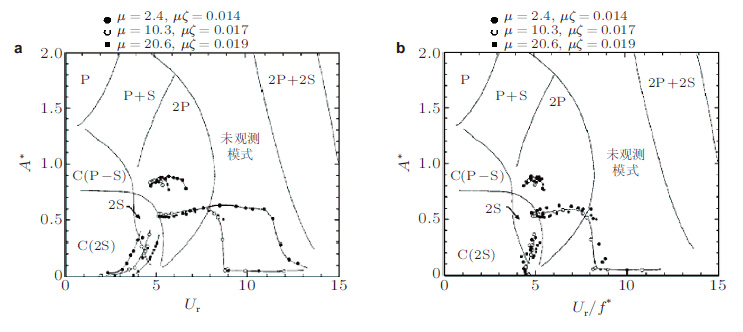
| 图 15 不同质量比结构锁频简缩速度范围 (Williamson & Roshko,1988) . (a) 以Ur = U=fND衡量锁频范围, (b) 以Ur/f* = U/frD衡量锁频范围 |
为了单独考察质量比μ 的影响, Williamson和Roshko(1988) 做了几组关于小阻尼比的弹性支撑刚性圆柱的涡激振动的实验并且测得了不同质量比锁频的响应和锁频区域, 如图 15(a), 可以看出: 响应幅值与μζ 有关, 当μζ 一定时, 对于不同质量比的结构其振幅峰值大致相等; 锁频范围受质量比的影响, 一般低质量比的结构锁频区域宽这与Griffin的结论一致.
以上讨论的是响应位移幅值, 如果关心锁频的范围即锁频开始和结束时的简缩速度. 从图 15(a)可以看出不同质量比系统进入"upper branch"所对应简缩速度(记为Ur_upper)几乎一致, 而"lower branch"结束所对应的简缩速度(记为Ur_lower)却不相同.这里的简缩速度是以结构固有频率计算得出的一般情况下取为静水中圆柱固有频率, 然而实际情况要复杂的多.
锁频阶段水中振动系统的固有频率不一定是常数因为附加质量系数Ca会随简缩速度的变化而改变的, 见图 16(a)(图中用于计算简缩速度的频率为静水中圆柱的固有频率fN), 所以实际振动频率随简缩速度的增大会略微地增大, 如图 16(b). 有趣的是, 如果以真实振动频率fr来定义简缩速度即Ur = U/frD则不同质量比系统的锁频范围是一样的, 大约为5~8, 如图 15(b).
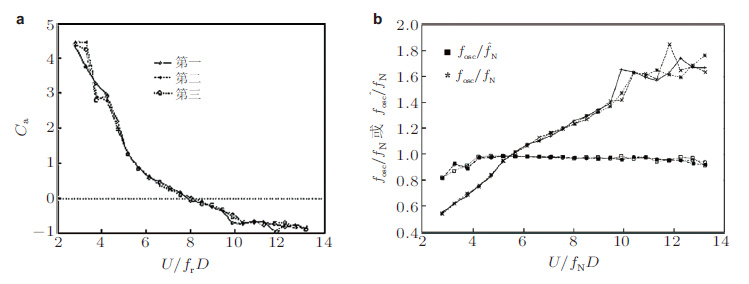
|
| 图 16 简缩速度对锁频阶段的附加质量系数和频率比的影响(Sarpkaya 2004) . (a) 简缩速度对附加质量系数的影响, (b) 简缩速度对频率之比的影响 |
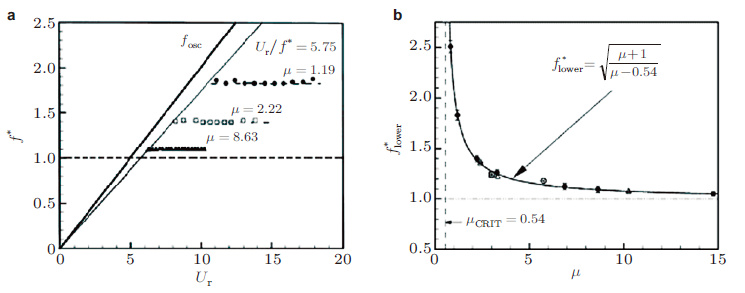
Govardhan和Williamson(2004) 认为VIV的实际振动频率fr主要与质量比有关, 大质量比时, 使CEA的作用可以忽略从而得到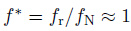
|
| 图 17 质量比与锁频阶段的频率比的对应关系 (Govardhan & Williamson 2004) . (a) 不同质量比对应的锁频阶段频率比, (b) 不同质量比对应的下枝频率比 |
锁频下分支对应的频率比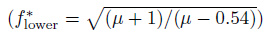
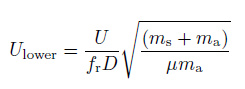
|
(7) |
式中, ma为静水中的圆柱附加质量. 式(7) 表明: 质量比小时锁频结束点对应的简缩速度大, 锁频区域范围大;质量比大时, 锁频结束点对应的简缩速度小, 锁频区域范围小.从涡激振动锁频发生的机理来看由于小质量比结构的流体附加质量相对于结构本身较大对整个耦合系统的固有频率影响较大, 流体的惯性作用更加明显(Govardhan & Williamson 2004)从而可以不断调整耦合系统的频率使其与涡脱频率接近, 使锁频持续下去(Vikestad et al. 2000), 因此小质量比结构锁频区域大而且响应振幅较大;反之亦然.
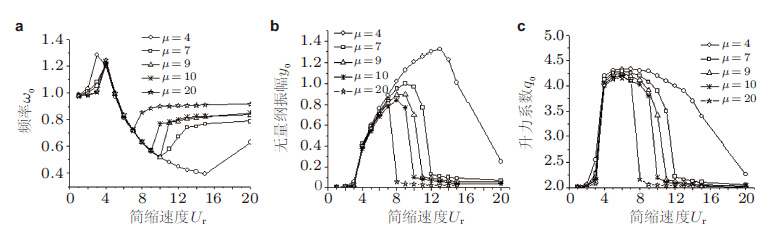
图 18(郑仲钦 2012a)给出了不同质量比下频率比ω0、振幅y0以及升力q0随简缩速度的变化, 其中, ω0 = ωv/ωst为涡脱落频率ωv(锁频时等于结构振动频率ωosc与Strouhal频率ωst=2πStU/D之比. 在耦合系统未进入锁频阶段时结构振幅以及升力接近零, 系统几乎处于静止状态此时的涡脱落频率即Strouhal频率, ω0=1, 如图 18(a)所示; 随着简缩速度继续增大, 涡脱落频率ωv接近结构固有频率ωn时, 结构发生锁频共振振幅与升力明显增大, 如图 18(b)和图 18(c)所示.在锁频阶段, 实际的涡脱落频率比ω0≠1.
|
| 图 18 质量比μ 对频率比、振幅、升力系数的影响. (a) 频率比;(b) 振幅; (c) 升力系数 |
(4) 长径比. 长径比是一个结构参数它主要影响边界条件、波的传播从而影响波型最终影响结构响应的幅值和其沿结构展向的分布. 有趣的是, 长径比L/D对∏的影响并不像拖曳力系数Cd、模态阶数n等参数的影响一样是单调的. 由图 8(a)的数值结果和ncri与L/D关系的拟合曲线可以看出, 随着L/D的增大∏值先增大后减小.即其他参数不变, 长径比L/D增大时结构会先出现驻波响应或中间状态, 然后会出现行波响应.
笔者认为出现这种现象的原因在于系统的总阻尼随着长径比L/D增大而变化, 阻尼包括结构阻尼ζsn和流体阻尼Cd两部分, 对于单位长度的立管来说, 其阻尼可以写为R = r + Rf(Cd), 其中, r和Rf(Cd)分别为单位长度上的结构阻尼和流体阻尼. 对于一个均匀的张力梁结构的模态阻尼可以写为
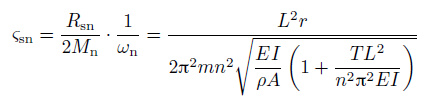
|
(8) |
当结构的长径比L/D较小时, 结构阻尼r比Rf(Cd)大, 在系统总阻尼R中占主导. 由于结构模态阻尼系数不变, 即ζsn不变, 根据式(8) , 如果长度增大则单位长度上的结构阻尼r应按1 / L2的比例减小在总阻尼R中结构阻尼占主导因此此时立管系统单位长度上的总阻尼会迅速减小这也就意味着结构的响应更容易出现驻波.因为当结构的长径比进一步增大时单位长度上的结构阻尼r小于流体阻尼Rf(Cd)后者保持为常数, 所以会占主导.此时结构的振幅会因为更远的传播距离而衰减更多可能没有传到端点就已经衰减为零也就是说结构的响应更容易出现行波效应. 若结构阻尼比流体阻尼小很多则随着长径比的增大, 立管响应易于出现行波, 这正是实际立管的情况.
其他的影响参数还有舍韦数(Schewe parameter)、频率参数等.舍韦数是Sarpkarya(1979, 2004)提出的一个综合参数用以涵盖一些不可控或难以定量化的影响因素例如实验中的边界条件、曲面表面分离点移动、非定常剪切层的扰动、流动在柔性结构尾迹中的三维效应、展向相关、涡脱落和升力频率的带宽等.频率参数ρ(fND)D/μ(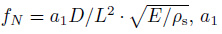
深水立管结构本身的特性使其涡激振动与以往刚性圆柱的有所不同由于立管的长径比很大(高达103量级), 其结构的柔性大自然模态的频率低且密集(相邻模态的频率差值很小), 因此在同样的来流条件下大长径比立管较一般的圆柱会出现"高阶模态"、"多模态参与"的涡激振动而且除了横向振动, 还伴随有扭转、轴向振动从而造成立管受力形式复杂, 增大了结构疲劳寿命分析的难度. 同时深水立管周围的流场也更加复杂例如海流速度沿结构展向的剪切变化、海流方向沿结构变化以及深水内波的作用等使得流场作用沿结构展向表现出幅值、方向、相位的非均匀性.
另外, 浮式平台多采用锚链式系泊系统进行位置约束深水平台的运动除了常规的波频运动, 还有低频漫漂(位移可达十几米)和高频振荡(ring和spring等), 随着水深的增加相对于浅水导管架平台和张紧式约束平台, 浮式平台的运动幅度(位移、速度等)明显增大对与上部平台相联的水下部分包括系泊链、立管等结构的影响增大平台浮体与水下立管的耦合作用明显增强. 总之深水立管的涡激振动更加复杂, 其响应预测也变得更加困难.
3.1 VIV分析方法 3.1.1 半经验模型和工程软件涡激振动在本质上是非线性的、自激又自限制的多自由度共振响应涉及结构运动的非线性(例如分叉、混沌)以及非定常剪切层和分离点移动、转捩、湍流等诸多复杂问题单纯根据理论分析给出响应的精确解非常困难(Sarpkaya 2004, Williamson & Govardhan 2008; Srinil & Zanganeh 2012). 因此大多数涡激振动预测是采用一些半经验的计算模型(Iwan 1981; Lyons & Patel 1986; Vandiver & Li 1999, Chen et al 2009, 潘志远等 2005, 雷松等 2010, 余建星等 2008)例如尾流振子模型、模态叠加模型、统计模型以及相关模型等.这些模型可以根据一些半经验的水动力和响应系数来预测涡激振动响应非常适用于工程问题的解决, 尤其尾流振子及其改进模型(Iwan & Blevins 1974, 1981; Lyons & Patel 1986; 葛斐等 2007陈伟民等 2010, 2011)由于物理意义明确、计算简便而且精度可靠得到了广泛应用. 但是, 半经验预报模型利用现有的实验数据结合唯象的经验系数结构动力和升力系数方程, 求得结构响应其缺点是对经验系数有比较大的依赖性而且不同模型间参数选取差别较大对同一研究对象可能会得到差别较大的结果.
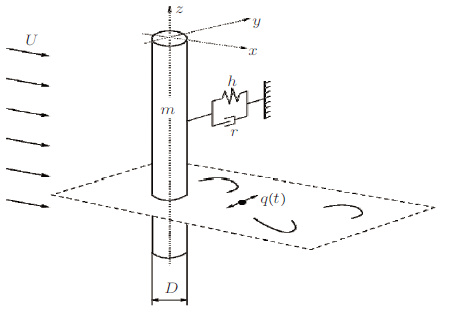
尾流振子模型不考虑流场和结构具体细节将流体和流体中的振荡物体视为一个整体系统把尾流看成一个非线性振子, 尾流振子的振动引起结构的振动, 反过来结构的振动又对尾流有反馈的作用.这个过程可以用适当的耦合方程来描述, 其中包括若干个由经验或实验确定的系数. 求解耦合方程可以较好地给出系统的运动特性并对运动现象本身从总体上和物理本质上能有较为直观的了解.Birkoff和Zarantanello(1957) 、Bishop和Hassan(1964) 首先考虑使用van der Pol 振子方程, 对于均匀来流(流速为U)中直径为D的圆柱如图 19所示, x轴为顺流向, y轴为垂直流向, 动力方程可表示为
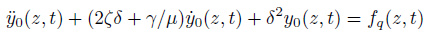
|
(9) |
|
| 图 19 尾流振子耦合系统示意图 |
其中, y0(z, t)= y(z, t)/D为无量纲横向位移, ζ为结构阻尼比, δ = ωn/ωv为结构固有频率ωn与涡脱频率ωv之比γ为附加阻尼比, 质量比μ=(ms+ma)/ma. 尾流振子对结构的无量纲作用力表示为fq=Cq0, C为系数. q0=2CL/CL0为无量纲涡激升力该变量也被称为简缩涡激升力系数, CL0为固定结构的升力系数.尾流振子满足非线性van der Pol方程
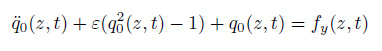
|
(10) |
其中, ε为van der Pol 参数, fy(z, t)为结构对尾流的作用力.
基于上述思路, 之后又发展了多种形式的尾流振子方程. Hartlen和Currie(1970)应用该概念并发展了类似的van der Pol振子方程来模拟圆柱体及尾流运动特性的尾流振子模型, Facchinetti等(2004a)通过不同的耦合项(位移、速度、加速度)研究了圆柱体运动对涡激升力的影响他们发现加速度耦合项可以定性地(并在一定程度上定量地)再现实验所观察到的关于弹性固定的刚性圆柱体的某些涡激振动响应.Facchinetti等(2004b)又把该模型扩展用于预测缆索的VIV响应、VIW (vortex-induced waves)响应, 并成功地预测出了拖曳线缆的响应. Mathelin和Lange(2005) 扩展了Facchinetti的工作预测了剪切流作用下线缆的VIV响应. 值得一提的是(1974, 1981)根据流体控制体的动量守恒方程给出了一种流体振子和结构动力的耦合方程组
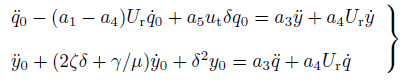
|
(11) |
其中, a,i=1,2,3,4,5是待定系数, ut是涡街的运动速度. 王艺(2010) 用该模型求解了弹性支撑刚性圆柱在均匀来流中的涡激振动问题Lyons和Patel(1986) 、Vandiver和Li(1999) 、陈伟民等(2010, 2011)提出了基于模态叠加的迭代模型可以预测波、流作用引起的立管、张力腿的单模态和多模态涡激振动响应.
为便于实际工程应用, 一些涡激振动预测软件也逐渐发展起来比较流行的有美国麻省理工学院(MIT)的Vandiver等开发的SHEAR7Lars等的VIVANA; Triantafyllou等的 VIVA等(Carl & Karl 1997). 它们之间的主要差别在于所基于的实验数据(自激振动、受迫振动或现场实验数据)不同同时经验参数的选取以及立管轴向流体力相关性的处理也存在较大差异.例如, VIVANA 是基于受迫振动实验数据(Gopalkrishnan 1993)和自激振动数据(Vikestad 1998), 所采取的升力系数模型为振幅A/D的函数. 但Gopalkrishnan( 1993) 并没有给出升力系数在振幅A/D<0.15条件下的值, 必须通过外推插值来获得. SHEAR7是当前国际上应用最为广泛的涡激振动分析软件之一. 它基于模态叠加法, 采用经验升力曲线(升力系数与振幅、简缩速度等因素相关)应用能量平衡原理计算结构的各阶模态响应并采用模态叠加方法计算结构总响应. VIVA软件基于麻省理工大学的大量实验数据包括对光滑圆柱体和与实际立管截面相同柱体的试验可以用于计算刚性立管、钻井立管、SCR和惰性波浪立管等不同结构的响应. 这些软件主要基于如下假设: 假定振动的响应发生在有限个离散的频率上、只考虑横向振动而且只适用于立管驻波响应, 不适用行波响应.
另外, 在海洋工程中还有一些可以对立管、锚链等结构进行静力和动力分析的细长海洋结构分析软件例如Orcina公司的OrcaFlex, 以及MARINTEK公司的RILEX等软件. OrcaFlex可以用于设计和分析包括SCR、TTR、脐带管、软管等在内的立管系统、系泊系统、拖曳系统等海洋结构系统它可以进行三维模拟、复杂准静态计算、时域非线性大位移分析、接触冲击分析、疲劳分析等功能比较强大, 但是对于VIV问题它需要调用其他专业软件和模型例如频域的SHEAR7和VIVA软件, 尾流阵子模型以及时域的涡跟踪模型(Orcina 1998). RILEX可以计算海洋柔性结构静动响应的有限元程序主要分析在浮体运动, 波浪等载荷作用下柔性结构的响应它对流体力的处理主要采用Morison公式没有考虑涡激升力引起的涡激振动.目前国内工程界主要引进以上国外分析软件有自主知识产权的经过实际工程考验的软件还尚需发展.
3.1.2 基于CFD的数值模型数值模拟方法可以分为两类: 一类是基于CFD, 另一类基于计算结构动力学(computational structural dynamics, CSD)或结构FEM(有限元方法).
基于CFD方法直接求解N-S方程因为无需做线性、无黏或是经验系数的假设所以能较详细地给出流场信息但是由于计算所需的资源量很大而且耗时长只能针对简单结构例如刚性圆柱、弹性短圆柱等而且尽管在理论上可以得到细致的流场信息但因其计算量太大在工程实际中很少采用. 近年来随着计算机速度提高和存储空间增大越来越多的文献给出了VIV的CFD结果. 较早地, Newman和Karniadakis(1997) 进行了低雷诺数(300) 下长径比为45的细长FR的3D CFD模拟随后的CFD模拟结果逐渐向更高雷诺数和更大长径比发展, Meneghini等(2004) 采用二维离散涡方法(discrete vortex method, DVM))模拟了真实的水下立管, 长径比达到了4 600, Pontaza等(2005, 2007)模拟了雷诺数高达107的立管VIV. 基于CFD的VIV数值模拟主要难点为湍流模型和流场网格技术, 所以下面主要介绍了这两点.按照对湍流模型的处理方式主要有以下几种:
(1) 基于DNS(direct numerical simulation)的VIV数值模拟. DNS 模型可以在空间域和时间域内详细地求解和描述结构响应和作用在结构上的流体力.Lucor等(2001, 2005)对较小长径比的圆柱体结构进行了计算但对较长的结构, 由于跨向长度太长而不能满足展向精度要求.Lucor等(2003) 的研究表明, 对较长的圆柱体结构初始条件、展向的精度、数值计算缓存域的大小都对预测的响应精度有影响.
(2) 基于 RANS(Reynolds-averaged Navier-Stokes)方法的VIV数值模拟. Sarpkaya(2004) 认为RANS方法不能对尾流边界层(wake-boundary-layer)交互机制做出较深层次的描述但RANS方法计算所需机时少, 已经作为实际设计分析工具在应用.
(3) 基于大涡模拟(large eddy simulation, LES)方法的VIV数值模拟. LES是DNS和RANS的折中. Beaudan和Moin(1994) , Mittal和Moin(1997), Kravchenko和Moin(1998) 最早在雷诺数Re = 3 900下进行LES数值模拟其平均速度、雷诺应力分布和实验的尾流数据非常一致.该雷诺数下的流场信息成为LES数值模拟的范例. 另外许多研究者对雷诺数Re = 3 900 时影响LES模拟效果的许多方面进行了研究. Breuer(1998) 利用了5种不同的数值求解方法和两种模型划分方法进行对比结果表明中心差分法所得结果比耗散法(dissipative methods)更符合实验, 低阶迎风方法(low-order upwind schemes)不能正确地预测一些重要的物理特性. Franke和Frank(2002) 的研究发现计算累积时间对圆柱体基底压力系数有重要影响.
(4) 基于离散涡方法(discrete-vortex method, DVM)的VIV数值模拟.在实际海洋环境中, 深水立管周围的流场非常复杂要想进行完全的三维模拟是不现实的. Yamamoto等(2004) 提出一种准三维模拟方法即流体力由沿圆柱展向划分的二维条带计算这些条带与三维圆柱体结构耦合.圆柱体结构的动力响应由基于欧拉-伯努利梁理论的有限元模型计算该模型基于 Patel和Witz(1991a)和Ferrari(1998) 的研究运动方程通过时域内数值积分求解. 每个条带的流体力计算采用DVM法即一种模拟二维、不可压缩黏性流体的拉格朗日数值方法.
近年来, VIV的CFD的结果也逐渐从最初较为容易的二维模拟向更加复杂的三维数值模拟发展. 早期有Newman和Karniadakis(1997)长径比为45的细长FR的3D CFD模拟. 后来, Lucor等(2001) 进行了更长立管(长径比为500) 在低雷诺数(103)下的CFD模拟. Willden和Graham(2001) 也给出了类似条件(长径比100雷诺数300) 的CFD模拟结果. 比较突出的是Yamamoto等(2004) 模拟中使用的长径比达到了500(一个120 m长的工程立管)雷诺数达到了2.0×105. Meneghini等(2004) 采用二维离散涡方法(DVM)可以模拟真实的水下立管长径比达到了4 600. Pontaza等(2005, 2007)模拟了雷诺数为1.0×106、长径比为20的立管VIV. Holmes(2006) 模拟了长径比1 400雷诺数1.0×104的柔性立管VIV.Constantinides(2008) 也给出了长径比L/D=4 200的细长立管VIV.他们使用了非结构网格技术, 单元数量达到了千万量级. 王成官等(2011) 利用Workbench 平台建立三维流固耦合模型进行了长径比为482的海洋隔水管涡激振动的三维数值模拟.按照对网格的处理方式(惯性和非惯性坐标系之间的利用和转换)三维CFD模拟网格技术大致可以分为以下几种:
(1) 非惯性系中的随体网格技术即在随柔性缆索一起运动的非惯性坐标系中采用使流场网格在非惯性坐标系中保持不变的方法来处理动网格问题.最初Newman和Karniadakis(1997) 的工作就是在随柔性缆索一起运动的非惯性坐标系中进行的使流场网格在非惯性坐标系中保持不变并将惯性坐标系中的N-S方程转化到非惯性坐标系中.利用谱有限元法对非惯性坐标系中流场进行直接数值模拟再将非惯性坐标系中的模拟结果通过坐标变换转化到惯性坐标系中从而展示了涡激振动缆索的驻波、行波现象和尾流中V字形的涡位错现象(Re=100和200) . Evangelinos等(2000) 基于谱有限元法和随柔性缆索一起运动的流场网格处理技术对锁频阶段的刚性圆柱、柔性圆柱周围的流场进行了三维数值模拟(Re =1 000), 得到了结构受力分布. 类似地, Blackburn(2001) 对低雷诺数的涡激振动分别进行了二维和三维数值模拟并且将数值模拟结果同实验结果进行了比较, 结果表明: 三维数值模拟可以获得和实验接近的数值模拟结果, 观察到2P涡尾流形态;采用二维数值模拟尽管结构最大振幅与实验结果较接近但是结构响应过程和涡尾流的结果与实验结构却有较大出入(即使雷诺数较低).
(2) 惯性系中的动网格技术即在三维惯性坐标系中采用网格变形或者网格更新技术.已经有不少文献采用该方法模拟流固耦合现象(So et al. 2001; Mittal & Kumar 2001, Chen et al. 2004, Tezduyar et al. 1992; Yu & Lin 2005), 例如较早的空气中机翼颤振、抖振和突风响应等以及后来的水中圆柱涡激振动等(气弹和水中VIV等).由于流场用3D单元划分, 可以给出立管展向的流场细节, 但是需要在立管表面划分更细的网格, 自此耗费的计算资源很大.
相比于机翼颤振的气动弹性问题, 细长立管的VIV问题的数值模拟难度更大.由于机翼颤振发生在气流中, 雷诺数较大, 边界层极薄机翼后面尖端的尾流分离现象又不明显因此常常不需要划分精细的层状边界层网格. 由于水流中的圆柱涡激振动相应的雷诺数较小, 边界层有一定的厚度圆柱后端的尾流分离现象又很明显, 因此无法忽略精细的层状边界层网格;机翼颤振的振幅较小, 往往只需采用弹性网格技术就可以了而对于VIV问题, 当结构运动的幅度较大时会引起流场网格畸变甚至出现负网格, 需要进行网格重新划分.
(3) 嵌合网格技术, 将流场分为两个区域, 一个是结构表面附近的区域(随体网格body grid), 其网格划分较为精细并且随结构运动而运动;另一个是远离结构的区域(背景网格background grid)采用较为略粗的网格而且网格是固定的; 在这两个区域之间的过渡区域采用变形(或局部更新)网格(Pontaza et al. 2005; 2007; 王艺 2010).采用这种混合的网格技术, 一方面通过结构表面精细的网格划分可以准确地描述边界层、分离点、涡脱落等局部流场细节另一方面计算量也不至于过大该方法非常适用于有移动物体的流场的CFD模拟.
环绕固体区域的精细网格区随着固体结构一起运动而不发生变形这样就既保证了网格的正交性, 同时又缩短了重新生成网格所需的CPU时间;通过采用上述惯性坐标系中的三维动态混合网格技术既保持了固体结构表面附近精细边界层网格的正交性从而保证了对流场、特别是固体结构表面流体载荷的数值模拟精度;又节约了重新生成网格所需要的CPU时间;同时上述不同形式的网格分区具有极大的灵活性不仅可以应用于模拟圆柱等简单几何形状固体结构的涡激振动而且还可以应用于模拟其他复杂不规则几何外形固体结构的涡激振动.
总之, 近年来CFD有了长足的发展有可能成为未来研究涡激振动的主要趋势但是目前的CFD在精度以及机时上仍然很难达到工程应用的要求工程实际应用中多采用半经验模型、由经验模型演化而来的工程软件另外, 还有近几年出现的基于水动力模型的FEM数值模拟.
3.1.3 基于CSD(或结构FEM)的数值模型理论或经验模型方法多针对理想Euler梁基于波共振假设然而工程实际立管的结构形式是多样的, VIV动响应的时空演化过程复杂.基于结构有限元方法的立管VIV响应数值模拟, 在这方面显出了其优点它不但可以比较方便地模拟工程实际中各种复杂结构形式的立管而且不受立管响应形式的制约既可以计算立管的驻波响应也适用于行波响应; 此外所建立的时域分析方法可以给出振动响应的时间和空间演化过程有助于观察立管的响应过程、分析振动在结构中的转播过程. Zhang和Chen(2010) 等利用该方法讨论了大长径比结构的VIV和VIW(vortex-induced wave), 给出了控制参数及其临界值.由于水动力用与结构的运动有关的涡激升力和流体阻力模型表达克服了CFD占用计算机资源量大、计算时间长的缺点. 当然水动力模型的精度直接影响了数值模拟的可靠性需要深入研究并辅以相应的实验以充实水动力数据库.
张立武(2010) 、郑仲钦和陈伟民(2012b)等通过有限元方法结合流体水动力模拟建立了一种适于深水立管的涡激振动的时域FEM方法可以针对复杂立管结构, 加载与运动相关的涡激升力和流体阻力并可以展示立管响应的时间空间演化过程从而更好地展示立管的振动的波动特性和非线性振动等规律.
对于结构动力和尾流水动力的耦合作用形式和表达一直是涡激振动模型的难点, 因为锁频阶段呈现的一些特有现象例如自激励、自限制、展向相关以及多模态参与、宽带随机振动等其机理至今仍不是非常清楚.为简化起见实际工程中通常采用定常升力系数模型, 即升力为
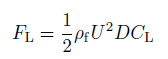
|
(12) |
其中, 升力系数CL为一个常数. 近年来随着对涡激振动研究的深入以及基于PIV的先进流场观测手段和基于CFD的数值计算的发展人们对涡激振动这种自激励同时又自限制的非线性现象以及在结构运动过程中尾迹流场的水动力和结构动力的耦合机理认识有了很大提高.研究表明(Sarpkaya 2004; Vandicer & Li 1999, Chen et al. 2012), 如果在升力模型中考虑结构动力与尾迹水动力的耦合作用可以得出更准确的升力模型. Sarpkaya(2004) 将涡激升力分解为拖曳力项和惯性项两部分测量了升力系数在几个振动周期内的傅里叶平均值指出在工程实际的雷诺数范围内与用结构运动的线性函数来表达的升力模型相比结构运动速度的非线性函数(二次函数)更能表征流体的主要作用;Govardhan和Williamson(2004) 进行了大量的VIV实验研究测量了涡激升力, 观察了升力随结构运动的变化规律; Vandiver和Li(1999) 则建议根据不同的结构振幅范围, 用分段双曲函数来表达升力曲线.
郑仲钦等(2012a)对涡激升力在整个锁频阶段的变化规律、与结构运动的关系进行了观察分析.图 20(a)为均匀流中弹性支承圆柱在受迫振动时的升力系数 (CL)实验结果(Govardhan & Williamson 2004), 以CL=0这条等高线(图中的黑粗线)为界, 内部CL > 0流体提供激励力; 外部CL < 0, 升力等效为阻力; CL = 0时, 圆柱和流体之间没有能量交换, 为理想锁频条件. 低阻尼圆柱自由振动的幅值试验结果见图 20(b)(Vikestad et al. 2000), 对比图 20(a)和图 20(b)可见, 振幅响应规律基本一致当Ur=5.5时振幅达到最大值最大振幅的平均值约为(A/D)max = 0.90.
|
| 图 20 涡激振动的升力系数和响应振幅实验结果. (a)升力系数等高线(Govardhan & Williamson, 2004) ; (b) 锁频阶段圆柱振动响应 (Vikestad et al., 2000) |
考虑到涡激振动锁频阶段的流体作用力与结构运动的非线性耦合, 张立武(2010) 、郑仲钦(2012a)和Chen等(2012a)提出与结构运动相关的假设升力模型, 进一步地为了非线性瞬态响应的时域计算的方便, 张立武(2010) 、Chen等(2012a)采用升力做功等效法给出涡激升力的结构速度多项式表达
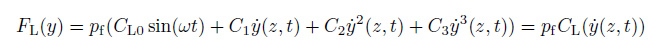
|
(13) |
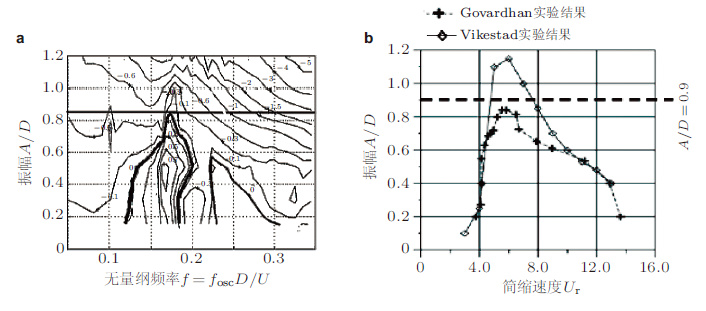
式中, 时变的涡激升力系数为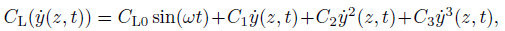
观察式(13) 中升力系数的各项在结构响应中的作用效果, 总体来说其在一定程度上能呈现涡激振动的主要特性.(1) 锁频阶段的自激特性常数项pfCL0sin(ωt)和线性项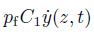
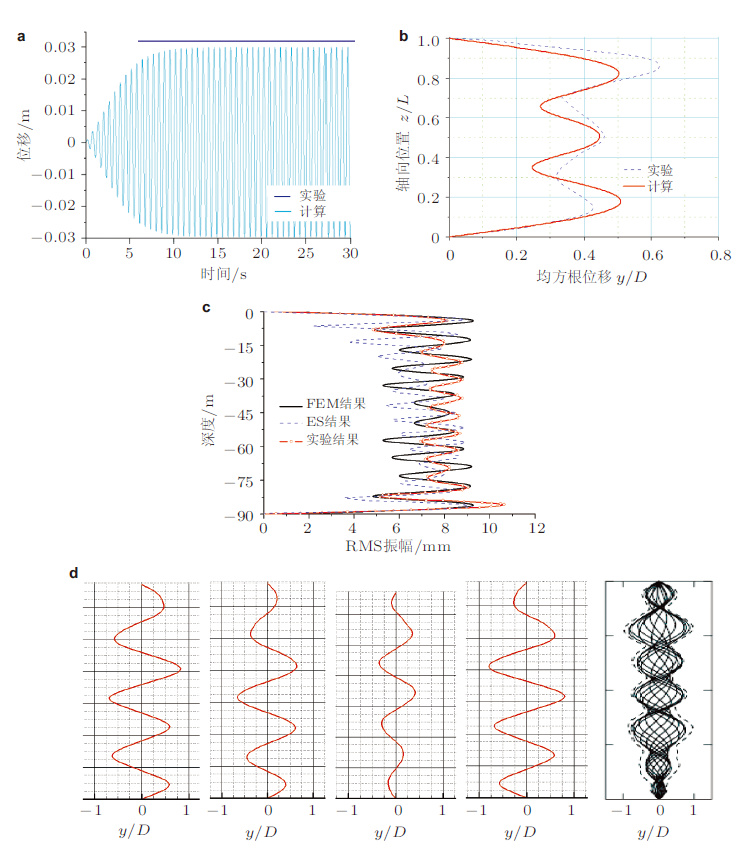
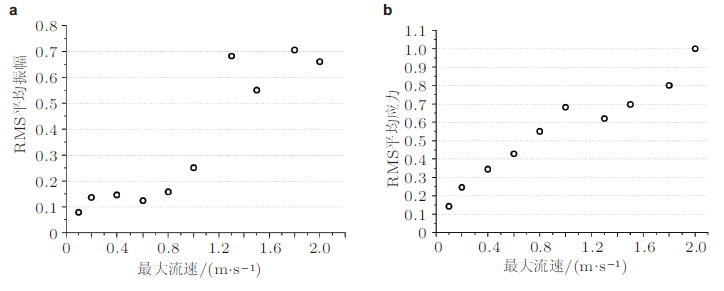
基于该涡激升力模型和有限元数值计算, Zhang和Chen(2011) 、Chen等(2015) 研究了多种流场(均匀流、阶梯流和剪切流)中刚性圆柱和FR的涡激振动(见图 21图 21(c)中的FEM结果、ES结果分别指Zhang(2011) 的有限元模型和Vandiver(1999) 的对等减缩模型的结果, 以下同)数值结果与实验结果吻合较好. 有趣的是在剪切流中, 随着流速的升高, 位移响应并不一定随之增大而结构应力却因为参与振动的模态阶数的升高而逐渐增大(见图 22)这种高应力响应的频率也很高, 将对结构的疲劳寿命带来较大影响需要在实际工程的立管设计中加以重视.
|
| 图 21 基于有限元数值模拟的FR在不同流场的涡激振动响应. (a) 刚性圆柱在均匀流中,(b) 柔性缆索在均匀流中, (c) 柔性缆索在剪切流中, (d) 柔性缆索在阶梯流中 |
|
| 图 22 剪切流中最大位移/应力响应随流速的变化. (a) 平均RMS振幅(A/D)随速度的变化, (b) 平均RMS应力随速度的变化 |
实验是研究和探索涡激振动规律的重要手段, 尤其在初期很多VIV基本现象的观察依靠实验完成多年来研究人员对不同类型的海洋立管做了大量的实验研究工作.随着流场观测手段的提高可以借助PIV和DPIV等先进实验手段细致地观测振荡圆柱的尾迹流场、涡脱落模式Williamson等(1988, 2008)在该方面进行了大量的研究分析了各种涡脱落模式(2S, 2PP+S等)的转换和响应的滞回、相位差之间的联系.
涡激振动实验分为以下几类:(1) 涡激振动机理实验主要为弹性约束刚性圆柱体实验, 此类实验一般是为了确定各参数的关系但是控制参数繁多, 而且很难在临界雷诺数范围内进行此类实验.(2) 模型(有比尺)实验, 这类实验主要是在相似模型上验证原型但因为实际实验较难使所有的无量纲数满足相似律所以验证结果需要进一步处理.(3) 原型(无比尺)实验实验中各参数都可以系统地改变, 其结果常被用来校准理论预测模型.(4) 现场实测, 是预测深海立管VIV最为理想的实验方式它可以提供真实雷诺数和模态下海洋立管 VIV的真实信息.
尽管涡激振动本身是自激振动, 但是由于实施方便很多实验采用受迫振动方式进行这些受迫振动实验主要观察振动圆柱体与流场之间的耦合以及水动力特性为涡激振动预报模型提供可靠的实验数据. 另外受迫振动实验可以消除自激振动实验的随机性且能在较大的范围内控制振幅与频率, 这些范围并不是自激振动能涵盖的.自激振动与受迫振动有着必然的内在联系和区别FR的涡激振动是一种自激振动, 如果把立管分成很多段各段之间的连接以及相互作用可以近似为受迫振动. 因此通过受迫振动实验数据可以判别柔性细长结构物自激振动条件下激发区间和阻尼区间.目前大多数FR涡激振动预报模型和软件, 诸如VIVANA(Carl & Karl 1997), SHEAR7(Vandiver & Li 1999)都基于受迫振动实验数据.Gopalkrishnan(1993) 进行了一系列的受迫振动实验所得实验数据广为工程模型引用. Sarpkaya(2004) 指出通过建立自激振动和受迫振动的理论模型并根据受迫振动实验数据来预报自激振动的流体信息或者通过自激振动的实验数据来反映受迫振动的动力特性可以为进一步理解立管的涡激振动的机理问题提供依据.近几年对自激振动和受迫振动的实验研究表明如果将弹性支撑圆柱体自激振动得到的振动曲线作为受迫振动的输入数据那么可得到几乎完全相同的流体力信息和尾涡模式, Morse和Williamson(2006) 、Hover等(2004)、Carberry等(2004, 2005)给出了详细介绍.
模型(有比尺)实验是指把模型按相似律进行缩小(或放大)在风洞或水槽中模拟实际工程环境来进行实验. 由于具有较好的操纵性一些学者在这方面做了细致的工作. Vandiver等(1996) 发现在剪切强度较小的剪切流条件下涡激振动激发的模态响应能被锁定到单一的响应模态之上这与均匀流条件下激发的单一模态较为相似. Vandiver等(1996) 进一步研究指出剪切流条件下的多模态响应由两个主要关键参数控制一个为泄涡频率带宽内潜在的响应模态数, 另一个为来流的剪切率.中等强度大小的剪切流所激发的频率带宽可包含多个响应模态数立管因此表现出多模态响应; 随着剪切强度增加频率带宽将以某一模态频率为主导. Chaplin等(2005a, 2005b)探究了阶梯流条件下细长管的涡激振动响应, 其中立管下部45%长度部分处于均匀来流中而上部55%长度部分处于静水中, 实验采用逐渐增加流速的方式分别得到横向与流向所激励的最大锁频模态阶数. Lie和Kaasen(2006) 在挪威卑尔根外的一个港口上做了大尺度柔性结构在线性剪切流下的涡激振动实验, 得到了立管在剪切流中的涡激振动响应规律.尽管由于有比尺实验往往不能同时满足长细比L/D和雷诺数Re的相似律, 而具有一定的局限性但是其在新现象探索和参数规律研究方面有比较大的优势.该文在建立水动力模型和研究大长径比立管的特有振动现象(剪切流中的多模态振动、行波效应等)时就充分利用了该类实验的一些结果.
现场实测由于不需要简化而且最符合工程实情是较为理想的涡激振动研究手段. 但是在实际作业环境下现场采集数据需要沿立管轴向布置多个传感器以采集数据, 成本较高;而且三维尺度较大, 很难在测量响应的同时测量流场;此外环境流场包含有较多的随机因素, 难以人为控制目前国际上实地测量实验并不多.较为著名的是挪威深水计划对3个装有测速仪和角速度测量仪的钻井立管进行的实时测量Kaasen等(2000) 详细介绍了实验装置使用以及测量数据处理过程实验得到的数据为立管涡激振动响应经验预报模型提供参考和比较.Lyons等(2003) 和Trarieux等(2006) 对锚链系统的涡激振动进行了现场实验并对实验结果进行了详细分析, 更多的实验研究可参考Furnes等(1998) Machado等(1992) , Willis和Thethi(1999) , Halse(2000) Cornut和Vandiver(2000) , 以及 Kaasen(2001).
总体而言, 尽管由于技术和操作等原因每种实验都有自身的优势和局限性单靠实验本身并不能解决所有的涡激振动问题.但是系统地分析已有的实验结果并合理利用实验数据可以为更好地理解VIV问题和建立预测模型提供帮助尤其是在建立计算模型和分析涡激振动的特有现象等研究工作中可以充分利用已有实验结果(张立武 2010; 郑仲钦和陈伟民 2012b; Chen et al. 2012a; Vandiver & Li 1999, 2005).
4 面临的热点问题与展望 4.1 多模态-宽带随机振动在实际海油工程中, 研究较多的单模态锁频VIV相对于刚性圆柱而言FR的涡激振动响应更为复杂. 因为细长柔性结构具有多阶模态不同阶模态的锁频对应着不同的流速范围而各阶模态所对应的锁频速度范围往往又相互重叠如果来流速度处在两阶模态的锁频速度的重叠区域就涉及到模态选择的问题. ;更为复杂的情况是如果流场是非均匀的如剪切流还涉及到多模态锁频的模态选择以及各阶模态锁频区域确定等问题新的预测模型需要针对这些问题给出解决方案.
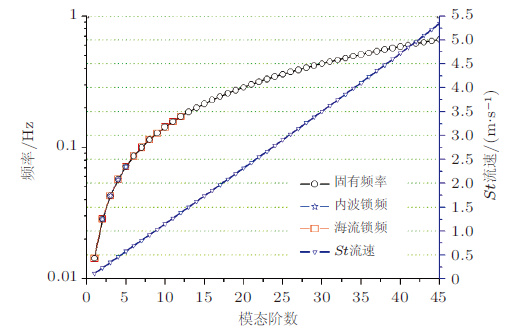
图 23为某3 000 m水深立管的固有振动频率以及各阶模态对应的Strouhal速度VStn=fnD/St, 发生锁频的模态分别为2~5阶和1~12阶.这种高阶模态、多阶模态参与振动, 不但使锁频带宽增加不容易确定立管展向各阶模态锁频区域的位置和长度;而且由于高阶模态的参与, 结构的高频应力提高严重影响了结构的疲劳寿命.
|
| 图 23 立管的固有振动频率及St速度曲线 |
剪切流的实验结果(Huarte et al. 2006; Huse & Kleiven 1998, Lie & Kaasen 2006)表明, 尽管水流速度沿圆柱体轴线连续变化但旋涡以单元的形式脱落.其脱落频率从一个单元到另一个单元是跳跃式变化的.因此沿结构的轴向可以分成若干个单元在每个单元上旋涡脱落频率是常数, 并且锁定在结构的某一阶固有频率上.通常涡脱落单元的数目取决于沿结构轴向的流速分布情况以及结构的固有频率.由于各个单元的旋涡脱落频率可以不同结构的振动模态不止一个可以被激发, 每一个模态对应一个锁频区域结构通过这个区域从流体获得能量. 而在之外的非锁频区域上结构能量被流体阻尼消耗.
根据Strouhal数St和流速范围可以初步给出发生锁频的频率范围以及对应的模态阶数n再根据锁频时的简缩速度范围以及流速沿结构轴向的分布可以计算出各阶锁频模态的锁频区域Ln.由于流场的剪切分布、结构模态的低频密集仅按照锁频速度范围确定锁频模态和区域时可能出现很多阶模态同时锁频而且锁频区域重叠的情况.
事实上, 从已有的试验结果看, 锁频模态的个数是有限的而以往的"高频占优"准则(Lyons & Patel 1986, Chen et al. 2009)直接将高阶模态作为主导模态, 对等减缩模型(Vandiver & Li 1999)均匀地将各阶模态锁频长度减缩直至模态不重叠这很难准确地挑选出锁频模态, 尤其不能确定响应中的主导模态. 陈伟民等(2011) 提出了模态能量法通过比较模态能量值的大小来确定最终参与锁频模态的阶数及相应的锁频区域.第n阶激振模态的功率与模态激振力Fn和模态阻尼Pn的关系为Pn=(Fn)2/(2Rn), 其中
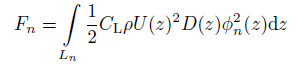
|
(14) |
式中, φn(z)为第n阶模态振型; Rn包括了模态水动力和结构阻尼.考虑到各阶模态之间的相互影响以及模态之间的"竞争"真正参与振动的模态的个数是有限的也就是说只有"竞争力"强的模态才能参与锁频. 因此, 取满足条件Pn=Pn/(Pn)max≥0.20的模态为锁频模态. 图 24为利用模态能量法得到的多模态涡激振动响应的模态加权结果与Huse等(1998, 1999)和Lie等(1997, 2006)的大尺度深水试验基本吻合(陈伟民等 2011).
|
| 图 24 基于模态能量法的多模态涡激振动响应的模态加权结果. (a) 最大流速为0.54 m/s, (b) 最大流速为1.14 m/s |
张杰等(2013) 考虑了立管内部张力沿轴线变化所引起的固有频率和振型的变化以及因此带来的模态耦合效应进而研究参数激励下深海立管的多模态耦合振动特性(唐友刚等2013) 并与未考虑模态耦合的计算结果进行对比分析. 结果表明考虑模态耦合立管参激振动不稳定区域增大, 多模态耦合参激振动发生时小激励也能激起大响应, 特别是弯曲应力将显著增大.
张立武(2010) 和Chen等(2016) 的研究表明: 无论在均流中(见图 25(a)和图 25(b))、还是剪切流中(见图 25(c)和图 25(f)), 都会发生多模态振动; 尤其是在剪切流中这种多模态竞争参与的振动, 表现出宽带多频的动响应特点需要在确定各阶模态的锁频区域时考虑模态能量或者模态简缩速度的综合影响;在立管的两端, 因为界面的反射作用, 以驻波波型为主导但是在立管展向的中间, 由于较长的传播路径和大阻尼作用容易出现行波波型.
|
| 图 25 均匀流和非均匀流中细长FR的多模态涡激振动响应. (a) 均匀流中的RMS 位移响应, (b) 均匀流中的位移时空演化, (c) 剪切流的RMS 位移 (最大流速0.54 m/s), (d) 剪切流的位移时空演化(最大流速0.54 m/s), (e) 剪切流的RMS 位移 (最大流速1.14 m/s), (f) 剪切流的位移时空演化 (最大流速1.14 m/s) |
近年来, 随着试验手段的提高和试验条件的改进大尺度的深水试验得到很大发展为多模态锁频振动的研究提供了很有价值的试验结果. Huarte等(2006)观察到了多模态振动并测得了拖曳力放大系数, Vandiver等(2009) 测得的振动模态阶数达10~25阶, Huse等(1998, 1999)通过模态分析法推算出立管轴线位移变化函数, Lie和Kaasen(2006) 用模态法分析了Huse的试验数据, 得到了响应的模态加权系数分析了振动中各阶模态的参与量. 但是对于多模态参与的模态竞争机制、模态参与量与简缩速度的关系以及实际工程中经常会出现的宽带的、随机的立管振动响应还需要更深入的研究并发展相应的计算模型.
4.2 上部浮体与水下立管的耦合事实上, 除了波浪载荷与海流载荷浮式平台的水下立管还要承受上部平台运动带来的载荷.浮式平台多采用锚链式系泊系统进行位置约束深水平台的运动除了常规的波频运动, 还有低频漫漂(位移可达十几米)和高频振荡(ring和spring等). 随着水深的增加相对于浅水导管架平台和张紧式约束平台, 浮式平台的运动幅度(位移、速度等)明显增大对与上部平台相联的水下部分包括系泊链、立管等结构的影响增大因此平台浮体-水下立管的耦合作用明显增强二者耦合的动力响应已成为国际上深水平台研究的一个热点问题.
这种平台浮体-水下立管的耦合作用引发了一系列新问题.例如由于上部平台的运动(以平台垂荡为例), 会引起立管的动态张力造成结构参数(刚度)的时变特性从而影响立管整体结构的涡激振动响应.研究结果表明与不计平台运动的情况相比平台垂荡除了激发了更高阶模态共振外, 还提高了原本锁频模态的振幅(增加了10%), 并且应力增幅显著(增加20%至1倍). 而且平台振荡带动结构的顺流向运动(inline motion)造成结构与流场在顺流向的非定常的相对运动这与以往的定常流场中的涡激振动有很大的不同. 实验结果(Liao 2002)表明尽管浮体的小幅运动本身不会激发立管的涡激振动但是由于运动边界造成的"振幅放大"效应上部浮体的小幅度运动可能会在立管某处引起较大的顺流向运动从而引发立管的涡激振动. 另外还涉及动边界条件改变展向相关性的问题因为平台的周期运动造成立管上端部的振荡边界条件圆柱端部边界条件对圆柱涡激振动的实验结果(Morse et al. 2008)表明这种运动边界条件会造成结构周围流场改变使得尾流的展向相关性变化、相关长度减小(或增大)从而改变响应尽管实验是在弹性支持的刚性圆柱上进行的但是它说明了边界条件的重要性.
关于平台和立管的耦合问题目前多见于针对平台动响应的研究通常有两种方法: 准静态法(Heurtier et al. 1998, Stansberg et al. 2002)和耦合法(Arcandra & Kim 2003; Heurtier et al. 2001;Chen et al. 2001; 2006; Tahara & Kim 2008; Garrett 2005;谷家扬等 2012). 准静态法把立管部分简化为无质量弹簧主要考虑下部立管对平台的静恢复力基于三维衍射/辐射理论计算上部大浮体的水动力和运动通常用线性频域或解耦时域方法求解问题. Spanos等(2005) 将平台质量集中在重心处用水平弹簧模拟立管和平台主体的相互作用用简化模型研究了立管刚度对SPAR平台总体运动响应的影响. Heurtier等(2001) 、 Chen等(2006) 和Wichers等(2001) 研究了多种深海平台浮体与立管(或系泊系统)的相互作用比较了时域耦合和准静态两种方法结果表明准静态方法忽略了水下立管的惯性和阻尼效应会低估系泊系统抵御环境载荷的能力.
耦合方法多见于上部浮体的动响应研究考虑了立管对平台的阻尼力、惯性力等动力作用立管的结构可以用有限元模型模拟. 细长立管水动力采用Morison公式上部浮体的水动力用势流辐射/绕射理论求解(例如WAMIT和WADAM程序)最后用迭代的方法进行有限元程序和浮体水动力程序的"耦合"求解为保证二者的耦合特性, 在平台和立管的联接处要求力和位移是连续的.因为"同时"求解了浮体和立管的动力方程所以隐式地包含了立管的阻尼力、惯性力等动力效应. Lee和Wang(2000) 采用线性弦线模拟张力腿, 分析了平台纵荡下的张力腿动力响应结果表明张力腿的振动模式与平台的运动模式类似但是振幅会随着入射波周期的改变而变化. Tahara和Kim(2008) 采用Bosman和Hooker(1999) 提出的计算杨氏模量的经验公式计算了SPAR平台垂荡时系泊系统的响应并将结果与线弹性系泊模型进行了对比发现两种情况下的响应会差别很大. 但是耦合法中立管的水动力采用Morison公式, 并不适用于立管的涡激振动问题.
另外需要指出的是, 不同的平台运动形式与下部立管的动力耦合机理不同.例如, 立管的水平运动即横荡和纵荡会沿着立管展向往底部传播并直接与立管涡激振动的横向运动相互耦合;而且平台运动边界还会造成新的非线性耦合现象. Liao(2002) 研究了非定常流中细长结构的涡激振动实验测量了端部周期振荡对FR的顺流向运动(inline motion)速度沿展向分布的影响, 发现了平台运动对立管的振幅放大效应.
而平台的垂荡运动主要造成立管的动张力使得立管的结构参数发生周期性的变化, 而导致参数激励问题(Patel & Paek 1991b, Simos & Pesce 1997, Chandrasekaran et al. 2006, 唐友刚等 2013, Chen et al. 2014; Yang & Xiao 2014毕勤胜等 2003). 关于参数激励的研究, 关注多的是立管结构稳定性问题即对如何确定稳定区域的边界进行理论求解并对不同的稳定性进行理论分析(Chatjigeorgiou 2004, Chandrasekaran et al. 2006; Yang & Xiao 2014, 肖飞和杨和振 2014).Chandrasekaran等(2006) 对TLP平台的张力腿的张力变化引起的Mathieu不稳定性进行了分析;Yang和Xiao(2014) 对在涡激和多频参数激励共同作用的多种组合条件下TTR立管的不稳定性进行了详细讨论比较了参数激励和涡脱落激励在不同海况下的作用指出在极端海况下会出现立管的高频-多模态参与的振动; 肖飞和杨和振(2014) 对深海钢悬链立管Hill不稳定性进行了预测.
还有一些研究针对简化模型, 如理想简支梁或简化水动力模型(Morrison公式或者定常涡激升力系数模型), 给出了响应的数值解(王东耀和凌国灿 1998; 徐万海等 2009; 唐友刚等 2013; 唐驾时和贺新柱 2001; 菅永军等 2003; Wu et al. 2012a, 2012b). 徐万海等(2009) 基于Euler梁和定常升力系数模型研究了参数激励下的立管稳定性区域以及响应; Wu(2012b)考虑了梁结构的截面旋转和剪切变形基于实验结果对定常涡激升力模型进行了修正研究了参数激扰的不同环境荷载作用对立管响应的影响. Wang等(2014) 进行了大尺度模型的水池实验进一步分析了平台强迫运动条件下的水下结构的涡激振动引起的SCR的疲劳破坏给出了平台运动频率和幅度对锚链的关键位置例如触地点和上顶部的疲劳破坏的影响规律;唐友刚(2013) 利用定常升力系数模型研究了深海CTTR在参数激励和涡激振动耦合作用下的动响应结果表明, 立管的横向振动响应频率存在0.5倍参激亚谐成分参数激励对于立管横向振动具有重要影响.
Chen等(2014, 2015)建立了具有时变结构刚度特性的有限元结构模型以及与结构运动相耦合的非定常涡激升力系数模型利用有限元数值模拟分析了平台运动-立管涡激振动整体系统的动力响应.研究了平台运动与立管涡激振动的动力耦合规律及响应过程中的振幅放大(见图 26)、参数激励过程中的模态转换(见图 27)等新现象考察了平台运动频率等参数对水下立管模态位移、振动波传播和演化的影响.
|
| 图 26 平台的横荡运动与水下立管涡激振动的动力耦合响应. (a) 平台横档运动引起的立管振幅放大, (b) 不同平台振荡幅度下的立管振动位移 |
|
| 图 27 平台的垂荡运动与水下立管涡激振动的动力耦合响应. (a) 考虑与不考虑平台垂荡的立管最大位移, (b) 立管参数激励响应中出现的模态转换 |
最后, 平台运动对立管形成了一个上端部振荡边界条件这种运动边界条件影响了结构周围流场. 研究表明(Slaouti & Gerrard 1981)端部边界条件对无论是短圆柱还是长径比达102的长圆柱的绕流具有重要影响Prasad和Willaimson(1997) 和Szepessy和Bearman(1992) 的研究结果证明在雷诺数Re<190的层流中和Re=5 000时圆柱上的涡动力的大小以及沿圆柱展向的分布情况均受端部边界条件影响.对于圆柱涡激振动尽管结构的振动提高了流体力的展向相关长度和涡形成的相关性但是Hover等(2004)和Morse等(2008) 的研究结果表明端部条件的改变会改变尾流的展向相关长度最终影响了结构的涡激振动发生条件以及响应幅值.目前这些研究还仅限于弹性支持的刚性圆柱.
目前国际上比较通用的VIV软件, 如SHEAR7、VIVA等(Carl & Karl 1997), 主要是针对单独立管的没有将平台运动对FR涡激振动的影响考虑进来.深水立管本身的结构和流场较为复杂而且平台运动对其运动的影响越来越重要, VIV响应预测更加困难需要进一步分析不同平台运动形式和水下立管涡激振动的相互作用机理建立考虑平台运动影响的深水立管涡激振动的预测模型在该方面的研究还有待继续开展.
4.3 悬链线等复杂结构的VIV实际工程中的立管结构形式多种多样, 根据结构形式和用途的不同可以大致将立管分为4种形式: TTR, SCT, FR和混合式立管(hybrid tower riser, HTR). 其中, SCR是近年来发展起来的一种新型深水立管系统其结构形式较为简单, 由具有标准长度的钢管焊接而成兼有海底管线与立管的特性, 其适用的水深可超过3 000 m很大程度上突破了顶部张紧式立管在深水海域的局限性被认为是深水工程中较有潜力的立管概念.
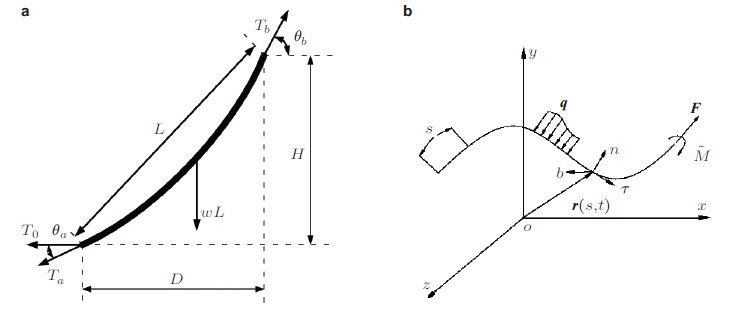
但是, 与以往垂直的TTR不同SCR具有初始的悬垂和沿结构展向变化的曲率结构与流速的夹角不再是90°对于这种具有倾斜角和初始曲率的结构其结构/位移的非线性、固有动力特性、尾迹流场的模式、VIV响应等的特点和规律还缺乏足够的认识和合理的预测模型.SCR的动力平衡方程与弯曲梁或者张力弦线的不同, 对于静态问题由于结构的自重作用, 悬链线自动悬垂而形成了悬链线形态. 对于如图 28所示的悬链线, 其几何构型和顶端张力的关系式为(郭双喜 2015)
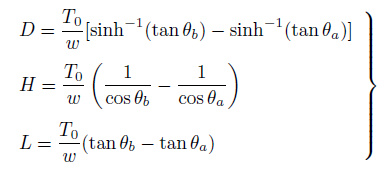
|
(15) |
|
| 图 28 悬链线结构示意图. (a) 悬链线结构静力平衡(b)三维系泊系统示意图 |
其中, L为悬链线的长度, D为悬链线的水平投影H为悬链线的垂直投影, θa, θb分别为悬链线两端点与水平线的夹角.
随着水深的增大, 系泊线上的动态效应包括惯性力和水动阻力对张力的影响越来越明显应考虑系泊线上的动力作用. 细长锚链运动方程的矢量形式如下
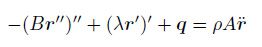
|
(16) |
其中, B为系泊线的弯曲刚度, r为位移矢量, ρ为系泊线密度, q为系泊线单位长度上作用的外力A为系泊线横截面积. λ(s,t)为系泊线上的有效张力, λ=F⋅r′+(Br")′⋅r′, 其中, F为作用于杆中心线上的合力, r′满足变形协调条件r′⋅r′=(1+ε)2(ε表示锚链的弹性伸长). 对于上述非线性动力方程通常不能直接得到解析解, 需要通过数值方法求解得到其动力响应.
尽管SCR在深水中的应用前景被看好但是目前较多的研究多集中在基于静力平衡的变形理论或实验观察(Karayaka et al. 2009, Chevron et al. 2011, Wang et al. 2014 段梦兰等 2011)关于考虑其惯性和阻尼效应的动态特性、尤其是VIV的研究还在发展中.Karayaka等(2009) 对实际工程中的SCR进行了现场监测分析了SCR流场之间相互作用的行为尤其是浮体导致的悬链线立管的响应、悬链线立管的涡激振动、触地区管道和海床的相互作用等问题.Chevron等(2011) 根据SCR在极端环境下的实测资料(浮体运动导致的立管加速度以及应力等数据), 分析了SCR的动力响应.段梦兰等(2011) 进行SCR触地区疲劳试验考虑了张力、弯曲、内外压与管土相互作用等因素的变化.
SCR的分析模型尚需进一步发展有的研究用等效的垂直张紧式的TTR来等效SCR或者借助VIV商用软件SHEAR7(基于模态叠加的尾流振子模型)分析其模态和VIV响应的RMS位移(Rao et al. 2011). 事实上, 对于具有曲率的弯曲结构其振型和频率与直梁结构不完全等效, 由于结构几何的差异SCR有初始曲率和几何非线性, 二者的VIV响应, 尤其是in-line方向的振动存在不可忽略的差异(Srinil et al. 2009).剪切流中的大尺度的深水实验(Huse & Kleiven 1998)表明对于SCR, 无论是一端铰支一端自由还是两端铰支其VIV会引起结构的轴向振动这种轴向振动可能导致远比弯曲疲劳应力更高的结构应力. 更困难的是如何利用目前常规的VIV的抑制措施来达到同时降低横向和轴向应力的目的目前还少有实验结果.
4.4 VIV抑制措施目前抑制涡激运动主要从两个方面来考虑:(1) 从结构动力学控制方面设计和调整立管结构参数, 使系统的自然频率远离涡激振动的频率范围;(2) 从尾迹流场的流体力学控制方面, 对流体边界层进行控制改变和控制旋涡的形成和脱落, 或减小旋涡脱落所造成的流体激励.所用的控制方法可以是被动控制或者主动控制:(1) 被动控制是目前使用较多的, 即事先对结构进行改变如改变结构的外形或增加附加的装置, 从而改变尾迹流场破坏或延迟规则的尾迹涡脱落, 弱化或减小流动对结构振动的激励作用达到抑制响应的目的;(2) 主动控制技术是正在发展中的即利用实时监测和计算机自动控制等技术通过对实测数据的分析和控制算法将主动控制律(外部干扰措施)反馈回系统从而控制旋涡脱落或增加阻尼降低结构振动位移.
附加装置的形式多种多样(Kumar et al. 2008; Gad-el-Hak & Bushnell 1991; Griffin & Hall 1991; Zdravkovich 1981, 1997 ;Lim & Lee 2004): 有的是干扰展向相关性例如在立管表面缠绕螺旋边条(helical strakes)或布置O形圈(O-rings)、利用突起或波浪形结构表面等;有的是影响钝体表面产生剪切层, 例如立管尾部加整流罩(fairings)、附属管线(axial rods)、附加薄带(ribbons)等阻止圆柱尾迹的旋涡形成及发展;还有的是阻止剪切层之间相互作用, 例如分离盘(splitter plates)等.
螺旋边条是被较早和普遍采用一种涡激振动抑制手段, 一些研究(Lee & Kim 1997, Baarholm et al. 2005, Zhang et al. 2011, Lubbad et al. 2011; Korkischko & Meneghini 2010)对能够取得最优化涡激振动抑制效果的螺旋边条的高度、间隔距离进行了分析结果表明增大边条的高度对振动的抑制效果明显但会给隔水管带来更高的流向阻力而另一个缺点是其抑制有效性会随着自由来流的湍流度以及约化速度的增大逐渐降低.采用直接修改结构的外形(波浪型圆柱)的方法这种沿展向不均匀的周期分布的结构的三维尾迹涡结构能得到很好的控制它在轴向方向呈现周期性正负涡的交替分布特性. 随着幅值的增大波浪型圆柱表面的自由剪切层得以延展使得旋涡的脱落发生在波浪型圆柱下游较远处, 从而达到减阻的目的.波浪型圆柱与普通直圆柱相比其幅值对平均阻力系数及脉动升力系数的减少及尾迹控制有着更重要的影响最大减阻可达16%(Lam et al. 2004; 2010; 王沣浩 2006).
横截面为流线型的整流罩在抑制隔水管旋涡脱落的同时能够有效减小隔水管的振幅(Grant & Patterson 1977; Allen & Henning 2001; Masters & Griffith 2012; Coakley & Knutson 2003)其抑制VIV的可靠性似乎要高于螺旋条纹但是其安装、维护和经济性不如螺旋边条.附属管作为钻井隔水管系统中的必要设备, 除起到作业的基本功能外也可通过影响隔水管周围的流场进而抑制其涡激振动(Song et al. 2009)通过适当布置其外形尺寸以及在隔水管周围的排布方式便能取得涡激振动抑制效果而且不需要太多的附加成本.分离盘能够起到稳定近流尾迹和抑制旋涡脱落的作用近流尾迹的流场形态在分离盘的长度L>5D时, 旋涡脱落基本消失并且阻力系数基本不再随着分离盘长度L的变化而变化(谷斐 2012).但是, 分离盘和整流罩均受来流方向影响, 现实中海洋流向是时常变化的.
除了以上这些抑制装置, 人们还提出了对流动直接控制的方法, 如喷射(或抽吸)方法, 即将流体以某一速度射出(或吸进)缝隙(或流孔)特别当射流速度周期性变化, 保持总质量流量为零时, 称为合成射流技术(synthetic jettechnique).这种流动控制方法较早地应用于控制机翼流动分离并调节升阻比(Clarke et al. 1955; Carriere & Eichelbrenner 1961, Chang 1976)该方法因为取得了一定成效, 后来向其他领域扩展用于钝体尾流控制的研究文献在最近几年增加较快(Glezer & Amitay 2002, Dong et al. 2008, Layek et al. 2008; Feng & Wang 2010). 邵传平等(2014) 通过一系列风洞实验研究了尾部喷射、隔离板和窄条控制件等3种控制方法及其对非锁频和锁频、谐波锁频及亚谐波锁频等3种锁频状态旋涡脱落的抑制效果并从尾流稳定性观点出发对振荡柱体绕流旋涡脱落的产生机制及其控制机理进行了探讨.
附加装置抑制措施的负面效应是由于顺流方向有效横截面积的增大导致水流的阻力增大, 如何能在两者之间取得平衡?需要对不同构型几何和布局条件下立管的位移幅值、尾迹流场、流体力沿展向的分布等进行系统的观测.另外, 对于CFD来说这种缠绕了边条或扰流片的立管的三维VIV数值模拟更是难上加难.
4.5 In-line与Cross-flow的双向振动耦合由于横向振动的幅值一般为顺流向振动的2倍因此多数研究关注的是横向涡激振动.然而尾迹中顺流向涡脱落的频率近似为横向涡脱落的2倍也就是说顺流向涡激振动的幅值尽管较小, 但是频率却比较高造成的疲劳损伤与横向振动可能会在同一数量级(Baarholm et al. 2006)因此对于海洋工程中的立管或者管线结构的疲劳寿命分析有时需要考虑横向和顺流向两种运动(Dahl et al. 2007; 2010) .
对于同时具有顺流向和横向双向自由度的结构不能简单地将单自由度横向涡激振动和单自由度流向涡激振动叠加起来因为顺流向运动会对尾涡脱落造成一定影响从而与横向振动产生一定的耦合. 对于柔性圆柱的双向涡激振动其发生条件为当频率比(顺流向与横向固有频率的比值)接近2(Dahl et al. 2010), 这时结构的运动轨迹为稳定的8字形双向振动的主要影响参数是质量比、频率比.
Jauvtis和Williamson(2003, 2004)的试验表明, 在高质量比条件下双自由度涡激振动响应与单自由度横向的结果区别并不明显.但是在低质量比条件下, 实验结果(Moe & Wu 1990; Jauvtis & Williamson 2004; Pesce & Fujarra 2000)表明顺流向振动将对横向振动有显著的影响:横向振动响应出现了新的上分支并伴随较大的振幅峰值 (A/D≈1.5), 同时在横向锁频范围内顺流向也形成了响应振幅峰值(Aymax/Axmax≈5.4)尾涡模式呈现出现了"2T"形式该尾涡模式会导致横向激振力中存在三阶高谐分量(Tryantafyllou et al. 2004). Fujarra等(2001) 的实验(质量比为1.3) 表明如果提高结构的流向刚度流向刚度与横向刚度的耦合造成超出锁频区域的高流速区的高振幅响应.双向运动的流向刚度和横向刚度的耦合加强使得柔性圆柱双向涡激振动变得复杂相应的动力分析也变得困难.
不同频率比(Sarpkaya 1995, Dahl et al. 2006, Sanchis 2009)的实验表明: 在频率比1.0附近, 横向振幅 (A/D)大约为1.2;当频率比为2.0时, 横向振幅随简缩速度的变化将出现两个不同的振幅峰值.随着频率比(在1.0~2.0范围内)增大横向的振幅响应、频率和相位角会有显著的改变锁频区内的振幅响应峰值和滞后均变得显著;频率比的增加将导致顺流向共振的延迟即锁频区域的简缩速度增大Sanchis(2009) 指出当顺流向共振靠近横向上端响应分支的前端时将显著地改变旋涡的分离点.
关于双向振动的计算模型, Furnes和Srensen(2007) 、Ge等(2011) 、Srinil和Zangane(2012) 、黄智勇等(2007) 分别提出多振子耦合振子模型尽管各个模型描述结构运动的振子不同, 但都使用了van der Pol振子来描述顺流向和横向的脉动水动力, 其中顺流向尾流振子的固有频率为横向的2倍.这种方法能够给出较为准确的响应振幅, 但是相位角与试验结果差别较大;另外, 模型中引入了较多的经验性参数, 对预测结果影响较大. 秦伟(2013) 考虑了横向运动对顺流向运动的影响基于涡强尾流振子模型对二维刚性圆柱体的双自由度涡激振动进行了数值模拟进一步验证了质量比和阻尼比对双向振动响应的影响十分显著.质量比减小将导致横向锁频范围增大, 但顺流向初始峰值无显著变化阻尼比减小将导致顺流向/横向振幅峰值增大, 但对锁频范围无显著影响.
4.6 管道内外流共同作用等其他问题工程中的海洋立管内部通常需要输送油、气或它们的混合体如果考虑内部输送流体的存在, 流体从变形管道的一端流向另一端时流体质点会产生离心加速度和科氏加速度从而使得流体动压力周期性作用于管壁, 诱发立管弯曲振动.而且管道在外部载荷下的振动和内部流体运动会相互加速从而引起管道的附加振动(郑哲敏 1958, Chen 1971; Moe & Chucheepsakul 1998), Feodosev(1956) , Paidoussis和Issid(1974) 的研究表明, 内部流体的作用会影响管道的动力特性及动力响应随着内流速度的增大, 结构刚度和固有频率降低当达到临界速度时系统振动发散而出现失稳.
内流对立管涡激振动的影响(Keber & Wiercigroch 2008; Meng & Chen 2011), 主要有两个方面:(1) 附加的内部流体质量改变总体立管结构质量, 流体产生附加轴向压力(附加结构刚度), 使得结构固有动力特性改变(例如固有频率的降低)从而改变锁频发生的流速范围和响应的幅值. 研究表明(Chen 1971, Wu 1991, Chen 2012b), 如果立管的顶端张力较小, 当内流足够大时内部流体流动产生的动力作用可以抵消顶端张力的作用从而显著降低立管的自振频率; 而顶端张力较大时内流体的影响则不明显.(2) 变形管内流体运动的离心力和科氏力在结构动力平衡方程中增加了附加项也会改变总体结构的动力特性和响应幅值(郭海燕等 2005).
关于考虑内流影响的立管VIV问题, Hong和Huh(1999) 、付强(2004) 、Guo和Lou(2008) 分别基于升力系数模型和尾流振子模型研究了内部流体对立管VIV的影响结果表明随着内流速度的增大, 位移幅值增大但立管的频率和振动的展向相关性都降低. Dai和Wang(2012) 利用多尺度法和单自由度模型讨论了内输液管线的定常响应的稳定性发现在锁频阶段会出现不稳定的动响应.
另外值得注意的是, 当立管外的流场沿展向为非均匀分布时(如剪切流)因为结构变形的曲率是非对称的, 所以不同流向的内部流体, 如下行流体(从立管顶部向海底输送)和上行流体(从海底向上输送)对结构响应的影响是不同的(Chen & Kim 2012b, 付强 2004郭海燕等 2005), 尤其当内部流体的运动速度较高的时候这个差别会更明显.
最后, 实际工程中的工作环境更复杂, 例如从地下抽出的原油稠度较大、温度较高, 为保障正常输送输送压力可以达到20 MPa左右, 设计温度普遍达到或超过100°C甚至可能达到150°C的高温(Aiten 1978; Ketar & Patil 2014), 远高于立管外部的海洋环境温度和压力如此条件下立管结构面临着发生屈曲的风险.较大的屈曲变形会导致结构弯曲应力急剧增大达到或超过钢材的屈服极限强度, 对立管的安全性造成严重威胁.屈曲变形导致结构配重层、保温层结构遭到破坏, 影响立管的正常使用;当屈曲变形达到一定数值时, 在复杂的海洋环境中受到外界作用的干扰屈曲幅值将会逐渐增大而导致海底结构发生破坏(Sun et al. 2011, Herlianto et al. 2012).高温油气所产生的内外温差对立管结构的固有动力特性也有影响随着温差的增大固有频率逐渐降低(赵丽刚 2006).
立管往往不是单个而是多个同时工作的立管束多个立管系统的模态组合会成倍数地增加, 系统的固有动力特性变得复杂;更重要的是, 下游立管位于上游立管的尾涡中立管之间的作用力在一定条件下变成吸引力从而引起立管的互相碰撞或倒塌(clashing or collapse)(Grundy & Hewitt 2002, Baarholm et al. 2007). He和Low(2010) 通过分析立管动响应的时域结果基于极值理论给出了立管之间碰撞概率的评估方法但是已有研究针对多立管之间的相互作用的流体动力和碰撞过程分析还较少有涉及VIV立管的碰撞问题.
4.7 新近的发展趋势以下谈几点涡激振动研究的发展趋势, 尤其是国外已经开展而国内尚显不足的方面.
4.7.1 高雷诺数的实验(或CFD数值模拟)虽然已经有不少涡激振动的实验在实验室开展但是有两个参数难以达到实际工程的要求, 一个是雷诺数另一个是长径比. 目前的许多结果是在低雷诺数(102~104)的条件下, 或者在中小尺度的实验室或一定的控制条件(例如强迫振动)下得到的.尽管雷诺数对物理和数值实验的结果有不可忽略的影响但是因为实验室条件和数值计算的困难目前还很少见到雷诺数大于5.0×105而且没有自由面、边界条件干扰的实验缺乏整个锁频区域的尾迹涡三维模式、相关长度、压力分布、分离点位置等的观测.
目前关于圆柱涡激振动的研究大都局限在雷诺数1.5×102<Re<1.5×105 的范围内, 在该雷诺数范围内, 斯特哈尔数约等于0.2, 随着雷诺数的升高 (4.0×105~1.0×106) Strouhal数有一个变动范围(0.18 ~ 0.24该值与结构的相关长度有关), 尾迹的宽度也从1.0D降低到0.7 D相应的流体阻力系数也会降低. Sarpakaya(2004) 指出很多的关于尾迹流场中涡脱落模式的多样性观察结果都是在低雷诺数下进行的Williamson和Erovardhan(1988, 2004, 2008)给出的2P和2S涡模式的详细分布图也是在雷诺数低于1 000的条件下得到的;甚至没有人在雷诺数大于20 000的条件下观察到响应的初始分支等因此对于高雷诺数的实验观察还需要进行尤其需要诸如相关长度、压力分布、分离点位置等实验数据.
高雷诺数的物理或数值实验的意义不仅仅在于与低雷诺数层流的不同现象的展示和发现高雷诺数条件的响应特点是非理想正弦、非确定周期的因为流场的持续变化, 所以不容易出现跳跃等突变(sharp change);而是希望通过高雷诺数实验来补充现有的水动力、响应数据库来更好地定量化地处理剪切效应、边界效应实现在更宽雷诺数范围内有效抑制VIV而且不增加阻力, 避免在工程实际中因缺乏实验数据和理论分析, 设计者只能采用保守设计方法的弊端.遗憾的是至今还缺乏高雷诺数的详细实验结果不清楚高雷诺数与低雷诺数数据结果的差异到底在哪里这需要进一步的研究.
4.7.2 大尺度的现场实验实验室的尺度范围通常小于10 m而实际海洋工程的立管长度大于1 000 m深水立管多数超过了3 000 m. 大尺度(large-scale)模型实验介于一般实验室和实际工程的尺度之间目前能实现的大尺度试验的尺度通常在几十米和几百米之间.
这种大尺度的实验不但有助于更好地理解实际海洋工程中经常发生的高阶-多阶模态参与、宽带随机振动、行波-驻波混合的立管涡激振动现象和机理所建立的水动力和响应数据库可以为预测模型提供必要和可靠的依据.事实上, 正是基于这些系统的大尺度实验工业设计部门才可以比较放心地使用目前的各种半经验计算模型这些模型本身并不一定很复杂其预测的准确程度在很大程度上依赖于模型中系数的数值和取法. 另外实际过程中的立管形式复杂多样现有的计算模型不可能完全真实地模拟出实际立管的工作环境和响应状况尤其是当新的立管概念提出时往往需要通过更接近实际情况的大尺度或现场试验来验证新概念的可行性并且观察可能发生的振动模式.
与刚性圆柱的涡激振动实验不同柔性圆柱的涡激振动试验会存在尺度效应实验室规模的小尺度模型试验不能直接推广到工程实际的大尺度立管. 李曼(2013) 比较了3种不同尺度的柔性圆柱模型的阻力系数、主导频率和模态阶数发现均存在尺度效应, 由于缩尺使轴向力主导的振动范围变大拖曳力的作用使得轴向力变大, 缩比模型的立管响应阶数偏低;不同尺度的模型VIV位移响应表明, 如果考虑弗雷德数相似不同模型的位移响应并不一致, 不能用简单的线性关系换算;模型的雷诺数相似性比弗雷德数略好, 但是也不能完全满足相似性原则.
实现大尺度实验的难度很大, 因为实验需要的场地大、设备多、费用高而且还存在一些棘手的具体问题: 测量仪器的附加质量/刚度影响大可以实现的长径比、雷诺数、流速受实验室条件限制(不够大)流场的湍流度大、响应模态阶数低; 能够安装的传感器的个数有限反应和捕捉多阶-高阶模态响应比较困难; 加速度计的信号含有杂波当立管的位移和变形较大使得加速度计倾斜的时候数据的水平分量因含有垂直分量而不纯.
国外首个大尺度实验是在均匀流中进行的, Vandiver和Mazel(1976) 观察了一根23.4 m长的常张力立管的锁频, 最大雷诺数为6 859观察到的最高阶模态为7阶, 当时只采用了两个加速度传感器测量模态位移;随后的实验雷诺数提高到22 000, 传感器个数增加到7对测量到的阻力系数超过了3.0. 剪切流中的实验(Kim et al. 1985)发现:细长立管(267 m)的动响应近似于张力弦线, 而且没有单模态锁频发生;最高的模态阶数从17.7 m长的缆索的11阶(Vadiver 1983)提高到了122 m长缆索的25阶(Vandiver et al. 2005; Lie & Kaasen 2006, Murrin 2007, Ordonez 2007)传感器的个数也增加到了24个, 雷诺数达到了34 000. 遗憾的是尽管国外在该方面已经开展了一些工作但是国内在这方面的实验工作还比较缺乏尤其是对较长尺度的、多个测量点的、高阶模态参与的VIV的观测数据还不多见.
4.8 总结与展望(1) VIV的非线性流固耦合
近二十多年来的VIV研究经常伴随着新现象的发现从最初的结构响应的锁频、分叉到后来的位移跳跃、与步长和路径的相关、尾迹涡的多模式脱落以及海洋工程中的多模态-高阶模态参与、宽带随机振动、行波-驻波交互传播等等对这些新现象的发生条件和内在物理机理的解释一直存在着争议还难以给出定论.困难的根源在于对VIV这种经典又独特的流固耦合现象的认识和掌握如何理解其流体动力和结构动力在锁频不同阶段的各自演化过程和互相耦合(相互促进、抵消、分解、消散)关系?结构在一个运动周期中如何改变其近壁面边界层中的脱离和涡量的大小?
当然, 发现和解释各种现象的最终目的, 不仅仅是为了促进本学科的进步;更重要的是有助于理解VIV问题的本质, 提炼出主要的影响因素从而建立更合理的预测模型, 服务于海洋工程实际.
(2) 用于工程设计的预测模型
海洋立管VIV的预测模型仍然需要完善, 不同于基于CFD和FEM的数值模拟这些应用于实际工程的预测模型应该具有比较高的计算效率可以方便地应用于深水FR的结构设计.今后的工作可以主要在两个方面加以完善: 一是适用于实际工程问题也就是说这样的模型应该繁简有度, 即可以反映VIV问题的基本特征又不会因为参数冗余或者其值的选取过于依赖模型使用者的个人经验或者选取过程繁琐而失去可操作性;更理想地, 这些模型能够反应涡激振动中的特殊现象, 例如考虑涡脱落模态变化对模型中涡脱落频率和流体载荷大小的影响给出响应的跳跃和不同分支等非线性现象; 另一方面这些模型的精度需要在更广泛范围进行验证, 这个工作可能是非常困难的.目前, 尽管已经有各种模型, 而且各自能在某些条件下得到很好的验证但是背对背的验证计算会出现较大的差异(Larsen & Halse 1997, Chaplin et al. 2005b), 还没有哪一个模型具有绝对的优势可以在每一个(或者大多数)情况下和实验吻合较好.
(3) 基于CFD与CSD的精细模型
随着数值方法的不断进步以及计算机和计算技术的迅速发展同时受科学研究需要的牵引CFD和CSD在海油工程领域的作用和优势越来越明显现在已成为与理论分析、水池试验相并列的3种主要研究手段之一在海洋平台设计、结构安全可靠性分析中发挥越来越重要的作用. 事实上在很多科学领域例如航空航天飞行器的设计与优化、针对地层特征和油气藏数据的石油天然气高效和环保的勘探和开采、核能的安全利用、生物医学的染色体和蛋白质的物理反应等基于大型计算的数值模拟都是至关紧要的常常被称作虚拟风洞、数值水槽. 尤其在某些技术刚出现时不使用仿真就无法理解、发展和使用计算机仿真的工程和科学已经成为核心竞争力(张晓欣 2007)高效大规模并行分析系统的开发研制将是未来海洋工程界提高竞争力的一个重要方向.
大长径比立管VIV的三维数值模拟, 需要流体力学计算程序(如Fluent, CFX等)和结构动力学计算程序(如ANASYS, ABQUAS和NASTRAN等)两类计算程序, 在耦合交界面进行流体动力和结构位移(变形)两种数据的交换, 涉及到流体和固体两种介质的网格数据之间的映射(或插值)和协调(流体网格的重构), 和由此带来的精度降低的问题. 另外计算技术方面还涉及不同求解器之间的高效交互使用、经济实用的并行算法和并行编程等关键技术问题探索更有效的算法来进一步提高精度并降低计算费用仍是近期研究的重点之一.这些问题随着结构尺寸的增大(大长径比)、形式的复杂(悬链线式、复合式立管带有边条、分离盘等附属设备的工业立管)以及雷诺数的增加(海洋工程的实际雷诺数通常大于105变得更加难以解决.
好的数值模拟应该是建立在科学、数学、计算、工程知识与方法的基础之上而发展的随着计算机技术和数值计算方法的不断进步以及人们对涡激振动这种流固耦合非线性现象认识的加深基于CFD与CSD结合的数值模拟不仅代表了建立在数学模型基础之上的理论科学的延伸给出更好的VIV响应预测结果, 还可以被用来探索新的流固耦合现象和理论在新的工程立管概念设计和测试中将会发挥越来越大的作用.
(4) 大尺度/高雷诺数的物理实验
目前的大尺度实验主要都是在国外开展的, 国内在该方面还尚需发展(唐国强等 2011, Fu et al. 2014, Xu et al. 2013).尽管在计算模型方面国内已经开展了大量工作而且在国际上已经具有一定的影响和地位但是还欠缺大尺度和高雷诺数的实验一些实验也多数是和国外先进研究机构合作的. 缺乏实验数据和深刻理解设计者只能采用保守设计方法设计水平的欠缺造成不必要的浪费和成本的提高;而且这些实验是验证VIV计算模型以及将其向工业应用推广所必须的手段尤其是目前, 我国的经济实力和科研项目经费管理已经到达了一定的水平与工业界联合组织和操作这种大尺度的大规模系统实验是完全有可能实现的.
目前仅有的实验数据主要是针对某种具体条件的而且多数是不完全公开的, 希望数据公开和共享, 事实上这些数据的公开和共享.可以很好地帮助理解本文所提到的一些尚未解决的难题从而进一步推动整个领域的科学研究和应用技术的进步.
| 毕勤胜, 陈章耀, 朱玉萍, 邹勇. 2003. 参数激励耦合系统的复杂动力学行为分析. 力学学报 , 35 :123–127. |
| Bi Q S, Chen Z Y, Zhu Y P, Zou Y. 2003. Dynamical analysis of coupled oscillators with parametrical excitation. Acta Mechanica Sinica , 35 :123–127. |
| 陈伟民, 张立武, 李敏. 2010. 采用改进尾流振子模型的柔性海洋立管的涡激振动响应分析. 工程力学 , 27 :240–246. |
| Chen W M, Zhang L W, Li M. 2010. Prediction of vortex-induced vibration of flexible riser using improved wake-oscillator model. Engineering Mechanics , 27 :240–246. |
| 陈伟民, 郑仲钦, 张立武, 李敏. 2011. 内波波致剪切流作用下深海立管的涡激振动. 工程力学 , 28 :250–256. |
| Chen W M, Zheng Z Q, Zhang L W, Li M. 2011. Vortex-induced vibration of deep water flexible risers experiencing internal-wave-induced shear flow. Engineering Mechanics , 28 :250–256. |
| 陈伟民, 郑仲钦, 郭双喜. 2014. 浮式平台的横荡运动对水下柔性立管涡激振动的影响. 海洋工程 , 32 :8–13. |
| Chen W M, Zheng Z Q, Guo S X. 2014. Impact of floating top sway on the vortex-induced vibration of submarine riser. The Ocean Engineering , 32 :8–13. |
| 段梦兰, 胡知辉, 曹静, 赵天奉, 房军. 2011. 深水钢悬链线立管触地区疲劳实验系统设计. 力学与实践 , 33 :15–19. |
| Duan M L, Hu Z H, Cao J, Zhao T F, Fang J. 2011. The design of fatigue experimental system for steel catenary riser in touchdown zone. Mechanics in Engineering , 33 :15–19. |
| 付强. 2004. 海洋输液立管动力特性及涡激振动响应理论研究.[硕士论文]. 青岛:中国海洋大学. |
| 葛斐, 惠磊, 洪友士. 2007. 水中悬浮隧道锚索在剪切流中的涡激响应. 中国科学院研究生院学报 , 24 :352–356. |
| Gei F, Hui L, Hong Y S. 2007. vortex-induced vibration of submarine floating tunnel undergoing shear flow. Journal of University of Chinese Academy of Sciences , 24 :352–356. |
| 谷家扬, 吕海宁, 杨建民. 2012. 随机波浪中张力腿平台耦合运动及系泊系统特性研究. 海洋工程 , 30 :42–48. |
| Gu J Y, Lu H N, Yang J M. 2012. Studies on coupling dynamic response and characteristics mooring system of TLP in stochastic waves. The Ocean Engineering , 30 :42–48. |
| 谷斐. 2012. 隔水管涡激振动抑制装置的流动控制实验研究.[博士论文]. 上海:上海交通大学. http://cdmd.cnki.com.cn/article/cdmd-10248-1013003761.htm |
| http://cdmd.cnki.com.cn/article/cdmd-10248-1013003761.htm |
| 郭双喜. 2015. 考虑结构耦合的浮式风机整体系统动响应分析.[硕士论文]. 北京:中国科学院力学研究所. |
| 郭海燕, 付强, 娄敏. 2005. 海洋输液立管涡激振动响应及其疲劳寿命研究. 工程力学 , 22 :220–224. |
| Guo H Y, Fu Q, L M. 2005. Vortex-induced vibrations and fatigue life of marine risers conveying flowing fluid. Engineering Mechanics , 22 :220–224. |
| 黄智勇, 潘志远, 崔维成. 2007. 两向自由度低质量比圆柱体涡激振动的数值计算. 船舶力学 , 11 :1–9. |
| Huang Z Y, Pan Z Y, Cui W C. 2007. Numerical simulation of VIV of a circular cylinder with two degrees of freedom and low mass-ratio. Journal of Ship Mechanics , 11 :1–9. |
| 菅永军, 鄂学全, 柏威. 2003. 参数激励圆柱形容器中的非线性Faraday 波. 应用数学和力学 , 24 :60–66. |
| Jian Y J, E X Q, Bai W. 2003. Nonlinear Faraday waves in a parametrically excited circular cylindeical container. Applied MAthmatics and Mechanics , 24 :60–66. |
| 雷松, 张文首, 赵岩, 岳前进. 2010. FDPSO 立管涡激振动响应分析. 工程力学 , 27 :294–298. |
| Lei S, Zhang W S, Zhao Y, Yue Q J. 2010. Influence of heave motion on vortex-induced vibrations of FDPSO risers. Engineering Mechanics , 27 :294–298. |
| 李曼. 2013. 立管涡激振动模型试验中的尺度效应问题研究.[硕士论文]. 上海:上海交通大学. http://cdmd.cnki.com.cn/article/cdmd-10248-1013021137.htm |
| http://cdmd.cnki.com.cn/article/cdmd-10248-1013021137.htm |
| 潘志远, 崔维成, 刘应中. 2005. 低质量- 阻尼因子圆柱体的涡激振动预报模型. 船舶力学 , 9 :115–124. |
| Pan Z Y, Cui W C, Liu Y Z. 2005. A predicting model for self-excited VIV of a circular cylinder at low mass-dam ping. Journal of Ship Mechanics , 9 :115–124. |
| 秦伟. 2013. 双自由度涡激振动的涡强尾流振子模型研究.[博士论文]. 哈尔滨:哈尔滨工程大学. http://cdmd.cnki.com.cn/article/cdmd-10217-1014133951.htm |
| http://cdmd.cnki.com.cn/article/cdmd-10217-1014133951.htm |
| 邵传平, 陈野军, 王赛, 秦广素. 2014. 流向振荡柱体尾流控制研究进展. 力学进展 , 44 :188–235. |
| Shao C P, Chen Y J, Wang S, Qin G S. 2014. Advances in the control of wakes behind an in-line oscillating cylinder. Advances in Mechanics , 44 :201405. |
| 唐国强, 吕林, 滕斌, 谢彬, 宋吉林, 张建侨, 吴浩. 2001. 大长细比柔性杆件涡激振动实验. 海洋工程 , 29 :18–25. |
| Tang G Q, Lü L, Teng B, Xie B, Song J L, Zhang J Q, Wu H. 2001. Laboratory measurement of vortex-induced vibration of long flexible riser. The Ocean Engineering , 29 :18–25. |
| 唐驾时, 贺新柱. 2001. 参数振动系统的共振分析. 岳阳师范学院学报.自然科学版 , 14 :34–40. |
| Tang J S, He X Z. 2001. Response analysis of parametrically excited system. Journal of Yueyang Normal University (Natural Science , 14 :34–40. |
| 唐友刚, 邵卫东, 张杰, 王丽元, 桂龙. 2013. 深海顶张力立管参激- 涡激耦合振动响应分析. 工程力学 , 30 :282–286. |
| Tang Y G, Shao W D, Zhang J, Wang L Y, Gui L. 2013. Dynamic response analysis for coupled parametric vibration and vortex-induced vibration of top-tensioned riser in deep-sea. Engineering Mechanics , 30 :282–286. |
| 王东耀, 凌国灿. 1998. 在平台振荡条件下TLP 张力腿的涡激非线性响应. 海洋学报 , 20 :119–128. |
| Wang D Y, Ling G C. 1998. Vortex-induced nonlinear vibration of TLP tethers under circumstances of platform oscillation. Acta Oceanologica Sinica , 20 :119–128. |
| 王成官, 王嘉松, 田中旭, 乔信起, 蒋世全, 许亮斌. 2011. 海洋隔水管涡激振动的三维数值模拟研究. 水动力学研究与进展 , 26 :437–443. |
| Wang C G, Wang J S, Tian Z X, Qiao X Q, Jiang S Q, Xu L B. 2011. Three dimensional numerical simulation of vivon marine riser. Chinese Journal of Hydrodynamics , 26 :437–443. |
| 王沣浩, 姜东歌, 罗昔联, 梅雪松. 2006. 波状圆柱绕流减阻的实验研究. 西安交通大学学报 , 40 :93–96. |
| Wang F H, Jiang G D, Luo X L, Mei X S. 2006. Experimental investigation on drag reduction of wavy cylinder in cross flow. Journal of Xi'an Jiaotong University , 40 :93–96. |
| 王艺. 2010. 均匀来流条件下的圆柱涡激振动研究.[博士论文]. 北京:中科院力学研究所. |
| 肖飞, 杨和振. 2014. 深海钢悬链立管hill 不稳定性预测. 上海交通大学学报 , 48 :583–588. |
| Xiao F, Yang H Z. 2014. Hill stability prediction of deep-sea steel catenary riser. Journal of Shanghai Jiao Tong University , 48 :583–588. |
| 徐万海, 曾晓辉, 吴应湘. 2009. 深水张力腿平台与系泊系统的耦合动力响应. 振动与冲击 , 28 :145–150. |
| Xu W H, Zeng X H, Wu Y X. 2009. The coupled dynamic responses of the tension leg platform and tendon in deep-water. Journal of Vibration and Shock , 28 :145–150. |
| 余建星, 许华力, 袁从敏, 王衷畅. 2008. 张力腿系缆系统涡激振动疲劳可靠性分析. 船舶力学 , 12 :592–598. |
| Yu J X, Xu H L, Yuan C M, Wang Z C. 2008. Fatigue reliability analysis of vortex induced vibration of TLP tethers in waves and current. Journal of Ship Mechanics , 12 :592–598. |
| 张杰, 唐友刚, 黄磊, 李伟. 2013. 参数激励下深海立管多模态耦合振动特性分析. 振动与冲击 , 32 :51–56. |
| Zhang J, Tang Y G, Huang L, Li W. 2013. Multi-mode coupled vibration behavior of a deep-water riser under parametric excitations. Journal of Vibration and Shock , 32 :51–56. |
| 张立武. 2010. 深海柔性立管涡激振动响应研究.[硕士论文]. 北京:中国科学院力学研究所. |
| 张晓欣. 2007. 美国科学基金委蓝带工作组报告:基于仿真的工程科学. 高性能计算发展与应用 , 18 :4–12. |
| Zhang X X. 2007. Ribbon panel report on simulation-based engineering science by NFS blue. Development and Application of High Performance Computing , 18 :4–12. |
| 赵丽刚. 2006. 高温高压条件下海燕立管的动态极值响应研究.[硕士论文]. 哈尔滨:哈尔滨工程大学. |
| 郑哲敏. 1958. 输水管的振动问题. 力学学报 , 2 :100–111. |
| Zheng Z M. 1958. Vibration of pipe line. Acta Mechanica Sinica , 2 :100–111. |
| 郑仲钦. 2012a. 平台运动对水下柔性立管动响应的影响分析.[硕士论文]. 北京:中国科学院力学研究所. |
| 郑仲钦, 陈伟民. 2012b. 结构与尾流非线性涡激振动预测模型. 海洋工程 , 30 :37–41. |
| Zheng Z Q, Chen W M. 2012. Prediction of vortex-induced vibration of cylinder based on the nonlinear coupling of structure and wake oscillator. The Ocean Engineering , 30 :37–41. |
| Aiten J. 1978. An account of some experiment on rigidity produced by cent force. Philosophical Magazine , 5 :81–105. |
| Alexander C M. 1981. The complex vibrations and implied drag of a long oceanographic wire in cross-flow. Ocean Engineering , 8 :379–406. doi:10.1016/0029-8018(81)90033-0 |
| Arcandra T, Kim M H. 2003. Hull/mooring/riser coupled dynamic analysis and sensitivity study of a tanker-based FPSO. Applied Ocean Research , 25 :367–382. doi:10.1016/j.apor.2003.02.001 |
| Baarholm G S, Larsen C M, Lie H. 2005. Reduction of VIV using suppression devices-An empirical approach. Marine Structures , 18 :489–510. doi:10.1016/j.marstruc.2006.01.003 |
| Baarholm G S, Larsen C M, Lie H. 2006. On fatigue damage accumulation from in-line and cross-flow vortex-induced vibrations on risers. Journal of Fluids and Structures , 22 :109–127. doi:10.1016/j.jfluidstructs.2005.07.013 |
| Balasubramanian S, Skop R A. 1996. A nonlinear oscillator model for vortex shedding from cylinders and cones in uniform and shear flows. Journal of Fluids and Structures , 10 :197–214. doi:10.1006/jfls.1996.0013 |
| http://cn.bing.com/academic/profile?id=1575953289&encoded=0&v=paper_preview&mkt=zh-cn |
| Berger E, Wille R. 1972. Periodic flow phenomena. Annual Reviews of Fluid Mechanics , 4 :313–340. doi:10.1146/annurev.fl.04.010172.001525 |
| Birkoff G, Zarantanello E H.1957. Jets, Wakes and Cavities. New York: Academic Press, ) . |
| Bishop R E D, Hassan A Y. 1964. The lift and drag forces on a circular cylinder oscillating in a flowing fluid. Mathematical Physical & Engineering Sciences , 277 :51–75. |
| Blackburn H M, Henderson R D. 1999. A study of two-dimensional flow past an oscillating cylinder. Journal of Fluid Mechanics , 385 :255–286. doi:10.1017/S0022112099004309 |
| Blackburn H M, Govardhan R N, Williamson C H K. 2001. A complementary numerical and physical investigation of vortex-induced vibration. Journal of Fluids and Structures , 15 :481–488. doi:10.1006/jfls.2000.0345 |
| Breuer M. 1998. Numerical and modeling influences on large eddy simulations for the flow past a circular cylinder. International Journal of Heat and Fluid Flow , 19 :512–521. doi:10.1016/S0142-727X(98)10015-2 |
| Brika D, Laneville A. 1993. Vortex-induced vibrations of a long flexible circular cylinder. Journal of Fluid Mechanics , 250 :481–508. doi:10.1017/S0022112093001533 |
| Brika D, Laneville A. 1995. An experimental study of the aeolian vibrations of a flexible circular cylinder at different incidences. J. Fluids Struct , 9 :371–391. doi:10.1006/jfls.1995.1021 |
| Carberry J, Govardhan R, Sheridan J, Rockwell D, Williamson C H K. 2004. Wake states and response branches of forced and freely oscillating cylinders. European Journal of Mechanics-B/Fluids , 23 :89–97. doi:10.1016/j.euromechflu.2003.05.007 |
| Carberry J, Sheridan J, Rockwell D. 2005. Controlled oscillations of a cylinder:forces and wake modes. Journal of Fluid Mechanics , 538 :31–69. doi:10.1017/S0022112005005197 |
| Carl M L, Karl H H. 1997. Comparison of models for vortex induced vibrations of slender marine structures. Marine Structure , 10 :413–441. doi:10.1016/S0951-8339(97)00011-7 |
| Chandrasekaran S, Chandak N R, Anupam G. 2006. Stability analysis of TLP tethers. Ocean Engineering , 33 :471–482. doi:10.1016/j.oceaneng.2005.04.015 |
| Chang P K.1976. Control of Flow Separation. Washington DC: Hemisphere Publication Corporation, ) . |
| Chaplin J R, Bearman P W, Huera Huarte F J, Pattenden R J. 2005a. Laboratory measurements of vortex-induced vibrations of a vertical tension riser in a stepped current. Journal of Fluids and Structures , 21 :3–24. doi:10.1016/j.jfluidstructs.2005.04.010 |
| Chaplin J R, Bearman P W, Cheng Y, Fontaine E, Graham J M R, Herfjord M, Isherwood M, Lambrakos K, Larsen C M, Meneghini J R, Moe G, Triantafyllou MS, Willden R H J. 2005b. Blind predictions of laboratory measurements of vortex-induced vibrations of a tension riser. Journal of Fluids and Structures , 21 :25–40. doi:10.1016/j.jfluidstructs.2005.05.016 |
| Chatjigeorgiou I K. 2004. On the parametric excitation of vertical elastic slender structures and the effect of damping in marine applications. Applied Ocean Research , 26 :23–33. doi:10.1016/j.apor.2004.08.001 |
| Chen S S. 1971. Dynamics stability of tube conveying fluid:Proceedings of the American society of civil engineers. Journal of the Engineering Mechanics Division , 97 :1469–1485. |
| Chen W M, Li M, Zheng Z Q, Guo S X, Kuan Gan K. 2015. Impacts of top-end vessel sway on vortex-induced vibration of the submarine riser for a floating platform in deep water. Ocean Engineering , 99 :1–8. doi:10.1016/j.oceaneng.2015.03.002 |
| Chen W M, Li M, Zhang L W, Tan T C. 2016. Study on Multi-mode VIV of deep water riser in different flow fields by finite element simulations. J. of Offshore Mechanics and Arctic Engineering , 138 :1–8. |
| Chen W M, Li M, Guo S X, Gan K. 2014. Dynamic analysis of coupling between floating top-end heave and riser's vortex-induced vibration by using finite element simulations. Applied Ocean Research , 48 :1–9. doi:10.1016/j.apor.2014.07.005 |
| http://cn.bing.com/academic/profile?id=2312821755&encoded=0&v=paper_preview&mkt=zh-cn |
| Chen W M, Li M, Zheng Z Q, Tan T C. 2012. Dynamic Characteristics and VIV of deep water riser with axially varying structural properties. Ocean Engineering , 42 :7–12. doi:10.1016/j.oceaneng.2011.12.019 |
| Chen X H, Zhang J, Ma W. 2001. On dynamic coupling effects between a spar and its mooring lines. Ocean Engineering , 28 :863–887. doi:10.1016/S0029-8018(00)00026-3 |
| Chen X H, Ding Y, Zhang J, Liagre P, Niedzwecki J, Teigen P. 2006. Coupled dynamic analysis of a mini TLP:comparison with measurements. Ocean Engineering , 33 :93–117. doi:10.1016/j.oceaneng.2005.02.013 |
| Chen Z S, Kim W J. 2012. Effect of bidirectional internal flow on fluid-structure interaction dynamics of conveying marine riser model subject to shear current. International Journal of Naval Architecture and Ocean Engineering , 4 :57. doi:10.3744/JNAOE.2012.4.1.057 |
| Clarke J H, Menkes H R, Libby P A. 1955. A provisional analysis of turbulent boundary layers with injection. Journal of Aeronautical Science , 22 :255–260. doi:10.2514/8.3322 |
| Clausen T, D'Souza R. 2001. Dynamic risers key component for deep water drilling floating production. Offshore , 61 :89–93. |
| Dahl J M, Hover F S, Triantafyllou M S. 2006. Two-degree-of-freedom vortex-induced vibrations using a force assisted apparatus. Journal of Fluids and Structures , 22 :807–818. doi:10.1016/j.jfluidstructs.2006.04.019 |
| Dahl J M, Hover F S, Triantafyllou M S. 2007. Resonant vibrations of bluff bodies cause multi vortex shedding and high frequency forces. Physical Review Letters , 99 :144503. doi:10.1103/PhysRevLett.99.144503 |
| Dahl J M, Hover F S, Triantafyllou M S. 2010. Dual resonance in vortex-induced vibrations at subcritical and supercritical Reynolds numbers. Journal of Fluid Mechanics , 643 :395–424. doi:10.1017/S0022112009992060 |
| Dai H L, Wang L. 2012. Vortex-induced vibration of pipes conveying fluid using the method of multiple scales. Theoretical & Applied Mechanics Letters , 2 :022006. |
| Davies, M. E.. 1976. A comparison of the wake structure of a stationary and oscillating bluff body. Using a conditional averaging technique. Journal of Fluid Mechanics , 75 :209–231. doi:10.1017/S0022112076000189 |
| Di Silvio G. 1969. Self-controlled vibration of cylinder in fluid stream. Journal of Engineering Mechanics Division , 95 :347–361. |
| Dickens W R. 1979. The self-induced vibration of cylindrical structures in fluid flow. Ice Proceedings , 67 :13–30. |
| Dong S, Triantafyllou G S, Karniadakis G E. 2008. Elimination of vortex streets in bluff-body flows. Physical Review Letters , 100 :204501. doi:10.1103/PhysRevLett.100.204501 |
| Evangelinos C, Lucor D, Karniadakis G E. 2000. DNS-derived force distribution on flexible cylinders subject to vortex-induced vibration. Journal of Fluids and Structures , 14 :429–440. doi:10.1006/jfls.1999.0278 |
| Facchinetti M L, de Langre E, Biolley F. 2004a. Coupling of structure and wake oscillators in vortex-induced vibrations. Journal of Fluids and Structures , 19 :123–140. doi:10.1016/j.jfluidstructs.2003.12.004 |
| Facchinetti M L, de Langre E, Biolley F. 2004b. Vortex-induced travelling waves along a cable. European Journal of Mechanics B-Fluids , 23 :199–208. doi:10.1016/j.euromechflu.2003.04.004 |
| http://cn.bing.com/academic/profile?id=2304275807&encoded=0&v=paper_preview&mkt=zh-cn |
| Feng L H, Wang J J. 2010. Circular cylinder vortex-synchronization control with a synthetic jet positioned at the rear stagnation point. Journal of Fluid Mechanics , 662 :232–259. doi:10.1017/S0022112010003174 |
| Feodosev V P. 1956. Vibrations and stability of a pipe when liquid flows through it. Inzhenernyi Sbornik , 10 :169–170. |
| https://www.researchgate.net/publication/34019573_Hydrodynamic_loading_and_response_of_offshore_risers |