首页> 欢迎您访问力学进展网站！               «上一年                      2016年文章目录                      下一年»
0
引用本文 Download PDF  
杨基明, 李祝飞, 朱雨建, 翟志刚, 罗喜胜, 陆夕云 . 激波的传播与干扰[J]. 力学进展, 2016, 46:201613
YANG Jimingy, LI Zhufei, ZHU Yujian, ZHAI Zhigang, LUO Xisheng, LU Xiyun . Shock wave propagation and interactions[J]. Advances in Mechanics, 2016, 46:201613.
激波的传播与干扰
杨基明, 李祝飞, 朱雨建, 翟志刚, 罗喜胜, 陆夕云     
中国科学技术大学近代力学系, 合肥 230027
收稿日期: 2016-02-26; 录用日期: 2016-05-05; 在线出版日期: 2016-05-09
通讯作者:杨基明,男,1992年获中国科学技术大学流体力学博士学位,现为教授,博士生导师;长期从事空气动力学、高速气流中的燃烧与爆轰、多相流、仿生力学以及流体力学实验与测量等领域的科研和教学工作;曾先后赴日本东北大学、德国亚琛工业大学、加拿大麦吉尔大学和我国台湾成功大学等进行合作研究;迄今已在《中国科学》,ShockWaveJ,PhysicsofFluids,AIAAJ等国内外杂志和国际会议发表论文100余篇;现为中国力学学会、中国空气动力学学会理事、安徽省力学学会理事长,ShockWaves、《中国科学G辑》《空气动力学学报》《实验流体力学》《推进技术》《气体物理》等杂志编委,第27?31届(2008|2017年)国际激波学术会议顾问委员会成员;曾获"全国模范教师"称号和"全国五一劳动奖章"等.E-mail:jmyang@ustc.edu.cn
© 2016《力学进展》版权所有
摘要: 激波的传播特性既取决于激波的产生条件,也与所处的传播环境密切相关.驱动条件、几何边界、介质的物理化学属性等发生变化时,都会引起激波传播特性的改变,而激波的变化反过来又会对其波及的流场产生影响.尽管激波传播及其干扰现象广泛存在于自然界和人类科技活动之中,其复杂机理的认识、规律的描述乃至应用潜力的挖掘仍有漫长的路要走.本文根据气体中激波传播和干扰现象以及与之相关的理论描述特征,在对激波传播以及反射、折射等基本现象进行简要阐述的基础上,重点围绕目前的热点问题,包括激波/激波干扰、激波/边界层干扰、激波与湍流作用、激波的聚焦与点火以及激波作用下气体界面不稳定性等研究进行了介绍和讨论,旨在对近年来该领域的进展及获得的成果做一个概述和归纳,期望对将来的深入研究有一个鉴借意义.
关键词: 激波传播     激波反射     激波/边界层相互作用     激波/界面相互作用     激波极线    
Shock wave propagation and interactions
YANG Jimingy, LI Zhufei, ZHU Yujian, ZHAI Zhigang, LUO Xisheng, LU Xiyun     
Department of Modern Mechanics, University of Science and Technology of China, Hefei 230027, China
Received: 26 February 2016; accepted: 05 May 2016; online: 09 May 2016
Abstract: The propagation of a shock wave depends not only on the conditions that it is generated, but also on the media where it propagates. Variations in driver condition, boundary condition and/or physical/chemical properties of the media may alter the behav-iors of the shock wave propagation, while the flowfield also varies along with the shock wave motion. Although shock wave propagation and interactions exist widely in the nature and human activities, there is still a long way to go for a better understanding of its complex mechanism, for theoretical descriptions of the phenomena, as well as for enrichment of the application. In this paper, we review the shock wave interactions and related analyses, and further discuss several hot topics, including shock/shock interaction, shock/boundary layer interaction, shock/turbulence interaction, shock focusing/ignition and instability of shocked interface.
Key words: shock wave propagation     shock wave reflection     shock wave/boundary layer interaction     shock wave/interface interaction     shock polar    
1 引 言

激波的传播及其与非均匀介质、复杂流动、障碍物等相互作用现象在自然界和人类活动中广泛存在，鉴于其能量具有时空集中释放的特点，使之不论在和平利用还是军事攻防等方面都展现出特有的潜力和价值(Glass 1975). 因此，深入认识激波传播及其作用机理，正确把握其运动规律并加以有效利用，既可望为造福人类提供关键支撑和指导，也可能成为克敌制胜的智慧源泉.

我们知道，平面运动激波在均匀介质的传播过程具有自持性，但一旦激波本身或传播的环境发生改变，包括驱动条件、几何边界、介质的物理化学以及运动等属性发生变化时，都会造成激波传播特性的改变，而激波的变化反过来又会对其波及的流场产生影响. 这种相互作用所产生的效果有时是让人敬畏的，例如通过采用合适的边界约束、固壁反射以及初始条件等产生内向汇聚的激波聚焦所获得高温、高压不仅可以达到点火燃烧(Tsang & Lifshitz 1990)、体外碎石等威力(Chaussy 1987)，也是为数不多的可望满足核聚变所需初始起爆条件的途径之一(王淦昌和袁之尚 1996); 强激波无坚不摧的破坏力给安全防护方法和工程设计不断提出新的课题(朱建士等，2010，乐嘉陵和倪鸿礼 1999)，而其神奇的创造力则又给新材料制备、物质在极端环境下的物理化学性质研究等提供了难得的机遇(Erskin & Nellis 1991); 在以激波为重要特征的超声速流动中，减少波阻使得超声速飞行器构型明显有别于传统的亚声速飞行器(Anderson et al. 1990，黄志澄，1994，黄伟等 2009)，而由激波/边界层干扰、激波/激波干扰造成的流场品质恶化和热力载荷剧增等现象，可以说是目前高超声速飞行器研究所面临的最具挑战性难题之一(Dolling 2001，姜宗林和俞鸿儒，2009，Babinsky & Harvey 2011).

值得注意的是，激波所涉及的领域之宽，不仅仅只体现在上述诸多工程应用背景方面. 鉴于其强非线性和间断性等特征，激波不但成为数学经典问题之一(如黎曼问题，激波管问题)，而且也是作为考核目前仍在不断发展的计算方法优劣的关键一环(如刘儒勋和舒其望 2003); 激波所特有的瞬间产生高温、高压等可控的参数设置环境也为诸如物理上的高温非平衡过程(Anderson 2006)以及化学上的点火与延迟燃烧特性(Lee 2008)等研究提供了独到的方法途径. 因此，当人们发现在激波相关的学术活动中，数理化天地生等诸多领域专家学者参与时也就不足为奇了. 历史上有不少科学巨匠涉足激波现象的探索，尽管有的大科学家所迈出的第一步未必正确. 例如牛顿所提出的声速传播速度关系实际上是与等温过程相对应，因而与实际观测结果存在约20%的差别，这一状况直到一个多世纪后的1816年Laplace纠正为绝热过程之后才得到彻底改观(Bernard Finn 1964)，从而为快于声速传播的激波现象的认识及其理论描述(如Earmshaw 1860)奠定了基础.

关于激波的传播与干扰的研究极其丰富，例如，Courant和Friedrichs(1948)系统地总结了截至二战时期的研究成果; Glass(1975)进一步整理了二战后的代表性进展; 高山喜(1995)、Ben-Dor(2001a)在20与21世纪之交前后分别组织撰写了力图能够全面反映当时该领域进展的《激波手册》; 按照激波作用类型、牵涉的领域或研究方法等不同特点，有针对性的专著则更多，如Han和Yin(1992)的《Shock Dynamics》，Ben-Dor(2007)的《Shock Wave Reflection Phenomena》，Babinsky和Takayama(2011)的《Shock Wave-Boundary-Layer Interactions》等. 然而，随着研究的不断深入和拓展，新的成果一直在不断地涌现. 每两年一次的国际激波学术会议在一定程度上反映了该领域的研究状况和发展趋势. 2015年7月在以色列特拉维夫举行的第30届国际激波学术会议有300多篇稿件参与交流. 在我国，历届全国力学大会上都设有激波与激波管分会; 此外，与力学大会相间之年还举行更大规模的系列激波学术会议，如不久前在洛阳召开的全国第16届激波学术会议(2014)就有约120篇文章参与交流，反映出有关激波及其相互作用的研究不仅自身在不断获得发展，同时也因其所特有的学科交叉性而受到其他相关领域的高度关注.

本文根据激波传播和干扰现象以及与之相关的理论描述特征，为简化难点、综合共性和突出特点，按照从一维到多维的思路，力图对该领域的一些进展情况作一简明介绍，继而在此基础上选取若干有应用背景的研究热点加以讨论，期望能起抛砖引玉之效.

2 典型的波系相互作用与描述 2.1 一维波系相互作用

激波的强间断性带来复杂性，但也给问题的简化带来便利. 因为这一特点使得在法向穿过波面的尺度相对于其他方向可以忽略，且两侧的参数变化成为主要矛盾，从而为建立激波前(下标1)后(下标2)参数(如压力p、密度ρ、速度u、焓h等)的简化描述关系提供了可能. 其中较为典型的代表应属兰金-雨贡纽关系(为便于全文符号统一，其形式已有别于原始的兰金-雨贡纽关系(Henderson 2001))，如式(1)所示

(1)

当然，该关系式是将坐标系固定在激波面上，亦即定常正激波所满足的; 另一种常见的描述形式是通过坐标变换的方法获得所谓非定常运动激波的关系式. 一旦给定介质的状态方程和热力学描述，激波前后参数随激波强度的变化即可得出(陈强 1978). 对于激波管、激波风洞等脉冲型实验设备来说，其足够大的长径比给一维非定常近似理论分析提供了便利，同时也给运用一维波系干扰理论来灵活设计实验方法给予了充分的施展空间(Lu & Marren 2002). 当然，这里限于篇幅，仅简要介绍一下一维波系相互作用的几个典型示例.

激波极线法是一种有效的分析波系干扰的方法. 在一维近似下，鉴于压力和速度作为反映力学平衡的关键要素，因此采用所谓压力-速度(p，u)极线能够很好地描述和分析波系干扰中的参数变化特征和规律(Courant & Friedrichs 1948). 在完全气体条件下，上述式(1)所描述的激波关系可用实验室坐标系下，激波前后速度与压力的关系表示为

(2)

其中，α和γ分别为气体的声速和比热比，下标"1"和"2"分别代表波前和波后参数(文中所有公式中的下标均为此意，因此与图中的区域代号并不一定对应)，"+"和"-"分别代表激波的传播方向为右行和左行. 该式表明，对于给定的波前初始状态(p1，u1)，某一强度的激波p2/p1将产生与其传播同向的相应幅度的诱导速度u2-u1，因此波后状态对应于(p，u)图上一确定的点. 而所有不同强度的激波波后状态则构成相应的p-u激波极线(如图 1所示).

图 1 一维激波干扰图(左) 和(p,u) 图(右) 示例. (a) 激波在端壁反射,(b) 激波在(慢/快) 界面折射,(c) 同向二激波(追赶) 作用,(d) 典型激波管流动问题

图 1(a)~图 1(d)分别给出了激波在封闭的端壁反射、激波通过接触面("慢/快"界面)时的折射、同向激波追赶以及激波管问题的典型波系干扰示例. 从中可以看出，基于这些干扰所应满足的约束条件，借助于(p，u)激波极线，能够方便地分析和得出作用后所能达到的后续流动状态. 如右行入射激波与静止端壁作用后，产生的左行反射激波应满足波后气流再次静止，以与端壁条件相协调(图 1(a)); 激波通过接触面时(见图 1(b))，透射激波在声速较快的一侧诱导更高的气流速度(图 1(b)中u4>u3，其作用将导致一束反射稀疏波以加速另一侧气体与之匹配(图 1(b)中u3<u5=u4; 两道同向运动的激波合并为一道激波时(见图 1(c))，需产生一道接触面(图 1(c)中④、⑤区)来表征不同的熵增，以及反向稀疏波(图 1(c)中③→④)来协调多次压缩(①→②→③)与单次压缩(①→⑤)所产生的速度和压力的不同; 用(p，u)激波极线法来分析典型的激波管问题亦有其独到之处(见图 1(d)): 破膜后，低压①区被驱动段在受到高压④区驱动段压缩(即激波)扰动的同时，也给驱动段产生了稀疏扰动，而被驱动段经激波压缩的②区气体和驱动段经稀疏波膨胀的③区气体则是二者矛盾协调的结果. 稍需补充说明的是，图 1(b)~图 1(d)中的稀疏波在p-u图中的数学描述则是式(3)所表征的等熵关系.

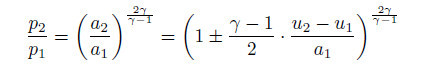
(3)

鉴于这种一维波系干扰的分析方法已较为成熟，这里就不再详细展开. 不过值得一提的是，其灵活运用至今仍在实验方法的创新思维中起到事半功倍之效(姜宗林等 2012).

2.2 二维波系相互作用及相关理论

当激波传播过程中的传播条件发生改变，包括壁面条件、传播介质的属性以及流场参数等出现变化时，激波都难免会与之产生相互作用. 其中激波受壁面"压缩"作用产生的反射，穿越声抗变化介质出现的折射以及与其他波系相遇产生的相交等现象作为典型的干扰形式而受到关注和较为系统的研究. 尽管自然界和工程实际中的激波干扰一般均具有三维性，但鉴于激波面极薄以及在垂直于波面法向的参数变化和作用剧烈的特征，前人为突出重点和分解难点，巧妙地寻求出基于激波法向剖面内进行二维简化的分析方法，从而为这类相互作用的简明理论描述和分析提供了一条简洁的途径.

如果说压力-速度(p-u)激波极线有助于分析一维激波干扰的话，那么在二维波系相互作用中，描述压力-气流偏转角关系的所谓(p-θ)激波极线则是极为有用的分析工具，尽管其理论描述只是气体动力学中所熟知的斜激波关系.

(4)

由式(4)的斜激波关系易知，在超声速来流M1给定的条件下，气流经斜激波折转的角度θ与斜激波前后的压比p2/p1有着确定的关系. 所有可能的p2/p1-θ解用p-θ图示的方法就能得到清晰明了的激波极线. 作为示例，图 2}给出了二维定常激波极线法分析激波反射问题的典型案例(Ben-Dor 2007). 结合流场图和激波极线图可以看出，斜劈所产生的贴体头激波将来流从(0)状态压缩至(1)状态，对应激波极线I的(0)点到(1)点; 由于反射激波以(1)区状态作为来流参数，因而反射激波极线R也就以激波极线Ⅰ上的(1)点作为起始点; 而反射波后流动参数能否满足壁面约束条件则给反射类型，如规则反射(图 2(a)，其中2 s和2 w分别对应强解和弱解)和/或马赫反射(图 2(b))的多样化提供了丰富的素材.

图 2 二维定常激波极线法分析激波反射问题. (a)规则反射,(b)马赫反射

固壁反射的作用主要来自壁面对气流方向的约束，该约束条件在波系干扰的分析中相对容易得到体现. 与之相比，多激波相交的情况则相对较为复杂，因为多波间相互作用后所能达到的平衡状态由流动自身来协调，这一复杂性使得p-θ激波极线分析的优越性得到进一步展现. 具体表现在，多道激波相交和相互作用后，最终能达到平衡状态的应该是相邻流体质点间压力相等、流动方向相同，而p-θ图示正是提供流动状态是否平衡的快捷分析手段. 图 3}给出了两激波规则相交和非规则相交(出现马赫杆)的典型示例(Ben-Dor 2007).

图 3 二维定常激波极线法分析多激波干扰问题(Ben-Dor 2007).(a)规则反射，(b)马赫反射

二维激波折射问题相对于一维的激波与界面(接触面)迎面相互作用来说要复杂得多. 随着激波与界面交角以及界面两侧声速等参数的不同，既有可能出现透射波的传播速度快于交点的移动速度，也有可能出现入射波在触及界面之前就过早地受到界面扰动的情况，这些所谓非规则折射给简化的波系分析带来较大难度(Abd-EL Henderson 1989). 即使对于较为理想的入射波、透射波和反射波均交于界面的所谓规则折射，尽管以固连于交点的参考系可获得临近区域的准定常化流场从而采用上述类似的分析方法，所得到波系干扰类型仍呈现不同的特点. 仅以激波在所谓"慢/快"声速界面的规则折射为例(见图 4)，即便在入射激波和界面两侧参数确定的情况下，随着激波与界面交角的不同，二者相互作用既可能出现反射稀疏波(图 4(a))，也可能出现反射激波(图 4(b))的情况. 鉴于后文中有关激波与界面的相互作用问题还有更为详细的介绍，这里不再过多赘述.

图 4 二维准定常激波极线法分析激波规则折射问题(Abd-EL Fattah 1978b).(a)界面反射稀疏波，(b)界面反射激波

有意思的是，从上述激波极线分析中可以发现，常常存在多解的情况，而这一般又对应于实际激波干扰过程中的迟滞现象，其中不乏当今的热点课题(杨旸等，2012，陶渊和范晓樯 2014). 总之，除了成为早期激波研究先驱者们(如Kawamura & Saito 1956)得力助手之外，即使是在目前数值模拟手段非常发达的情况下，具有快捷高效及其揭示机理特点的激波极线等分析方法仍受到广泛的欢迎，不仅在基础科学前沿问题研究方面受到关注(高波，2010，李季 2015)，而且在诸如高超声速飞行器控制等应用方面也展示出诱人的潜力(焦晓亮等 2012).

3 激波干扰的若干热点问题 3.1 典型的激波/激波干扰问题

激波-激波干扰现象是超声速及高超声速流动中最具挑战性难题之一，相关的机理认识及其准确描述和预测有着重要的学术和应用价值. 在激波-激波相互作用的局部区域，物体表面会产生过高的力热载荷，新一代高超声速飞行器的研制对此必须予以高度重视. 另一方面，激波-激波干扰的流动特征也十分复杂，流动中剪切、压缩和热力过程间的相互作用等仍有待进一步探索和揭示.

激波-激波干扰的一个典型示例是平面入射斜激波与钝头体弓形激波的相互作用问题. Edney(1968)根据入射激波与弓形激波之间交点的位置及激波的强度，将激波-激波干扰问题分为6种类型(见图 5)，其中，Ⅲ和Ⅳ 类的交点均位于弓形激波的亚声速段(即弓形激波的波后为亚声速流动); Ⅰ，Ⅱ，Ⅴ和Ⅵ 类的交点位于弓形激波的超声速段(即弓形激波的波后为超声速流动). 这六类干扰表现出不同的近壁流动结构，Ⅰ，Ⅱ和Ⅴ 类表现为激波与边界层相互作用;Ⅲ类表现为剪切层与边界层相互作用; Ⅳ 类会形成超声速"射流"; Ⅵ 类表现为膨胀扇与边界层相互作用. 其中第Ⅳ类激波干扰以其产生超声速射流并引起壁面局部区域压力和热流剧增而倍受关注. 针对第Ⅳ类激波干扰，国内外学者做了大量的实验和数值研究工作. Keyes和Hains(1973)、Wieting和Holden(1989)、Boldyrev 等(2001)通过风洞实验和激波-膨胀波理论分析了激波干扰流场结构，对壁面压力、热流进行了预测，为数值计算提供了丰富的实验数据. Wieting和Holden(1989)指出第Ⅳ类激波干扰具有非定常性，实验条件下流动振荡频率在3~10 kHz之间. Gaitonde和Shang(1995)采用改进的Steger-Warming格式求解了第Ⅳ类激波干扰的非定常流场，计算的振荡频率为32 kHz. Zhong(1994)采用高阶格式求解二维Navier-Stokes方程，分析和探讨了相关非定常流场的特征. Chu和Lu(2012)详细揭示和分析了第Ⅳ 类激波-激波相互干扰的非定常流场演变过程(图 6(a))，发现超声速"射流"的非定常运动形成沿壁面向上或向下发展的两个剪切层. "射流"激波(jet bow shock)后的圆柱表面会出现很小的滞止区，在这个区域内，非定常脉动的压力、温度和热流峰值均非常高.

图 5 6类激波/激波干扰及其在钝前缘上的位置分布(Albertson & Venkat 2005)

最近，肖丰收等(2016)考察了在驻点开设凹腔对第Ⅳ类激波干扰的影响(见图 6(b))，结果表明，虽然凹腔的引入强化了Ⅳ类激波干扰的非定常振荡特性，但这种振荡特性的要因并非来自凹腔的谐振，而是与射流/凹腔间的相互作用过程密切相关; 此外，以内转式进气道唇口等构型为背景，重点关注和考察了V形钝化前缘的激波干扰流场(见图 6(c)). 研究发现，随着来流参数、V形前缘的几何条件如倒圆半径、钝化半径等的不同，不仅会出现多种复杂的波系干扰结构，而且局部热流会出现数量级的上升，达到与Ⅳ类激波干扰相当的程度. 有意思的是，该结果表明，过大的钝化半径可能会反而增加局部热流(张志雨等 2016). 因此，相关的机理认识和优化设计无疑需要予以重视和开展进一步深入研究.

图 6 几种典型的激波-激波干扰研究进展.(a)第Ⅳ 类激波干扰的非定常瞬时流场(Chu & Lu 2012，左: 结构示意; 右: 涡量和胀压云图);(b)带凹腔钝头体第Ⅳ类激波干扰流场(肖丰收等，2016，左: 实验瞬时纹影; 右: 数值瞬时温度云图和流线图);(c)V形钝化前缘激波干扰流场(张志雨等 2016)，前缘钝化半径r=2 mm，3种倒圆半径分别为: R=0 mm，2 mm，6.5 mm; 上图: 实验纹影照片; 下图: 数值流场结构和表面热流云图
3.2 激波/边界层干扰

激波/边界层干扰(shock wave/boundary layer interaction，SBLI)现象广泛存在于国防和航空航天领域跨声速、超声速和高超声速流动中，其更深层次的机理是黏性和无黏干扰. 由于要满足物面无滑移边界条件，在离开物面很近的一层薄层内，黏性的作用不可忽略，即物面附近存在边界层. 在超声速流动中，主流区一般认为是无黏的. 主流区的激波在物面附近会与边界层产生相互作用，即所谓的激波/边界层干扰. 超/高超声速飞行器在机身外表面、翼面以及进气道内，不可避免地会遇到激波/边界层干扰的问题(如图 7). 在激波/边界层干扰的区域，流动现象很复杂，可能会发生流动分离、激波非定常运动、旋涡运动、压力波动、混合、湍流等等(Kim 2007). 流动分离决定性地影响了流动的总体特征，是激波/边界层干扰的重要方面. 一旦出现流动分离，产生了分离泡，激波波系会发生变化，进而引起压力载荷的变化，在流动再附点还会引起热流的增加. 因此，研究激波/边界层干扰的问题，准确的预报流动分离和壁面热流，对于高超声速飞行器的减阻和防热设计具有重要意义.

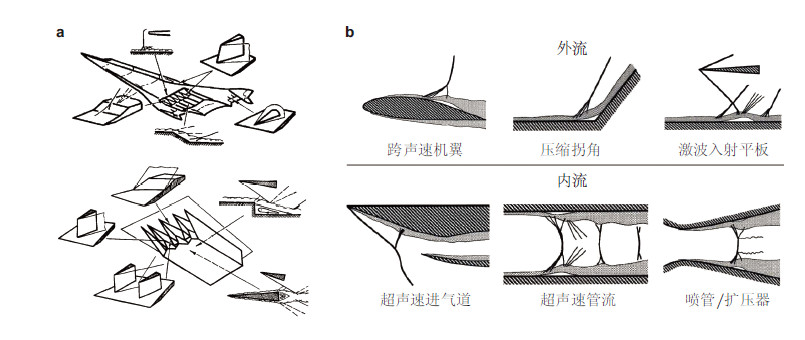
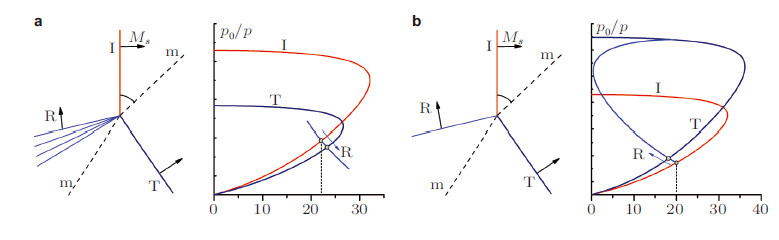
图 7 发生激波/边界层干扰的几种基本构形示意图.(a)高速飞行器各部件干扰(Zheltovodov 1996)，(b)内/外流形式(Kim 2007)

1939年Ferri在翼型风洞实验中，发现了激波/边界层干扰的现象(Ferri 1940). 而对此问题首次系统地进行实验研究则是在20世纪40年代中后期，Liepmann(1946)和Ackeret 等(1947)研究了跨声速和低马赫数超声速下，激波与层流和湍流边界层干扰. 此后，各国的学者在较宽的马赫数和雷诺数范围，对多种几何构形的激波/边界层干扰进行了广泛的研究. 对于二维的激波/边界层干扰(Adamson & Messiter，1980，易仕和等，2015，李新亮 2015)，最常见的研究是正激波/斜激波与湍流/层流平板边界层的干扰，以及流动经过一个凸起或是压缩拐角时的干扰(如图 8). 三维激波/边界层干扰研究的常见构形是，单翼板产生的后掠激波与边界层干扰(Charwat & Redekeopp，1967; West & Korkegi，1972)、双翼板产生的交叉激波与边界层干扰(Garrison et al. 1993，1996)，以及三维进气道内激波与边界层主导的流动(Goonko et al. 2003). 美国宾夕法尼亚州立大学气体动力学实验室(PSU，Gas Dynamics Laboratory)Settles教授等收集了大量的激波/边界层干扰的实验数据，并建立了数据库(Settles & Dodson，1991，1993，1994a，1994b)，最近Marvin 等(2013)在NASA的支持下，针对二维和轴对称构型的高超声速激波/湍流边界层干扰问题，收集整理了实验数据库，用于CFD验证. 北大西洋公约组织航天研究与发展咨询组(NATO，RTO，AGARD)曾专门针对激波/边界层干扰进行了研讨(Degrez 1993，Saric et al. 1996，Muylaert et al. 1998)，激波/边界层干扰也是国际激波会议(ISSW)的议题之一. 国内也开展了许多激波/边界层干扰的研究，中国航天科技集团公司第十一研究院的李素循出版了激波/边界层干扰的专著(李素循2007).

图 8 激波/边界层干扰的实例.(a)斜激波入射平板(纳米散射(NPLS)切片(易仕和等 2015))，(b)压缩拐角(左: DNS(李新亮 2010)，右: NPLS显示(易仕和等 2015))

对激波/边界层干扰这一问题的研究，虽然已经持续了七十多年，在流场显示、壁面压力和热流测量方面获得了一些认识，但是仍然还有许多物理、化学上的机理没有完全认识. 比如，激波导致流动分离(shock-induced separation，SIS)发生的清晰的具体的判据如何(Kim & Setoguchi，2007)，干扰区域内热载荷的准确预测方法，激波/边界层干扰对可压缩边界层稳定性以及转捩的影响，高超声速下包含化学反应的激波/边界层干扰等等.

随着各国吸气式高超声速飞行器研究热潮的到来，激波/边界层干扰问题又受到了新的更广泛的关注(Panaras 1996，Dolling 2001，Knight et al. 2003，Zheltovodov 2006，Edwards 2008，Gaitonde 2015). 近年来，激波/边界层干扰中低频的自持振荡现象(Dussauge & Piponniau，2008，Clemens & Narayanaswamy，2014)，引起了研究者的广泛关注，主要是为了揭示分离激波运动的频率比来流边界层的特征频率低一个数量级这一问题的产生机理(Wu & Martin，2008). 目前已经提出了多种机制，如分离泡、分离剪切层和激波波系之间的反馈回路机制(Wu & Martin，2008)，分离泡连续的收缩和扩张机制(Piponniau et al. 2009)，剪切层的脱涡(Smits & Dussauge，2005)，以及这些物理机制的耦合作用. 但是，对于这一问题还没有定论. 随着激波/边界层干扰问题中非定常特征的实验测量、CFD以及理论研究的不断深入，Dussauge 等(Dussauge & Piponniau，2008，Délery & Dussauge，2009，Debiève & Dupont，2009)多位研究者建议，借助流动稳定性理论，可能会有所突破，提供一种解决方案.

近年来随着吸气式高超声速飞行器研究的不断深入，以高超声速进气道的脉冲起动过程(范晓樯等2007，Li et al. 2011，李祝飞，2013，蔡佳等，2013，Wang et al. 2013)、飞行实验中进气道保护罩打开过程(Tahir 2003，李宇飞等2007，Ogawa et al. 2010，Grainger et al. 2012，徐骁等 2015)、进气道激波振荡过程(喘振)(Tan et al. 2011，李祝飞 2012; Li et al. 2013)、进气道自起动过程等(李祝飞，2013，李祝飞等，2013，李祝飞和杨基明 2016)为典型代表的，与进气道性能息息相关的复杂流动现象，均伴有激波的非定常运动，而借助于x-t图、激波极线法等一维和二维的分析方法，有利于从整体上把握流动的演化过程，揭示其流动机理.

超/高超声速进气道在超额定或反压条件工况下，可能出现由于波系干扰引起的进气道不起动(如图 9)，近年来受到研究人员和工程部门的重视(Mahapatra & Jagadeesh，2009，Yao et al. 2013，Tao et al. 2014，Wang et al. 2015，Jiao et al. 2015，高雄等，2015，焦晓亮等，2015，陶渊等 2015). 借助于二维的激波极线分析方法，所获得的出现马赫反射的条件，对于进气道设计和工作范围的选定具有一定的指导意义.

图 9 波系干扰引起的进气道不起动.(a)实验纹影(Mahapatra & Jagadeesh 2009);(b)结构示意图(陶渊等 2015): IS入射激波，DS脱体激波，RS反射激波，SL滑移线，EW膨胀波

随着新型高超声速内转式进气道逐步进入工程视野，内转式进气道中三维曲面激波/边界层干扰，给实验观测和理论分析都提出了新的挑战，激波研究不断地涌现出新的活力和研究热点.

3.3 激波/湍流作用与脉动压力问题

激波和湍流相互作用广泛存在于自然界和工程实际问题中，其自身所蕴含的复杂非线性相互作用机制以及诸如航空航天等重大需求背景不断给相关研究提出新的挑战. 激波和湍流相互作用会引起速度、压力脉动的增强，不仅会引起飞行器非定常脉动载荷环境的显著恶化，也给传统的预测方法增加了新的难度和要求. 这一状况尤其随着马赫数的提高和热耦合的显现而进一步加剧. 采用吸气式冲压发动机的高超声速飞行器多采用机体/推进一体化气动外形，外形特征为升力体类前体、不规则弹身及布局复杂的控制面，外流场存在复杂的绕流环境及激波与边界层主导的复杂流动，激波-激波干扰、逆压梯度导致分离激波、弹身型面拐角复杂流动、激波相交及碰撞、翼舵干扰等特征明显; 内型面一般采用前体预压缩来流，并捕获来流供给燃烧室，燃料与空气掺混燃烧后经尾喷管喷出产生推力. 前体、进气道、尾喷管内存在复杂的分离区及激波干扰区，喷流引起干扰流动等. 因此，内外流并存，且飞行操纵与动力推进密切交织与耦合，这些非定常特质明显的流动现象会带来严酷的压力脉动，峰值压力部位会随着气动外形及飞行条件的不同而改变，且多与峰值热流相交织.

就基础研究而言，在激波和湍流旋涡分离的流动问题中，存在着许多更为复杂的湍流问题的机理尚未得到深刻的认识. 例如，激波/湍流相互作用问题广泛存在于各类复杂的可压缩流动中，人们迫切需要深化认识此类问题的流动物理机理. 激波/湍流相互作用可分为如下典型问题(Andreopoulos et al. 2000): 激波/均匀各向同性湍流、激波/湍流边界层、激波/湍流尾迹以及激波/湍射流相互作用等. 近年来，关于激波与均匀各向同性湍流和湍流边界层相互作用问题已有不少研究. 数值研究方面，直接数值模拟(direct numerical simulation，DNS)和大涡模拟(large eddy simulation，LES)方法是研究激波和湍流相互作用问题的主要手段. 常见的研究模型主要有激波与均匀各向同性湍流作用(Larsson & Lele，2009)、入射激波与平板湍流边界层相互作用(Pirozzoli & Grasso，2006，Humble et al. 2009)以及斜坡形成的激波与湍流边界层相互作用(Ringuette et al. 2008)等. 而关于激波与湍流旋涡分离流、尾迹以及湍射流相互作用的研究还很少(Andreopoulos et al. 2000)，其原因可以归结为: 一方面，这类问题包含的流动现象更为复杂，并亟待探索; 另一方面，这些流动问题也为湍流模拟和计算方法提出了新挑战(王国蕾和陆夕云 2012).

可压缩湍流的实验研究对风洞流场的要求苛刻，用于激波与湍流相互作用研究的实验不仅需要对激波条件有着准确的把握，也需要对干扰前的来流条件进行有效地掌控和预测; 在此基础之上，激波与湍流相互作用的精细流场结构信息的获得，对非接触测量和显示技术的时间和空间分辨率也提出了严格的要求. 值得注意的是，近些年来，随着超声速、高超声速相关湍流机理的探索，以及气动光学效应等需求背景的推动，相关的实验与测量技术取得了令人瞩目的进展(Andreopoulos et al. 2000，Wyckham et al. 2005). 尤其令人欣慰的是，我国学者在实验技术方面所取得的成果显著，以基于纳米粒子示踪的平面激光散射观测技术(易仕和等，2015，全鹏程等 2014)为代表的非接触流场显示为将来实验研究的新突破给人以较大期待.

激波/湍流相互作用问题的流动机理很复杂，所涉及的影响因素也很多. 激波/湍流相互作用会直接导致流场中湍流尺度的改变，并能够影响流体的混合效应(Budzinski 1992); 在激波/湍流相互作用区，湍流的增强不仅与Rankine-Hugoniot 关系相关，还受到其他因素的影响，如流线弯曲引起的失稳效应、流动分离以及胀压效应等(Andreopoulos et al. 2000); 激波/湍流相互作用特性还依赖于激波的强度、位置和形状以及流动的几何构型和边界条件等(Deville et al. 2008); 来流的湍流状态和可压缩效应也是影响激波/湍流相互作用问题的重要因素(Ganapathisubramani et al. 2007). 上述这些复杂流动特性和诸多影响因素所带来的多种效应，尚未能在现有的湍流模式中得到很好的反映(Roy & Blottner，2006，Fureby 2008)，复杂湍流问题的机理尚未得到有效和深刻的认识. 因此，针对激波/湍流相互作用的复杂流动问题，在湍流模式和湍流机理等方面尚待进一步研究.

3.4 激波的聚焦与点火

由于激波对气体热状态的提升在近乎瞬间完成，并且跨激波的热力学和动力学状态参数具有很好的可确定性，激波诱导点火方法被大量应用于预混可燃气体的点火特性、火焰传播规律以及基于点火延迟的反应机理研究(Berets et al. 1950; Mooradian & Gordon，1951; Strehlow 1962，1963; Voevodsky & Soloukhin，1965; Belford & Strehlow，1969; Burcat et al. 1971，1972; Trang & Lifshitz，1990; Yamashita et al. 2012; Chaumeix et al. 2014). 另一方面，由于激波具有很好的可控性以及传播中的可增强性，激波诱导点火也是工程实际中(如脉冲爆轰发动机(Jackson et al. 2002，2003)、惯性约束核聚变(Perkins 2009))一个具有相当应用前景的点火方式.

不管是基础学术研究还是工程应用，激波诱导点火的实践通常需要经历一个激波由弱至强的发展过程. 以激波管实验研究为例，如图 10所示，为了避免膜片破裂、接触面混合等诸多不确定因素干扰点火过程，同时也由于直接生成强激波的代价更高，通常首先产生波后温度低于点火温度的弱激波，在激波稳定建立后，再通过一定的激波增强方法来实现有的放矢的可控点火. 相应的，工程应用则本来就有以较弱的能量实现可靠点火的实际需求，因此也必须对常规容易获取的、能量密度较低的弱激波进行有效的后续增强. 从这一角度看，激波增强方法是激波诱导点火研究一个具有普遍性的关键环节. 不同激波增强方法下，其激波诱导点火的过程和特点也各有差异; 而设计更为先进和有效的激波增强方法也是该领域研究一个重要方面.

图 10 激波诱导点火的一般途径

对激波诱导点火的基本认识和研究动机最早主要来自对可燃混合气体的燃烧化学反应动力学机理的关注(Strehlow & Dyner，1962，1963; Gaydon & Hurle，1963; Greene & Toennies，1964; Voevodsky & Soloukhin，1965; Burcat et al. 1971，1972). 受益于理想激波和激波管运行环境的简洁性和可知性，经激波处理直至点火发生的时间尺度(即点火延迟时间)可通过简单的数据处理直接获得. 此类研究自20世纪50年代到今天仍在继续，文献数量极其庞大，难以枚举. Belford和Strehlow(1969)、Tsang和Lifshitz(1990)对此进行了较为详尽的综述. Schultz和Shepherd(2000)则对已有研究中关于氢等常见燃气的大量点火延迟时间数据进行了整理.

利用激波管形成的平面激波进行点火实验，实际运行方式主要有两种. 一是直接采用入射激波点火(Myers & Bartle，1969，Gray & Westbrook，1994，Chaumeix et al. 2014)，如图 11所示. 这种点火方式需要较强的入射激波，由于激波最先扫过的介质处于稳定高能状态的累积时间最长，因此点火通常在接触间断下游附近发生，破膜过程及接触面扩散混合不可避免地对此产生影响; 此外，由于该方式下点火位置处于随气流的运动之中，实验室坐标下的测得的点火延迟需经过相应换算求得. 另一更为普遍的点火方式是利用反射激波点火(Strehlow et al. 1962，1963; Voevodsky & Soloukhin，1965; Burcat et al. 1971，1972; Cooke & Williams，1975; Brown & Thomas，1999)，如图 12所示. 这种激波在端壁的反射是一种最具代表性的激波增强方法. 在理想激波管假设前提下，可认为激波端壁反射波后气体(5区)处于静止状态，点火在静止气体中发生方便于点火位置的确定以及点火延迟时间等参量的测量，这对于预混燃气反应特性的研究具有独特优势. 尽管如此，实际激波管流远非理想流动(Gaydon & Hurle，1963，Belford & Strehlow，1969，Fujii et al. 1979，Petersen & Hanson，2001). 早期研究(Meyer & Oppenheim，1971)认为反射激波诱导点火存在两种不同点火模式，一种是强点火，发生在5区温度较高情况下，点火由端壁整体平面发展，这种点火态势较为符合理想的激波管假设; 另一种是弱点火，发生在较低温度情况下，5区出现多处随机散布的着火点，这也就给延迟时间的测量带来很大的偏差和不确定性. Yamashita等(2012)最近的研究则表明，所谓强弱点火的模式差异实际上是一个随5区温度连续变化的过程(如 图 13). 另一重要的非理想因素是流体的黏性效应无法忽略，激波反射后在回传过程中不可避免地会与来流边界层发生相互作用，形成"λ"形激波(如图 13(b)). 这种激波/边界层干扰难免将会改变激波波后流场特性，影响下游的点火及火焰传播过程. 特别是随着反射激波强度减弱，波后流场温度降低，点火延迟时间变长，诱导距离增加，边界层的影响效应将变得尤为显著. 此外，根据不同的实验条件，入射激波对气流的预处理、湍流、热非平衡弛豫等同样会对实验结果和测量形成干扰.

图 11 平面入射反射激波诱导点火
图 12 平面反射激波诱导点火
图 13 不同反射激波诱导点火模式(Yamashita et al. 2012).(a)T5=1 291 K，(b)T5=988 K

通过端壁反射增强激波的方法实际是利用端壁阻滞将入射激波所诱导的气流动能转化为内能并叠加至入射波后的气流内能上去. 与此相异的另一类方法则是基于减小激波传播面积以增强激波强度的思想，即所谓激波聚焦. 这类激波增强方法的基本原理可追溯到早期Guderley(1942)关于柱面和球面汇聚激波的自相似解以及Chester(1954)、Chisnell(1957)和Whitham(1957，1959)所提出的激波动力学理论. 后者以变分法分析缓变截面管中激波传播的流动和波系方程，并通过省略高阶项获得激波强度与传播面积的一维近似关系(简称CCW关系)

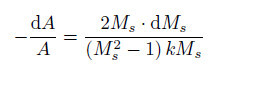
(5)

Whitham(1957，1959)在这一关系基础上进一步建立了二维和三维的"Ray-tube"理论，用于估算激波在不同边界约束下的波面形态及其演变. 该理论尽管并未切实纳入波后气流的流动物理，却获得了与流体动力学结果相当的一致性，从而被广泛采纳和运用，并为早期数值模拟匮乏情况下的工程计算和科学研究提供了极大的便利.

式(5)表明减小激波传播面积即可增大激波强度. 这一原理最为直观和典型的应用就是柱面或球面激波的汇聚. 理论上，完全对称的柱面/球面汇聚激波的面积将收缩至一个无穷小的奇点，激波强度趋于无穷大. 若这一增强过程发生在预混可燃气体中，则汇聚激波必然扫过该气体的点火极限.

目前已有关于柱面/球面汇聚激波的研究以理论和数值模拟为主，研究关注点一是理论和相关数据的进一步完善(Dyke & Guttmann，1982，Hafner 1988，Bilbal & Gratton，1996，Ponchaut et al. 2006)，特别是奇点邻域汇聚激波强度增长规律、汇聚指数等; 二是考虑实际应用环境的非理想性影响，如汇聚激波的稳定性(Gardner et al. 1982)、多边形汇聚(Schwendeman & Whitham，1987)、高温气体效应(Radha & Sharma，1993，Kjellander et al. 2010)等等. 此类研究以理论和数值为主的一个重要原因是，完整的柱面/球面汇聚激波的实验室生成始终是一个巨大的挑战(尤其是球面汇聚激波)，并造成开展此类汇聚实验的困难.

当前一种行之有效的生成完整柱面汇聚激波的方法是采用环形激波管并以壁面引导和约束环形激波在端部向心折转汇聚，如图 14(a)所示. Perry和Kantrowitz(1951)、Takayama等(1984，1987)、Watanabe和Takayama(1991)等研究了这种柱面汇聚激波的生成效果以及它的稳定性; Eliasson等(2006，2007)研究了不同形状柱面激波(圆柱和多边形)汇聚和反射的特性; Kjellander 等(2010，2012)则从实验上对柱面激波汇聚的热辐射和能量情况进行了详细的探讨. 放宽严格的柱面约束，一些基于相似概念的环状激波汇聚增强的方法也大量见诸发表. Skews等(2002)将 图 14(a)所示的平面端部约束腔改为锥形腔(如图 14(b))，于是实现并研究了锥形激波的汇聚问题; Jiang和Takayama(1998)、 Hosseini和Takayama(2010)等则研究了一种环形激波的绕射、反射和聚焦过程，其汇聚的相干构型如图 14(c)所示; 以脉冲爆轰发动机的高效点火为背景，Jackson等(2002，2003)采用如图 14(d)所示的相干原理，巧妙设计了一种形成环状爆轰波汇聚的点火装置，并在氢/空气混合气体中实现成功点火; 基于同一构型原理，他们的另一项工作则实现了环状射流激波的汇聚点火(Jackson & Shepherd，2007，2008). 这种点火方式被认为是两级脉冲爆轰发动机的一项关键技术(Leyva et al. 2003). 我国也在相关工程背景下对此展开了深入的数值和实验研究(李海鹏等 2010; 曾昊等，2011，2013; 荣康等2012; 包醒东等 2013).

图 14 柱面激波聚焦设置及其变种

除上述直接利用球面、柱面、环形激波的汇聚来增强激波外，另一种激波汇聚方法通过激波在凹面腔上的迎面反射实现. 激波凹面反射聚焦实际可视为端部反射与激波汇聚这两种机制的组合，如图 15所示. 显然，就局部激波的增强而言，凹面腔反射聚焦效果大大优于平面端部的反射作用，而轴对称凹腔的聚焦效果又优于柱面凹腔，从而点火效能也以轴对称凹腔更强(Borisov et al. 1990，Kisbige et al. 1992). Izumi 等(1994)对几种不同焦距二维抛物面的对比研究认为，不管何种反射面，反射波系均会出现上下两个对称的三波点(图 16中(T))，两个三波点在对称面的碰撞形成全场压力的极大值，表征着汇聚的发生. 董刚等(2006)对冷态凹面反射汇聚的研究揭示了与此相似的规律. Babinsky和Takayama(1998)研究发现凹腔边界的类型对聚焦的波系可产生大的影响. Skews和Kleine(2007)以高速摄影方法捕捉到激波在半圆柱凹腔反射汇聚的更多更精细流场结构. 在热态点火方面，Gelfand等(2000)对氢空气混合空气中楔形凹腔和抛物面凹腔的聚焦点火开展实验研究，观测到强弱两种不同的聚焦点火模式，其中强点火立即形成爆轰，而弱点火则首先发展出凹腔内的湍流火焰，进而在适当条件下转化为爆轰(图 17). Bartenev等(2000)结合数值模拟分析了上述情况下点火发生的位置、条件和机制. Jackson等(2005)考察了碳氢燃料混合气体中N2稀释、燃料种类、凹腔深度对激波反射聚焦点火的影响. Khomik等(2007)对已有的临界点火入射激波马赫数进行了综合分析，发现当凹腔深度不变，凹腔形状的改变对临界马赫数影响甚微. 滕宏辉等(2007)的数值模拟显示，在高入射激波马赫数下，除一般激波聚焦点的着火点外，入射激波在凹面上的马赫反射可在壁面附近诱发另一着火点.

图 15 凹面端部反射汇聚示意图.(a)平面端部反射，(b)凹面端部反射汇聚
图 16 凹面端部反射汇聚实验照片(Izumi et al. 1994)
图 17 反射激波汇聚点火起爆实验结果(Gelfand 2000).(a)楔腔反射，(b)抛物面反射

近期，我国空军工程大学的何立明等(2015)对激波环形聚焦点火和凹面反射激波聚焦点火的研究现状进行了充分详尽的综述. 该文结合两级脉冲爆轰发动机的工程背景，从冷态聚焦流场、聚焦点火实验研究和数值模拟研究3个方面展开. 文章最后指出，不管是环形射流聚焦点火还是凹腔激波聚焦点火，其流场均充斥着复杂激波系以及与火焰的相互作用，各种作用机制错综复杂，需要进一步深入探究.

然而从理解纯粹的激波诱导点火机制的角度，我们实际希望能将复杂问题分解并逐一解析. 为了尽可能的降低流场激波波系的复杂度，除平面激波，柱面或球面激波是另一种均衡简洁的波面. 问题在于，早期的尝试中，实验装置较为复杂，所产生的柱面汇聚激波强度较弱，进行点火及火焰传播过程研究较为困难，而且实验可观察的时间尺度和空间尺度也极为有限. 近年来，有研究希望通过某种方法将平面激波转变为在锥形腔内汇聚传播的球面激波或楔形腔内汇聚传播的柱面激波. 然而，如果不加任何过渡环节，入射激波迎面的锥形腔或楔形腔实际与凹腔汇聚相同，必将伴随复杂的激波反射而形成不利干扰(Setchell et al. 1972，Bond et al. 2009). Dimotakis和Samtaney(2006)提出一种平面激波汇聚的"激波透镜"理论(如图 18). 不过，这种"透镜"界面的实际设置仍需要排除诸多难题，后续并没有看到满意的实验结果公开发表.

图 18 激波透镜方法(Dimotakis & Samtaney 2006)

Zhai等(2010)提出了一种通过合理地设计壁面型线将平面激波转变成圆柱形汇聚激波的方法. 典型实验段构型如图 19所示，汇聚通道由光滑衔接的过渡段(PQ)和楔形段(QO)两部分组成，其中过渡段壁面型线主要依据激波动力学理论(Chester 1954; Chisnell 1957; Whitham 1957，1959)进行反设计获得. 这一方法简单有效且可行性强，已被后续研究者效仿，并拓展至球面汇聚激波的生成(Kjellander 2012，Liverts & Apazidis，2016). 杨剑挺等近期以此为基础，研制了扇形收缩契腔内圆弧汇聚激波点火研究实验装置，并开展了相应的预混可燃气体点火以及火焰传播特性研究. 图 20所示为一种典型的柱面汇聚激波点火过程的高速摄影图. 研究发现: 这种依据激波动力学方法设计的过渡型面可以很好地将平面激波平滑过渡为均衡的柱面汇聚激波; 当入射激波马赫数超过一定值，点火发生，着火点位置并不位于温度最高的激波波面附近，而是滞后于波后一定距离. 点火后的火焰结构迅速发展为向上下游分别传播的爆轰波(杨剑挺等 2016).

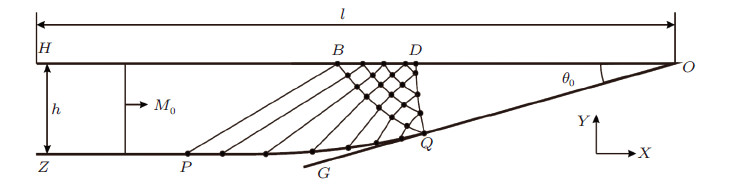
图 19 激波动力学方法设计楔形腔(Zhai et al. 2010)
图 20 纹影图30% H2+70%Air，初压6.0 kPa，初始激波马赫数3.0(杨剑挺等 2016)
3.5 激波作用下气体界面不稳定性研究 3.5.1 研究背景

激波穿越两种不同气体的界面时，激波对界面两侧气体不同的压缩效果和界面对激波的折射使得流场中呈现出强烈的耦合作用. 在初始界面或入射激波存在扰动的情况下，初始扰动随着激波诱导后的界面运动逐渐演化发展，并最终形成湍流混合层. 这就是Richtmyer-Meshkov(RM)界面不稳定性问题(Richtmyer 1960，Meshkov 1969). 从Richtmyer于1960年提出理论分析和Meshkov在1969 年实验验证后，各国研究者展开了大量的研究工作. 这不仅因为RM不稳定性是一种十分复杂的多尺度强非线性的物理问题，而且也由于其广泛和重要的应用背景. 例如在惯性约束核聚变中，由反冲力形成的聚心冲击波，将靶芯千百倍地压缩，并产生上亿度的高温发生聚变. 一旦在冲击波压缩的过程中出现RM 不稳定性，引起的湍流混合会降低靶的产额，甚至影响其成败(Lindl et al. 2014). 此外，在超燃冲压发动机的燃料混合(Yang et al. 1993)，超新星爆发(Arnett et al. 1989)，爆燃向爆轰的转变，水下爆炸，国防尖端武器等领域都有着广泛而重要的应用. 经过半个多世纪的努力，RM不稳定性的研究进展迅速，已成为当今流体力学研究领域的一大热点，相关研究水平正在不断提高. 1999年，针对加州理工学院Sturtevant研究小组 1995年发表的激波管中带隔膜界面RM不稳定性实验结果，利弗莫尔实验室与明尼苏达大学合作，利用PPM方法进行了可压缩湍流高精度数值计算，这一工作荣获了当年Gordon Bell奖. 同年，Los Alamos国家实验室研究了RM不稳定性后期湍流混合区的发展，详细地分析了一些以前从未发现过的新现象，他们的工作获得了Fernbach奖. 《流体力学年鉴》近十多年来不断有RM不稳定性和湍流混合问题的综述文章发表(Zabusky 1999，Brouillette 2002，Dimotakis 2005，Ranjan et al. 2011). 2005年《Los Alamos Science》发表了一系列关于湍流混合问题的研究方法和结果. 这些事实说明，随着未来对于实验现象和数值模拟工作深入研究的需要，以及目前超级计算机计算能力和精密光电诊断技术的迅速发展，国际学术界越来越重视RM不稳定性方面的研究工作.

RM不稳定性问题具有较大的空间跨度，大尺度如天体物理超新星爆发，小尺度如惯性约束核聚变中氘氚(DT)气芯和金属壳体的混合. 当前国际上关于RM不稳定性的实验研究方法主要分为4种: 激光惯性约束聚变、电磁套筒内爆、炸药驱动金属材料、激波加载流体界面. 由于耗资巨大、周期较长或诊断困难等原因，前3种实验方法在短期内难以得到大量可靠的实验数据. 目前国际上主要是依靠上述第4种方法，因为在激波管中开展的激波加载流体界面实验具有可控的实验条件，在研究不同密度气体间的RM不稳定性及湍流混合问题具有得天独厚的优势:(1)投资小;(2)周期短;(3)实验条件易控，有效时间长;(4)结合当代先进光电测试技术，可以得到高时空分辨率的实验结果. 作为基础性研究课题，美、英、俄、法等核武器单位以及部分高校、研究院所开展了大量的激波管研究界面不稳定性实验. 这类实验运用高速摄影、纹影、粒子图像测速和激光诱导荧光等光学测量技术，在激波管中对流体介质的RM不稳定性发展过程进行测量，获得精确的实验结果. 2000年美国能源部研发报告中，开展不稳定性实验的激波管与Omega、Z机器和Pegasus等一起被列为研究高能量密度物理和流体动力学效应的实验装置. 2002年阿拉莫斯实验室主任John Browne指出，类似于激波管中RM不稳定性问题研究这样的小实验可以得到高质量的实验数据，这些数据对于校验程序是至关重要的，这些小实验是预测整个核武器性能的基石. 芝加哥大学天体物理中心的ASCI超新星模拟程序FLASH和阿拉莫斯实验室的辐射流体动力学程序RAGE，都将激波管中RM不稳定性研究的实验结果作为首选的校验数据. 这些事实表明，利用激波管设备开展RM不稳定性研究是当前国际上的重要研究手段.

3.5.2 RM不稳定性的理论研究

RM 不稳定性的研究最早是以理论研究开始的，经过几十年的发展，理论研究也越来越深入. RM不稳定性的演化发展是一个复杂的物理过程，理论研究方面，以单模态正弦界面为研究重点，产生了多种模型，其它类型初始扰动界面的理论研究极少. 经典的RM 不稳定性的发展过程一般认为包括3个阶段. 初始阶段扰动的线性增长，典型代表工作如Richtmyer(1960)对激波与两个不同密度流体之间可压缩界面的扰动增长进行了分析. Richtmyer 认为，当激波较弱时，激波诱导的速度是很小的，因此界面随后的运动可以认为是不可压的. 这样，通过用一个冲击函数δ(t)来代替重力加速度g，得到了扰动幅度随时间线性增长的结果; 随后Meyer和Blewett(1972)、 Wouchuk和Nishiara(1996)、 Vandeboomgaerde等(1998)不断对脉冲模型进行修正，使其具有更好的适用性. 由于脉冲模型公式实际上是基于一种不可压缩线性理论，所以它只在振幅较小时才是正确的. 由于简洁且易于计算，脉冲模型引起了广泛的兴趣. 在小扰动和弱激波情况下，这一模型能够给出很好的结果. 当初始激波干扰后的可压缩性效应较弱时，各种脉冲模型之间的差别也很小. 对于强激波情况，以及激波冲击界面后瞬间的界面现象，需要使用可压缩线性理论. Yang等(1994)针对反射激波和反射稀疏波两种情况，数值求解了线性化扰动方程，并系统地与Richtmyer的冲击模型做了对比. 他们发现当入射激波强度减弱以及流体比热比增大时，二者比较吻合，显然这两种效应都与可压缩效应相关. 之后 Fraley(1986)以及Velikovich(1996)等分别采用类似的方法针对反射激波以及反射稀疏波的情况，得到了一个解析解. 在强激波极限条件下，气体实验的RM不稳定性问题中，气体的分解变得非常重要. 针对反射激波的情况，这种分解效应已经被Samtaney和Meiron(1997)从理论和数值模拟上予以证实.

扰动线性发展时间是比较短暂的，随后即进入非线性发展阶段. 在非线性发展阶段，线性理论不再适用. Velikovich和Dimonte(1996)对Richtmyer 的冲击模型进行了非线性修正，提出了单模态非线性的高阶扰动理论. 但该理论并不局限于此，同样适用于多模态扰动、连续界面扰动以及三维流动等非线性问题. 同时也对"尖钉"和"气泡"的增长理论进行了高阶修正. Zhang和Sohn(1997)针对冲击加速不可压的问题导出了四阶弱非线性的解法，随后Vandenboomgaerde 等(2002)更是将这种方法延伸至11 阶. Zhang和Sohn 理论的一个缺陷就是得不到普遍公认的扰动增长的渐近行为，而这一问题在Sadot 等(1998)理论中得到了较好地解决. Collins和Jacobs(2002)，Jacobs和Krivets(2005)的实验表明，扰动早期的增长与很多不可压的线性稳定性理论符合的都比较好. 在非线性阶段初期，Sadot 等的模型与实验结果吻合相对较好.

对于单模态扰动的增长，在上述理论的基础上，Zhang和Sohn(1996，1997)运用级数高阶展开和Padé近似扩展有效区间的方法处理了关于非线性发展的问题. 利用这种匹配技术，类似于边界层理论中的渐近方法，在反射激波和反射稀疏波两种情况下，他们研究了二维和三维初始扰动的发展过程，得到了气泡和尖钉不同的速度公式，以及界面发展的总体增长率，适用于从早期到晚期(Li & Zhang，1997). Sadot等(1998)提出单模态界面从早期到后期的演化过程，可以通过联合线性脉冲模型结果和渐近气泡/尖钉势流模型得到，对于非常后期的情况，可以得到对所有气体组合的扰动增长率. 这一模型的计算结果和激波管中的低、中入射马赫数实验结果吻合得很好.

但在绝大多数应用问题中，初始扰动是多模态的，波数分布在多个数量级. 而且，随着RM不稳定性的发展，Kelvin-Helmholtz不稳定性将导致涡的卷曲，从而进一步增加物理尺度的分布范围. 最终，界面将演化成一个三维的湍流混合区，即便初始扰动是二维的，最终也将如此. 由于宽广的时空尺度分布范围需要求解，直接数值模拟(DNS)研究RM不稳定性是不切实际的，需要发展一些物理模型来解决这一问题. 由于界面后期的演化可看做由各种尺寸、各种速度的气泡和尖钉之间的竞争所主导(Sharp 1984)，这种情况下，气泡和尖钉可以分别处理，总的界面厚度可由气泡和尖钉的尺寸之和得到. 在各种各样的初始条件下，产生了一些相关的理论，然而实验结果表明增长因子的宽广变化特性，这说明这个问题实际上很可能对初始条件非常敏感. 针对任意初始扰动的情况，Mikaelian提出了一种能够预测扰动增长的模型(Mikaelian 2015)，该模型经验证具有较好的适用性. 随着研究的深入，强激波以及汇聚激波逐渐成为研究热点. 在强激波条件下，可压缩效应不能忽略，界面发展有可能很快由线性区进入非线性区，弱非线性理论也将不再适用. 而已有的理论模型多是针对于平面激波，汇聚激波条件下的相关理论仍需要开展大量的研究.

三维界面的不稳定性发展是当前RM不稳定性研究的主要方向. 然而，由于观测与分析困难，这方面的实验与理论研究比较少，对三维界面的RM不稳定性发展与演变规律认识非常有限. 在三维 RM不稳定性情况下，扰动增长规律与二维 RM不稳定性情况不同(Chapman & Jacobs，2006，Long et al. 2009). 相对二维情形，界面的演变发展将受到由于第3个维度的加入而产生的额外涡量的影响. 已有结果表明，当扰动界面的主曲率的方向相同时，扰动幅度增长率高于二维 RM不稳定性情况，当扰动界面的主曲率方向相反时，扰动幅度增长率低于二维 RM不稳定性情况，但目前仍缺少一个统一的关于三维界面不稳定性发展的认识与理论. 已有的三维 RM不稳定性研究主要关于三维 单模扰动和随机扰动界面在激波作用下的演化规律(Chapman & Jacobs，2006，Long et al. 2009)，其他初始形状的扰动界面的三维 RMI 研究较少. Luo 等(2013)采用无支撑的约束环技术，生成了具有极小曲面特征的三维单模界面，系统开展了三维界面的RM不稳定性的实验研究，并 提出了一个适用于任意形状初始界面的扰动线性增长理论模型，可以正确描述二维界面(只有一个主曲率)、一般三维界面(具有相同指向的主曲率)和极小曲面三维界面的线性增长过程. 此外，根据实验结果，还提出了一个三维非线性理论公式，适用于三维界面演变的发展后期.

3.5.3 RM不稳定性的实验研究

Meshkov最早用实验验证了Richtmyer的冲击理论，采用硝化纤维膜形成了正弦界面，观测了正弦界面在平面激波冲击下的前期演化过程. 自此以后，大量的实验研究逐渐开展起来，从激波的形状和强度、界面形状和气体组分以及各种高时空分辨率的观测手段3个方面不断改进和优化. 归纳起来，平面激波作用气体界面RM不稳定性主要有三类实验类型: 第1种激波运动方向与界面垂直，初始界面多为小扰动正弦结构等，开展的实验工作较多. 最初多采用高分子膜形成初始正弦界面，但这种成膜方式通常需要网格的支撑，网格的存在对激波的行为以及界面的发展演化都有一定的干扰作用，而且高分子膜破碎后，较大的膜片同样对流场产生影响(Meshkov 1969). 通过不断对高分子膜的改进，如减小高分子膜的厚度，能够得到不断优化的实验结果(Brouillette & Sturtevant，1989，Sadot et al. 1998). 为了消除膜的破碎对流场的观测和测量带来的干扰，Brouillette和Strutevant(1993)采用一道薄金属板来分隔两种气体，金属板能够快速伸缩，利用气体分子之间的扩散效应形成一个连续的分界面. 抽平板技术属于无隔膜技术，可以形成多种形状的初始界面，但平板抽离会引入较大的扰动. 此外，在竖直激波管中，Jones和Jacobs(1997)让两种气体分别从激波管两侧充入并在实验段处相遇，通过加载在激波管上的振动来形成界面，同时利用先进的片光技术得到了无膜正弦界面的发展演化. 除了二维单模界面之外，三维单模界面近些年来也得到了广泛关注(Chapman & Jacobs，2006). Luo等(2013)采用细线约束肥皂膜的方法形成了具有极小曲面特征的单模界面，并实验研究了界面的三维性对不稳定性发展的影响(如图 21所示)，同时提出了三维界面扰动增长规律的理论模型. Likhachev和Tsiklashvili(2014)也从实验和理论方面研究了任意三维扰动界面在激波冲击下的发展演化规律.

图 21 平面激波冲击具有极小曲面特征的单模界面的实验结果(Luo et al.2013)

在单模界面的基础上，研究人员逐渐也将注意力集中到其他形状的界面，即初始界面具有一定的曲率，如气柱、气泡等，这类实验有些学者认为不纯是RM不稳定性问题，存在激波和物体绕流，但作为检验数值程序，研究不同尺度涡的演化不失为一种好的实验方法. 在这类实验中，较为典型的是Haas和Sturtevant(1987)采用肥皂膜和硝化纤维膜分别形成的球形和柱形界面，采用阴影方法得到了大量的实验数据. 之后法国的Layes等(2003，2009)，中国科学技术大学的Zhai等(2011)，Si等(2012)也采用类似的方法形成界面，利用高速摄影技术研究了不同工况下的界面演化规律. 在这些实验中，界面易受到支杆的影响，而且多集中于弱激波的冲击. Ranjan等(2005，2007)采用了一种新的球形界面形成方法，让界面在激波管中自由上浮或自由落体，同时采用片光技术研究了高马赫数激波的冲击作用. 这种方法避免了支杆的影响，也消除了阴影纹影等光学测量手段的积分效应，得到了高马赫数下特有的现象. 同样，为了消除膜的影响，Jacobs(1992)利用射流技术形成了无膜气柱界面，并结合先进的PLIF技术获得了气柱界面的演化形态(如图 22所示). 无膜界面易于结合先进的片光诊断技术，能够得到流场的定量信息，因此，射流方法形成无膜界面被各国研究者广泛采用，并被进一步改进，用来形成多气柱(Tomkins et al. 2002，2003)，气帘界面(Orlicz et al. 2009，Tomkins et al. 2008)以及椭圆形气柱(Zou et al. 2010)等. 但射流技术形成的界面仅仅局限在气柱或气帘界面，难以形成其他形状气体界面. 而且这种方法形成的气体界面具有一定的运动速度，边界易于扩散，因此具有三维效应(Weirs 2008). 而三维界面的不稳定性发展是当前RM不稳定性研究的主要方向. 但由于观测与分析困难，这方面的实验与理论研究比较少，对三维界面的RM不稳定性发展与演变规律认识还非常有限. 相对二维情形，界面的演变发展将受到由于第3个维度的加入而产生的额外涡量的影响，目前仍缺少一个统一的关于三维界面不稳定性发展的认识与理论. 除了已有的截面形状为圆形或椭圆形的二维柱形外，Wang 等(2013)、 Zhai 等(2014)、Luo 等(2015)利用细针约束肥皂膜的方式在实验中形成了各种多边形界面，如正方形、三角形等，并研究了激波在界面上的折射现象以及多边形界面在激波冲击下的演化规律(如 图 23所示). 除了以上两种实验类型外，第3种实验类型为激波与界面具有一定夹角，如斜界面和"V"型界面. 最初斜界面仅是用于研究激波的折射现象(Abd-EL Fattah & Henderson，1978a，1978b)，后来斜界面的不稳定性发展才逐渐得到关注. 激波与界面有较大的夹角时，激波在界面处发生非正规折射使得激波与界面的相互作用变得较为复杂，对此类界面演化发展问题很难用理论分析，主要通过实验和数值计算进行研究，得到界面演化发展中后期的发展特征.

图 22 平面激波冲击氦气气柱的PLIF图像(Jacobs 1992)
图 23 平面激波作用下，SF6/N2界面(左，Zhai et al.2014)和N2/SF6界面(右，Luo et al. 2015)的演化图像

最初形成斜界面或V形界面时仍是依赖于网格的支撑(Wang et al. 2012). 近几年来，美国德州农工大学的研究人员在其倾斜的激波管中利用气体相遇形成了相对于激波倾斜的无膜气体界面，并开展了大量的数值和实验研究(McFarland et al. 2013，2014). 董平等(2015)采用细针约束肥皂膜的方式形成了不同顶角的V形界面，并开展了相关的实验研究.

平面激波由于生成简单，其诱导下的RM不稳定性得到了广泛研究. 至于圆柱或球形激波冲击气体界面的实验，由于汇聚激波冲击界面与ICF的实际情形更吻合，汇聚激波的产生与应用成为RM不稳定性研究中最重要的前沿方向之一. 然而，由于汇聚激波的产生十分困难，设备复杂，测量难度大，汇聚激波作用下界面不稳定性的实验研究非常少. 日本东北大学Takayama教授曾在竖直激波管中形成了柱形汇聚激波，并开展了汇聚激波与柱形界面相互作用的过程(Hosseinia & Takayamam，2005). 但随着Takayama教授的退休，相关的汇聚激波研究也停滞不前. 利用气体透镜技术，Dimotakis和Samtaney(2006)年提出了一种柱形激波的产生方法，但直到 2015年，法国马赛大学Biamino等(2015)第一次在其汇聚激波管中开展了汇聚激波与单模界面的相互作用，获得了初步的实验结果. 南非金山大学Skews等(2015)这些年也致力于汇聚激波方面的研究，但其主要研究激波的汇聚效应以及汇聚激波的壁面反射等，较少涉及界面不稳定性的研究内容. 中国科学技术大学的Zhai等(2010，2012)曾利用激波动力学理论设计了能够产生汇聚激波的弯曲壁面，并在该激波管中开展了汇聚激波与球形和柱形相互作用的实验研究(Si et al. 2014); 此外，Luo等(2015)，Si等(2015)分别在半圆形激波管和竖直激波管中生成了柱形汇聚激波，并初步研究了汇聚激波与单模界面以及多边形界面相互作用的实验研究(如 图 24所示). 在汇聚激波作用下，由于能量汇聚、激波形状不同导致不同的斜压涡量堆积等因素的影响，界面的演化将表现出许多新的现象与规律. 关于RM不稳定性实验方面的研究进展，可参见文献(罗喜胜等 2014).

图 24 汇聚激波作用下，单模界面(左，Luo et al. 2015)和正六边形界面(右，Si et al. 2015)的演变规律
3.5.4 RM不稳定性的数值研究

数值模拟作为一种重要的研究手段在RM不稳定性研究中得到了广泛应用，特别是后期的非线性阶段和湍流混合阶段的细节信息基于现有的手段还难以观察和测量，而数值模拟在这方面则有很好的互补性. RM不稳定性就是Richtmyer在1960年首次通过数值计算发现的. 1972 年，Meyer和Blewett(1972)运用Lagrange算法对RM 不稳定性进行了数值模拟，结果与Meshkov 的实验结果定性一致. 20世纪80年代开始，高精度高分辨率计算方法和超级计算机的发展给界面不稳定性数值模拟研究注入了更大的活力. 美国就先后实施了加速战略创新计划(ASCI)、万亿尺度和千万亿尺度数值模拟等的大型研究计划，力图将高精度高分辨率数值方法和高性能计算机相结合，通过大型数值计算深入研究重要的物理问题. Holmes 等(1995)、Zhang和Graham(1998)等采用界面追踪技术的数值方法也对RM不稳定性进行了数值模拟. Latini 等(2007)运用五阶和九阶的WENO格式的激波捕捉方法数值模拟了激波与单模界面相互作用，数值结果与Collins和Jacobs(2002)的实验进行了对比，吻合较好. Baltrusaitisa等(1996)运用自适应网格技术模拟了激波和气柱相互作用，结果与实验吻合. Tritschler等(2014)采用DNS方法考察了初始条件的不确定性对气柱界面发展的影响，认为激波马赫数以及气柱界面内用于示踪的丙酮浓度对混合宽度的发展影响较大.

随着平面激波作用下二维界面不稳定性研究的深入，三维界面不稳定性以及汇聚激波诱导下的界面不稳定性逐渐得到关注. Malamud等(2014)采用数值方法研究了反射激波作用下三维多模界面的RM不稳定性，考察了初始扰动的分布对界面发展的影响. Olson和Greenough(2014)采用二维和三维大涡模拟方法研究对比了平面激波作用下多模初始扰动的发展规律. 结果表明在三维计算中，在二次激波冲击界面之后，界面很快进入湍流混合状态，界面总体长度基本不再发生变化. Lombardini等(2014a，2014b)采用大涡模拟研究了球形汇聚激波及其反射激波作用下的界面不稳定性问题，获得了界面混合宽度以及相关的湍流特征等数据. 此外Gallis等(2015)采用分子动力学的direct simulation Monte Carlo(DSMC)方法模拟了单模扰动界面的RM不稳定性问题，并且取得了较好的结果.

总而言之，实验研究方面，产生激波的尺度和强度范围在不断拓宽，强度和形状精确可控的手段日趋完善; 界面生成方法也一直在持续革新，扰动小、模式多样的界面生成方法在不断涌现; 另外，流场显示测量手段的高时空分辨能力将可获得更精细的演变过程信息. 数值研究方面，计算方法的科学高效与计算机容量和速度的飞速发展无疑也给相关模拟研究实现多影响因素和更宽时空尺度的湍流混合计算带来新的机遇. 需要强调的是，实验和数值研究的有机结合将有望为相关研究向纵深突破提供强大的驱动力.

4 结束语与展望

在对激波传播以及反射、折射等基本现象进行简要阐述的基础上，着重针对目前的热点问题，包括激波/激波干扰、激波/边界层干扰等研究进行了介绍和讨论，以期对当今开展的研究起到有价值的参考.

激波的传播与波系相互作用现象在自然界以及人类科技活动中广泛存在，与之相关的研究涉及众多学科，在航空航天、生物、医药以及材料等诸多领域有着重要的应用价值，是科技界最为活跃且经久不衰的领域之一. 尤其是随着当今以高超声速飞行器、惯性约束核聚变等研究为典型代表的重大需求的驱动，正在不断给激波及其相互作用研究领域提出新的挑战，所带来的难题较以往要复杂得多，包括几何构型的复杂性、流动介质的复杂性(如高温效应、相变、化学反应等)、相互作用的复杂性(如流/固/热/电磁多场耦合)等等. 值得庆幸的是，新的研究方法、手段和条件也在提供着越来越强有力的支撑. 地面模拟设备的发展，包括流场品质的提高(如静风洞)、模拟参数和能力的拓展(如高焓、长时间、大尺度风洞等)等，为某些苛刻流动条件的实现提供了可能; 测量方法和技术的发展则不仅为流场多种参数信息的获取打开新局面，而且也为实验与数值模拟的有机结合建立起直接的桥梁. 目前高时空分辨的精细化测量与数值计算的多尺度模拟研究发展遥相呼应，而激波干扰现象则正好涵盖从宏观到微观跨尺度的丰富内涵. 可以说，激波干扰更深层次的机理认识和规律的总结与数值计算和测量方法的进步相辅相成，共同发展.

近些年来，随着我国空天科技的蓬勃发展，为高速流动所伴随的基础科学研究既提供了难得的机遇，也不断带来新的挑战. 其中，激波干扰问题的研究当属关键环节之一，在工程应用中如果处理得巧妙得当，可望起到"四两拨千斤"之效; 当然，如果处理不当，则也可能是"差之毫厘失之千里". 相信激波相关研究必将在推动以新一代飞行器为代表的科技进步的同时，获得自身的发展.

致 谢 国家自然科学基金资助项目(11132010).
参考文献
包醒东, 李志强, 妥欢, 董鹤.2013. 斜向环形激波聚焦诱导直接起爆的大涡模拟[J]. 航空动力学报, 28 :2455–2461 . ( Bao X D, Li Z Q, Tuo H, Dong H.2013. LES of direct detonation induced by incident circular shock wave focusing[J]. Journal of Aerospace Power, 28 : 2455–2461 ) .
蔡佳, 苏纬仪, 张堃元, 李永洲.2013. 高超声速二元进气道脉冲起动双波结构的理论与数值研究[J]. 推进技术, 34 :1165–1171 . ( Cai J, Su WY, Zhang K Y, Li Y Z.2013. Theoretical and numerical study of double shock structure during 2D hypersonic inlet pulse-starting process[J]. Journal of Propulsion Technology, 34 : 1165–1171 ) .
陈强. 1978. 激波管流动的理论和实验技术. 中国科学技术大学讲义
董刚, 叶经方, 范宝春.2006. 激波聚焦反射的实验和数值研究[J]. 高压物理学报, 20 :359–364 . ( Dong G, Ye J F, Fang B C.2006. Experimental and numerical investigation of shock wave focusing and reflection[J]. Chinese Journal of High Pressure Physics, 20 : 359–364 ) .
董平, 罗喜胜, 翟志刚.2015. 平面激波与V 形air/SF6 肥皂膜界面相互作用的研究[J]. 中国科学: 物理学力学天文学, 45 :044701. ( Dong P, Luo X S, Zhai Z G.2015. Research on the interaction of planar shock with ‘inverse chevron’ air/SF6 soap film interface[J]. Scientia Sinica Physica, Mechanica & Astronomica, 45 : 044701 ) .
范晓樯, 贾地, 冯定华, 李桦.2007. 脉冲风洞中进气道起动过程试验研究[J]. 推进技术, 28 :60–64 . ( Fan X Q, Jia D, Feng D H, Li H.2007. Experimental investigation on starting process of hypersonic inlet in gun tunnel[J]. Journal of Propulsion Technology, 28 : 60–64 ) .
高波. 2010. 二维定常超音速流中激波马赫反射的波系结构与转捩研究. [博士论文]. 北京: 清华大学
高山和喜. 1995. 衝擊波ハンドブック. 东京: Springer 1-1256
高雄, 满延进, 李大进, 朱守梅. 2015. 试验研究高超二元进气道超额定状态//第五届冲压发动机技术交流会. 厦门, 下册: 348-353
何立明, 荣康, 曾昊, 陈鑫, 张强, 于鹏祥.2015. 激波聚焦及起爆爆震波的研究进展[J]. 推进技术, 36 :1441–1458 . ( He L M, Rong K, Zeng H, Chen X, Zhang Q, Yu P X.2015. Advances in shock wave focusing and induced detonation initiation[J]. Journal of Propulsion Technology, 36 : 1441–1458 ) .
HuangW, WangZ G, LuoS B, LiuJ.2009. An overview of research on engine/airframe integration for hypersonic waverider vehicles[J]. Journal of Solid Rocket Technology, 32 :242–248 .
黄志澄.1994. 空天飞机的乘波外形[J]. 气动实验与测量控制, 6 :1–10 . ( Huang Z C.1994. Waverider shapes for aerospace plane[J]. Aerodynamic Experiment and Measurement & Control, 6 : 1–10 ) .
姜宗林, 李进平, 赵伟, 刘云峰, 俞鸿儒.2012. 长试验时间爆轰驱动激波风洞技术研究[J]. 力学学报, 44 :824–831 . ( Jiang Z L, Li J P, Zhao W, Liu Y F, Yu H R.2012. Investigating into techniques for extending the test-duration of detonation-driven shock tunnels[J]. Acta Mechanica Sinica, 44 : 824–831 ) .
姜宗林, 俞鸿儒.2009. 高超声速激波风洞研究进展[J]. 力学进展, 39 :766–776 . ( Jiang Z L, Yu H R.2009. Progress of the research on hypersonic shock tunnels[J]. Advances in Mechanics, 39 : 766–776 ) .
焦晓亮, 崔涛, 于达仁. 2012. 超声速气流中双楔块结构的激波反射滞后现象及突变模型//高超声速专题研讨会暨第五届全国高超声速科学技术会议论文集
焦晓亮, 常军涛, 王仲奇, 于达仁. 2015. 高马赫数下高超声速进气道迟滞现象研究//第五届冲压发动机技术交流会. 厦门, 下册: 58-66
乐嘉陵, 倪鸿礼.1999. 激波(爆炸波) 与物体相互作用的数值模拟[J]. 流体力学实验与测量, 13 :1–9 . ( Le J L, Ni H L.1999. Numerical simulation of shock (blast) wave interaction with bodies[J]. Experiments and Measurements in Fluid Mechanics, 13 : 1–9 ) .
李海鹏, 何立明, 陈鑫, 曾昊.2010. 凹面腔内激波聚焦起爆爆震波过程的数值模拟[J]. 推进技术, 31 :87–91 . ( Li H P, He L M, Chen X, Zeng H.2010. Numerical investigation of detonation initiation by shock wave focusing over parabolic reflector[J]. Journal of Propulsion Technology, 31 : 87–91 ) .
李季. 2015. 高温非平衡效应下的激波干扰与激波反射. [博士论文]. 合肥: 中国科学技术大学
李素循.2007. 激波与边界层主导的复杂流动[M]. 北京: 科学出版社, . ( Li S X.2007. . Complex flows domi-nated by shock waves and boundary layers[M]. Beijing: Beijing Science Press, ) ) .
李新亮, 傅德薰, 马延文, 梁贤.2010. 压缩折角激波- 湍流边界层干扰直接数值模拟[J]. 中国科学: 物理学力学天文学, 40 :791–799 . ( Li X L, Fu D X, Ma Y W, Liang X.2010. A direct numerical simulation on shock wave-turbulent boundary layer interaction over a compression ramp[J]. Scientia Sinica Physica, Mechanica & Astronomica, 40 : 791–799 ) .
李新亮.2015. 高超声速湍流直接数值模拟技术[J]. 航空学报, 36 :147–158 . ( Li X L.2015. Direct numerical simulation techniques for hypersonic turbulent flows[J]. Acta Aeronautica et Astronautica Sinica, 36 : 147–158 ) .
李宇飞, 何国强, 刘佩进.2007. 一种辅助高超音速进气道起动方法研究[J]. 固体火箭技术, 30 :392–395 . ( Li Y F, He G Q, Liu P J.2007. Investigation on one aid hypersonic inlet starting method[J]. Journal of Solid Rocket Technology, 30 : 392–395 ) .
李祝飞, 高文智, 李鹏, 姜宏亮, 杨基明.2013. 一种进气道自起动特性检测方法[J]. 实验流体力学, 27 :14–18 . ( Li Z F, Gao W Z, Li P, Jiang H L, Yang J M.2013. A test method for inlet self-starting ability detection[J]. Journal of Experiments in Fluid Mechanics, 27 : 14–18 ) .
李祝飞, 杨基明.2016. 预设堵块法检测进气道自起动能力的数值研究[J]. 推进技术, 10 :. ( Li Z F, Yang J M.2016. A numerical investigation of the pre-setting-blockage method to detect the self-starting ability of an inlet[J]. Journal of Propulsion Technology, 10 : ) .
李祝飞, 高文智, 李鹏, 姜宏亮, 杨基明.2012. 二元高超声速进气道激波振荡特性实验[J]. 推进技术, 33 :676–682 . ( Li Z F, Gao W Z, Li P, Jiang H L, Yang J M.2012. Experimental investigation on the shock wave oscillation behaviors in a two-dimensional hypersonic inlet flow[J]. Journal of Propulsion Technology, 33 : 676–682 ) .
李祝飞. 2013. 高超声速进气道起动特性机理研究. [博士论文]. 合肥: 中国科学技术大学
刘儒勋, 舒其望. 2003. 计算流体力学的若干新方法. 北京: 科学出版社, 42-76
罗喜胜, 翟志刚, 司廷, 杨基明.2014. 激波诱导下的气体界面不稳定性实验研究[J]. 力学进展, 44 :201407. ( Luo X S, Zhai Z G, Si T, Yang J M.2014. Experimental study on the interfacial instability induced by shock waves[J]. Advances in Mechanics, 44 : 201407 ) .
全鹏程, 易仕和, 武宇, 朱杨柱, 陈植.2014. 激波与层流湍流边界层相互作用实验研究[J]. 物理学报, 63 :084703. ( Quan P C, Yi S H, Wu Y, Zhu Y Z, Chen Z.2014. Experimental investigation of interactions between laminar or turbulent boundary layer and shock wave[J]. Acta Phys. Sin., 63 : 084703 ) .
荣康, 何立明, 张建邦, 曾昊, 张强.2012. 喷口导流环结构对激波聚焦起爆的影响分析[J]. 推进技术, 33 :299–305 . ( Rong K, He L M, Zhang J B, Zeng H, Zhang Q.2012. Investigation on the effects of deflector structure on detonation initiation by shock wave focusing[J]. Journal of Propulsion Technology, 33 : 299–305 ) .
陶渊, 范晓樯. 2014. 二维定常激波反射迟滞现象研究进展// 第十六届全国激波与激波管学术会议论文集. 洛阳, 1: 75-82
陶渊, 刘卫东, 范晓樯. 2015. 进气道前体激波与唇口边界层相互作用流场结构分析// 第五届冲压发动机技术交流会. 厦门, 下册: 33-42
滕宏辉, 姜宗林, 韩肇元.2004. 环形激波绕射、反射和聚焦的数值模拟研究[J]. 力学学报, 36 :9–15 . ( Teng H H, Jiang Z L, Han Z Y.2004. Numerical investigation of diffraction, focusing and reflection of toroidal shock waves[J]. Acta Mechanica Sinica, 36 : 9–15 ) .
滕宏辉, 王春, 邓博, 姜宗林.2007. 可燃气体中激波聚焦的点火特性[J]. 力学学报, 39 :171–180 . ( Teng H H, Wang C, Deng B, Jiang Z L.2007. Ignition characteristics of the shock wave focusing in combustive gases[J]. Chinese Journal of Theoretical and Applied Mechanics, 39 : 171–180 ) .
王淦昌, 袁之尚.1996. . 惯性约束核聚变[M]. 合肥: 安徽教育出版社, : 96 -238. ( Wang G C, Yuan Z S.1996. Inertial Confinement Fusion[M]. Hefei: Anhui Education Press, : 96 -238) ) .
王国蕾, 陆夕云.2012. 激波和湍流相互作用的数值模拟[J]. 力学进展, 42 :274–281 . ( Wang G L, Lu X Y.2012. Numerical simulation of shock wave/turbulent boundary layer interactions[J]. Advances in Mechanics, 42 : 274–281 ) .
肖丰收, 李祝飞, 朱雨建, 杨基明.2016. 带凹腔钝头体第Ⅳ 类激波干扰特性研究[J]. 推进技术, 37 :1–7 . ( Xiao F S, Li Z F, Zhu Y J, Yang J M.2016. Effects of forward-facing cavity on behaviors of type Ⅳ shock interaction of blunt body flows[J]. Journal of Propulsion Technology, 37 : 1–7 ) .
徐骁, 岳连捷, 卢洪波, 肖雅彬, 张新宇.2015. 高超声速进气道快速破膜开启的流动特性[J]. 航空学报, 36 :1795–1804 . ( Xu X, Yue L J, Lu H B, Xiao Y B, Zhang X Y.2015. Flow characteristics of hypersonic inlet starting with diaphragm rupture[J]. Acta Aeronautica et Astronautica Sinica, 36 : 1795–1804 ) .
杨剑挺, 朱雨建, 詹东文, 杨基明.2016. 收缩楔腔内激波汇聚诱导点火实验[J]. 气体物理, 1 :25–30 . ( Yang J T, Zhu Y J, Zhan D W, Yang J M.2016. Yang J T, Zhu Y J, Zhan D W, Yang J M. Experiment on the shock-induced ignition in a converging wedged cavity[J]. Physics of Gases, 1 : 25–30 ) .
杨旸, 姜宗林, 胡宗民.2012. 激波反射现象的研究进展[J]. 力学进展, 42 :141–161 . ( Yang Y, Jiang Z L, Hu Z M.2012. Advances in shock wave reflection phenomena[J]. Advances in Mechanics, 42 : 141–161 ) .
易仕和, 陈植, 朱杨柱, 何霖, 武宇.2015. 高超声速流动试验技术及研究进展[J]. 航空学报, 36 :98–119 . ( Yi S H, Chen Z, Zhu Y Z, He L, Wu Y.2015. Progress of experimental techniques and studies on hypersonic/supersonic flows[J]. Acta Aeronautica et Astronautica Sinica, 36 : 98–119 ) .
岳连捷, 刘红, 徐骁, 彭辉, 张新宇. 2013. 激波风洞进气道自起动实验方法// 第九届全国实验流体力学学术会议论文集. 杭州
张志雨, 肖丰收, 李祝飞, 朱雨建, 杨基明. 2016. 钝化V 形前缘激波干扰特性研究//第17 届全国激波与激波管学术会议. 成都
曾昊, 何立明, 章雄伟, 李海鹏, 陈鑫.2010. 环形射流喷口位置对激波聚焦起爆的影响分析[J]. 航空动力学报, 25 :1964–1970 . ( Zeng H, He L M, Zhang X W, Li H P, Chen X.2010. Investigation on the influence of jet pressure on detonation initiation via imploding annular shock waves[J]. Journal of Aerospace Power, 25 : 1964–1970 ) .
曾昊, 陈鑫, 何立明, 吴春华.2013. 凹面腔内二维激波会聚特性研究[J]. 空气动力学学报, 31 :316–320 . ( Zeng H, Chen X, He L M, Wu C H.2013. Investigation of two-dimensional shock wave focusing[J]. Acta Aerodynamica Sinica, 31 : 316–320 ) .
中国力学学会激波与激波管专业委员会. 2014//第16 届全国激波与激波管学术会议论文集. 洛阳, 1: 1-726
朱建士, 胡晓棉, 王裴, 陈军, 许爱国.2010. 爆炸与冲击动力学若干问题研究进展[J]. 力学进展, 40 :400–423 . ( Zhu J S, Hu X M, Wang P, Chen J, Xu A G.2010. A review on research progress in explosion mechanics and impact dynamics[J]. Advances in Mechanics, 40 : 400–423 ) .
Abd-EL Fattah A M, Henderson L F.1978a. Shock waves at a fast-slow gas interface[J]. Journal of Fluid Mechanics, 86 : 15–32 .
Abd-EL Fattah A M, Henderson L F.1978b. Shock waves at a slow-fast gas interface[J]. Journal of Fluid Mechanics, 89 : 79–95 .
Adamson T C, Messiter A F.1980. Analysis of two-dimensional interactions between shock waves and boundary layers[J]. Annual Review of Fluid Mechanics, 12 : 103–138 .
Anderson J D.2006. Hypersonic and High-Temperature Gas Dynamics[J]. Second Edition, AIAA Education, 449 : .
Andreopoulos Y, Ag ui, J H, Briassulis G.2000. Shock wave-turbulence interactions[J]. Annual Review of Fluid Mechanics, 32 : 309–345 .
Arnett W D, Bahcall J N, Kirshner R P, Woosley S E.1989. Supernova 1987A[J]. Annual Review of Astronomy and Astrophysics, 27 : 629–700 .
Babinsky H, Takayama K.1998. The influence of entrance geometry of circular reflectors on shock wave focusing[J]. Computers and Fluids, 27 : 611–618 .
Babinsky H, Harvey J K.2011. Shock Wave-Boundary-Layer Interactions[M]. Cambridge: Cambridge Univer-sity Press, ) .
Baltrusaitis R M, Gittings M L, Weaver R P, Benjamin R F, Budzinski J M.1996. Simulation of shock-generated instabilities[J]. Physics of Fluids, 8 : 2471–2483 .
Bartenev A M, Khomik S V, Gelfand B E, Gronig H, Olivier H.2000. Effect of reflection type on detonation initiation at shock-wave focusing[J]. Shock Waves, 10 : 205–215 .
Belford R L, Strehlow R A.1969. Shock tube technique in chemical kinetics[J]. Annu. Rev. Phys. Chem., 20 : 247–272 .
Ben-Dor G, Igra O, Elperin T.2001. Handbook of Shock Waves[M]. New York: Academic Press, ) .
Ben-Dor G.2007. [J]. Shock Wave Reflection Phenomena. (2nd edition), : .
Berets D J, Greene E F, Kistiakows G B.1950. Gaseous detonations.Ⅱ. Initiation by shock waves.[J]. Journal of the American Chemical Society, 72 : 1086–1091 .
Bernard Finn S.1964. Laplace and the speed of sound[J]. ISIS Journal, 55 : 7–19 .
Biamino L, Jourdan G, Mariani C, Houas L, Vandenboomgaerde M, Souffland D.2015. On the possibility of studying the converging Richtmyer-Meshkov instability in a conventional shock tube[J]. Experiments in Fluids, 56 : 26 .
Bilbal L E, Gratton J.1996. Spherical and cylindrical convergent shocks[J]. Il Nuovo Cimento, 18 : 1041–1060 .
Boldyrev S M, Borovoy V Y, Chinilov A Y, Gusev V N, Struminskaya I V, Yakovleva L V, Delery J, Chanetz B.2001. A thorough experimental investigation of shock/shock interference in high Mach number flows[J]. Aerospace Science and Technology, 5 : 167–178 .
Bond C, Hill D J, Meiron D I, Dimotakis P E.2009. Shock focusing in a planar convergent geometry:Experiment and simulation[J]. Journal of Fluid Mechanics, 641 : 297–333 .
Borisov A A, Zamanskii V M, Kosenkov V V, Lisyanskii V V, Skachkov G I, Troshin K Y, Gelfand B E.1990. Ignition of gaseous combustible mixtures in focused shock waves[J]. AIP Conference Proceedings, 208 : 696–701 .
Brouillette M.2002. The Richtmyer-Meshkov instability[J]. Annual Review of Fluid Mechanics, 34 : 445–468 .
Brouillette M, Sturtevant B.1989. Growth induced by multiple shock waves normally incident on plane gaseous interfaces[J]. Physica D, 37 : 248–263 .
Brouillette M, Sturtevant B.1993. Experiments on the Richtmyer-Meshkov instability: Small-scale pertur-bations on a plane interface[J]. Physics of Fluids A, 5 : 916–930 .
Brown C J, Thomas G O.1999. Experimental studies of shock-induced ignition and transition to detonation in ethylene and propane mixtures[J]. Combustion and Flame, 117 : 861–870 .
Burcat A, Scheller K, Lifshitz A.1971. Shock tube investigation of comparative ignition delay times for C1-C5 alkanes[J]. Combustion and Flame, 16 : 29–33 .
Burcat A, Crossley R W, Scheller K, Skinner G B.1972. Shock tube investigation of ignition in ethane-oxygen-argon mixtures[J]. Combustion and Flame, 18 : 115–123 .
Chapman P R, Jacobs J W.2006. Experiments on the three-dimensional incompressible Richtmyer-Meshkov instability[J]. Physics of Fluids, 18 : .
Charwat A F and Redekeopp L G.1967. Supersonic Interference along the Corner of Intersecting Wedges[J]. AIAA Journal, 5 : 480–488 .
Chaumeix N, Imbert B, Catoire L, Paillard C E.2014. The onset of detonation behind shock waves of moderate intensity in gas phase[J]. Combustion Science and Technology, 186 : 4–5 .
Chester W.1954. The quasi-cylindrical shock tube[J]. Phil. Mag., 45 : 1293–1301 .
Chisnell R F.1957. The motion of a shock wave in a channel, with applications to cylindrical and spherical shock waves[J]. Journal of Fluid Mechanics, 2 : 286–298 .
Chu Y, Lu X.2012. Characteristics of unsteady type Ⅳ shock/shock interaction[J]. Shock Waves, 22 : 225–235 .
Clemens N T, Narayanaswamy V.2014. Low-frequency unsteadiness of shock wave/turbulent boundary layer interactions[J]. Annual Review of Fluid Mechanics, 46 : 469–492 .
Collins B D, Jacobs J W.2002. PLIF flow visualization and measurements of the Richtmyer-Meshkov instability of an air/SF6 interface[J]. Journal of Fluid Mechanics, 464 : 113–136 .
Cooke D F, Williams A.1975. Shock tube studies of methane and ethane oxidation[J]. Combustion and Flame, 24 : 245–256 .
Courant R, Friedrichs K O.1948. . Supersonic Flow and shock waves[M]. New York: Interscience Publishers, Pure and Applied Mathematics (Academic Press), ) .
Debiève J F, Dupont P.2009. Dependence between the shock and the separation bubble in a shock wave boundary layer interaction[J]. Shock Waves, 19 : 499–506 .
Délery J, Dussauge J P.2009. Some physical aspects of shock wave/boundary layer interactions[J]. Shock Waves, 19 : 453–468 .
Deville M, Le T H, Sagaut P.2008. Special issue of the "Turbulence and Interaction" conference[J]. Flow Turbulence Combust, 80 : 1–2 .
Dimotakis P E.2005. Turbulent mixing[J]. Annual Review of Fluid Mechanics, 37 : 329–356 .
Dimotakis P E, Samtaney R.2006. Planar shock cylindrical focusing by a perfect-gas lens[J]. Physics of Fluids, 18 : 031705 .
Dolling D S.2001. Fifty years of shock-wave/boundary-layer interaction research: What next?[J]. AIAA Journal, 39 : 1517–1531 .
Dussauge J P, Piponniau S.2008. Shock/boundary-layer interactions: Possible sources of unsteadiness[J]. Journal of Fluids and Structures, 24 : 1166–1175 .
Dyke M, Guttmann A J.1982. The converging shock wave from a spherical or cylindrical piston[J]. Journal of Fluid Mechanics, 120 : 451–462 .
Earmshaw S.1860. On the mathematical theory of sound (communicated in Nov[J]. 1858). Phil. Trans. Roy. Soc. London, 150 : 133–148 .
Edney B.1968. Anomalous heat transfer and pressure distributions on blunt bodies at hypersonic speeds in the presence of an impinging shock[J]. Technical Report, 115 : .
Edwards J R.2008. Numerical simulations of shock/boundary layer interactions using time-dependent modeling techniques: A survey of recent results[J]. Progress in Aerospace Sciences, 44 : 447–465 .
Eliasson V, Apazidis N, Tillmark N, Lesser M B.2006. Focusing of strong shocks in an annular shock tube[J]. Shock Waves, 15 : 205–217 .
Erskin D J, Nellis W J.1991. Shock-induced martensitic phase transformation of oriented graphite to diamond[J]. Nature, 349 : 317–319 .
Fraley G.1986. Rayleigh-Taylor stability for a normal shock wave-density discontinuity interaction[J]. Physics of Fluids, 29 : 376–386 .
Fujii N, Koshi, M Ando H, Asaba T.1979. Evaluation of boundary layer effects in shock-tube studies of chemical kinetics[J]. Int. J. Chem. Kinet., 11 : 285–304 .
Fureby C.2008. Towards the use of large eddy simulation in engineering[J]. Progress in Aerospace Sciences, 44 : 381–396 .
Gaitonde D, Shang J S.1995. On the structure of an unsteady type Ⅳ interaction at Mach 8[J]. Computers and Fluids, 24 : 469–485 .
Gaitonde D V.2015. Progress in shock wave/boundary layer interactions[J]. Progress in Aerospace Sciences, 72 : 80–99 .
Gallis M A, Koehler T P, Torczynski J R, Plimpton S J.2015. Direct simulation Monte Carlo investigation of the Richtmyer-Meshkov instability[J]. Physics of Fluids, 27 : 084105 .
Ganapathisubramani B, Clemens N T, Dolling D S.2007. Effects of upstream boundary layer on the unsteadiness of shock-induced separation[J]. Journal of Fluid Mechanics, 585 : 369–394 .
Gao B, Wu Z N.2010. A study of the flow structure for Mach reflection in steady supersonic flow[J]. Journal of Fluid Mechanics, 656 : 29–50 .
Gardner J H, Book D L, Bernstain I B.1982. Stability of imploding shocks in the CCW approximation[J]. Journal of Fluid Mechanics, 114 : 41–58 .
Garrison T J, Settles G S, Narayanswami N, Knight D D.1996. Measurements of the triple shock wave turbulent boundary-layer interaction[J]. AIAA Journal, 34 : 57–64 .
Garrison T J, Settles G S, Narayanswami N, Knight D D.1993. Structure of crossing-shock-wave turbulent-boundary-layer interactions[J]. AIAA Journal, 31 : 2204–2211 .
Garrison T J, Settles G S, Narayanswami N, Knight D D.1994. Laser interferometer skin-friction measure-ments of crossing-shock-wave turbulent-boundary-layer interaction[J]. AIAA Journal, 32 : 1234–1241 .
Gaydon A G, Hurle I R.1963. The shock tube in high temperature chemical physics[J]. Journal of Chemical Education, 41 : 114 .
Gelfand B E, Khomik S V, Bartenev A M, Medvedev S P, Gronig H, Olivier H.2000. Detonation and deflagration initiation at the focusing of shock waves in combustible gaseous mixture[J]. Shock Waves, 10 : 197–204 .
Glass Ⅱ.1975. . Shock Wave and Man[M]. Toronto: Toronto University Press, ) .
Goonko Y P, Kharitonov A M, Latypov A F, Mazhul I I, Rostand P, Yaroslavtsev M I.2003. Structure of flow over a hypersonic inlet with side compression wedges[J]. AIAA Journal, 41 : 436–447 .
Gray J A, Westbrook C K.1994. High-temperature ignition of propane with MTBE as an additive: Shock tube experiments and modeling[J]. J. Chem. Kinet., 26 : 757–770 .
Greene E F, Toennies J P.1964. . Chemical Reactions in Shock Waves[M]. New York: Academic Press, ) .
Guderley G.1942. Starke kugelige und zylindrische VerdichtungsstÄosse in der NÄahe des Kugelmittelpunk bzw. der Zylinderachse[J]. Luftfahrtforschung, 19 : 302–313 .
Haas J F, Sturtevant B.1987. Interaction of weak shock waves with cylindrical and spherical gas inhomo-geneities[J]. Journal of Fluid Mechanics, 181 : 41–76 .
Hafner P.1988. Strong convergent shock waves near the center of convergence[J]. Siam J. Appl. Math., 48 : 1244–1261 .
Han Z Y, Yin X Z.1992. Shock Dynamics[M]. Beijing: Science Press, ) .
Henderson L F.1989. On the refraction of shock waves[J]. Journal of Fluid Mechanics, 198 : 365–386 .
Holmes R L, Grove J W, Sharp D H.1995. Numerical investigation of Richtmyer-Meshkov instability using front tracking[J]. Journal of Fluid Mechanics, 301 : 51–64 .
Hosseini S H R, Takayama K.2010. Experimental study of toroidal shock wave focusing in a compact vertical annular diaphragmless shock tube[J]. Shock Waves, 20 : 1–7 .
Hosseini S H R, Takayama K.2005. Experimental study of Richtmyer-Meshkov instability induced by cylindrical shock waves[J]. Physics of Fluids, 17 : 084101 .
Humble R A, Scarano F, van Oudheusden B W.2009. Unsteady aspects of an incident shock wave/turbulent boundary layer interaction[J]. Journal of Fluid Mechanics, 635 : 47–74 .
Izumi K, Aso S, Nishida M.1994. Experimental and computational studies focusing process of shock waves reflected from parabolic reflectors[J]. Shock Waves, 4 : 213–222 .
Jacobs J W.1992. Shock-induced mixing of a light-gas cylinder[J]. Journal of Fluid Mechanics, 234 : 629–649 .
Jacobs J W, Krivets V V.2005. Experiments on the late-time development of single-mode Richtmyer-Meshkov instability[J]. Physics of Fluids, 17 : 034105 .
Jackson S I, Shepherd J E.2008. Detonation initiation in a tube via imploding toroidal shock waves[J]. AIAA Journal, 46 : 2357–2367 .
Jiang Z L, Takayama K.1998. Reflection and focusing of toroidal shock waves from coaxial annular shock tubes[J]. Computers and Fluids, 27 : 553–562 .
Jiao X, Chang, J, Wang Z, Yu D.2015. Mechanism study on local unstart of hypersonic inlet at high Mach number[J]. AIAA Journal, 53 : 3102–3112 .
Jones M A, Jacobs J W.1997. A membraneless experiment for the study of Richtmyer-Meshkov instability of a shock-accelerated gas interface[J]. Physics of Fluids, 9 : 3078–3085 .
Kawamura R, Saito H.1956. Reflection of shock waves-pseudo-stationary case[J]. Journal of the Physical Society of Japan, 11 : 584–592 .
Khomik S V, Medvedev S P, Polenov A N, Gelfand B E.2007. Conditions of detonation initiation by focusing shock waves in a combustible gas mixture[J]. Combustion, Explosion, and Shock Waves, 43 : 697–702 .
Kisbige H, Tesbima K, Nishida M.1992. Focusing of shock waves reflected from an axisymmetrically parabolic wall[J]. Shock Waves, 1 : 341–345 .
Kjellander M, Tillmark N, Apazidis N.2010. Shock dynamics of strong imploding cylindrical and spherical shock waves with real gas effects[J]. Physics of Fluids, 22 : 116102 .
Knight D, Yan H, Panaras A G, Zheltovodov A.2003. Advances in CFD prediction of shock wave turbulent boundary layer interactions[J]. Progress in Aerospace Sciences, 39 : 121–184 .
Larsson J, Lele SK.2009. Direct numerical simulation of canonical shock/turbulence interaction[J]. Physics of Fluids, 21 : 126101 .
Latini M, Schilling O, Don W S.2007. High-resolution simulations and modeling of reshocked single-mode RMI comparison to experimental data and to amplitude growth model predictions[J]. Physics of Fluids, 19 : 024104 .
Layes G, Jourdan G, Houas L.2003. Distortion of a spherical gaseous interface accelerated by a plane shock wave[J]. Physics Review Letters, 91 : 174502 .
Layes G, Jourdan G, Houas L.2009. Experimental study on a plane shock wave accelerating a gas bubble[J]. Physics of Fluids, 21 : 074102 .
Lee J H S.2008. . The Detonation Phenomenon[M]. New York: Cambridge University Press, ) .
Li X L, Zhang Q.1997. A comparative numerical study of the Richtmyer-Meshkov instability with nonlinear analysis in two and three dimensions[J]. Physics of Fluids, 9 : 3069–3077 .
Li Z, Gao W, Jiang H, Yang J.2013. Unsteady behaviors of a hypersonic inlet caused by throttling in shock tunnel[J]. AIAA Journal, 51 : 2485–2492 .
Liepmann H W.1946. The interaction between boundary layer and shock waves in transonic flow[J]. Journal of the Aeronautical Sciences, 13 : 623–637 .
Likhachev O A, Tsiklashvili V.2014. Integral constraints in the study of Richtmyer-Meshkov turbulent mixing[J]. Physics of Fluids, 26 : 102101 .
Lindl J, Landen O, Edwards J, Moses E, Team N.2014. Review of the national ignition campaign 2009-2012[J]. Physics of Plasmas, 21 : 020501 .
Liverts M, Apazidis N.2016. Limiting temperatures of spherical shock wave implosion[J]. Physical Review Letters, 116 : 014501 .
Lombardini M, Pullin D I, Meiron D I.2014a. Turbulent mixing driven by spherical implosions.Part 1. Flow description and mixing-layer growth[J]. Journal of Fluid Mechanics, 748 : 85–112 .
Lombardini M, Pullin D I, Meiron D I.2014b. Turbulent mixing driven by spherical implosions.Part 2. Turbulence statistics[J]. Journal of Fluid Mechanics, 748 : 113–142 .
Long C C, Krivets V V, Greenough J A, Jacobs J W.2009. Shock tube experiments and numerical simulation of the single-mode, three-dimensional Richtmyer-Meshkov instability[J]. Physics of Fluids, 21 : 114104 .
Lu F, Marren D.2002. Advanced hypersonic facilities//Zarchan P, ed[J]. Progress in astronautics and aero-nautics. AIAA Inc, 198 : 1–616 .
Luo X, Ding J, Wang M, Zhai Z, Si T.2015. A semi-annular shock tube for studying cylindrically converging Richtmyer-Meshkov instability[J]. Physics of Fluids, 27 : 091702 .
Luo X, Wang X, Si T.2013. The Richtmyer-Meshkov instability of a three-dimensional air/SF6 interface with a minimum-surface feature[J]. Journal of Fluid Mechanics, 722 : R2 .
Luo X, Wang M, Si T, Zhai Z.2015. On the interaction of a planar shock with an SF6 polygon[J]. Journal of Fluid Mechanics, 773 : 366–394 .
Ma Y B, Zhong X L.2003. Receptivity of a supersonic boundary layer over a flat plate[J]. Part 1. Wave structures and interactions. Journal of Fluid Mechanics, 488 : 31–78 .
Mahapatra D, Jagadeesh G.2009. Studies on unsteady shock interactions near a generic scramjet inlet[J]. AIAA Journal, 47 : 2223–2231 .
Malamud G, Leinov E, Sadot O, Elbaz Y, Ben-Dor G, Shvarts D.2014. Reshocked Richtmyer-Meshkov instability: Numerical study and modeling of random multi-mode experiments[J]. Physics of Fluids, 26 : 084107 .
McFarland J A, Greenough J A, Ranjan D.2013. Investigation of the initial perturbation amplitude for the inclined interface Richtmyer-Meshkov instability[J]. Physica Scripta, 155 : 014014 .
McFarland J, Reilly D, Creel S, McDonald C, Finn T, Ranjan D.2014. Experimental investigation of the inclined interface Richtmyer-Meshkov instability before and after reshock[J]. Experiments in Fluids, 55 : 1640 .
Meshkov E E.1969. Instability of the interface of two gases accelerated by a shock wave[J]. Fluid Dynamics, 4 : 101–104 .
Meyer K A, Blewett P J.1972. Numerical investigation of the stability of a shock accelerated interface between two fluids[J]. Physics of Fluids, 15 : 753–759 .
Myers B F, Bartle E R.1969. Reaction and ignition delay times in the oxidation of propane[J]. AIAA Journal, 7 : 1862–1869 .
Mikaelian K O.2015. Testing an analytic model for Richtmyer-Meshkov turbulent mixing widths[J]. Shock Waves, 25 : 35–45 .
Mooradian A J, Gordon W E.1951. Gaseous detonation.Ⅰ. Initiation of detonation[J]. The Journal of Chemical Physics, 19 : 1166–1172 .
Ogawa H, Grainger A L, Boyce R R.2010. Inlet starting of high-contraction axisymmetric scramjets[J]. Journal of Propulsion and Power, 26 : 1247–1258 .
Olson B J, Greenough J.2014. Large eddy simulation requirements for the Richtmyer-Meshkov instability[J]. Physics of Fluids, 26 : 044103 .
Orlicz G C, Balakumar B J, Tomkins C D, Prestridge K P.2009. A Mach number study of the Richtmyer-Meshkov instability in a varicose, heavy-gas curtain[J]. Physics of Fluids, 21 : 064102 .
Panaras A G.1996. Review of the physics of swept-shock boundary layer interactions[J]. Progress in Aerospace Sciences, 32 : 173–244 .
Perkins L J, Betti R, LaFortune K N, Williams W H.2009. Shock ignition: A new approach to high gain inertial confinement fusion on the national ignition facility[J]. Physical Review Letters, 103 : 045004 .
Perry R W, Kantrowitz A.1951. The production and stability of converging shock waves[J]. J. Appl. Phys., 22 : 878–886 .
Petersen E L, Hanson R K.2001. Non-ideal effects behind reflected shock waves in a high pressure shock tube[J]. Shock Waves, 10 : 405–420 .
Piponniau S J, Dussauge P, Debieve J F, Dupont P.2009. A simple model for low-frequency unsteadiness in shock-induced separation[J]. Journal of Fluid Mechanics, 629 : 87–108 .
Pirozzoli S, Grasso F.2006. Direct numerical simulation of impinging shock wave/turbulent boundary layer interaction at M = 2:25[J]. Physics of Fluids, 18 : 065113 .
Ponchaut N F, Hornung H G, Pullin D I, Mouton C A.2006. On imploding cylindrical and spherical shock waves in a perfect gas[J]. Journal of Fluid Mechanics, 560 : 103–122 .
Radha C, Sharma V D.1993. Imploding cylindrical shock in a perfectly conducting and radiating gas[J]. Physics of Fluids B, 5 : 4287 .
Ranjan D, Anderson M H, Oakley J, Bonazza R.2005. Experimental investigation of a strongly shocked gas bubble[J]. Physics Review Letters, 94 : 184507 .
Ranjan D, Niederhaus J H J, Motl B, Anderson M H, Oakley J, Bonazza R.2007. Experimental investigation of primary and secondary features in high-mach-number shock-bubble interaction[J]. Physics Review Letters, 98 : 024502 .
Ranjan D, Oakley J, Bonazza R.2011. Shock-bubble interactions[J]. Annual Review of Fluid Mechanics, 43 : 117–140 .
Richtmyer R D.1960. Taylor instability in shock acceleration of compressible fluids[J]. Communication on Pure and Applied Mathematics, 13 : 297–319 .
Ringuette M J, Wu M, Mart-n M P.2008. Coherent structures in direct numerical simulation of turbulent boundary layers at Mach 3[J]. Journal of Fluid Mechanics, 594 : 59–69 .
Roy C J, Blottner F G.2006. Review and assessment of turbulence models for hypersonic flows[J]. Prog. Aerospace Sci., 42 : 469–530 .
Sadot O, Erez L, Alon U, Oron D, Levin L A, Erez G, Ben-Dor G, Shvarts D.1998. Study of nonlinear evo-lution of single-mode and two-bubble interaction under Richtmyer-Meshkov instability[J]. Physical Review Letters, 80 : 1654–1657 .
Saillard Y, Barbry H, Mournier C.1985. Transformation of a plane uniform or spherical shock by wall shaping//Shock waves and shock tubes, Proc. 15th Intern. Symp[J]. Stanford, CA: Stanford University Press, : 147–154 .
Samtaney R, Meiron D I.1997. Hypervelocity Richtmyer-Meshkov instability[J]. Physics of Fluids, 9 : 1783–1803 .
Schwendeman D W, Whitham G B.1987. On converging shock waves[J]. Proc. R. Soc. Lond. A, 413 : 297–311 .
Setchell R E, Storm E, Sturtevant B.1972. An investigation of shock strengthening in a conical converging channel[J]. Journal of Fluid Mechanics, 56 : 505–522 .
Settles G S, Dodson L J.1994. Supersonic and hypersonic shock boundary-layer interaction database[J]. AIAA Journal, 32 : 1377–1383 .
Sharp D H.1984. An overview of Rayleigh-Taylor instability[J]. Physical D, 12 : 3–18 .
Si T, Long T, Zhai Z, Luo X.2015. Experimental investigation of cylindrical converging shock waves interacting with a polygonal heavy gas cylinder[J]. Journal of Fluid Mechanics, 784 : 225–251 .
Si T, Zhai Z, Luo X.2014. Experimental study of Richtmyer-Meshkov instability in a cylindrical converging shock tube[J]. Laser and Particle Beams, 32 : 343–351 .
Si T, Zhai Z G, Yang J M, Luo X S.2012. Experimental investigation of reshocked spherical gas interfaces[J]. Physics of Fluids, 24 : 054101 .
Skews B, Gray B, Paton R.2015. Experimental production of two-dimensional shock waves of arbitrary profile[J]. Shock Waves, 25 : 1–10 .
Skews B W, Menon N, Bredin M.2002. An experiment on imploding conical shock waves[J]. Shock Waves, 11 : 323–326 .
Skews B W, Kleine H.2007. Flow features resulting from shock wave impact in a cylindrical cavity[J]. J. Fluid Mech., 580 : 481–493 .
Strehlow R A, Cohen A.1962. Initiation of detonation[J]. Physics of Fluids, 5 : 97–101 .
Strehlow R A, Dyner H B.1963. One-dimensional detonation initiation[J]. AIAA Journal, 1 : 591–595 .
Takayama K, Onodera O, Hoshizawa Y.1984. Experiments on the stability of converging cylindrical shock waves[J]. Theor. Appl. Mech., 32 : 305–329 .
Takayama K, Kleine H, Gronig H.1987. An experimental investigation of the stability of converging cylin-drical shock waves in air[J]. Experiments in Fluids, 5 : 315–322 .
Tan H J, Li L G, Wen Y F, Zhang Q F.2011. Experimental investigation of the unstart process of a generic hypersonic inlet[J]. AIAA Journal, 49 : 279–288 .
Tao Y, Fan X, Zhao Y.2014. Viscous effects of shock reflection hysteresis in steady supersonic flows[J]. Journal of Fluid Mechanics, 759 : 134–148 .
Tomkins C D, Kumar S, Orlicz G C, Prestridge K P.2008. An experimental investigation of mixing mechanisms in shock-accelerated flow[J]. Journal of Fluid Mechanics, 611 : 131–150 .
Tomkins C D, Prestridge K P, Rightley P M, Marr-Lyon M, Vorobieff P, Benjamin R F.2003. A quantitative study of the interaction of two Richtmyer-Meshkov-unstable gas cylinders[J]. Physics of Fluids, 15 : 986–1004 .
Tomkins C D, Prestridge K P, Rightley P M, Vorobieff P, Benjamin R F.2002. Flow morphologies of two shock accelerated unstable gas cylinders[J]. Journal of Visualization, 5 : 273–283 .
Tsang W, Lifshitz A.1990. Shock tube techniques in chemical kietics[J]. Annu. Rev. Phys. Chem., 41 : 559–599 .
Vandenboomgaerde M, Gauthier S, Mugler C.2002. Nonlinear regime of a multimode Richtmyer-Meshkov instability: A simplified perturbation approach[J]. Physics of Fluids, 14 : 1111–1122 .
Vandenboomgaerde M, Mugler C, Gauthier S.1998. Impulsive model for the Richtmyer-Meshkov instability[J]. Physical Review E, 58 : 1874–1882 .
Velikovich A L.1996. Analytic theory of Richtmyer-Meshkov instability for the case of reflected rarefaction wave[J]. Physics of Fluids, 8 : 1666–1679 .
Velikovicha A L, Dimonte G.1996. Nonlinear perturbation theory of the incompressible Richtmyer-Meshkov instability[J]. Physical Review Letters, 76 : 3112–3115 .
Wang M, Si T, Luo X.2013. Generation of polygonal gas interfaces by soap film for Richtmyer-Meshkov instability study[J]. Experiments in Fluids, 54 : 1427 .
Wang T, Liu J H, Bai J S, Jiang Y, Li P, Liu K.2012. Experimental and numerical investigation of inclined air/SF6 interface instability under shock wave[J]. Applied Mathematic and Mechanics, 33 : 37–50 .
Wang W, Guo R.2013. Numerical study of unsteady starting characteristics of a hypersonic inlet[J]. Chinese Journal of Aeronautics, 26 : 563–571 .
Wang Z, Zhao Y, Zhao Y, Fan X.2015. Prediction of massive separation of unstarted inlet via free-interaction theory[J]. AIAA Journal, 53 : 1108–1112 .
Watanabe M, Takayama K.1991. Stability of converging cylindrical shock waves[J]. Shock Waves, 1 : 149–160 .
Weirs V G, Dupont T, Plewa T.2008. Three-dimensional effects in shock-cylinder interactions[J]. Physics of Fluids, 20 : 044102 .
West J E, Korkegi R H.1972. Supersonic interaction in the corner of intersecting wedges at high Reynolds numbers[J]. AIAA Journal, 10 : 652–656 .
Whitham G B.1957. A new approach to problems of shock dynamics[J]. Part Ⅰ. Two-dimensional problems. Journal of Fluid Mechanics, 2 : 145–171 .
Whitham G B.1959. A new approach to problems of shock dynamics[J]. Part 2. Three-dimensional problems. Journal of Fluid Mechanics, 5 : 369–386 .
Wouchuk J G, Nishihara K.1996. Linear perturbation growth at a shocked interface[J]. Physics of Plasmas, 3 : 3761–3776 .
Wieting A R, Holden M S.1989. Experimental shock-wave interference heating on a cylinder at Mach 6 and 8[J]. AIAA Journal, 27 : 1557–1565 .
Wu MW, Martin M P.2008. Analysis of shock motion in shockwave and turbulent boundary layer interaction using direct numerical simulation data[J]. Journal of Fluid Mechanics, 594 : 71–83 .
Yamashita H, Kasahara J, Sugiyama Y, Matsuo A.2012. Visualization study of ignition modes behind bifurcated-reflected shock waves[J]. Combustion and Flame, 159 : 2954–2966 .
Yang J, Kubota T, Zukoski E E.1993. Applications of shock-induced mixing to supersonic combustion[J]. AIAA Journal, 35 : 854–862 .
Yang Y, Zhang Q, Sharp D H.1994. Small amplitude theory of Richtmyer-Meshkov instability[J]. Physics of Fluids, 6 : 1856–1873 .
Yao Y, Li S G, Wu Z N.2013. Shock reflection in the presence of an upstream expansion wave and a downstream shock wave[J]. Journal of Fluid Mechanics, 735 : 61–90 .
Zabusky N J.1999. Vortex paradigm for accelerated inhomogeneous flows: Visiometrics for the Rayleigh-Taylor and Richtmyer-Meshkov environments[J]. Annual Review of Fluid Mechanics, 31 : 495–536 .
Zhai Z G, Liu C L, Qin F H, Yang J M, Luo X S.2010. Generation of cylindrical converging shock waves based on shock dynamics theory[J]. Physics of Fluids, 22 : 041701 .
Zhai Z G, Si T, Luo X S, Yang J M.2011. On the evolution of spherical gas interfaces accelerated by a planar shock wave[J]. Physics of Fluids, 23 : 084104 .
Zhai Z G, Si T, Luo X S, Yang J M, Liu C L, Tan D W, Zou L Y.2012. Parametric study on the cylindrical converging shock waves generated based on shock dynamics theory[J]. Physics of Fluids, 24 : 026101 .
Zhai Z, Wang M, Si T, Luo X.2014. On the interaction of a planar shock with a light polygonal interface[J]. Journal of Fluid Mechanics, 757 : 800–816 .
Zhang Q, Graham M J.1998. A numerical study of Richtmyer-Meshkov instability driven by cylindrical shocks[J]. Physics of Fluids, 10 : 974–992 .
Zhang Q, Sohn S I.1996. An analytical nonlinear theory of Richtmyer-Meshkov instability[J]. Physical Letter A, 212 : 149–155 .
Zhang Q, Sohn S I.1997. Nonlinear theory of unstable fluid mixing driven by shock wave[J]. Physics of Fluids, 5 : 1106–1124 .
Zhong X.1994. Application of essentially nonoscillatory schemes to unsteady hypersonic shock-shock inter-ference heating problems[J]. AIAA Journal, 32 : 1606–1616 .
Zou L Y, Liu C L, Tan D W, Huang W B, Luo X S.2010. On interaction of shock wave with elliptic gas cylinder[J]. Journal of Visaulization, 13 : 347–353 .
主办单位: 中国科学院力学研究所、中国力学学会
《力学进展》从2014年起正式变更为年刊，重点刊登力学领域的高水平综述性文章。

文章信息

杨基明, 李祝飞, 朱雨建, 翟志刚, 罗喜胜, 陆夕云
YANG Jimingy, LI Zhufei, ZHU Yujian, ZHAI Zhigang, LUO Xisheng, LU Xiyun
激波的传播与干扰
Shock wave propagation and interactions
力学进展, 2016, 46:201613
Advances in Mechanics, 2016, 46:201613
DOI: 10.6052/1000-0992-16-009

文章历史

收稿日期: 2016-02-26
录用日期: 2016-05-05
在线出版日期: 2016-05-09

引用本文

杨基明, 李祝飞, 朱雨建, 翟志刚, 罗喜胜, 陆夕云 . 激波的传播与干扰[J]. 力学进展, 2016, 46:201613
YANG Jimingy, LI Zhufei, ZHU Yujian, ZHAI Zhigang, LUO Xisheng, LU Xiyun Shock wave propagation and interactions[J]. Advances in Mechanics, 2016, 46:201613.

工作空间