木质复合材料制造过程中，胶黏剂以流动状态与木材单元接触、渗透、固化后，便形成了彼此结合的界面(连海兰等，2012)，该界面在木材与树脂复合构件中起桥梁作用，是决定复合构件性能的关键因素(Jesson et al., 2012)。研究表明，在两相材料之间形成结构完整、性能稳定的胶合界面，有助于传递和分散复合材料的内部应力(Lee et al., 2007)，然而，界面往往也是复合材料中的弱相区，在外载或外部环境作用下容易发生失效破坏，因此，深化对胶合界面区域材料力学行为的认识，将有助于理解木材胶合界面胶接力形成机制。

纳米压痕技术是一种在微纳尺度下可以有效表征材料力学性能的测试手段。Wimmer等(1997)首次采用该技术研究木材管胞细胞壁力学行为，引起了木材科学界广泛关注，目前纳米压痕技术已被大量用于评价木质材料、高分子聚合物等材料在微纳尺度下的力学性能(江泽慧等，2004；Yu et al., 2007；2010；Wang et al., 2013；林兰英等，2015)。纳米压痕技术的快速发展，也给木材界面理论研究带来了新的发展机遇。Konnerth等(2006)率先将纳米压痕技术用于木材胶合界面力学性能研究中，Qin等(2018)探讨了胶合界面区域的弹性模量和硬度分布情况。木材是一种天然有机高分子聚合物材料，无论在长期静态载荷还是短期动态载荷作用下均会表现出黏弹性特征，如蠕变、力学损耗等(詹天翼等，2017)，而木质复合材料在许多实际应用中常常受长期静载或交变应力作用，因此，研究木材胶合界面的黏弹性行为十分必要。目前，所开展的准静态力学研究并不能完整揭示实际应用中复合材料界面的力学响应行为，普通的动态力学分析(DMA)可用于研究材料的宏观黏弹性(Salmén et al., 2016)，但不能检测材料在纳米尺度下的性能。鉴于此，本研究采用纳米压痕技术中的静态和动态加载模式(Nano-DMA)，系统研究木材胶合界面区域各相材料的静态和动态力学行为，探讨树脂渗透对木材管胞壁层力学性能的影响，以期为木质复合材料制造工艺优化和增强改性提供理论依据。

1 材料与方法 1.1 试验材料

以火炬松(Pinus taeda)为试验材料，于树高1.3 m处截取一个25 mm厚圆盘，在圆盘上沿第32个年轮附近径向截取尺寸5 mm×5 mm×10 mm(弦向×径向×纵向)的木块若干，并将其含水率调至8%左右。试验所用胶黏剂有酚醛树脂(PF)和脲醛树脂(UF)2种，固含量分别为45%和60%，pH分别为10.5和7.5，黏度分别为150和300 mPa·s左右(25 ℃)。

1.2 仪器与设备

试验所用仪器和设备包括微型台虎钳台钳Primus100(Proxxon Inc., Germany)、滑走切片机、Leica MZ6超薄切片机(Leica Inc., Germany)、钻石刀(Micro Star Tech., USA)、纳米压痕仪Nanoindentation(Hysitron, Inc., Minneapolis，MN)、纳米动态力学测试(nano-dynamic mechanical analysis)配件等。纳米压痕仪载荷分辨率为1 nN、位移分辨率为0.01 nm，Berkovich金刚石探针曲率半径低于100 nm。

1.3 纳米压痕静载测试 1.3.1 样品制备

1) 胶合试件压制  在一块木材的径切面和另一块木材的弦切面分别按75 g·m^-2涂胶量涂布胶黏剂，陈化10 min后，将2块木材贴合在一起，采用微型台虎钳台钳对胶合试件加压至0.8 MPa；将木材-PF和木材-UF胶合试件分别在140和120 ℃下固化30 min，再调温调湿72 h备用。每种胶合试件制作5个样品。

2) 试样表面抛光  采用滑走切片机将胶合试件一端刨切成四棱锥形，用玻璃刀将试样尖端刨出面积为1 mm²的光滑平面，再用钻石刀抛光，获得表面粗糙度低于10 nm的胶合界面区域。

1.3.2 测试方法

1) 测试条件  抛光后的样品固定在纳米压痕仪试验台上，测试环境温度和湿度分别为25 ℃和51%±3%。

2) 测试区域确定  采用纳米压痕仪内置光学显微镜观察样品表面(图 1)，重点研究木材第32个年轮附近胶合区域3个不同部位材料的力学性能：A——界面区域树脂；B——未与树脂接触的木材管胞壁；C——与树脂接触的木材管胞壁。

3) 测试位置确定  对选定的测试区域扫描成像，如图 1b、c所示，在A、B和C处选择测试位置。测试位置选择在木材管胞壁S₂层，每个试样选取6个管胞。测试结束后重新扫描测试位置，获取压痕图像，选取有效数据。

4) 测试操作  采用三段恒速率加卸载模式(加载压入5 s、最大载荷保持5 s、卸载5 s)，试验设定最大载荷为400 μN。

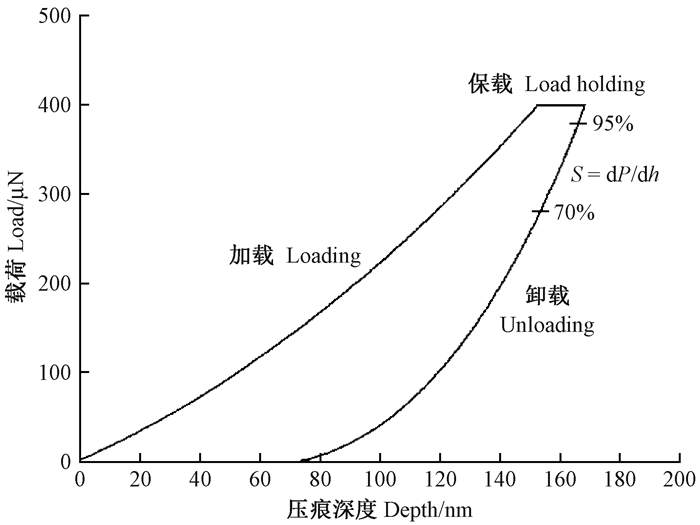
5) 统计计算  根据测试后的压痕质量，选取30个有效数据，采用Oliver等(1992)方法对加载-位移曲线(图 2)进行统计分析，计算材料的弹性模量和硬度。复合弹性模量(E_r)的计算公式如下：

$ E_{\mathrm{r}}=\frac{\sqrt{\pi}}{2 \beta} \frac{S}{\sqrt{A}}。$

(1)

式中：β为常数，本研究所用探针β为1.034；S为弹性接触刚度，由卸载曲线顶部斜率计算得出；A为材料与探针的接触投影面积。

样品的硬度(H)为：

$ H=\frac{P_{\max }}{A\left(h_{\mathrm{c}}\right)。} $

(2)

式中：P_max为最大载荷。

1.4 界面蠕变性能测试 1.4.1 理论基础

1) 纳米压痕-流变学理论  胡克定律认为，弹性体受力后应变达到平衡所需时间极短，理想弹簧可准确描述弹性体的力学行为，其应力-应变关系如下：

$ \sigma=E \cdot \varepsilon。$

(3)

式中：σ、E和ε分别为应力、弹性模量和应变。

理想黏壶可准确描述黏性材料的力学性能，其应力-应变关系如下：

$ \sigma=\eta \cdot \frac{\mathrm{d} \varepsilon}{\mathrm{d} t}=\eta \cdot \dot{\varepsilon}。$

(4)

式中：η、t和$ \dot{\varepsilon}$分别为黏壶内的液体黏度、时间和应变率。

在蠕变过程中，材料的应变和应力比值称为蠕变柔量，测试时应力是恒定的，蠕变柔量可用下式计算：

$ J(t)=\frac{\varepsilon(t)}{\sigma_{0}}。$

(5)

式中：J(t)、ε(t)和σ₀分别为蠕变柔量、任意时刻的应变和恒应力。

基于流变学理论，Schiffmann等(2006)研究发现，在压痕过程中，材料所受应力σ=P/A，产生的应变dε=cotδ·dh/h。因此，木材细胞壁的纳米压痕蠕变柔量可描述为：

$ J(t)=\frac{1}{c} \frac{A(t)}{P_{0}} ; c=2\left(1-v^{2}\right) \cdot \tan \delta。$

(6)

式中：υ、δ和P₀分别为泊松比、探针的半开角(本研究为70°)和初始阶段载荷。

接触投影面积(A)由下式计算得到：

$ A=C_{o} h_{\mathrm{c}}^{2}+C_{1} h_{\mathrm{c}}+C_{2} h_{\mathrm{c}}^{1 / 2}+C_{3} h_{\mathrm{c}}^{1 / 4}+C_{4} h_{\mathrm{c}}^{1 / 8}+C_{5} h_{\mathrm{c}}^{1 / 16}。$

(7)

式中：C₀~C₅为探针常数；h_c为压入深度。

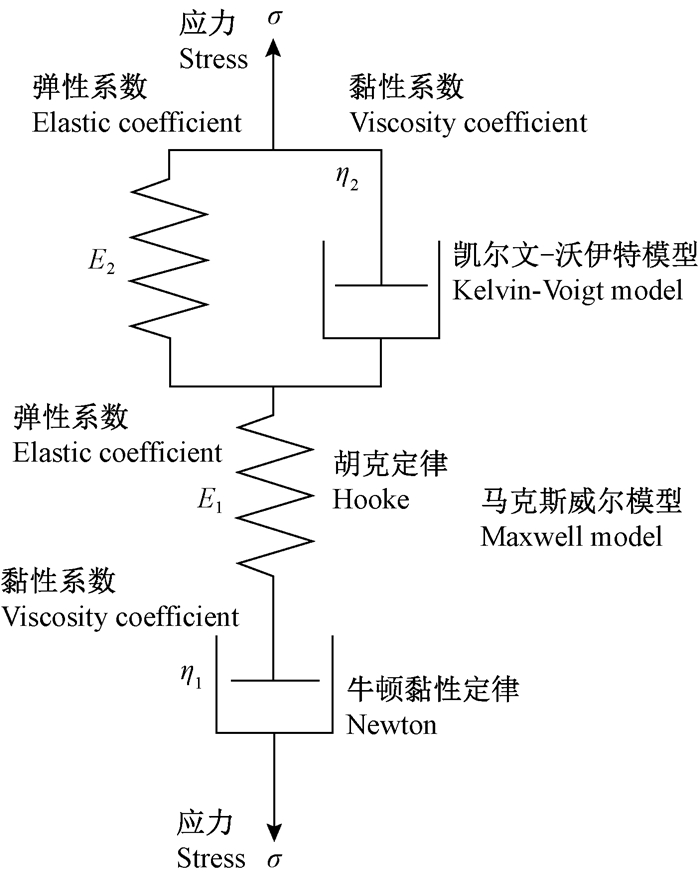
2) Burgers力学模型  木材细胞壁中高度结晶化的微纤丝骨架具有弹性，可理想化为弹簧元件；而细胞壁中的无定形物质在受力时易产生伸展滑移，进而引起延时弹性形变和黏性流动，可理想化为阻尼器。因此，由这2种元件串联或并联组成的Maxwell模型、Kelvin模型被广泛应用于木材黏弹性研究中(Findley et al., 1977)，如图 3所示。

由Burgers力学模型可知，材料的应力与应变之间具有如下关系：

$ \sigma+p_{1} \dot{\sigma}+p_{2} \ddot{\sigma}=q_{1} \dot{\varepsilon}+q_{2} \dot{\varepsilon}。$

(8)

式中：$ \dot{\sigma}、\ddot{\sigma}、\dot{\varepsilon}、\ddot{\varepsilon}$分别为应力和应变的一次求导和二次求导。

p₁、p₂、q₁、q₂定义为：

$ p_{1}=\frac{\eta_{1}}{E_{1}}+\frac{\eta_{1}}{E_{2}}+\frac{\eta_{2}}{E_{2}} ; p_{2}=\frac{\eta_{1} \eta_{2}}{E_{1} E_{2}} ; q_{1}=\eta_{1} ; q_{2}=\frac{\eta_{1} \eta_{2}}{E_{2}}。$

(9)

式中：E₁、E₂为弹性系数；η₁、η₂为黏性系数。

测试过程中，材料所受应力为定值，$\dot{\sigma}=\ddot{\sigma}=0 $，因此可将式(8)简化为：

$ \sigma=q_{1} \dot{\varepsilon}+q_{2} \ddot{\varepsilon}。$

(10)

将式(10)代入式(5)，蠕变柔量计算公式变为：

$ J(t)=J_{0}+J_{1} t+J_{2}\left[1-\exp \left(-t / \tau_{0}\right)\right]。$

(11)

式中：J₀=1/E₁；J₁=1/η₁；J₂=1/E₂；τ₀=η₂/E₂; t为延迟时间。

1.4.2 测试步骤

纳米压痕蠕变测试采用恒速率加载，加载曲线为三段式。为了获取材料在较长时间的蠕变性能，结合以往研究实践经验(Schiffmann，2006；Zhang et al., 2012；Meng et al., 2015)，延长保载时间至200 s。根据蠕变柔量公式计算木材胶合界面的蠕变柔量，采用Burgers模型对实测压痕数据进行拟合获得材料的弹性和黏性系数。

1.5 Nano-DMA测试 1.5.1 工作原理

纳米动态力学测试方法(Nano-DMA)的工作原理为：在静态载荷上叠加动态载荷，使探针以额定频率在试样表面高速振动接触，从而获得材料的黏弹性能(Chakravartula et al., 2006)。Pethica等(1989)提出纳米尺度的动态力学模型，动态负载(F₀)、角频率(ω)和探针位移(X₀)的关系如下：

$ X_{0}=\frac{F_{0}}{\sqrt{\left(K-m \omega^{2}\right)^{2}+\left[\left(C_{{\rm s}}+C_{{\rm i}}\right) \omega\right]^{2}}} $

(12)

式中：C_i和X₀可由仪器空气校准获得。

位移和力之间的相位移(ϕ)根据下式计算：

$ \varphi=\tan ^{-1} \frac{\left(C_{\mathrm{s}}+C_{\mathrm{i}}\right) \omega}{K-m \omega^{2}}。$

(13)

式中：m为探针质量；C_i为位移传感器空气间隙的阻尼系数；C_s为被测试样的阻尼系数；相位移ϕ由锁定放大器获得。

复合刚度(K)由下式计算：

$ K=K_{\mathrm{i}}+K_{\mathrm{s}}。$

(14)

式中：K_s为叶片弹簧的弹簧常数；K_i为探针支撑弹簧的弹簧常数，由仪器空气校准获得。

储能模量(E′_r)、损失模量(E″_r)和损耗因子(tanδ)由下列方程式计算：

$ E_{\mathrm{r}}^{\prime}=\frac{K_{\mathrm{s}} \sqrt{\pi}}{2 \sqrt{A}}; $

(15)

$ E_{\mathrm{r}}^{\prime \prime}=\frac{\omega C_{\mathrm{s}} \sqrt{\pi}}{2 \sqrt{A}}; $

(16)

$ \tan \delta=\frac{C_{{\rm s}} \omega}{K_{{\rm s}}}。$

(17)

1.5.2 测试步骤

首先进行空气校准以获取仪器自身动态特征参数，然后进行动态加载测试，设定静态载荷为200 μN，动态载荷为10 μN，动载谐波频率由10逐级增加到200 Hz，循环100次。样品测试区域选择与静态测试保持一致。

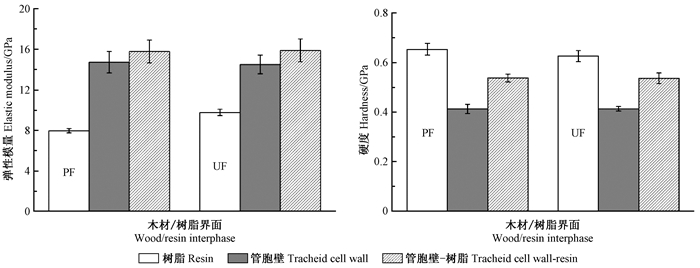
2 结果与分析 2.1 弹性模量和硬度

由图 4可知，火炬松木材管胞壁的弹性模量(E_r)为14.72 GPa，硬度(H)为0.42 GPa。在PF胶合界面区域，与树脂接触的木材管胞壁弹性模量和硬度分别增加7%和26%，说明PF对木材管胞壁起到增强效果，与化学分析法研究结果(Wang et al., 2016)一致。胶黏剂分子渗透进入木材管胞壁层，既可以填充管胞壁物质间空隙，增加管胞壁密度，进而增强管胞壁层，也可与细胞壁物质如纤维素、半纤维素等发生化学交联作用，形成弹性网络结构，从而提高其硬度和弹性模量。木材-UF胶合界面测试结果表明，与树脂接触的木材管胞壁弹性模量和硬度也得到提高，且UF的增强效果比PF略好。分析其原因在于，pH 6左右的火炬松木材为UF提供了更好的固化环境，在相同固化时间下UF固化程度较高(Xing et al., 2007)，且UF自身的力学性能也高于PF，因此对管胞壁层的增强效果相对较好；但UF黏度比PF大，不利于其对细胞壁的渗透，故二者的增强效果无明显区别。

2.2 蠕变性能

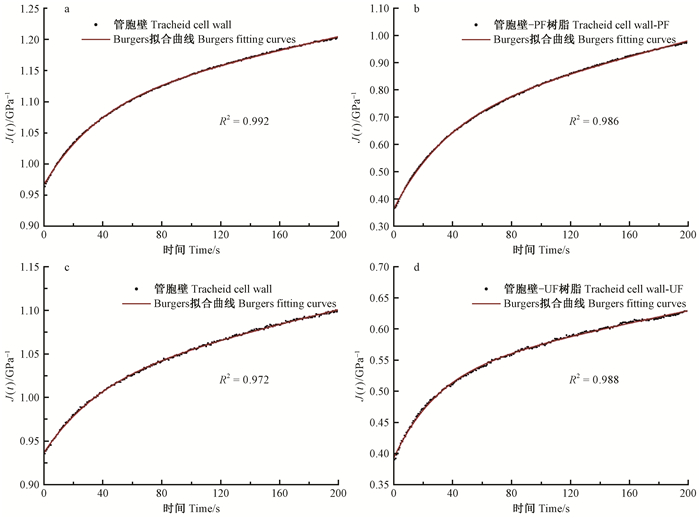
根据Burgers力学模型对实测的木材管胞壁纳米压痕蠕变数据进行拟合，如图 5所示。可以看出，拟合曲线的拟合优度(R²)均大于0.97，表明Burgers力学模型适用于分析木材管胞壁的蠕变性能。在测试过程中，加载至最大载荷进入保载时(t=0)，管胞壁初始蠕变柔量为J(0)=J₀。在木材-PF胶合试件中，未与树脂接触管胞壁和与树脂接触管胞壁的J₀分别为0.934和0.363 GPa^-1，表明管胞壁与树脂接触后蠕变柔量约下降60%。随着保载时间延长，细胞壁的蠕变柔量增大，当保载即将结束时(t=200 s)，J₀分别增加至1.21和0.95 GPa^-1，与树脂接触管胞壁的蠕变柔量仍比未与树脂接触管胞壁低20%。综合分析得出，随着树脂分子进入木材管胞壁，管胞壁弹性模量增加，蠕变柔量变小，说明界面中的树脂可在短周期内改善木材管胞壁的抗蠕变性能。另外，对比图 5a、b可以看出，随着应力作用时间延长，经树脂渗透后管胞壁蠕变柔量的增加程度明显大于纯管胞壁，说明应力作用时间对聚合物树脂的蠕变柔量具有重要影响(Eftekhari et al., 2016；Wang et al., 2017)，但长期受载时，树脂渗透作用可能不能有效改善管胞壁的抗蠕变性能。在木材-UF胶合试件中，相同加载时间时与树脂接触管胞壁的蠕变柔量也低于未与树脂接触管胞壁，说明UF也可提高管胞壁的短期抗蠕变性能。

表 1所示为木材管胞壁压痕蠕变特征参数的拟合方程。根据式(11)，J(t)表示材料的瞬时蠕变柔量；J₀表示管胞壁受载时的弹性行为，与时间无关，为常数；J₁t表示管胞壁的黏弹性行为，与加载时间正相关；J₂t表示管胞壁的黏性；τ₀表示松弛速率。

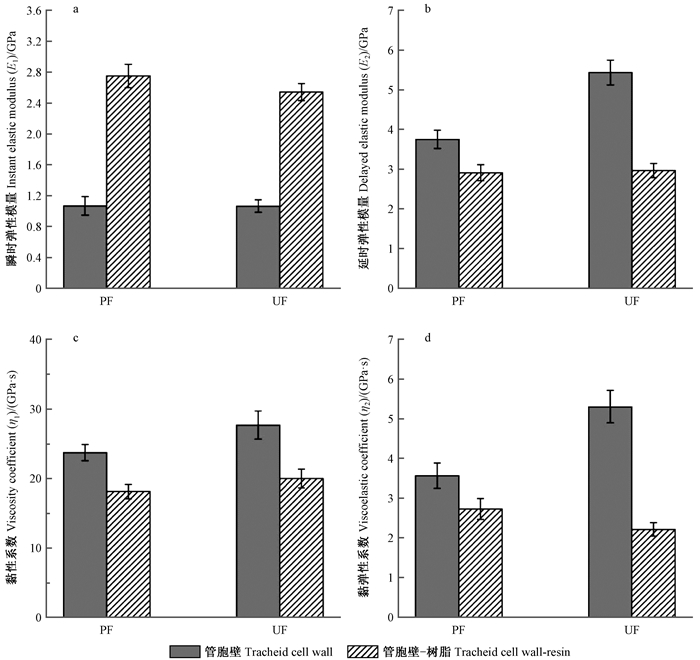
由式(11)可知，瞬时弹性模量E₁=1/J₀，黏性系数η₁=1/J₁，延时弹性模量E₂=1/J₂，黏弹性系数η₂= E₂×τ₀。根据表 1可获得特征参数J₀、J₁、J₂和τ₀，进而可计算出木材胶合界面区域管胞壁的蠕变特性参数。如图 6所示，胶黏剂影响管胞壁的黏弹性，当木材与胶黏剂接触后，PF和UF分子渗透进入管胞壁层，使得管胞壁的瞬时弹性模量(E₁)分别增加157%和138%，延时弹性模量(E₂)分别下降22%和45%，黏性系数(η₁)分别下降24%和28%，黏弹性系数(η₂)分别下降24%和58%。木材管胞壁中半纤维素以无定形状态渗透于骨架物质中，在受力状态下，当管胞壁发生形变超过弹性形变范围时，半纤维素在微纤丝骨架之间起到润滑作用，使得微纤丝之间产生滑移，即产生塑性形变；而当胶黏剂分子进入微纤丝间隙后，自身固化反应以及与胞壁物质发生交联反应有效限制了半纤维素滑动，进而使得胶合界面中与树脂接触管胞壁的弹性增加、黏性降低。

2.3 动态力学性能

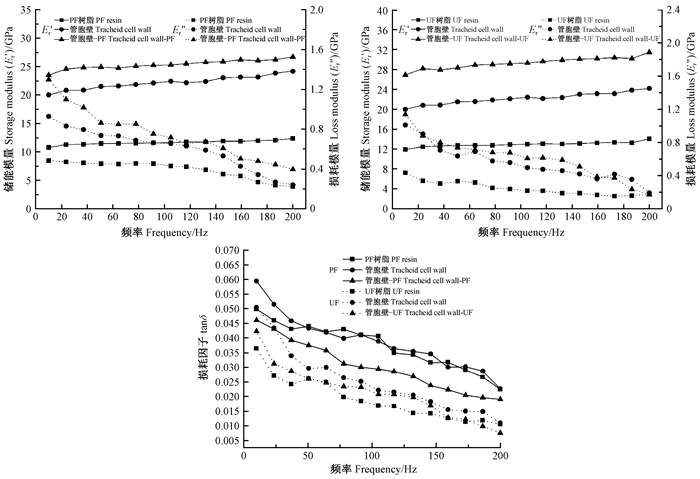
图 7所示为动态载荷作用下木材胶合界面区域管胞和胶黏剂的储能模量(E′_r)、损耗模量(E″_r)和损耗因子(tanδ)与加载频率之间的关系。由图可知，随着加载频率逐渐增大，界面区域各相材料的E′_r呈增加趋势，E″_r和tanδ均逐渐减小，与Furuta等(2011)、Chakravartula等(2006)关于宏观动态黏弹性的研究结果一致。由黏弹性理论可知，损耗因子(tanδ)的变化表明在低载荷频率下材料以黏性响应为主，随着载荷频率增加，区域物质的弹性响应增加，与Zhou等(2007)关于树脂材料的纳米尺度动态力学行为研究结果一致。加载频率也会对管胞壁中分子链段运动模式产生影响，当加载频率较低时，分子链段具有较好的柔韧性，可以有效耗散能量，因此损耗模量高；当加载频率较高时，分子链段运动将受到限制，管胞壁表现出较大的刚性，即储能模量高而损耗模量低(Li et al., 2015)。另外，界面区域中胶黏剂的E′_r和tanδ均小于木材管胞壁，说明固化后树脂吸收和消耗能量的能力较差，这是因为本研究所用树脂均为热固性树脂，固化后形成交联网络结构，受力状态下三维网络结构难以发生分子的链段运动。

通过对比分析与树脂接触管胞壁和未与树脂接触管胞壁的动态力学参数可以看出，胶黏剂对界面区域木材管胞壁的动态力学性能具有一定影响。如当加载频率为10 Hz时，与PF和UF接触后木材管胞壁的E′_r分别提高16%和29%，树脂分子渗透使得管胞壁的储能模量增加，与静态弹性模量具有相同的变化趋势。随着加载频率增加，界面区域与树脂接触管胞壁的损耗模量下降，这是由于树脂分子渗透进入会限制管胞壁物质的分子运动。综合分析来看，胶合过程中胶黏剂对木材管胞壁的动态黏性贡献低，甚至降低其动态黏性，与静载过程中黏性变化趋势一致。

综合静态和动态压痕结果可知，木材管胞壁自身兼具黏弹性特征，当受外力时可以储存和耗散能量，有利于胶合界面中应力的传递和分散。但在胶合过程中，胶黏剂进入管胞壁后，使得管胞壁弹性增强，黏性下降，导致胶合界面耗散能量的能力下降，将对胶合界面应力的传递和分散产生不利影响。

3 结论

1) 胶合界面区域胶黏剂进入管胞壁层，使得木材管胞壁的静态弹性模量、硬度和瞬时弹性模量增加，而黏弹性模量和黏性系数减小，可改善管胞壁的短期抗蠕变能力。

2) 木材管胞壁的储能模量和损耗模量高于树脂；经树脂渗透后，管胞壁的储能模量增加，而损耗因子呈减小趋势，不利于界面应力的传递和分散。

3) 将纳米动态力学检测技术用于复合材料界面研究，可为界面胶合机制提供新思路，但在获取有效信息、力学现象分析等方面仍存在一定局限性，后续研究中需进一步加强。