了解树干(去皮)横截面面积年增长量(即年轮面积增长量，ring area increment，RAI)及其垂直分布，是优化单木生长模型、揭示干形变化机制、准确预测叶生物量和材积年增长量、研究林木生长和气候等关系的基础(Biondi et al., 2008；Ogawa，2015；Latte et al., 2016)。树干木质部的主要功能是水分传输和机械支持，管道模型理论认为，总叶量或当年生叶量的垂直分布决定RAI垂直分布，活树冠(第一活枝到梢顶)内的RAI随树干各位置离梢顶的长度(以下简称为“距离”)增大而显著增加，冠下恒定(Pressler，1864；Shinozaki et al., 1964；Kershaw et al., 2000)；最优水分传输系统理论认为，针叶树种活树冠内的RAI随距离增大以节间(相邻轮生枝间的树干)为单元均匀增加，冠下恒定(West et al., 1999；Enquist，2002)；均匀应力理论认为，为保持应力沿树干均匀分布，RAI随距离增大而增加(Dean et al., 2002；Moore et al., 2014)。但目前尚不完全清楚这些理论对RAI实际变异的解释能力和相对重要性，比较各理论模式与实测结果的异同，进一步阐明相关机制，仍是当前研究的重点(Gaffrey et al., 2001；Bouriaud et al., 2005；Cortini et al., 2013；Moore et al., 2014)。

为准确模拟预测RAI垂直分布，一些学者构建了以树干区段为单元的分段模型(Max et al., 1976；Courbet，1999)、基于管道模型理论的RAI和叶面积关系模型(Jajr et al., 2000)、基于光合产物分配的半机制模型(Deleuze et al., 2002；Barczi et al., 2008)等，但总的来看各模型通用性普遍不高。Cortini等(2013)以易于获取的因子为自变量构建了一个包含3分量的模型，并对加拿大4个针叶树种RAI垂直分布进行模拟，认为该模型建模方法和模型形式在理论上适用于多数树种，通用性较好，但实用效果还需继续验证。

长期以来，研究者们普遍在胸高处测定RAI并据其预测材积年增长量(annual volume increment，VAI)，假设胸高处RAI能代表全树干径向增长量，并与VAI呈显著、稳定的线性函数关系(Arbaugh et al., 1993；Corona et al., 1995)。但实际情况并非完全如此，各树干位置RAI与全树干水平的差异(反映代表性高低)及其与VAI的关系均与RAI垂直分布模式有关(Bouriaud et al., 2005；Latte et al., 2016)，根据树干有效输水组织(部分边材)及其垂直分布而非采用边材面积或横截面面积确定叶生物量(leaf biomass，LB)的理想预测模型和位置是目前研究的重点(West et al., 1999；Lehnebach et al., 2018)。常绿针叶树种的有效输水组织主要分布在树干木质部外侧、数量上与针叶寿命相等的几个年轮层(Kershaw et al., 2000；Lehnebach et al., 2018)，目前对有效输水组织和LB的关系鲜见报道。鉴于此，本研究在山西油松(Pinus tabulaeformis)主要分布区选择不同特征的油松林进行树干解析和RAI测算，研究：1) RAI的垂直分布特征及主要控制机制；2)根据Cortini等(2013)建模方法和模型形式构建油松RAI垂直分布模型，验证其应用效果；3)在不同RAI垂直分布模式下，探究不同树干位置RAI与全树干水平的差异及其与VAI、LB的关系。

1 研究区概况与研究方法 1.1 研究区概况

以山西油松主要分布区为研究区，包括山西森林生态系统监测网络覆盖的太原西山(TX)、偏关(PG)、中条山泗交(SJ)、关帝山隆兴(GL)、太行山海眼寺(TH)和坪松(TP)、临县城庄沟(LX)及太原东山(TD)8个林场。

1.2 研究方法 1.2.1 样地调查及林分因子测算

2014—2017年10月，在8个林场选择9个不同年龄和竞争状态的油松林，于典型地段分别布设1块100 m×100 m的样地，并将其划分为25个20 m×20 m的样方进行每木检尺。根据检尺结果，在每块样地的25个样方内分别选择1株最高木(每400 m²选1株)，依其平均高度确定林分优势高(stand dominant height，SDH，m)；在每块样地随机选择50株林木，采用生长锥在树干基部分别钻取1个样芯，依其平均年轮数确定林龄(Age，a)；基于各林分的SDH和Age，查询立地指数表(杨继镐等，1993)，确定其立地指数(site index，SI，m)；以各样地林木胸径变化范围的第33.3、66.7百分位数，将林木划分为小、中、大3级，推算各林分的大树胸高断面积(basal area of breast height of big trees，BBA，m²·hm^-2)。各样地特征见表 1。

1.2.2 树干解析和叶生物量测定

在每块样地各级林木中，分别选择1株标准木作为样木，每块样地共3株，对其编号并测定相关生长指标后齐地伐倒。依第一活枝着生处到梢顶长度将树冠等分为3区，按区去除枝叶并称其鲜质量，每区选择3~5个标准枝进行枝叶分离和含水量测定，求算各样木的叶生物量(LB，kg)。

在每株样木树干基部、0.3 m和1.3 m以及其余部分每隔0.5 m(树高≤5 m)或1 m(树高>5 m)处，分别截取1个5 cm厚圆盘，直到形成层年龄小于3年(依枝轮数判断)时停止，并同步截取所有样木活树冠基部(形成层年龄均≥3年)的圆盘。采样时对各圆盘编号并记录其高度(截取处高度，m)，从27株样木上(表 2)共截取形成层年龄≥3年的圆盘312个。

1.2.3 不同树干位置RAI及样木材积年增长量测算

将各圆盘打磨至年轮清晰可辨，采用Lintab 6年轮分析仪(德国Rinntech公司，精度1/100 mm)在与其不同方位平均半径最接近的位置逐年测量轮宽，并据圆盘所属样木的采伐时间为各年轮定年，运用COFECHA程序检测轮宽和定年的准确性。利用TSAPWin(Scientific 4.64)将轮宽转换为面积，以圆盘最近3年(样木采伐当年及前2年，与针叶寿命一致)的平均年轮面积作为其所在树干位置的横截面面积年增长量(RAI，cm²)。

依据圆盘截取处将树干分成不同区段，梢头区用树高年生长量内插法和圆锥体差值法(Carmean，1972)，其余区段用平均断面近似求积式和差值法，测算各样木最近3年的平均材积增长量作为其材积年增长量(VAI，dm³)。此外，测算各样木总材积，结合年龄确定其多年平均材积增长量(many years annual volume increment，MVAI，dm³)。

1.2.4 有效树冠长度及有效树冠基部RAI

郁闭林分中，林木中上部树冠受株间竞争等影响较小，生长相对旺盛，称为有效树冠；下部受遮荫和挤压等影响较大，呈衰退迹象(Courbet，1999)。以单木为单元，绘制RAI随距离变化的折线图，目视与判别分析相结合将折线分为斜率等明显不同的区段，对距梢顶最近和次近的2个区段分别拟合，拟合线交点的x、y分别为有效树冠长度(CLY，m)和其基部RAI(Deleuze et al., 1995)，CLY占活树冠长度和树高的比例分别为有效树冠的比例和其冠长率(CTY，%)。

1.2.5 RAI垂直分布模拟

根据Cortini等(2013)建模方法，RAI垂直分布的基础模型为：

${\rm{RA}}{{\rm{I}}_{ij}} = {a_0} \times {\rm{DIC}}_{ij}^{{a_1}} + {b_0} \times {\rm{DBC}}{{\rm{B}}_{ij}} + {c_0} \times {\rm{EXP}}\left( {{c_1} \times } \right.{\rm{ RD}}{{\rm{H}}_{ij}}) + {\varepsilon _{ij}}。$

(1)

式中：i、j分别为样木和圆盘编号；DIC_ij为圆盘上方的有效树冠长度(m)；DBCB_ij为有效树冠基部下方圆盘距该处的距离(m)；当圆盘高度高于有效树冠基部高度时，DIC_ij=树高-圆盘高度，DBCB_ij=0；当圆盘高度小于等于有效树冠基部高度时，DIC_ij为有效树冠长度，DBCB_ij=有效树冠基部高度-圆盘高度；RDH_ij为圆盘高度占树高的比例；a₀、a₁、b₀、c₀和c₁为模型参数；ε_ij为组内误差。

分别测算312个圆盘的DIC_ij、DBCB_ij和RDH_ij，采用R语言(R version 3.2.5，R Core Team 2014)的GNLS(广义非线性最小二乘法)程序包估算模型1[式(1)]参数。在模型1中引入样木变量(表 2中各变量及样木的CLY_i和CTY_i)，保留效应显著(P < 0.05)者构建模型2[式(2)]；在模型2中引入林分变量(表 1)，保留效应显著者(P < 0.05)构建模型3[式(3)]；模型2和3的参数估计方法与模型1相同。根据各模型赤池信息量准则值(AIC)、拟合优度(R_adj²)、绝对或相对均方根误差(RMSE)及似然比检验结果评价并比较其拟合效果。

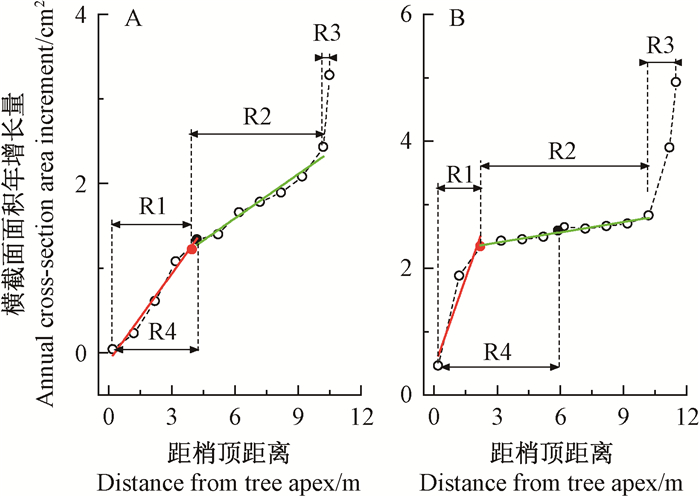
2 结果与分析 2.1 RAI的垂直分布特征

各样木RAI随距离变化的折线均明显分为斜率中等、较小和较大3个区段(图 1)，分别与有效冠区、树干中间区和膨大区相对应，样木有效树冠比例为0.42~1.00，平均为0.86，说明在整体水平上，有效树冠区占活树冠区的86%。

对各样木3个区段RAI和距离的关系分别拟合，可以发现RAI垂直分布包括2种模式(以2株代表性样木展示)：一是各区段的RAI均随距离增大而显著增加(P < 0.05)(图 1A，模式Ⅰ)；二是树干中间区的RAI相对稳定(P>0.05)，其他2个区段的RAI均随距离增大而显著增加(图 1B，模式Ⅱ)。2种模式的差异主要源自树干中间区。模式Ⅰ和Ⅱ样木分别占总样木的51.9%和48.1%，前者略多。

2.2 RAI的垂直分布模拟

模型2和3的表达式如下：

$\;\;\;\;\;\;\;\;{{\rm{RA}}{{\rm{I}}_{ij}} = \left( {{a_0} + {a_2} \times {\rm{SAG}}{{\rm{E}}_i} + {a_3} \times {\rm{C}}{{\rm{R}}_i} + {a_4} \times {\rm{CL}}{{\rm{Y}}_i}} \right) \times }\\ {{\rm{DIC}}_{ij}^{{a_1}} + \left( {{b_0} + {b_1} \times {\rm{CT}}{{\rm{Y}}_i}} \right) \times {\rm{DBC}}{{\rm{B}}_{ij}} + \left( {{c_0} + {c_2} \times {\rm{CL}}{{\rm{Y}}_i}} \right) \times }\\ {\exp \left( {{c_1} \times {\rm{RD}}{{\rm{H}}_{ij}}} \right) + {\varepsilon _{ij}}} ; $

(2)

$\begin{array}{c}{\mathrm{RAI}_{i j}=\left(a_{0}+a_{2} \times \mathrm{SAGE}_{i}+a_{3} \times \mathrm{CR}_{i}+a_{4} \times \mathrm{CLY}_{i}+a_{5} \times\right.} \\ {\mathrm{SI}_{i}+a_{6} \times \mathrm{BBA}_{i}+a_{7} \times \mathrm{DT}_{i} ) \times \mathrm{DIC}_{i j}^{a_{1}}+\left(b_{0}+b_{1} \times \mathrm{CTY}_{i}\right) \times} \\ {\mathrm{DBCB}_{i j}+\left(c_{0}+c_{2} \times \mathrm{CLY}_{i}+c_{3} \times \mathrm{R} \mathrm{HT}_{i}\right) \times \exp \left(c_{1} \times \mathrm{R} \mathrm{D} \mathrm{H}_{i j}\right)+\varepsilon_{i j }}。\end{array} $

(3)

各模型参数见表 3。模型1~3的残差变异均以G(fitted_ij, δ)=|fitted_ij|^δ(fitted_ij为拟合值)描述为好，不同树干位置RAI的相关性均以Γ_i(ε)=CAR(1)(一次自回归模型)描述为好。

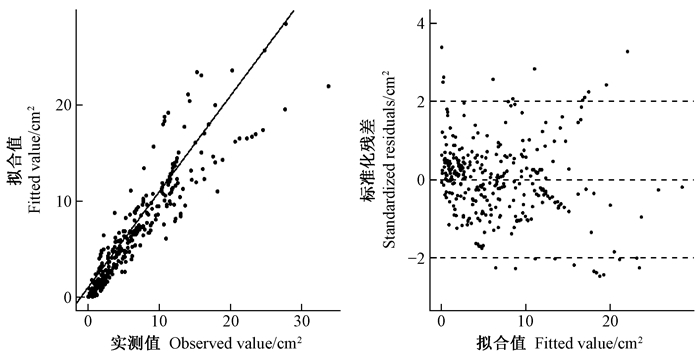
模型1~3对RAI垂直分布的拟合效果依次显著提高(似然比检验，P < 0.05)，模型2比模型1的R_adj²提高11.03%，模型3比模型2的R_adj²提高13.73%，最优模型(即模型3)的R_adj²达82.76%(表 4)，其拟合值为实测值的无偏估计(图 2)。

3个模型的第1分量(含DIC_ij的分量)描述的是有效冠区RAI随距离增大而增加，冠下RAI为恒量。模型3中，该分量的乘幂函数指数(a₁)为0.983 7，说明有效冠区RAI与距离略呈曲线关系，该区RAI随CR、CLY、SI、DT的增大而增加，随SAGE和BBA的增大而减小。

3个模型的第2分量(含DBCB_ij的分量)描述的是DBCB的函数及累加计算有效树冠基部到树干基部不同位置RAI的分量。模型3中，DBCB的斜率是CTY的线性函数，其参数(b₀和b₁)均与0差异显著，意味着冠下RAI并不恒定。

3个模型的第3分量(含RDH_ij的分量)描述的是树干横截面的膨大生长现象，是RDH的负指数函数及累加计算全树干不同位置RAI的分量。模型3中，负指数函数的系数(c₁)为-34.709 0，意味着膨大生长随RDH增大快速而显著下降，RDH为6.6%时(平均为0.63 m)，该分量降至树干基部的10.1%。

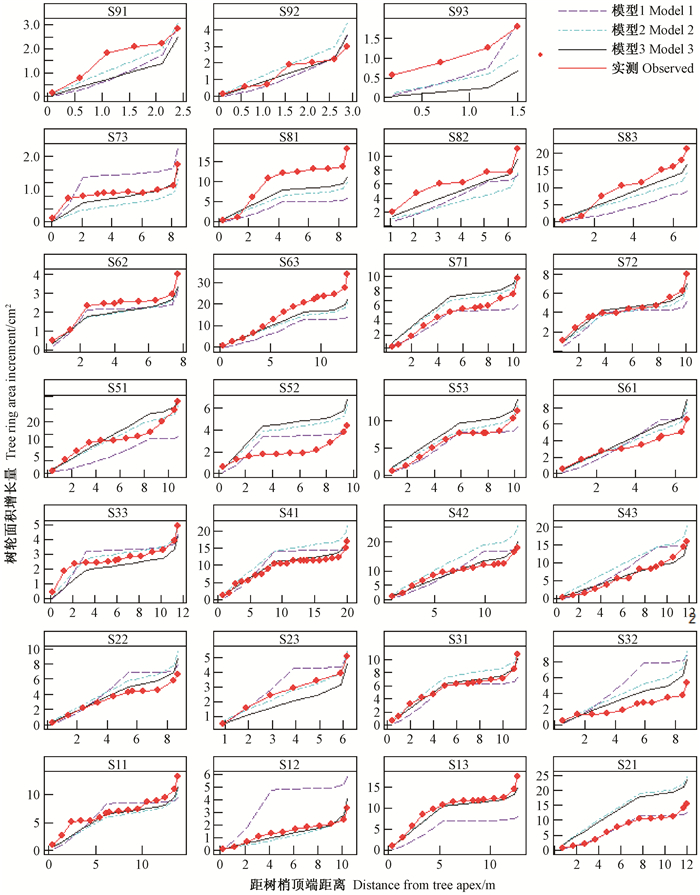
模型3对样木整体RAI垂直分布模拟最好，但对每株样木并不尽然，52.0%的样木以模型3拟合最好，30.0%的样木以模型2或模型1拟合为好，18.0%的样木均不理想(图 3)。

2.3 不同树干位置RAI与全树干水平的差异及与VAI的关系

312个圆盘的平均RAI为6.10 cm²，与各样木有效冠基的RAI均值相近。全树干水平的RAI、VAI在2种模式间无显著差异(P>0.05)。RAI垂直分布模式明显影响不同位置RAI的差异及各位置RAI与全树干水平的差异(表 5)。

模式Ⅰ、Ⅱ及整体水平(即全部样木)，4个位置RAI与全树干水平的差异由大到小依次为树干基部、胸高处、活树冠基部和有效树冠基部，说明有效树冠基部的代表性最高；4个位置间，树干基部的RAI明显高于其他3个位置，3个位置RAI在模式Ⅱ中的平均差异最小，在模式Ⅰ中最大，整体水平上居中，说明其在模式Ⅱ中对全树干代表性的相近程度高于模式Ⅰ和整体水平。总体来看，胸高处RAI分别比全树干高40.1%(模式Ⅰ)、16.4%(模式Ⅱ)和27.0%(整体水平)，代表性相对较小且随模式变异较大。

模式变化对4个位置RAI与VAI关系函数类型的一致性及拟合优度的差异性具明显影响(表 5)。模式Ⅰ及全部样木中，树干基部和胸高处的RAI与VAI呈显著乘幂函数关系，活树冠基部和有效树冠基部的RAI与VAI呈显著一元一次函数关系，均以胸高处RAI为自变量的模型模拟效果最好；模式Ⅱ中，4个位置的RAI和VAI呈显著乘幂函数关系，具同等的模拟预测效果，有效树冠基部的略好。总体来看，2种模式的有效树冠基部、活树冠基部RAI与VAI关系函数的类型及拟合优度明显不同，其他2个位置的相近，胸高处RAI在各模式及整体水平上均能有效模拟预测VAI，拟合优度均在0.906 9以上。

以全部样木的最优模型(胸高处RAI为自变量的模型)对模式Ⅰ和Ⅱ各样木VAI进行预测，平均相对误差分别达30.6%和-21.2%，而据2种模式各自的最优模型，分别为3.2%和2.0%，说明依整体水平上优选的模型对不同模式林木的VAI进行预测时误差很大。

2.4 不同树干位置RAI与单木叶生物量的关系

模式变化对4个位置RAI与LB关系函数类型的一致性及拟合优度的差异性存在明显影响(表 6)。模式Ⅰ及全部样木中，树干基部和胸高处的RAI与LB呈显著乘幂函数关系，活树冠基部和有效树冠基部的与LB呈显著一元一次函数关系，均以胸高处RAI为自变量的模型模拟效果最好；模式Ⅱ中，4个位置的RAI和LB呈显著乘幂函数关系，具同等的模拟预测效果，胸高处的略好。总体来看，胸高处RAI在各模式及整体水平上均是模拟预测LB的最优自变量，拟合优度均在0.918 4以上。

2.5 单木叶生物量与单木材积年增长量的关系

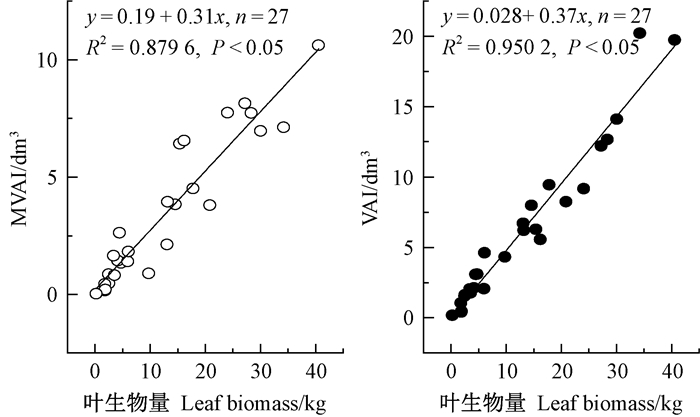
各样木多年和近3年的年均材积增长量分别为3.46±0.59和6.17±1.08 dm³，前者是后者的56.1%，二者均与叶生物量呈显著一元一次函数关系，叶生物量可分别解释二者株间变异的87.96%和95.02%，对近3年的年均材积增长量的预测效果明显较好(图 4)。

3 讨论 3.1 RAI垂直分布模式及与理论模式的异同

本研究结果表明，3个树干区段中，中间区RAI垂直分布的株间变异最大，是分布模式划分的主要依据(Cortini et al., 2013)。RAI垂直分布主要包括3种模式，除本研究发现的2种外，另一种发生在被压木上，其中间区RAI随距离增大而显著下降(Courbet，1999；Cortini et al., 2013)。

实际与理论模式相比可知，管道模型和最优水分传输系统理论能较好解释有效树冠区RAI的垂直分布，均匀应力理论能有效解释膨大区明显较大的RAI及其垂直分布，说明这2个区段的RAI分布分别受控于水分传输和机械支持需求，但二者对中间区RAI分布的相对重要性存在明显不确定性，这可能是生理(Uggla et al., 1998；Lovisolo et al., 2002)、生态(Chhin et al., 2010；Latte et al., 2016)等因子共同作用的结果，相关机制尚需继续探索。

3.2 RAI垂直分布模拟

验证结果表明，Cortini等(2013)建模方法和模型形式在油松上应用效果良好，也说明基于易于获取的林木和林分因子能对RAI垂直分布进行较好的模拟预测，不过入选最优模型(模型3)的变量与Cortini等(2013)并不完全相同，可能是树种、环境差异等所致。此外，模型3适于模拟预测林木整体的RAI垂直分布，在单木水平的应用效果因样木而异。此外，针叶树种膨大区的相对高度一般为5.0%(Fonweban et al., 2011)~10.0%(Cortini et al., 2013)。据模型3预测，油松膨大区的相对高度为6.6%，在合理范围内。

本研究采用27株标准木的312个圆盘，分析油松RAI的垂直分布特征，构建了相关模型。目前此类研究选用的样木多为20~30株(Courbet，1999；Kershaw et al., 2000；Bouriaud et al., 2005；Cortini et al., 2013)，Chenlemuge等(2015)认为，对人工林而言，该样本量可以满足相关研究要求。

3.3 不同树干位置RAI与全树干水平的差异及与VAI、LB的关系

本研究发现，在4个广为关注的树干位置中，有效树冠基部RAI对全树干水平的代表性最高，但Bouriaud等(2005)发现欧洲山毛榉(Fagus sylvatica)代表性位置的高度为6.7 m，说明该位置还与林木的生长发育状态等有关，并非稳定不变，对代表性位置随林木生长的变化还需进一步研究。

与其他研究结果(Bouriaud et al., 2005；Stephenc et al., 2010；Latte et al., 2016)相似，本研究发现胸高处RAI对全树干水平的代表性不高且明显受RAI垂直分布模式的影响，直接以该处观测结果估算树干径向增长量有时会造成很大误差；不同模式中，胸高处RAI与材积增长量的关系或优于其他位置或略差于理想位置，因此本研究结果支持Leblanc(1990)的观点，即在胸高处测算RAI并据此预测VAI是有效但存有缺陷的方法。此外，代表性较高的有效树冠基部RAI对VAI的模拟预测效果总体上不及胸高处，主要源于VAI是RAI和高增长共同作用的结果，胸高处较大的RAI弥补了高增长效应。

RAI垂直分布模式不同，各位置RAI与叶生物量关系的一致性存在差异，模式变化的影响不可忽略(West et al., 1999)。多数研究认为活树冠基部比其他位置的边材面积对单木叶生物量的预测效果要好(Stancioiu et al., 2005；Marchand，2011)，但本研究发现各模式及整体水平，胸高处RAI均是预测叶生物量的理想变量，活树冠基部的仅在树干中间区RAI较为恒定的模式中较好，与Grier等(1974)的研究结论相近，这可能也是根据有效输水组织与边材面积分别模拟预测单木叶生物量的差异之一。

4 结论

油松树干RAI垂直分布存在明显的株间和株内变异。株内水分传输和机械支持需求分别决定了有效树冠区及膨大区的RAI垂直分布，二者的相对重要性及生物环境等因子共同决定了树干中间区的分布。株间变异主要源自中间区RAI垂直分布的差异。

Cortini等(2013)建模方法和模型形式在油松上的应用效果良好，根据该建模方法和模型形式构建的最优RAI垂直分布模型可解释油松RAI垂直变异的82.76%，但入选最优模型的变量受树种和生物环境等影响，与Cortini等(2013)并不完全相同。

在当前研究4个广为关注的树干位置中，有效树冠基部RAI对全树干水平的代表性较高。胸高处RAI对全树干水平的代表性明显受RAI垂直分布模式影响；不同模式中，胸高处RAI与材积增长量的关系或优于其他位置或略差于理想位置。因此，在胸高处测算RAI并据此预测VAI是有效但存有缺陷的方法。不同模式和整体水平，基于不同树干位置的有效输水组织构建的单木叶生物量预测模型中，胸高处RAI始终是预测叶生物量的理想自变量。