在森林火灾场合，蔓延中火焰对森林周边环境和设施产生热辐射。因其非接触式传播和全方位作用特点，火焰辐射成为点燃未燃区可燃物的重要能量来源，即使一定距离之外的可燃物也会因受到火焰辐射的攻击而被点燃(Cohen, 2004)。林火蔓延过程中只有树冠火才会真正意义上对环境构成影响，才会直接产生辐射引燃现象。地表火因火焰尺度因素和热辐射传输过程中植被遮挡效应，对环境的影响可以忽略。

以往研究工作中采用临界辐射热流强度来确定被保护林分和设施的安全距离。Zárate等(2008)以4.7 kW·m^-2作为临界值分析特定林火场合火焰宽度与长度之比对消防员安全距离的影响；Rossi等(2011)计算不同类型植被形成林火对附近房屋的辐射换热水平，并以10 kW·m^-2作为临界值推算出相应的安全距离。由于这些工作停留于林火辐射热交换的层面，未涉及接受体辐射能量的积累过程，因而并不能真正从阻隔林火辐射点燃的角度为隔离带宽度设置提供依据。目前世界上多林各国在建设防火隔离带时大多基于经验设置其宽度：预防型隔离带宽度一般为数十米至上百米(王海晖等, 2015)，火灾现场临时开设的阻火线宽度则通常 > 10 m。

林火蔓延过程中，随着辐射源向目标物不断接近，目标物接受到的火焰辐射热流通量(强度)会不断变化。与此同时，目标物接受面微元的朝向严重影响其接受的辐射热流强度(Butler et al., 1998; Bergman et al., 2011)。例如，森林中通常易于点燃的2类可燃物，枯立木(dead standing timber, DST)和枯倒木(dead fallen timber, DFT)；它们因辐射接受面分别与地面垂直和平行，接受到的辐射热流强度存在明显差异。研究表明，辐射点燃其实是接受体接受能量不断积累和达到一定程度而引发的。Cohen等(1998)依据辐射累积量和临界辐射累积量的概念提出了辐射点燃条件。辐射累积量表征热辐射攻击过程中接受体吸受热辐射能量的积累水平。具体在何种林火条件下可以实现有效辐射点燃，目前缺乏相应的量化分析。这不利于确认实际林火管理作业中相关预防和控制措施的有效性。

本文致力于探索特定林火场合中辐射换热的特性和引燃的条件。由火焰辐射基本原理出发，构建与火行为参数相关联的林火辐射点燃模型。通过算例分析，在验证模型可靠性的同时，分析林火蔓延过程中对典型接受体辐射换热的特点及辐射换热量累积的规律。在此基础上，探讨不同环境风速条件下林缘与接受体之间间距对辐射点燃现象的影响，评估隔离带阻隔辐射点燃的效能，为防火隔离带的设计提供理论依据。

考虑树冠火情形，其火焰尺度通常大于5 m。火焰在所有表面向未燃区均匀释放辐射能，相应可等效为矩形辐射面，其边长分别对应火焰长度l_f和火线宽度2w_f (Knight et al., 2004; Zárate et al., 2008)。火焰等效热辐射面在环境风作用下出现偏角γ。图 1为移动火焰对前方枯立木的辐射换热示意图(Rossi et al., 2011)。

图 1 移动火焰对枯立木辐射换热示意 Fig. 1 Schematic of a moving flame and the heat exchange with an element on a targeted dead standing timber by radiation

依据热辐射换热基本原理(Bergman et al., 2011)，火焰面对目标物的辐射换热通量为

式中，F为火焰面对目标物辐射换热效率(即视角系数)，T_f为火焰温度，其在整个火焰面上为常数(Butler et al., 1998; Zárate et al., 2008; Rossi et al., 2011)。ε_f为火焰发射率，σ为斯蒂芬-玻尔兹曼常数(5.67×10^-8 W·m^-2 K^-4)，τ为热辐射在大气环境中透过率。由于目标物温度远低于T_f，式1忽略目标物温度及其变化所带来的影响。

火焰辐射面特定微元dA₁中心坐标为(z₁tanγ, y₁, z₁)，表面法向量n₁=(cosγ, 0, sinγ)。枯立木与火焰面底端在x轴方向的距离为x，接受微元中心B距离地面高度z₂，其坐标为(x, 0, z₂)；接受体表面与地面垂直，表面法向量n₂=(-1, 0, 0)。代入枯立木接受微元视角系数计算式(Rossi et al., 2011)，方程1变换成

式中，x=x₀-S_ft，为蔓延中火焰面与目标物水平距离。l_fcosγ为火焰高度，属火灾现场常规观测量。

对于枯倒木来说，目标物位于地面，并且接受微元中心点坐标为(x, 0, 0)。目标物表面与地面平行，表面法向量n₂=(0, 0, 1)。采用类似推导方法，枯倒木表面微元接受辐射热流通量为

火焰面偏角γ由经验公式确定(Pagni et al., 1973; Wang, 2011):

式中，g为重力加速度，U_w为风速。

火焰在平地面以速度S_f向林缘推进。至林缘后，可燃物逐渐消耗殆尽，火焰衰弱至熄灭，最终长度降至零。据此将林火辐射分为2个阶段。阶段Ⅰ是林火从远处蔓延推进至林缘的过程，持续时间t_s；阶段Ⅱ则是至林缘后火焰衰弱直至熄灭的过程，持续时间t_r。其中，阶段Ⅰ火焰长度保持不变，火线强度与火蔓延速度存在以下关系(Byram, 1959; Alexander, 1982)：

式中，H_c=18 620 kJ·kg^-1，为森林可燃物热值(Pyne et al., 1996)，w_a为蔓延过程中单位面积可燃物消耗量。

火线强度与火焰长度满足经验关系式(Thomas, 1971; Pagni et al., 1973; Wang, 2011):

对于树冠火而言，火线强度与火焰持续时间的乘积表征林火蔓延过程中瞬间释放出的能量，与单位面积可燃物消耗量成正比(Wang, 2011):

式中，k为待定常数。

阶段Ⅱ因燃料供应中断火焰衰变至熄灭。考虑到实际情况和便于后续计算，假定在t_r内火焰长度呈线性下降:

一般而言，森林火灾的规模(火焰长度)随单位面积可燃物消耗量单调增大，相应符合以下经验关系w_a=w₀ exp(-c/l_f)，其中w₀为常数。文献中的两组林火现场观测数据，一组与2003年堪培拉大火有关(Wang, 2011)，l_f=35 m，I_b=48 063 kW·m^-1，S_f=11 km·h^-1，t_r=60 s；另一组为野外试验获得(Wotton et al., 2012)，l_f=3.8 m，I_b=1 719.9 kW·m^-1，t_r=39 s。代入方程式5—7可得w₀= 1.336 kg·m^-2，c=16.033 m，然后由方程式7确定出常数k=183.30 m。

目标物微元接受能量的累积量用FTP表示，其定义式为(Cohen et al., 1998)

式中，$ {\dot q} $″_cr表示产生FTP的临界辐射热流通量，即当$ {\dot q} $″_e > $ {\dot q} $″_cr目标物微元才会有能量积累。该计算式不但基本抵消火蔓延过程中前方未燃区对火焰辐射换热的稍许遮挡作用，同时还在很大程度上消除因忽略接受体升温对拦截热辐射通量产生的影响。当FTP达到临界值FTP_ig，目标物成功点燃。对于典型木质可燃物而言，$ {\dot q} $″_cr =13.1 kW·m^-2，FTP_ig=11 501 s·kW^1.828 m^-3.656 (Cohen et al., 1998)。这里认定接受体处于实验室条件下相同并且最有利于点燃的状况，相应忽略火灾现场的环境因素对接受体点燃条件的影响。这其实是给林火辐射点燃的安全评估放出余量。

特定目标物接受到的FTP同样可分为2部分：第一部分为林火蔓延向目标物推进直至林缘处的过程(阶段Ⅰ)中产生的FTP1，第二部分则为林火到达林缘处至熄灭过程(阶段Ⅱ)中产生的FTP2。目标物与林缘之间的距离d等效于通常意义上的隔离带宽度，其因改变林火蔓延过程中对目标物的辐射热流强度而影响FTP。阶段Ⅰ火焰持续时间t_s=(x₀-d)/S_f。

开展林火辐射换热计算时，同样按“最糟糕情形”考虑，即取τ=1.0、ε_f =1.0、T_f=1 200 K (Butler et al., 1998; Zárate et al., 2008; Rossi et al., 2011)。火焰宽度2w_f=50 m，这是基于林火现场观测结果统计分析给出的(Butler et al., 1998; Zárate et al., 2008)。火灾现场的火线宽度有较强的偶然性，但其能对所考虑接受体微元构成辐射换热的有效长度一般为50 m，并且因辐射换热的特点其宽度呈对称状分布于接受微元的正前方。DST接受体微元距离地面高度z₂通常设定为1.5 m，该设定源于森林火灾场合枯立木分布状态和接受辐射换热的基本方式，同时也为文献中同类安全评估结果的比较提供便利。对于DFT接受体微元，其距离地面高度z₂=0 m。

在计算辐射热流通量和累积量的过程中，通常取火源起点离目标物距离x₀=500+d m，因为更远处的火焰无法构成任何影响。使用环境风速和火焰长度这两个参数作为林火特性参数中的因变量，借助于方程式5和6，由火焰长度估算火蔓延速度，然后计算动态火蔓延过程中火源与目标物之间的距离。根据风速估出火焰锋面偏角(式4)，计算阶段Ⅰ中任意时刻林火对目标物的辐射热流通量(式2或3)，相应算出FTP1(式9)。由方程式6—8确定火焰长度在林缘衰变过程，然后计算阶段Ⅱ中不同时刻的辐射热流通量(式2或3)，再积分计算出FTP2(式9)。将FTP最终值与FTP_ig比较以确定特定工况下接受体是否具备辐射点燃的条件，由此确定有效分隔距离d_s。

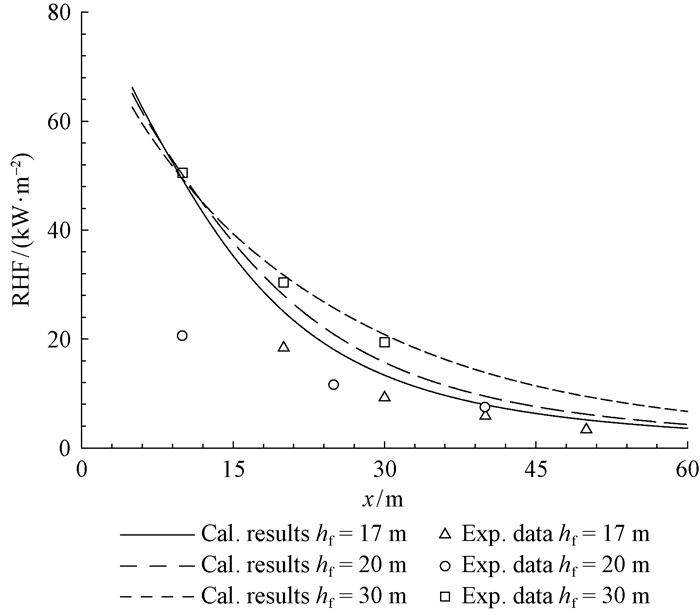
针对不同尺度火焰计算获得DST接受体拦截到的辐射热流通量RHF ($ {\dot q} $″_e)随距离变化的曲线，见图 2。结果与野外现场观测数据进行了对比。依据现场试验条件设定计算参数有，T_f=1 200 K，h_f分别为17、21和33 m，2w_f=20 m；U_w分别为11、15和25 km·h^-1；目标高度z₂=1.2 m (Butler et al., 2000)。模型预测结果与实验测量数据的高度一致性，证明了模型和算法的可靠性。随着火源与目标物间距减小，目标物接受到的辐射热流强度迅速增加，但其量阶基本保持在100 kW·m^-2以内。辐射热流强度近似与距离的平方成反比，因而在距离很近时辐射热流强度出现陡升，这与文献中报道的计算结果亦相吻合(Zárate et al., 2008)。

图 2 设定工况下理论计算结果与野外观测数据对比 Fig. 2 Comparisons of model predictions with the field observations under specific fire scenarios (RHF为DST接受的辐射热流通量(Butler et al., 2000) (RHF specifying the radiant heat flux intercepted by the DST receiver (Butler et al., 2000).

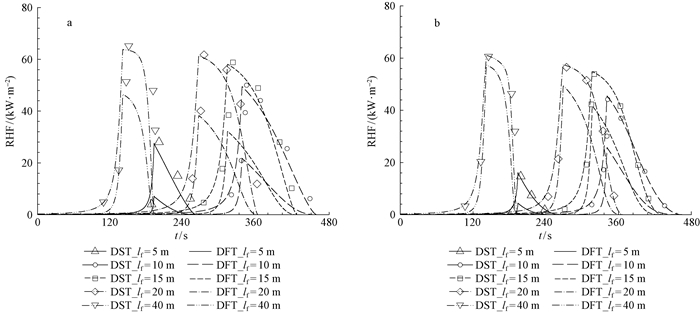
计算获得典型工况下林火蔓延直至熄火过程中火焰面对枯立木DST和枯倒木DFT接受微元的热辐射通量随时间变化曲线见图 3。取2w_f =50 m，并设定林缘与目标物间隔d=10 m。可以观察到，RHF随时间变化迅速上升到峰值后下降。曲线上升阶段对应于林火蔓延向林缘推进的过程(阶段Ⅰ)。随着火焰面与目标物之间距离不断减小，RHF逐渐增大；曲线到达峰值标志着林火蔓延至林缘。曲线下降阶段对应林火到达林缘后渐渐熄灭的过程(阶段Ⅱ)。由于火焰长度不断减小直至为零，RHF逐渐减小至零。模型计算获得的RHF呈现先增大后减小的变化规律，是林火发展直至熄灭过程的具体反映，与林火现场观测现象一致(Butler et al., 2000)。

图 3 不同风速条件下林火蔓延及熄灭过程中2类典型接受体辐射换热通量RHF随时间的变化[Uw=2 m·s-1(a) and 6 m·s-1(b)] Fig. 3 Time-dependent variations of radiation heat flux intercepted by two typical receivers during the fire spread and extinction process at the conditions of different wind speeds[ Uw=2 m·s-1(a) and 6 m·s-1(b)]

由图 3可知，随着火焰长度的增加，RHF峰值有所增大，这是火焰面面积增大导致辐射换热效率增加的结果。火焰长度的不同反映着火灾现场可燃物载量和燃烧速率的变化，导致火蔓延速度随火焰长度呈现先减小后增大的变化规律，因而5 m长火焰产生的RHF峰值出现的时间早于10 m长火焰产生的。RHF到达峰值后下降至零所持续时间为林火到达林缘后的火焰持续时间。图 5中展示出的火焰持续时间在50~130 s之间，与通常树冠火火焰持续时间的量阶相符(Cohen, 2004; Wang, 2011)。

图 4 典型工况下阶段Ⅰ和阶段Ⅱ两类目标物接受累积辐射能FTP对比[Uw=2 m·s-1(a)，6 m·s-1(b)] Fig. 4 Comparisons of the magnitudes of accumulated flux-time products by two types of receivers during the attack of fires at Stages Ⅰ and Ⅱ [Uw=2 m·s-1 (a) and Uw=6 m·s-1(b), respectively]

图 5 典型工况下枯立木和枯倒木微元体接受的FTP随火焰长度lf的变化[d=10 m(a) and 20 m(b)] Fig. 5 Variations of accumulated flux-time products by the receiver elements on DST and DFT as a function of the sizes of fires at the conditions of two distinct separation distances for the receivers [d=10 m(a) and d=20 m (b)]

图 4将典型工况下2类接受体的累积辐射能FTP1和FTP2进行对比。撇开FTP1~FTP2~0的情形，无论对于枯立木还是枯倒木，均有FTP1$ \ll $FTP2。尽管阶段Ⅰ时间t_s长于阶段Ⅱ时间t_r，但随着火焰长度l_f由5 m增大至40 m，阶段Ⅱ有效辐射时间，即RHF大于临界值$ {\dot q} $″_cr的时间段，呈倍数增加。换句话说，在通常林火场合(l_f ≤40 m)，阶段Ⅰ能影响FTP的时间段远短于阶段Ⅱ的。加上在阶段Ⅱ目标物距离火焰面最近，导致FTP2远大于FTP1。

FTP1$ \ll $FTP2意味着实际林火蔓延过程中2类接受体的能量累积很少，林火蔓延至林缘后至火焰熄灭过程中能量积累占主导地位，这揭示了林火蔓延至林缘停止前进后对目标物的热辐射是点燃目标物的主要原因。由此可以确认，文献中以静止火源作为辐射源开展的建筑构件点燃试验，尽管略去了林火动态蔓延的特性，其测试结果仍具有实际参考意义(Cohen et al., 1998)。

由图 4可知，相同工况下枯立木接受微元的辐射累积量FTP远大于枯倒木。在无风条件下，枯立木辐射接受面与火焰面平行，而枯倒木的接受面与火焰面垂直，因而林火对枯立木的辐射换热效率更高，对枯立木的RHF相对较大。随着风速出现，火焰面倾斜，火源对枯立木的辐射换热效率变化幅度不大，但对枯倒木的辐射换热效率影响则较显著；相应地，枯立木相对于枯倒木的优势有所下降。随着风速进一步增大，枯立木接受到的RHF相对于枯倒木的甚至基本相当，这与图 3中相同火焰长度条件下风速从2 m·s^-1增大到6 m·s^-1时枯立木和枯倒木接受的RHF峰值接近的现象一致。对于累积量FTP，枯立木的FTP总是大于枯倒木的，但这种优势同样随风速增大有所下降。

图 5为典型工况下枯立木和枯倒木微元接受到的FTP随l_f变化曲线。对于枯立木DST，随着火焰长度的增大，辐射换热通量不断增大，有效辐射时间(即$ {\dot q} $″_e≥$ {\dot q} $″_cr的时间段)起初也呈增大趋势，因而FTP曲线呈上升趋势；火焰长度增大到一定值后，有效辐射时间缩短导致对应FTP曲线呈下降趋势。FTP曲线先上升后下降趋势使得其出现最大值，表明特定火焰长度条件下目标物接受到能量水平最高。对于枯倒木DFT来说，在l_f增大过程中，其FTP曲线基本呈上升趋势。

比较图 5a和5b的结果可以看出，当隔离带宽度从10 m增大到20 m时，枯立木和枯倒木接受到的FTP减至约为原来的1/3。这反映隔离带宽度显著影响林火辐射点燃效率，增大隔离带宽度明显增强其阻隔林火辐射点燃的效能。不难推断，目标物与林缘之间距离为一适当值d_s时，林火蔓延及到达林缘后熄灭过程中对目标物产生的FTP刚好达到临界值FTP_ig，以实现目标物与林缘间的安全分隔。正如前面提及的，在特定林火条件下，与处在相同位置的枯倒木相比，枯立木因能量积聚水平更高而更容易被林火辐射点燃，因而基于枯立木确定的有效分隔距离d_s大于基于枯倒木的。

随着风速增大，枯倒木微元接受的FTP增加幅度较大；枯立木的FTP则有所波动，相对上升幅度不明显(图 5)。这是因为随着风速增大，火焰面偏角增大，针对枯倒木的辐射换热效率增大幅度明显，而针对枯立木的辐射换热效率变化幅度不大，导致枯倒木接受到的热辐射累积量与枯立木的差距有所减小。此现象也与图 4展示的结果一致。基于工程中计算结果的有效性考虑，在评估林火热辐射对环境影响时，枯立木可以作为判别特定地域是否会出现辐射点燃的重要参考物。当然，实际火灾现场对应的亦可以是干燥的树皮或树枝，还可以是林间房屋设施的木质外墙、窗户、遮阳篷立柱或篱笆等(Cohen et al., 1998; Zárate et al., 2008; Wang, 2011)。

图 6给出不同风速条件下针对枯立木计算出d_s随l_f变化的曲线。由图 6可知，随着l_f增大，d_s由数米增大至30 m，风速对这种变化规律的影响基本可以忽略。l_f增大意味着火焰面面积增大，因而目标物接受的RHF不断增加。尽管有效辐射时间先增大后减小，RHF却始终对FTP的变化占据主导地位，从而导致d_s随l_f呈持续增大趋势。

图 6 不同林火条件下避免辐射点燃的分隔距离的变化 Fig. 6 Separation distances for preventing ignition by flame radiation sourced from forest fires under different fire scenarios

计算结果表明，当d_s设定为10 m时，能阻隔l_f~10 m林火的辐射点燃，与工程实际中构筑阻火线的经验相吻合。野外试验中观察到30 m高度火焰的热辐射无法点燃20 m外目标物(Butler et al., 2000; Cohen, 2004)。本模型计算结果为，不同风速条件下针对30 m长火焰面的有效分隔距离d_s在20~25 m间，与野外试验结果相符。这进一步验证了模型计算结果的可靠性。

以往文献基于特定参照物(目标物)接受辐射热流强度界定林火易发地域房屋设施的安全距离。缘于选定热流强度阈值的差异，其取值变化范围为30~65 m(Cohen et al., 1998; 王海晖, 2008; Zárate et al., 2008)。例如，Cohen等(1998)基于20 m高火焰对40 m外目标物的辐射热流强度低于20 kW·m^-2这一判据推算出安全距离为40 m。尽管本项工作获得的结果与此接近，但结果的来源存在本质差别。本文采用的辐射点燃模型，不但考虑环境风对火焰面的影响，还兼顾真实林火蔓延和熄灭过程中热辐射换热的动态变化，通过计算目标物接受到的热辐射累积量推断目标物点燃条件。与以往工作相比，本文的结果有更坚实的物理基础和明确的物理内涵。需要强调的是，本模型计算是针对特定木质材料的(Cohen et al., 1998)。一旦选取聚集在特定房屋或设施边缘干燥易燃的松针或落叶为热辐射点燃物，因其对应的FTP_ig数值显著降低，会导致d_s取值大幅增加。

与传统隔离带(即无可燃物生土带)阻火原理不同，生物防火林带通过密植树冠浓郁的常绿阔叶树和抑制地表可燃物的生长以阻隔火蔓延，遮荫型防火隔离带则通过清除地表可燃物、保留胸径较粗抗火性较强树木使林火强度降低至无法持续和发展的程度以达到阻隔效果(王海晖等, 2015)。这2种防火隔离带对林火热辐射亦具有一定的吸收、遮挡作用。遮挡作用强弱可以以不同的遮挡率来体现，这里定义遮挡率为防火林带吸收以及反射的热辐射能与投射进防火林带的总热辐射能之比(等效于1-τ)。表 1为计算出的不同风速条件下受40 m长度火焰攻击的有效分隔距离d_s随遮挡率变化结果。火焰长度40 m认定为文献中所报道的火焰长度上限，以此数值开展计算相应能获得d_s最大值并观察防火林带带来的影响。由表 1结果可知，随遮挡率增大d_s显著减小，而环境风速的变化则会导致d_s的稍许波动。与生土带(工程阻隔带)和火灾控制过程中临时开设的阻火线相比，设置防火林带所需有效分隔距离大为减小。由此可见，防火林带的防火功能除了体现在隔断地表可燃物和吸收火源形成的飞火屑块外，对林火辐射点燃现象还有相对高效的阻隔作用。

表 1 火焰长度40 m林火条件下有效分隔距离d_s (m)随遮挡率的变化情况^① Tab.1 Variations of the separation distance d_s (m) as a function of the blocking ratio of the thermal radiation for the forest fire with a length of 40 m and located at different wind speeds

表 1 火焰长度40 m林火条件下有效分隔距离ds (m)随遮挡率的变化情况① Tab.1 Variations of the separation distance ds (m) as a function of the blocking ratio of the thermal radiation for the forest fire with a length of 40 m and located at different wind speeds 遮挡率Blocking ratio (1- τ) 0 m·s-1 2 m·s-1 4 m·s-1 6 m·s-1 8 m·s-1 10 m·s-1 0.2 18.5 20.6 21.5 21.5 20.6 18.6 0.3 14.9 16.7 17.4 17.0 15.2 11.9 0.4 10.8 12.2 12.4 — — — ①在大火焰尺度和高环境风速情形下常规生物防火林带难以达到0.4的遮挡率，因而相应计算结果没有实际意义。Some calculation results may have no practical significance given that the radiation blockage rate of 0.4 is not achievable by an usual biological fire-prevention belt during large-scale forest fire in the presence of a high-speed wind.

由于预定工作目标的限制，本项工作中没有能涉及坡度因素对火蔓延过程辐射换热以及对辐射点燃现象的影响。根据以往的认识可以推测，如果隔离带处于林火蔓延的上坡方向，目标物接受微元对火源视角系数势必会增大，热辐射输运效率将有所提高，有效分隔距离相应应有所扩大才能有效降低枯立木点燃几率；当隔离带处于林火蔓延的谷底，则会出现相反的结果。另外，一旦隔离带处于上坡火蔓延的顶端(即山顶)，由于枯立木接受微元与上坡火空间位置的变化，其视角系数和热辐射输运效率应介于单纯上坡火和下坡火之间，相应对分隔距离的要求亦介于这两种火灾蔓延情形之间。具体的量化结果，有待进一步的理论计算获取。

在实际林火管理工作中实施火灾预防和阻隔，无论是采用工程阻隔带抑或是生物防火林带技术，均需结合当地林分的植被分布状况和潜在林火行为开展相关设计，因为不同林分结合当地地形条件和气象条件会产生不同林火行为，其中包括火焰长度的变化以及包括飞火现象在内的特殊林火行为。这对于确保具体森林防火工作的有效性和经济性的统一至关重要(王海晖等, 2015)。

本文建立起特定林火行为条件下的火焰辐射换热和累积量计算模型。针对特定野外试验数据计算验证，确认了模型的可靠性。源于热交换过程中的辐射换热效率差异，林火对林缘附近枯立木的辐射换热通量大于枯倒木的辐射换热通量。

林火到达林缘后衰灭的过程中对目标物的辐射换热为其能量积累做出主要贡献，是造成辐射点燃的主要原因。随着目标物与林缘之间距离的增大，林火热辐射对目标物产生的能量积累水平迅速降低；火焰长度和环境风速则通过改变热辐射持续时间和辐射换热效率影响辐射点燃的效率。以林缘附近特定枯立木作为热辐射接受体计算结果表明，避免林火辐射点燃的有效分隔距离随火焰长度的增加而加大，而30 m宽度以上隔离带则能有效避免长度至40 m的火焰辐射造成的点燃现象。一旦将通常隔离带替换成生物防火林带，由于林带自身对林火热辐射的吸收和遮挡作用，所需分隔距离明显缩短。本项工作为森林阻隔系统的设计以及林区设施的有效保护提供理论指导。