文章信息
- 曾伟生, 贺东北, 蒲莹, 肖前辉.
- Zeng Weisheng, He Dongbei, Pu Ying, Xiao Qianhui.
- 含地域和起源因子的马尾松立木生物量与材积方程系统
- Individual Tree Biomass and Volume Equation System with Region and Origin in Variables for Pinus massoniana in China
- 林业科学, 2019, 55(2): 75-86.
- Scientia Silvae Sinicae, 2019, 55(2): 75-86.
- DOI: 10.11707/j.1001-7488.20190208
-
文章历史
- 收稿日期:2017-02-06
- 修回日期:2017-05-19
-
作者相关文章
2. 国家林业和草原局中南林业调查规划设计院 长沙 410014
2. Central South Forest Inventory and Planning Institute, National Forestry and Grassland Administration Changsha 410014
森林生物量约占陆地生态系统地上碳储量的80%和地下碳储量的40%(Dixon et al., 1994),是陆地生态系统最大的碳库,在应对气候变化中具有独特功能,在维持全球碳平衡中具有重要作用。森林生物量信息不仅有助于弄清森林生态系统中的能量积累,而且其本身就是森林可持续性的重要指标,森林生物量估计值既可用于评估生物质能源、碳储量和碳汇能力,又能用于研究气候变化、森林健康、森林生产力及营养循环(Clark et al., 2011),准确估计森林地上生物量和地下生物量,对森林生态系统的结构和功能分析具有重大意义。
生物量可以通过树干材积和生物量扩展因子进行估计,也可基于生物量方程进行估计(Somogyi et al., 2007)。生物量方程是指生物量与易测因子(如胸径、树高)之间的回归方程,从已有文献看,目前所建生物量方程已经涵盖世界上不同生态地理区域的很多树种(Ter-Mikaelian et al., 1997;Zianis et al., 2005;Snorrason et al., 2006;Návar,2009;Fayolle et al., 2013;Djomo et al., 2016);同时,有不少学者试图把特定条件或局部区域的生物量方程通过简化等手段推至区域、国家乃至全球水平(Jenkins et al., 2003;Zianis et al., 2004;Vallet et al., 2006;Muukkonen,2007;Henry et al., 2013);另外,也有学者为解决生物量数据累加性与相容性等问题而研究和探索新的方法,取得了不少成果(Parresol,1999;2001;Tang et al., 2001;Zeng et al., 2011;2012;董利虎等,2011;2013;曾鸣等,2013;Dong et al., 2014;Dong et al., 2016;Zeng,2015;Fu et al., 2014)。近年来,我国为建立统一的生物量计量标准体系,正在积极推进主要树种通用性立木生物量模型的研建(Zeng,2014)。
马尾松(Pinus massoniana)是我国南方重要的针叶树种,广泛分布于长江流域的10多个省份。根据第八次全国森林资源清查结果,马尾松林面积1 001万hm2,蓄积5.91亿m3(国家林业局,2014)。目前,已经建立了很多马尾松立木生物量模型(吕勇等,1996;贺东北等,1998;吴守蓉等,1999;曾伟生等,2010;Zeng et al., 2012;李际平等,2013),但这些模型多数是基于局部地域采集的较少样本建立的,将其应用于其他地域或较大尺度范围会导致结果不可信;同时,地上生物量和地下生物量通常分别独立建模,未考虑系统的完整性;此外,大尺度生物量模型是否需要分不同地域和起源建立,也无人做出过定论。基于此,本研究利用采自全国马尾松分布区的代表性样本,研建相容性立木生物量和材积模型系统,研究目标包括:1)利用误差变量联立方程组方法和哑变量模型方法,解决地上生物量、地下生物量和立木材积等多变量之间的相容性问题,以及在地上生物量和地下生物量样本单元数不相等情况下如何建立一体化联立模型系统的问题;2)构建含地域和起源因子的全国尺度立木生物量联立模型系统,分析按不同地域和起源建模能否显著提高模型的预估精度,并按最优建模方案构建联立方程组,为准确估计马尾松生物量提供依据。
1 数据与方法 1.1 数据采集本研究所用数据由国家森林资源连续清查生物量调查建模项目组提供。根据《立木材积表》(国家林业局,1999),马尾松二元材积表分2个地理区域范围编制,也称建模总体。总体1的地域范围包括湖南、江西、广东、广西、福建、浙江、江苏、安徽、贵州等省区,总体2的地域范围包括四川、重庆、湖北3省市。项目组收集的建模数据涉及2个总体,其中总体1包括150株样木的地上生物量和立木材积实测数据,其中54株样木同时还实测了地下生物量;总体2包括151株样木的地上生物量和立木材积实测数据,其中50株样木同时还实测了地下生物量。在全部301株样木中,164株来自天然林,137株来自人工林;在104株测定地下生物量的样木中,67株来自天然林,37株来自人工林。样本在马尾松2个总体分布范围内具有广泛的代表性。
每个总体的样木均匀配置2、4、6、8、12、16、20、26、32及38 cm以上10个径阶,每个径阶约15株样木,要求尽可能均匀配置不同的树高级。如果每个径阶分高、中、低3个树高级,则每个树高级应选择5株样木。对每株样木,采伐前准确测量胸径和树高,以确认是否符合预定的径阶和树高级要求。样木伐倒后,测量树高(或树长)、冠长和年龄等因子。将所有树枝从树干上砍下,测量其总鲜质量。将树干从0、0.05、0.1、0.2、0.3、0.4、0.5、0.6、0.7、0.8和0.9相对树高处分成11段,测量每段基部直径,根据Smalian公式计算树干材积。分上、中、下3段测量树干鲜质量,并分别截取3个圆盘,称其总鲜质量和树皮鲜质量。然后分上、中、下3层挑选3个样枝,将针叶从树枝上摘除。根据针叶和无叶枝条的鲜质量比,推算整株样木树枝和树叶鲜质量。最后,从3个样枝中选取3个样品,从全部树叶中混合选取1个样品,称其鲜质量。从全部样木中选取约1/3同时测量地上和地下生物量。根据样木大小,采用机械或手工方法将整个根系挖出,将根上的泥土清除干净后,分树桩(根蔸)、粗根(大于10 mm)和细根(2~10 mm,不包括2 mm以下须根)称其总鲜质量,并选取样品称重。样木的选取,树干、树皮、树枝、树叶和树根等各部分的测量和取样,都严格执行林业行业标准规定(国家林业局,2015a)。所有样品带回实验室,85 ℃下烘至恒重。根据干质量和鲜质量之比,计算出各部分的生物量和样木的总生物量。表 1给出了马尾松2个总体生物量建模样本的统计特征值。
|
|
立木生物量和树干材积方程的一般形式(Parresol,1999;Zeng et al., 2012)表述如下:
| $ y = {\beta _0}{x_1}^{{\beta _1}}{x_2}^{{\beta _2}} \cdots {x_j}^{{\beta _j}} + \varepsilon 。$ | (1) |
式中:y为生物量(kg)或树干材积(dm3);xj为反映林木大小的变量,如胸径(D,cm)和树高(H,m);βj为待估参数;ε为误差项,假定其服从正态分布。
生物量和材积数据都具有显著的异方差性,在参数估计时必须消除异方差。本研究采用加权回归估计方法,其特定权函数根据最小二乘法拟合的独立回归方程的残差推导而来(Parresol,1999;2001;曾伟生等,2011a)。因为基于胸径D的一元模型与基于胸径D和树高H的二元模型都得到广泛应用,因此本研究将建立一元和二元2套模型。地上生物量、地下生物量和树干材积方程的二元模型分别表述如下:
| $ {M_{\rm{a}}} = {a_0}{D^{{a_1}}}{H^{{a_2}}} + \varepsilon ; $ | (2) |
| $ {M_{\rm{b}}} = {b_0}{D^{{b_1}}}{H^{{b_2}}} + \varepsilon ; $ | (3) |
| $ V = {c_0}{D^{{c_1}}}{H^{{c_2}}} + \varepsilon 。$ | (4) |
式中:Ma和Mb分别为地上生物量和地下生物量(kg);V为树干材积(dm3);ai、bi和ci为待估参数。
1.2.1 相容性联立方程组地上生物量通过生物量转换因子(BCF)与树干材积相关联,而BCF等于生物量扩展因子(BEF)与基本木材密度的乘积(IPCC,2006)。因为BCF是森林生物量估计的重要参数,在生物量建模实践中一般都同时建立与树干材积方程相容的地上生物量方程和BCF方程(曾伟生等,2012;Zeng,2015)。类似地,地下生物量通过根茎比(RSR)与地上生物量相关联(Wang et al., 2008;Mugasha et al., 2013)。因为RSR也是森林生物量估计的重要参数,一般也同时建立与地上生物量方程相容的地下生物量方程和RSR方程(曾伟生等,2011b)。但是,由于测定地下生物量和地上生物量的样木数量不相等,前者仅为后者的1/3,通常做法是分别建立地上生物量和地下生物量联立方程组(曾伟生等,2015;国家林业局,2015b)。为了建立一体化联立方程组,本研究引入一个哑变量或指示变量I,对于已测定地下生物量的样木,令I=1;对于未测定地下生物量的样木,令I=0(Crecente-Campo et al., 2010; Zeng et al., 2017)。构建一体化联立方程组,可保证地上生物量、地下生物量、树干材积、生物量转换因子和根茎比之间的相容性,其二元模型表述如下:
| $ \left\{ \begin{array}{l} {M_{\rm{a}}} = {a_0}{D^{{a_1}}}{H^{{a_2}}} + \varepsilon ;\\ {M_{\rm{b}}} = {b_0}{D^{{b_1}}}{H^{{b_2}}}I + \varepsilon ;\\ V = {c_0}{D^{{c_1}}}{H^{{c_2}}} + \varepsilon ;\\ {\rm{BCF}} = {a_0}{D^{{a_1}}}{H^{{a_2}}}/{c_0}{D^{{c_1}}}{H^{{c_2}}} + \varepsilon ;\\ {\rm{RSR}} = {b_0}{D^{{b_1}}}{H^{{b_2}}}I/{a_0}{D^{{a_1}}}{H^{{a_2}}} + \varepsilon 。\end{array} \right. $ | (5) |
式中:BCF和RSR分别为生物量转换因子和根茎比;I为标识是否有地下生物量数据的指示变量,其他符号同式(2)~(4)。
如果删除式(5)中所有包含H的指数项,二元模型就变成了一元模型,限于篇幅,这里不再列出。
估计上述联立方程组参数的方法有多种。Borders(1989)提出采用二段或三段最小二乘回归方法估计林分生长和收获模型系统的参数;Parresol(1999)采用似然无关回归(SUR)解决联立方程组的可加性问题;Tang等(2001)提出估计联立方程组参数的误差变量(EIV)建模方法,该方法近年来得到广泛应用(董利虎等,2011;Zeng et al., 2012;李际平等,2013;曾鸣等,2013;Zeng,2015)。Fu等(2014)对采用SUR和EIV这2种方法建立的非线性可加性生物量方程系统进行比较,结果表明EIV方法比SUR方法更有潜力。因此,本研究采用EIV建模方法,通过ForStat软件估计式(5)中的参数,其中Ma、Mb、V、BCF和RSR作为误差变量,D和H作为无误差变量(唐守正等,2008)。
1.2.2 含地域和起源因子的联立方程系统为了分析不同地域(建模总体)和起源对生物量和树干材积变动的影响,在前述联立方程组的基础上,本研究再引入2个哑变量J和K。当样木属于总体1的地域范围时J=1,属于总体2的地域范围时J=0;当样木来自天然林时K=1,来自人工林时K=0。含地域和起源因子的一元联立方程组表述如下:
| $ \left\{ \begin{array}{l} {M_{\rm{a}}} = \left({{a_0} + {a_{01}}J + {a_{02}}K} \right){D^{\left({{a_1} + {a_{11}}J + {a_{12}}K} \right)}} + \varepsilon ;\\ {M_{\rm{b}}} = \left({{b_0} + {b_{01}}J + {b_{02}}K} \right){D^{\left({{b_1} + {b_{11}}J + {b_{12}}K} \right)}} \cdot I + \varepsilon ;\\ V = \left({{c_0} + {c_{01}}J + {c_{02}}K} \right){D^{\left({{c_1} + {c_{11}}J + {c_{12}}K} \right)}} + \varepsilon ;\\ {\rm{BCF}} = \left({{a_0} + {a_{01}}J + {a_{02}}K} \right){D^{\left({{a_1} + {a_{11}}J + {a_{12}}K} \right)}}/\\ \;\;\;\;\left[ {\left({{c_0} + {c_{01}}J + {c_{02}}K} \right){D^{\left({{c_1} + {c_{11}}J + {c_{12}}K} \right)}}} \right] + \varepsilon ;\\ {\rm{RSR}} = \left({{b_0} + {b_{01}}J + {b_{02}}K} \right){D^{\left({{b_1} + {b_{11}}J + {b_{12}}K} \right)}} \cdot I/\\ \;\;\;\;\left[ {\left({{a_0} + {a_{01}}J + {a_{02}}K} \right){D^{\left({{a_1} + {a_{11}}J + {a_{12}}K} \right)}}} \right] + \varepsilon 。\end{array} \right. $ | (6) |
式中:a01、a02、a11、a12、b01、b02、b11、b12、c01、c02、c11和c12为哑变量J和K的待估参数;其他符号同前。
如果其中部分参数在统计上与0无显著差异,可将其从模型中剔除。如果在式(6)中增加包含H的指数项,一元模型就变成了二元模型,限于篇幅,这里不再列出。
1.3 模型评价用于评价立木生物量或材积模型的统计指标有很多(Parresol,1999)。根据曾伟生等(2011c)研究结果,评价立木生物量模型的基本统计指标有6项,即确定系数(R2)、估计值的标准误(SEE)、平均预估误差(MPE)、总体相对误差(TRE)、平均系统误差(ASE)和平均百分标准误差(MPSE),这些指标在立木生物量建模中得到广泛应用(Zeng et al., 2012;曾鸣等,2013;曾伟生等,2015;Zeng,2015;Zeng et al., 2017)。本研究采用6项指标中的4项,其计算公式如下:
| $ {R^2} = 1 - \sum {{{\left({{y_i} - {{\hat y}_i}} \right)}^2}} /\sum {{{\left({{y_i} - \bar y} \right)}^2}} ; $ | (7) |
| $ {\rm{SEE}} = \sqrt {\sum {{{\left({{y_i} - {{\hat y}_i}} \right)}^2}} /\left({n - p} \right)} ; $ | (8) |
| $ {\rm{TRE}} = \sum {\left({{y_i} - {{\hat y}_i}} \right)} /\sum {{{\hat y}_i}} \times 100; $ | (9) |
| $ {\rm{MPE}} = {t_\alpha } \cdot \left({{\rm{SEE}}/\bar y} \right)/\sqrt n \times 100。$ | (10) |
式中:yi为观测值;ŷi为估计值;y为样本观测值的平均数;n为样本单元数;p为参数个数;tα为置信水平为α、自由度为n-p时的t值。
根据传统做法,建立回归模型包括模型建立和模型检验。有学者对模型检验的理论和方法学基础提出质疑(Picard et al., 1984;Kozak et al., 2003;曾伟生等,2011c),认为交叉检验不能对回归模型的评价提供额外信息,因此为慎重起见,本研究首先利用全部样本数据进行建模和分析,然后对建立的相容性模型系统采取“抽1/10检验10次”的刀切法方式开展交叉检验,以评价模型的适用性。
另外,为分析不含地域和起源因子与包含地域和起源因子的模型之间是否存在显著差异,采用F检验方法。F统计量按下式(Meng et al., 2008;Zeng et al., 2011)进行计算:
| $ F = \frac{{\left({{\rm{SS}}{{\rm{E}}_2} - {\rm{SS}}{{\rm{E}}_1}} \right)/\left({{\rm{d}}{{\rm{f}}_2} - {\rm{d}}{{\rm{f}}_1}} \right)}}{{{\rm{SS}}{{\rm{E}}_1}/{\rm{d}}{{\rm{f}}_1}}}。$ | (11) |
式中:SSE2和SSE1分别为不含地域和起源因子与包含地域和起源因子模型的残差平方和,而df2和df1分别为不含地域和起源因子与包含地域和起源因子模型的自由度。利用式(11)计算的F与临界值进行比较,以确定2个模型之间是否存在显著差异。一元和二元模型之间的差异也可采用上述F统计指标进行检验。
对于自由度相同的模型之间的比较,如不同地域或起源的一元模型或二元模型,可以检验二者之间线性回归方程y=a+bx 的参数(a, b)与(0, 1)是否有显著差异。F统计量按下式(唐守正等,2008;曾伟生,2010)进行计算:
| $ F = \frac{{\frac{1}{2}\left({a\sum {{y_i}} + b\sum {{x_i}{y_i}} - 2\sum {{x_i}{y_i}} + \sum {x_i^2} } \right)}}{{\frac{1}{{n - 2}}\left({\sum {{{\hat y}_i}} - a\sum {{y_i}} - b\sum {{x_i}{y_i}} } \right)}}。$ | (12) |
其服从自由度f1=2、f2=n-2的F分布。利用式(12)计算的F与临界值进行比较,以确定2个模型之间是否存在显著差异。
2 结果与分析基于马尾松2个总体的全部生物量样本,通过ForStat软件的“非线性误差变量联立方程组”方法,拟合以下4组模型:一是不含地域和起源因子的二元联立方程组式(5)及简化的一元联立方程组;二是包含地域因子的一元和二元联立方程组;三是包含起源因子的一元和二元联立方程组;四是同时包含地域和起源因子的一元联立方程组式(6)及其对应的二元联立方程组。表 2列出了4组模型的参数估计值,表 3列出了4组模型中一元和二元地上生物量方程、地下生物量方程和树干材积方程的统计指标。
|
|
|
|
从表 2可以看出,不论在一元还是二元联立方程组中,地下生物量的估计均只取决于直径,而与树高无关;二元地上生物量方程中的树高参数a2及二元材积方程中的直径参数c1和树高参数c2均与地域和起源无关。
从表 3各项统计指标的对比可进一步看出,对于地上生物量的估计,不论是一元还是二元回归方程,包含地域和起源因子没有改进模型的拟合效果;对于地下生物量的估计,包含地域因子的方程可以显著改进模型的拟合效果(对应于一元和二元联立方程组,其F统计量分别为54.11和45.70,远大于临界值3.09),而包含起源因子的方程反而造成一定负面效果;对于树干材积的估计,包含起源因子的一元方程可以显著改进模型的拟合效果(其F统计量为18.38,大于临界值2.99),而包含地域因子的一元方程及包含地域和起源因子的二元方程反而不如其对应的总体平均模型(不含地域和起源因子的方程)。
从以上分析知,一元联立方程组中,地上生物量与地域和起源无关,地下生物量与地域有关,树干材积与起源有关;二元联立方程组中,地上生物量和树干材积均与地域和起源无关,仅地下生物量与地域有关。据此,重新建立一元和二元联立方程组,参数估计结果见表 4。由表 4可知,10次拟合的参数估计值是稳定的,其平均数非常接近利用全部数据拟合的结果。
|
|
另外,对这10组共60个模型(地上生物量、地下生物量、树干材积一元和二元模型各10个)用抽出的未参与建模的1/10数据进行检验,计算总体相对误差(TRE),看是否满足以下条件(中华人民共和国林业部,1990):
| $ {\rm{TRE}} \le {\rm{MPE}} \cdot {{t'}_a}/{t_a} \cdot \sqrt {n/n'} 。$ | (13) |
式中:MPE为所建模型的平均预估误差;n和n′分别为建模样本和检验样本的样木株数;ta和ta′分别为其对应置信水平为a的t分布值。
结果表明,60个模型中有59个均满足式(13),仅第1组模型中的二元立木材积模型不满足,但也接近临界值。因此,按照传统建模方法,可以认为这10组模型都可以通过适用性检验。很显然,这10组模型中的任何一组都不会比其平均模型更好,而平均模型的数学期望值就是利用全部样本所建的模型。据此,可以得到马尾松的相容性一元和二元地上生物量、地下生物量、树干材积方程以及生物量转换因子和根茎比方程(表 5)。
|
|
另外,从一元和二元模型的对比看,对地上生物量和树干材积的估计,二元模型均显著优于一元模型,如不含地域和起源因子的地上生物量和树干材积方程,二元模型和一元模型的F统计量分别为55.22和631.86,远远大于临界值3.84。对地下生物量的估计,尽管在2个联立方程组中都采用一元模型,但二者依然存在显著差异[按式(12)计算的F统计量为42.48,远大于临界值3.09],一元联立方程组中的地下生物量方程效果更好,这从表 4的统计指标对比中也能反映出来。
3 讨论本研究建立的马尾松一元和二元相容性立木生物量方程和材积方程拟合效果良好,其中,对地上生物量和树干材积的估计,二元模型的效果更好;而对地下生物量的估计,一元模型的效果反而要好一些,与曾伟生等(2010)对南方马尾松立木生物量建模的结论是基本一致的。由于已报道的部分马尾松生物量模型(吕勇等,1996;贺东北等,1998)其建模预估变量不完全一致,本研究选用5篇文献(吴守蓉等,1999;曾伟生等,2010;李海奎等,2010;李际平等,2013;国家林业局,2015c)中的马尾松生物量方程来作对比。利用本次建模的生物量实测值作为对比基础,计算文献中马尾松生物量方程估计值的相对误差,结果见表 6。可以看出,吴守蓉等(1999)及李海奎等(2010)的地上生物量和地下生物量模型误差过大,曾伟生等(2010)的模型误差在10%左右,而国家林业局(2015c)发布的模型,不论是地上生物量还是地下生物量模型,也不论是一元还是二元模型,其误差都在±3%以内,预估效果最好。
|
|
关于地上生物量的估计,本研究表明,地上生物量与地域和起源无关,与Fu等(2014)的结论不完全一致。West等(1997;1999)基于林木分支网络和林木结构的生物力学原理提出了一个通用的地上生物量模型M=aD8/3(也称WBE模型);Zianis等(2004)对包括WBE模型在内的3种简化生物量估计方法进行了对比分析,认为大量研究结果得到的平均参数为2.37,与WBE模型的理论值2.67在统计上有明显差异;曾伟生等(2012)基于几何学观点提出WBE模型的指数参数b应为7/3,并用1 441株样木的实测数据进行了验证,还得出参数a≈0.3ρ(ρ为木材基本密度)。本研究所用301株马尾松样木的平均木材基本密度为0.447 6,据此可以直接得到一个新的地上生物量模型M=0.1 343D7/3。利用该模型估计301株马尾松样木的地上生物量,其相对误差仅为-1.13%,效果非常好,再次验证了曾伟生等(2012)提出的地上生物量模型的通用性,也与本研究得出的马尾松地上生物量估计与地域和起源无关的结论是相符的。
关于地下生物量的估计,从表 4可知不同地域的模型存在显著差异。图 1给出了总体1和总体2地下生物量实测值与估计值之间的差异。可以看出,相同直径的林木,总体1地域范围内的地下生物量要大于总体2。由于总体1的地域范围位于长江流域东南部,而总体2的地域范围位于长江流域中西部,温度、降水等气候条件存在显著差异。为此,利用全国1971—2000年30年的气象资料和每株样木的地理坐标,通过内插法得到每株样木位置的年均温度和年均降雨量,以此为基础分析气候因子对立木地下生物量的影响,结果未发现存在统计上的差异。因此,马尾松不同总体之间地下生物量估计存在差异的原因还有待于进一步探究。
关于树干材积的估计,本研究表明马尾松二元材积方程具有很强的通用性,与地域和起源无关。李晖等(2016)在分析不同区域落叶松二元立木材积表的差异时,通过建立含区域特定参数的立木材积方程,发现3种建模方案(全国1个总体、2个总体和4个总体)之间的差异并不大,得出了与马尾松完全类似的结论。一元材积方程因与树高-胸径回归模型高度相关,而不同起源的马尾松林其龄组结构存在差异(据第八次清查结果,天然马尾松林中近成过熟林面积仅占23%,而人工马尾松林中近成过熟林面积占40%),从而会影响树高-胸径之间的回归关系。尽管表 4中的2个一元材积方程在统计上存在显著差异,人工林的材积估计值大于天然林,但其相对差异都在5%以内,且林木胸径越大相对差异越小,如林木胸径从5 cm增加到50 cm,其相对差异从4.57%逐渐下降到2.66%。
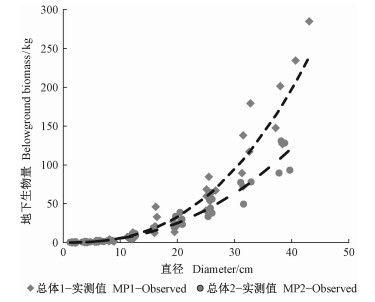
|
图 1 不同建模总体的地下生物量实测值与估计值之间的对比 Fig. 1 Comparison between observed and estimated values of belowground biomass in different modeling populations |
对马尾松地上生物量和树干材积的估计,二元模型比一元模型效果好;但对地下生物量的估计,二元模型反而不如一元模型。地域和起源对马尾松地上生物量的估计均无显著影响,其地上生物量模型具有良好的通用性;但地域对马尾松地下生物量的估计有显著影响,而起源对基于一元模型的树干材积估计有显著影响,人工林的估计值大于天然林。以上结论都是针对本文研究对象马尾松而言的,不一定具有普遍性,对其他树种是否适用,还有待进一步研究。
本研究所建马尾松一元和二元相容性立木生物量方程与树干材积方程,确定系数(R2)均在0.92以上,其中地上生物量方程的平均预估误差在4%以内,地下生物量方程的平均预估误差在8%以内,达到了《立木生物量建模方法技术规程》(国家林业局,2015b)等相关技术规定的预估精度要求,可以推广应用。将哑变量引入误差变量联立方程组,可同时解决多个变量之间的相容性及样本单元数不相等时如何联合建模的问题,是切实可行的生物量建模方法,可为其他类似研究提供参考和借鉴。
董利虎, 李凤日, 贾炜炜, 等. 2011. 含度量误差的黑龙江省主要树种生物量相容性模型. 应用生态学报, 22(10): 2653-2661. (Dong L H, Li F R, Jia W W, et al. 2011. Compatible biomass models for main tree species with measurement error in Heilongjiang Province of northeast China. Chinese Journal of Applied Ecology, 22(10): 2653-2661. [in Chinese]) |
董利虎, 李凤日, 贾炜炜. 2013. 东北林区天然白桦相容性生物量模型. 林业科学, 49(7): 75-85. (Dong L H, Li F R, Jia W W. 2013. Compatible tree biomass models for natural white birch (Betula platyphylla) in northeast China forest area. Scientia Silvae Sinicae, 49(7): 75-85. [in Chinese]) |
国家林业局. 1999. 立木材积表(LY/T 1353-1999). 北京: 中国标准出版社. (State Forestry Administration. 1999. Tree volume tables(LY/T 1353-1999). Beijing: China Standard Press.[in Chinese]. [in Chinese]) |
国家林业局. 2014.中国森林资源报告(2009-2013).北京: 中国林业出版社. (State Forestry Administration. 2014. Report of Forest Resources in China (2009-2013). Beijing: China Forestry Publishing House.[in Chinese]) |
国家林业局. 2015a. 立木生物量建模样本采集技术规程(LY/T 2259-2014). 北京: 中国标准出版社. (State Forestry Administration. 2015a. Technical regulation on sample collections for tree biomass modeling(LY/T 2259-2014). Beijing: China Standard Press.[in Chinese]. [in Chinese]) |
国家林业局. 2015b. 立木生物量建模方法技术规程(LY/T 2258-2014). 北京: 中国标准出版社. (State Forestry Administration. 2015b. Technical regulation on methodology for tree biomass modeling(LY/T 2258-2014). Beijing: China Standard Press. [in Chinese]) |
国家林业局. 2015c. 立木生物量模型及碳计量参数-马尾松(LY/T 2263-2014). 北京: 中国标准出版社. (State Forestry Administration. 2015c. Tree biomass models and related parameters to carbon accounting for Pinus massoniana(LY/T 2263-2014). Beijing: China Standard Press. [in Chinese]) |
贺东北, 骆期邦, 曾伟生. 1998. 立木生物量线性联立模型研究. 浙江林学院学报, 15(3): 298-303. (He D B, Luo Q B, Zeng W S. 1998. Study on linear simultaneous model of tree biomass. Journal of Zhejiang Forestry College, 15(3): 298-303. [in Chinese]) |
李海奎, 雷渊才. 2010. 中国森林植被生物量和碳储量评估. 北京: 中国林业出版社. (Li H K, Lei Y C. 2010. Estimation and evaluation of forest biomass and carbon storage in China. Beijing: China Forestry Publishing House.[in Chinese]. [in Chinese]) |
李晖, 曾伟生. 2016. 不同区域落叶松二元立木材积表的检验及差异分析. 林业科学, 52(6): 157-162. (Li H, Zeng W S. 2016. Validation and comparison of two-variable tree volume tables for Larix spp. in different regions of China. Scientia Silvae Sinicae, 52(6): 157-162. [in Chinese]) |
李际平, 郭文清, 曹小玉. 2013. 基于非线性度量误差的马尾松相容性立木生物量模型. 中南林业科技大学学报, 33(6): 22-25. (Li J P, Guo W Q, Cao X Y. 2013. Compatible nonlinear tree biomass models with measurement error for Masson pine (Pinus massoniana). Journal of Central South University of Forestry & Technology, 33(6): 22-25. [in Chinese]) |
吕勇, 曾思齐, 邓湘文, 等. 1996. 马尾松林分生物量的研究. 中南林学院学报, 16(4): 28-32. (Lü Y, Zeng S Q, Deng X W, et al. 1996. A study of stand biomass of Pinus massoniana. Journal of Central South Forestry University, 16(4): 28-32. [in Chinese]) |
唐守正, 郎奎建, 李海奎. 2008. 统计和生物数学模型计算(ForStat教程). 北京: 科学出版社. (Tang S Z, Lang K J, Li H K. 2008. Statistics and computation of biomathematical models (course of ForStat). Beijing: China Science Press.[in Chinese]. [in Chinese]) |
吴守蓉, 杨惠强, 洪蓉, 等. 1999. 马尾松林生物量及其结构的研究. 福建林业科技, 26(1): 18-21. (Wu S R, Yang H Q, Hong R, et al. 1999. Studies on the biomass of Pinus massoniana plantations and its structure. Journal of Fujian Forestry Sci & Tech, 26(1): 18-21. [in Chinese]) |
曾鸣, 聂祥永, 曾伟生. 2013. 中国杉木相容性立木材积和地上生物量方程. 林业科学, 49(10): 74-79. (Zeng M, Nie X Y, Zeng W S. 2013. Compatible tree volume and aboveground biomass equations of Chinese fir in China. Scientia Silvae Sinicae, 49(10): 74-79. [in Chinese]) |
曾伟生. 2010. 二元立木材积方程的检验与更新方法探讨. 中南林业调查规划, 29(3): 1-5. (Zeng W S. 2010. Discussion on verification and updating of two-way tree volume equations. Central South Forest Inventory and Planning, 29(3): 1-5. DOI:10.3969/j.issn.1003-6075.2010.03.001 [in Chinese]) |
曾伟生, 唐守正. 2011a. 非线性模型对数回归的偏差校正及与加权回归的对比分析. 林业科学研究, 24(2): 137-143. (Zeng W S, Tang S Z. 2011a. Bias correction in logarithmic regression and comparison with weighted regression for non-linear models. Forest Research, 24(2): 137-143. [in Chinese]) |
曾伟生, 唐守正. 2011b. 东北落叶松和南方马尾松地下生物量模型研建. 北京林业大学学报, 33(2): 1-6. (Zeng W S, Tang S Z. 2011b. Establishment of below-ground biomass equations for larch in northeastern and Masson pine in southern China. Journal of Beijing Forestry University, 33(2): 1-6. [in Chinese]) |
曾伟生, 唐守正. 2011c. 立木生物量模型的优度评价和精度分析. 林业科学, 47(11): 106-113. (Zeng W S, Tang S Z. 2011c. Goodness evaluation and precision analysis of tree biomass equations. Scientia Silvae Sinicae, 47(11): 106-113. [in Chinese]) |
曾伟生, 唐守正. 2012. 一个新的通用性相对生长生物量模型. 林业科学, 48(1): 48-52. (Zeng W S, Tang S Z. 2012. A new general biomass allometric model. Scientia Silvae Sinicae, 48(1): 48-52. [in Chinese]) |
曾伟生, 肖前辉, 胡觉, 等. 2010. 中国南方马尾松立木生物量模型研建. 中南林业科技大学学报, 30(5): 50-56. (Zeng W S, Xiao Q H, Hu J, et al. 2010. Establishment of single-tree biomass equations for Pinus massoniana in southern China. Journal of Central South University of Forestry & Technology, 30(5): 50-56. DOI:10.3969/j.issn.1673-923X.2010.05.010 [in Chinese]) |
曾伟生, 姚顺彬, 肖前辉. 2015. 中国湿地松立木生物量方程研建. 中南林业科技大学学报, 35(1): 8-13. (Zeng W S, Yao S B, Xiao Q H. 2015. Construction of individual tree biomass equations for Pinus elliottii in China. Journal of Central South University of Forestry & Technology, 35(1): 8-13. [in Chinese]) |
中华人民共和国林业部. 1990. 林业专业调查主要技术规定. 北京: 中国林业出版社. (Forestry Ministry of P. R. China. 1990. Major regulations on special surveys in forestry. Beijing: Chinese Forestry Publishing House.[in Chinese]. [in Chinese]) |
Borders B E. 1989. Systems of equations in forest stand modeling. Forest Science, 35(2): 548-556. |
Clark J, Murphy G. 2011. Estimating forest biomass components with hemispherical photography for Douglas-fir stands in northwest Oregon. Canadian Journal of Forest Research, 41(5): 1060-1074. DOI:10.1139/x11-013 |
Crecente-Campo F, Soares P, Tomé M, et al. 2010. Modelling annual individual-tree growth and mortality of Scots pine with data obtained at irregular measurement intervals and containing missing observations. Forest Ecology and Management, 260(11): 1965-1974. DOI:10.1016/j.foreco.2010.08.044 |
Dixon R K, Solomon A M, Brown S, et al. 1994. Carbon pools and flux of global forest ecosystems. Science, 263(5144): 185-190. DOI:10.1126/science.263.5144.185 |
Djomo A N, Picard N, Fayolle A, et al. 2016. Tree allometry for estimation of carbon stocks in African tropical forests. Forestry:An International Journal of Forest Research, 89(4): 446-455. DOI:10.1093/forestry/cpw025 |
Dong L H, Zhang L J, Li F R. 2014. A compatible system of biomass equations for three conifer species in northeast, China. Forest Ecology and Management, 329: 306-317. DOI:10.1016/j.foreco.2014.05.050 |
Dong L H, Zhang L J, Li F R. 2016. Developing two additive biomass equations for three coniferous plantation species in northeast China. Forests, 7(7): 136. DOI:10.3390/f7070136 |
Fayolle A, Doucet J L, Gillet J F, et al. 2013. Tree allometry in central Africa:testing the validity of pantropical multi-species allometric equations for estimating biomass and carbon stocks. Forest Ecology and Management, 305: 29-37. DOI:10.1016/j.foreco.2013.05.036 |
Fu L Y, Zeng W S, Zhang H R, et al. 2014. Generic linear mixed-effects individual-tree biomass models for Pinus massoniana Lamb. in southern China. Southern Forests:A Journal of Forest Science, 76(1): 47-56. DOI:10.2989/20702620.2013.870389 |
Henry M, Bombelli A, Trotta C, et al. 2013. GlobAllomeTree: international platform for tree allometric equations to support volume, biomass and carbon assessment. iForest (early view): e1-e5.[2013-07-18]. http://www.sisef.it/iforest/contents/?id=ifor0901-006.
|
IPCC. 2006. IPCC guidelines for national greenhouse gas inventories-agriculture, forestry and other land use. Volume 4. Hayama: IGES.
|
Jenkins J C, Chojnacky D C, Heath L S, et al. 2003. National-scale biomass estimators for United States tree species. Forest Science, 49(1): 12-35. |
Kozak A, Kozak R. 2003. Does cross validation provide additional information in the evaluation of regression models?. Canadian Journal of Forest Research, 33(6): 976-987. DOI:10.1139/x03-022 |
Meng S X, Huang S, Lieffers V J, et al. 2008. Wind speed and crown class influence the height-diameter relationship of lodgepole pine:nonlinear mixed effects modeling. Forest Ecology and Management, 256(4): 570-577. DOI:10.1016/j.foreco.2008.05.002 |
Mugasha W A, Eid T, Bollandsas O M, et al. 2013. Allometric models for prediction of above- and belowground biomass of trees in the miombo woodlands of Tanzania. Forest Ecology and Management, 310: 87-101. DOI:10.1016/j.foreco.2013.08.003 |
Muukkonen P. 2007. Generalized allometric volume and biomass equations for some tree species in Europe. European Journal of Forest Research, 126(2): 157-166. DOI:10.1007/s10342-007-0168-4 |
Návar J. 2009. Allometric equations for tree species and carbon stocks for forests of northwestern Mexico. Forest Ecology and Management, 257(2): 427-434. DOI:10.1016/j.foreco.2008.09.028 |
Parresol B R. 1999. Assessing tree and stand biomass:a review with examples and critical comparisons. Forest Science, 45(4): 573-593. |
Parresol B R. 2001. Additivity of nonlinear biomass equations. Canadian Journal of Forest Research, 31(5): 865-878. DOI:10.1139/x00-202 |
Picard R R, Cook R D. 1984. Cross-validation of regression models. Journal of American Statistical Association, 79(387): 575-583. DOI:10.1080/01621459.1984.10478083 |
Snorrason A, Einarsson S F. 2006. Single-tree biomass and stem volume functions for eleven tree species used in Icelandic forestry. Icelandic Agricultural Sciences, 19: 15-24. |
Somogyi Z, Cienciala E, Mäkipää R, et al. 2007. Indirect methods of large-scale forest biomass estimation. European Journal of Forest Research, 126(2): 197-207. DOI:10.1007/s10342-006-0125-7 |
Tang S Z, Li Y, Wang Y H. 2001. Simultaneous equations, error-in-variable models, and model integration in systems ecology. Ecological Modelling, 142(3): 285-294. DOI:10.1016/S0304-3800(01)00326-X |
Ter-Mikaelian M T, Korzukhin M D. 1997. Biomass equations for sixty-five north American tree species. Forest Ecology and Management, 97(1): 1-24. DOI:10.1016/S0378-1127(97)00019-4 |
Vallet P, Dhôte J F, Le Moguédec G, et al. 2006. Development of total aboveground volume equations for seven important forest tree species in France. Forest Ecology and Management, 229(1/3): 98-110. |
Wang X P, Fang J Y, Zhu B A. 2008. Forest biomass and root-shoot allocation in northeast China. Forest Ecology and Management, 255(12): 4007-4020. DOI:10.1016/j.foreco.2008.03.055 |
West G B, Brown J H, Enquist B J. 1997. A general model for the origin of allometric scaling laws in biology. Science, 276(5309): 122-126. DOI:10.1126/science.276.5309.122 |
West G B, Brown J H, Enquist B J. 1999. A general model for the structure and allometry of plant vascular systems. Nature, 400: 664-667. DOI:10.1038/23251 |
Zeng W S. 2014. Development of monitoring and assessment of forest biomass and carbon storage in China. Forest Ecosystems, 1: 20. DOI:10.1186/s40663-014-0020-5 |
Zeng W S. 2015. Integrated individual tree biomass simultaneous equations for two larch species in northeastern and northern China. Scandinavian Journal of Forest Research, 30(7): 594-604. DOI:10.1080/02827581.2015.1046481 |
Zeng W S, Tang S Z. 2012. Modeling compatible single-tree aboveground biomass equations of Masson pine(Pinus massoniana) in southern China. Journal of Forestry Research, 23(4): 593-598. DOI:10.1007/s11676-012-0299-4 |
Zeng W S, Zhang H R, Tang S Z. 2011. Using the dummy variable model approach to construct compatible single-tree biomass equations at different scales-a case study for Masson pine(Pinus massoniana) in southern China. Canadian Journal of Forest Research, 41(2): 1547-1554. |
Zeng W S, Zhang L J, Chen X Y, et al. 2017. Construction of compatible and additive individual-tree biomass models for Pinus tabulaeformis in China. Canadian Journal of Forest Research, 47(4): 467-475. DOI:10.1139/cjfr-2016-0342 |
Zianis D, Mencuccini M. 2004. On simplifying allometric analyses of forest biomass. Forest Ecology and Management, 187(2/3): 311-332. |
Zianis D, Muukkonen P, Mäkipää R, et al. 2005. Biomass and stem volume equations for tree species in Europe. Silva Fennica Monographs 4, 63.
|
 2019, Vol. 55
2019, Vol. 55
