林业科学  2015, Vol. 51 Issue (11): 50-59   PDF    
DOI: 10.11707/j.1001-7488.20151107
0

文章信息

杨会肖, 刘天颐, 刘纯鑫, 王金榜, 黄少伟
Yang Huixiao, Liu Tianyi, Liu Chunxin, Wang Jinbang, Huang Shaowei
火炬松基因资源林的空间分析
Spatial Analysis of Loblolly Pine Trees as Gene Resources
林业科学, 2015, 51(11): 50-59
Scientia Silvae Sinicae, 2015, 51(11): 50-59.
DOI: 10.11707/j.1001-7488.20151107

文章历史

收稿日期：2014-11-04
修回日期：2015-01-30

作者相关文章

杨会肖
刘天颐
刘纯鑫
王金榜
黄少伟

引用本文
杨会肖, 刘天颐, 刘纯鑫, 王金榜, 黄少伟. 2015. 火炬松基因资源林的空间分析[J]. 林业科学, 51(11): 50-59.
Yang Huixiao, Liu Tianyi, Liu Chunxin, Wang Jinbang, Huang Shaowei. 2015. Spatial Analysis of Loblolly Pine Trees as Gene Resources. Scientia Silvae Sinicae, 51(11): 50-59.  DOI: 10.11707/j.1001-7488.20151107
火炬松基因资源林的空间分析
杨会肖1, 2, 刘天颐1, 3, 刘纯鑫1, 3, 王金榜4, 黄少伟1, 3    
1. 广东省森林植物种质创新与利用重点实验室 广州 510642；
2. 广东省林业科学研究院 广州 510520；
3. 华南农业大学林学院 广州 510642；
4. 英德市林业科学研究所 英德 513055
收稿日期：2014-11-04；修回日期：2015-01-30
基金项目：国家林业局引进国际先进林业科学技术项目"高脂火炬松种质资源与定向选育技术引进"(2014-4-72); 广东省科技计划项目"基于家系林业的火炬松第3代遗传改良与杂交育种"(2011B020302004)。
通讯作者：黄少伟
摘要：【目的】我国南方山地地形复杂，林木遗传试验林大多建立在丘陵地带，环境一致性相对较差，相邻的单株间在空间上存在相互作用关系，空间分析能够减少试验误差，提高遗传效应估算的准确性。【方法】利用不同的空间分析模型对火炬松第1代种子园控制授粉子代和第1代种子园自由授粉子代进行AIC值和方差分量比较，利用最佳的空间模型(AR1η+Rep·；Fam)对火炬松2个子代类群10年生树高、胸径、通直度和枝下高进行遗传参数估算。【结果】不同空间分析模型显示所有性状的最佳空间模型为AR1η模型。空间分析可增加家系方差，减少环境误差方差，从而增加遗传增益的估计值，这使得BLUP预测各亲本的育种值更加准确；所有性状的相邻行间的相关和相邻列间的相关基本一致且均为极强相关，但相邻列间的相关要大于行间的相关。对于第1代种子园控制授粉子代类群，树高的加性方差提高9.1%，残差方差减少7.3%；胸径的加性方差提高0.7%，残差方差减少1.6%；枝下高的加性方差未有变化，残差方差减少18.2%；通直度的加性方差提高50.0%，残差方差减少1.9%。除通直度的单株狭义遗传力提高30.7%外，树高、胸径和枝下高的单株狭义遗传力分别降低24.4%，38.7%和18.7%。对于自由授粉子代，树高的加性方差未有变化，残差方差减少4.9%；胸径的加性方差提高3.2%，残差方差减少2.9%；枝下高的加性方差增加100.0%，残差方差减少20.8%；通直度的加性方差提高33.3%，残差方差减少2.5%。枝下高和通直度的单株狭义遗传力分别提高61.5%，5.8%，树高和胸径的单株狭义遗传力分别降低42.1%，34.2%。若将家系入选率定为15%，对于第1代种子园控制授粉子代，前6名家系与没有使用空间分析模型时的家系号完全相同，其胸径遗传增益比没有使用空间分析模型时提高7.2%；对于第1代种子园自由授粉子代类群，前6名家系中有5个与没有使用空间分析模型时相同，占83%，其胸径遗传增益比没有使用空间分析模型时提高24.5%。【结论】与混合线性模型相比，空间分析可降低残差方差，增加各性状的遗传增益，但不可以忽略试验设计，合理的田间试验设计和空间分析的联合分析能降低环境方差，准确地估算遗传参数，提高林木遗传试验的效率。
关键词： 火炬松    空间分析    遗传参数    育种值    
Spatial Analysis of Loblolly Pine Trees as Gene Resources
Yang Huixiao1, 2, Liu Tianyi1, 3, Liu Chunxin1, 3, Wang Jinbang4, Huang Shaowei1, 3    
1. Guangdong Key Laboratory for Innovative Development and Utilization of Forest Plant Germplasm Guangzhou 510642;
2. Guangdong Academy of Forestry Guangzhou 510520;
3. College of Forestry, South China Agricultural University Guangzhou 510642;
4. Yingde Institute of Forestry Yingde 513055
Abstract: [Objective]The landforms of mountains are complex in the south of China, most genetic trials of forest species were established in hilly areas where the consistency of environmental conditions was relatively poor, spatial interactions exist among adjacent individuals. Spatial analysis can help us decrease experimental errors and enhance the accuracy of estimation of genetic parameters. [Method]The Akaike Information Criterion (AIC) values and variance components for controlled-pollinated family group(G8) and open-pollinated family group(G5) from first-generation seed orchard of Pinus taeda were compared using different models of spatial analysis, and the genetic parameters for height (H), DBH, stem straightness (STR), and clear bole height (CH) were estimated using the best spatial analysis model (AR1η+Rep·Fam). [Result]The best spatial analysis was applied to G8 and G5 using individual-tree models, which improved the additive genetic variance, decreased experimental errors and increased genetic gains. In contrast to the results from base design model, the spatial analysis of field data for G8 and G5 indicated that the autocorrelations were high, and they were consistent between rows and columns. For G8, the additive variance for H was increased by 9.1%, and residual variance was reduced by 7.3%; the additive variance for DBH was increased by 0.7%, and residual variance was reduced by 1.6%; the additive variance for CH was kept the same in the two models, and residual variance was reduced by 18.2%; the additive variance for SSTR was increased by 50%, and residual variance was reduced by 1.9%. Heritability for SSTR was increased by 30.7%, and heritability for H, DBH and CH were reduced by 24.4%, 38.7% and 18.7% respectively. For G5, the additive variance for H was kept the same in the two models, and residual variance was reduced by 4.9%; the additive variance for DBH was increased by 3.2%, and residual variance was reduced by 2.9%; the additive variance for CH was increased by 100.0%, and residual variance was reduced by 20.8%; the additive variance for SSTR was increased by 33.3%, and residual variance was reduced by 2.5%. The narrow-sense heritability of H and DBH for individuals were respectively reduced by 42.1% and 34.2%, and the narrow-sense heritability of CH and SSTR for individuals were increased by 61.5% and 5.8% respectively. For the controlled-pollinated family group(G8), the six top families at a selection rate of 15% of all the tested families, were identical between the groups with and without spatial analysis. For the open-pollinated family group(G5), five of the top six families were identical between the groups with and without spatial analysis. Increased gains for DBH from selection with rate at 15% were 7.2% for G8 and 24.5% for G5.[Conclusion]Compared to the mixed linear model, spatial analysis reduces residual variance and increases genetic gains of various characters, but we cannot ignore the field experimental design, appropriate combination of field experimental design and spatial analysis can reduce the environmental variance, improve the accuracy of estimation of genetic parameters, and improve the efficiency of forest genetic trials.
Key words: Pinus taeda    spatial analysis    genetic parameter    breeding value    

在农业和林业的遗传测定中，合理的田间试验设计结合相应的线性模型是处理地点变异的通用方法(Dutkowski et al., 2002)。林业上常用的试验设计方法是随机完全区组设计(RCB)，它通过设置区组，对试验地不同地块间的条件差异实行有效控制，减少试验误差，提高试验精度(黄少伟等，2001)。但随着技术的发展，尤其是计算机辅助设计技术的发展，传统的随机完全区组设计已经被随机不完全区组和使用区组间信息复原的模型所取代(Dutkowski et al., 2002；Nguyen et al., 1993)。这是因为林业试验中所用的区组通常比较大，区组内的环境差异往往显著，从而大大降低了遗传方差与遗传参数估算的准确性，而采用平衡不完全区组(balanced incompleted blocks，BIB)，则可避免RCB设计的缺陷。

田间试验的目的是准确估算环境效应中的处理效应，但即使是再先进复杂的试验设计，也难以根据地点变异的实际模式来确定设计单元(区组)的边界。田间试验中，地点的变异可以是空间连续的(土壤和小气候效应的相似模式)，也可以是不连续的(栽培措施和测量方法的不同效应)，还可以是随机的(微小环境的异质性)。即使在同一块地点内，试验地的空间连续性变异还可以表现为局部趋势(块状)或总体趋势(梯度型)的差异。在田间试验的分析中，可以解释地点变异和改善处理效应估计的分析方法有：趋势面分析法、后区组处理法(post-blocking)、空间模型分析法等。其中，趋势面分析法是采用空间坐标的多项式函数来模拟环境的变异(Bartlett，1978：Cullis et al., 1991; Gleeson，1997; Singh et al., 2003; Stram et al., 1994; Yang et al., 2004; Pearce，1980)：空间模型分析法是通过行和列的空间自相关分析剔除地点内的空间相关误差来提高遗传试验分析的精确性(Gilmour et al., 2009)。

在我国，林木主要种植在山上和不规则的地形上，而且参试材料多，单株需要较大的空间，因此，林木在重复间和区组间具有很强的空间异质性(Costa e Silva et al., 2013)。当存在空间异质性时，较近的单株间在表现上存在更多的相似性，即近邻效应。空间分析不仅降低了试验误差，而且影响了家系效应的估计，使各家系的排序发生了很大的变化，提高选择精度(White et al., 2007; Hamann et al., 2002; Reed et al., 1985)。本研究的目的是根据试验设计建立单地点生长和形质性状的空间分析模型，在行和列的二维坐标上检验剔除空间变异后研究各方差分量、家系育种值以及遗传增益的变化情况，分析行和列的空间自相关，并检验空间残差方差的独立性，提高遗传效应估算的准确性。

1 材料与方法 1.1 试验材料和试验设计

在联合国发展计划署援建的火炬松(Pinus taeda)改良种子园项目(CPR/91/153，1992—1996)资助下，从美国引进258个不同改良程度的火炬松优良家系。由于试验地难以一次性安排全部258个家系，同时为控制试验区内环境误差，按材料来源和类型划分为8个类群，本研究只对第1代种子园的控制授粉子代(G8)和自由授粉子代(G5)的生长和形质性状展开研究(表 1)，采用随机完全区组设计，栽植密度为3 m×3 m，1997年春季造林。其中，第1代种子园的控制授粉子代林包含47个家系，7次重复，5株行式小区：第1代种子园的自由授粉子代林包含53个家系，5次重复，5株行式小区。

表 1 10年生试验林生长和形质性状① Tab.1 Growth and form traits of progeny groups at age 10 years
1.2 数据收集

造林10年生和14年生时分别对试验林进行每木调查，测量树高与胸径。10年生时进行通直度和枝下高调查，通直度最高分为5分，其中通直无弯曲得5分，1个弯曲得4分，2个弯曲得3分，3到4个弯曲得2分，4个以上弯曲或分叉得1分。空缺或死株以缺失值表示，对试验点中的每株树给定一个行号和列号，利用10年生和14年生的胸径，10年生的通直度和枝下高数据进行不同模型的拟合比较。主要对10年生试验林的生长和形质数据(表 1)进行遗传参数分析。

1.3 统计模型

所有线性模型的一般表达式：y=Xb+Zf+e。式中：y为性状表型观测值构成的向量：b为固定效应构成的向量，且第1个元素为群体均值：f为随机效应构成的向量：e为剩余误差向量：X为固定效应的关联矩阵：Z为随机效应的关联矩阵。

固定效应的估计和随机效应的预测通过解混合模型方程组得到(Henderson，1980)：

$\left[ \begin{gathered} X'{R^{ - 1}}X{\text{ }}X'{R^{ - 1}}Z \hfill \\ Z'{R^{ - 1}}X{\text{ }}Z'{R^{ - 1}}Z + {G^{ - 1}} \hfill \\ \end{gathered} \right]\left[ \begin{gathered} {\hat b} \hfill \\ {\hat f} \hfill \\ \end{gathered} \right] = \left[ \begin{gathered} X'{R^{ - 1}}y \hfill \\ Z'{R^{ - 1}}y \hfill \\ \end{gathered} \right]$
式中：G为每个随机效应的方差协方差直接求和(direct sum);R为残差的方差协方差矩阵，它被认为是独立的误差项且等于σe2I，I为单位矩阵。在空间分析中，R被分成空间自变量方差(σξ2)和空间因变量残差方差(ση2)，R矩阵变为：
$\begin{gathered} R = \sigma _\xi ^2\left[ {{\text{AR1}}\left( {{\rho _{{\text{col}}}}} \right) \otimes {\text{AR1}}\left( {{\rho _{{\text{row}}}}} \right)} \right] + \sigma _\eta ^2I; \hfill \\ \sigma _\xi ^2 = \frac{1}{{n \times m}}\Sigma _{i = 1}^n\Sigma _{j = 1}^n{\left( {{\text{Tre}}{{\text{e}}_{i,j}} - {\text{Tre}}{{\text{e}}_{i + 1,j + 1}}} \right)^2} \hfill \\ \end{gathered} $
式中：⊗为克罗内克(Kronecker)积，AR1(ρ)为一阶自回归相关矩阵，n为行数，m为列数，Treei，j和Tree i+1，j+1分别表示第i行第j列及第i+1行第j+1列上单株同一性状的观测值。

行和列的二维空间当作是可分离的AR1过程，用以下相关矩阵表示：

${\text{AR1}}\left( \rho \right) = \left[ \begin{gathered} 1{\text{ }}\rho {\text{ }}{\rho ^2} \cdots {\rho ^{n - 1}} \hfill \\ \rho {\text{ }}1{\text{ }}\rho {\text{ }} \cdots {\text{ }} \vdots \hfill \\ {\rho ^2}{\text{ }}\rho {\text{ }}1{\text{ }} \cdots {\text{ }} \vdots \hfill \\ \vdots {\text{ }} \vdots {\text{ }} \vdots {\text{ }} \ddots {\text{ }} \vdots \hfill \\ {\rho ^{n - 1}} \cdots {\text{ }} \cdots {\text{ }} \cdots {\text{ }}1 \hfill \\ \end{gathered} \right]$
式中：ρ是自回归系数，在AR1模型下，ρ是相邻误差的相关系数，ρ2是间隔2行或2列的误差相关系数，ρn是间隔n行或n列的误差相关系数。

2个类群空间分析模型的选择过程如表 2，主要采用单株模型，其中μ表示平均均值，Rep表示区组效应，Plot表示小区内单株效应，tree表示加性效应，η表示残差误差(或空间不相关误差)，ξ表示空间自相关误差，e表示环境残差。上述因子中，除了μ作为固定效应外，其余都作为随机效应。模型中各项的方差分量显著性水平可根据单侧似然比检验(one-tailed likelihood ratio tests)，公式可参考文献Stram等(1994)的报道。模型的比较通过赤池信息准则(Akaike Information Criterion，AIC值)，AIC值越小，模型模拟得越好。AIC值的计算公式：AIC=-2 ×(logL-ρ)，式中：logL(log-likelihood)是模型中的极大似然函数值，ρ是模型中评估参数的数量。用AIC值比较模型时，固定效应的参数需要一致。

表 2 火炬松第1代种子园控制授粉子代(G8)和自由授粉子代(G5)2个类群空间分析模型的选择① Tab.2 Selecting best spatial analysis model for controlled-pollinated family group (G8) and open-pollinated family group (G5) from first-generation seed orchard

第1代种子园控制授粉子代类群和自由授粉子代类群的遗传参数估算及其家系和单株育种值的评估模型为y=μ+Rep·Fam+tree+ξ+η，即最佳模型中加入Rep·Fam的随机效应。ASReml软件基于限制性极大似然法(restricted maximum likelihood，REML)估计随机效应的方差组分和利用最佳线性无偏预测法(best linear unbiased prediction，BLUP)预测所有家系和单株的育种值。

空间分析将环境方差(σe2)分为2部分，即σe2=σξ2+ση2，σξ2是由空间变异引起的环境方差，ση2是由非空间变异引起的环境方差。空间分析的目的是从环境方差中剔除部分或全部的σξ2，从而减少环境方差，增加遗传率估计值和选择的增益。单株狭义遗传力计算公式(Falconer，1996; Dutkowski，2005; Dutkowski et al., 2002; Piepho et al., 2007)为：

$h_{\text{i}}^{\text{2}} = \frac{{\sigma _{{\text{tree}}}^{\text{2}}}}{{\sigma _{{\text{Rep \times Fam}}}^2 + \sigma _{{\text{tree}}}^{\text{2}} + \sigma _{\text{\xi }}^{\text{2}} + \sigma _{\text{\eta }}^{\text{2}}}}$
式中：hi2是单株狭义遗传力，σtree2为控制授粉子代和自由授粉子代的加性方差，σRep·Fam2为家系与区组互作的方差。

遗传增益的计算公式如下：

$\Delta G = \frac{1}{m}\sum\limits_{i = 1}^m {{{\hat a}_{i{\text{S}}}}} - \frac{1}{n}\sum\limits_{i = 1}^n {{{\hat a}_{i{\text{ALL}}}}} $
式中：ΔG表示遗传增益，$\hat a$iS表示群体中被选择的第i个家系的BLUP预测育种值，$\hat a$iALL表示群体中第i个家系的BLUP预测育种值，m表示被选择的家系数，n表示群体中所有的家系数。公式用文字表述为在同一群体中，遗传增益等于被选择家系BLUP预测育种值的平均值减去全部家系BLUP预测育种值的平均值。

1.4 ASReml的实现过程

本研究中，利用ASReml进行空间分析时数据格式和程序见图 1。图 1仅列出第1代种子园自由授粉家系和控制授粉家系子代原始数据文件(.csv)内的部分数据。数据文件中的第4列(Group)中，“1”代表第1代种子园自由授粉子代，“2”代表第1代种子园控制授粉子代。在计算第1代种子园控制授粉子代胸径单株狭义遗传力和育种值时，将计算第1代种子园自由授粉子代胸径的单株狭义遗传力和育种值的程序语句“！filter Group !select 1”中的1改成2。

图 1 ASReml进行空间分析的数据和程序 Fig. 1 The data and program by spatial analysis using ASReml softpackage 第4列(Group)中，“1”代表第1代种子园自由授粉子代，“2”代表第1代种子园控制授粉子代。“1” represents open-pollinated family group from first-generation seed orchard; “2”represents controlled-pollinated family group from first-generation seed orchard in the fourth column.
2 结果与分析 2.1 不同模型的拟合效果比较

不同模型的AIC值计算结果表明，完全随机区组设计(RCB)的模型模拟效果都不佳(表 3)。对于自由授粉子代的试验(G5)，除性状SSTR10用AR1模型拟合不如RCB模型外，其余性状的AR1空间模型显著提高了线性拟合效果。同时，AR1η模型拟合的效果比AR1模型更好。仅从AIC值上来看，BaseAR1η模型大多数模拟比AR1η模型好，但后续的模型参数评估结果(表 4)发现，除了性状SSTR10外，其余模型中Rep和Plot的方差分量均不显著，因此，BaseAR1η模型模拟效果与AR1η模型基本一致。对于控制授粉子代的试验(G8)，除了性状SSTR10最佳模型为BaseAR1η外，其余性状的最佳拟合模型都是AR1η模型。第1代种子园自由授粉子代类群的模型结果与控制授粉子代类群的模型相似，经过比较和参数评估值权衡后，所有性状的最佳模型均为AR1η模型。

表 3 不同分析模型的AIC值① Tab.3 AIC values of different analysis models
表 4 不同空间分析模型的参数方差评估值① Tab.4 Variance parameters estimates of different spatial analysis models
2.2 不同模型拟合的参数评估值

模型拟合的参数评估值(表 4)结果表明，对于RCB模型，Plot效应都不显著，而区组效应中，控制授粉子代类群除DBH14不显著外，其他性状均在0.05水平上显著，但是自由授粉子代试验中，所有性状的区组效应σR2都不显著。

在所有拟合的模型中，加性遗传方差在0.05水平上都达到了显著。与RCB模型相比，AR1模型显著提高了σtree2的值，但在后续的最佳模型AR1η中，σtree2的值又下降了，这说明AR1模型拟合效果不佳导致σtree2异常地增大，这与Dutkowski等(2006)的研究结果相似。

关于AR1模型中的误差方差，除了控制授粉子代SSTR10和DBH14的自相关误差方差显著增大外，其他性状的空间自相关误差方差σξ2明显低于RCB的误差方差σe2，同时行、列自回归相关值的趋势类似并且相关值接近1。而最佳模型AR1η中的大多数误差方差是以随机误差方差ση2的形式存在，且ση2和σξ2的比值超过1。

2.3 各性状最佳模型的自相关和空间残差方差

利用最佳的空间模型(AR1η+Rep·Fam)对火炬松第1代种子园控制授粉子代和自由授粉子代中的10年生树高、胸径、通直度和枝下高进行分析，结果见图 2、图 3。从空间残差方差图 2和图 3中可以看出，所有性状的空间残差都不为0，表明这些性状在空间行和列分布上存在空间自相关，且空间上存在变异。从表 5可以看出，所有性状的行相关和列相关均为极强相关，除控制授粉子代枝下高和通直度外，其他性状列相关均大于行相关。基于空间分析的加性方差比之前没有使用空间分析的方差有所提高。对于控制授粉子代类群，树高的加性方差提高9.1%，残差方差减少7.3%：胸径的加性方差提高0.76%，残差方差减少1.6%：枝下高的加性方差未有变化，残差方差减少18.2%：通直度的加性方差提高50.0%，残差方差减少1.9%。除通直度的单株狭义遗传力提高30.7%外，树高、胸径和枝下高的单株狭义遗传力分别降低24.4%，38.7%和18.7%。对于自由授粉子代，树高的加性方差提高50.0%，残差方差减少1.9%：胸径的加性方差未有变化，残差方差减少4.9%：枝下高的加性方差增加100.0%，残差方差减少20.8%：通直度的加性方差提高33.3%，残差方差减少2.5%。枝下高和通直度的单株狭义遗传力分别提高61.5%，5.83%，树高和胸径的单株狭义遗传力分别降低42.1%，34.2%。从这个结果中可以看出，残差方差都有所降低，这是因为一部分方差转换成空间残差方差了。

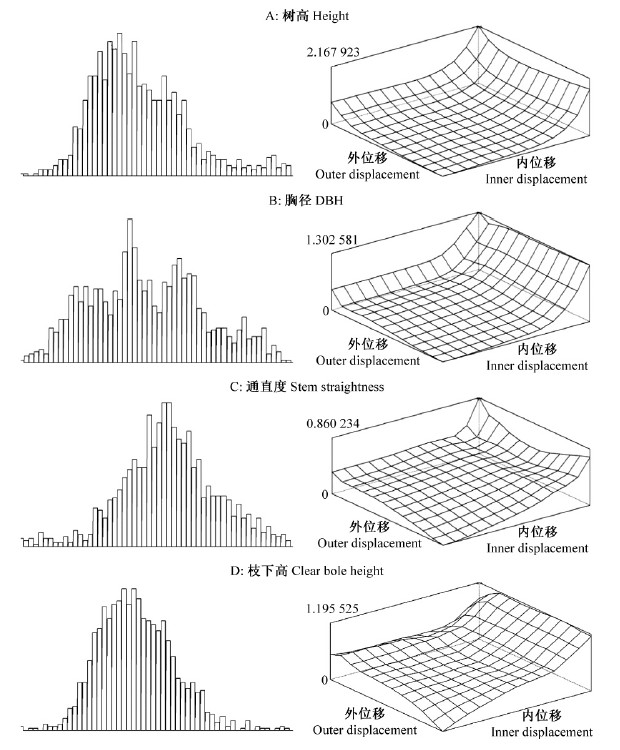图 2 10年生火炬松第1代种子园控制授粉子代生长和形质性状的空间残差方差柱状分布和趋势 Fig. 2 Histogram distribution and variogram of spatial residuals of Loblolly Pine for G8 for growth and form traits at age 10 years
图 3 10年生火炬松第1代种子园自由授粉子代生长和形质的空间残差方差柱状分布和趋势 Fig. 3 Histogram distribution and variogram of spatial residuals of Loblolly Pine for G5 for growth and form traits at age 10 years
表 5 利用空间分析模型估计火炬松第1代种子园控制授粉子代和自由授粉子代10年生性状的遗传参数① Tab.5 Estimated genetic parameters of growth and form traits for G8 and G5 at age 10 years based on spatial analysis model
2.4 育种值预测及遗传增益估算1)

1)利用单株模型预测亲本和单株育种值时，育种值的计算结果保存在后缀名为“.sln”的文件中。第1代种子园自由授粉子代的计算结果共含2 838个BLUP值，其中有53个母本育种值、1 176个子代育种值，其余为交互效应。第1代种子园控制授粉子代计算结果中共含4 572个BLUP值，其中有36个母本育种值和35个父本育种值、1 856个子代育种值，其余为交互效应。以下显示的是部分母本、父本和子代育种值。根据最佳的空间分析模型(AR1η+Rep·Fam)预测控制授粉子代和自由授粉子代10年生时生长和形质的家系育种值，表 6列出了2个类群10年生时胸径育种值大于0的家系。根据预测的胸径育种值，结合10年生树高、通直度和枝下高的育种值，以15%入选率进行2个类群的家系选择。对于第1代种子园控制授粉子代类群，前6名家系与没有使用空间分析模型时的家系号完全相同，只是排列顺序有略微差异，入选家系的遗传增益为1.41 cm，比没有使用空间分析模型时提高了7.2%(没有使用空间分析的各家系育种值未列出)。对于第1代种子园自由授粉子代，前6名家系与没有使用空间分析模型时的148，144，151，149和214共5个家系号相同(占83%)，入选家系的遗传增益为1.53 cm，比没有使用空间分析模型时提高了24.5%。本研究得出的遗传增益是中等的，而Costa e Silva等(2001)获得了较高的遗传增益。

表 6 基于空间分析第1代种子园控制授粉子代和自由授粉子代10年生时生长和形质性状及其预测的育种值 Tab.6 Growth performance and predicted breeding values based on spatial analysis model of families for G8 and G5 at the age of 10 years
3 结论与讨论

火炬松子代试验林中第1代种子园的控制授粉子代和自由授粉子代的树高、胸径、通直度和枝下高性状存在极强的空间自相关，表明它们之间存在跨区组的环境梯度和地块差异，并且列之间的环境相似性要大于行之间的相似性。以往的空间分析表明林木的生长性状有较低的空间自相关。Magnussen(1993)发现北美短叶松(Pinus banksiana)的树高自相关介于0～0.4之间，这些值通过模拟研究增加到0.5。Anekonda等(1996)发现北美红杉(Sequoia sempervirens)无性系的自相关值是0.4。本研究的结果显示生长性状有较高的空间自相关，这是由于独立误差项从自相关成分中分离出来，而不是仅使用单独的自相关误差项。性状具有较高的自相关，表明试验误差是有相关性的而且是不独立的。空间分析的一个主要优势是把相关的误差整合到残差的方差和协方差矩阵中。在一个试验林中，区组间是不同质的和不连续的，但空间变异和空间自相关是连续的，因此区组设计不能完全消除空间变异和空间自相关，故为使试验效果更好需要采用正确的试验设计和空间分析方法。

随着数量遗传学的发展，空间分析在林木遗传试验中的作用越来越大。试验设计能排除供试因子的系统变异，而对于剩余的偶然变异是不能完全控制的。要想从试验数据中得出正确的结论就必须在设计试验时考虑到系统误差和试验的偶然性误差。由于林木试验设计通常不能完全代表环境变异来源，因此把空间组分加入到设计模型中会使得模型在统计上得以改良，也在一定程度上反映了测量性状的本质，同时空间模型提供了一个地点变异更加逼真和满意的描述，从而能更好地阐述地理变异的本质。

空间分析模型的合理选择，能够得到较好的分析结果。在本研究的试验设计中，把自回归误差项加入到设计模型中，并保留了独立误差项。空间分析模型中固定和随机效应的设定基于似然比检验，由于它把环境方差分成空间变异的残差方差和非空间变异的环境方差2个部分，因此与没有使用空间分析模型时相比减少了环境误差方差，增加了预测的精度，减少了遗传方差估计值的标准差，增加了家系方差，这使得遗传力和遗传变异系数的估算值得到了一定的增加，使林木育种者可以更加准确地推断某个特定性状的遗传控制情况和变异幅度等遗传参数。本研究的结果已经说明在一个试验点内树高和胸径空间的局部变异是显著的，剔除这部分变异后火炬松树高、胸径、通直度和枝下高性状的家系方差增加而残差方差减小，这使得遗传参数的估计发生变化。BLUP 预测各家系的育种值也相应地发生变化，使得各亲本的排序发生变化，在给定的入选率下，遗传增益明显提高。

参考文献(References)
[1] 黄少伟,谢维辉.2001.实用SAS编程与林业试验数据分析.广州:华南理工大学出版社.
Huang S W, Xie W H. 2001. Practical SAS programming and anlysis of forestry test data. Guangzhou:South China University of Technology Publishing House.[in Chinese](1)
[2] Anekonda T S, Libby W J. 1996. Effectiveness of nearest-neighbor data adjustment in a clonal test of redwood. Silvae Genetic, 45(1):46-51.(1)
[3] Bartlett M S. 1978. Nearest neighbor models in the analysis of field experiments. Journal of the Royal Statistical Society Series Statistical Methodology, 40(2):147-174.(1)
[4] Costa e Silva J, Dutkowski G W, GilmourA R. 2001. Analysis of early tree height in forest genetic trials is enhanced by including a spatially correlated residual. Canadian Journal of Forest Research, 31:1887-1893.(1)
[5] Costa e Silva J, Potts B M, Bijma P, et al. 2013. Genetic control of interactions among individuals:contrasting outcomes of indirect genetic effects arising from neighbour disease infection and competition in a forest tree. New Phytol, 197(2):631-641.(1)
[6] Cullis B R, Gleeson A C. 1991. Spatial analysis of field experiments:an extension two dimensions. Biometrics, 47(4):1449-1460.(1)
[7] Dutkowski G W, Costa e Silva J, Gilmour A R, et al. 2002. Spatial analysis methods for forest genetic trials. Canadian Journal of Forest Research, 32(12):2201-2214.(3)
[8] Dutkowski G W, Costa e Silva J, Gilmour A R, et al. 2006. Spatial analysis enhances modelling of a wide variety of traits in forest genetic trials. Canadian Journal of Forest Research, 36(7):1851-1870.(1)
[9] Dutkowski G W. 2005. Improved models for the prediction of breeding values in trees. Melbourne,Australia:PhD thesis of University of Melbourne.(1)
[10] Falconer D S. 1996. Introduction to quantitative genetics. 4th ed. New York:Longman.(1)
[11] Gilmour A R, Gogel B J, Cullis B R, et al. 2009. ASReml User Guide Release 2.0. Hemel Hempstead:VSN International Ltd.(1)
[12] Gleeson A C. 1997. Spatial analysis//Kempton R A, Fox P N. Statistical methods for plant variety evaluation. London:Chapman and Hall.(1)
[13] Hamann A, Namkoong G, Koshy M P. 2002. Improving precision of breeding values by removing spatially auto-correlated variation in forestry field experiments. Silvae Genetica, 51(5/6):210-215.(1)
[14] Henderson C R. 1980. A simple method for unbiased estimation of variance components in the mixed model. Journal of Animal Science, 58(1):119.(1)
[15] Magnussen S. 1993. Bias in genetic variance estimates due to spatial autocorrelation. Theoretical and Applied Genetics, 86(2):349-355.(1)
[16] Nguyen N, Williams E R. 1993. An algorithm for constructing optimal resolvable row-column designs. Aust Journao Stat, 35(3):363-370.(1)
[17] Pearce S C. 1980. Randomized blocks and some alternatives:A study in tropical conditions. Trop Agriculture, 57(1):1-10.(1)
[18] Piepho H P, Möhring J. 2007. Computing heritability and selection response from unbalanced plant breeding trials. Genetics, 177(3):1881-1888.(1)
[19] Reed D D, Burkhart H E. 1985. Spatial autocorrelation of individual tree characteristics in loblolly pine stands. Forest Science, 31(3):575-587.(1)
[20] Singh M, Malhotra R S, Ceccarelli S, et al. 2003. Spatial variability models to improve dryland field trials. Genetics, 39(2):151-160.(1)
[21] Stram D O, Lee J W. 1994. Variance components testing in the longitudinal mixed effects setting. Biometrics, 50(4):1171-1177.(1)
[22] White T L, Neale D B, Adams W T. 2007. Forest genetics. Cambridge:CAB International.(1)
[23] Yang R C, Ye T Z, Blade S F, et al. 2004. Efficiency of spatial analyses of field pea variety trials. Crop Science, 44(1):49-55.(1)