杉木(Cunninghamia lanceolata)是我国亚热带地区特有的优良用材树种，也是我国南方主要的造林树种。第7次全国森林资源清查表明，全国杉木人工林面积为853.86万hm2，占全国造林面积的21.35%，在我国森林资源中占有重要的地位。林分蓄积量是反映森林数量的主要指标，蓄积量的大小标志着林地生产力的高低及经营措施的效果。杉木林分蓄积量模型的研究，为改善杉木的经营管理、揭示杉木的生长规律提供重要的参考依据。正是由于林分蓄积量的重要性，因此林分蓄积量模型的研究是林分测算因子建模中的主要对象，国内学者对杉木林分蓄积量模型做了不少研究(杜纪山等，2000;许炜敏等，2012)。根据模拟对象的不同，可以分为基于单木材积生长模型(单木水平)预测林分蓄积量和基于林分蓄积量生长模型(林分水平)预测林分蓄积量。这2种方法各有优缺点:基于林分蓄积量生长模型能够直接预测林分蓄积量，但却无法反映出详细的单木信息;基于单木材积生长模型预测林分蓄积量，可以得到详细的单木信息，如各单木的生长状况，但是利用该模型预测林分蓄积量相对比较复杂，而且会导致误差积累(Qin et al.，2006;Zhang et al.，2010;孟宪宇，1996;张雄清等，2011)。

从理论上来讲，上述2类模型所得到的林分蓄积量预测值应该是一致的;但是由于模型的误差及模型自身结构的问题，这2类模型所预估的林分蓄积量却有可能不一致。随着林分蓄积量模型研究的深入，考虑到单木水平模型和林分水平模型的特点，在模拟过程中利用单一水平的模型预估林分蓄积量有一定的局限性。研究如何综合利用这2类模型所提供的信息和特点、提高杉木林分蓄积量模型的兼容性显然很有意义。解聚法使得单木水平模型所得的林分蓄积量尽可能地与林分水平模型所得的林分蓄积量相匹配，进而提高林分蓄积量模型的兼容性(Ritchie et al.，1997; Qin et al.，2006)，但是该方法仅是缩小了单木水平预测结果与林分水平预测结果的差别，实际上并没有解决林分蓄积量模型的兼容性问题。Yue等(2008)提出利用组合预测法提高林分断面积预测模型的兼容性，该方法能够充分利用单个模型所提供的有效信息，减少单个模型中随机因素的影响，分散不同的模型预测误差，最终提高模型预测精度。然而对于林分蓄积量模型兼容性的研究未见报道。

本文以江西杉木林为研究对象，利用组合预测法研究杉木林分蓄积量模型，将林分模型和单木模型进行组合，从而达到杉木林分蓄积量预测的一致性，既解决了杉木林分蓄积量模型的兼容性问题，同时也提高了杉木林分蓄积量预测的精度。

试验地位于江西省分宜县大岗山年株林场场部后山，属于罗霄山脉北端的武功山支脉，114°30'—114°45'E，27°30'—27°50'N。年株林场场部后山海拔250 m，低山，母岩为砂页岩，年平均气温16.8 ℃，降雨量1 656 mm，年蒸发量1 503 mm，属南亚热带季风气候区。

该试验林使用1年生苗木于1981年造林，采用随机区组试验设计，5个密度: A密度(2 m×3 m)、B密度(2 m×1.5 m)、C密度(2 m×1 m)、D密度(1 m×1.5 m)、E密度(1 m×1 m)，每个密度3次重复，共15个样地，每个样地面积为600 m²。样地内每株树进行编号，造林当年对样地内林木进行每木检尺。1989年前逐年调查，1989年后隔年调查。本研究数据从1989年到2007年。由于1998年受到冰冻灾害的影响，在1999—2001年间，高密度林分中出现了大量死亡林木，因此，本研究中去掉这期的调查数据。利用这些复测数据可以组成调查间隔期2年的120个样地，随机选取75块样地用于建模，45块样地用于模型检验。杉木林分变量因子统计量见表 1。

表 1 杉木林分及林木因子统计 Tab.1 Statistics of stand variables and tree variables

表 1 杉木林分及林木因子统计 Tab.1 Statistics of stand variables and tree variables 变量 Variables 建模数据Fit data 检验数据Validation data 最小值 Min. 最大值 Max. 均值 Mean 标准差 S. D. 最小值 Min. 最大值 Max. 均值 Mean 标准差 S. D. 年龄Age/a 10.00 28.00 18.00 6.07 14.00 26.00 20.00 4.25 优势高Dominant height/m 8.82 18.44 13.69 2.37 10.37 18.13 14.17 1.80 林分蓄积量Stand volume /(m3·hm-2) 95.01 339.72 226.09 58.79 115.62 324.11 242.92 41.20 株数Number of trees/hm-2 1 450.00 9 883.00 4 153.95 2 177.12 1 500.00 8 950.00 4 160.00 2 011.48 林分平方平均直径Quadratic mean diameter/cm 7.50 20.16 12.87 3.09 8.68 19.75 13.18 2.84 林分断面积Stand basal area/ (m2·hm-2) 20.07 423.28 111.00 110.65 28.04 297.71 97.05 78.09 单木胸径Diameter at breast height/cm 1.30 32.40 11.24 3.91 1.60 31.50 11.68 3.75

首先根据单木胸径值，利用部颁杉木一元材积表经验公式计算出单木材积:

然后以林分年龄、林分优势高、林分密度等为自变量，建立单木材积模型和林分蓄积量模型(Qin et al.，2006;2007;张雄清等，2010)。

单木水平:

林分水平:

式中: RS₁为相对植距指标，RS₁=$\left({\sqrt {10\;000/{N_1}} } \right)/{H_1}$;A₁为前期林分的平均年龄，a;H₁为前期林分的优势木平均高，m;N₁为前期林分的公顷株树，株hm^-2;D_q1为前期林分平方平均直径，cm;B₁为前期林分胸高断面积，m²·hm^-2;M₁^s为前期林分蓄积量，m³ hm^-2;V_i，1为前期第i株树的材积，m³;d_i，1为前期第i株树的胸径，cm;P_i，2为第i株林木的存活概率;α₁，α₂，…δ₄为待估参数。

根据方程(2)，可以得出第2期单木材积预估值${{\hat V}_{i，2}}$，然后结合单木存活概率预测值${{\hat P}_{i，2}}$，可以计算出第2期林分蓄积量预估值，即得到了单木水平的林分蓄积量预估值M^t: ${M^{\rm{t}}} = \sum\limits_{i = 1}^j {{{\hat P}_{i，2}}{{\hat V}_{i，2}}/S} $(S为样地面积，hm²;j为样地林木株数)。根据林分蓄积量方程(4)，可以得到林分水平的林分蓄积量预估值M^s。

根据Bates等(1969)提出的组合预测法，林分蓄积量的组合预测模型如下:

式中: M^c为林分蓄积量的组合预测值;μ₁为权重因子(0 ＜ μ₁ ＜ 1)。

组合预测模型权重系数估计的常见方法有标准差法、方差协方差法(Granger et al.，1977;Yue et al.，2008)、误差平方和法(Winkler et al.，1983)、最优加权法(唐小我，1992)等。张雄清等(2011)对以上4种不同的权重计算方法进行了比较分析，发现最优加权法能够去除单个预测模型在组合预测模型中有偏的影响，从而使得组合预测模型的预测精度最高。因此，在本研究中，利用最优加权法计算林分蓄积量组合预测模型的权重系数。

首先，构造目标函数$\min \sum\limits_{k = 1}^k {{{\left[ {{M_k} - \left({{\omega _1}M_k^{\rm{t}} + {\omega _2}M_k^{\rm{s}}} \right)} \right]}^2}} $，约束条件ω₁+ω₂=1。式中: M_k为第k个样地林分的公顷蓄积量。

记W=(ω₁，ω₂)^T，R=(1，1)^T，e_i=(e_i1，e_i2，…e_in)。式中: T表示转置;W表示组合预测权重系数列向量;R表示元素全为1的n维列向量;e_i表示第i种模型的预测误差向量;n为样地数;i=1，2，即单木水平模型和林分水平模型。

令J=(e₁，e₂)，则J^TJ=$\left(\begin{array}{l} e_1^T\\ e_2^T \end{array} \right)\left({{e_1}\;\;\;{e_2}} \right)= \left(\begin{array}{l} e_1^T{e_1}\;\;\;e_1^T{e_2}\\ e_2^T{e_1}\;\;\;e_2^T{e_2} \end{array} \right)= E$，那么可以推导得到权重向量，详细推导过程见张雄清等(2011):

式中: E^-1为逆矩阵。

林分蓄积量模型、单木材积模型和单木存活概率模型等可以通过统计量平均误差(MD)、平均绝对误差(MAD)、均方根误差(RMSE)和决定系数(R²)、对数似然值(lgL)进行评价。它们的数学表达式分别为:

式中: y_i为实际值(林分蓄积量、单木材积、单木存活概率);${{\hat y}_i}$，${{\bar y}_i}$分别为它们的预测值和平均值;p_i为单木存活概率;n为观察个数。本研究参数估计、模型检验均利用SAS软件完成。

经过模型参数的检验，单木材积模型、单木存活概率模型和林分蓄积量模型的参数估计值及统计检验见表 2。由表 2可知，各参数估计在0.05水平上显著。林分蓄积量模型的MD为0.154 3，MAD为5.522 4，RMSE为6.824 1，R²为0.983 7;单木材积模型的MD为-6.91E-5，MAD为0.003 9，RMSE为0.007 3，R²为0.981 2;单木存活概率模型的RMSE为0.171 0，lgL为4 180.58。根据各模型的评价统计量值发现，各模型的拟合效果较好。经过Kolmogorov-Smirnov正态性检验，单木材积模型的残差和林分蓄积量模型的残差均服从正态分布，且对自变量没有明显的估计偏差(图 1，图 2)。

表 2 模型参数估计值及模型评价统计量 Tab.2 Parameter estimates and model evaluations

表 2 模型参数估计值及模型评价统计量 Tab.2 Parameter estimates and model evaluations 属性 Attribute 参数 Parameter 估计值 Estimate 标准误 Std. error 平均误差 MD 平均绝对误差 MAD 均方根误差 RMSE 决定系数 R2 林分蓄积量 Stand volume/(m3·hm -2 ) δ1 6.026 4 1.093 5 0.154 3 5.522 4 6.824 1 0.983 7 δ2 4.779 2 2.256 4 δ3 -0.641 2 0.077 6 δ4 -8.352 7 4.193 4 单木材积 Tree volume/m3 α1 2.149 9 0.298 9 -6.91E -5 0.003 9 0.007 3 0.981 2 α2 24.780 4 0.492 5 α3 -1.219 5 0.062 2 α4 -7.565 9 0.443 6 α5 1.154 0 0.014 6 单木存活概率 Tree survival β1 -6.821 9 2.150 8 - - 0.171 0 4 180.58 (lgL) β2 0.191 4 0.015 2 β3 -1.891 4 0.075 8 β4 0.795 8 0.227 4

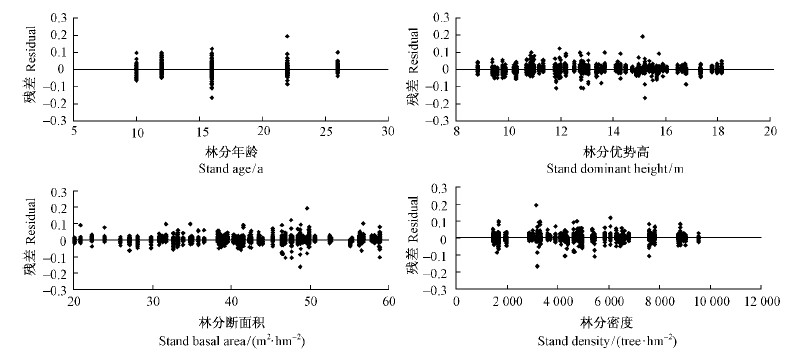	图 1 单木材积模型的残差 Fig. 1 Residuals of the tree volume model

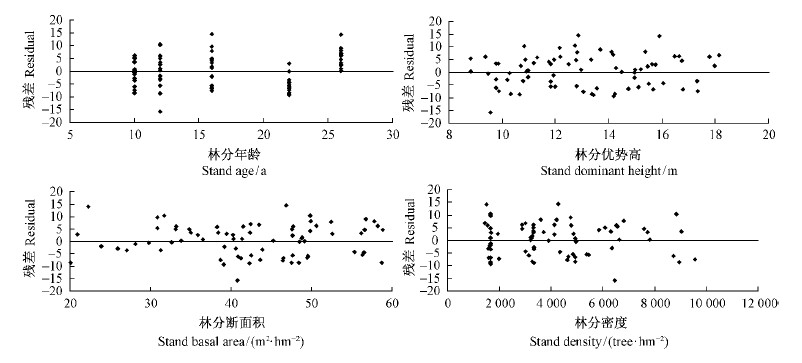	图 2 林分蓄积量模型的残差 Fig. 2 Residuals of the stand volume model

根据最优加权法得到组合预测模型中的权重系数: ω₁=0.170 8，ω₂=0.829 2，然后利用式(5)可以得到林分蓄积量的组合预测值。根据这2个权重系数，可以计算出林分蓄积量的组合预测值。各种不同水平模型所预测的林分蓄积评价统计量比较见表 3。由表 3可知，在建模数据中，通过单木水平模型所得的林分蓄积量的MD为-0.565 8，MAD为6.332 4，RMSE为7.949 1，R²为0.977 9;通过林分水平模型所得的林分蓄积量的MD为0.154 3，MAD为5.522 4，RMSE为6.824 1，R²为0.983 7;通过组合预测模型所得的林分蓄积量的MD为0.031 3，MAD为5.472 8，RMSE为6.769 9，R²为0.984 0。根据这些模型的评价统计量值，可以发现通过组合模型预测林分蓄积量的精度最高。最优加权法是组合预测模型确定权重系数的重要方法之一，在其他领域的研究中也有广泛应用(于晓秋等，2007;李秀珍等，2008)。这种方法以误差平方和最小为目标函数，这也解释了组合预测模型中均方根误差RMSE在这3个模型中最小、决定系数R²最大的原因。

表 3 各种不同模型的评价统计量(建模数据) Tab.3 Model evaluations based on different models(fit data)

表 3 各种不同模型的评价统计量(建模数据) Tab.3 Model evaluations based on different models(fit data) 属性Attributes 单木水平Tree-level 林分水平Stand-level 组合预测模型Forecast combination 平均误差MD -0.5658 0.1543 0.0313 平均绝对误差MAD 6.332 4 5.522 4 5.4728 均方根误差RMSE 7.9491 6.824 1 6.7699 决定系数R2 0.9779 0.983 7 0.984 0

表 4列出了利用检验数据所得的各种不同模型的评价统计量。根据这些评价统计量，发现在检验数据中通过组合预测法预测林分蓄积量也比通过单项预测(单木水平模型、林分水平模型)的效果都要好，这与表 3的结果一致。

表 4 各种不同模型的评价统计量(检验数据) Tab.4 Model evaluations based on different models(validation data)

表 4 各种不同模型的评价统计量(检验数据) Tab.4 Model evaluations based on different models(validation data) 属性Attributes 单木水平Tree-level 林分水平Stand-level 组合预测模型Forecast combination 平均误差MD -4.4920 -4.3737 -4.3494 平均绝对误差MAD 8.0380 6.800 8 6.6957 均方根误差RMSE 9.6880 8.224 8 8.1989 决定系数R2 0.9360 0.9538 0.9542

各不同模型的林分蓄积量预测值与实际值的线性相关见图 3。由图 3可知，通过组合预测法预测林分蓄积量的相关系数R²比其他单项预测的R²都高，精度最高。因此，利用组合预测法预测林分蓄积量相对于其他2种方法预测精度较高，效果较好。同时利用组合预测法使得不同水平模型预测所得的林分蓄积量趋于一致，保证了林分蓄积量预测的一致性，提高了林分蓄积量模型的兼容性。

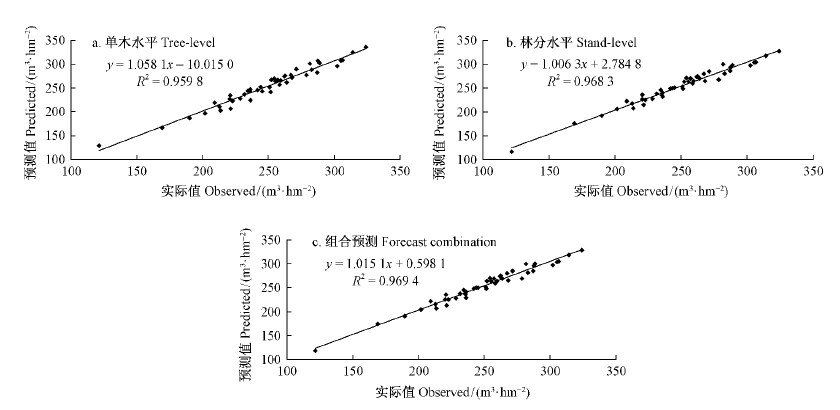	图 3 3种不同方法的林分蓄积量预测值与实际的值线性相关 Fig. 3 Correlations of predicted and observed stand volume based on 3 methods

杉木林分蓄积量模型，是杉木生长模型系统的一个重要组成成分。随着杉木林分蓄积量模型研究的深入，考虑到单木水平模型和林分水平模型的特点，在模拟过程中利用单项模型预估杉木林分蓄积量都有一定的局限性。因此，提高杉木林分蓄积量模型的兼容性显然很有意义。Zhang等(1993)利用解聚法使得单木材积模型所得的林分蓄积量尽可能地与林分蓄积量模型所得的林分蓄积量相匹配，进而提高单木生长模型和林分生长模型预测林分蓄积量的兼容性，但是并没有考虑利用单木水平和林分水平生长模型的组合估计量来彻底解决兼容性。组合预测方法能够充分利用单项预测模型所提供的有效信息，减少单项模型中随机因素的影响，使单项模型之间优势互补，分散预测误差，因而提高了模型的精度(Bates et al.，1969;张雄清等，2009)。在本研究中，利用组合预测法预测杉木林分蓄积量，既包含了单木水平的详细信息，也包含了林分水平的信息，并综合利用了这2种水平所提供的信息和特点，分散预测误差，其预测精度比单木水平和林分水平模型的预测精度都要高。同时，利用组合预测法预测杉木林分蓄积量，使单木水平和林分水平模型所得的林分蓄积量组合成一个林分蓄积量值，保证了杉木林分蓄积量预测的一致性，提高了杉木林分蓄积量模型的兼容性。

在组合预测模型中，权重的计算对提高组合预测结果的精度非常重要。Newbold等(1974)认为在单项预测模型之间不存在相关性的前提下利用误差平方和法计算组合预测模型的权重系数，预测精度较高。Bates等(1969)首先提出了组合预测方法，并在研究中利用方差协方差法来计算组合预测模型的权重系数。该方法以组合预测模型的方差最小为目标从而计算得到最优的权重系数组合，如果各单项模型权重值可以保持稳定，那么该方法的预测结果稳定性比较好。但是在通常情况下，单项模型权重值不稳定，因此应用该方法确定组合预测模型的权重有一定的局限性(张艳等，2006)。张雄清等(2011)对以上几种不同的权重计算方法进行了比较分析，研究发现最优加权法能够去除单项预测模型在组合预测模型中的有偏估计，从而提高组合模型的预测精度。然而在本研究中通过最优加权法得到的杉木林分蓄积量组合模型权重系数是不变的。若权重值假定为常数，那么组合预测模型可能不能很好地反映预测模型的有效性，将会导致组合预测模型的精度降低。引起权重系数变化的原因主要是样地数据结构的变化，相同蓄积模型的表现不同，这会使得每个预测模型可能表现出“时好时坏”，反映在权重系数上表现为“时大时小”，若继续采用这种固定权重的组合预测模型，预测结果可能会有误差。因此，今后应该研究非负变权重组合预测模型的构建，从而进一步提高杉木林分蓄积量的预测精度。