文章信息
- 朱臻, 沈月琴, 张耀启, 石文, 王枫
- Zhu Zhen, Shen Yueqin, Zhang Yaoqi, Shi Wen, Wang Feng
- 碳汇经营目标下的林地期望价值变化及碳供给——基于杉木裸地造林假设研究
- Change of Forestland Expected Value and Carbon Supply in the Objective of Carbon Sequestration: Based on the Chinese Fir Plantation in Bared Land
- 林业科学, 2012, 48(11): 112-116.
- Scientia Silvae Sinicae, 2012, 48(11): 112-116.
-
文章历史
- 收稿日期:2011-04-25
- 修回日期:2011-06-29
-
作者相关文章
2. 美国奥本大学 阿拉巴马 36849
2. Auburn University Alabama, USA 36849
当今全球气候变化问题已成为世界各国面临的最重大挑战之一,森林生态系统是全球碳循环重要组成部分,研究表明通过森林固碳方式来减缓碳释放不仅潜力巨大,而且具明显的成本优势(van Kooten et al., 1995;Murry,2000;Benítez et al., 2004)。因此,通过林业活动增加森林碳汇(减缓碳释放)是应对气候变化的重要途径。我国也将森林碳汇作为应对气候变化的重要选择,并提出相应的行动方案与发展目标。但是应认识到基于森林碳汇目标的林业经营方式将发生极大改变,此种变化体现在物质和技术等生产要素投入以及产出的增加。基于资金时间价值和碳价格变化的因素影响,林业经营者所面对的最佳经营决策也将发生改变。从“经济人”角度出发,林业经营主体追求林地收益最大化是林业经营的目标,因此模拟碳市场价格变动,比较基于碳汇和单一木材收益经营目标之间最佳轮伐期和林地期望值变化,从而帮助森林经营者选择林业经营最优决策方案就具有重要的研究价值和实践意义。
目前国外学者对森林碳汇经营决策方面已作了一定的相关研究。利用Hartman模型分析不同树种在最佳轮伐期和碳供给下不同碳支付形式所带来的影响(Stainback et al., 2002)。Nhung(2009)以马占相思(Acacia manqium)和尾叶桉(Eucalyptus urophylla)为例,分析了确保木材采伐和碳汇价值最大化下2个树种的森林经营模式,比较分析了有无碳市场情况下林业经营的最佳决策方案。对碳供给进行了研究,在森林碳汇成本研究基础上,开始尝试估计特定树种的碳汇供给曲线。如Guitart等(2010)模拟了不同立地条件的森林碳汇供给曲线,Benitez等(2004)通过敏感性分析发现,土地价格、木材价格和碳吸收率是影响碳汇供给的重要因素。国内则对森林碳汇相关研究刚刚开始,对碳储量的计算主要集中在自然科学领域,如刘国华等(2000)利用我国第1~4次森林资源清查资料,通过拟合回归方程对我国20年的森林碳储量进行了估算。周国模等(2004)研究毛竹(Phyllostachys edulis)林的碳储量;在社会科学方面的研究主要集中在森林碳汇市场交易方面,以定性分析为主。如何英等(2007)分析了中国森林碳汇交易市场现状与潜力;冯亮明等(2009)提出在国内成立一个自愿碳排放权交易市场等。研究相关文献可以发现,国内对碳市场背景下林地期望值变化和森林碳汇供给潜力方面的系统研究缺乏,更缺少实地的调查案例研究。
本文以浙江省杉木(Cunninghamia lanceolata)为对象,以林种生长模型以及实地调查等数据为基础,利用改进的Faustmann模型模拟不同碳价格下树种所属林地期望值和最佳轮伐期的变化,从而分析不同碳价格和轮伐期水平下最优林种经营方案。以此为基础获得树种碳汇供给曲线和区域水平的供给潜力和前景,既可以有效弥补国内研究的相对空白,也为政府促进森林碳汇供给提供决策依据。
1 案例点和数据 1.1 案例点杉木是与中国南方环境相适应的重要速生树种,是南方首要的商品材树种。20世纪50年代杉木造林面积迅速增加(浙江森林编辑委员会,1993)。2009年浙江省森林资源清查数据显示,杉木林蓄积量达到7 294.70万m3,仅归属为生态公益林的杉木林面积就达到10.53万hm2(张骏等,2010),因此选择杉木作为案例树种,研究碳汇经营目标下的浙江省林地期望价值及碳供给具有典型性。本文以浙江省昌化林场作为案例点开展实地调查。昌化林场地处浙江省西北部。场部设在临安市龙岗镇西1 km处,地理坐标为119°07′25″ E、30°10′05″ N。林场经营总面积2 110 hm2,2010年末职工总数113人,林场职工人均年收入9 737元。
1.2 数据和模型设计笔者基于裸地造林的假设,了解林场目前每公顷裸地造林的相关成本。经营成本由3部分构成:1)种植成本。主要包括种苗和人工劳务成本。据调查,种苗成本为1 350元· hm-2,人工劳务成本为4 500元· hm-2。一般在第1年种植后,林场会在第2,3,4年进行补植,保证造林存活率和种植规模。其中补植成本中种苗成本每年217元· hm-2,人工劳务成本每年1 500元· hm-2;2)管护成本。主要包括每年人工抚育成本,目前营林活动中没有化肥农药成本。据调查,每年人工抚育成本为81.75元· hm-2;3)采运成本。包括采伐和运输成本。据调查,该林场采伐成本为140元·m-3,运输成本为40元·m-3。目前采运过程中已经无需缴纳各项税金。根据调查,2010年木材的市场价格为胸径10 cm以下为600元·m-3;10~20 cm为850元·m-3;20 cm以上为1 000元·m-3。
传统木材经营模式中轮伐期设计是基于林地收获的最高期望值,而在碳汇林经营中存在2个目标且同时又矛盾(Guitart,2010):即木材和碳收益的最大化。因此可以称为复合林业经营目标。基于复合林业经营目标下的森林经营,由于考虑到碳价值,轮伐期会相应的延长(van Kooten et al., 1995),因此不但需要承受正常的生产资料投入成本,还需要承受是否改变轮伐期的机会成本(即为延长轮伐期带来更多的碳收益),这部分机会成本也可以看作森林碳汇的价值。由于目前没有杉木碳汇林经营的相关样地数据,笔者只考虑现有经营模式下增加碳汇经营目标后对于林地期望值和最佳轮伐期的影响。
1) 采用的杉木生长模型国内学者开展了大量的杉木生长模型和经济成熟龄的研究,但时间相对较早。如周国模等(2001)、吴载璋等(2004)和陈则生(2004)的研究。为了测算杉木不同生长年份的蓄积量,笔者采用陈则生(2004)设计的生长模型其生长模型:
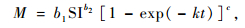
|
(1) |
其中:M表示为杉木蓄积量,SI表示为立地指数,t为林分年龄。b1=4.535 47,b2=1.609 31,c=3.720 004,k=0.096 004,立地指数SI=15。
杉木的平均胸径和树高模型:

|
(2) |
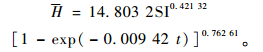
|
(3) |
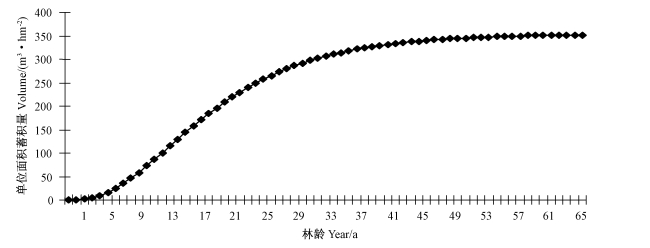
鉴于缺少碳汇林生长模型的研究,笔者考虑的是在现有经营强度下的复合经营最佳决策问题,并与单一目标进行比较,因此在复合经营目标下仍然采用单一目标下的生长模型(图 1)。
|
图 1 杉木蓄积量变化 Fig.1 Volume change of Chinese fir |
2) 不同目标经营情景下的林地期望值模型在本研究中主要是基于裸地造林的假设。笔者采用林地期望价法来预测复合经营目标下杉木的最佳轮伐期和林地期望值,并与单一经营目标相比较。可以发现,在单一目标和复合目标2种情景下森林经营的收益是不同的。传统的森林经营收益只有木材收益,可以表示为(4)式;而复合经营目标的森林经营收益既包括传统的木材收益,同时也包括碳收益,可以表示为(5)式:
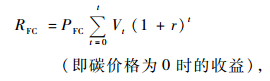
|
(4) |
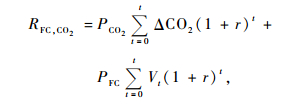
|
(5) |
其中:RFC,CO2代表复合经营目标的林种收益,PCO2代表碳价格,ΔCO2代表轮伐期中碳的净储量,r表示利率,在这里使用利率5%水平,t表示轮伐期,PFC表示木材价格,Vt表示t轮伐期内的蓄积量,RFC表示单一经营目标的林种收益。考虑到不同目标下林地经营的成本也有差异,基于Faustmann模型,则2类目标的林地期望价值可以分别表示为:
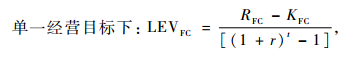
|
(6) |
其中: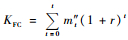
复合经营目标下:
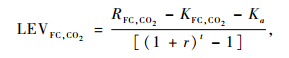
|
(7) |
其中: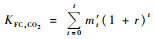
采用朱向辉等(2008)的研究成果,测定杉木各器官的含碳量,各器官烘干质量含碳率Pi分别为:干52.34%,根47.22%,枝49.95%,叶51.28%。立木平均单株碳质量Ci= ΣWiPi,其中Wi为烘干的各器官生物量,Pi为各器官的含碳率。其中烘干的各器官的生物量模型分别为下式:
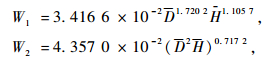
|
(8) |
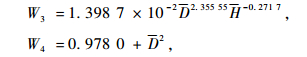
|
(9) |
其中:W1,W2,W3和W4分别为干、根、枝和叶的烘干生物量,D,H分别为平均胸径和树高(式2,3)。计算得到立木平均单株碳质量Ci后,根据标准造林密度,计算得到杉木样地的碳密度(kg·hm-2)。根据样地单位面积蓄积量101.65 m3·hm-2,换算得到杉木每m3的碳密度。本研究采用的碳价格为11美元·t-1(李峰等,2011)。在计算碳汇林经营中的固碳量时除了应计算净碳含量外,还需要注意2个问题:应考虑杉木采伐加工成产品后,其生命周期结束后存在的碳释放。笔者假设杉木制品的生命周期为50年;另一方面,木材在采伐、加工成产品时必然存在损失消耗,笔者假设木材利用率为95%。
2 碳价格变化对林地期望值和碳供给的影响林业经营者所面对的最佳经营决策主要考虑最佳轮伐期问题。以杉木为例,单一和复合经营目标的区别可能导致最佳轮伐期会发生变化;另一方面碳价格的波动也会影响到最佳轮伐期乃至碳储量的供给,因此有必要进行深入分析。
2.1 基于两类经营目标的最佳轮伐期和林地期望值比较基于裸地造林的假设,利用上述改进的Faustmann模型,笔者分别计算了单一目标和复合经营目标下的林地期望值和最优轮伐期。在单一木材收益最大化目标下,根据现有杉木价格和经营成本则最优轮伐期为18年,与陈则生(2004)计算得到最佳轮伐期接近,林地期望值为83 776元·hm-2;复合经营目标下,在目前碳和杉木价格水平以及经营成本下,最优轮伐期也为18年,林地期望价达到86 767元·hm-2。在原来的经营强度下,增加碳汇的经营目标并没有延长最佳轮伐期,即林业经营者在复合经营目标下并不会改变原来的采伐决策。这主要原因是目前木材市场价格远远高于碳的市场价格,导致杉木经营者所面对的改变最佳轮伐期的机会成本很小,所以两类目标下最佳轮伐期保持不变。计算得到的林地期望值远高于陈则生(2004)、Stainback(2002)的相关研究,主要原因有多方面:1)本研究所采用的现有木材市场价格远大于之前学者所采用的价格,如Stainback等(2002)所采用的市场价格仅为10.24~28.96美元·m-3,而陈则生(2004)采用的木材价格为410~530元·m-3;2)近年来由于各种税费的减免使得营林成本大大减少;3)本研究采用的样地为立地条件最好的一类地。
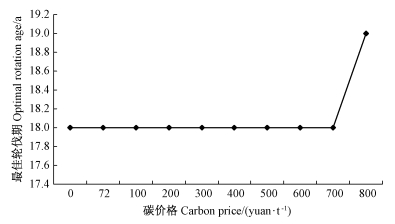
2.2 碳价格变化对于杉木最佳轮伐期和林地期望值的影响为了解碳价格变化对杉木最佳轮伐期及林地期望值所产生的影响,笔者设置碳价格在0~800元·t-1的变动区间,利用改进的Faustmann模型计算最佳轮伐期和林地期望值。其中碳价格为0元·t-1也就意味着单一经营目标。发现碳价格在较长的变动范围内并没有对杉木的最佳轮伐期产生影响,只有当碳价格上升到800元·t-1时,杉木的最佳轮伐才往后推移了1年,为19年(图 2)。可以说,在目前木材市场价格处于高位的水平下,碳价格变动对于杉木最佳轮伐期并不敏感。
|
图 2 不同碳价格水平下的最佳轮伐期变化 Fig.2 Optimal rotation change in different carbon price level |
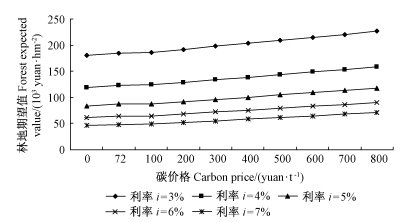
从林地期望价值来看,碳价格水平越高,不同轮伐期的林地期望值变化范围越大。同时,最佳轮伐期下的林地期望值也呈增长趋势。基于利率5%水平下,单一经营目标从碳价格为0元·t-1下的83 776元·hm-2增加到碳价格800元·t-1下的117 047元·hm-2,上升39.71%(图 3)。
|
图 3 不同利率和碳价格下的林地期望值变动 Fig.3 Forestl and expected value change in different interest and carbon price |
笔者模拟不同的利率水平(3%~7%),对最佳轮伐期和林地期望值进行敏感度分析。可以发现(表 2),利率每提高1%,使得杉木最佳轮伐期基本提前1年;而在较高利率水平下(如i=6%,7%),最佳轮伐期都会在较低的碳价格(碳价格=72~300元·t-1)发生变动。但总体而言,利率变动对于最佳轮伐期的影响相对较小。从利率变动对林地期望值的影响来看(图 3),在单一经营目标下的林地期望值从180 410元·hm-2减少到45 782元·hm-2;而在复合经营目标下,以目前碳价格(72元·t-1)计算则林地期望值从184 525元·hm-2下降到48 027元·hm-2。可以发现利率从3%提高到7%,在不同碳价格水平下,其林地期望值下降达到75%~70%,即利率变动会对林地期望值产生巨大影响。
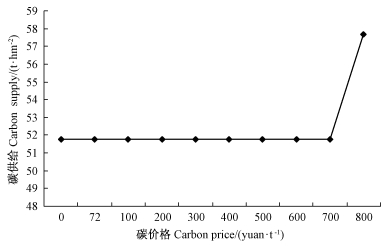
2.4 案例地杉木的碳供给曲线分析笔者基于5%的利率水平,计算了在不同碳价格下最佳轮伐期下的碳供给,并绘出了碳供给曲线(图 4)。可以发现,碳供给量没有因为碳价提高而有显著增加,基本维持在同一水平,其原因和之前类似,即现有杉木木材价格远高于碳价格,造成不同碳价下最佳轮伐期基本维持不变,基于现有的杉木生长模型则杉木蓄积和碳供给量保持稳定。
|
图 4 案例地杉木的碳供给曲线 Fig.4 Carbon supply curve of Chinese fir |
|
|
森林碳汇已成为我国乃至全球应对气候变化的重要策略。在此背景下,林业经营主体在经营活动中不但可以得到预期的木材收益,同时还可以得到潜在的碳汇收益,这可能会导致林业经营决策发生相应的变化,以促进更多的碳供给。从本文的案例研究可以发现:1)基于目前的杉木市场价格远高于碳价格的现实,在现有的经营模式下,林业经营主体基于复合经营目标的决策将不会改变,杉木的最佳轮伐期没有发生延长,从而导致在大范围的碳价格变动下碳的供给也没有显著增加。这一方面说明碳汇林必须改变原来的经营方式才能促进碳供给的增加,另一方面也说明木材收益和碳收益的2个不同经营目标是兼容的,林业经营者不用延长轮伐期以获取更多的碳收益,这对于林业经营者从事碳汇林经营是一个积极的信号;2)基于碳汇经营模式下的杉木林地期望值增长迅速,即碳汇林地的潜在投资价值巨大,这势必推动部分立地条件较差的农地转化为碳汇林地,即森林碳汇会对土地利用变化产生深远影响。政府可以给予当地农民造林补贴,推动闲置农地开展碳汇造林项目。本研究过程中也存在一些需要改进之处:1)本研究采用杉木生长模型仍然基于传统经营模式,在碳汇林经营模式下需要对其进行修正;2)由于案例样本较少,无法反映大区域范围内的碳汇供给情况;另一方面,目前采用的案例地数据是立地条件最高的林地,今后应基于不同立地条件的林地进行评估将更具说服力;3)本文的研究基于裸地造林假设,今后需要深化对现有林的碳供给研究,也需要考虑不同营林措施如间伐等的影响。
| [] | 陈则生. 2010. 杉木人工林经济成熟龄的研究. 林业经济问题, 30(1): 22–26. |
| [] | 冯亮明, 刘伟平, 肖友智. 2009. 基于森林资源保护的碳排放权交易问题的研究. 林业经济问题, 29(1): 15–19. |
| [] | 何英, 张小全, 刘云仙. 2007. 中国森林碳汇交易市场现状与潜力. 林业科学, 43(7): 106–111. |
| [] | 李峰, 刘桂英, 王力刚. 2011. 黑龙江省森林碳汇价值评价及碳汇潜力分析. 防护林科技(1): 87–88. |
| [] | 刘国华, 傅伯杰, 方精云. 2000. 中国森林碳动态及其对全球碳平衡的贡献. 生态学报, 20(5): 733–740. |
| [] | 吴载璋, 吴锡麟. 2004. 福建杉木人工林生长模型的研究. 福建林业科技, 31(4): 11–14. |
| [] | 浙江森林编辑委员会. 1993. 浙江森林. 北京, 中国林业出版社. |
| [] | 张骏, 葛滢, 江波. 2010. 浙江省杉木生态公益林碳储量效益分析. 林业科学, 46(6): 22–26. DOI:10.11707/j.1001-7488.20100604 |
| [] | 周国模, 郭仁鉴, 韦新良. 2001. 浙江省杉木人工林生长模型及主伐年龄的确定. 浙江林学院学报, 8(3): 219–222. |
| [] | 周国模, 姜培坤. 2004. 毛竹林的碳密度和碳贮量及其空间分布. 林业科学, 40(6): 20–24. DOI:10.11707/j.1001-7488.20040604 |
| [] | 朱向辉, 汪传佳, 王仁东. 2008. CDM-ARP杉木林碳汇监测方法学研究. 浙江林学院学报, 25(3): 336–341. |
| [] | Benítez P, McCallum I, Obersteiner M. 2004. Global supply for carbon sequestration: Identifying least-cost afforestation sites under country risk considerations. Laxenburg, Austria: IIASA. |
| [] | Guitart L C, Rodriguez. 2010. Private valuation of carbon sequestration in forest plantations. Ecological Economics, 69: 451–458. DOI:10.1016/j.ecolecon.2009.10.005 |
| [] | Murray B C. 2000. Carbon values, reforestation, and 'perverse' incentives under the Kyoto protocol: an empirical analysis. Mitigation and Adaptation Strategies for Global Change, 5(3): 271–295. DOI:10.1023/A:1009636028776 |
| [] | Nhung N T H. 2009. Optimal forest management for carbon sequestration: a case study of Eucalyptus urophylla and Acacia mangium in Yen Bai Province, Vietnam. Singapore:EEPSEA. |
| [] | Stainback G A, Alavalapati J R R. 2002. Economic analysis of slash pine forest carbon sequestration in the sourthern U.S.. Journal of Forest Economics, 8(2): 105–117. DOI:10.1078/1104-6899-00006 |
| [] | van Kooten C G, Binkley C S, Delcourt G. 1995. Effect of carbon taxes and subsidies on optimal forest rotation age and supply of carbon services. American Journal of Agricultural Economics, 77(2): 365–374. DOI:10.2307/1243546 |
 2012, Vol. 48
2012, Vol. 48


