文章信息
- 李春明
- Li Chunming
- 基于两层次线性混合效应模型的杉木林单木胸径生长量模型
- Individual Tree Diameter Increment Model for Chinese Fir Plantation Based on Two-Level Linear Mixed Effects Models
- 林业科学, 2012, 48(3): 66-73.
- Scientia Silvae Sinicae, 2012, 48(3): 66-73.
-
文章历史
- 收稿日期:2010-08-05
- 修回日期:2010-11-04
-
作者相关文章
单木生长模型是定量研究林木生长过程的有效手段,既可对林木的生长做出现实的评价,也可用来预估未来林分各因子的变化;既是编制和修订各种林业数表的基础,也是森林经营中各种措施实施的依据(王孝安等,2005)。单木胸径生长模型的研究结果可应用于异龄林、混交林等多种林分类型,并能够描述不同经营措施对林木生长的影响,可以直接判定单株木的生长状况和生长潜力,以及判定采用林分密度控制措施后各保留木的生长状况,这些信息对于林分的集约经营很有价值(张惠光,2006)。
国内一些学者在单木生长模型方面开展了一些研究(杜纪山, 1999;黄家荣等,2000;刘兆刚,2004;王文斗等,2005),所用的建模数据通常来自于林分内多个样地在一定时间间隔内多次的重复观测:首先,这些数据之间存在着序列相关性,且相邻测量时间的数据相关性较大,而离得较远的数据相关性减小;其次,由于分布区域、竞争环境和立地条件不同,以及林木个体之间的差异,树木之间存在着生长上的差异;再次,这些数据之间不满足独立性要求,而且存在着异方差性。以往这些问题经常被忽略,这样就可能会造成很大的估计和预测误差,给林业生产经营和决策部门提供错误的信息和依据。混合效应模型方法被广泛地用来解决这类问题,该方法主要优点在于它不仅考虑固定效应,也考虑随机效应,使得信息利用更为充分;不仅可以满足常规要求的重复测量数据,而且还可用于说明分析变量水平及其变化趋势;对个别观察单位重复测量次数不完全相同的情况,也同样有效。
国外很多学者研究了混合模型在模拟和预测单木胸径生长中的应用:Adame等(2008)利用截距效应混合模型方法研究西班牙西北部比利牛斯栎(Quercus pyrenacia)的胸径生长,考虑了林木大小、林木竞争、立地条件和生物地理气候等因子;Uzoh等(2006)利用多层次线性混合模型研究美国西部美国黄松(Pinus ponderosa)同龄林分的单木胸径生长,与Adame等(2008)不同的是没有考虑生物地理气候对单木生长的影响; Rafael等(2005)在建立石松(Pinus pinea)的胸径生长量模型时, 与Adame(2008)的方法和考虑的因子相同; Weiskittel等(2007)在分析花旗松(Pseudotsuga menziesii var. menziesii)、异叶铁杉(Tsuga heterophylla)和美国赤杨(Alnus rubra)3个树种的胸径生长时,利用混合效应模型方法,并考虑了气候和经营相互作用的影响;Kiernan等(2008)在研究不同采伐方式下糖枫(Acer saccharum)异龄林的单木胸径生长时,用混合效应模型来解释重复测量产生的时间序列相关性。这些学者在利用线性混合效应模型模拟单木胸径生长时,均认为考虑随机效应后,模型精度会有很大的提高。
线性混合效应模型包括随机截距效应和随机系数效应2种(Littell et al., 2000),上述学者利用线性混合效应模型方法在构建单木胸径生长模型时都采用了随机截距效应。到目前为止,利用随机系数效应线性混合模型方法构建单木胸径生长模型的研究还未见诸于文献。本研究根据所用不同区域和不同样地数据之间存在着嵌套性的特点,采用SAS软件进行模拟。在模拟过程中利用参数随机效应方法分别对嵌套的样地层次、区域层次及同时考虑2个层次进行模拟,并考虑异方差和序列相关性问题,利用LRT(似然比检验)进行方差分析,最后利用均方根误差、平均绝对残差和确定系数对独立的验证数据进行验证。
1 研究数据和方法 1.1 数据来源数据来源于江西省的人工杉木(Cunninghamia lanceolata)(杉木树种蓄积占样地总蓄积80%以上)固定样地调查。共计82个区域365块杉木样地,从中选择了5 416株树木(树木起测胸径为5 cm,从1991年开始每5年测量1次, 共4次,4 500株树木作为模拟数据,其余树木为验证数据)进行研究。样地面积为0.08 hm2。样地基本调查因子包括单木胸径、海拔、平均年龄、平均胸径、样木总株数等。样地汇总因子统计结果见表 1。
|
|
大量研究表明,影响单木个体生长的因素很多,包括树木大小及活力指标、立地、竞争及林分特征等,其中以个体间的竞争作用最为重要,是影响林木生长、形态变化和存活的主要因素之一(张大勇等, 1989)。目前很多学者在模拟单木胸径生长时,同时考虑了单木胸径大小、生活力状况、竞争状态及立地条件等因素的影响(Mailly et al., 2003;Trasobares et al., 2004)。
1) 树木大小影响 一般来说,胸径越大的树木其生长量就越大,因此树木的生长量与调查期初的胸径有一定的关系。本研究分别采用期初胸径、期初胸径的对数或期初胸径的平方等函数形式进行模拟。考虑单木生长量与期初胸径的关系如式(1):
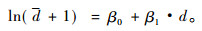
|
(1) |
式中: d为单木胸径生长量;d为胸径,考虑对数形式时换成lnd,考虑平方形式时换成d2。
2) 立地条件影响 对于一个模型来说,如果能够充分说明和表达树木胸径的生长,必须包括立地条件因子方面的调查(Spurr et al., 1980),这些调查通常包括纬度、经度、坡度、坡向、海拔及立地指数等。这些因子对树木的生长没有直接的影响,但是却间接影响湿度、温度、光照及其他物理和化学方面的特征。本研究考虑了坡度、坡向及海拔对胸径平均生长量的影响。坡度和坡向利用Stage(1976)提出的转化公式:

|
(2) |
式中: SL为坡度;ASP为坡向;Hb为海拔。
3) 竞争影响 每株树木的生长并不只受初始胸径和立地条件的影响,最重要的是受到相邻树木与其竞争地位和经营措施的影响。本研究选择了样地内大于对象木(具体指正被模拟的树木)断面积之和与对象木胸径的比值及对象木单木胸径与林分平方平均胸径的比值来衡量竞争对单木胸径生长的影响。具体公式如下:

|
(3) |
式中: BLI为大于对象木断面积之和与对象木胸径的比值;BDBH为对象木单木胸径与样地林分平均胸径的比值。
4) 林分因子影响 单木胸径生长量还受林分因子的影响,在外业调查中容易获取的林分因子包括林分单位面积株数、林分断面积等,本研究分别考虑了这2个因子的影响。
由于直径生长量都大于或等于0,为了避免在模拟过程中估计值可能出现负值,另外,当直径生长量小于1时,在拟合过程中一些小的变化可能会导致大的误差,因此把因变量变成ln(d+1)。首先把数据分成2部分:一部分为建模数据,一部分为验证数据。在构建模型时,自变量考虑单木大小、立地条件、林分因子及竞争对单木胸径生长量的影响。模拟过程中,为了避免出现自变量之间存在严重的共线性问题,利用方差膨胀因子去除存在多重贡献性的变量,只有回归系数显著(P<0.05)且方差膨胀因子小于10的变量才进入模型。综合考虑对胸径生长有影响的因子,选择不同的自变量形式分别进行模拟,并去除存在多重共线性的自变量,最终拟合结果如表 2。
|
|
传统最小二乘方法模拟效果评价指标值为AIC=21 964.9,BIC=21 972.6,-2Log Likelihood=21 962.9。从表 2可看出,杉木受初始胸径大小的影响,随着胸径增大,生长量增大。BA反映林分的密度特征,从模拟结果看,密度与胸径生长量呈现负相关,密度越大的林分胸径生长量越小。海拔虽然在模型中差异显著,但其值很小,与其他几个变量相比,作用极其微弱,因此本研究没有作为随机效应参数。对胸径生长量影响最大的是BLI变量,这个指标越大胸径生长量越小,充分说明了处于竞争有利地位的杉木胸径生长迅速,而处于劣势的树木生长缓慢。
最后确定的混合模型的基础形式如式(4):

|
(4) |
式中: d为胸径;BA为样地总断面积;Hb为海拔;BLI为样地内大于对象木断面积之和与对象木单木胸径的比值;d为单木胸径生长量;ε为估计误差。
1.2.2 误差方差协方差结构样地内方差协方差结构也称为误差效应方差协方差结构。对固定样地进行长期观测的森林生长收获数据通常都存在自相关和异方差问题,为了确定样地内的方差协方差结构,必须解决这2方面的问题, 在林业上通常利用式(5)进行描述:
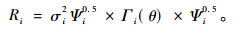
|
(5) |
式中:Ri是样地内方差协方差矩阵;σi2为未知样地i的残差方差;Ψi为描述样地内误差方差结构的异质性方差的对角矩阵;Γi(θ)是描述样地内误差的自相关结构矩阵。
为了表达样地内的时间序列相关性,一阶自回归模型[AR(1)]、一阶自回归与滑动平均模型相结合的矩阵模型[ARMA(1, 1)]及复合对称矩阵模型(CS)经常被用在森林生长收获模拟中(Wang et al., 2007)。异方差结构包括幂函数和指数函数2种,具体形式见Vonesh等(1997)。
1.2.3 混合效应模型参数估计当利用混合效应模型进行预测时,需要计算随机效应参数。在本研究中,随机效应参数值可通过抽样样地部分已知信息、最好线性无偏估计以及限制性极大似然方法来预测,具体预测公式见式(6)(Vonesh et al., 1997):

|
(6) |
式中:
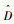



在研究过程中,分别从样地层次、区域层次或同时考虑2个层次3方面来考虑参数的随机效应,在此基础上考虑误差效应中的时间序列相关性和异方差问题。利用AIC、BIC和-2Log Likelihood 3个指标值对模拟效果进行评价。由于以往模型参数估计方法大多采用最小二乘方法,只考虑平均水平而没有考虑个体差异(本文称为传统方法),因此本文最后选择验证数据,利用均方根误差、平均绝对残差和确定系数对二者的精度进行比较(Uzoh et al., 2006)。
2 结果与分析 2.1 随机参数效应根据本研究所采用的数据情况,在模拟参数的随机效应时,主要包括样地层次、区域层次以及二者同时作用3种效应。
2.1.1 样地层次随机参数效应因选择的参数个数组合不同而会产生出很多模拟结果。因此,本部分首先把每个参数分别作为混合参数,然后再把多个参数组合作为混合参数来模拟,利用AIC、BIC和-2Log Likelihood等3个评价指标对模拟效果进行评价,最后找出一个模拟效果最好的模型作为随机参数线性混合效应模型。模拟结果见表 3样地层次。
|
|
样地效应收敛的情况共有14种,AIC、BIC和-2Log Likelihood 3个指标值都比传统方法(表 2)要小。另外,单个变量为混合参数时,变量d的模拟效果最好;2个变量组合时,int BA的模拟效果最好;3个变量组合时,int d BLI的模拟效果最好。总体来说,截距、单木胸径、样地总断面积和样地内大于对象木断面积之和与对象木单木胸径的比值(int d BA BLI)4个变量上的参数同时作为混合参数的模拟精度最高。对这4种结果进行方差分析,d与int BA差异显著(LRT=1 205.422 0,P<0.000 1),int BA与int d BLI差异显著(LRT=352.644 7,P<0.000 1),int d BLI与int d BA BLI差异显著(LRT=54.965 9,P<0.000 1)。这说明增加参数个数能够明显提高模型的估计精度。
考虑了参数的随机效应后,还需要考虑误差效应的方差协方差矩阵,包括自相关和异方差2部分。考虑自相关矩阵的模拟结果见表 4样地层次,考虑异方差的模拟结果见表 5样地层次。
|
|
|
|
表 4表明,考虑时间序列相关性后,与不考虑自相关结构相比,这3个结构模拟效果有很大的改善,并且差异都达到了极显著水平,存在着明显的自相关性。根据3个评价指标值的大小,最终选择ARMA(1,1)作为自相关矩阵结构。从表 5的比较结果看出,无论是指数函数还是幂函数作为异方差函数,模拟效果都显著提高。选择幂函数或指数函数并没有大的差别,由于指数函数的3个指标值更小一点,因此选择指数函数作为最终的异方差方程。
确定了最佳的混合参数、自相关矩阵结构和异方差方程后,把这几方面综合考虑进行模拟,确定的模型形式如式(7):

|
(7) |
式中:i为区域编号;j为样地编号;k为样木编号;m为观测次数;b0ij,b1ij,b2ij和b3ij分别为样地层次随机效应参数;xi为自变量。
对式(7)的模拟效果分别与考虑样地的随机参数效应、样地随机参数效应及自相关结构组合、样地随机参数效应及异方差组合这3种模拟结果进行方差分析,LRT的比较结果显示全部差异显著(P<0.000 1)。因此,在实际模拟胸径生长量时要综合考虑参数的随机效应、自相关结构和异方差,这样能够获得更准确的模拟结果。式(7)最终的模拟结果见表 6样地层次。综合的模拟结果可在实际中运用,例如在模拟整个调查区域内的胸径生长量时可用固定参数进行模拟,如要获得具体样地的胸径生长量时,可以利用获得参数的随机效应方差协方差矩阵、误差效应方差协方差矩阵计算出某个样地的随机参数,然后再预测具体样地的胸径生长量。
|
|
区域间存在的随机效应在实际应用中也不能忽略,本部分同样首先把每个参数分别作为混合参数,然后再把多个参数同时作为混合参数来模拟,最后找出一个模拟效果最好的模型作为随机参数线性混合效应模型。最后收敛的模型模拟结果见表 3区域层次。
收敛的形式包括13种,截距、单木胸径、样地总断面积和样地内大于对象木断面积之和与对象木单木胸径的比值(int d BA BLI)同时作为混合参数的模拟精度最高,所得出的结论与样地层次一致。对各个组合最高的模型进行方差分析,胸径d与int BA差异显著(LRT=1 064.8220,P<0.000 1),int BA与int d BLI差异显著(LRT=180.028 8,P<0.000 1),int d BLI与int d BA BLI差异显著(LRT=172.171 8,P<0.000 1)。
与考虑样地参数随机效应一样,在考虑区域的参数随机效应时,也要考虑误差效应的方差协方差矩阵。考虑自相关矩阵的模拟结果见表 4区域层次,考虑异方差的模拟结果见表 5区域层次。
表 4的模拟结果与考虑样地参数随机效应的结论一致,选择ARMA(1,1)结构作为自相关矩阵结构。另外通过表 5的比较结果看出,采用幂函数作为异方差函数后方差分析不显著;但是采用指数函数形式差异显著,因此选择指数函数作为异方差的方程。
在考虑区域的随机参数效应影响时,也把混合参数效应、自相关矩阵结构和异方差函数方程综合考虑进行模拟,采取的模型形式如式(8):

|
(8) |
式中:i为区域编号;j为样地编号;k为样木编号;m为观测次数;b0i,b1i,b2i和b3i分别为区域层次随机效应参数;m为某次测量次数。
对式(8)的模拟效果分别与考虑区域的随机参数效应、区域随机参数效应及自相关结构组合、区域随机参数效应及异方差组合3种的模拟结果进行方差分析比较,LRT的比较结果显示全部差异显著(P<0.000 1),这与考虑样地层次的模拟结果一致。最后确定的区域层次模型参数和各种矩阵模拟结果见表 6区域层次。
2.1.3 两层次影响在实际中,样地效应和区域效应同时存在,存在着嵌套性,因此应把样地效应和区域效应结合起来同时考虑。本研究在模拟过程中所有参数都考虑样地效应和区域效应,模型不能够收敛,因此可随机去掉一个参数进行模拟,然后选择模拟精度最高的模型形式作为基础的线性混合效应模型,结果如表 7所示。从表 7可以看出,区域效应包括int,ZBA和BLI,样地效应所有参数都作为混合参数时的模型模拟效果最好(模拟2),但是当区域效应去掉BLI时(模拟5),与其没有显著差异(LRT= 7.496 7,P=0.057 6),模拟6和模拟7与其有显著差异(P<0.000 1)。当所有参数都作为区域的混合参数、而部分参数考虑样地效应时,均不收敛。因此为了避免在模拟中过参数化问题,可采用模拟5的混合参数。最终确定的方程如式(9):

|
(9) |
|
|
式中:vi(0)和vi(2)分别为区域的参数随机效应;uij(0),uij(1),uij(2)和uij(3)分别为样地的参数随机效应;D1为区域间随机效应矩阵;D2为样地间随机效应矩阵。当此方程考虑异方差和时间序列自相关时,模型均不能够收敛。最后对此式进行模拟,如果实际应用中存在着两层次效应,则可按表 6的两层次模拟结果对未来林分的单木胸径进行预测。
2.2 模型验证对胸径生长量模型进行模拟后,利用独立的验证数据进行验证,比较线性混合模型与传统最小二乘方法的精度。传统最小二乘方法的3个指标值计算结果为平均绝对残差为0.387 2、均方根误差为0.474 9、确定系数为0.323 5。下面分不同层次进行验证。
1) 样地效应 只考虑样地随机效应而不考虑误差效应的混合效应模型平均绝对残差为0.292 1、均方根误差为0.368 1、确定系数为0.680 9;既考虑样地随机效应又考虑误差效应的混合效应模型平均绝对残差为0.296 9、均方根误差为0.372 7、确定系数为0.671 9。
2) 区域效应 只考虑样地随机效应不考虑误差效应的混合效应模型平均绝对残差为0.343 5、均方根误差为0.426 8、确定系数为0.526 1;既考虑样地随机效应又考虑误差效应的混合效应模型平均绝对残差为0.354 3、均方根误差为0.438 1、确定系数为0.487 8。
3) 两层次效应 在计算两层次效应时,由于考虑误差效应时模型不能够收敛,因此只考虑了参数的随机效应,计算结果为平均绝对残差为0.282 6、均方根误差为0.356 2、确定系数为0.693 5。
经过这3个效应的计算,可以看出均方根误差和平均绝对残差均小于最小二乘方法,而确定系数全部大于传统最小二乘方法。
3 结论与讨论1) 在模拟胸径生长量时,误差结构矩阵(包括异方差和观测的时间序列自相关结构)是不能忽略的。方差分析表明,与不考虑误差结构矩阵相比,模拟效果差异显著。本研究中,ARMA(1, 1)作为时间序列自相关结构矩阵模拟效果最好,但和AR(1)的值相差不多,并且参数要比AR(1)多1个。因此在实际应用中,可以利用AR(1)代替ARMA(1, 1)进行模拟。指数函数在描述样地效应或区域效应异方差时模拟效果最好。
2) 在对模型进行验证时,不考虑误差效应与考虑误差效应的3个评价指标值没有大的差异,从而可以说明,误差效应方差协方差是不稳定的因子,在实际应用中是否必须考虑二者之间的差异有待于进一步研究。
3) 对3种情况(样地、区域及两层次)的效应进行比较,结果为两层次效应模拟精度要略高于样地效应,但两层次效应和样地效应模拟精度都远高于区域效应,说明在拟合单木胸径生长量时,误差的主要来源是样地之间的差异。在实际应用中可根据不同情况及不同的需要,选择不同的层次进行模拟和预测。本文考虑到生产实际中的应用性,没有考虑树木层次的混合效应,如特别需要可参考文中方法加以考虑。
| [] | 杜纪山. 1999. 用二类调查样地建立落叶松单木生长模型. 林业科学研究, 12(2): 160–164. |
| [] | 黄家荣, 万兆溟. 2000. 马尾松人工林与距离有关的单木模型研究. 山地农业生物学报, 19(1): 10–15. |
| [] | 刘兆刚. 2004. 落叶松人工林单木模型的研究. 植物研究, 23(2): 237–244. |
| [] | 王文斗, 李凤日, 那冬晨, 等. 2005. 辽东栎单木生长模型的研究. 林业科技, 30(2): 11–13. |
| [] | 王孝安, 段仁燕, 王明利. 2005. 太白红杉单木胸径生长模型的研究. 武汉植物学研究, 23(2): 157–162. |
| [] | 张大勇, 赵松岭, 张鹏云. 1989. 青杄林演替过程中的邻体竞争效应及邻体干扰指数模型. 生态学报, 9(1): 53–59. |
| [] | 张惠光. 2006. 福建柏单木生长模型的研究. 中南林业调查规划, 25(3): 1–4. |
| [] | Adame P, Hynynen J, Canellas I, et al. 2008. Individual-tree diameter growth model for rebollo oak(Quercus pyrenacia Willd.)coppices. Forest Ecology and Management, 255(3/4): 1011–1022. |
| [] | Fang Z, Bailey R L. 2001. Nonlinear mixed effects modeling for slash pine dominant height growth following intensive silvicultural treatments. Forest Science, 47(3): 287–300. |
| [] | Kiernan D H, Bevilacqua E, Nyland R D. 2008. Individual-tree diameter growth model for sugar maple trees in uneven-aged northern hardwood stands under selection system. Forest Ecology and Management, 256(9): 1579–1586. DOI:10.1016/j.foreco.2008.06.015 |
| [] | Littell R C, Milliken G A, Stroup W W, et al. 2000. SAS for mixed models(second edition). SAS Institute Inc., Cary, NC, USA. |
| [] | Mailly D, Turbis S, Pothier D. 2003. Predicting tree growth increment in a spatially-explicit individual tree model: a test of competition measures with black spruce. Canadian Journal of Forest Research, 33(3): 435–443. DOI:10.1139/x02-122 |
| [] | Rafael C, Gregorio M. 2005. Multilevel linear mixed model for tree diameter increment in stone pine (Pinus pinea): a calibrating approach. Silva Fennica, 39(1): 37–54. |
| [] | Spurr S H, Barnes B V. 1980. Forest Ecology. 3rd ed. New York, Wiley: 687. |
| [] | Stage A R. 1976. An Expression for the effect of slope aspect and habitat type on tree growth. Forest Science, 22(4): 457–460. |
| [] | Trasobares A, Pukkala T, Miina J. 2004. Growth and yield model for uneven-aged mixtures of Pinus sylvestris L. and Pinus nigrarn Arn. in Catalonia, north-east Spain. Annals of Forest Science, 61(1): 9–24. DOI:10.1051/forest:2003080 |
| [] | Uzoh F C C, Oliver W W. 2006. Individual tree height increment model for managed even-aged stands of ponderosa pine throughout the western United States using linear mixed effects models. Forest Ecology and Management, 221(1/3): 147–154. |
| [] | Vonesh E F, Chinchilli V M. 1997. Linear and nonlinear models for the analysis of repeated measurements. New York, Marcel Dekker Inc. |
| [] | Wang Y, Lemay V M, Baker T G. 2007. Modelling and prediction of dominant height and site index of Eucalyptus globules plantations using a nonlinear mixed-effects model approach. Canadian Journal of Forest Research, 37(8): 1390–1403. DOI:10.1139/X06-282 |
| [] | Weiskittel A R, Garber S M, Johnson G P, et al. 2007. Annualized diameter and height growth equations for Pacific Northwest plantation-grown douglas-fir, western hemlock, and red alder. Forest Ecology and Management, 250(3): 266–278. DOI:10.1016/j.foreco.2007.05.026 |
 2012, Vol. 48
2012, Vol. 48