木工带锯机是木材加工行业中应用最广的设备，带锯条的张紧力是带锯机设计与制造的重要参数。为了保证锯材质量、提高锯切效率，有效措施之一就是提高锯条的张紧力; 同时，张紧应力不应超过材料的许用应力。国产MJ397型高速带锯机，没有采用液压自动调整张紧机构，而是通过旋转手轮和螺杆的传动实现锯轮的升降来控制锯条的张紧力，显然较难控制张紧力的大小。对此，笔者在通过应变测量得出锯条静态张紧力的基础上，利用频谱分析法实测木工带锯条在静态和动态下的固有频率，并将木工带锯条的复杂振动简化为弦的振动，得出带锯条动态张紧力，对木工带锯条理论的深入研究和装备技术的改进有现实意义。

1 测量仪器与设备

南京安正CRAS振动及动态信号采集分析系统; CA-YD-107电荷型加速度计1只，其灵敏度为5.29 pc·m^-1 s^-2; CWY-DO-501电涡流位移传感器(位移计) 2只，其灵敏度为8 mv·μm^-1; 橡胶锤1把; MJ397型高速木工带锯机1台，主要技术参数见表 1。

本机床所用木工带锯条为直背齿形，材料为65Mn，有效宽度(不含齿高) b = 76.5 mm，厚度h =1.0 mm，总长度L = 5 400 mm，紧边长度l =(5 400-3.14 × 700) ÷ 2 = 1 600 mm = 1.6 m，松边长度= 1.6 m，密度ρ = 7 800 kg·m^-3，横截面面积A = 7.65 × 10^-5 m²。

2 试验设计 2.1 试验方法

由于带锯条固有频率属于低频，根据随机振动理论(柯拉科特，1983; 汤姆逊，1980; 马岩，1998)，采用橡胶锤激振带锯条，应用频谱分析法测量带锯条的固有频率(戴诗亮，1984)，试验框图如图 1所示。

2.2 试验过程

本试验环境温度19 ℃、环境湿度21%，无外界强磁场干扰和无腐蚀气体侵蚀，电源电压220 V，频率为50 Hz。

带锯轮静止时，根据电测法测得的带锯条张紧力T₀ = 3 412 N(王正等，2008)。

用电涡流位移传感器测量带锯条在不开机时的频率和开机空载时的紧、松边频率，电涡流传感器与带锯条测量面间距约1 mm，电涡流传感器信号经放大滤波后接采集箱第1通道(Ch1)，其参数设置:分析频率和低通滤波频率均为50 Hz。用电涡流传感器，工程单位设为μm，校正因子设为8，Hanning窗计权; 若用加速度计，其信号经放大滤波后接采集箱第2通道(Ch2)，工程单位设为m·s^-2，校正因子529 (放大100倍)。

3 带锯条固有频率测试结果与分析

测试频谱见图 2~4，基频测试结果见表 2。

图 2表明带锯机在不开机静止状态下，分别用电涡流传感器测得的紧、松边的频率。测量时用单通道分别测量带锯条紧边和松边的频谱，然后用程序进行通道合成为双通道作业，其带锯条紧边和松边的实测基频均为23.63 Hz。

图 3，4分别显示了开机空载状态下带锯条紧边和松边的测量频谱，其所示紧边、松边频谱有多个频率，为了认定开机空载状态下紧边和松边的频率(动频)，又进行了双通道测量。在双通道测量中，Ch1接电涡流传感器，电涡流传感器分别距带锯条紧边和松边为1 mm; Ch2接加速度计，加速度计安装于锯床的床身上，其带锯条紧边、松边的实测基频分别为24.90和21.68 Hz。从图 3，4中发现，f =16.21 Hz的频率是锯轮转动频率是干扰力频率(970 /60 = 16.2 Hz)。

4 简化带锯条振动为弦振动(Queiroz et al., 1999; Yang et al., 1991; 张宏志等，2002)的动力学模型理论计算 4.1 不开机静止时

带锯条张力T = T₀ = 3 412 N时，如图 5a所示，带锯条横向振动的固有频率计算公式为:

当n = 1时，

此时，带锯条张紧力无紧边、松边变化，静态频率(静频)将T = 3 412 N代入基频为23.6 Hz。

4.2 开机空载时

带锯轮转动中的带锯条张力T = T₀ ± ΔT /2，带锯条两边的张力不再相等，T₁为紧边张力，T₂为松边张力，扭矩引起带锯条松边、紧边的张力差ΔT =T₁-T₂，如图 5b所示。带锯轮转动时，基频动力学理论计算如下。

驱动带锯轮扭矩M_e的计算式为:

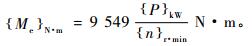
由此得:

将T₀ = 3 412 N、P = 7.5 kW和锯轮转速n = 970r·min^-1代入ΔT公式，计算如下:

显然，其紧边张力

松边张力

不开机静止时，带锯条静止张紧力为:

开机空载时，带锯条紧松边的动态张紧力为:

5 结论

1) 在带锯条张紧力T₀ = 3 412 N条件下，不开机静止时，带锯条两边的基频相等; 开机空载时，带锯条紧边基频大于松边基频，说明弦振动简化理论模型给出的规律符合木工带锯条的实际情况。

2) 带锯机静止时，其带锯条两边实测张紧力相同。开机空载时，带锯条紧边的张紧力较不开机时的紧边张紧力高; 而松边张紧力比不开机静止时的松边张紧力低，这是由于其动频率变小，相当于转动的带锯条张紧力降低，锯条的张紧程度变“松”了，这就是带锯条晃动或抖动现象的原因，从松边的频谱也反映了这一点。开机空载时，用频率推算的动张紧力与常规扭矩计算的张紧力，紧边约高7%，松边约低15%。

3) 65Mn材料的σ_s = 350 MPa，一般带锯条的张紧应力σ≤130 ~ 140 MPa。根据生产经验，细木工带锯机的带锯条张紧应力σ = 30 ~ 50 MPa，相应的带锯条张紧力T = 2 295 ~ 3 825 N，固有频率f₁ =20 ~ 25 Hz。本试验测得的最大张紧力T_max =3 788 N，最小张紧力T_min = 2 877 N; 固有频率f_1(max) = 24.9 Hz，f_1(min) = 21.7 Hz，因此用测量频率可作为带锯条调整的验收手段。

4) 即使频率推算的动张紧力与常规扭矩计算的张紧力在紧边误差约高7%，在松边误差约低15%，但由于一方面在计算松紧边拉力差时，本研究用的是全功率，而空载时，消耗的功率小于全功率，即使按全功率计算，ΔT /2 = 106 N，仅占张力的3% (106 /3 412 = 3.1%)，，因而频率误差约占1.5%;另一方面，频率推算动张紧力精度能滿足带锯条正常工作时的松、紧边张紧力范围。因此，用本文提出的测动静频方法，作为调整带锯条动态张紧力验收手段这一问题的研究和工程应用是完全可以接受的。

5) 本文通过介绍实测木工带锯机运转时带锯条系统固有频率的方法，可正确得到带锯轮的实时动态张紧力值，一方面有助于指导用户及时调整带锯条张紧力在合理范围内，以便有效锯切材料，达到稳定锯切质量:提高功效和节约成本的目的; 另一方面有助于指导带锯机制造商开展产品动态结构设计、检测等技术优化和验收工作，进一步提高国产带锯机产品的基础研发能力，改善产品质量，增收节支。上述通过激振的方式检测带锯条的固有频率而判定其张紧状态，进而实现带锯条张紧的动态调整，对木工带锯条理论的深入研究和装备技术的改进有指导意义。