森林生态系统作为陆地生态系统的主体，在维护全球气候系统、调节全球碳平衡、减缓大气温室气体浓度上升等方面具有不可替代的作用。因此，世界各国越来越重视对森林生物量的监测(Tomppo et al., 2010)。开展全国森林生物量监测和评估、建立适合较大区域范围的通用性立木生物量模型将成为必然趋势，事实上很多国家已经在朝着这个方向努力，不少学者也在积极探索建立适合国家、区域乃至全球水平的通用性立木生物量模型(Hansen，2002; Chojnacky，2002; Jenkins et al., 2003; Snorrason et al., 2006; Vallet et al., 2006; Repola et al., 2007; Muukkonen，2007; Case et al., 2008; Návar，2009)。

特别值得关注的是，West等(1997; 1999)基于林木分支网络和林木结构的生物力学原理，在多种假设(将林木视为多级分支网络、各级分支的面积和体积守恒、最终的分支单元大小不变等)的基础上提出了符合相对生长规律的通用模型，并通过非常复杂的推导过程得到林木直径D∝M^3/8，即认为地上生物量模型M=aD^b中的指数参数b=8/3(≈ 2.67)。此后，该理论模型(简称WBE模型)引起了广泛关注。Chojnacky(2002)针对美国森林资源清查中林木生物量估计方法的多样性和复杂性，认为WBE模型为简化生物量的计算过程提供了可能; Zianis等(2004)对包括WBE模型在内的3种简化生物量估计的方法进行了对比分析，结果表明大量研究结果得到的平均参数为2.37，与WBE模型的理论值2.67在统计上有明显差异; Zianis等(2006)利用来自世界各地的多个树种的地上生物量M与树干直径D数据对理论模型进行了验证，结果表明WBE模型不能描述经验数据库中M-D相对生长的形状; Pilli等(2006)对不同年龄阶段的a，b值进行了研究，其结果表明成林阶段的b值与WBE模型的理论值无明显差异，而a值与木材密度显著相关。

本文以几何学为基础，研究提出一个新的通用性相对生长生物量模型，并利用大量立木生物量实测数据和文献资料对模型进行验证。新的模型将为简化大尺度森林生物量估计提供可行途径。

1 数据

本文所用数据包括2部分:第一部分为立木地上生物量实测数据，具体包括1997年全国生物量课题组采集的样木数据447株，涉及北方和南方2片，其中北方片8个树种组，即落叶松(Larix gmelinii)、冷杉(Abies fabri)、红松(Pinus koraiensis)、椴树(Tilia amurensis)、水曲柳(Fraxinus mandshurica)、胡桃楸(Juglans mandshurica)、黄菠萝(Phelodondrom amurense)和色木槭(Acer mono)，共295株，南方片3个树种组，即杉木(Cunninghamia lanceolata)、马尾松(Pinus massoniana)和阔叶树，共152株; 2007年贵州省编制杉木、马尾松系列数表采集的样木数据694株，其中杉木399株样木，马尾松295株样木; 2009年全国连续清查生物量调查建模项目收集的数据300株，涉及东北落叶松和南方马尾松2个树种，每个树种各150株。3个部分的样木数据共计1 441株。第二部分为各类文献资料上收集的地上生物量模型参数结果，包括北美146个方程和欧洲61个方程的参数，以及美国、加拿大、墨西哥和我国已经发表的一些方程参数。

2 模型的提出

按照经典几何学的观点，规则物体的维数是整数，而自然界存在的各种物体通常是非规则的，因此可以利用分形几何学来描述非规则物体的维数(Mandelbrot，1983)。分形几何学的特性之一是可以用非整数维来描述客观存在的物体(Theiler，1990)。在理论上，林木的表面形状可以作为平面和立方体的混合物体来描述，因为它既不是三维的立体，又不是二维的平面，其维数应该介于二维和三维之间。将其拓展到林木生物量的估计，则公式M=aD^b中的b值相当于维数，其值应在2~3之间; 如果采用公式M=aD^bH^c，则2＜b+c＜3(Zianis et al., 2004)。对于应用最广的一元模型，West等(1999)提出其理论b值应为8/3，但Zianis等(2004; 2006)利用大量数据进行检验后认为，这一理论值并不能描述M与D之间的关系，与经验参数值存在显著差异，而且是明显偏大。基于几何学的观点，下面对b值进行分析。

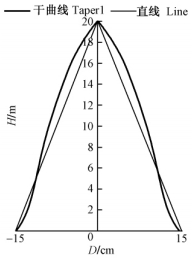
首先来分析树干的形状。图 1为根据杉木的削度方程(曾伟生等，1997)绘制的干曲线与直线的对比示意图。不规则的树干可以用规则的圆锥体来近似描述。我们知道，树干基部直径D₀构成的横断面面积∝D₀²，是二维的; 横断面与树高H构成的圆柱体体积∝D₀³(假设H∝D₀)，是三维的。依此类推，假设横断面与树高构成的圆锥体体积∝ D₀^b(假设H∝D ₀)，则b值就相当于圆锥体的非整数维。由于圆锥体体积等于圆柱体体积的1/3，按照直观的推断，可以得到b=2+1/3=7/3或b=3-2/3=7/3。因为圆锥体可以看成是树干的近似描述，所以树干的非整数维可以近似取7/3(或≈2.33)。由于林木树冠与树干具有类似的分形维(Zeide，1990)，而且林木地上生物量大约80%由树干构成，因此，整个林木的维数也可以取近似值7/3，从而地上生物量公式M=aD^b可以取b=7/3。

然后再来分析参数a值。一方面，由于a值与b值存在着明显的负相关(Zianis et al., 2004; Pilli et al., 2006)，即使采用一个固定的b值(如2.33) 可能与实际不完全相符，但可以在很大程度上从a值得到弥补; 另一方面，a值与木材密度显著相关(Pilli et al., 2006)，因此可以建立a值与木材密度ρ之间的回归关系。由于木材密度是树种的重要特性之一，不同树种地上生物量模型的差异主要由参数a来体现。这也暗示着，木材密度相同的树种，其地上生物量模型也相同。因此，木材密度比较接近的树种，可以合并建立地上生物量模型。

3 模型的验证

通过前述分析，得到以下基于林木直径的通用性地上生物量模型M=aD^b，其中b=7/3(近似取2.33)。该模型能否反映生物量数据的实际情况，本文采取如下2个途径进行验证:一是与已经发表的各类文献中的有关结果或生物量模型参数进行对比分析; 二是利用收集的立木生物量实测数据通过建模分析进行验证。

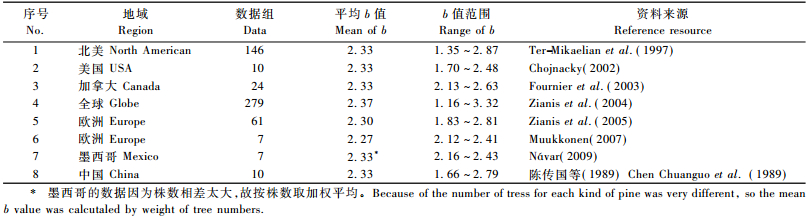
3.1 与已有研究结果的对比

Zianis等(2004)从全球汇集了279项研究结果计算得到的平均b值等于2.367 9，标准差为0.27，标准误为0.016 3，大约69%的b值在2.18~2.54之间，13%在2.68~2.80之间; 其平均值与WBE模型的理论值2.67存在显著差异，但与本文提出的理论值2.33非常接近。利用Ter-Mikaelian等(1997)收集的北美65个树种146个地上生物量方程的b值进行计算，其算术平均值2.33，中位数为2.35;利用Zianis等(2005)收集的欧洲39个树种61个地上生物量方程的b值进行计算，其算术平均值2.30，中位数为2.33;利用Fournier等(2003)的加拿大24个树种地上生物量方程的b值进行计算，平均为2.33;利用Chojnacky(2002)建立的美国10个树种组的通用性地上生物量方程的b值进行计算，平均为2.33;利用Muukkonen(2007)建立的欧洲7个树种的通用性地上生物量方程的b值进行计算，平均为2.27;利用Návar(2009)建立的墨西哥7个松类树种组(n=721) 的地上生物量方程的b值进行计算，平均为2.29(因为株数相差太大，从27~384不等，如按株数加权平均为2.33);利用陈传国等(1989)建立的中国东北10个树种组的地上生物量方程的b值进行计算，平均为2.33。很明显，上述各项研究结果的平均b值与本文提出的理论值非常接近，有些甚至几乎没有差异。上述对比数据见表 1。

3.2 利用实测数据进行验证

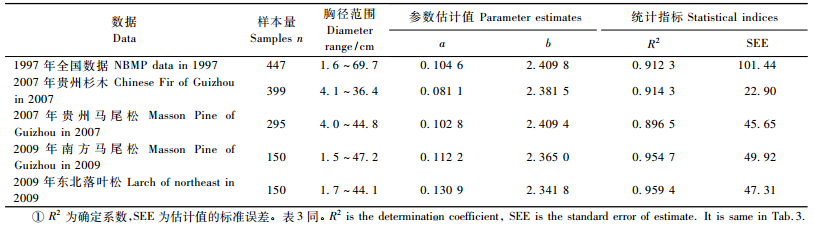
利用前面提到的5组立木地上生物量实测数据，按加权最小二乘回归拟合模型M=aD^b，其结果见表 2。回归估计的权函数采用W=1/f(x)²(曾伟生等，1999)。从表 2的结果可以看出，参数b值与本文提出的理论值2.33差异不大，而与WBE模型的理论值2.67则有明显差异。

如果将参数b设置为固定值2.33，对上述5组数据进行重新拟合，其结果见表 3。从表 3的2项统计指标看，与表 2的结果出入不大，其中1997年全国数据和2007年贵州马尾松数据的拟合结果还要好于表 2。由于模型只有1个参数，不同树种之间的比较就更为简单方便，如贵州马尾松和南方马尾松模型，参数a的差异不到5%(贵州的偏大3.68%); 而且因为参数a与木材密度显著相关，所以根据参数a的估计值就能知道不同树种的木材密度差异，如马尾松的木材密度大于杉木，落叶松的木材密度又大于马尾松。

最后，再利用1997年全国生物量课题组采集的447株样木数据，来分析参数a与木材密度ρ的关系。每株样木的木材密度ρ(g·cm^-3)由树干生物量除以树干带皮材积得到，参数a由地上生物量M除以D^2.33得到。通过线性回归模型a=b₀+b₁ρ进行分析，截距参数b₀与0没有显著差异，从而参数a与木材密度ρ之间的关系变成了简单的比例关系a=kρ。经拟合，其结果为:

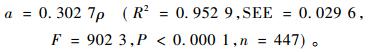
(1)

如果利用表 2中全部样木数据进行拟合，其结果为:

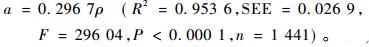
(2)

从(1)，(2) 式知，只要获知了某树种的木材密度信息，就可对参数a进行估计。

综上所述，立木的地上生物量模型可以表述为M = aD^7/3，其中a≈0.3ρ，ρ为木材密度。

4 结论与讨论

本文从West等(1997; 1999)提出的理论生物量模型出发，对大范围多树种的一元生物量模型M=aD^b的2个参数进行了研究。基于几何学的观点推断出参数b的理论值为7/3(≈2.33)，并通过与已发表文献的大量研究结果进行对比，说明新提出的参数值能够很好地描述地上生物量与胸径之间的平均相对生长关系; 同时还利用5组立木生物量实测数据(共计1 441株样木)对新提出的理论模型参数进行了验证; 最后还分析了参数a与木材密度ρ之间的相关性，并建立了二者之间的线性回归模型。结果表明:参数a与木材密度ρ呈显著正相关，将木材密度乘以0.3就能得到参数a的近似估计值。新的模型既简单明了，又能反映不同树种之间的生物量差异，为建立用于大尺度范围森林生物量估计的通用性生物量模型提供了可行途径。

当然，本文提出的理论参数只是基于几何学知识所做的直观推断。事实上，依据同样的推断，一元树干生物量模型甚至一元材积模型也应该具有类似的b值参数。因为这方面收集的资料较少，这里仅对树干生物量提供一些相关结果:一是利用Ter-Mikaelian等(1997)收集的北美65个树种134个树干生物量方程的b值进行计算，其算术平均值为2.31;二是利用Zianis等(2005)收集的欧洲11个树种30个树干生物量方程的b参数进行计算，算术平均值为2.28;三是利用1997年全国生物量课题组采集的11个树种组的447株样木数据进行拟合，参数b的估计值为2.32。显然，它们与前述理论值的差异并不大。因为不同树种的干曲线方程是存在差异的，因此2.33只能是一个近似的平均估计值。