削度是描述树干直径沿其树干向上随干径位置的升高而逐渐减小变化的程度，是用来说明干形变化的一种指标。由于树干削度方程不仅能预测树干总材积，还能预测基于树干任何高度和直径的经济材积, 在欧美等国家，树干削度方程已经逐渐取代材积表和材积方程。削度方程也是森林经营和林产品加工业的重要工具，广泛应用于估算树干材积、出材率和重建树干的三维空间及仿真与优化造材。

树干削度的研究已有100多年的历史。任何一个削度方程都不可能完满地描述所有树种树干形状的变化; 同时，也不会完全适应某一树种的所有林分。按发展阶段削度方程大致可归为3类:简单模型、变指数模型和分段模型。简单模型是用一个简单函数来描述削度的变化, 如Kozak等(1969)提出的简单树干削度方程, 这个简单模型很难准确描述干形的变化。Max等(1976)构造了分段树干削度模型, 这个模型由3个多项式组成，分别代表树干下部、中部和上部，取得了较好的预估精度。Cao等(1980)、Fang等(2000)、Jiang等(2005；2008)和Brooks等(2008)针对不同的树种建立分段模型。Kozak (1988)构建了变指数模型，通过变化指数来描述树干凹曲线体和抛物线体。这些模型较准确地预测了树干形状。随后，Newnham (1992)，Bi (2000)和Sharma等(2004)针对不同的树种建立可变参数树干削度模型。但是，变指数模型的缺点是不能直接积分得到材积估算，必须通过计算机程序来实现预测。Avery等(2002)把枫香(Liquidambar styraciflua)树干根部、中部和上部分别设想为凹曲线体(neiloid)、抛物线体(paraboloid)和圆锥体(cone)，较好地模拟了树干形状。然而，Valentine等(2001)发现湿地松(Pinus elliottii)和北美鹅掌楸(Liriodendron tulipifera)并不遵循这些形状。

在我国, 从事削度方程的研究起步较晚，孟宪宇(1982)应用一致性削度-材积比方程，探讨了材种出材率表的编制方法以及最适合模型, 在技术方法上做出了有益贡献。严若海等(1992)用变形形数导出新的削度模型，结果优于简单削度模型和分段模型。胥辉等(1995)以天山云杉(Picea schrenkiana var. tianshanica)为对象, 提出了新的削度模型, 能较好地满足各项预估能力。曾伟生等(1997)综合国内外学者提出的众多削度模型, 以湖南杉木(Cunninghamia lanceolata)为例, 提出了一个参数少而精度高的可变参数模型。

由于干形数据具有层次结构及重复测量的特点，近年来混合模型技术已应用于树干削度模型中(Tasissa et al., 1998; Valentine et al., 2001; Garber et al., 2003; Leites et al., 2004; Trincado et al., 2006; Yang et al., 2009a; 2009b)。与传统的回归分析相比，混合模型能满足独立同分布的假设，能得到渐进无偏参数估计，并用方差-协方差结构来反映数据间的相关性及异质性。混合模型包括总体和个体预测，总体预测只能反映平均水平而不能体现林分或树木之间的差异，而个体预测通过二次抽样校正随机参数来反映林分或树木之间的差异。目前国内应用混合模型研究削度方程还未见报道。本文以落叶松(Larix gmelinii)人工林为例，采用非线性混合模型技术建立树干削度混合效应模型，并对混合效应模型中随机参数值的校正进行探讨，然后对混合效应模型与传统模型拟合效果进行检验及比较分析。

1 数据与方法 1.1 数据

研究地点位于黑龙江省带岭林业实验局境内。带岭局位于小兴安岭南麓，地处低山丘陵带，隶属伊春市。128°37′—129°17′E, 46°50′—47°21′N。带岭地处中温带，属于大陆性湿润季风气候。受西伯利亚冷空气和太平洋季风的双重影响，冬季长且干燥、寒冷、多雪；夏季湿润而温暧。全年平均气温1.4 ℃左右。年最高气温37 ℃; 年最低气温-40 ℃。无霜期115天左右。全年平均降雨量661 mm，年降雨量最大值836.5 mm。降雨期全年为130天左右，多集中在7—9月，占全年降雨量的一半以上。带岭秋冬季多刮西北风，春夏多刮西南风。土壤种类以山地暗棕色森林土为主，少量草甸土、沼泽土和石质土。

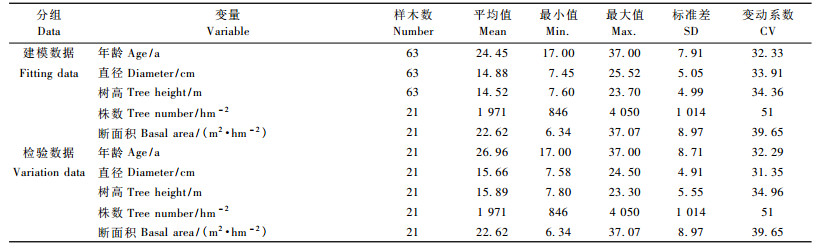
用来建立模型的数据为该局大青川林场的21块落叶松人工林样地。样地面积为0.04 hm², 实测样地内每株林木的胸径和树高。在每块标准地内随机选取4株标准木，树木被伐到后，测量以下指标: 1)树高; 2)第一活枝高和第一死枝高；3)树冠高度和冠幅; 4)树干采用中央断面积区分法进行区分: ①树高在15 m(含15 m)以上者按2 m区分; ②树高在14.9 m以下者按1 m区分, 测量各区分段梢头和梢底直径及中央位置处的带皮直径。将所收集全部干形数据按75%和25%的比例分成建模数据样本和独立检验样本，分别用于建立和检验削度方程。落叶松人工林各样木测树因子的统计量见表 1。

1.2 方法 1.2.1 基础模型

本研究采用能直接积分及拟合精度较高的Max等(1976)分段削度模型作为基础模型，该模型由3个多项式组成，分别代表树干下部、中部和上部的不同几何形状，其模型形式：

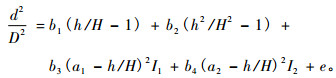
(1)

式中：d为树干h高处的带皮直径；D为带皮胸径；H为树高；h为从地面起算的高度; 当h/H≤a₁, I₁=1;当h/H>a₁, I₁=0;当h/H≤a₂, I₂=1;当h/H>a₂，I₂=0; b₁，b₂，b₃，b₄为模型待定参数；a₁，a₂为树干下部和上部拐点处的相对高度；e为模型的误差项。

1.2.2 混合模型

在基本模型基础上构建混合模型，混合模型包含固定参数、随机参数和方差协方差结构。根据Pinheiro等(1998), 混合模型的构建需要3个步骤：

1) 确定参数效应。一般情况下有2种方法确定模型中固定参数和随机参数。一种直观的方法是将样地(树木)间数据分别拟合，然后画出基于每一样地(树木)间参数的置信区间，如果该参数的置信区间重合，则把该参数确定为固定参数，否则认为该参数为混合参数，即包括随机参数。这种方法显然要求有足够的样地(树木)抽样确保削度方程能收敛。此外本文所用削度方程有6个参数，在实际拟合过程中发现对于部分样地(树木)模型很难收敛，因此该方法不适合确定复杂削度方程的参数效应。另一种方法是将不同随机参数组合的模型进行拟合，比较模型拟合的统计量，即比较AIC、BIC和对数似然值指标，这3个指标越小越好。本文选第2种方法确定参数效应。

2) 确定样地(树木)内方差协方差结构(R_i)。本文所使用数据具有层次结构, 包括样地间、树木间和观察值。应采用3层混合模型理论来建立削度模型; 但在一个模型中综合考虑3个层次，模型很难收敛且不能得到完整的方差协方差结构，因此本研究分别考虑2个层次，即样地间和树木间，将样地间随机效应和树木间随机效应分开建模，这样也能体现样地效应和树木效应对削度方程的影响。本研究使用Davidian等(1995)来计算样地(树木)内方差协方差结构：

(2)

式中：σ²指某一样地(树木)内观测值的残差方差值，Γ_i(ρ)为连续时间函数[CAR(1)]，即描述同一样地(树木)内不同测量值相关性，ρ为自回归参数ρ>0，d_jk=|h_ij-h_ik|，j≠k(Pinheiro et al., 2000)，I_ni为描述样地(树木)内方差的n_i×n_i维单位矩阵。

3) 确定样地(树木)间方差协方差结构(D)。样地(树木)间的方差协方差结构反映了组间的变化。本研究所用的方差协方差结构取决于随机参数的个数，以包括2个随机参数(u, v)的方差协方差结构为例，结构如下：

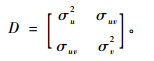
(3)

式中：σ_u²为随机参数u的方差，σ_v²为随机参数v的方差，σ_uv为随机参数u和v的协方差。

1.2.3 模型评价和检验指标

拟合和检验结果通过以下统计量和指标评价：AIC、BIC和-2Log Likelihood 3个统计量指标, 确定系数(R²), 误差(Bias), 均方根误差(RMSE)。

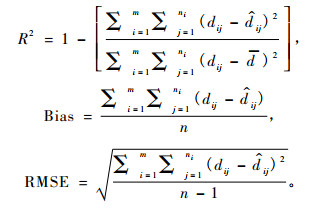
其中：d_ij为观测值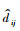，为预测值，d为观测值的平均值，n_i为样地(树木)内观察值数量，m为样地(树木)个数，n为样本数。

基础模型的参数估计采用SAS软件模型模块(proc model)中的似乎不相关回归过程(seemingly unrelated regression, SUR)进行拟合。混合模型的参数估计采用SAS软件的NLMIXED模块进行拟合。

1.2.4 模型检验

模型的独立性检验采用建模时未使用独立样本(检验样木)数据，对所确定模型的预测性能进行综合评价。混合效应模型中固定效应部分的检验与传统的检验方法相同; 然而，随机效应部分的检验需要二次抽样来计算随机参数值。本研究使用Vonesh等(1997)的方法来计算随机参数 ：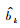

(4)

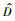
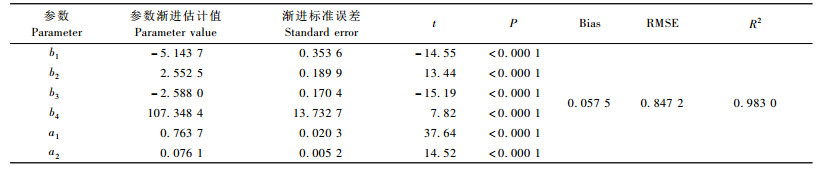
式中：为随机效应参数的方差协方差矩阵，为样地(树木)内方差协方差结构，Ẑ_k为设计矩阵，ê_k为实际值减去用固定效应参数计算的预测值。

2 结果与分析 2.1 基本模型

利用SAS软件模型模块中的似乎不相关回归过程，编写程序解决分段削度模型(1)的4个参数和2个拐点的参数同时估计以及参数估计显著性检验。由表 2可知：落叶松树干干形的下部拐点位置为0.076 1，上部拐点位置为0.763 7。t检验证明所有参数估计都是显著的(P < 0.000 1)。模型检验(F=31 392.30，P < 0.000 1)及拟合统计量(R²=0.983 0)都表明该削度模型对于描述落叶松树干干形变化具有显著意义。

2.2 非线性混合模型 2.2.1 基于样地效应混合模型随机参数确定

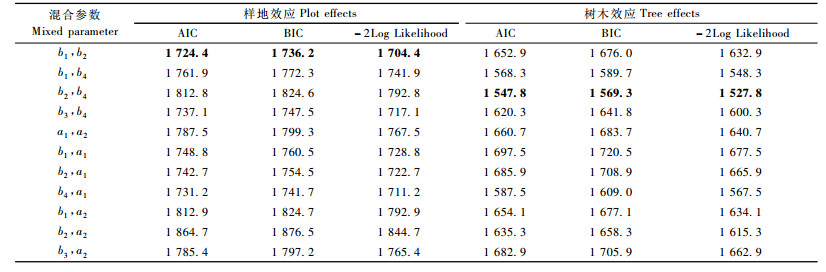
基于样地效应和不同随机参数的组合，利用SAS软件的NLMIXED模块对模型(1)进行拟合。利用AIC、BIC和-2Log Likelihood 3个统计量指标对模型的拟合优度进行比较，3个指标越小说明拟合的精度越高。拟合结果见表 3。可以看出:模型收敛的情况共有11种，其中具有混合参数b₁, b₂模型的3个指标值最小。因此，把该模型选为基于样地效应的最优混合模型。

2.2.2 基于树木效应混合模型随机参数确定

与2.2.1的研究方法相同。考虑树木效应和不同随机参数的组合，对模型(1)进行拟合，拟合结果见表 3。可以看出:模型收敛的情况共有11种，其中具有混合参数b₂, b₄模型的3个指标值最小。因此，把该模型选为基于树木效应的最优混合模型。

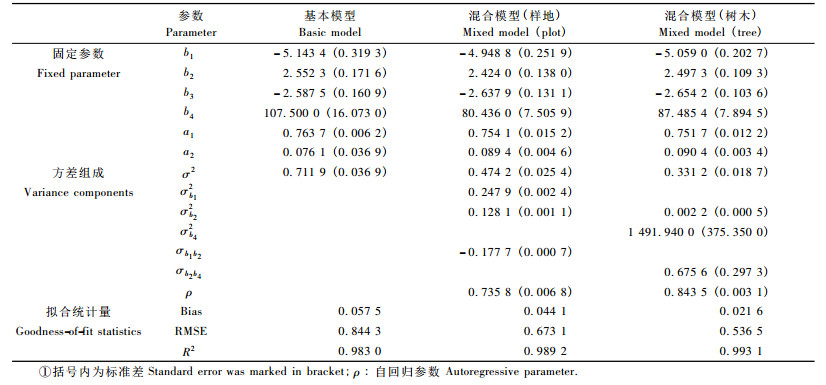
2.2.3 模型评价

表 4给出了基于样地和树木效应的最优混合模型与传统基本模型的比较。无论考虑样地效应还是树木效应的随机影响时，混合模型的确定系数大于基本模型的确定系数，而混合模型的误差和均方根误差均小于基本模型的误差和均方根误差，这些评价指标说明引入随机参数提高了模型的拟合精度。此外，考虑树木效应混合模型的确定系数(R²=0.993 1)大于考虑样地效应混合模型的确定系数(R²=0.989 2)，而考虑树木效应混合模型的误差(Bias=0.021 6)和均方根误差(RMSE=0.536 5)均小于考虑样地效应混合模型的误差(Bias=0.044 1)和均方根误差(RMSE=0.673 1)。这3个评价指标说明考虑树木效应混合模型的拟合精度比考虑样地效应混合模型的拟合精度高。

2.2.4 模型检验

独立样本数据包括21株样木，因此本研究只检验基本模型基于树木效应混合模型中的固定效应和随机效应。混合模型中随机效应部分的检验需要计算随机参数值。每株样木随机抽取2个样本，即高度和直径测量值，用公式(2~4)计算随机参数值，具体计算采用SAS软件的PROC IML模块计算。检验结果如表 5示。可以看出:通过计算随机效应混合模型的预测精度比基本模型和固定效应模型高; 而固定效应模型的预测精度比基本模型低，这也说明混合模型强调的是随机效应而不是固定效应。

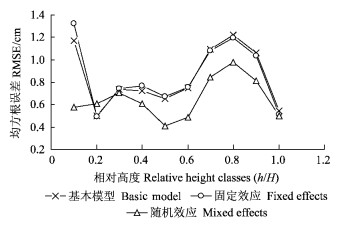
图 1给出了不同模型在不同相对树高处的均方根误差。可以看出:除相对高度在10%~20%外，随机效应混合模型在不同树干高度处预测精度是最高的。

3 结论与讨论

本研究采用非线性混合模型的方法建立落叶松人工林树干削度模型。分别考虑样地效应和树木效应，将不同随机参数组合的模型进行拟合，利用AIC、BIC和对数似然值评价非线性混合模型的效果表明:当考虑样地效应影响时，b₁，b₂同时作为混合参数时模型拟合最好; 当考虑树木效应影响时，b₂，b₄同时作为混合参数时模型拟合最好。无论考虑样地效应影响还是考虑树木效应影响，混合模型的拟合精度都比基本模型的拟合精度高，与国外文献的研究结果一致(Tasissa et al., 1998; Valentine et al., 2001; Garber et al., 2003; Leites et al., 2004)。为了进行混合模型检验，本研究还探讨了随机参数值的校正过程，通过校正随机参数值混合模型能提高模型的预测精度。因此混合模型在应用上不但能反映总体干形预测, 还能反映个体干形差异，而传统的非线性回归分析只能反映总体干形变化。由于样本数量有限，本研究没有探讨随机参数的变化规律，当考虑样地效应时，随机参数应当与林分变量(如年龄、林分密度等)有一定线性关系；当考虑树木效应时，随机参数应当与树木变量(如树冠长度、宽度、冠长率等)有一定线性关系。随着数据的积累，这方面将进一步深入研究。