文章信息
- 刘恩斌, 周国模, 施拥军, 葛宏立
- Liu Enbin, Zhou Guomo, Shi Yongjun, Ge Hongli
- 测树因子二元概率分布:以毛竹为例
- Bivariate Theoretic Probability Distribution of Forest Mensuration:A Case of Moso Bamboo Forest
- 林业科学, 2010, 46(10): 29-36.
- Scientia Silvae Sinicae, 2010, 46(10): 29-36.
-
文章历史
- 收稿日期:2009-01-20
- 修回日期:2010-06-25
-
作者相关文章
测树因子的概率分布对森林生物量估算及现代森林经营活动起着非常重要的作用, 它可以预估树木各径阶、各龄阶株数与蓄积变化, 生长量测定、产量预估、枯损量计算等, 还可以对抚育间伐设计与森林碳库估算提供科学依据。在林业与生态实践中, 研究较多的是测树因子的一元概率分布(洪利兴等, 1995; 周国模等, 1996; Diane et al., 2008; Lindsay et al., 1996; Wang et al., 2005; 吴承祯等, 1998; 刘君然等, 1997), 但一元概率分布只能描述一个测树因子的概率分布规律, 不能全面反映林分测树因子的联合概率分布状况。
Hafley等(1976)、Schreuder等(1977)应用二元SBB 函数研究了林分胸径、树高分布信息, 结果显示二元SBB 函数非常适合描述胸径、树高联合分布规律; Li等(2002)用二元Beta函数也研究了林分胸径、树高分布规律, 经卡方检验表明二元Beta函数适合于描述胸径、树高分布规律; Wang等(2007)应用二元SBB 、二元Beta等4个函数再次研究了林分胸径、树高分布信息, 结果表明二元SBB 函数拟合精度最高, 要优于二元Beta函数; 葛宏立等(2008)应用二元Weibull分布函数研究了浙江毛竹(Phyllostachys edulis)胸径、年龄分布规律, 表明二元Weibull分布函数具有较高的测量精度; 还有文献介绍的测树因子二元概率密度函数是通过修改一元Weibull概率密度函数3参数得到的, 不满足概率模型的性质(周国模等, 2006)。从以上研究可以看出, 已有测树因子联合分布的研究不是建立在充分利用现有数据提供信息的基础上, 而是事先指定一种概率模型, 然后用它来测量测树因子的概率分布状况, 如果测量精度高, 则说明该分布适合描述测树因子的联合分布规律, 这样做的缺点是事先指定的概率模型不一定是最佳模型, 因为适合描述测树因子联合分布的概率模型可能有很多。因此, 在最大限度地利用现有资料提供信息的基础上, 如何构建适应范围更广、测量精度更高的测树因子概率模型值得研究。熵是信息论中的一个基本概念, 是用以度量信息源不确定性的量, 熵最大就意味着获得的总信息量最少, 即所添加的信息最少, 故本文对测树因子二元最大熵函数做了详细推导, 并用构建的模型与已有二元SBB 函数、二元Beta函数分别测量了浙江毛竹胸径、年龄联合分布信息, 旨在说明二元最大熵函数的优越性。
综上所述, 本文研究测树因子二元概率分布具有如下意义:1) 2个测树因子的联合分布是全面认识林分结构、精确估算区域尺度生物量的有力工具; 2) 可以更精确、更全面地预估树木各径阶、各龄阶株数与蓄积变化等; 3) 在林业生产实践中, 要作出科学的决策需要2个测树因子的联合分布信息, 故只研究测树因子的一元概率分布不能满足现代林业实践的需求; 4) 构建了测数因子二元最大熵函数, 从而为精确测量测树因子概率分布信息提供了一种新的途径。
1 理论与方法 1.1 测树因子二元最大熵函数构建要构建测树因子的二元概率密度模型, 必须有一个构造的标准, 那就是使所构造的模型在数据不充分的情况下, 既要与已知的数据相吻合又必须对未知的部分做最少的假定, 即对数据的外推或内插采取最超然的态度。因此模型的构造过程可以认为是从数据中提取信息的过程, 而信息来自2个部分:一是己知数据, 二是由于数据不完全而不得不对未知部分所做的假定, 这种假定相当于人为地“添加”了一些信息。由于熵可以用来度量测树因子的不确定性, 熵最大就意味着获得的总信息量最少, 即所添加的信息最少, 所以最大熵是超然的。本文利用最大熵超然的特点, 仿照一元最大熵函数的推导过程(朱坚民等, 2005), 导出了二元最大熵函数, 进而把它作为测树因子的二元概率密度模型。
为了能在理论上导出测树因子二元最大熵概率密度函数, 在此先介绍几个相关的概念与性质。
1.1.1 相关概念与性质
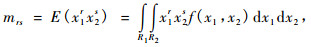
|
(1) |
(1) 式就是随机变量x1, x2的联合分布混合矩。

|
(2) |
(2) 式就是随机变量x1, x2的联合分布熵函数。
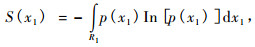
|
(3) |
(3) 式就是随机变量x1的连续型熵函数。类似的可定义随机变量x2的连续型熵函数为:
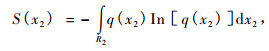
|
(4) |
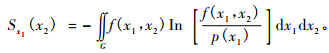
|
(5) |
(5) 式就是在试验x1实现条件下的试验x2的条件熵函数。
定理:
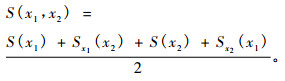
|
(6) |
因为S(x1, x2) = S(x1) + Sx1(x2) = S(x2) + Sx2(x1), 证明过程详见参考文献(李贤平, 2006)。
1.1.2 二元最大熵概率密度模型构建利用样本信息的一种简便方法是计算样本的各阶矩。利用以上的概念与定理, 仿照一元最大熵函数的构建思路(朱坚民等, 2005), 本文详细推导了连续型随机变量的二元最大熵函数:
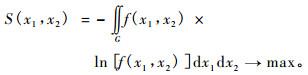
|
(7) |
约束条件为:

|
(8) |
通过调整f(x1, x2), 使其熵达到最大, 设S为拉格朗日函数, 其余为拉格朗日乘子。
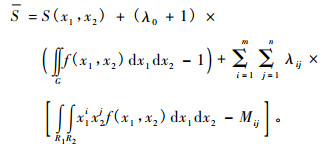
|
(9) |
(9) 式中的S(x1, x2)用(6)式替代, 得:
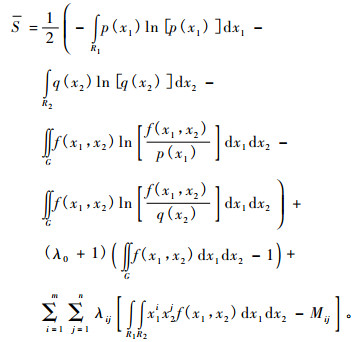
|
令d S/df(x1, x2)等于0, 求得:
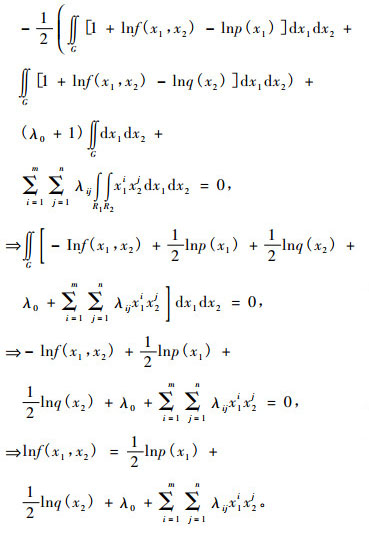
|
(10) |
在(10)式中, 把p(x1), q(x2)分别用x1, x2一元最大熵函数的统一表达式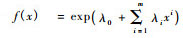
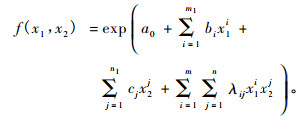
|
(11) |
(11)式就是本文提出的二元最大熵函数, 该函数的表达式符合指数族分布, 因此可以把它看作是二元多参数指数族分布。从(11)式还可以看出, 二元最大熵函数的指数幂是二维连续函数空间基{1, x1, x12, …, x1m1, …, x2, x22, …, x2n1, …, x11x21, …, x1mx2n, …}(当x1的阶矩取至m1, x2的阶矩取至n1, x1与x2的混合矩取至m, n时可达到精度要求)的线性组合, 这与一元最大熵函数类似。以此类推可以得到二元以上最大熵函数, 它可以作为2个以上测树因子的概率密度函数。
1.2 二元SBB 函数在已有的二元分布函数中, 用二元SBB 函数研究测树因子二元概率分布规律报道最多(Hafley et al., 1976; Schreuder et al., 1977), 其函数表达式为:
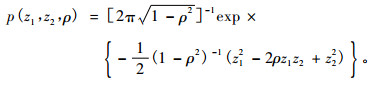
|
(12) |
其中:
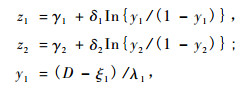
|
(13) |
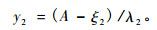
|
(14) |
在式(12)中ρ是z1, z2的相关系数, 式(13), (14)中γ1, γ2, δ1, δ2, ξ1, ξ2, λ1, λ2都是系数, D, A分别是胸径与年龄。
在用二元SBB 函数测量测树因子二元概率分布信息时, 如果这9个系数的初值选取不当, 迭代很难收敛, 经多次尝试, 按如下初值选取方法迭代很快收敛且测量精度很高:ξ1, ξ2的初值一般取在[0, 4.5], ξ1 + λ1, ξ2 + λ2的取值分别要大于max(Dj) (j = 1, 2, …, n)与max(Aj)(j = 1, 2, …, n) (Schreuder et al., 1977):
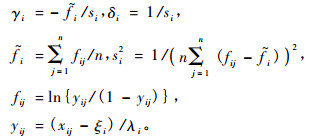
|
这里x1j =Dj, x2j = Aj, 以上各式中i = 1, 2;j = 1, 2, …, n。
1.3 二元Beta函数二元Beta函数有5参数形式与3参数形式2种(Gupta et al., 1985), 5参数二元Beta分布密度函数为:

|
(15) |
式(15)中, 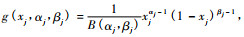
3参数二元Beta分布密度函数为:
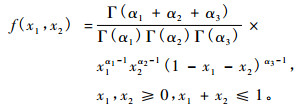
|
(16) |
从以上2个Beta函数的表达式可看出其自变量的定义域在0至1之间, 而树种测树因子的取值不完全在其自变量的取值范围内, 因此需要先进行变量的区间变换。在本文中经多次尝试, 选取如下变换公式: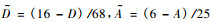
由于柯尔莫哥洛夫检验综合考虑了每一样本单元累积频率值与其相应理论累积频率值的偏差, 因此它比χ2检验精确(北京林学院, 1979), 故用柯尔莫哥洛夫检验方法对3种函数做拟合优度检验。现假设Fn(x, y)为随机样本n次观察值的累积概率分布; F(x, y)为理论分布函数, 并定义
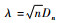
下面用浙江省森林资源连续清查有关毛竹的样地资料对本文介绍的3种二元概率函数进行检验与分析, 并根据方程dθ =(B′B)-1 B′y, θ(k + 1)= θ(k) + dθ(θ为参数矩阵, B为自变量组成的矩阵, y为因变量组成的矩阵, k为迭代次数), 用SPSS软件拟合3种函数的参数。
2 模拟案例毛竹是浙江省的主要经济植物, 在全省分布范围很广, 具有很强的固碳能力(周国模等, 2004; 2006), 还是浙江省农民经济收入的重要来源。在我国, 毛竹是一种特殊的地域性植物, 与其他植物不同的是:1) 毛竹的胸径生长与高生长在第1年内完成; 2) 对单株毛竹而言, 当胸径生长与高生长完成后, 胸径与竹高不再发生变化, 但其生物量还在变化, 生物量的这种变化主要是由年龄引起的。本文研究省域尺度毛竹胸径、年龄分布主要基于以下3方面的考虑:1) 毛竹林是一种异龄林, 故除胸径外, 年龄也是其林分结构的重要特征; 2) 对于区域尺度的毛竹林而言, 由于立地条件等的不同, 使得相同胸径的毛竹, 其年龄并不完全一样, 相同年龄的毛竹, 其胸径也并不完全一样, 这样区域尺度毛竹胸径、年龄具有某种分布规律; 3) 由于胸径与年龄是影响毛竹生物量的主要因素, 故利用区域尺度毛竹胸径、年龄的联合概率分布信息与毛竹径阶生物量, 可以推算区域尺度的毛竹生物量。
2.1 资料来源浙江省于1979年建立了森林资源连续清查体系, 以5年为一个复查周期。共设置固定样地4 250个, 样点格网为4 km × 6 km, 样地形状为正方形, 边长28.28 m, 面积800 m2。本研究利用2004年的调查数据, 选择基本为毛竹纯林的样地245个, 每个毛竹样地毛竹胸径从5 ~ 15 cm, 年龄1 ~ 4度以上, 毛竹株数18 ~ 461株不等。样地内5 cm以上的竹子均要调查记载, 调查内容主要有量测胸径, 测定年龄(1年生竹记为1度竹; 2 ~ 3年生竹记为2度竹, 依此类推)。本文研究的是全省区域的宏观模型, 所以将245个样地的数据合并统计, 见表 1。
|
|
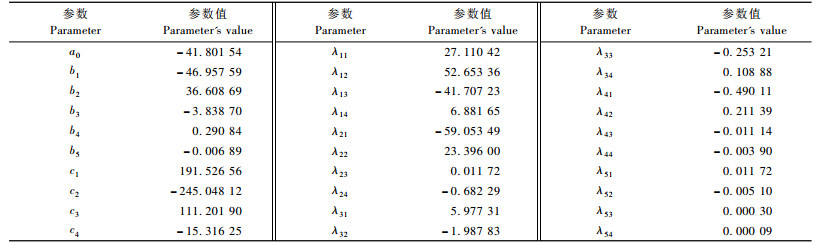
一般来说, 胸径x1、年龄x2阶数的取值范围为2 ≤ x1, x2 ≤6, 经多次尝试知, 当胸径x1取至5阶矩与年龄x2取至4阶矩时, SPSS软件提供非线性最小二乘算法的拟合精确最高, 具体的拟合步骤为:1) 打开SPSS软件; 2) 利用表 1的株数值计算某径阶、某龄阶实测概率, 并以此实测概率为因变量, 对应的胸径、年龄为自变量; 3) 将因变量与自变量的值复制到SPSS的Data View表中, 再把Variable View中Name字段的相应单元格分别命名为概率、胸径与年龄; 4) 在SPSS任务栏中选择Analyze→ Regression →Nonlinear; 5) 将概率作为因变量导入Dependent栏中, 当m = 5, n = 4, m1 = 5, n1 = 4时, 把(11)式按照SPSS软件语法输入到Model Expression框中, 并在Parameters栏中设置每个参数的初始值; 6) 点击Save选项, 并选择Predicted values和Residuals, 点击Option选项, 并选择Levenberg-Marquardt; 7) 点击OK进行计算, 系统运算后, 在Data View表中即可得到毛竹在各径阶、各龄级上相应实测概率的估计值与偏差。SPSS软件拟合的二元最大熵函数各参数见表 2。
|
|
此时毛竹估计株数为: 29 577 (实际株数为29 951),回归离差平方和: 9. 976 77e - 05,R2 = 0.996 0。柯尔莫哥洛夫检验统计量1-Q(λ) = 0.999 83, 是个很大的概率, 故二元最大熵函数适合于描述浙江毛竹胸径、年龄分布规律。从表 2可以看出, 30号变量的系数几乎为0, 说明在用最大熵函数描述毛竹胸径、年龄分布规律时, 对应变量x15x24提供信息较其他变量相对较少。
2.2.2 二元最大熵函数测量结果的直观描述由于二元最大熵函数指数幂的组成很有规律, 在此用Matlab软件根据表 2参数绘制省域尺度毛竹胸径、年龄二元最大熵概率密度图, 见图 1。

|
图 1 省域尺度毛竹胸径、年龄二元最大熵概率密度 Figure 1 Bivariate maximum probability entropy density distribution on moso bamboo's diameter-age for province dimension |
从图 1可以看出:虽然对单株毛竹而言, 其胸径、年龄的相关性不大, 但由于立地条件等原因使省域尺度毛竹胸径、年龄具有某种分布规律。图 2可以更直观地反应二元最大熵函数的测量精度。
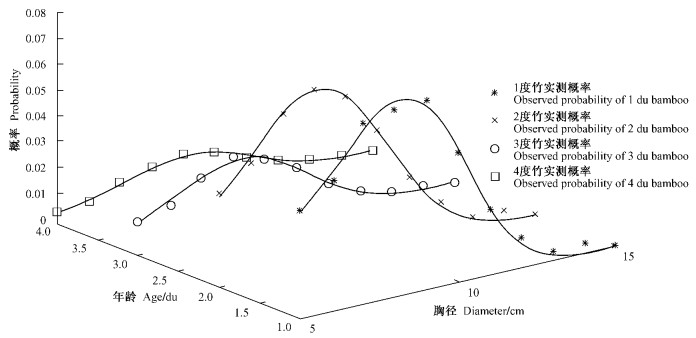
|
图 2 毛竹胸径在每一度上的二元最大熵函数曲线 Figure 2 Diameter distribution curve of bivariate maximum entropy for each moso bamboo's age |
从图 2可以看出:二元最大熵函数对浙江省域尺度毛竹胸径、年龄分布信息的测量精度非常高。
由于二元Weibull概率密度函数比较复杂, 所以其图像与毛竹各径阶、各龄阶实测概率的直观描述在此不便说明。
2.2.3 二元SBB 函数评价检验及其参数利用表 1株数值计算某径阶、某龄阶实测概率, 用SPSS软件提供的非线性最小二乘算法拟合SBB 函数各参数为:(ρ, γ1, γ2, δ1, δ2, ξ1, ξ2, λ1, λ2) =(-0.433 36, 0.717 76, 0.489 39, 2.288 50, 0.883 01, 0.991 51, -1.563 97, 15.460 38, 6.609 77), 此时回归离差平方和为0.000 84, R2 = 0.964 00, 柯尔莫哥洛夫检验统计量1-Q(λ) = 0.979 98, 是个很大的概率, 故二元SBB 函数适合于描述浙江毛竹胸径、年龄分布规律。
2.2.4 二元Beta函数评价检验及其参数利用表 1株数值计算某径阶、某龄阶实测概率, 用SPSS软件提供的非线性最小二乘算法拟合5参数Beta函数各参数为:(α1, α2, β1, β2, λ) =(1.882 61, 6.061 89, 0.562 85, 48.801 58, -0.803 45), 此时回归离差平方和为0.006 91, R2 = 0.701 00, 柯尔莫哥洛夫检验统计量1-Q(λ) = 0.776 36。
拟合3参数二元Beta密度函数参数为:(α1, α2, α3) =(1.828 83, 2.577 62, 0.248 77), 此时回归离差平方为0.007 26, R2 = 0.687 00。可以看出, 2种二元Beta函数的测量精度相差不大。
2.2.5 模型分析及对比1) 二元SBB 函数分析 从回归离差平方和与R2 可以看出:该模型的测量精度很高, 故二元SBB 函数能精确描述浙江毛竹胸径、年龄联合分布规律, 原因在于二元SBB 函数具有严格的概率模型性质, 其边际分布是一元SB分布(Haffley et al., 1977; Schreuder et al., 1977), 而一元SB 分布能非常精确地描述一个测树因子概率分布规律(Haffley et al., 1977)。SBB 函数还具有其他二元函数不具有的优点即可以说明2个随机变量的相关性与独立性, 这一特点可由参数ρ反映。从ρ的值可以看出, 浙江毛竹胸径与年龄的相关性不大, 同时也说明毛竹胸径、年龄分布不属于2个相互独立随机变量的联合分布。故有关2个相互独立随机变量联合分布的性质不适用于研究毛竹胸径、年龄分布。
2) 二元Beta函数分析 从回归离差平方和与R2 可以看出:该模型测量精度最低, 故二元Beta函数很少被用于研究测树因子的联合概率分布规律, 这也可以从二元Beta函数的柯尔莫哥洛夫检验统计量得出。估计精度低的原因是:①二元Beta函数初值选取不像二元SBB 函数一样形成了一套固定的理论; ②目前有关测树因子二元Beta函数初值给定的例子很少见报道, 故本文对二元Beta函数初值的选取完全是盲目的, 因此得出的参数可能不是全局最优解; ③在应用二元Beta函数时, 须先进行变量的区间变换, 但到底哪个变换公式最理论还未见报道, 本文的变换公式只是经多次尝试后确定的, 带有很大的主观随意性。
3) 测树因子二元最大熵函数与二元Weibull分布函数对比分析 二元Weibull函数是分布函数而不是概率密度函数, 因此需要先计算各径阶、各龄阶实测概率的累积值才能用二元Weibull分布模型, 其计算结果也是累积概率, 故要做相应的减法运算才能得到各径阶、各龄阶的概率; 而最大熵模型已经是概率密度函数, 可以直接使用各径阶、各龄阶的实测概率。从二元Weibull分布的表达式可以看出:通过求2阶偏导得到的其概率密度函数相当复杂。从与Weibull分布函数评价检验指标(回归离差平方2.364 2e-004, R2 = 0.990 11, 柯尔莫哥洛夫检验统计量0.996 97)的对比可以看出:2种方法拟合结果都非常好, 二元最大熵函数拟合结果比二元Weibull分布略好, 主要是由于二元最大熵函数有更广的适应性且可以逼近二元Weibull概率密度函数, 这从以下分析可以得出, 现用函数逼近理论对二元最大熵函数的性质做如下推导:
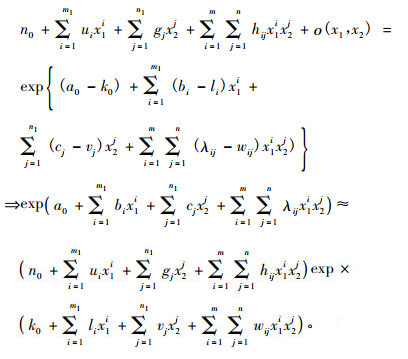
|
(17) |
在(17)式中, ο(x1, x2)是高阶无穷小。
对(17)式的每一项再做同样的推导如:
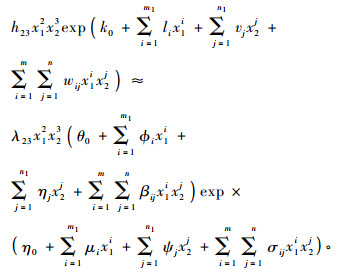
|
从这里可以看出(17)式的每一项都含有2组二维连续函数空间基的线性组合, 即
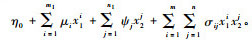
由于毛竹的生物量与胸径、年龄都有关, 一元概率密度函数或分布函数不能全面反映毛竹林测树因子的概率分布规律, 因而不能精确估算区域尺度毛竹生物量, 而本文所述的3种方法可以弥补一元概率函数的这一不足。综合本文的研究得到如下结论:
1) 本文在充分利用现有资料提供信息的基础上构建了测树因子的二元概率密度函数即二元最大熵函数, 它的幂是二维连续函数空间基的线性组合, 是二元多参数指数族分布。
2) 二元最大熵函数的测量精度最高, 适应范围最广, 二元SBB 函数的测量精度次之, 二元Beta函数的测量精度最低, 从本文模型评价检验与分析对比可以得出二元最大熵函数是描述测树因子联合分布信息的最佳模型。
3) 通常确定某种分布函数能不能反映毛竹胸径、年龄联合分布规律的方法是假设检验, 显然符合假设检验的分布函数并不唯一, 二元最大熵函数测量精度优于其他函数的根本原因在于:第一, 二元最大熵函数能最大限度地挖掘测量数据本身所固有的规律; 第二, 表达式所含参数比其他函数多。
4) 二元最大熵函数、二元SBB 函数的测量精度都非常高, 都适合于描述毛竹胸径、年龄联合分布规律:回归离差平方和、R2 与与柯尔莫哥洛夫检验统计量依次为9.976 77e-05, 0.996 0, 0.999 83; 0.000 84, 0.964 00, 0.979 98。
5) 二元Beta函数在林业上的应用还有待于进一步研究。
6) 当考虑2个以上影响毛竹生物量的因素、估算区域尺度毛竹生物量时, 要用到测树因子的2元以上概率密度函数或分布函数, 而二元以上Weibull分布函数与SBB 函数的表达式, 作者查阅了大量有关资料, 还未发现有相关报道; 但从一元与二元最大熵概率密度函数的组成, 结合相关的理论, 可以推出二元以上最大熵概率密度函数的表达式即指数幂是相应空间基的线性组合。
7) 从二元最大熵函数的表达式可以看出:本文构建的二元概率密度函数具有统一的结构形式, 可作为研究测树因子二元概率分布信息的统一模型, 且这种统一形式可以根据数据类型与精度要求, 非常灵活地选用不同的样本阶矩, 从而灵活选择不同阶数的二元最大熵函数。
8) 在用二元SBB 函数测量毛竹胸径、年龄联合分布时, 其参数初值选取方法与胸径、树高参数初值选取(Schreuder et al., 1977)相同, 原因在于这种初值选取方法是根据二元SBB 函数的结构特点与性质提出的, 按照该方法选取的初值在二元SBB 函数的收敛域内, 这从Schreuder等(1977)与本文的研究可以得到验证。
北京林学院. 1979. 数理统计[M]. 北京: 中国林业出版社: 167-168.
|
葛宏立, 周国模, 刘恩斌, 等. 2008. 浙江省毛竹直径与年龄的二元Weibull分布模型[J]. 林业科学, 44(12): 15-20. DOI:10.3321/j.issn:1001-7488.2008.12.003 |
洪利兴, 杜国坚, 张庆荣, 等. 1995. 天然常绿阔叶异龄幼林胸径的Weibull分布及动态预测[J]. 植物生态学报, 19(1): 29-42. |
李贤平. 2006. 概率论基础[M]. 2版. 北京: 高等教育出版社: 210-213.
|
刘君然, 赵东方. 1997. 落叶松人工林威布尔分布参数与林分因子模型的研究[J]. 林业科学, 33(5): 412-417. |
吴承祯, 洪伟. 1998. 杉木人工林胸径的Weibull分布及其最优拟合研究[J]. 江西农业大学学报, 20(1): 86-90. |
周国模, 姜培坤. 2004. 毛竹林的碳密度和碳贮量及其空间分布[J]. 林业科学, 40(6): 20-24. DOI:10.11707/j.1001-7488.20040604 |
周国模, 刘恩斌, 刘安兴, 等. 2006. Weibull分布参数辨识改进及对浙江毛竹林胸径年龄分布的测度[J]. 生态学报, 26(9): 2918-2924. |
周国模, 王瑞铨, 俞双群, 等. 1996. 庆元县人工杉木林直径分布的研究[J]. 华东森林经理, (1): 18-32. |
朱坚民, 郭冰菁, 王中宇, 等. 2005. 基于最大熵方法的测量结果估计及测量不确定度评定[J]. 电测与仪表, 42(8): 5-8. |
Diane H K, Eddie B, Ralph D, N. 2008. Individual-tree diameter growth model for sugar maple trees in uneven-aged northern hardwood stands under selection system[J]. Forest Ecology and Management, 256: 1579-1586. DOI:10.1016/j.foreco.2008.06.015 |
Gupta A K, Wong C F. 1985. On three and five parameter bivariate Beta distributions[J]. Metrika, 32(1): 85-91. DOI:10.1007/BF01897803 |
Haffley W L, Schreuder H T. 1977. Statistical distributions for fitting diameter and height data in even-aged stands[J]. Can J For Res, 7(3): 481-487. DOI:10.1139/x77-062 |
Hafley W L, Schreuder H T. 1976. Some non-normal bivariate distributions and their potential for forest application[J]. International Union Forest Research Organizations, ⅩⅥ World Congress Proceedings: 104-114. |
Li F, Zhang L, Davis C J. 2002. Modeling the joint distribution of tree diameters and heights by bivariate generalized beta distribution[J]. Forest Science, 48(1): 47-58. |
Lindsay S R, Wood G R, Woollons R C. 1996. Modelling the diameter distribution of forest stands using the Burr distribution[J]. Journal of Applied Statistics, 23(6): 609-620. DOI:10.1080/02664769623973 |
Schreuder H T, Hafley W L. 1977. A useful bivariate distribution for describing stand structure of tree heights and diameters[J]. Biometrics, 33(3): 471-478. DOI:10.2307/2529361 |
Wang M, Rennolls K. 2007. Bivariate distribution modeling with tree diameter and height data[J]. Forest Science, 53(1): 16-24. |
Wang M, Rennolls K. 2005. Tree diameter distribution modelling:introducing the logit-logistic distribution[J]. Can J For Res, 35(6): 1305-1313. DOI:10.1139/x05-057 |
 2010, Vol. 46
2010, Vol. 46