文章信息
- 朱光玉, 雷渊才
- Zhu Guangyu, Lei Yuancai
- 两阶段自适应群团抽样在沙漠边缘植被调查中的比较
- Comparison among Different Designs of Two-Stage Adaptive Cluster Sampling in Vegetation Survey in Desert Edge
- 林业科学, 2010, 46(6): 71-77.
- Scientia Silvae Sinicae, 2010, 46(6): 71-77.
-
文章历史
- 收稿日期:2008-12-04
- 修回日期:2010-04-06
-
作者相关文章
2. 中南林业科技大学林业遥感信息工程研究中心 长沙 410004
2. Research Center of Forestry Remote Sensing Information Engineering, Central South University of Forestry and Technology Changsha 410004
对于稀少、积聚群团状总体,Thompson (1990)提出了一种新的抽样设计,自适应群团抽样(adaptive cluster sampling,ACS)。随后,出现了多种自适应群团抽样设计,如分层自适应群团抽样(Thompson, 1991)、两阶段自适应群团抽样(Salehi et al., 1997a)、两相自适应群团抽样(Felix-Medina et al., 2004)等,并且被广泛用于各种领域(Turk et al., 2005)。
两阶段抽样有着悠久的历史和广泛的应用领域(Salehi et al., 1997b)。但是两阶段自适应群团抽样的研究却比较少。Salehi等(1997b)描述了两阶段自适应群团抽样设计,初级单元采用不放回简单随机抽样,然后,在每个初级单元中,对次级单元进行适应性群团抽样。设计中提出了2种适应性抽样计划:1)群团允许横跨初级单元边界的设计;2)群团不允许横跨初级单元边界设计。
Muttlak等(2002)提出了调整的两阶段自适应群团抽样设计,将总体中的网络分成两大类:大网络和小网络,如果网络单元个数大于临界值Cα1,则为大网络,反之则为小网络。对小网络进行一阶段适应性抽样,对大网络进行两阶段抽样。
Salehi等(2005)阐述了不考虑邻域的两阶段序贯抽样,初级单元采用不放回简单随机抽样,然后,在每个初级单元中,对次级单元也采用不放回简单随机抽样,如果抽取的次级单元至少有1个单元满足某一条件(如大于临界值Cα),则对该初级单元,再进行不放回简单随机抽样。
为了探讨两阶段自适应群团抽样设计的适用性,本文以内蒙古磴口县巴彦高勒镇西南约8 km,乌兰布和沙漠边缘地区为研究区,该地区的珍稀植物花棒(Hedysarum scoparium),分布稀少且呈群团状,所以选取花棒为具体对象,利用VB 6.0编制的抽样程序,对调查的花棒数据进行了多次模拟试验,并对这4种两阶段自适应群团抽样种设计的效率做了比较,寻求最佳的、适用于花棒调查的抽样设计。
1 两阶段自适应群团抽样的原理与方法对于稀少、集聚总体的参数估计,自适应群团抽样(ACS)是一种非常有效的抽样方法。然而,也存在的一些问题:1)最终样本的不确定性,因此对于给定效率的情况,适应性抽样有其局限性;2)当临界值选取不当时,可能导致最终样本量过大或过小;3)样本单元调查时,可能会因为单元之间的距离,耗时太多。而两阶段自适应群团抽样,可以合理的解决上述问题。
两阶段自适应群团抽样是对次级(二阶)单元进行适应性群团抽样计划,它包括2种适应性抽样方式,一种是不可以跨越初级(一阶)单元的适应性群团抽样,另一种是可以跨越初级(一阶)单元的适应性群团抽样。针对这2种抽样设计,Salehi等(1997b)设计了2种相应的无偏估计量:一种是修正的HT(Horvitz and Thompson)两阶段ACS估计量,另一种是修正的HH(Hansen and Hurwitz)两阶段ACS估计量。
1.1 相关概念邻域或邻近(neighborhood)、网络(network)、边缘单元、群团、自适应群团抽样的概念和自适应群团抽样的相关估计量公式见Thompson(1990)、雷渊才等(2007),本文采用一阶邻域。
由群团和网络的定义可以知道,总体可以划分为网络之并,各网络相互独立;而群团则并一定相互独立,因为不同的群团可能有共同的边缘单元。所以,当样本量一定时,群团的包含概率是未知的或边缘单元的交叉包含概率是未知的,而最初样本单元与网络交叉的包含概率是可以确定的。正是因为网络之并构成总体,网络的相互独立性,Thompson(1990)将部分包含概率(partial inclusion probabilities)引入了Horvitz-Thompson估计量和Hansen-Hurwitz估计量,得到了基于网络的修正的HT估计量和HH估计量,因此网络相互独立、同分布是这2种方法的应用前提。
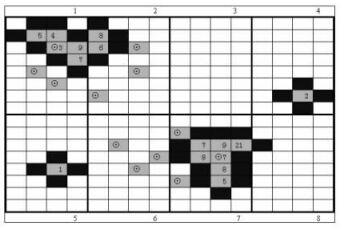
两阶段自适应群团抽样:假定总体中有NT个单元,依据需要将总体划分成M个初级单元(primary units),这样每个初级单元包括Ni个次级单元(second units)(如图 1所演,总体单元NT=256,初级单元M=8,每个初级单元所包含的次级单元个数相等,Ni=32)。首先采用等概率或不等概率抽取m个初级单元(图中标记⊙所在的单元即为最初抽取的样本单元),然后,在所抽取的m个初级单元中,分别抽取ni个次级单元,依据适应性抽样原则,当抽取的次级单元的观测值满足条件C(如大于临界值Cα)时,其相邻(预先定义)的额外单元也应入样。按照这种运行规则,如果额外单元也满足条件C(如大于临界值Cα),与额外单元相邻的单元也应入样,直至遇到不满足条件的额外单元,抽样才停止,这种抽样称为跨越边界的两阶段自适应群团抽样。如果是不跨越边界的两阶段自适应群团抽样,当额外单元处于一阶单元边界时,抽样就会停止; 否则,直至遇到不满足条件的额外单元,抽样才停止。
|
图 1 两阶段自适应群团抽样 Figure 1 Two-stage adaptive cluster sampling |
网络、群团和包含概率等概念与自适应群团抽样一致。
两阶段自适应群团抽样有4种不同的抽样设计:
1) 跨边界基于修正的HH估计量的两阶段自适应群团抽样;
2) 跨边界基于修正的HT估计量的两阶段自适应群团抽样;
3) 不跨边界基于修正的HH估计量的两阶段自适应群团抽样;
4) 不跨边界基于修正的HT估计量的两阶段自适应群团抽样。
1.2 跨越边界的抽样设计通常情况下每个初级单元Ni所包含的单元数是相等的。单元(i, j)表示第i个初级单元中的第j个次级单元,用yij表示单元观测值。令Ti= 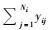
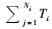
在抽样的第一阶段,从M个初级单元中不放回随机抽取m个初级单元,在第二阶段从第一阶段抽取的初级单元i(i=1, 2, …, m)中,不放回随机抽取ni个次级单元,则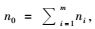
不考虑最初抽样单元(primary sampling unit,PSU)的边界,将NT个单元分割成K个网络。
1.2.1 修正的HT估计量由Thompson (1990)得总体均值估计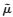
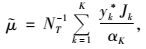
|
(1) |
总体均值方差var(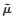
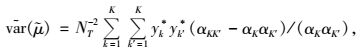
|
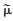
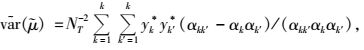
|
(2) |
其中,K为总体网络单元数, k为抽取的网络单元数, Jk为随机变量(Jk=1或Jk=0),Jk=1表示网络k被抽中, 否则,网络k未被抽中。αk表示网络k被抽取的包含概率, αkk′表示网络k和网络k′被同时抽取的包含概率, yk*,yk′*表示网络k中所有单元值之和,αk和αkk′的计算见Salehi等(2005)。
1.2.2 修正的HH估计量pi为初级单元的包含概率,pij为初级单元i和初级单元j都入样的包含概率,Aij为包含单元(i, j)的网络,Aijl表示网络Aij位于初级单元l的部分。fij.表示初级单元样本n0落入网络Aij中的单元数,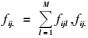
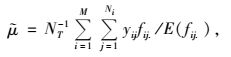
|
(3) |
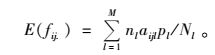
|
(4) |
由公式(3)中的yijfij.可知,网络Aij与最初样本单元交叉了fij.次,则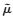
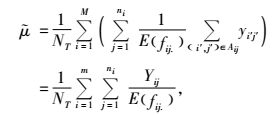
|
其中, Yij表示网络Aij单元值之和。
为了求出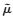
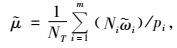
|
(5) |
其中,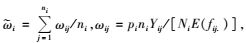
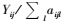
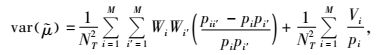
|
其中,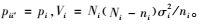
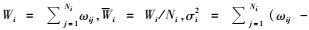
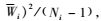
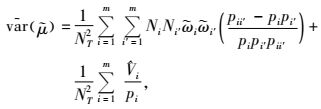
|
(6) |
其中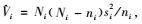
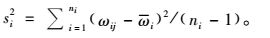
|
如果初级单元的选取采用不放回简单随机抽样,则pi=m/M,pii′=m(m-1)/M(M-1),方差公式可转化为:
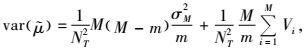
|
(7) |
其中,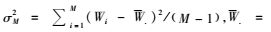
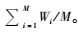
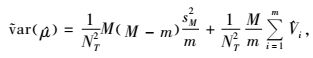
|
(8) |
其中,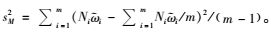
总体均值估计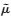
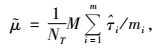
|
(9) |
式中,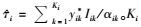
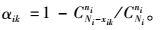
|
(10) |
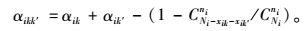
|
(11) |
由于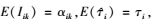
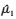
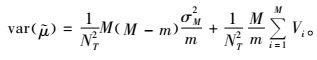
|
不同的是:
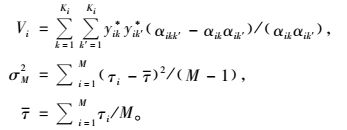
|
式中Vi为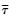
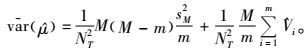
|
(12) |
不同的是:
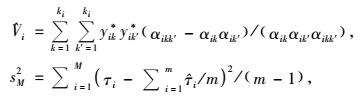
|
式中yik*,yik′*分别表示网络k与k′的单元值之和。
1.3.2 修正的HH估计量不跨越边界修正的Hansen-Hurwitz估计量与跨越初级抽样单元边界的估计量公式是一致的, 只是被抽中的网络经过修剪,相应的参数值也会变化。
2 研究区概况与数据采集 2.1 研究区概况本研究地点位于内蒙古自治区磴口县境内,地处内蒙古西部,属于黄河河套地区,灌溉农业发达,境内自然环境分割明显,西部为沙漠戈壁。研究区为黄河西岸绿洲向乌兰布和沙漠过渡区,分布有典型的沙地植被,是林业治沙技术试验区。根据项目区的生态系统结构、功能及其环境特点,在研究区选择具有典型代表性质的稀少且呈群团状的沙漠植被类型。试验区总面积为100 hm2。
研究区植被隶属亚非荒漠植物区,亚洲中部区,阿拉善省,东阿拉善州。阿拉善荒漠省的东界就在乌兰布和沙漠的东缘,也就是亚洲中部荒漠区与草原区的分界线,而且是极为重要的植物地理学分界线。沙漠植物基本上都是沙生、旱生、盐生类灌木和小灌木组成,这些植物对当地生境有极强的适应性和抗逆性。植被以天然灌木白刺(Nitraria tangtorum)为主, 主要分布在圆锥沙丘,人工种植沙枣(Elaeagnus angustifolia)、梭梭(Haloxylon ammodendron)和肉苁蓉(Cistanche deserticola)等。乔木有沙枣。灌木主要有白刺、梭梭、柽柳(Tamarix chinensis)、花棒、盐爪爪(Kalidium foliatum)、柠条锦鸡儿(Caragana korshinskii)和沙蒿(Artemisia ordosica)等。草本植物主要有沙米(Agriophyllum squarrosum)、芦苇(Phragmites australis)、沙鞭(Psammochloa villosa)、沙地旋覆花(Inula salsoloides)、苦豆子(Sophora alopecuroides)、细叶砂引草(Messerschmidia sibirica var. angustior)、雾冰藜(Bassia dasyphylla)、盐地碱蓬(Suaeda salsa)、苦苣菜(Sonchus oleraceus)和猪毛菜(Salsola collina)等。
2.2 样地设置与数据采集首先在调查区内,选择具有代表性的稀少且呈群团状样地作为试验大样地,大样地设置为方形,面积为1 000 m×1 000 m,在该大样地内按行(编号依次为0,1,2, …)列(编号依次为A,B,C, …)交叉设置100块样地,面积为100 m×100 m。方形样地4个边界测量以样地的边界西南角为起点,然后用全站仪实测各测点的距离和三维坐标。
在每个样地内再依次细分设置小样方100个,面积为10 m×10 m。每个样方的境界测量精度原则上要求达到1/100,即每10 m的误差为10~20 cm。小样方均以样地的左下角点为编号起点,向右(由西向东)、向上(由北向南)按行列编号。
2.2.1 样地基本因子调查各样地(100 m×100 m)的基本因子调查内容主要包括样地编号、样地面积、每个样地的4个地面控制点坐标点的三维地理坐标、样地在大样地的位置图、小地形、土壤类型、土层厚度(cm)、优势种、起源、林种、权属、造林时间、株行、植被类型、设置者、设置日期等内容。
2.2.2 样地乔木、灌木等因子调查样地的因子调查是分别基于以每个小样方(10 m×10 m)为单位进行乔木、灌木植物各因子的调查,根据样方的调查结果即可统计整个样地的乔木、灌木植物等各调查因子种类、数量及分布情况。
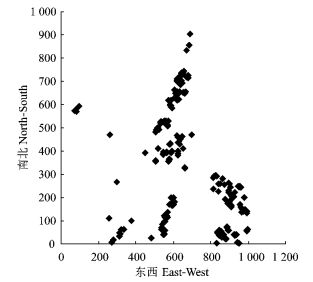
2.2.3 花棒总体分布本文以花棒数据作为研究总体,其分布状况如图 2。本文以小样方(10 m×10 m)为最小单元,以单元内花棒株数为感兴趣的研究指标。由于花棒株数的总体分布表数据太多(100×100),共有1 000个最小单元,故没有在此显示出来,而以花棒平面坐标图显示其分布状况,原点为样地西南角点,横坐标为东西方向,纵坐标为南北方向。由图 2分析可以得知:花棒分布稀少、集聚成群且分布广泛。
|
图 2 花棒总体分布 Figure 2 Distribution of H. scoparium population |
将总体(10 000 m×10 000 m)分为100个初级单元(100 m×100 m),每个初级单元包括100个次级单元(小样方:10 m×10 m)。总体总值为2 108株,总体均值为每个单元0.211株,总体单元的方差为7.00。邻域的定义采用一阶邻域,临界值Cα=0,扩充条件C>Cα。
模拟试验以两阶段简单不放回抽样、跨边界修正的HH两阶段不放回自适应群团抽样、跨边界修正的HT两阶段不放回自适应群团抽样、不跨边界修正的HH两阶段不放回自适应群团抽样和不跨边界修正的HT两阶段不放回自适应群团抽样为研究对象。
3.1 样本量对7种不同的样本量进行重复抽样,50×ni(ni=4, 6, 8, 10),50为抽取的初级单元个数,ni为抽取的次级单元个数。
3.2 抽样重复次数对这4种不同样本量, 设计了19种(100, 200, 300, 400, 500, 600, 700, 800, 900, 1 000, 2 000, 3 000, 4 000, 5 000, 6 000, 7 000, 8 000, 9 000和10 000次)不同重复抽样次数的模拟抽样方案。本研究总共进行了76次抽样模拟试验。
3.3 程序设计本次抽样模拟工具,采用的是自编的程序。开发语言为VB6.0。
由于抽样设计的中英文名太长,在图中显示不便,所以,在此处对各种抽样设计估计量参数做一个临时的简捷表示。
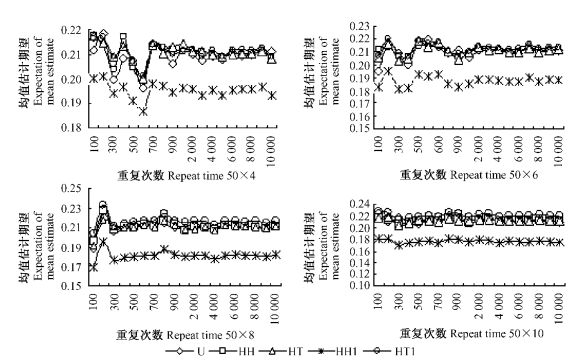
图 3,4中的横坐标表示重复抽样次数,纵坐标表示重复抽样得到的参数。图中的50×ni(ni=4, 6, 8, 10)表示最初样本总量,50表示抽取的最初单元数,ni表示抽取的次级单元数。图中的U表示两阶段抽样的均值估计的期望,HH表示跨越边界HHACS均值估计的期望,HH1表示不跨越边界HHACS均值估计的期望,HT表示跨越边界HTACS均值估计的期望,HT1表示不跨越边界HTACS均值估计的期望。图中的V表示两阶段抽样的方差估计的期望,VH表示跨越边界HHACS方差估计的期望,VH1表示不跨越边界HHACS方差估计的期望,VT表示跨越边界HTACS方差估计的期望,VT1表示不跨越边界HTACS方差估计的期望。
4 结果与分析 4.1 样本均值分析由图 3分析可知:随着样本量的增加,均值估计的期望,开始呈波浪型曲线,然后逐渐趋向于常数,除了不跨越边界HHACS均值估计的期望没有明显接近总体均值,其他4种方法均值估计的期望均趋向于总体均值。这表明模拟试验从实际上验证了这5种抽样方法的无偏性。
|
图 3 均值估计期望 Figure 3 Expectation of mean estimate |
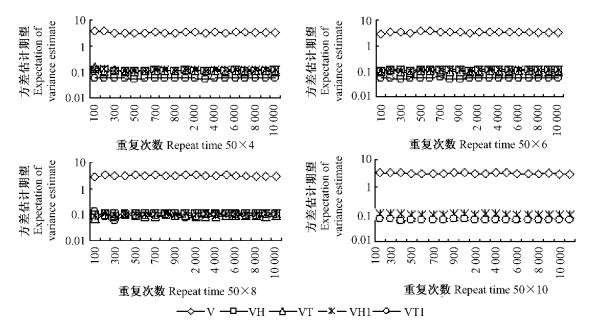
此处的方差是指,重复抽样得到的方差估计的期望。由图 4分析可知:1)两阶段简单随机抽样方差估计的期望波动比较大,且其方差估计的期望始终远大于其他4种抽样的方差估计的期望;2)除了两阶段简单随机抽样,其他4种抽样的方差估计的期望一直比较稳定,且趋近于0。这些说明,两阶段自适应群团抽样比简单的两阶段抽样方法要好。
|
图 4 方差估计期望 Figure 4 Expectation of variance estimate |
由样本均值分析可以,无法判断4种两阶段自适应群团抽样的优劣,所以,需要进一步对它们的样本方差估计期望。4种两阶段自适应群团抽样(跨边界修正的HH两阶段不放回自适应群团抽样(HHACS)、跨边界修正的HT两阶段不放回自适应群团抽样、不跨边界修正的HH两阶段不放回自适应群团抽样和不跨边界修正的HT两阶段不放回自适应群团抽样)的样本方差估计期望的均值依次为:0.108 5,0.094 7,0.108 2,0.066 8。
方差估计期望的均值越小,说明其对应的抽样方法效率越高。这4种抽样方法的优越性从高到低的顺序为:不跨边界HTACS1、跨边界HTACS、不跨边界HHACS1、跨边界HHACS。
5 结论以花棒数据研究对象,通过对4种方法的模拟研究得出以下结论。
1) 通过对样本均值的分析,可知:随着样本量的增加,均值估计的期望,开始呈波浪型曲线,然后逐渐趋向于常数。表明模拟试验从实际上验证了这5种抽样方法的无偏性。
2) 通过对样本方差分析和样本方差估计期望的分析,得出针对研究区植被花棒,这5种抽样设计的效率排序从高到低依次为:不跨边界HTACS1、跨边界HTACS、不跨边界HHACS1、跨边界HHACS、简单两阶段抽样。
3) 不跨越边界的设计优于跨越边界的设计。
雷渊才, 唐守正. 2007. 适应性群团抽样技术在森林资源清查中的应用[J]. 林业科学, 43(11): 132-138. DOI:10.3321/j.issn:1001-7488.2007.11.022 |
Dryver A. 2003. Performance of adaptive cluster sampling estimators in a multivariate setting[J]. Environmental and Ecological Statistics, 10: 107-113. DOI:10.1023/A:1021937508414 |
Felix-Medina M H, Thompson S K. 2004. Adaptive cluster double sampling[J]. Biometrika, 91(4): 877-891. DOI:10.1093/biomet/91.4.877 |
Muttlak H, Khan A. 2002. Adjusted two-stage adaptive cluster sampling[J]. Environmental and Ecological Statistics, 9: 111-120. DOI:10.1023/A:1013723226430 |
Rocco E. 2003. Constrained inverse adaptive cluster sampling[J]. Journal of Official Statistics, 19: 45-57. |
Salehi M, Seber G. 1997a. Adaptive cluster sampling with networks selected without replacement[J]. Biometrika, 84: 209-219. DOI:10.1093/biomet/84.1.209 |
Salehi M, Seber G. 1997b. Two-stage adaptive cluster sampling[J]. Biometrics, 53: 959-970. DOI:10.2307/2533556 |
Salehi M, Smith R. 2005. Two-stage sequential sampling: a neighborhood-free adaptive sampling procedure[J]. Journal of Agricultural, Biological and Environmental Statistics, 10: 84-103. DOI:10.1198/108571105X28183 |
Thompson S. 1991. Stratified adaptive cluster sampling[J]. Biometrika, 78(2): 389-397. DOI:10.1093/biomet/78.2.389 |
Thompson S. 1990. Adaptive cluster sampling[J]. Journal of the American Statistical Association, 85: 1050-1059. DOI:10.1080/01621459.1990.10474975 |
Turk P, Borkowski J J. 2005. A review of adaptive cluster sampling: 1990-2003[J]. Environmental and Ecological Statistics, 12(1): 55-94. DOI:10.1007/s10651-005-6818-0 |
 2010, Vol. 46
2010, Vol. 46
