虽然林木遗传育种的理论研究已进入基因组时代, 但是目前在林木遗传改良的实践中, 子代测定仍然是林木遗传改良工作的关键环节, 遗传测定工作的好坏直接关系到遗传增益能否获得提高和育种工作能否获得持续发展(王明庥, 2001)。林木遗传测定的一项重要任务就是估算亲本性状的遗传方差、协方差以及遗传相关、遗传力等遗传参数, 这些参数是进一步估算遗传增益或计算多性状选择指数的先决条件。林木遗传参数的估计需要建立线性模型进行分析, 模型中会包含种源、家系、单株、地点、年份等因素的效应, 这些效应有的是固定的, 有的则是随机的, 这样的线性模型称为混合线性模型或方差分量模型。林木遗传育种学家通常采用方差分析法(ANOVA)对模型中的方差分量进行估计, 进而估计其他的遗传参数。由于混合线性模型是数理统计学领域里一个比较复杂的专题, 这使得不少林木遗传育种学家在估算遗传参数时感到比较困难。事实上, 文献中对林木遗传模型, 特别是非平衡数据的林木遗传模型的参数估计理论和方法论述得不多或不够详尽, 并且到目前为止还没有开发出比较好的应用软件来估计林木遗传育种参数。

方差分量模型在遗传育种模型分析中的应用由来已久, 并且还在不断地发展和完善之中。方差分析法是估计方差分量模型中方差分量的一种统计方法, 最早由Fisher(1925)提出, 后来由Tippett(1931)、Neyman等(1935)和Daniels(1939)等得到发展。Henderson(1953)提出了3种估计方差分量的方差分析法, 其最大的贡献在于其能够处理不平衡数据, 且能分析较为复杂的方差分量模型, 随后方差分析法在动植物遗传模型分析中得到了广泛的应用。虽然20世纪70年代后提出了估计方差分量的极大似然法(ML)(Hartley et al., 1967)、边缘极大似然法(REML)(Patterson et al., 1971)和最小范数二次无偏估计(MINQUE)(Rao, 1971)等, 但是迄今为止方差分析法在遗传育种模型分析中的应用仍然是最为广泛的。最近20多年来, 对方差分量估计的抽样方差和假设检验也展开了一些研究(Dieters et al., 1995; Khuri et al., 1998; Zhu et al., 2004; Giampaoli et al., 2009)。经典的林木遗传育种模型大多属于方差分量模型, 其理论方法来源于一般的方差分量模型, 其研究对象有别于动物和农作物。国内外林木数量遗传学文献(Wright, 1976; Namkoong, 1979; Williams et al., 2002;续九如, 2006)中有关林木遗传模型分析大多只涉及平衡数据模型, 对非平衡数据模型以及有关方差分量估计的统计性质, 如标准误差、假设检验等, 没有详尽的论述或根本没有论述。

半同胞子代测定在林木家系选择中有着重要应用, 目前仍然有不少研究报道(季孔庶等, 2005; 黄少伟等, 2006; 翟思万等, 2007; Blada et al., 2007; Sebbenn et al., 2008)。本文针对林木单地点半同胞子代测定试验, 给出遗传模型不同形式的表达式, 采用方差分析法推导了平衡数据和不平衡数据条件下方差分量估计式, 并给出方差分量估计的抽样方差以及方差分量假设检验统计量的计算方法。在此基础上, 给出了不平衡数据条件下家系遗传力的计算公式以及家系遗传力和单株遗传力抽样方差近似计算方法。对于2个数量性状, 给出了不平衡数据下遗传相关系数估计式, 而且还给出了遗传相关系数估计的方差近似计算方法。最后, 用VC++6.0编写了计算单地点半同胞子代测定模型中各种遗传参数的Windows应用软件, 供林木遗传育种工作者使用。

1 统计方法 1.1 统计模型

林木单地点半同胞家系子代测定为随机区组试验, 被测的某个数量性状值可用线性模型表示为

(1)

式中, μ为总体均值; B_i为第i个区组的固定效应, i = 1, 2, …, b; F_j为第j个家系的随机效应, j = 1, 2, …, f, E(F_j)=0, Var(F_j)=σ_F²; (BF)_ij为第i个区组第j个家系的随机效应, E[(BF)_ij]=0, Var[(BF)_ij]=σ_BF²; e_ijk为第i个区组第j个家系第k个单株的随机误差, k=1, 2, …, n_ij, E(e_ijk)=0, Var(e_ijk)=σ_e²。同时假定所有因子间的协方差为0(White et al., 1989)。对于模型(1), 主要任务是对方差分量σ_F²、σ_BF²和σ_e²作出估计, 并考察它们的统计性质。

模型(1)还可以用矩阵表达为

(2)

式中, β=(μ, B₁, …, B_b)′, F=(F₁, …, F_f)′, (BF)=[(BF)₁₁, (BF)₁₂, …, (BF)_bf]′, X为n×(b+ 1)矩阵, U₁为n×f矩阵, U₂为n×bf矩阵, y为n×1的数量性状观测向量, e为n×1的随机误差向量, 这里为观测的总株数。

当小区单株个数均为p时, 即数据是平衡的, 那么上述遗传模型还可以表示为

(3)

式中, 符号表示矩阵的Kronecker乘积, I_b表示b阶单位矩阵, 1_b表示元素全为1的b维向量, 其他符号类似。

1.2 方差分析法

方差分析法估计方差分量的主要思想是将方差分量模型中的随机效应看作固定效应, 按通常的方差分析法算出各效应对应的平方和, 再根据随机效应模型计算这些平方和的数学期望, 它们是方差分量的线性函数, 然后令这些数学期望等于各自对应的平方和, 便得到关于方差分量的1个线性方程组, 解此方程组就得到方差分量的估计(王松桂等, 2007)。对于模型(1), 可按如下方法估计方差分量。

1) 先将F和(BF)看作随机效应向量, 设D₁=I-X(X′X)^-X′, 式中右上角“-”号表示矩阵的广义逆, 则模型的误差平方和为ESS(β)=y′D₁y; 再将F看作固定效应向量, 而(BF)仍然看作随机效应向量, 并记D₂=I-(X, U₁)[(X, U₁)′(X, U₁)]^-(X, U₁)′, 则模型的误差平方和为ESS(β, F)=y′D₂y; 最后将F和(BF)都看作固定效应向量, 并设D₃=I-(X, U₁, U₂)[(X, U₁, U₂)′(X, U₁, U₂)]^-(X, U₁, U₂) ′, 则模型的误差平方和为ESS(β, F, BF)=y′D₃y。

2) 设A₀=I-D₁, A₁=D₁-D₂, A₂=D₂-D₃, A₃=D₃, 则区组间、家系间、小区间和小区内的误差平方和分别为ESS_B=y′A₀y, ESS_F=y′A₁y, ESS_BF=y′A₂y及ESS_e=y′A₃y。不难验证矩阵A₀、A₁、A₂和A₃都是投影阵, 而且它们所张成的向量空间相互正交, 因此数量性状值的平方和可以分解为

(4)

此外, 家系间、小区间和小区内的误差平方和的数学期望分别为

(5)

式中, Tr表示矩阵的迹。

3) 记λ₁=Tr(U′₁D₁U₁), λ₂=Tr(U′₂D₂U₂), 并根据矩阵的广义逆和迹运算的性质, 则(5)式中方差分量的系数可以作如下简化:

(6)

这样就得到了不平衡数据的方差分析表(表 1)。

令家系间、小区间和小区内的误差平方和的数学期望等于各自的误差平方和, 解线性方程组, 得到各方差分量的估计为

(7)

当数据平衡时, 即小区单株数均为p时, 则n=bfp, λ₁=bp(f-1), λ₂=p(b-1)(f-1)。此时, 家系间、小区间和小区内的误差平方和可表示为

(8)

1.3 方差分量估计的抽样方差

由于模型(1)中各随机效应均服从正态分布, 所以y~N(Xβ, Σ), 其中Σ=cov(y)=U′₁U₁σ_F²+U′₂U₂σ_BF²+Iσ_e²。对于平衡数据, 根据多元正态分布的二次型理论(Searle et al., 1992), 可知

(9)

由上式并注意到区组间、小区间和小区内的误差平方和互不相关, 得到各方差分量估计方差的无偏估计为:

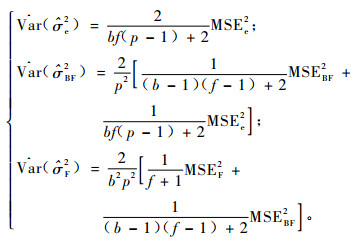
(10)

式中, MSE为误差平方和的均方。

对于不平衡数据, 用上述方法仍然可以得到Var(ESS_e)的无偏估计为

(11)

但对于Var(ESS_F)和Var(ESS_BF)的估计, 情况却有所不同, 因为ESS_BF和ESS_F不再服从χ²分布, 不相关不再成立。但是根据二次型的方差和协方差的有关结论(Searle, 1997), 可以得到

(12)

(13)

由(12)和(13)式, 并注意到Var(ESS_e)=, 根据(7)式得到在不平衡数据条件下和的方差的估计为

(14)

1.4 方差分量的假设检验

常用Wald方法对方差分量是否显著为零进行假设检验(王松桂等, 2007)。首先考虑σ_BF²的假设检验问题, 此时零假设为H₀:σ_BF²=0, 备择假设为H₁:σ_BF²>0。将模型(2)中的随机效应向量F和BF视为固定效应, 则模型拟合后的误差平方和为ESS_e=y′D₃y。若零假设成立, 则模型(2)变为y=Xβ+U₁F+e, 此时同样将F视为固定效应向量, 模型拟合后的误差平方和为ESS_e0=y′D₂y。可以验证:1) ESS_e/σ_e²~χ_n-bf²; 2) 当σ_BF²=0时, (ESS_e0-ESS_e)/σ_e²~χ_(b-1)(f-1)²且与ESS_e相互独立。因此在零假设成立时, 有

(15)

这就是检验σ_BF²是否显著为零的统计量。

由此可以看出, 无论是平衡数据还是不平衡数据, 利用(15)式均可对σ_BF²是否为零进行显著性检验。下面考虑σ_F²是否显著为零的假设检验问题, 即零假设为H₀:σ_F²=0, 备择假设为H₁:σ_F²>0。对于平衡数据, 由(9)式可知, 在零假设成立的条件下, 有

(16)

此为平衡数据条件下σ_F²是否显著为零的假设检验问题的统计量。

当数据不平衡时, σ_F²的假设检验问题比较复杂, 这里采用Ofversten(1993)提出的方法推导出σ_F²假设检验的统计量及其计算方法。首先存在一个正交矩阵P, 使得,

(17)

式中, R是行满秩矩阵, (R₁₁, R₁₂, R₁₃)的秩为b, (R₂₂, R₂₃)的秩为f -1, R₃₃的秩序为(b-1)(f-1)。设

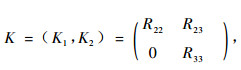
则存在正交矩阵Q, 使得K₂K′₂=QΛQ′, 其中Λ为对角矩阵, 而且对角线元素均大于零。记L=Λ^-1/2Q′, 令, 并设s=b(f-1), 则有

设λ为Λ^-1对角线元素中的最大值, t_s为t₄的1个子向量, 令

(18)

那么有

由于K₁的秩为f-1, 因此存在正交矩阵T, 使得TLK₁=(S′, 0′)′, 其中S为行满秩矩阵, 其秩为f-1。定义随机向量

式中, w₁含有f-1个元素, w₂含有(b-1)(f-1)个元素, 并有

这里σ_s²=σ_BF²+λσ_e²。由于w₁与w₂相互独立, 因此检验零假设H₀:σ_F²=0是否成立的统计量为

(19)

1.5 遗传力的估计及其抽样方差

对于单地点半同胞子代林测定模型(1), 家系j的平均值为

(20)

其方差为

(21)

显然, 当数据不平衡时, 各家系均值的方差不全相同, 因此在定义家系遗传力时用其平均值来代替, 即家系遗传力定义为

(22)

式中, 当数据平衡时, 上式简化为

(23)

从理论上来讲半同胞家系间的遗传差异只能解释加性遗传方差的1/4, 因此在计算单株遗传力时, σ_F²则要乘以4, 而分母则以单株的方差Var(y_ijk)来代替(Wright, 1976), 即单株遗传力的计算公式为

(24)

很明显, 单株遗传力计算公式对平衡和不平衡数据都适用。

遗传力是方差分量函数的比, 其抽样方差可用2种近似的方法得到。一种是由Dickerson(1969)提出的比较简单的方法:

(25)

此法将分母看作常量而非随机变量, 这是由于遗传力计算公式中的分母是表型方差, 在通常情况下表型方差比加性方差更容易得到精确估计, 因此在实际操作中常把表型方差当作1个已知的参数(Dieters et al., 1995)。

另一种是基于一阶太勒展开式而得到的2个随机变量比值方差的近似计算公式:

(26)

式中, θ₁=E(X₁), θ₂=E(X₂)。上式在Kempthorne(1957)、Becker(1984)和Namkoong(1979)中有所提及或应用, 但没有给出完整的推导过程, 详细推导过程可参见Dieters等(1995)。式(25)和(26)均可用来估计遗传力的方差, 但(26)式较为常用(Dieters et al., 1995)。

这里采用(26)式估计家系遗传力和单株遗传力的方差。由于方差分析法所获得的方差分量估计都是无偏估计, 因此各方差分量估计的数学期望等于其自身。根据(7)式和(13)式, 可以得到方差分量估计间的协方差。为了计算不平衡数据条件下家系遗传力的方差, 只需在(26)中设并计算即可。类似地可以计算单株遗传力的方差以及平衡数据下的遗传力的方差。

1.6 遗传相关系数估计及其抽样方差

对于2个数量性状y₁和y₂, 在(7)式中令ESS_F=y′₁A₁y₂, ESS_BF=y′₁A₂y₂, ESS_e=y′₁A₃y₂, 则可以得到这2个性状家系间及区组内家系间的遗传协方差。根据遗传协方差可以得到2个性状的遗传相关系数的估计为

(27)

式中, θ=(θ₁₁, θ₂₂, θ₁₂)′, θ₁₁和θ₂₂分别为性状y₁和y₂的遗传方差, θ₁₂为这2个性状的遗传协方差, 和分别为这2个性状的遗传方差估计, 为这2个性状的遗传协方差估计。利用(27)式在θ处的一阶太勒展开式, 得到遗传相关系数估计的抽样方差的近似式为

(28)

该式最早由Tallis(1959)提出, 后来Scheinberg(1966)应用此式推导了1个遗传相关系数的抽样方差近似表达式。根据正态分布的二次型有关结论(Searle, 1997)可以计算y′₁A₁y₂, y′₁A₂y₂和y′₁A₃y₂的方差以及它们之间的协方差, 进而可以计算遗传协方差的方差及其与方差分量之间的协方差, 最后利用(28)式就可以近似计算出遗传相关系数估计的抽样方差。

2 结果与讨论

本文详细地分析了林木单地点半同胞子代测定遗传模型, 给出了模型不同表达形式, 用方差分析法推导了不平衡数据条件下方差分量估计的表达式, 并给出了方差分量的抽样方差和假设检验统计量的计算方法; 给出了不平衡数据条件下家系遗传力的计算表达式以及计算家系遗传力和单株遗传力抽样方差的方法; 描述了任意2个数量性状遗传相关系数及其抽样方差的计算方法。由于篇幅的限制, 文中有些结果(如遗传力和相关系数的抽样方差)只描述了其方法步骤和理论依据, 没有给出详细的推导过程和表达式。但是为了弥补这点不足, 根据本文的理论结果, 用VC++ 6.0编写了Windows应用软件HalfsibSS 1.0。该软件可以对单地点半同胞子代测定的多性状数据进行分析, 对于无论是平衡数据还是非平衡数据, 可以计算每个性状的方差分量、方差分量的标准误、方差分量的假设检验统计量、家系遗传力和单株遗传力及其标准误、性状间的遗传相关系数及其标准误。HalfsibSS 1.0可以免费得到使用, 下载网址为http://fgbi o.njfu.edu.cn/tong/halfsibss/halfsibss.htm。

在计算方差分量及模型中的其他参数时, 本文在计算方法上有所突破, 使得在很短的时间内可以处理上万个单株数据。如果按照理论表达式(7)计算方差, 那么就会涉及到广义逆矩阵的计算, 当数据量较大时, 如大于2 000个单株数据, 个人电脑是难以承担的。利用正交变换将模型中的设计阵变成(17)式中R矩阵, 同时也变换数量性状数据, 可以简化计算各个误差平方和以及有关二次型的方差和协方差, 避免了广义逆矩阵的计算。

虽然SAS等软件也可以分析方差模型, 但它们不能够完全直接解决林木遗传模型中许多参数计算问题。SAS中的VARCOMP过程可对方差分量模型计算分析, 然而VARCOMP过程的方差分析法只给出方差分量的估计, 不能给出方差分量估计的抽样方差以及方差分量假设检验结果, 当然不可能给出遗传力和遗传相关系数的估计以及它们的抽样方差。20世纪90年代初南京林业大学开发的SPQG软件包在国内林木遗传育种界颇受好评(施季森等, 1991), 但它的大多功能是进行多元统计分析, 在林木遗传模型方面只涉及到林木双列杂交遗传模型, 而且迄今为止只有DOS版本, 再没有继续发展新的版本。

通过林木单地点半同胞子代测定遗传模型分析可以看出, 林木遗传模型的统计理论比较复杂。因此, 文献中关于林木遗传模型, 尤其是不平衡数据模型描述得不够详细, 这正是多年来不少林木遗传育种工作者在分析处理林木试验数据时感到困难的最主要原因。本文所研究的林木遗传模型形式上比较简单, 但其统计理论和计算方法可用来分析和计算其他林木遗传模型, 如多地点半同胞子代测定模型、双列杂交遗传模型等。