文章信息
- 于建芳, 王喜明.
- Yu Jianfang, Wang Ximing.
- 木材干燥应力应变宏观模型的构筑
- The Development of Macroscopic Model on Wood Drying Stress-Strain
- 林业科学, 2005, 41(5): 214-218.
- Scientia Silvae Sinicae, 2005, 41(5): 214-218.
-
文章历史
- 收稿日期:2003-06-23
-
作者相关文章
木材是天然的复合材料,它可能是正常材,也可能是缺陷材。组成的不同引起木材各个方向上产生的应变也不同。一般来说,正常材的弦向应变最大,纵向应变最小,而对应压木或幼龄材等这些缺陷材,它们可能表现出相当高的纵向应变。即使在含水率相同时,由于材种不同,其横纵向应变也不相同。为了搞清木材的应变特性及其影响因素,很多研究者在这方面做了研究。然而,由于木材应变的复杂性和木材结构、化学成分的多样性,关于木材产生应变的机制还没有提出完整的解释。Skaar(1988)提出早晚材相互作用理论,但是在实际应用中多层试样是很普遍的,而且他在研究中没有考虑对应压木来说较重要的纵向应变。Pang(2002)建立了由多种材种组成的多层试样模型,但在分析中没有考虑干燥过程中重要的机械吸湿应变。为了分析在干燥中木材产生的应变对木材变形的影响,有必要考虑组成正常材、缺陷材的早晚材相互作用和机械吸湿应变。
在干燥过程中,当木材所处的环境条件变化时,木材内部结构会做出相应的反应,所以了解木材内部结构及对外部条件变化的反应是很重要的,这一点需从分子水平来研究,但从宏观水平研究也很有意义。在实验中测量的由多层材种组成的试样的宏观应变值,是多层材种表现出的总的应变,并不是单层的应变,所以利用层合理论建立数学模型,可把木材总的可测量的应变和各层的应变联系起来考察应力应变的关系。
本构方程就是能描述材料行为的一个数学模型。建立一个准确的模型,可以对干燥过程进行模拟,这为发展更好的干燥基准提供了一个工具。一维模型的优点是便于应用,可以此为基础来证明一些干燥中发生的最重要的现象,也可证明不同干燥条件和力学限制对干燥过程的影响。但是在干燥板材时,情况复杂得多,应力应变关系是三维的,而且受木材不均匀结构的影响。在大多数情况下,建立三维模型来描述木材干燥时应力应变关系是有必要的,但若考虑所有这些影响来建立三维模型是很困难的,而且很难用试验验证。在研究板材横断面性质时,二维模型就足够了,不过在研究中忽略了纵弦径向的弯曲影响。
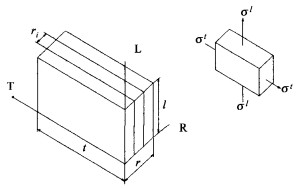
1 模型的构筑建模时所用的由早晚材组成的多层试样模型图见图 1(Pang,2002)。图中L、T、R为试材纵向、弦向、径向;l、t、r为试材纵向、弦向、径向的长度;σl、σt为试材纵向应力和弦向应力;ri为i层试样的径向长度。
|
图 1 木材多层模型图 Fig. 1 Schematic diagram of a model with a speciman containing several layers of different types of wood |
所用的假设如下:1)各层的总应变相同;2)径向应力为零;3)所有剪切应变为零。建模时主要考虑含水率变化对干燥过程中应力与应变的影响,并认为干燥总应变包括弹性应变、干缩应变和机械吸湿应变。下面对这3种应变分别进行分析。
1.1 弹性应变对小变形,弹性理论给出的广义虎克定律张量表达式是:

|
(1) |
式中:εij为应变张量,σij为应力张量,Cij为刚度矩阵。
对长试样而言,若垂直平面的应变为零,则为平面应变条件;对薄试样而言,若垂直平面的应力为零,则为平面应力条件。虽然这2种条件下的应力应变关系的差异很小,但是平面应变条件下的应力应变关系复杂(徐芝伦,1983),所以本文应用平面应力条件下的应力应变关系,由假设2)和假设3)可知虎克定律简化为:
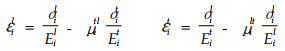
|
(2) |
式中:εi为i层试样的应变;σi为i层试样的应力;Ei为i层试样的弹性模量;μ为泊松比。
1.2 干缩应变干缩应变是木材在无抑制时失水所发生的尺寸变化。因为木材是正交各向异性体,所以木材中各点在发生主方向上的线干缩应变时,任一个对称面上都不会产生剪切变形。在纤维饱和点以下,干缩应变与含水率变化成正比(李维桔,1983),所以可得出干缩应变的张量表达式:
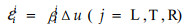
|
(3) |
式中:βij为线干缩系数张量;Δu为含水率变化量。
线干缩系数张量βj为:
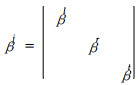
|
(4) |
式中:βl、βr、βt分别表示木材纵向、径向和弦向干缩系数。
1.3 机械吸湿应变机械吸湿应变是木材干燥中重要的应变,它是应力和含水率变化相互作用的结果,值不随时间而变化,且在水分稳态时不发生,这种应变是在试验时观察得出的,木材在受常应力作用下,当含水率改变时(失水或吸水),木材的收缩或膨胀会延长。干燥中,这种应变是有用的,它可以减少木材层与层之间的内部抑制(Pang,2000)。已经提出几个计算机械吸湿应变的公式(Salin,1992;Ranta-Maunus,1993),若只考虑“泊松比”影响,本文采用机械吸湿应变表达式为:
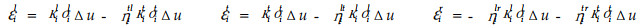
|
(5) |
式中:κi为机械吸湿常数;η为机械吸湿“泊松比”。
所以试样i层的应力与总应变的关系为:
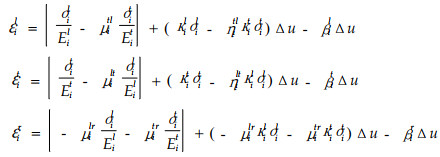
|
(6) |
为保证应变协调性,运用假设1),边界条件是:

|
(7) |
式中:ε0为试材总应变。
力平衡条件是:
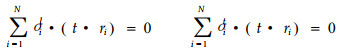
|
(8) |
从式(6)中解得:
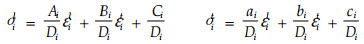
|
(9) |
把式(9)代入力平衡条件(8)并结合边界条件(7)可得:

|
(10) |
式(10)中系数如下:
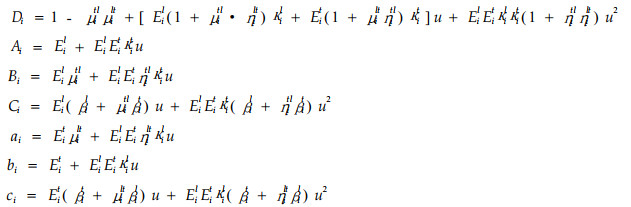
|
如果建立模型时所作的假设正确,那么不管试样由几层组成,上面建立的模型都适用。树种不同,相应的参数也不同,所以预测的理论曲线和试验曲线不会太一致,且这种差别随树种而不同。然而利用理论曲线可以定性地分析和考察各参数间的依存关系和变化趋势,也可以定性地检验改变干燥基准而产生的不同结果。下面就针对由早材和晚材2层组成的樟子松(Pinus sylvestris var. mongolica)试样对模型进行预测,所选参数见表 1(Ylinen et al., 1967; Martensson et al., 1997)。
|
|
|
图 2 樟子松材总应变与含水率的关系图(v=0.2) Fig. 2 Total strain of Scots Pine vs MC |
|
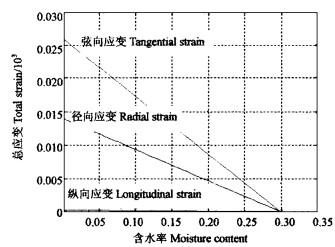
图 3 全干时樟子松材总应变与早材率的关系图 Fig. 3 Total strain of Scots Pine vs earlywood ratio |
|
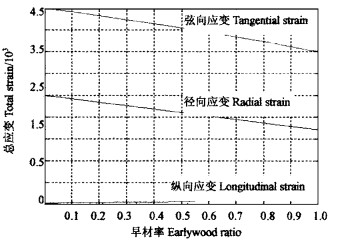
图 4 樟子松早晚材弦纵向应力与含水率的关系图(v=0.8) Fig. 4 Stress of earlywood and latewood of Scots Pine in longitudinal and tangential directions vs MC |
|
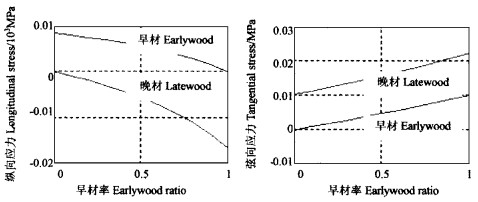
图 5 全干时樟子松早晚材弦纵向应力与早材率的关系图 Fig. 5 Stress of earlywood and latewood of Scots Pine in longitudinal and tangential directions vs earlywood ratio |
图 2、3反应了总应变随含水率和早材率的变化情况,具体结果如下:1)纵向总应变在含水率变化过程中几乎不发生变化,且数值接近于零,而弦径向总应变较大。这与干燥理论一致,主要是由于纤丝、微纤丝和微晶在细胞壁的内外层的排列方向的不同引起的。2)弦向总应变比径向总应变大,由于原因复杂,同时又因树种而异,与木材的宏观、微观和亚微观都有关系,所以对这种差异的解释至今没有定论。对樟子松而言,早材至晚材略急变,早材管胞径壁纹孔直径约接近径壁直径,这可能是其中一个原因。虽然早晚材各自的弦向应变比径向应变大,但是从图中可以看出,晚材的差异干缩比早材的略小,含水率为0时晚材的弦径向应变比T/R约为1.1,早材的T/R约为2.1;含水率为25%时,晚材的T/R约为1.8,早材的T/R约为2。这也说明随含水率的降低晚材的应变差异在减小,而早材的应变差异在增加,且晚材比早材的差异变化要大。3)早材率越低,弦径向总应变越大,纵向总应变越小。这是由于早材细胞壁次生壁中层较薄,微纤丝角大的部分(S1层和S3层)相对数量多,即早材中纵缩大的部分比例多,而且早材细胞壁次生壁中层的纤丝角比晚材的大,导致晚材纵向应变比早材纵向应变小。另外,在同一年轮中,由于晚材胞壁比早材厚,晚材胞壁物质比早材多,因而晚材胞壁内含有水分绝对量也比早材的多,所以在含水率相同的情况下,晚材横向应变比早材的大(申宗圻,1990)。4)从图中还可以看出,三向总应变都随含水率的减小而增加,增加的幅度是弦向最大,增加约2.6%,径向次之,增加约1.4%,纵向最小,增加不到0.1%。弦向约为径向的1.8倍。当含水率降到0时,晚材率为0.8,与0.2时相比,弦向总应变增加约2.2个百分点,而径向总应变增加约0.3个百分点,因为此时晚材受早材的牵制渐弱,总应变接近于晚材。5)含水率从25%降到0时,晚材的弦向应变增加约2.25%,径向应变增加约1.25%,早材的弦向应变增加约1.8%,径向应变增加约0.9%,这说明弦向比径向增的多,同一方向晚材比早材增的多。
图 4、5反应了弦纵向应力与含水率、早材率的关系,从图中可以看出:1)早材纵向受拉应力,弦向受压应力,而晚材纵向受压应力,弦向受拉应力。原因是早材纵向应变大于晚材,横向应变小于晚材。2)当早材率增加时,早材应力在减小,而晚材应力在增大,且晚材应力增加的幅度比早材应力减小的幅度要大,主要由于早材越多,早材对晚材的抑制越大,而晚材对早材的抑制逐渐减小。3)早材含量少时,早材受力大于晚材,随含水率的减小,早材应力增加的幅度比晚材增加的幅度大,这是因为晚材比早材硬,晚材硬的弦向带强迫早材软的弦向带发生和晚材同样的应变,即晚材对早材的抑制变大,反之亦然。4)含水率为30%时,应力为零,随含水率的减小,应力均先急剧增加,达到一最大值时,又逐渐减小,最后趋于稳定。在含水率略小于30%,早晚材的弦纵向应力均达到最大值,例如,早材含量为0.2时, 早材纵向拉应力达到7.8 kPa, 弦向压应力达到2.5 kPa, 晚材纵向压应力达到2 kPa,弦向拉应力达到7 kPa。5)在早晚材含量为4:1的情况下,当试材全干时,早晚材各自的弦向应力都约为纵向应力的2倍。
3 小结上面所建模型适用于分析材种沿厚度方向对称分布的多层试样的干燥特性,否则应力的对称分布会使试样向应变较高的表层发生弯曲。当试样只有早材和晚材2层组成时,模型预测结果与Pang(2002)的应力应变发展趋势及其与早材率的关系基本相似,由于Pang(2002)建立的模型没有考虑机械吸湿应变,所以3个主方向上的应变值比本文的应变值小,弦向和纵向的应力比本文的大。建立模型时假设试样由多层组成,且各层的总应变相同,径向应力为零,所有剪切应变为零。建模时考虑弹性应变、干缩应变和机械吸湿应变,并主要考虑含水率变化和各层所占试样比率对干燥过程中应力与应变的影响,所建立的应力与应变模型如下:
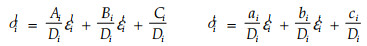
|
推导出应变的变化规律为:
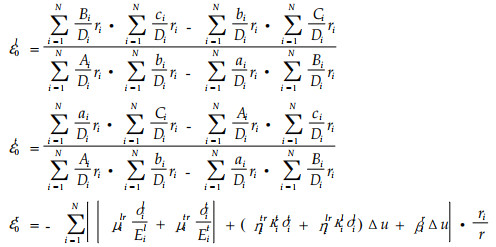
|
从理论上不管试样由几层组成,上面建立的模型都适用。对某一树种,确定其物性参数后,当改变含水率或各层所占试样比率时,就能预测各层应力与应变的变化规律。由于建模时作了假设,所以预测的理论曲线和试验曲线可能不会太一致。然而利用理论曲线可以定性地分析和考察各参数间的依存关系和变化趋势,也可以定性地检验改变干燥基准而产生的不同结果。这样就可定性地分析干燥过程,更好地理解各参数之间的定量关系和规律,有助于制定合理的干燥基准。
李维桔. 1983. 木材弹性及木材干燥应力Ⅱ.木材干燥应力. 南京林产工业学院学报, 2: 107-122. |
申宗圻. 1990. 木材学. 北京: 中国林业出版社.
|
徐芝伦. 1983. 弹性力学. 北京: 人民教育出版社.
|
Martensson A, Svensson S. 1997. Stress-strain relationship of drying wood. Holzforschung, 51: 472-478. DOI:10.1515/hfsg.1997.51.5.472 |
Pang S. 2000. Modelling of stress development during drying and relief during steaming in Pinus radiata lumber. Drying Technology, 18(8): 1677-1696. DOI:10.1080/07373930008917806 |
Pang S. 2002. Predicting anisotropic shrinkage of softwood. part 1:theories.Wood Science and Technology, 36: 75-91. DOI:10.1007/s00226-001-0122-4 |
Ranta-Maunus A. 1993. Rheological behaviour of wood in directions perpendicular to the grain. Materials and Structures, 2: 362-369. |
Salin J G. 1992. Numerical prediction of checking during timber drying and a new mechamo-sorptive creep model. Holzals Rol-und Werkstoff, 50: 195-200. DOI:10.1007/BF02663286 |
Skaar C.1988.Wood-water relations.Springer, Berlin
|
Ylinen A, Jumppnen P. 1967. Theory of the shrinkage of wood. Wood Science and Technology, 1: 241-252. DOI:10.1007/BF00349757 |
 2005, Vol. 41
2005, Vol. 41

