木材的性质直接关系着木材的用途及加工利用方式。树种的遗传特性、立地条件、气候条件及抚育管理方式等都会影响木材的组织构造，进而影响木材的力学性质。即使是同一树种，不同树龄形成的木质部，材性也不同。因此在讨论树体内材性的变化时，一般把树干划分为2部分考虑：髓附近的树木生长初期形成的材性变化较大、材质较差的木质部称为是幼龄材；靠近树皮部分材性较稳定、材质较优的木质部称为成熟材。准确地区分幼龄材和成熟材，有利于合理利用现有的木材资源。培育材性成熟早、幼龄材半径小的良种是材性育种的重要研究内容，但由于形成层细胞的成熟期很难直接观测，通过测定木材的力学性质来确定成熟期又较复杂，因此找到一种简单、准确的方法区分幼龄材和成熟材是具有重要意义的。

杨树分布广泛、适应性强、生长迅速，是我国北方的主要造林树种，也是我国的重要木材资源。以往的研究中(Huang et al., 2000)，以2种杨树为对象分析了导管分子长度和木纤维长度的径向变化。本文在此基础上探讨了以导管分子长度、木纤维长度和导管腔径等材性指标为因变量，以年轮数为自变量，应用分段回归分析建立非线性回归模型的方法，对树体内的成熟材和幼龄材的区分进行了界定，并对幼龄材在树体内的径向和纵向分布进行了分析，以期为今后的材性育种，选择材性成熟早、幼龄材半径小的良种提供科学依据。

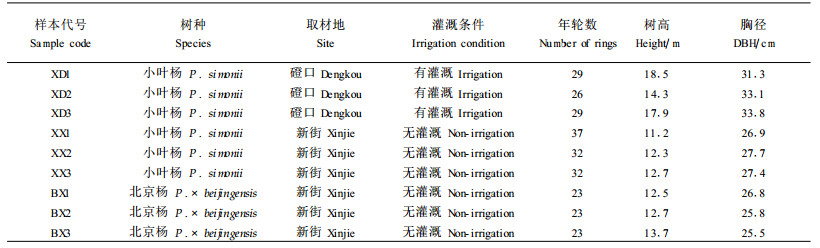
1 材料与方法 1.1 材料

试验材料采自内蒙古伊克昭盟新街治沙站无灌溉的小叶杨(Populus simonii)和北京杨(P.×beijingensis)人工林，以及巴盟磴口沙漠林业试验中心灌溉的小叶杨农田防护林。首先从各林分内分别选择3株平均木作为试材，9株试材的概况见表 1。样树伐倒后在1.2 m高处各截取一个圆盘，再分别从新街治沙站2株小叶杨的2.2 m、4.2 m、6.2 m、8.2 m高处截取一个圆盘，从每个圆盘上取1根通过髓心的木条。

1.2 导管分子长度和木纤维长度的测定

从髓心到树皮的每个年轮中央切取一个1 cm长的轴向小薄片，用Jeffrey溶液(10%硝酸+10%铬酸)离析后，制作临时切片。用OLMPUS万能投影仪在每个切片上测定30根导管分子的长度和50根木纤维的长度，计算其平均值和变异系数。以每个切片的平均值作为该年轮的导管分子长度或木纤维长度。

1.3 导管腔径的测定

制作髓心到树皮的横切面连续切片，用彩色摄像机(CCD-IRIS、DXC-108 SONY)通过光学显微镜(BH-2、PM10-AK OLYMPUS)放大100倍，从每个年轮的中部摄取图像，用数字形式保存到计算机内。应用WinROOF(Version2)图像分析系统在每个年轮内测定30根导管分子的腔径，以每个切片的平均值作为该年轮导管分子的腔径。

1.4 数据处理和模型的建立

应用统计分析系统SAS(SAS Institute Inc., 1988)及SPSS(SPSS Inc., 1999)，以年轮数为自变量，以从髓心到树皮的每个年轮的导管分子长度、木纤维长度和导管腔径为因变量，在同时满足二次函数y=ax²+bx+c(if x≤x₀)和常数函数y=p(if x > x₀)的程序上对上述数据进行处理，建立分段回归的非线性回归模型(NLIN)，同时自动计算出材性成熟龄。

1.5 幼龄材半径的确定

用年轮测定显微镜测定树木不同高度上每个年轮的宽度，根据模型计算出不同高度的材性成熟龄和年轮宽度测定值，推算出不同高度上达到材性成熟龄时的幼龄材半径。

2 结果与讨论

木材的性质是由构成木质部的各类细胞的大小、数量、形态及其空间排列方式所决定的。在阔叶树中，导管分子和木纤维占木质部细胞的70%以上，杨树可达90%以上(鲍甫成等，1998)，因此导管分子和木纤维的大小、数量和形态是影响杨树材性的重要指标。

导管分子和木纤维是由形成层原始细胞分裂、分化后形成的，所以导管分子和木纤维的大小主要取决于形成层原始细胞的大小。一般木纤维的长度在分化过程中会增加50%~8 00%，而导管分子在分化过程中长度几乎不发生变化，因此可以把导管分子的长度看成是形成层原始细胞的长度(古野毅等，1994)。根据这一观点，本研究把导管分子长度作为判断材性成熟的主要指标。以往的研究结果表明，杨树木纤维的长度及导管分子的腔径与导管分子的长度密切相关(Huang et al., 2000)，因此本研究把这2个指标作为区分成熟材和幼龄材的辅助指标。

2.1 杨树材性成熟龄非线性回归模型的建立

导管分子及木纤维的大小等材性指标从髓心到树皮方向的变化有很多种类型，对不同树种的不同材性指标建立同一成熟龄模型是不可能的。国外一些学者以管胞长度及木材密度为材性指标，对一些针叶树木质部成熟材和幼龄材的区分方法进行了研究(高义, 1982；Roos et al., 1990；Shepard et al., 1992)。我国关于木材材性指标的径向变异也做了大量的研究工作，建立的木材密度径向变异模型数学方程种类有多项式、双曲线、指数方程等(鲍甫成等, 1995)，也有应用有序样本分类的最优分割法对杉木(Cunninghamia lanceolata)、长白落叶松(Larix olgensis)、湿地松(Pinus elliottii)和马尾松(Pinus massoniana)的幼龄材和成熟材进行界定的研究报道(鲍甫成等, 1998)。

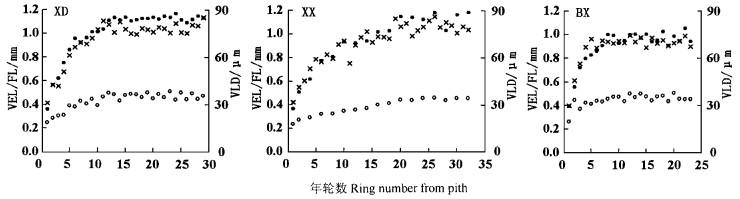
本文所用2种杨树的导管分子和木纤维的长度及导管腔径的径向变化如图 1所示。髓心附近导管分子和木纤维的长度最短，导管腔径最小，之后随着形成层年龄的增加其长度也随之增加，导管腔径也随之增大，磴口小叶杨约12年轮后、新街小叶杨约23年轮后、新街北京杨约10年轮后3个材性指标均趋于稳定。

根据杨树导管分子和木纤维的长度及导管腔径的变化特征，以年轮数为自变量，分别以导管分子长度、木纤维长度、导管腔径为因变量，应用分段回归法建立非线性回归数学模型。方程拟合的思路为：从髓心到树皮方向导管分子长度和导管腔径及木纤维长度呈曲线形增加部分用二次函数拟合，趋于稳定后的部分用常数函数拟合，求出这2个连续函数残差达到最小时的2个函数的交叉点(即二次函数的最大值)，把这个点作为材性达到稳定时的年龄，即成熟龄(Hudson, 1966)。模型方程为：

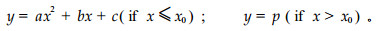
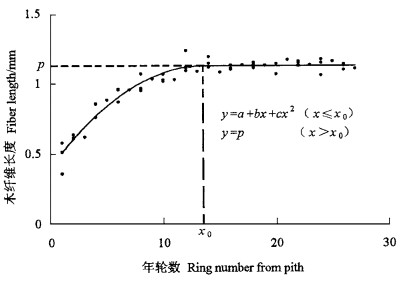
这里x为年轮数，y为材性指标的大小(导管分子长度或木纤维长度或导管腔径)，x₀为推算的成熟龄，p为稳定后的材性指标大小(导管分子长度或木纤维长度或导管腔径)，a、b、c为参数。图 2是这个非线性模型的图例。

把年轮数和材性指标值输入计算机，应用SPSS或SAS在模型程序中计算，SAS或SPSS自动调整残差，达到最小时计算自动结束，可获得残差最小时的a、b、c参数值及p值，同时还可以打印出残差值、决定系数和显著性检验结果。

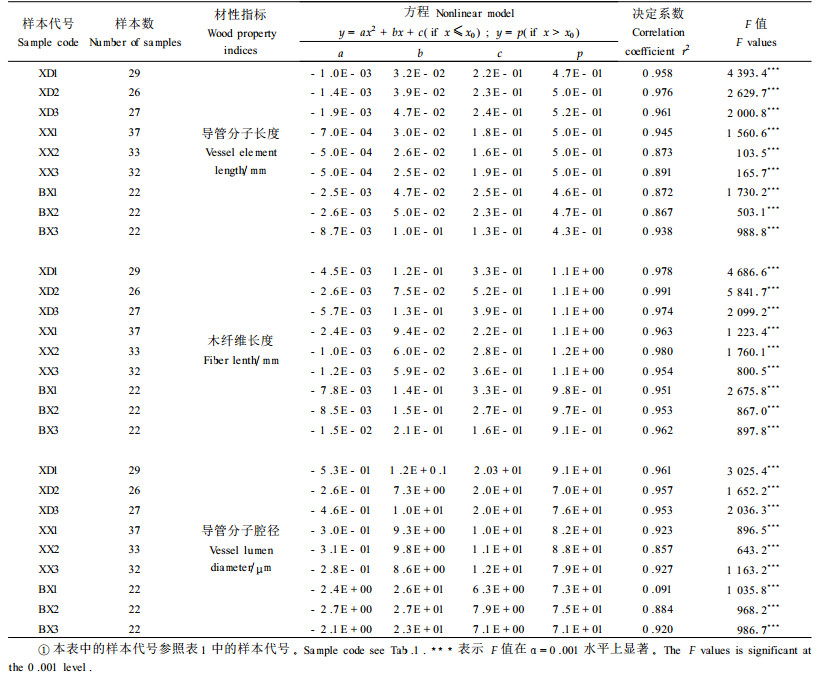
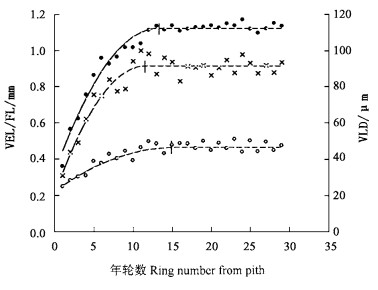
应用上述方法对所有个体(磴口和新街的小叶杨及新街北京杨)的3个材性指标分别进行了方程拟合，结果见表 2。从模型分析结果可以看出，这3个材性指标对该模型有很好的拟合性，决定系数的范围在0.857~0.991之间，其中木纤维长度指标的决定系数均在0.95以上；所有方程均在0.1%水平上达到显著。说明导管分子长度、木纤维长度和导管腔径均可作为判断材性成熟指标，这个模型有望在杨树材性成熟龄的判断、材性育种及木材有效利用方面发挥作用。图 3是用磴口小叶杨(XD1)的导管分子长度、导管腔径和木纤维长度的径向变动实测值建立的非性形回归方程模型曲线的一例，从图中可见这3个模型的理论值曲线与实测值的变化趋势是一致的。

2.2 杨树材性成熟龄及其幼龄材在树干内的分布 2.2.1 杨树材性成熟龄

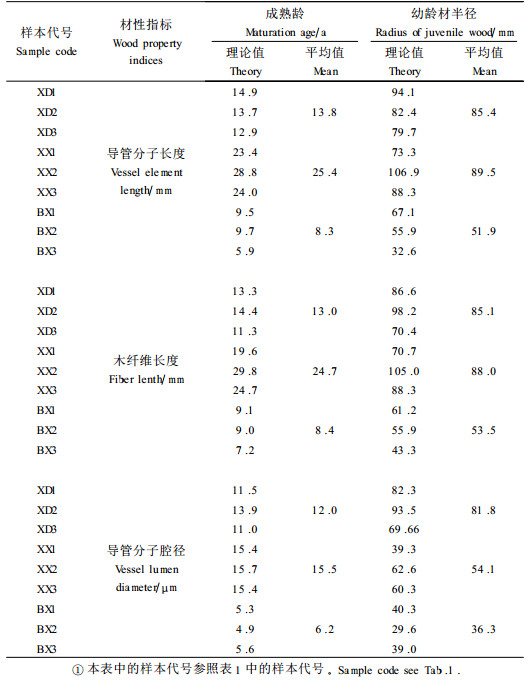
应用上述非线性模型推算的杨树材性成熟龄如表 3所示。首先从同一材性指标的成熟龄来分析，以最能反映形成层原始细胞大小的导管分子长度的稳定作为判断材性成熟的标准时，磴口灌溉条件下的小叶杨14年达到材性成熟，新街无灌溉的人工林小叶杨25年达到成熟，无灌溉北京杨8年达到成熟。由此可见，同一材性指标的杨树材性成熟龄，因树种不同和有无灌溉而差异很大。同样无灌溉条件下，北京杨比新街小叶杨早13年成熟，灌溉小叶杨比无灌溉小叶杨早11年成熟。

从同一树种的不同材性指标的材性成熟龄来看，灌溉和无灌溉小叶杨导管分子长度的平均成熟龄均比木纤维长度早近1年，无灌溉北京杨的导管分子长度和木纤维长度的平均成熟龄几乎没有差异。磴口灌溉条件下生长的小叶杨及无灌溉北京杨的导管腔径成熟龄比导管分子长度或木纤维长度的成熟龄平均早约2年，新街无灌溉小叶杨的导管腔径成熟龄比导管长度或木纤维长度的成熟龄平均早近10年。以上比较分析的结果表明，3种试材(磴口和新街的小叶杨及新街北京杨)的导管分子长度与木纤维长度的成熟龄差异不大，但导管腔径与这2个材性指标的材性成熟龄差异很大。

以上分析结果表明，杨树材成熟龄因树种不同和有无灌溉而差异很大，成熟龄也因材性指标不同而有差异。导管分子和木纤维是由形成层原始细胞分裂、分化形成的，木纤维长度在分化过程中会增加50%~800%，而导管分子在分化过程中长度几乎不发生变化，所以可以把导管分子的长度看成是形成层原始细胞的长度(古野毅等，1994)。因此，该模型在应用时如果研究的目的在于从理论上推算形成层细胞的成熟龄，可选择导管长度为材性指标拟合方程；如果研究的目的在于木材加工利用，因为木纤维占木质部细胞的60%以上，可选择木纤维长度作为材性指标拟合方程。

2.2.2 幼龄材在树干中的分布

1) 径向分布  根据各材性指标的成熟龄计算的幼龄材半径如表 3所示亦因树种不同和有无灌溉而不同。以同一材性指标如以导管分子长度作为材性指标计算成熟龄时，磴口灌溉条件下的小叶杨幼龄材的半径平均85 mm，新街无灌溉的小叶杨幼龄材的半径平均90 mm，新街无灌溉的北京杨幼龄材的半径平均52 mm。同样无灌溉条件下，北京杨比小叶杨幼龄材的半径小33 mm；同一树种，灌溉小叶杨比无灌溉小叶杨幼龄材半径小5 mm。

从同一树种的不同材性指标来看，以木纤维长度作为材性指标时幼龄材的半径与导管分子长度作为材性指标时幼龄材的半径差异不明显，但对于无灌溉小叶杨和北京杨，以导管腔径作为材性指标时计算的幼龄材的半径分别为54 mm和36 mm，分别比以导管分子长度或木纤维长度作为材性指标计算的幼龄材半径小约36 mm和16 mm。

结果表明，幼龄材的半径因树种、有无灌溉而差异很大；不同材性指标计算的幼龄材半径，其中以导管分子长度和木纤维长度计算的幼龄材半径差异不大，但以导管腔径计算的幼龄材半径明显小于以导管分子长度和木纤维长度计算的幼龄材半径。

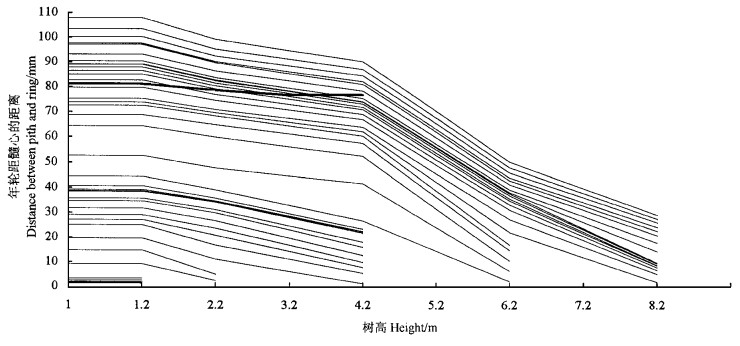
2) 纵向分布  图 4表示的是以导管分子长度作为材性指标时，新街小叶杨(XX1)树干内幼龄材的分布情况。从表 4可见，1.2 m高处的成熟龄为第24年，此时距髓心的距离为81.2 mm；2.2 m高处的成熟龄为第26年，此时距髓心的距离为78.6 mm；4.2 m高处的成熟龄为第28年，此时距髓心的距离为76.7 mm；6.2 m处导管分子长度未达到成熟。随着树高的增加，成熟龄稍有推迟，但幼龄材的半径有减小的趋势。

3 结论

杨树导管分子长度、木纤维长度和导管腔径的径向变动适合于非线性回归模型：y=ax²+bx+c (if x≤x₀)；y=p (if x > x₀)。

这里x为年轮数，y为材性指标的大小(导管分子长度或木纤维长度或导管腔径)，x₀为推算的成熟龄，p为稳定后的材性指标大小(导管分子长度或木纤维长度或导管腔径)，a、b、c为参数。

应用这个非线性回归模型拟合了杨树导管分子长度、木纤维长度和导管腔径的材性成熟方程，方程的决定系数在0.857~0.991之间，所有方程均在0.1%水平上达到显著，表明导管分子长度、木纤维长度和导管腔径都可以作为区分幼龄材与成熟材的指标，通过建立模型，有效地判断材性成熟龄。该模型不仅能够反映材性指标的径向变化特征，而且推算材性成熟龄的方法也比较简单、准确。具体应用时，如果研究的目的在于从理论上推算形成层细胞的成熟龄，依据导管分子在分化过程中长度变化很小这一特性，可选择导管长度为材性指标拟合方程；如果研究的目的在于木材加工利用，因木纤维占木质部细胞的60%以上，所以可选择木纤维长度作为材性指标拟合方程。

成熟龄及幼龄材的半径因树种及立地条件的不同，存在很大差异。同一树木的不同高度，成熟龄及幼龄材的半径也存在着差异，随着树干高度的增加，成熟龄推迟，幼龄材的半径减小。这些差异的存在为选择成熟早、幼龄材半径小的良种提供了可能性。在今后的材性育种中，成熟龄应该作为材性优良品种选择的指标，列入选择育种的范畴，使有限的木材资源得到更有效、合理的利用。