我国有丰富的竹材资源，开发与利用竹材资源方兴未艾。竹材因其强度高、韧性好等特点被广泛地用于结构材料。竹木复合空心板(图 1)是根据造船工业的特殊需要研究开发的一种特殊结构板。为克服竹材质重、刚性差的弱点，采用空心夹层型式。其上下面板为结构、性能相同的竹篾层积材，芯层为松木条；板具有厚面板、硬夹心的特点。由于受其板重和结构尺寸的限制，准确预测其弯曲性能对减少盲目试制起到非常重要的作用。研究发现(王泉中等，2001a; 2001b)，竹篾层积材具有很强的正交各向异性和显著的横向剪切效应。以这样性能的面板作为主要构件的竹木复合空心板，在横向集中载荷作用下，势必具有更为显著的横向剪切效应。为能准确预测其弯曲性能，本文运用高阶剪切理论对竹木复合空心板的弯曲性能进行了详细与深入的分析，并与(王泉中等，2001a; 2001b)中的有关分析结果进行了比较。

1 高阶剪切理论概述

一阶剪切理论对横向剪切效应明显弯曲问题的变形计算有了较大改善，但因其平截面的近似假设，对弯曲强度的分析仍与经典理论一样，没有得到任何改善。高阶剪切理论放弃了与实际不符的平截面假设，避免了一阶剪切理论人为地选择剪切变形系数所产生的影响。不但对变形的分析更趋精化，而且涉及了横向剪切效应对强度的影响。

利用罗祖道等(1994)给出的高阶剪切理论的位移模式，该位移模式是依据梁的横截面上剪应力为抛物线分布的假设。针对两端简支、中间受一集中载荷的空心夹层梁模型，运用最小势能原理，导出了高阶剪切理论下的位移函数表达式。其主要过程如下：

对上述空心夹层梁，设定的位移模式为

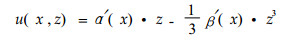
(1)

(2)

对第n层，其应力分量可表示为

(3)

(4)

式中：E⁽ⁿ⁾、G⁽ⁿ⁾为第n层材料的纵向弹性模量与横向剪切弹性模量。本问题共3层。

整梁的变形能为

(5)

梁的总势能为

(6)

根据最小势能原理δπ＝0，可得到关于α, β的微分方程组和相应的边界条件。求解后可得到空心夹层梁的位移函数为

(7)

(8)

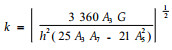
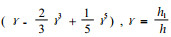
式中：, A₃=bE_f+(b₁E_c-bE_f)γ³, A₅=bE_f+(b₁E_c-bE_f)γ⁵, A₇=bE_f+(b₁E_c-bE_f)γ⁷, G=bG_f+(b₁G_c-bG_f)。

这里：u、w分别为梁横截面的纵向位移和横向位移；E_f、E_c分别为面板与芯层的纵向弹性模量；G_f、G_c分别为面板与芯层的板厚向剪切弹性模量；b、b₁分别为面板与芯层的宽度；h、h₁分别为板与芯层的高度；L为梁的跨度；P为作用于梁跨中的载荷；x、z分别为梁横截面位置坐标与其上点的高度坐标。材料性能常数和结构尺寸等具体数据见文献(王泉中等，2001a; 2001b)。

2 变形与强度的分析

对于变形分析，研究其跨中挠度。根据式(8)，其跨中挠度计算式为：

(9)

为说明高阶剪切理论下的分析结果，图 2同时给出了经典理论和一阶剪切理论下跨中挠度随跨高比(L/h)变化的情况。图 2表明，对弯曲变形的分析, 高阶剪切理论与一阶剪切理论非常接近，这说明一阶剪切理论对弯曲变形的分析比经典理论不但有了很大改进，而且具有相当精度。另一方面，一阶剪切理论中针对竹木复合空心板的弯曲问题所选择的截面剪切变形系数是合适的，由于一阶剪切理论分析表达式简单，因此，在一般工程应用中，采用一阶剪切理论进行分析计算完全合适。

对于强度分析，利用式(7)与(3)，可得到第n层的正应力表达式为：

(10)

对于横截面上剪应力，可通过平衡微分方程求得，其表达式为：

(11)

图 3表明，跨中横截面上的正应力，高阶剪切理论下为非线性分布，一阶剪切理论为线性分布，且在面板与芯层之间应力有突变。随着跨高比的增加，高阶理论下的应力分布线性化趋势越明显，且能清楚地反映出面板与芯层间的应力突变。在应力的数值上，高阶剪切理论下的应力明显地大于一阶剪切理论下的应力。计算发现，不同跨高比下，2种理论计算的应力数值相差的绝对值是相等的。这说明，高阶剪切理论反映的横向剪切效应对弯曲强度的影响不随跨高比而变；但随着跨高比的增加，相对差距在显著地缩小，表明横向剪切效应在不断地减弱。

对式(11)分析可知，在载荷不变的情况下，横截面上的剪应力分布与跨高比无关。图 4反映出，在高阶剪切理论下，横截面上剪应力分布随横截面的位置而变；但随着距跨中截面距离的增加，横截面上剪应力分布趋向于一阶剪切理论下的分布。图中显示了每增加10 mm时横截面上剪应力的分布情况。约在距跨中50 mm处，2种理论下剪应力分布基本相同。

在等值的集中载荷作用下，竹木复合空心板面内最大正应力σ_max比值[绝对比=σ_(HSDT)/σ_(FSDT); 相对比=(σ_(HSDT)-σ_(FSDT))/σ_(FSDT)]随跨高比(L/h)变化曲线如图 5所示。在跨高比很小时，横向剪切效应对弯曲应力的影响是十分显著的。

3 结束语

计算分析表明，横向剪切效应对竹木复合空心板的弯曲性能有显著影响。在跨高比较小时，高阶剪切理论表达的变形是经典理论表达的几倍。横截面上的正应力和剪应力分布与一阶剪切理论表达的完全不同，尤其是剪应力，不仅跨中截面上存在较大差异，而且还随截面的位置而变。另外，由高阶剪切理论表达的横向剪切效应产生的附加弯曲应力以及剪应力仅与载荷有关，而与跨高比无关。总之，在弯曲变形的表达上，高阶剪切理论对一阶剪切理论改进不大，一阶剪切理论已具有相当精度。对弯曲强度的表达，高阶剪切理论较一阶剪切理论有很大改进。本文的研究结果，对以竹篾层积材为主的层合型结构的分析具有指导意义。