以往在构建林分生长和收获模型时，多注重林分密度、整地、施肥、抚育间伐等经营措施及立地条件等环境因素对林分生长和收获量影响的研究，忽视了种植材料本身遗传效应的影响。随着林木育种工作的进展，越来越多的遗传改良材料大规模地应用于生产实践，如果继续沿用原有的基于一般未改良林分建立的生长模型系统来预测改良林分的未来收获量势必造成很大的偏差，带来经营决策上的失误(孙晓梅等，2004)。如何在林分生长模型中体现改良材料引起的遗传增益已成为近年来生长模型研究的一个热点。80年代以来，学者们开始致力于针对遗传改良林分的生长和收获模型的研究，建立了反映不同改良材料生长过程的各类生长和收获模型，并依此预测改良林分的遗传增益(Nance et al., 1979；Nance，1982；Buford，1986；1989；Buford et al., 1987；Hamilton et al., 1994；Nance et al., 1981a；1981b；Rehfeldt et al., 1991；Tang et al., 2001)。

与林业发达国家相比，我国林木改良工作起步较晚，现有的改良材料试验林主要是以从大量的备选材料中选择优良育种材料为目的种源试验林、子代测定林，或无性系评比林，尚没有以反映遗位改良林分轮伐期内生长规律信息的改良林分标准地资料(孙晓梅等，2004)。Buford等(1987)通过比较火炬松改良林分与未改良林分树高-年龄关系、树高-直径关系、树干削度和干形等因子，认为遗传因素导致林分生长最根本的变化在于对树高-年龄关系(立地指数曲线)的影响。因此，本文利用15年生日本落叶松自由授粉家系子代测定林连年观测资料研究不同家系的生长变异情况，讨论家系对树高-年龄关系影响的假设、假设检验的方法、过程和检验结果，根据上述研究结果构建了反映日本落叶松不同家系生长过程的树高生长模型。

1 研究方法 1.1 优势高的确定

日本落叶松自由授粉家系子代测定林建于湖北建始长岭岗林场，1988年造林，完全随机区组设计，4次重复，47个家系，6株双列小区，株行距2 m×2 m。从1990年开始每年每木定株观测树高和胸径，至2000年。其中，1999年只对小区单株进行观测，本文在计算时未包括在内。本文以家系小区内2株最高树的平均高定义小区优势高。由于参试家系较多，数据量大，为了简化计算过程，从参试的47个家系中随机选择23个家系参与计算。

1.2 模型的统计假设检验

选择应用最为广泛的Richards方程和Schumacher方程的对数线性回归形式作为基础模型来描述日本落叶松家系树高-年龄关系，其模型形式如下：

(1)

式中:H_d表示优势高；A表示树木年龄；β₁、β₂、β₃依次为渐近参数、速率参数和形状参数；ε表示模型的随机误差。

(2)

式中：a、b分别表示线性模型的截距(或水平)参数和斜率(或形状)参数。

1.2.1 以Richards方程为基础模型的统计假设检验

利用再参数化的方法，将家系效应以哑变量的形式引入Richards基础模型，分别对模型的形状、渐近和速率3参数展开家系影响的显著性检验。模型的各扩展形式如下：

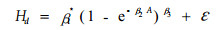
(3)

式中：; m表示家系数；当第i个家系时，x_i=1，其余家系x_i=0。

(4)

式中：；当第i个家系时，x_i=1，其余家系x_i=0。

(5)

式中：；当第i个家系时，x_i=1，其余家系x_i=0。

根据上述统计模型，检验各家系的渐近参数、速率参数和形状参数是否相同，即检验下述零假设：

1.2.2 以线性Schumacher方程为基础模型的统计假设检验

利用哑变量的方法将Schumacher方程扩展为(Buford et al., 1987)：

(6)

式中：当第i个家系时，x_i=1；其余家系时，x_i=0。

(7)

式中：当第i个家系时，x_i=1, z_i=A^-1；其余家系时，x_i=0, z_i=0。

根据上述统计模型，检验各家系的模型截距和斜率参数a、b是否相同，即检验下述零假设：

计算引入家系效应的扩展模型和没有家系效应的基础模型的残差平方和及自由度，检验家系对各参数是否存在显著性影响(Neter et al., 1985)：

(8)

式中:df^*和RSS^*为扩展模型的自由度和残差平方和；df和RSS为基础模型的自由度和残差平方和。

Richards方程及其扩展模型的拟合，采用SAS/STAT 6.12软件中PROC NLIN过程的麦夸特法(Marquardt)和正割法(DUD)计算：Schumacher方程及其扩展模型经对数变换后转为线性方程，采用PROC REG过程计算(高惠璇等，1997)。

2 结果与分析 2.1 优势高生长的家系效应分析

对自由授粉子代测定林逐年优势高数据方差分析表明，除12 a时家系间优势高差异不显著外，其余各年均存在显著差异，而大部分年龄(6个年龄)区组间优势高生长差异不显著，说明该测定林树高生长变异主要受家系影响(表 1)。

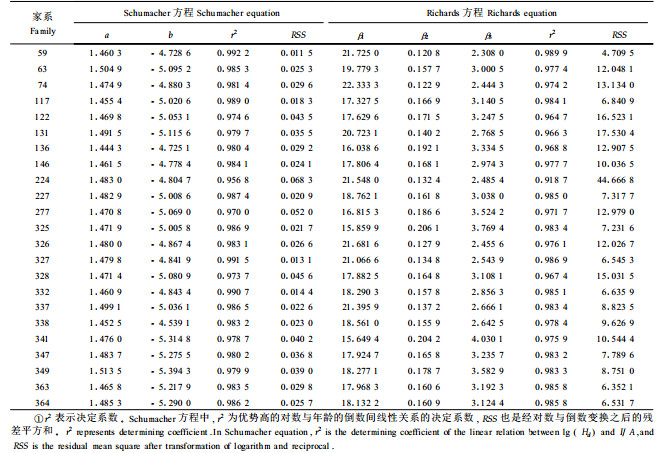
将测定林连年优势高观测数据分家系代入1式进行拟合，比较不同生长方程对各家系的拟合结果及模型参数(表 2)，发现Schumacher线性方程和Richards方程对描述幼中龄日本落叶松家系优势高生长均可达到令人满意的效果，家系间各模型参数存在一定的差异，说明家系对落叶松树高生长曲线的渐近值和形状存在一定的影响。

2.2 家系效应对优势高生长曲线影响模式分析

为了进一步明确家系对各模型参数影响的显著程度，利用子代测定林优势高数据对Schumacher和Richards方程及其扩展模型分区组进行拟合，并根据拟合结果逐项对两模型的参数进行F检验。

2.2.1 以Richards方程为基础模型的假设检验结果

表 3列出了各区组根据Richards基础模型和扩展模型拟合的残差平方和、自由度及相应的F值。由此可以看出，4个区组的F₁值远远大于查表F值，F₂值略高于查表F值，拒绝各家系树高模型具有相同渐近参数、速率参数的H₀₁和H₀₂假设，说明同一立地不同家系的树高-年龄曲线的渐近值和增长速率存在显著差异；4个区组的F₃值均低于查表F值，不足以推翻各家系树高-年龄曲线具有相同形状参数的H₀₃假设，说明同一立地不同家系具有相同的形状参数。因此，不同家系树高-年龄生长模型的最终形式为：

(9)

式中：；当第i个家系时，x_i=1, 其余家系x_i=0。

从模型预测值与观测值的分布来看(图 1)，预测值和观测值的散点基本上分布在与坐标轴成45°角的直线上，说明该模型对不同家系树高生长过程的拟合效果非常理想。观察日本落叶松各家系优势高预测的生长曲线趋势(图 2，选择6个家系作图)，发现随着年龄的增长家系间优势高的差异不断拉大，至15 a时家系间优势高最大差异达3.3 m，说明家系间生长潜力存在很大的变异。为进一步了解家系间生长速率的变化，以生长最快的224号家系和最慢的136号家系为代表画出了这两个家系优势高的连年生长量变化曲线(图 2)。从中看出，224号家系的连年生长量明显高于136号家系，且两个家系连年生长量曲线出现最高峰值的时间也不相同。136号家系在7年生时连年生长量开始呈下降趋势，224号家系9年生以后才出现明显下降的趋势。

2.2.2 以Schumacher方程为基础模型的假设检验结果

表 4列出了根据Schumacher基础模型及其扩展模型拟合的各区组残差平方和、自由度及其相应的F值。4个区组的F₄和F₅均显著大于查表F值，拒绝家系间模型截距和斜率参数相同的H₀₄、H₀₅假设，说明同一立地不同家系的树高-年龄对数线性模型的截距和斜率存在极显著的差异。因此，不同家系的树高生长模型的最终形式为7式。

表 5列出了根据7式和9式拟合的各家系参数及相关系数。同样画出了模型预测值与观测值的分布图(图 3，数据经对数变换)。各家系的预测值和观测值的对应散点基本上分布在与坐标轴成45°角的直线上，说明利用该模型对家系树高生长过程进行拟合可以取得令人满意的效果。日本落叶松各家系优势高预测生长曲线(图 3)同样随着年龄的增长家系间优势高的差异不断拉大。

3 结论与建议

树高-年龄曲线是建立遗传改良林分生长模型的基础。根据Richards模型的统计假设检验结果，日本落叶松不同家系树高生长过程为多形曲线，模型的渐近和速率参数不同(该结论与Knowe和Foster (1989)对火炬松自由授粉家系树高生长模型分析得出的结论一致)，说明遗传变异也是导致树木优势高生长差异的原因之一，树高生长潜力(立地指数)随着遗传改良材料的应用而增大，这已被很多的研究所证实(Buford，1989；Danjon，1995；Knowe et al., 1989：Nance et al., 1981b；Schmidtling，1988；Schmidtling et al., 1993)。

由Schumacher模型的统计假设检验可知，同一立地不同家系的树高生长曲线的渐近值(对数线性方程的截距参数)和形状(对数线性方程的斜率参数)发生明显变化，说明日本落叶松不同家系优势高生长规律不同，应采用不同的生长模式来描述。该结论与以往同类研究的结论有所不同。例如，Nance和Wells(1981b)、Buford和Burkhart(1987)通过比较火炬松种源和家系的树高-年龄关系，认为遗传因素仅引起曲线的渐近值(截距)发生改变，但其形状(斜率)不变，即基本生长模式一致；李希菲等(1999)通过对杉木不同种源的立地指数曲线研究也认为各种源的立地指数值不同，但曲线的斜率相同；Golden等(1981)的研究表明不同种源的生长模式存在差异，但这种差异并不重要；也有研究认为不同遗传材料的渐近值也不发生改变(Sprinz et al., 1989)。

在选择生长模型拟合不同遗传材料的生长过程时，一般认为灵敏度高的Richards方程更能反映出不同材料间生长过程的细微变化，比对数线性模型的拟合效果要好(Knowe et al., 1989；Sprinz，1987)。但从本文对2类模型的比较来看，Schumacher线性方程和Richards方程对日本落叶松幼龄阶段家系的优势高生长过程的模拟均能达到令人满意的效果。

从不同家系优势高生长趋势看出，家系间优势高的生长差异随年龄而增大，说明家系间生长潜力存在着很大的变异，同时不同家系的连年生长速率也不相同。生长快的家系的连年生长量明显高于生长慢的家系，且连年生长量曲线的高峰值到来的时间也明显滞后于生长慢的家系。

如果模型的选择和计算得当，在缺乏改良林分固定样地观测数据的情况下，利用子代测定林资料能够获得比较合理的树高-年龄曲线，再结合已建立的一般的未改良林分的生长模型系统完全能够实现改良林分的生长和遗传增益的预测。但是，子代测定林内小区株数毕竟有限，根据这么有限的小群体的表现来推断林分水平的生长表现，必然存在一定的局限性。因此，要想深入地研究现实改良林分与未改良林分的生长和收获量的差异，预测改良林分的遗传增益，需要建立改良林分与对照(未改良林分)接近现实林分生长状态的标准地，并依据标准地的长期连年观测资料模拟和评估现实改良林分的遗传增益。

林分生长的动态关系包括：优势高随时间的动态变化过程(树高-年龄关系)、树高-直径生长关系、林木株数随时间的变化过程(自然稀疏模型)等，本研究只开展了日本落叶松家系对树高-年龄关系的影响的研究，对于其它关系的影响有待进一步的验证，以便更全面地理解日本落叶松改良林分的生长动态过程，同时为进一步建立改良林分的生长模型提供科学的理论依据。