文章信息
- 于海鹏, 刘一星, 张斌, 李永峰.
- Yu Haipeng, Liu Yixing, Zhang Bin, Li Yongfeng.
- 应用空间灰度共生矩阵定量分析木材表面纹理特征
- Application of Spatial Gray Level Cooccurrence Matrix in Wood Surface Texture Quantitative Analysis
- 林业科学, 2004, 40(6): 121-129.
- Scientia Silvae Sinicae, 2004, 40(6): 121-129.
-
文章历史
- 收稿日期:2003-06-25
-
作者相关文章
纹理在日常生活中频繁出现,但究竟什么是纹理,却一直未有准确的定义。一般认为,纹理就是在图像中反复出现的局部模式和它们的空间排列规则,是任何事物构成成分的分布和特征。霍金斯总结了判别纹理属性的3要素:一是某种局部的序列性,在该序列更大的区域内不断重复;二是序列是由基本部分非随机排列组成的;三是各部分大致都是均匀的统一体,纹理区域内任何地方都有大致相同的结构尺寸。木材表面所呈现的图案符合霍金斯的纹理判别3要素,应属于纹理型事物。
长期以来,木材科学工作者应用传统方法对木材表面纹理进行了许多定性的研究分析,取得了一些研究成果(刘一星,1994),但在定量化分析方面的研究并不多。京都大学的增田稔正在积极进行木材纹理定量化的研究,主要采取以简单的线形通过排列模式的变换来模拟木材的纹理特征,并在此基础上构建模型(增田稔,1983;仲村匡司等,1995)。此种方法的优点在于思路清晰、方法简便、特征参数明确,缺点是其表达能力有限,对木材纹理的复杂性和变异性以及木材真实纹理的分布规律不能充分反映。这种问题的解决方法应是先充分分析木材纹理的特点和变化规律,寻找出能对之有较好表达效果的特征参数,然后再建立起数学表达模型,这是从繁到简的思路。不同类型木材的纹理,从目视上往往就能看出它们不仅具有一定的共性特征,而且绝大多数也有其鲜明的个性特征,同时各类木材纹理的分布基本都是有规律的,这些特征为计算机进行木材纹理的定量分析和合理的识别分类奠定了良好的基础。借助数字图像处理技术对木材表面的纹理特征进行定量分析,并实现计算机的识别分类将是一件非常有意义的工作(Haralick et al., 1973)。
空间灰度共生矩阵法是数字图像纹理分析的经典方法,这种方法也被证明是一种行之有效的方法,选用这种方法进行木材纹理分析应该是可行的(Haralick, 1979; Haddon et al., 1993; 黄桂兰等, 1995)。本文就应用空间灰度共生矩阵对木材表面纹理进行定量分析展开研究和讨论。
1 材料与方法 1.1 材料选取国内有代表性的树种50种,其中针叶树材17种,阔叶树材33种,对各树种均制取120 mm×80 mm的木材径、弦向切面试件。对所有试件进行离散数字化形式的转变,采样精度为512×512像素,灰度层次为256级,保存为标准图像格式,等待进一步分析处理。
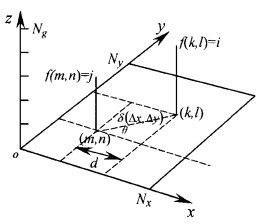
1.2 方法 1.2.1 构建空间灰度共生矩阵利用空间灰度共生矩阵对图像像素点的灰度值进行二阶统计。空间灰度共生矩阵建立在对图像的二阶组合条件概率密度函数估计的基础上,通过计算图像中任意两点灰度的相关性,能够反映图像灰度关于方向、相邻间隔、变化幅度的综合信息,是分析纹理特性的有效办法。具体方法为:将图像的灰度表面看成三维空间中的一个曲面(图 1),以oxy作为图像像素的坐标平面,设水平方向x的像素总数为Nx,则像素的水平空间域为Lx={1, 2, …, Nx}; 设垂直方向的像素总数为Ny,则像素的垂直空间域为Ly={1, 2, …, Ny};以z作为像素的灰度坐标轴,设z轴上每个像素出现的灰度量化的最高级为Ng, 则像素的灰度量化集为G={0,1,2,…,Ng}。由此,可以将图像函数f表示为一个Lx×Ly的图像像素集,且这个像素集的每一个像素均具有Ng个灰度层中的一个值G,即表示为f:Lx×Ly→G。
|
图 1 像素对的空间表达模式 Fig. 1 Spatial express mode of pixel pair |
定义像素点对的间隔距离参数为d, 像素点对的方向角度参数为θ, θ与x轴平行时值取零,绕逆时针旋转为正方向。统计纹理图像中在θ方向上相隔d像素距离的一对像素分别具有灰度层i和j的出现概率P(i, j, d, θ),生成灰度共生矩阵C(d, θ),记为C(d, θ)=[P(i, j, d, θ)]。
C(d, θ)是一个对称矩阵,关于θ变化时存在C(d, 0°)=CT(d, 180°), C(d, 45°)=CT(d, 225°), C(d, 90°)=CT(d, 270°), C(d, 135°)=CT(d, 315°),这样只需计算θ取0°、45°、90°、135°时的C(d, θ),即可得知C(d, θ)在θ的整个坐标空间的值。
当θ=0°、45°、90°、135°时,像素对G(k, l)=i和G(m, n)=j的共生率P(i, j, d, θ)计算如下:
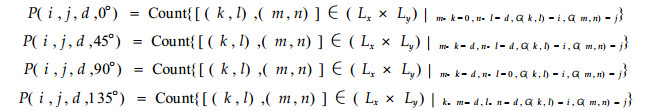
|
其中,Count表示在该集合中的元素数目。
1.2.2 基于空间灰度共生矩阵计算纹理特征参数值根据Haralick等(1973)的“图像分类的纹理特征”一文,14种纹理特征参数可基于灰度共生矩阵求得。本文应用波兰COST B11研究小组开发MaZda图像纹理分析软件对其中的11种进行计算(Szczypi'nski et al., 2001),这11种特征参数计算式如下。
(1) 二阶角矩: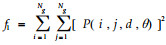
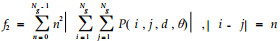
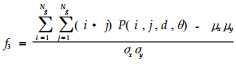
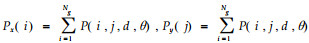
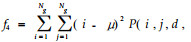
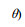
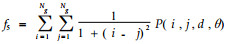
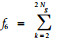
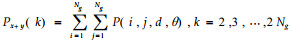
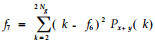
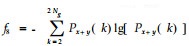
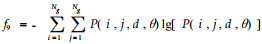
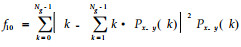
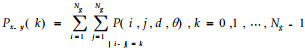
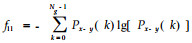
通过程序分别计算每幅图像在像素点对距离d取1、2、3、4、5,角度θ取0°、45 °、90°、135°时的11种纹理特征参数值,对所得全部数据进行统计分析。
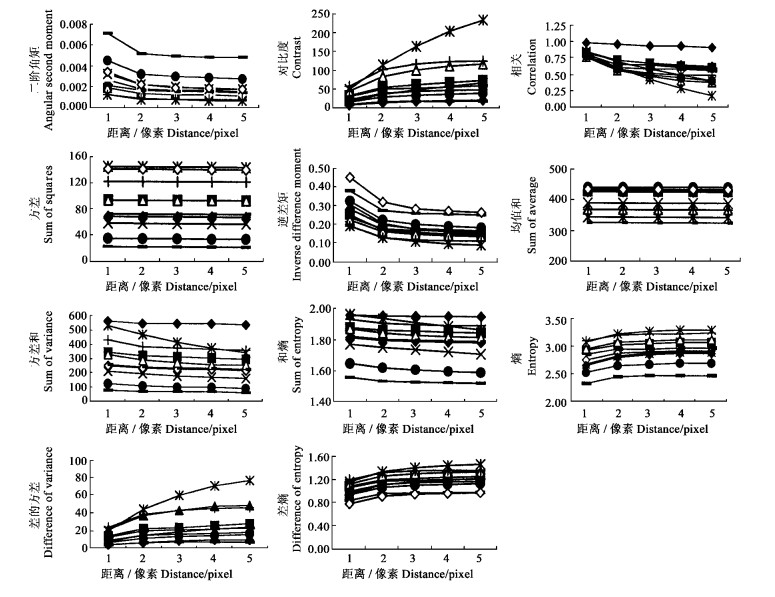
2 分析与讨论 2.1 d取值对纹理特征参数值的影响为忽略方向差异的影响,使特征参数值成为与图像旋转无关的量,此处计算的特征参数值取θ在0°、45°、90°、135° 4个方向的平均值。图 2为木材纹理特征参数值随d增大的变化情况。从图 2中可以看出,当像素点对间距d=1~5时,二阶角矩、对比度、相关、逆差矩、差的方差、差熵的值均受到一定影响;而方差、均值和、方差和、熵、和熵受影响较小或无影响。随d的增大,二阶角矩、相关、逆差矩的值呈下降趋势,至d=2时渐缓,在d=3~5无大的变化,基本保持一致;随d的增大,对比度、熵、差的方差、差熵呈上升趋势,至d=2时渐缓,在d=3~5基本保持一致:因此,认为d取3时,计算的纹理特征参数值具有较好的代表性。
|
图 2 纹理特征参数值随d的变化情况 Fig. 2 Changing of texture features with d
—◇—白桦B. platyphylla—■—大青杨P. ussuriensis; —△—柞木Q. mongolica;  红松P. Koraiensis; 红松P. Koraiensis;  兴安落叶松L. gmelinii; —●—鱼鳞云杉P.jczoensis; 兴安落叶松L. gmelinii; —●—鱼鳞云杉P.jczoensis;  春榆U. japonica 春榆U. japonica  黄菠萝P. amurense; 黄菠萝P. amurense;  紫椴T.amurensis —◆—银杏G. biloba. 紫椴T.amurensis —◆—银杏G. biloba.
|
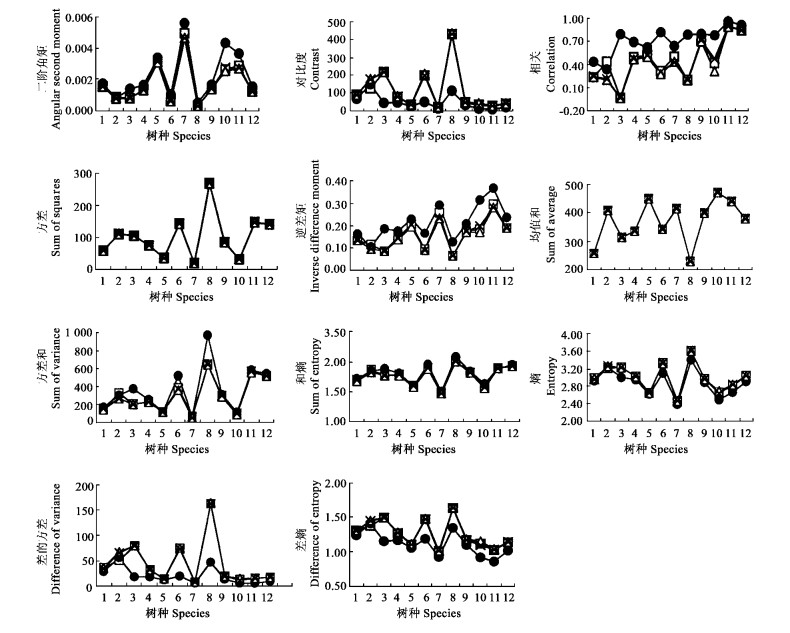
受θ的影响,不同方向上的纹理特征参数值存在差异。图 3反映了d取3时,纹理特征参数在θ的0°、45°、90°、135° 4个方向上的取值变化。从图 3中各条曲线的变化趋势看,4个方向上纹理特征参数值的变化规律基本相同(“相关”除外),说明各方向上的纹理参数值都具有对样本纹理特征的正确反映能力。但从图中各曲线的偏离程度可以看出,θ=90°方向上的纹理特征参数值明显异于其他3个方向上的纹理特征值,其他3个方向上的纹理特征值彼此之间无显著差异,这说明纹理特征参数的确受到木材竖向带状条纹的影响,竖向的共生率增大,使基于共生率计算的90°方向上的特征参数值也不同于其他3个方向。
|
图 3 纹理特征参数值在不同方向上的变化 Fig. 3 Changing of texture features in different directions —□—θ=0° or 180°;—●—θ=90° or 270°;—△—θ=45° or 225°;—×—θ=135° or 315°. |
根据木材纹理的特点,考虑到即使是同一种木材,其径、弦切面纹理也是完全不同的,因此对径、弦切面纹理应分别进行分析。对于径切面,考虑到都具有竖向的带状条纹理,每种木材的个性特点和变化规律主要集中在横向,这样分析方向只取θ=0°一种即可;对于弦切面,考虑到抛物线状纹理是其基本规律,每种木材的个性特点和变化规律主要集中在0°、45°和135°方向,这样分析时应取这3个方向纹理特征值的平均值。
受θ不同方向取值影响较明显的特征参数为:对比度、相关、逆差矩、差的方差、差熵;不明显或基本不受影响的特征参数为:二阶角矩、方差、均值和、方差和、和熵、熵。
2.3 纹理特征参数的筛选与归类在对纹理特征参数进行筛选和归类之前,应首先明确一下各参数所表征的纹理意义和变化规律。
二阶角矩:又称为能量,是图像灰度分布均匀程度和纹理粗细的一个度量。当图像较细致、均匀时,二阶角矩值较大,最大时为1,表明区域内图像灰度分布完全均匀;反之,当图像灰度分布很不均匀、表面呈现出粗糙特性时,此时二阶角矩值较小。
对比度:反映邻近像素的反差,是纹理定域变化的度量,可以理解为图像的清晰度、纹理的强弱。对比度值越大,表示纹理基元对比越强烈、纹理效果越不明显;对比度值较小,表示纹理效果越明显;当对比度值为0,表明图像完全均一、无纹理。
相关:衡量共生矩阵在行或列方向上的相似程度,是灰度线性关系的度量。不同图像的相关值之间并无太大差异,而同一幅图像自身4个方向的相关值之间却往往存在较大差异,一般表现为在纹理方向上的相关值明显高于其他方向的相关值。因此,相关可用来指明纹理的方向性。
方差、方差和:反映纹理变化快慢、周期性大小的物理量。值越大,表明纹理周期越大。方差、方差和的值均随图像纹理的不同有较大变异,可作为区分纹理的一个重要指标。
均值和:图像区域内像素点平均灰度值的度量,反映图像整体色调的明暗深浅。熵、和熵、差熵:代表图像的信息量,是图像内容随机性的量度,指示纹理的复杂程度。当图像复杂程度高时,图像熵值最大,分形值也相对较高;当图像复杂程度低时,熵值较小或为0。
差的方差:表明邻近像素对灰度值差异的方差,对比越强烈,差的方差值越大;反之,值越小。
逆差矩:反映纹理的规则程度。纹理杂乱无章、难于描述的,逆差矩值较小;规律较强、易于描述的,逆差矩值较大。
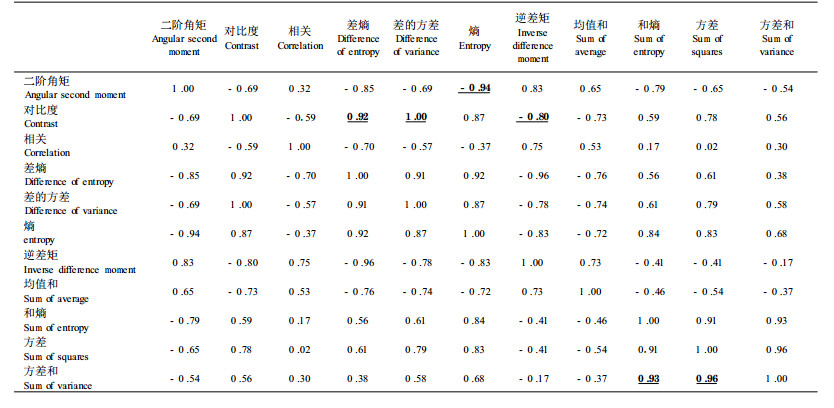
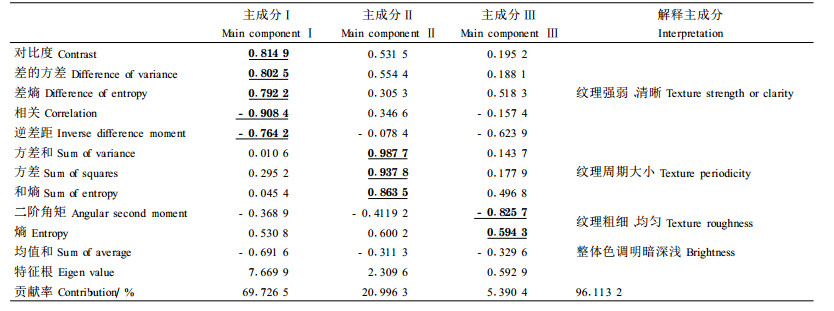
虽然以上这11种特征参数都能表达纹理的某些特定信息,但存在信息冗杂、重复表述的问题,所以应进行筛选并类,尽量选择出代表性好、独立性强的特征参数用于木材纹理分析。针对11种纹理特征参数所求得的相关系数矩阵见表 1,主成分因子构成见表 2。
|
|
|
|
通过相关系数分析、因子分析以及图 3中曲线的变化规律可以发现,许多特征参数是高度相关的,因子分析的主成分分类结果也反映了这一点。因此,若将相关系数大于0.8的特征参数去除,则相对比较独立的特征参数就只剩下4个:对比度(依此可去:差的方差、差熵、相关、逆差矩)、方差和(依此可去:方差、和熵)、二阶角矩(依此可去:熵)、均值和。实际上对比度、二阶角矩、方差和正是通常公认最重要的纹理特征参数。这里均值和虽然不是真正意义上的纹理特征参数,但它反映的是图像的总体灰度特征,可作为色度明暗深浅指标,对于加强纹理的表达、分类识别具有重要意义。
对特征参数的因子分析可得到3个纹理主成分,主成分I代表纹理基元的反差与对比,表示纹理的强弱、清晰程度;主成分Ⅱ代表纹理基元过渡变化的快慢,表示纹理的周期性:主成分Ⅲ代表纹理基元的大小与分布的均匀程度,表示纹理的粗细均匀性。主成分I越大表明纹理越强、纹理图案越清晰:主成分Ⅱ越大表明纹理变化越缓慢、周期越大;主成分Ⅲ越大表明纹理越细致均匀。
将筛选出来的纹理特征参数(对比度、二阶角矩、方差和)与3个纹理主成分比较纹理表达效果,发现3种纹理特征参数的表达能力接近于纹理主成分,能较好地反映不同树种木材的变化趋势。因此,在今后的分析中,只选择“对比度、方差和、二阶角矩、均值和”这4个纹理特征参数就可以较好地完成分析任务,而且还可以大大减少计算的工作量,节约分析时间。
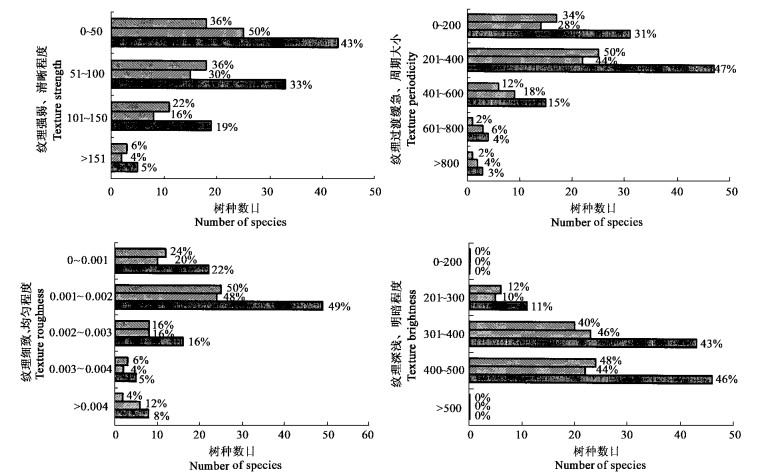
2.4 木材纹理主成分的分级统计为明确木材纹理在主成分空间的分布特征,采用等级差的分级方式,利用计算机统计各树种木材径、弦向纹理落入各主成分分级空间的情况,用统计分布图列出分析结果如图 4。从图 4中很容易看出木材径、弦向纹理以及全部纹理在纹理主成分空间的分布聚集程度。
|
图 4 木材纹理主成分的分级统计分布 Fig. 4 Gradational statistic of wood texture principal components
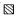 径向纹理Radial texture; 径向纹理Radial texture;  弦向纹理Tangential texture; 弦向纹理Tangential texture;  全部Whole. 全部Whole.
|
针对木材径向纹理的特点,计算其0°方向上的纹理特征值,统计、分析木材径向纹理的强弱、周期、粗细和明度的分布规律。图 5反映了各树种木材径向纹理在各主成分空间的分布。从中可以看出:各树种木材径向纹理在纹理强弱、粗细和明暗主成分空间分布都较均匀,而在纹理周期主成分空间分布却较集中,这说明了不同树种木材的径向纹理有着相近的过渡变化周期,但在纹理强弱、粗细和明暗方面却各有特色,差异很大。从图 5还可以看出,阔叶树材径向纹理在纹理粗细和纹理周期主成分空间的分布比较集中,显示了各阔叶树材间在粗细均匀方面有着相近的特征,在纹理过渡变化快慢方面也相近;而针叶树材径向纹理在明暗主成分空间分布较集中,显示各针叶树材的明度彼此相差不大,这与刘一星等(1995)的研究结果相同。
|
图 5 木材径向纹理在主成分空间的分布情况 Fig. 5 Distribution of wood radial texture in principal component space ●针叶树材Softwood; △阔叶树材Hardwood. |
表 3列出了木材径向纹理80%样本整体在主成分空间的分布范围(去除最小和最大样本各10%,保留中间的80%),表 3的平均值数据反映出针叶树材与阔叶树材的径向纹理在纹理周期和纹理粗细方面差异不大,而在纹理强弱和明暗程度上有着较明显的差异。
|
|
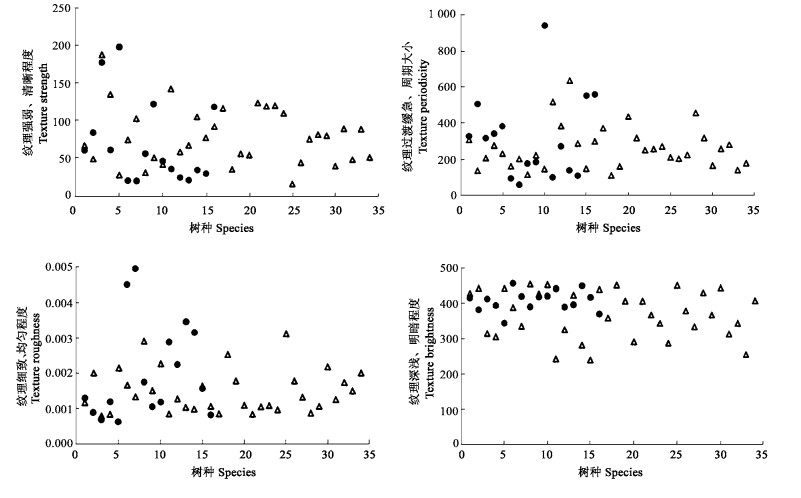
图 6反映了各树种木材弦向纹理在主成分空间的分布,从中可以看出各树种木材弦向纹理在纹理周期和纹理明暗主成分空间分布都较均匀,而在纹理强弱、纹理粗细主成分空间分布却较集中,这说明了不同树种木材的弦向纹理过渡变化周期存在差异,明暗也很不相同,但在纹理强弱和纹理粗细方面却很相似,彼此差异不大。从图 6还可以看出,针叶树材弦向纹理在纹理强弱、粗细和明暗主成分空间的分布都比较集中,阔叶树材弦向纹理在纹理周期和纹理粗细主成分空间分布较集中。
|
图 6 木材弦向纹理在主成分空间的分布情况 Fig. 6 Distribution of wood tangential texture in principal component space ●针叶树材Softwood; △阔叶树材Hardwood. |
表 4列出了木材弦向纹理80%样本整体的主成分分布范围,平均值数据反映出针叶树材与阔叶树材的弦向纹理在纹理强弱、周期、粗细和明暗4个方面均存在较大差异,数据上反映出的这种差异可以印证目视上针叶树材与阔叶树材弦向纹理存在的差别。关于木材径向纹理与弦向纹理之间的差别,这里不再分析,具体可参照2.5和2.6部分归纳得出。
|
|
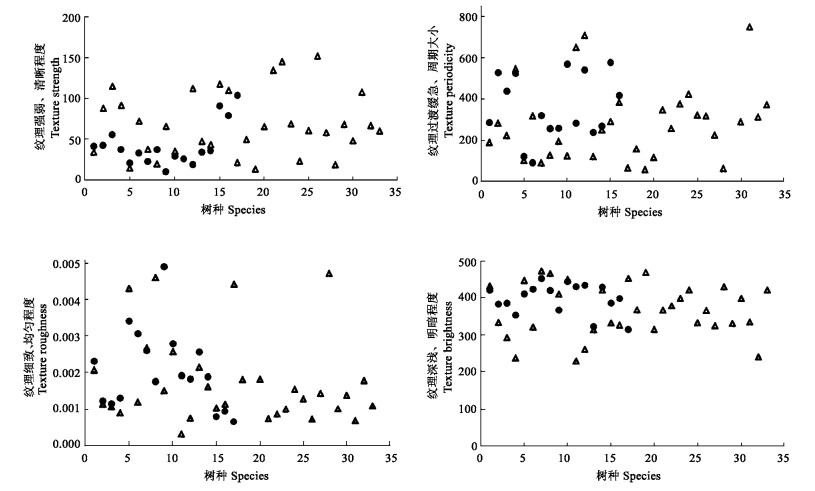
前面讨论了各树种木材纹理在各主成分空间中的临近程度,但主成分空间上的临近还不足以说明它们的纹理在视觉上就一定是相似的,因为任何一个主成分都只是对纹理某一方面特征的抽提,虽然具有专业意义,但不具备全面性和综合性,因此单独选择哪一个主成分来综合判定纹理间的相似性都不理想。而较容易想到、具有一定道理的方法应是对4个主成分的值再综合,利用各自贡献率的大小对其进行加权平均,得出每种木材纹理的综合值,综合值能比较全面地反映出该种纹理的基本特征,这点由4种主成分累积的96.11的贡献率可以证明,因此综合值是可以用作比较2种树种木材纹理相似性的依据。综合值的计算式如下:
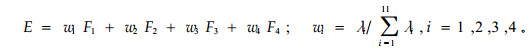
|
λi是因子分析时所得各主成分的特征根,wi是各主成分对解释原变量的贡献率,Fi是旋转后的纹理特征参数fi的线性函数,即主成分计算值。
2种木材纹理的相似性可以通过2种纹理综合值之差与它们综合值的平均值之比来计算,所得的百分比作为它们纹理不相似程度的量值。不相似度越小,表明2种木材纹理越相似,即相应的目视差异也越小;否则,二者之间越不相似,目视差异越大。可以设定几个判定范围和相应结论来加以界定:不相似度在1%以内,可判定为2种纹理极相似;大于1%而小于10%,可判定为相似;大于10%而小于20%,可判定为基本相似;大于20%而小于50%,判定为略相似;大于50%,判定为不相似。
通过对50个树种径、弦切面的分析,发现通过综合值来表征纹理的基本特征具有一定的理论意义和实际的可行性,通过不相似度计算来判定2种纹理的相似程度也取得了较好的效果,但应指出此种方法在同径向或同弦向纹理之间的判定效果要好于不同切面纹理之间相似度的判定效果。
3 结论本文探讨了空间灰度共生矩阵法在纹理定量化分析中的应用。在对国内50个树种径、弦向纹理计算、分析的基础上得出了d取3,θ在径向纹理时取0°,在弦向纹理时取0°、45°和135°的平均值对于反映木材纹理的特点较适宜。在11种纹理特征参数的基础上归纳出4个纹理主成分因子,分别反映纹理的强弱、纹理的变化周期、纹理的粗细均匀性以及整体灰度的明暗;讨论了木材纹理在各主成分空间上的分布规律和特点,并具体对木材径、弦向纹理分别进行了细致分析;最后提出了纹理综合评价值的计算方法,以及通过纹理综合值判定2种纹理间相似性的方法。综合而言,空间灰度共生矩阵具有较好的纹理表达能力,对于定量化分析、评价木材表面纹理能够发挥良好的作用,具有一定应用价值。
黄桂兰, 郑肇葆. 1995. 空间灰度相关在影像纹理分类中的应用及分析. 武汉测绘科技大学学报, 20(4): 301-304. |
刘一星著.木材视觉环境学.哈尔滨: 东北林业大学出版社, 1994
|
刘一星, 李坚, 徐子才, 等. 1995. 我国110个树种木材表面视觉物理量的综合统计分析. 林业科学, 31(4): 353-355. |
仲村匡司, 增田稔. 1995. まさ目パタ一ンの浓淡むらの视觉特性. 木材学会誌(日本), 41(3): 301. |
增田稔. 1983. 木目模样その他のパタ一ンの数量化に関すゐ研究一特に, ちらつきに基づくパタ一ンの数量化について. 材料(日本), 32(359): 893. |
Haralick R, Shanmugam K, Dinstein I. 1973. Textural features for image classification. IEEE Transactions on Systems, Man and Cybernetics, 3(6): 610-621. |
Haralick R. 1979. Statistical and structural approaches to texture. Proceedings IEEE, 67(5): 786-804. DOI:10.1109/PROC.1979.11328 |
Haddon J F, Boyce J F. 1993. Co-occurrence matrices for image analysis. IEEE Electronics and Communications Engineering Journal, 5(2): 71-83. DOI:10.1049/ecej:19930013 |
Szczypi'nski P, Kociolek M, Materka A, et al. 2001. Computer program for image texture analysis in PhD students laboratory. International Conference on Signals and Electronic Systems, L d'z-Poland: 255-262. |
 2004, Vol. 40
2004, Vol. 40