索网式缆索起重机(陈洁余等，2001)和双联式缆索起重机(史济彦，1965)比较，克服了双联式缆索起重机靠两条起重索绷拉提升和平移重物，容易绷断而造成事故的缺陷；和桥式起重机(机械工程手册编辑委员会，1997)比较，不但功能相同，运行同样平稳可靠，造价仅为桥式起重机的一半左右。但是，其索网承载结构和双联式缆索起重机的索网承载结构相似，设计计算十分困难。本文根据其部分结构的中央挠度已经超过了“抛物线”计算理论(杜盖尔斯基，1955；加藤诚平，1965)适应范围的实际情况，应用“悬索曲线”计算理论(单圣涤，1983；2000)，导出了索网式缆索起重机的设计计算方法。此方法有效解决了悬挂缆索斜向集中载荷的张力计算和索网承重结构的受力分析问题，同样适用于双联式缆索起重机的设计计算，为今后发展更为复杂的索道索系设计计算提供了新的理论依据。索网式缆索起重机，有双承载索网式缆索起重机和四承载索网式缆索起重机两种，本文以四承载索网式缆索起重机为例，计算索网式缆索起重机的设计计算法。

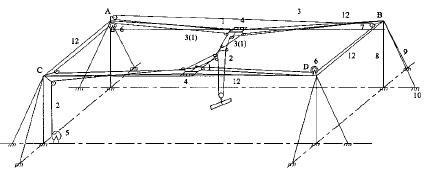
1 索网式缆索起重机的基本结构

图 1所示为双承载索网式缆索起重机，这种索网式缆索起重机的技术关键是用一条两端同时固结在B点的缆索3(1)，通过两个导向滑车7、两个摩擦卷筒6、两个跑车4及其两个相互联结的动滑轮配置而成的长度不变的副承载索。图中E表示由两个相互联结的动滑轮构成的移动滑规，当D处摩擦卷筒制动时，A处摩擦卷筒的转动可以控制移动滑规的纵向位置；当A处摩擦卷筒制动时，AEB间的副承载索长度被固定，D处摩擦卷筒的转动，可以通过牵连索的配合，控制两个跑车沿AB、CD两条承载索移动，使移动滑规E可以在ABDC平面内任意处定位。这种缆索起重机的起重结构，则由图中的缠绕卷筒5和起重索2，分别挂在C点架杆上、两个跑车4上、滑规E的两个动滑轮上的共5个滑车及动滑轮和挂勾构成，起重索2的尾端也被固结在架杆B上。于是当重物被提升后，悬挂在移动滑规上的重物，在ABDC平面内不论被移动到任何位置，运行中的起重索和副承载索的长度都不会发生变化，因而这种索网式缆索起重机只要张紧度合理，运行中便会平稳而安全，还可应用于林木的择伐和中幼林的抚育间伐及采种等林区作业。

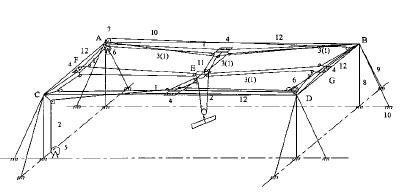
图 2所示为基本结构和双承载索网式缆索起重机相同的四承载索网式缆索起重机，这种索网式缆索起重机和双承载索网式缆索起重机的差别，只是在AC和BD之间各增加了一条承载索、一个跑车和一个动滑轮，因而四承载缆索起重机的移动滑规由四个增力滑轮组成，有四条承载索和四个跑车同时承重，其它结构和双承载索网式缆索起重机完全相同。

2 索网式缆索起重机的设计计算方法

索网式缆索起重机设计计算方法的主要困难，和双联式缆索起重机类似，在于其承重结构是一更为复杂的索网结构，而且有的是中央挠度系数远大于抛物线计算理论的适用范围0.08的(杜盖尔斯基，1955；加藤诚平，1965)承重结构，必须采用新的“悬索曲线”计算理论(单圣涤，1983；2000)。为便于推广，本文只介绍其中难度较大、最具代表性的四承载索网式缆索起重机的设计与计算方法。

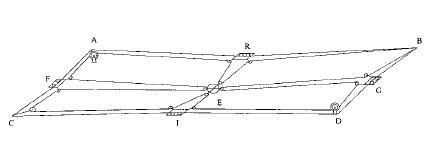
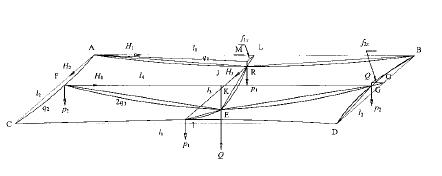
为便于计算，可将图 3所示的四承载索索网的承重结构简化成图 4所示的力学计算模型。图中ARB、CID、AFC、BGD分别表示此缆索起重机的四条承载索，R、I、F、G分别表示四个跑车的位置，由副承载索串连起来的四个跑车、两个摩擦卷筒、两个导向滑车和四个增力滑轮而成的承载索网，则被简化成由FEG和REI构成的两条同时承载重物的副承载索，在这种情况下，当重物Q的位置处于ABDC平面的中央位置E处平衡静止时，AB、CD、AC、BD、FG、RI等6条承重的缆索都处于最大受力状态，所以可以以此状态的计算作为索网式缆索起重机设计的依据。

设此起重机的集中荷重为Q，主承载索AC、BD索的单位长度自重为q₁，AC、BD的单位长度自重为q₂，副承载索的单位长度自重为q₃。对照图 4，MEI和FEG副承载索的单位长度自重则为2q₃，AB、CD的水平跨距为l₁，AC、BD的水平跨距为l₂，RI的水平跨距为l₃，FG的水平跨距为l₄，AB、CD索的水平中央挠度为f_1x，AC、BD的水平挠度为f_2x，RI的中央挠度为f_s，此索承担的荷重量为Q₁，FG的中央挠度为f₄，此索承担的荷重量为Q₂，并设，，，。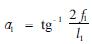

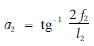
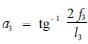
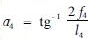
RI、FG两索的其水平张力分别为H₃、H₄，有

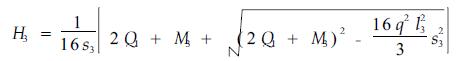
(1)

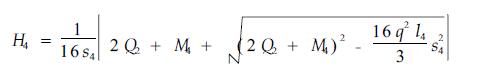
(2)

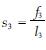
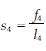
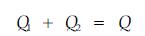
两式中，，，M₃，M₄分别为此两索之自重，q为此两索的单位长度重量，且q=2q₃。

(3)

设AB、CD和AC、BD索的中央水平挠度系数为

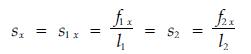
(4)

式中s_x可称为四承载索网式缆索起重机主承载索的水平中央挠度控制系数，因为图 4中的RI、FG两条副承载索，实际上是如图 2所示，由一根副承载索通过一个滑车、两个摩擦卷筒、四个跑车和承载滑规上的四个增力滑轮形成的，承载滑规在ABDC平面中央平衡的条件，即联结承载滑规各索的张力相等, 有

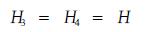
(5)

为计算两索分别承担的荷重量，可分别在ER、EG曲线的中间点附近，取一切线方向分别与RI、FG方向一致的一点进行受力分析，在这两个点上，有

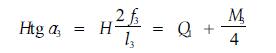
(6)

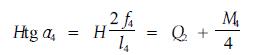
(7)

按照(5)、(6)、(7)式，有

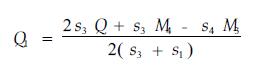
(8)

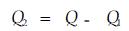
(9)

设索网式缆索起重机的中央总挠度为f，表示ABDC平面到E点的垂直距离，有

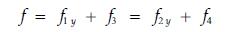
(10)

忽略主承载索之自重时，图 4中△LMR和△RJE及△OQG和△GKE是两对相似三角形，有

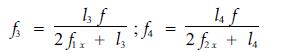
(11)

REI副承载索和FEG副承载索作用在ARB、CID、AFC、BGD承载索上R、I、F、G处的作用力应分别为

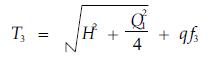
(12)

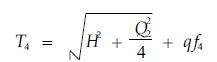
(13)

按照(10)式，这时f_1y=f-f₃，f_2y=f-f₄，ARB、CID和AFC、BGD的中央挠度分别为f₁和f₂，且

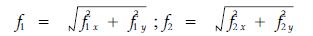
(14)

ARB、CID和REI、FEG的水平张力分别为H₁、H₂，且

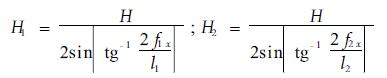
(15)

AR、RB两索同时作用在R处的张力分别为T_R(AR)、T_R(BR)，有

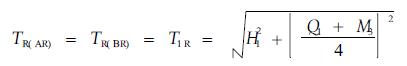
(16)

BG、DG两索同时作用在G处的张力分别为T_G(BG)、T_G(DG)，有

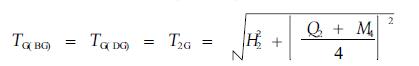
(17)

于是，ARB、CID两索分别作用在A、B、C、D的张力分别为

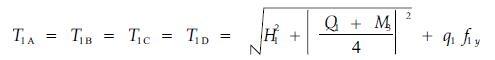
(18)

AFC、BGD两索分别作用在A、B、D的张力分别为

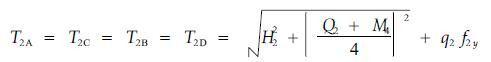
(19)

诸式中，各集中载荷缆索之自重分别为

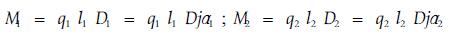
(20)

(21)

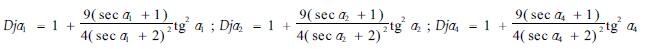
(22)

以上便是索网式缆索起重机的设计计算公式。

3 索网式缆索起重机的设计步骤

根据任务并考虑到载具和工作件的自重正确确定起重机的实际载量；按0.03~0.05的范围给定主承载索的水平中央挠系数s_1x=s_2x, 并根据地形条件和钢架杆的高低，给定此缆索起重机的中心挠度f，再按(15)式可算出f₃和f₄；以实际承重的2.5~3.5倍为破断张力T_p预选副承载索, 按(21)式算出副承载索的自重M₃、M₄；按(8)、(9)两式算出REP、FEG两索的载荷分布Q₁、Q₂，按(1)、(2)两式分别算出RI、FG索的水平张力H′₃、H′₄，再按(16)、(17)式可分别算出副承载索分别作用在主承载索上的张力T′_3R、T′_4G；对H′₃、H′₄取平均值，按(15)式可分别算出主承载索的水平张力H₁、H₂，再按(16)、(17)、(18)、(19)式，算出AR、RB分别作用在R处的张力T_R(AR)、T_R(BR)BG、DG两索同时作用在G处的张力T_G(BG)、T_G(DG)及ARB、CID两索分别作用在A、B、C、D的张力T_1A=T_1B=T_1C=T_1D；AFC、BGD两索分别作用在A、C、B、D的张力T_2A=T_2C=T_2B=T_2D；对承载索进行安全校核；按其实际起重量的n/2倍选取起重索和牵连索。

4 结论

索网式缆索起重机由于用了一条长度不变的副承载索和两个摩擦卷筒、一个导向滑车、四个跑车、四条主承载索和一个承载滑规相互配置而成的承重结构，能够随时连续平稳地把承载和起重结构平移到ABDC平面中的任意一点，而且起重结构中的起重索，在移动中的长度不会发生变化，可以确保在ABDC平面中的任意一点平稳垂直提升和移动重物，跨距可达数百米，作业面积可达数公顷，性能和桥式起重机十分接近，造价仅为同功能的桥式起重机造价的一半左右，适合于大型水利水霸的建造和控制及其它大型建筑工程。

架空索道设计中，双联式缆索起重机平面索网的出现，提出了关于悬挂缆索斜向集中载荷和索网承重的受力计算问题，近半个世纪一直末获解决，文中应用“悬索曲线”计算理论，导出了索网式缆索起重机的设计计算方法。此方法有效解决了悬挂缆索斜向集中载荷的张力计算和索网承重结构的受力分析问题，同样适用于双联式缆索起重机的设计计算，为今后发展更为复杂的索道索系的设计计算提供了新的理论依据。