文章信息
- 朱廷曜, 关德新, 吴家兵, 金昌杰.
- Zhu Tingyao, Guan Dexin, Wu Jiabing, Jin Changjie.
- 论林带防风效应结构参数及其应用
- Structural Parameters of Wind Protection of Shelterbelts and Their Application
- 林业科学, 2004, 40(4): 9-14.
- Scientia Silvae Sinicae, 2004, 40(4): 9-14.
-
文章历史
- 收稿日期:2002-11-18
-
作者相关文章
林带结构不同,其防护效益也有明显差异,这一点早为许多研究者所发现。营造具有最优结构的林带,可以取得最大的防护效益,因而林带结构的研究非常重要。早期的研究者将林带的结构分为3种或4种结构类型(玛恰金,1956; 曹新孙等,1983),其后许多研究者又提出了林带的结构参数:疏透度(β)和透风系数(α)作为评价林带优劣的指标,并给出了最适指标(Юдин, 1950;Caborn, 1957;Jensen, 1961;傅抱璞,1963;Cмaлько, 1963;Eimern et al., 1964;曹新孙等,1983)。但疏透度和透风系数本身还存在几何意义或实用性等问题,例如疏透度把立体结构的林带视作平面,几何意义与实际相差甚远,因而当林带疏透度相同而林带宽度不同时,其防风效应(及其它效应)并不相同;而透风系数测量较为复杂,特别是林带树木高大时,在野外测量非常困难,使许多研究成果的推广应用产生困难。
本文拟采用林带经营管理中最常用的数据,地上生物量和林带林木(或林带段)的材积(或蓄积)求得最优结构指标的方法,解决这一难题,并可根据林木的生长模型计算结果对农田防护林的规划设计、效益评价和预评价以及经营抚育等进行信息化管理。
1 林带地上生物量与风速削弱系数 1.1 林带地上生物量与林带结构林带的高度、宽度和林木干、枝、叶等地上部分的生物量在空间的分布状况称为林带的结构。设林带地上部分现存生物量为B,树枝部分为B1,树叶部分为B2,树干部分为B3(通常取质量单位),但林业经营管理中常用的数据为材积(取体积单位),而生物量则较少用,但两者有密切关系。实际上材积V0即为B3的体积。令g1Vo为B1的体积,g2V0为B2的体积,若B的体积为V,则有
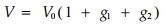
|
(1) |
或V=V0(1+g)。式中g=g1+g2, g1,g2分别为枝、叶的体积与材积V0的比值,其大小和树种、树龄、季节、立地类型、经营方式等有关。据徐文铎等(1998)的调查,东北部分地区小青杨(P. pseudosimonni)g1值在0.17~0.93之间,幼龄林g1值偏大,成熟林约为0.30~0.50,过熟林偏小。g2与季节有关,生长旺季偏大,林带防护期主要在春季和初夏,叶量尚少,所以取值不宜过大。
林分生长空间内,地上生物体积所占比例应是林分结构的重要特征之一。令W表示地上生物量的平均体积密度,即单位空间内的生物量的体积,其因次为〔L3L-3〕,L为长度,于是有
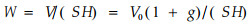
|
(2) |
式中V若代表林带内单株林木的地上生物量总体积,则V0为单株材积,S为单株林木的平均营养面积,H为株高;若令V代表长度为L段林带内的总地上生物量的体积,则V0为该段的蓄积量。S=LD为该段林带的总面积,D为带宽,H为平均高。计算结果表明,杨树林带W值约为10-3~10-4。W可为高度z的函数W(z),对于结构均匀的林带,沿水平方向一般可视为常数。
1.2 林带结构与风速削弱系数林带地上部分,林木的干、枝、叶,大致均匀的分布于所占空间,上部树梢部位偏小,向下接近根际部分由于修枝则更小,气流流过林带时,与干、枝、叶表面摩擦,产生阻力,林带地上生物量的总表面积越大,则气流受到的阻力也越大,因而气流速度减小越多。Кайгородoв(1916)在分析气流通过林带风速减弱的规律时,曾给出一个系数k,称为风速削弱系数。他假设林带水平结构均匀,k(z)只是高度z的函数.气流通过林带宽度Δx时,风速减弱Δu,则Δu的大小应和通过的路径Δx成正比,和风速u的大小成正比,比例系数为k(z),则有
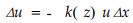
|
(3) |
或写成微分形式,并积分,则有
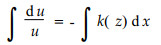
|
(4) |
令x=0时,u=uf, 即向风面林缘的风速;x=D时,u=u,即背风面林缘的风速。积分上式则有:
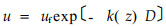
|
(5) |
由上式可以看出k的物理意义应是,气流经过单位距离林带时,由于气流与林带林木的干、枝、叶等表面的摩擦造成的气流动量的减少率。k值不是直接描述林带的物理量,但和林带结构特征直接相关。我们野外曾观测到最大的 k 值为0.16,最小为0.01,一般在0.02~0.08之间。通风结构类型林带枝下高部分的k值偏小,可小于10 -4。
由上面的分析可知k的大小应和林带内的干、枝、叶的表面积密度Cm密切相关,设Cm为单位空间内地上生物量干、枝、叶等的总面积,其因次为〔L2L-3〕。于是可以假定风速削弱系数k随Cm的增大而增大,k应是Cm的函数,即k=f(Cm),k的因次为[L -1 ]。由因次分析法(π定理)可知,k应是Cm的一阶函数。设林带地上生物量表面积密度Cm改变△Cm时,k值改变Δk,观测表明,Δk的大小和ΔCm成正比,和Cm的大小成反比,即与相对值(ΔCm/Cm)成正比, 于是有:
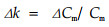
|
写成微分形式:
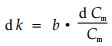
|
(6) |
在生产实践中Cm的数据不易求得,也几乎无法精确测量。假设干、枝、叶表面积密度和其体积密度(W)成正比,即Cm/W=Ra, 并认为比例参数Ra在数值上为一常数,其因次应为[L-1],于是有:Cm=RaW,d Cm=Ra d W,代入上式则有:
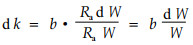
|
(7) |
积分上式则得:
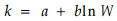
|
(8) |
式中a、b为待定积分常数。风速削弱系数k可用林带结构指标W表示,W为林带地上部分生物量的体积密度。W值大,则表示林带空间的干、枝、叶的分布茂密;W值小则表示林带空间干、枝、叶稀疏。应该指明的是,林带地上生物量的体积密度相同时,枝条的粗细、柔软程度和枝叶表面的粗糙度等也有一定的影响。但这些因素与表面积密度相比,影响较小,为使问题简化,未予考虑。但有些树种,特别是针叶树松、柏等的枝叶表面的特征与所占比重(分散程度)不同于阔叶树种,积分常数a、b会有较大变化。
由上面的分析可以认为林带地上生物量的体积密度W可直接表示林带的结构特征,是真正意义上的林带结构参数。而疏透度β、透风系数α、风速削弱系数k等,和林带的结构有密切的关系,习惯上仍可称为林带的结构参数。
2 林带结构参数之间的关系防护林研究中经常使用的林带参数为疏透度β、透风系数α和风速削弱吸收k,均和林带地上生物体积密度有密切关系,在一定条件下,可以互相换算。
2.1 透风系数α 2.1.1 α的定义透风系数α为林带背风面林缘在林带高度以下的平均风速u(或写成[ū])与未受林带影响的旷野同一高度的平均风速u0(或写成[ū0])之比,即
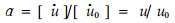
|
(9) |
式中符号[]表示对空间和时间的平均值。可以看出,该参数不能直接表示林带的结构,仅反映林带动力效应的特征。透风系数相同的林带,防风效应(及其它效应)基本相同,林带宽度对防风效应影响不大。观测研究表明,效能最适透风系数为0.32~0.36,即林带具有最大平均防风效能时的透风系数;距离最适透风系数为0.5~0.6,即林带具有最大有效防护距离时的透风系数(朱廷曜等,2001)。α的缺点是测量较为复杂,特别是林带树木高大时,在野外测量很困难。
2.1.2 α与林缘相对风速的关系据式(5)和式(9)可得
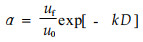
|
(10) |
式中uf为林带向风面林缘的风速。气流由旷野吹向林带时,由于林带阻力的影响,未至林带林缘,气流速度已逐渐降低。至向风面林缘,降到uf。uf降低的多少和林带透风系数有关。风洞实验测得的α和uf的数据列于表 1。α和uf取5个高度,株间取10测点,共50个数据的平均值。uf/u0和α的拟合关系式为:

|
(11) |
|
|
该模式在α特大或趋向零时,可能有较大的误差。为验证其可靠性,选取了Cмaлько(1963)野外的观测结果,利用该书表18中的向风面林缘、背风面林缘及对比点,1、2、5 m 3个高度的风速,计算了各林带(共11条)的 uf、u0 和透风系数α的平均值(表 2)。可以看出,uf/u0的实测值和计算值基本一致,差值很小。应该说明的是Смалвко观测的林带平均高约9 m。观测中他虽然作了系统的安排和精确的测量,但无意测定透风系数和向风面林缘、背风面林缘的风速,致使计算透风系数和uf的测点较少,但模拟结果还是令人满意的。
|
|
将式(11)代入式(10),可得透风系数和风速削弱系数的关系式为
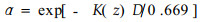
|
(12) |
两边取对数,可得
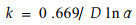
|
(13) |
由风速削弱系数与透风系数的关系式(12)不难看出,α也可以用林带地上生物体积密度W表示为下式:
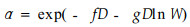
|
(14) |
式中f、g为常数,f=a/0.669,g=b/0.669。D为带宽。a, b为k的拟合常数。
2.2 疏透度β 2.2.1 β的定义β为林带林缘垂直面上透光孔隙的投影面积s与林带投影总面积S之比,以小数或百分数表示,即
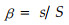
|
(15) |
可以看出,该定义把立体结构的林带视作平面,几何意义与实际相差甚远。因而当林带疏透度相同而林带宽度不同时,其防风效应(及其它效应)并不相同。故不能准确代表林带的结构特性。且野外测量,多用目测,误差很大。近来利用照片和图象数字化分析方法(kenney, 1987;姜凤岐等,1992),精度有明显提高,但也仅能比较宽度相近林带的优劣。如限定宽高比近于1时的林带,最适疏透度约为0.2。
2.2.2 β与透风系数的关系疏透度相同的林带防风效应并不完全相同。但当林带宽度变化不大时,相差不大。根据风洞模拟实验和野外观测结果,统计分析了林带宽高比近于1的林带透风系数和疏透度的关系,拟合模式为: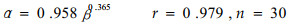
为简便计,且疏透度的观测精度不高,上式取为下列形式:
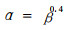
|
(16) |
对于平面模型林带(平板)的实验结果,得出下式:
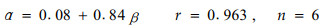
|
(17) |
该式可用于平板式风障透风系数和疏透度的换算,但与实际值的偏差较大。上述α与β关系的观测值与模式曲线详见文献(朱廷曜等,2001)。
3 风速削弱系数的拟合模型 3.1 风速削弱系数的参数拟合由式(8)可知,当测得林带的地上生物体积密度W时,可求得风速削弱系数k。杨树为东北地区农田防护林生态工程的主要树种之一。利用傅梦华等(1992)在辽宁省西部农田防护林地区的观测资料,用二元材积拟合式(李凤日等, 1993)计算了林带段和平均单株林木的材积V0,树种为北京杨(P. beijingensis)、小钻类杂交杨(P. xiaozhuanica)等。考虑到徐文铎等(1998)、李文华等(1981)在东北地区关于小青杨枝、叶与材积的比及与林龄等的关系,以及这些树种在这一地区的生长特性,g值的范围取为0.30~0.45。计算方法为:
(1) 疏透结构类型林带:林木全株地上生物量平均体积密度W为
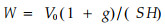
|
(18) |
式中S为林带内单株林木的平均营养面积,H为平均树高,计算结果及式(8)拟合的各系数列于表 3。由表可知疏透结构林带风速削弱系数k的拟合模型为
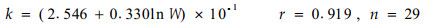
|
(19) |
W值的计算范围为0.492×10-3~3.093×10-3。
(2) 通风结构类型林带:枝下高树干部分的材积为
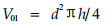
|
(20) |
取g=0, 即无枝叶,地上生物体积密度平均为
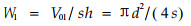
|
(21) |
式中d为胸径,h为枝下高;上部树冠部分的材积为V02=(V0-V01),生物量体积密度平均为:
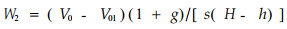
|
(22) |
通风结构类型林带的风速削弱系数亦分为两部分。林下高部位为k1,林冠部位为k2,拟合公式分别为
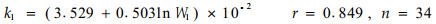
|
(23) |
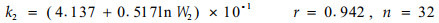
|
(24) |
W1、W2值的计算范围分别为0.832×10-3~5.403×10-3、0.331× 10-3~2.434×10-3,(19)、(23)、(24)式的拟合情况见图 1。
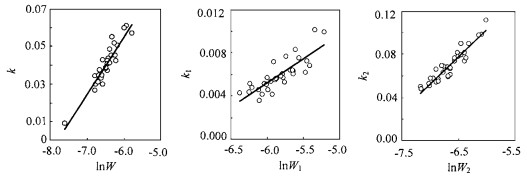
|
图 1 公式19(左)、23(中)、24(右)的拟合图 Fig. 1 Plots of regression of formula 19(left), 23(middle) and 24(right) |
由上述分析可以看出,当测得林带段平均单株林木材积V0或V01,V02,并确定g值后,即可求得地上生物体积密度W或W1,W2。由式(19)或(23)、(24)计算出k,k1,k2。当已知林带宽度D时,根据式(12)可以计算出疏透结构类型林带的平均透风系数α及通风结构类型林带枝下高部位的透风系数α1,林冠部位的平均透风系数α2,则林带的平均透风系数α按加权平均由下式求得:
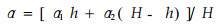
|
(25) |
式中H为平均带高,h平均枝下高。由得到的透风系数与最适透风系数指标比较可以判断林带结构的优劣,并据此确定需采取的抚育措施。
3.2 地上生物体积密度的测算地上生物体积密度可以采取多种方法得到:(1)采用测树学的方法直接测定现有林带的地上生物量(林业部调查规划院,1981),并测定干、枝、叶的比重,换算成体积密度;(2)测定林带树木的高度和胸径,采用一元材积式或二元材积式进行计算(李凤日等, 1993),并测定干、枝、叶的比重,换算成体积密度;(3)在立地类型划分的基础上,用测树学的调查方法获取大量数据,建立主要防护林树种的生长模型,利用生长模型计算地上生物量、材积等。经常采用的生长模型有Richards模型:
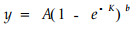
|
(26) |
或Logistic模型
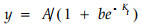
|
(27) |
式中y为t年的生长量,可代表地上生物量B、材积V0、高度H、胸径d等。A为树木生长的渐近最大值,K为与树木生长有关的参数,b为与初值有关的参数。根据上述模型可求得林带任一年的现存地上生物量或蓄积量。进而可求得地上生物体积密度,求出风速削弱系数kt及透风系数αt。故可利用效益评价模型作出农田防护林体系或林带的防护效益评价和预评价。
4 林带结构参数应用举例限于篇幅,本文仅在抚育措施方面举例说明其在生产中的应用方法。
设某地的快杨(P. xiaozhuanica)林带,带宽12 m,株行距1.5 m×2.0 m, 6行,初植成活密度为N0=3 333株·hm-2,现林龄15 a,据蒋伊尹等(1989a)给出林带蓄积量V0(m3·hm-2)的生长模型为
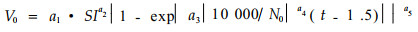
|
(28) |
其中:a1=60.450, a2=1.592, a3=-1.555×10-2, a4=-0.539, a5=1.222, t为年数。蒋伊尹等(1989b)划分标准设地位级指数为SI=15。根据她给出的高生长模型、径生长模型、保留株数模型计算结果为:15年时H=12.990 m,d=0.136 m, 密度N0=1 931株·hm-2。计算每公顷的蓄积量为V0=214.987 m3,单株材积v0=V0/N=0.111 m3。平均单株营养面积为s=5.180 m2, 设调查结果为,枝叶比g=0.40, 修枝高度为h= 3 m,则根据(21)、(22)式计算得到,地上部分枝下高材积密度或生物量体积密度为W1=2.784×10-3,林冠部分的生物量体积密度为W2=1.841×10-3,由式(23)、(24)计算得到的风速削弱系数k1=5.694×10-3,k2=8.837×10 -2。由式(12)计算得到的透风系数分别为α1=0.903, α2=0.205。则该林带平均透风系数为α=3×0.903+0.205×(12.99-3)/12.99=0.366,接近于效能最适透风系数,小于距离最适透风系数。考虑到林带林木正处于生长旺盛期,地上生物体积密度将进一步增大。透风系数将减小,因而决定间伐(伐除部分林木)和疏伐(伐除部分枝条)。
通风结构类型林带枝下高一般为林带平均高的1/4~1/3,林木在迅速长高,故可修枝到4 m。同时4 m以上的枝条也疏伐约12.5%,使g值由0.40降至0.35。则此时,枝下高(4 m以下)透风系数未变,仍为0.90;林冠部的生物量体积密度W2由未疏伐时的1.841×10 -3减至1.554×10-3。风速削弱系数减小为7.962×10-2,透风系数增大到0.24。林带平均透风系数增大到0.44。还可间伐部分林木以使透风系数达到0.50左右。利用式(25)使α1保持不变(0.90),改变α2使两边相等则可粗略的认为α2=0.32时。平均透风系数可增至0. 50左右。利用式(24)可求得此时的林冠部位生物量体积密度W2=1.138×10-3,须减小约27%(1.138/1.554=0.732),则可确定间伐强度为27%。即1 931株·hm-2, 应伐除521株·hm-2, 保留1 410株·hm-2。计算结果表明,间伐后的平均透风系数为0.51。若不疏伐侧枝,g保持为0.40,则平均透风系数为0.50。
根据上述分析可知,k值取决于地上生物体积密度及干、枝、叶表面积的大小和分散程度。虽然根据杨树测算得到的计算模型,也应适用于结构类似的其它阔叶树种林带,但当地上生物体积密度相同时,表面积的差异会使k值有较大差异,此外,有叶期和无叶期,阔叶树和针叶树等也可能引起误差。本文仅提供一种新的林带结构参数和应用方法,在今后实践中尚须进一步完善。
曹新孙, 朱廷曜, 姜凤岐, 等. 1983. 农田防护林学. 北京: 中国林业出版社.
|
傅抱璞. 1963. 论林带结构与防风效能. 南京大学学报(气象学), (1-2): 109-120. |
傅梦华, 姜凤岐, 杨瑞英. 1992. 杨树林带疏透度的研究及其在林带结构控制中的应用, 林带经营技术与理论基础. 北京: 中国林业出版社, 102-108.
|
姜凤岐, 徐吉炎, 傅梦华, 等. 1992. 林带经营技术与理论基础. 北京: 中国林业出版社, 54-57.
|
蒋伊尹, 李凤日, 李长胜, 等. 1989a. 防护林杨树生长的研究. 哈尔滨: 东北林业大学出版社, 59-70.
|
蒋伊尹, 李凤日, 李长胜, 等. 1989b. 杨树防护林地位指数表的编制. 哈尔滨: 东北林业大学出版社, 80-87.
|
蒋伊尹, 蒋伊尹, 刘志宏, 等. 1989b. 农田防护林杨树主要林业数表的编制研究(一元、二元立体材积表). 哈尔滨: 东北林业大学出版社, 45-57.
|
蒋伊尹, 蒋伊尹, 刘志宏, 等. 1989b. 农田防护林杨树主要林业数表的编制研究(一元、二元立体材积表). 哈尔滨: 东北林业大学出版社, 80-87.
|
李文华, 邓坤枚. 1981. 长白山主要生态系统生物生产量的研究. 森林生态系统研究, 2: 34-50. |
林业部调查规划院. 1981. 森林调查手册. 北京: 中国林业出版社.
|
玛恰金 N. 1956. 农田防护林和小气候. 北京: 科学出版社.
|
徐文铎, 邹春静. 1998. 中国沙地森林生态系统. 北京: 中国林业出版社, 274-275.
|
朱廷曜, 关德新, 周广胜, 等. 2001. 农田防护林生态工程学. 北京: 中国林业出版社, 88-89,93-96.
|
Caborn J M. 1957. Shelterbelts and microclimate. Bull For Comm Bull No.29, Edinburgh. |
Van Eimern J, Karschon R Razumova L A. 1964. Windbreaks and shelterbelts, WMO Technical note No.59, Geneva. Switzerland. |
Jensen M J. 1961. Shelter effect investigation into the aerodynamics of shelter and its effects on climate and crops. Copenhagen:Danish Technical Press. |
Kenney W A. 1987. A method for estimating windbreak porosity using digitized photographic silhouettes. Agirc For Meteorol, 39(1): 91-94. |
Cмaлько ЯА. ветрозащитные особенности лесных полос разных конструкчий, госселхо-издат усср, киев.1963
|
Юдин М И. 1950. Вхлияние пoлоса турбулетный оδмен И Оптимальная ширина доклады АН СССР Т. 71, (4): 655-658. |
 2004, Vol. 40
2004, Vol. 40



