随着全球范围内优质大径级原木日益减少，建筑用锯材和胶合板产量呈逐年下降趋势，而市场对人造板的需求却在不断增加，非单板类木质人造板(定向刨花板、普通刨花板和中密度纤维板)将是未来人造板领域的主力军。目前，定向刨花板和结构刨花板已在很大程度上替代结构胶合板用于房屋建筑。人造板性能与许多因素有关，其中密度是决定其物理和机械性能最主要的因素之一。由于木材原料本身的密度差异、产品结构特点以及热压工艺的不同，造成了板材内部存在一定的密度差异(density variation)，这种密度差异既存在于板材厚度方向，也存在于板面方向，密度差异的存在必将对产品性能产生影响。多年来，各国科学家对厚度方向上的端面密度分布(vertical density profile)一直非常关注，并进行了较系统深入的研究(Kelly, 1977; Wolcott et al., 1990)；但对于板面方向的平面密度分布(horizontal density distribution)却没有引起人们足够的重视，目前仅有少数科学家在此领域进行了一些研究(Suchsland et al., 1989; Dai et al., 1994a；1994b; Xu et al., 1995a；1995b)。本研究将对平面密度分布与板材性能的关系，特别是平面密度分布对内接合强度和尺寸稳定性的影响进行探讨。

1 平面密度分布模型

刨花板平面密度分布最早由Suchsland(1959)提出。他将刨花板简化成由相互不连续的刨花层组成的理想化结构，并且每层中刨花与刨花之间存有一定空隙。在此假设的基础上，Suchsland设计出了第一个用来研究刨花板平面密度分布的模型，该模型由多层单板组成，每张单板预先打上数目相同的孔，单板上孔的位置是随机分布的。在这个模型中，板面内任一小面积上单板重叠数(overlap)的分布(亦即压制成板材后的平面密度分布)，服从二项式分布：

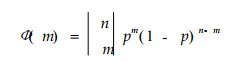
其中：Ф(m)为小面积上单板重叠数为m的概率；m为单板重叠数(密度)；n为总单板层数；p为每层内木材相对体积(%)。

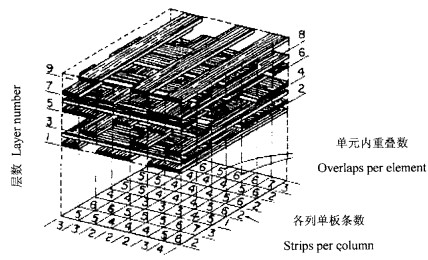
Dai和Steiner(1994a；1994b)应用二维随机场理论建立了计算机模型来预测随机铺装的刨花板坯内平面密度的分布情况。他们认为在随机铺装板坯内的任一点上刨花重叠的概率服从泊松分布，已知刨花的平均长度、宽度、刨花总数以及各层总面积就可以预测出板坯的结构特性，包括平面密度分布情况。Suchsland和Xu(1989;1991)又开发出了用单板条(veneer strip)来模拟刨花板平面密度分布的模型。该模型是由若干层组成的正方形板坯(图 1)，每层又由数根相互平行的单板条组成。每层板坯就如同N×N的格子方阵，单板条的宽度与方阵中格子的宽度一致，其长度与板坯长度相等。每层中单板条数X由计算机随机产生(1≤X≤N)，并由计算机随机安排每一根单板条在该层内的摆放位置，相邻两层之间单板条纹理互相垂直，这样一来最后形成的板坯各个单元格之间单板条重叠数就存在一定的差异，这种差异在板坯压制成板材之后会被保留下来，从而形成了刨花板的平面密度偏差(horizontal density variation)。该模型的优点在于利用计算机技术，试验者可以预知板材各处的密度，并可人为控制密度差异的大小，具有试验和测试上的方便性。本研究在该模型的基础上进行了部分改进，固定每层的单板条数，使试验操作更加方便。

2 材料与方法 2.1 材料

采用加拿大产美洲山杨(Populus tremuloides)为原料，气干密度约0.45 g·cm^-3。将杨木段首先旋切成0.8 mm厚的单板，室温下自然干燥至含水率10%左右，锯割成宽度25 mm、长度700 mm的单板条，烘干至含水率2.5%。采用4辊筒涂胶机对单板条进行双面精确涂胶，胶种为OSB生产用液态酚醛树脂胶，固体含量57%，施胶量5%(固体胶量与单板条绝干重量比)。涂胶后的单板条手工逐条逐层铺装成板坯。

2.2 制板方法

采用的板坯幅面尺寸为700 mm×700 mm，可视为28行×28列的矩阵(25×28=700)。每层共可不重叠摆放28根单板条(28个摆放位置)。为获得不均匀的密度分布，本试验中每一层仅放入18根单板条，每根单板条的位置由计算机在28个位置中随机产生，相邻两层单板条相互垂直摆放，铺装后的板坯共由784个25 mm×25 mm小单元组成，待热压成板材之后，各小单元的密度决定于其中单板的重叠数。铺装后的板坯放入由计算机精确控制的压机中进行热压，热压条件为：闭合时间40 s、温度210℃、热压时间240 s。热压过程中采用厚度程序控制，板子名义厚度11 mm。为了得到需要的重叠数，试验中采用4种名义密度(表 1)，每种密度重复3次，共压制700 mm×700 mm×11 mm试验板材12块。热压后的板材统一放入相对湿度65%和温度20℃的恒温恒湿箱中平衡至含水率12%。

2.3 测试方法

根据计算机产生的板坯模型确定并标出试验板上对应单元格的重叠数。就每一个单元格(25 mm×25 mm)来说，其重叠数各处是一样的，亦即单元内不存在平面密度差异，在研究密度与对内结合强度(IB)的影响时，以一个单元格作为试件大小，每块试验板上所有不同重叠数的单元各锯取3块进行IB性能测试。在研究不同密度分布对IB的影响时，除25 mm×25 mm的试件以外，还采用了包含4个单元(50 mm×50 mm)和9个单元(75 mm×75 mm)的试件尺寸。IB测试按1997年美国ASTM标准在4202型INSTRON万能力学试验机上进行，加载速度5.3 mm·min^-1。

3 结果与讨论 3.1 平面密度分布

板平面内密度变异性是非单板类木质人造板(刨花板、纤维板)生产中不可避免的固有现象(Suchsland，1962；Dai et al., 1994a)，其密度变异程度(即平面密度分布)主要决定于原料单元尺寸和板坯成型工艺。研究表明，铺装方式对板坯的三维结构起着至关重要的作用，单元(刨花或纤维)在铺装机内下落时自由度或随机性越大，铺装后的板坯结构均匀性越好，反之越差，一般来讲，定向刨花板的平面密度变异大于普通刨花板；构成单元的大小和几何形状对板平面密度变异亦有明显影响，单元越小，板坯结构均匀性越好，通常纤维板的均匀性优于普通刨花板和定向刨花板。

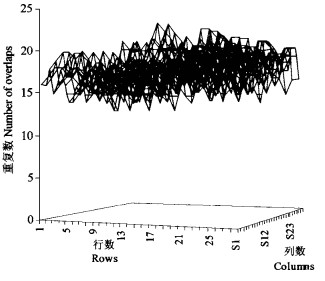
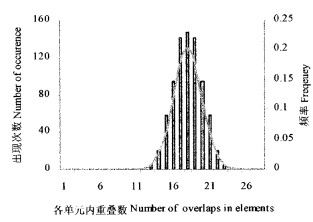
本试验基于随机铺装理论，利用计算机模型，以单板条代替大片刨花，构造出具有一定密度变异的板坯，旨在研究刨花板平面密度分布规律及其对板子性能的影响。图 2为29层(板名义密度0.60 g·cm^-3，标准偏差1.95)的板坯模型，显示出了各单元重叠数在板坯平面内的分布情况。重叠数代表单元格内所含木片的层数，待板坯被压制成厚度均匀的板材以后，重叠数越大的地方，最终密度将越高，故重叠数大小决定了热压后板子该处密度(local density)的高低。从图中可以看出板坯中各单元格重叠数分布具有明显的不均匀性，这种不均匀性是造成刨花板平面密度变异的根本原因。同时也观察到不同的重叠数在板坯内分布是随机的，统计分析表明，各重叠数出现的频率具有一定的规律性，出现频率较高的重叠数集中在所有单元重叠数的平均值附近，如图 3(平均密度0.60g·cm^-3)中柱状图所示。对比根据其均值(average overlap)和标准差(standard deviation)拟合出的正态分布曲线看出，重叠数在板坯中的分布遵循正态分布规律。板坯模型中，重叠数的均值和标准差是两个关键指标，其中均值反映了最终板材的平均密度，而标准差则体现了板坯结构均匀性的优劣，亦是板材平面密度变异程度的表征。试验中还可以通过计算机程序方便地调整标准差的大小，从而获得平均密度相同而密度分布不同的板材。

3.2 平面密度分布对内结合强度(IB)的影响 3.2.1 密度与内结合强度

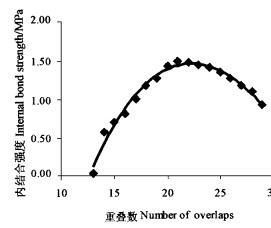
如前所述，密度与板材的物理力学性能密切相关，而内结合强度(IB)是衡量非单板类木质人造板性能的一个重要指标。在使用相同胶粘剂和施胶量的情况下，板材密度是决定IB大小的关键因素。由于密度变异的存在，故刨花板各处的IB也将有所差异。一般认为，密度的增加有助于提高板材的内结合强度，但是本研究表明，IB并非随密度的增加而线性增加。如图 4(试件尺寸25 mm×25 mm)所示，在低密度区，IB随密度的增加而迅速提高，在某个密度值(本试验中该值出现在第22个重叠数处，相当于0.72 g·cm^-3)IB达到最高值，然后随密度的增加IB反而呈下降趋势。可见，超过某一临界值后，密度的增加反而给内结合强度带来负面影响。刨花之间的胶合一方面取决于刨花表面胶粘剂的分布情况，另一方面又依赖于刨花表面之间相互接触的紧密程度。热压时，由于板坯结构不均匀性，导致板坯上压力分布不均，使得各处木材压缩率不等。重叠数高处承受了绝大部分的压力，压缩率高；而重叠数低处可能只有很小的压力，压缩率小。增加压力，有利于提高刨花之间的接触和刨花表面胶粘剂的流展和相互转移，从而有助于IB的提高，同时由于压缩率增加，单元密度亦随之增加；当压力增加到一定值时，刨花之间的接触达到最佳，IB也到达了最高点；压力进一步增加，刨花之间接触已不会改善，相反地，过高的压力将导致木材破坏(细胞壁压溃)和内应力增加，导致了IB减小。从IB试件的破坏形式也可以明显看出，重叠数较小的试件多表现为胶接面破坏，而重叠数较大的试件则多表现为木材破坏。

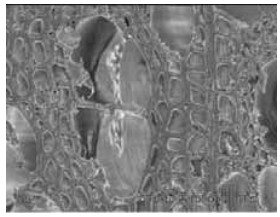
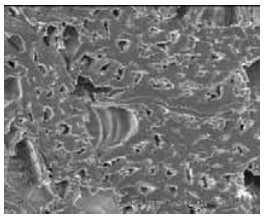
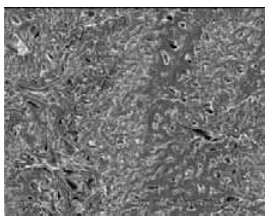
图 5~7分别为常温下径向压缩5%、25%和60%后加拿大杨木细胞结构的扫描电子显微镜图片(放大倍数500×)。比较压缩率不同的细胞结构发现，随着压缩率的提高，木材细胞壁断裂明显增多。勿庸置疑，细胞壁的破坏将导致木材横向抗拉强度下降，从而使IB降低。

综上所述，一定范围内增加密度，有助于内结合强度的提高，但密度过大则会对IB不利。生产中应从板坯结构着手，尽量提高板坯均匀性，既有利于材料性能的稳定，又可以节省原料，减小压机负荷，对降低生产成本有着积极的意义。

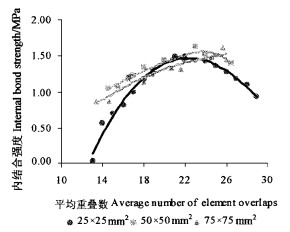
3.2.2 平面密度分布与内结合强度

为了探明平面密度分布对内结合强度的影响，试验中选择了分别包含一个单元(25 mm×25 mm)、4个单元(50 mm×50 mm)和9个单元(75 mm×75 mm)3种不同尺寸的试件进行IB测试，结果见图 8(横坐标50 mm×50 mm和75×75 mm试件的重叠数为其所含各单元重叠数的平均值)。不同尺寸的试件有着不同的密度分布，一个单元试件中不存在密度差异，而对于含有多个单元的试件，由于各单元重叠数不尽相同，密度不再是均匀分布，一定程度上其密度差异随试件尺寸的增加而增加。研究发现，具有不同密度分布的3种试件，内结合强度随密度的变化有着相似的规律性，但随着试件尺寸的增大，IB最高点向高密度区偏移。在低密度区，50 mm×50 mm和75 mm×75 mm试件的IB明显高于25 mm×25 mm试件的IB，研究认为密度偏差是造成这种现象的根本原因。内部具有密度差异的试件，各点IB有高有低，而整体试件的IB则取决于试件中IB较高的单元及其在试件中所占的比例。由此看来，对于低密度刨花板来讲，在标准范围内适当增加密度偏差，有利于提高内结合强度；而对于中高密度刨花板应尽量减少密度变异。

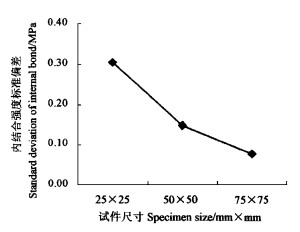
板密度分布还与其IB偏差(standard deviation)有关。理论上，若板内密度均匀分布，则IB应处处相等，不存在IB偏差问题。对于非单板类木质人造板来说，板内密度变异是一种不可避免的现象，所以IB偏差也就成为必然，但IB偏差又与被测试件大小有关。试验表明，随着试件尺寸的增加，IB偏差呈下降趋势(图 9)。说明试件尺寸增加，减小了试件之间(between-specimen)的密度偏差。Xu等(1995a; 1995b)对商业华夫板(wafer board)的研究亦证明了这一点。因此，在板材内接合强度性能测试时，应考虑选择合适的试件尺寸。

4 结论

非单板类木质人造板存在平面密度变异，计算机板坯模型研究证明随机铺装的刨花板，板坯内平面密度遵循正态分布规律；板材各处IB受其密度影响较大，增加密度(压缩率)有助于IB的提高，但密度过高将对IB不利；平面密度变异影响IB均匀性，适当增加试件尺寸，可以减小试件之间的密度差异，从而降低IB测试结果的离散性。