国内农业部门在肥料效应试验研究方面，已经取得了长足的进步和显著的进展(丁希泉，1986；张宽等，1990；王兴仁等，1996；马卫萍等，2002)，所得结果已在我国肥料计量中发挥了巨大的作用，尤其是近年来计算机技术的进步，更是推动了这一技术的发展。相比农业，在林业上利用肥料效应函数的试验研究很少。对竹林施肥，以提高产量的研究虽有众多报道(洪顺山等，1992；陈金林等，1996；吴立潮等，1997；邱立龙等，1998；黄当亮，1998；严伍明等，1998)，但共同的缺陷是所得结果都属定性描述，无法从整体上把握施肥量和肥料配比对竹林产量的影响。为使竹林施肥能从定性转为定量描述，顾小平等(1998)研究了毛竹纸浆竹林施用氮磷钾肥料效应。试验建立的施肥模型以及由此决策出的最佳施肥方案和肥料配比与传统的推荐施肥存在较大的出入；采用的三因素二次通用旋转组合设计也没能安排林分结构因子，对毛竹林丰产技术措施的整体把握尚欠缺。为此，本文在前期施肥试验结果的基础上，补充考虑了密度因子对产量的影响，重新选择试验林地，采用四因素二次回归最优设计，建立氮磷钾施肥及留竹密度与毛竹林产量间的回归模型，用以验证先期建立的肥料效应函数，同时也为生产上指导毛竹林的丰产培育提供规范的数量化依据。

1 材料与方法 1.1 林分状况

试验林分选择在江西省宜丰县云峰尖国营林场，东经114°50′，北纬28°30′，属毛竹林分布的中心产区。年平均降雨量1 560 mm，年均温17.1℃，环境气候条件与先期福建邵武的试验林分相仿(顾小平等，1998)。林分为大小年分明的毛竹纯林结构，逢单数年为出笋大年，全梢竹。1995年冬季已进行过全面垦复。林地除立竹较稀，林下长有杂草及小灌木外，与先期在福建的试验将竹木混交林改制成毛竹纯林相比，没有大量的枯落物和杂灌。施肥前采土样分析土壤基础肥力情况见表 1。

1.2 试验设计

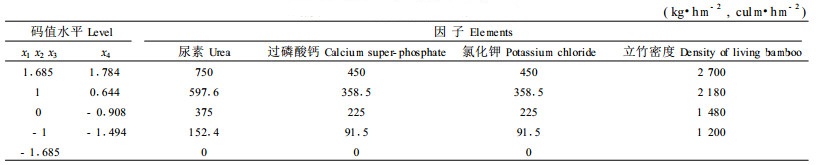
采用氮(x₁)、磷(x₂)、钾(x₃)、立竹密度(x₄)四因素二次回归最优混合设计，编码及设计水平见表 2。

试验小区N=16，每小区500 m²，随机排列于相对均等的一面山坡上，四周设立5 m以上的缓冲带，用以隔离各小区，加上重复1次，合计设立标地32块。依据对基础数据的调查，在1997年毛竹林大年的冬季采伐作业时，各试验小区按设计要求，调整立竹密度，定株采伐。原计划设计立竹密度水平为1 600~3 000株·hm^-2，但因林场在砍伐设计作业时，对个别地块增加了伐竹量，所以只好在翌年的小年6月份，竹林换叶期(施肥前)对原标地的立竹留养密度作了重新调整。毛竹林分平均胸径为10.2 cm。

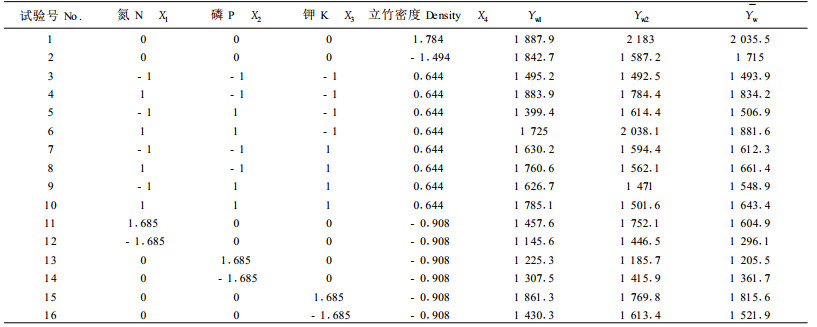
供试肥料为俄罗斯产的尿素(含N量460 g·kg^-1)，湖南永和的过磷酸钙(含P₂O₅120 g·kg^-1)，加拿大产的氯化钾(含K₂O 600 g·kg^-1)。于1998年毛竹林小年的9月份各试验小区按设计的施肥水平，林地开沟一次施入了全部肥料。试验结构矩阵见表 3。为防止挖笋、伐竹等人为因子对数据的干扰或破坏，与先期的试验一样(顾小平等，1998)，林地派人重点管护，出笋大年禁挖春笋(包括自然退笋)。1999年调查成竹情况。新竹产量的计算，仍按福建省地方标准(FDBT/LY29-90)编制的毛竹材重量公式计算。新竹产量指的是商品竹材产量，非毛竹地上部的生物产量，列于表 3的Y_w1和Y_w2列。

2 结果与讨论 2.1 新竹产量函数模型的建立

试验结果如表 3所示。用四因素二次回归最优设计的结构矩阵，以x₁、x₂、x₃和x₄为决策变量，施肥毛竹林新竹产量(Y)为目标函数，求出试验产量的回归方程为：

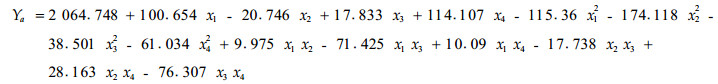
(1)

对回归方程进行方差分析，得回归均方F_回=3.813 7 > F_0.01=3.53，表明回归方程达极显著水平，复相关系数R=0.995 1，试验所建立的二次方程与氮、磷、钾肥及留养立竹密度间拟合很好，四因素对新竹产量之间的密切程度达到了极显著水平。对上述方程的回归系数进行t测验，b₁、b₄达到了显著水平，其余的不显著，表明施用氮肥和改变立竹留养密度是影响新竹产量的主导因素.

若以肥料价格：尿素P_x1=2元·kg^-1、过磷酸钙P_x2=0.5元·kg^-1、氯化钾P_x3=1.5元·kg^-1，竹材价格P_y=0.4元·kg^-1计，则相应的经济效益(Y_b)=产值(Y_a×P_y)-可变投入(P_x1×Z₁+P_x2× Z₂+P_x3×Z₃)。Z_i为各自施肥用量。同样，用四因素二次回归最优设计的结构矩阵，以x₁、x₂、x₃和x₄为决策变量，施肥毛竹林新竹产值(Y_b)为目标函数，可求得经济效益回归方程为：

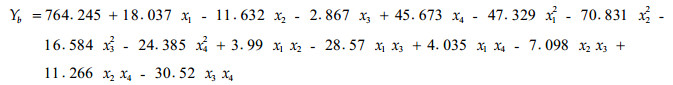
(2)

回归均方F_回=752.1 > F_0.01=3.53，达极显著水平, 复相关系数R=0.970 1，说明上述两方程可分别用于竹林产量和经济效益预测。

2.2 模型的极值判别

农业上的大量田间试验结果表明，由于受土壤肥力变异等多种因素的干扰，当试验因素增多时，往往得不到理想的、符合报酬递减律的凸形效应曲面方程(概率不足60%)，如果对凹形和鞍形效应曲面回归方程，利用边际分析方法求解最佳施肥量，就会得到肥料利润最小或中等利润的施肥建议，从而产生误导。因此，在做边际分析之前，必需先对回归方程进行极值判别。

对新竹产量方程Y_a进行极值判别，得回归式第奇数阶主子行列式均小于零，而偶数阶主子行列式均大于零，表明驻点为极大值，符合报酬递减律的凸形效应曲面方程，可用于模型的优化与解析。同样，对效益回归方程Y_b进行极值判别，得方程(2)驻点也为极大值，可用于边际分析。

2.3 边际分析与寻优 2.3.1 产量模型的最优解

最高产量必须是回归方程的极点，每一自变量的边际产量等于0。因此，对方程(1)求导。依据克莱姆法则，求得最大施肥量和最佳留养立竹密度的编码值为：x₁=0.512 6;x₂=0.057 9;x₃=-0.257;x₄=0.941 4。相对应的实际最大施肥量和立竹留养密度分别是：尿素=489 kg·hm^-2；过磷酸钙=233 kg·hm^-2；氯化钾=190.7 kg·hm^-2；立竹密度=2 316株·hm^-2。N:P₂O₅:K₂O=1:0.124:0.509。

将x₁ x₂ x₃ x₄代入式(1)得竹材最高产量Y_{a max}= 43.2 t·hm^-2。

2.3.2 经济最佳施肥量

产量的最大值并非经济效益的最优解。施肥利润受生产函数的投入和价格比控制，当边际产量等于投入与价格比值时施肥利润最大，此时的施肥量称经济最佳施肥量。

与求解产量最大值的方法类同，依据克莱姆法则，求得经济效益的最优解为：x₁=0.289；x₂=-0.111 6；x₃=-0.340 4；x₄=0.934 7。相对应的最大施肥量和立竹密度分别是：尿素=439.4 kg·hm^-2，过磷酸钙=209.6 kg·hm^-2；氯化钾=179.6 kg·hm^-2；立竹密度=2 320株·hm^-2。N:P₂O₅:K₂O=1:0.124:0.533。

将x₁ x₂ x₃ x₄代入式(2)得竹材(不包括笋、枝稍)最高经济效益Y_{b max}=15 966.5元·hm^-2。

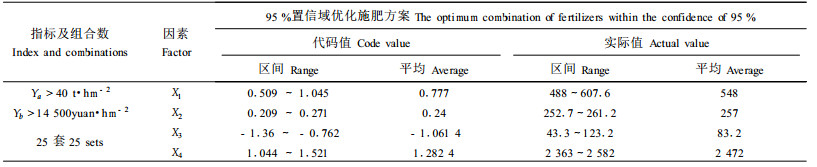
2.3.3 高产高效施肥优化方案

本次试验采用的四因素二次回归最优设计，在试验设计水平范围内共有500套组合方案。兼顾高产与高效同步增长的目标，采用产量和效益两目标函数的双频分析，从500套方案中，筛选出新竹产量 > 40 t·hm^-2，竹材经济效益 > 14 500元·hm^-2的优化组合方案25套，利用步长法，经频数分析得数据的编码平均值, 结果见表 4。由表 4可知，取95%置信域，毛竹林优化施肥方案是：尿素488~607.6 kg·hm^-2，平均548 kg·hm^-2；过磷酸钙252.7~261.2 kg·hm^-2，平均257 kg·hm^-2；氯化钾43.3~123.2 kg·hm^-2，平均83.2 kg·hm^-2。优化的立竹留养密度是：2 363~2 582株·hm^-2，平均2 472株·hm^-2。

2.4 各试验因素对产量的效应 2.4.1 各因素的独立效应

将回归式(1)的3个自变量分别固定在一定水平上，可得到另一变量的偏子回归解析模式。分别取3个施肥变量的编码下限水平-1.683(不施肥)，立竹密度的上限水平1.784(2 700株·hm^-2是普通推荐的立竹留养密度)时，得各施肥试验因子和立竹密度对新竹产量影响的单因子试验独立效应降维函数如下，见表 5。

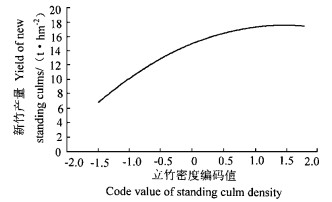
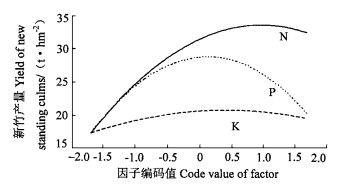
从表 5看出，试验因素对产量影响的独立效应大小顺序为x₄ > x₁ > x₂ > x₃。留养立竹密度过稀是限制新竹产量的主导因素。在立竹密度从1 200~2 700株·hm^-2的试验区段内，随立竹密度的增加，即便不施肥，新竹产量也有较大幅度增加(图 1)。当然，要想取得较高的新竹产量，尚需配合施用肥料。在氮、磷、钾中，以施用氮肥，增产作用最明显。另外，各施肥因子对产量的独立效应均呈二次抛物线形(图 2)，符合肥料“报酬递减律”，即毛竹林肥料的投入量有一定的限度，过量投入会导致肥料效益下降以致减产的后果。图 2清楚地显示了氮、磷、钾肥料各自对产量的影响。施用氮肥的增产幅度最大，磷肥次之，钾肥较为平缓。施用氮肥增产的最大值出现在1水平附近(施尿素550 kg·hm^-2)；而磷钾肥的增产最大值在0水平附近(施过磷酸钙、氯化钾225 kg·hm^-2)。施肥超过了这一最大值，新竹产量的下降也非常明显。

2.4.2 各试验因素的综合效应

以上分析的独立效应大小反映的是各试验因子在单独使用时对新竹产量的影响。要了解在综合因子作用下某因素的回归贡献，评价各因素的相对重要性，可以将各试验因素按贡献率大小排序。对线性模型，因素的重要性可用通径分析等方法判断，但对多元二次非线性模型，就不能只从线性化方程的某一项评价各因素的相对重要性，需要将因素的一次项、二次项和交互作用项综合加以考虑。

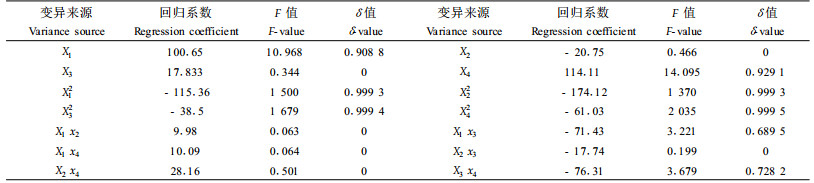
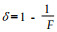
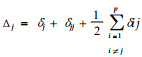
根据徐中儒的贡献率法，将二次回归方程式(1)的各项偏回归系数方差比按下式计算因素贡献列于表 6。然后，根据F≤1，δ=0；F > 1，，求得第j个因素的贡献率。因为贡献率，Δ₄ > Δ₁ > Δ₃ > Δ₂，所以，试验各因子对产量影响大小的顺序是：x₄ > x₁ > x₃ > x₂。与独立效应分析结果基本相同，只是磷、钾肥的重要性在独立效应分析和贡献率分析中不一致，其原因主要在于磷肥在单独施用时，虽然对新竹产量的影响比钾肥单独施用时要大，但由于施用钾肥与氮肥及立竹密度间都存在交互效应，所以从肥料配合后的各因子对产量的贡献来看，钾肥的重要性要大于磷肥。

2.5 不同立竹密度条件下的施肥优化方案

每次固定立竹留养密度因子(X₄)在不同的水平上对各施肥因素在-1.685 ~1.685的区间内进行回归模拟，可得到在不同立竹密度下的125套组合方案。对各自的125套方案中，新竹产量 > 30 t·hm^-2的组合方案进行频数分析，得不同留养立竹密度条件下的优化施肥方案(表 7)。从表中可以看出，在不同留养密度条件下，通过施肥，竹林取得高产(新竹产量 > 30 t·hm^-2)的组合方案数以在留养2 180株·hm^-2的水平下最多，有82套，占全部125套的65.6%；其次是在留养2 700株·hm^-2的水平，有72套，占全部125套的57.6%。这一结果与产量最优解得到的立竹密度2 320株·hm^-2大体吻合。

3 小结

采用四因素二次回归最优设计建立了毛竹材用林新竹产量与氮、磷、钾肥施用量及留养立竹密度间的回归模型：γ_a=2 064.748+100.654 x₁-20.746 x₂+17.833 x₃+114.107 x₄-115.36 x₁²-174.118 x₂²-38.501 x₃²-61.034 x₄²+9.975 x₁x₂-71.425 x₁x₃+10.09 x₁x₄-17.738 x₂x₃+28.163 x₂x₄-76.307 x₃x₄，同时，根据投入、产出价格建立了毛竹林施肥和留养立竹的经济效益方程：γ_b=764.245+18.037 x₁-11.632 x₂-2.867 x₃+45.673 x₄-47.329 x₁²-70.831 x₂²-16.584 x₃²-24.385 x₄²+3.99 x₁x₂-28.57 x₁x₃+4.035 x₁x₄-7.098 x₂x₃+11.266 x₂x₄-30.52 x₃x₄。

上述产量、效益回归模型经函数极值判别为典型效应方程，有极大值。进一步采用边际分析方法，求得产量模型的最优解为x₁=0.512 5；x₂=0.057 9；x₃=-0.257 0；x₄=0.941 4。相对应的最大施肥量和立竹密度分别是：尿素=489 kg·hm^-2；过磷酸钙=233 kg·hm^-2；氯化钾=191kg·hm^-2；立竹密度=2 316株·hm^-2。N:P₂O₅:K₂O=1:0.124:0.509。可得新竹最高产量Y_{a max}=43.2 t·hm^-2。此优化的施肥方案与顾小平等(1998)结果非常吻合，但与以往一些学者(吴立潮等，1997；洪顺山等，1992)推荐的氮磷钾肥料三要素配比为1:0.6:0.4和1:0.5:1的结论不甚一致。

求得效应模型的最优解x₁=0.289；x₂=-0.111 57；x₃=-0.340 4；x₄=0.934 7。相对应的最大施肥量和立竹密度：尿素=439.4 kg·hm^-2；过磷酸钙=209.6 kg·hm^-2；氯化钾=179.6 kg·hm^-2；立竹密度=2 320株·hm^-2。N:P₂O₅:K₂O=1:0.124:0.533。得竹材的最高经济效益Y_{b max}=15 966.5元·hm^-2。兼顾高产与高效同步增长的目标，采用产量和效益两目标函数的双频分析，得到95%置信域的毛竹林优化施肥方案是：尿素488~607.6 kg·hm^-2，平均548 kg·hm^-2；过磷酸钙252.7~261.2 kg·hm^-2，平均257 kg·hm^-2；氯化钾43.3~123.2 kg·hm^-2，平均83.2 kg·hm^-2，优化的立竹留养密度：2 363~2 582株·hm^-2，平均2 472株·hm^-2。

根据对参试各因素独立效应的分析，增加立竹的留养密度是提高毛竹林产量的主导因子，其次为增施氮肥；将各因子对产量的贡献率排序得x₄ > x₁ > x₃ > x₂。这一结果也与上次在毛竹纸浆林所得的氮磷钾的贡献率排序完全相同，与一些学者(张献义等，1995)提出的毛竹林应以增施磷肥为主的结果相背。

本次试验得到的在不同密度条件下的优化施肥配比方案，扩大了对试验点周边地区相同立地条件的不同密度毛竹林分的施肥指导。