森林可持续经营的理念发展200年了(Gadow et al. 2000)。一个好的森林经营计划，应能准确地描述未来的森林经营活动，同时预测出在其影响下预期生长。过去主要依靠林分生长表来推测森林生长，近年发展出各种新方法，其中线性规划就是应用最多的方法。在森林经营的基本单位(如林分)允许分割时，即在一个林分里可能同时采用几种经营措施时，线性规划可以提供最优解决，它特别能满足可持续经营“稳定产出”(even flow)的要求。如果一个包含成百上千个林分的大面积经营范围内，要求实现可持续经营并要求每个林分只能采用一种方案时，线性规划就往往显得无力了，0-1规划也比较困难(Wu et al. 2000)。

模拟退火和遗传算法这两种随机搜索方法可以很好地解决这类问题(Kirkpatrick et al. 1983)。本文以杉木(Cunninghamia lanceolata)人工林为例，介绍一个通用的森林可持续经营计划模型，用线性规划、模拟退火和遗传算法来求解，并对三者进行比较。

1 线性规划、模拟退火和遗传算法的原理简介 1.1 线性规划

线性规划的单纯型法求解，已有很多的文献介绍(Zionts，1974；Garca，1990；Lappi，1992)，本文不再赘述。

1.2 模拟退火

模拟退火是模拟热力学的降温过程。高温时，物质内部分子(或原子)高速随机运动，呈气体状态。随着温度的逐渐降低，能量的损失使分子运动速度降低，形成液态。当温度继续降低时，随机运动分子间会逐渐排列成有规则的晶体。晶体是能量最低的状态，只要温度的降低过程足够平稳，随机运动的分子就会逐渐排列成为整齐的晶体。分子间从无序的高能量进入有序的低能量状态，就是一个自然的优化过程(Press et al., 1992；Vidal，1993)。优化是不断地对不同目标方程值进行比较的过程，对于上述热力学的退火过程来说, 目标方程值就是内部分子的排列状态，用能量来衡量。

分子间的排列状态，既有从无序到有序的过程，也有从有序到无序的过程，随着温度的逐渐降低，后者出现的概率就越来越小。这个概率可以用Metropolis概率来描述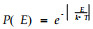：。式中，E表示能量的差值绝对值，T表示温度，k是Boltzmann常数，通常是正整数。

用模拟退火的方法来解决多林分的森林经营决策问题时，可以把每个林分看成是一个分子，所有林分各种可能的经营措施组合就是物质的不同能量状态。森林由多个林分组成，其目标方程值就相当于热力学中的能量值。通常，森林可持续经营追求的是目标方程的最大值，如木材产量或价值等，同时，森林可持续经营还要求木材等产品的产出呈稳定状态，如在一定的年限里每年的木材产量是一个常量，或者按一定的增长率增加，这些要求可用约束条件表示。模拟退火实际上就是在一个林分组合初始状态下，对现有的林分组合产生一个变化，即随机选择的一个林分的经营措施发生了变化，而其它林分保持不变，计算两者目标方程值。若新的变化使目标方程值提高了，就保留新的变化；如果目标方程值没有提高，则计算Metropolis概率，将Metropolis概率与随机产生的概率进行比较，若Metropolis概率更大就也保留新方案，反之则放弃新方案。重复这个步骤，直到目标方程值收敛到满意程度。模拟退火的过程可以用下列伪代码表示：

其中，T为温度，其初始值通常为100；r为温度下降系数，通常为0.9；L为迭代次数；E₀初始状态的能量；E_i为新状态的能量。能量在实际森林经营决策问题中通常为目标方程值。

以一定的概率接受目标方程值更差的新组合，目的是为了避免局部最优值，获得全局最优值。如果每次迭代过程只接受更优的组合，迭代过程将很快结束于一个局部最优解。这犹如登山者爬到一个小山峰的顶尖时就结束了攀登过程，因为他的周围都是更低的地方，而这很可能只是一个大山脉中的一个小山峰。要到达最高的山峰(或接近之)，就要放弃局部的最优，才能达到或接近全局的最优。

1.3 遗传算法

Holland根据群体遗传和进化理论，提出了遗传算法理论。其基本原理是模仿天然生物群体的自然选择杂交、遗传、变异和进化过程。在生物群体中，受到环境的压力，适应能力较高的个体具有较高的生存和繁殖机会。同时，群体在遗传过程中会有部分个体产生随机变异，好的变异类型具有较高的适应能力，具有较多的繁殖机会，而差的变异类型就更可能被淘汰。

将遗传算法应用到多林分的森林可持续经营过程时，可以把每一种林分经营措施的组合看成一个个体，用一个DNA序列来表示：假设有20个林分，每个林分有2种可选的经营措施，分别用0和1表示，那么20个林分的经营方式组合就可以用一个20位的二进制数字来表示，如01010110111010111011，可称为一个个体的“染色体”或“基因型” (单链DNA)。群体中任意—个个体都是一种20个林分的经营方式组合。

在开始时，设定初始群体数量，例如有50个个体，就由计算机随机产生50个10位的二进制数字来表示50个个体的基因型，构成了初始群体。据它们的基因型，分别计算出50个个体的目标方程值，并计算出群体的平均值，然后根据目标方程值的大小选择进入下一代繁殖的个体。可以依照目标方程值大的具有较多的生存和繁殖机会的原理选择个体。一种比较适用的方法是森林调查时经常采用的PPS(probability proportional to size)样地抽样方法(Akca，2000)。为了保证下代群体的质量，可以使用强制的方法把排名最前面的若干名个体无条件进入下一代群体，其余的名额由PPS抽取。

这种“优胜劣汰”的方法有可能使群体的遗传基础越来越窄。为了扩大遗传基础，获得全局性的最优解，有必要采取措施，在每一代群体中产生一定数量的新基因型个体：在新选出的群体中根据预定的机率，随机选取若干对个体进行“交配”，即交换它们的部分“染色体”。例如有两条基因型分别为01010110111010111011和10100111111010111101的个体，在第3和第4个“位点”之间发生交换，其结果为：

其中^表示交换的位置, 发生交换的位置也是仿照生物学而随机产生的。

除了这种称为“基因重组”的变异方式之外，还有一种重要的方式就是“基因突变”，即按照预定的几率发生在某些个体在某个随机的基因位点上发生“突变”，变成另一个等位基因，如基因型为0100111111010111101的个体在第4个位点发生突变，就变成0101111111010111101了。为了保证群体的质量，也可以强制规定最优秀的若干个体不发生基因突变。

重复计算每个个体的目标方程值和群体平均值，进行下一代的自然选择杂交、遗传、变异过程，直到满足某个条件时结束，例如群体平均值提高到稳定的状态或群体内最优个体的目标方程值收敛到满意的程度，这时群体内最优个体的基因型就是最优解。

对于林分只有2种可选经营方案的情况，一个位点的变异就是简单地变成相应的另一个等位基因，如0变成1或者1变成0。而对于林分有2个以上的可选经营方案时，需要引入“复等位基因”的概念，如一个林分具有编号从0到4的共5个可选经营方案，变异就可以有4个可能的选择方向，也是由随机数来选择。

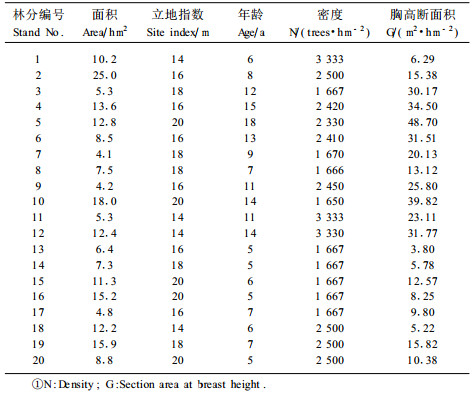
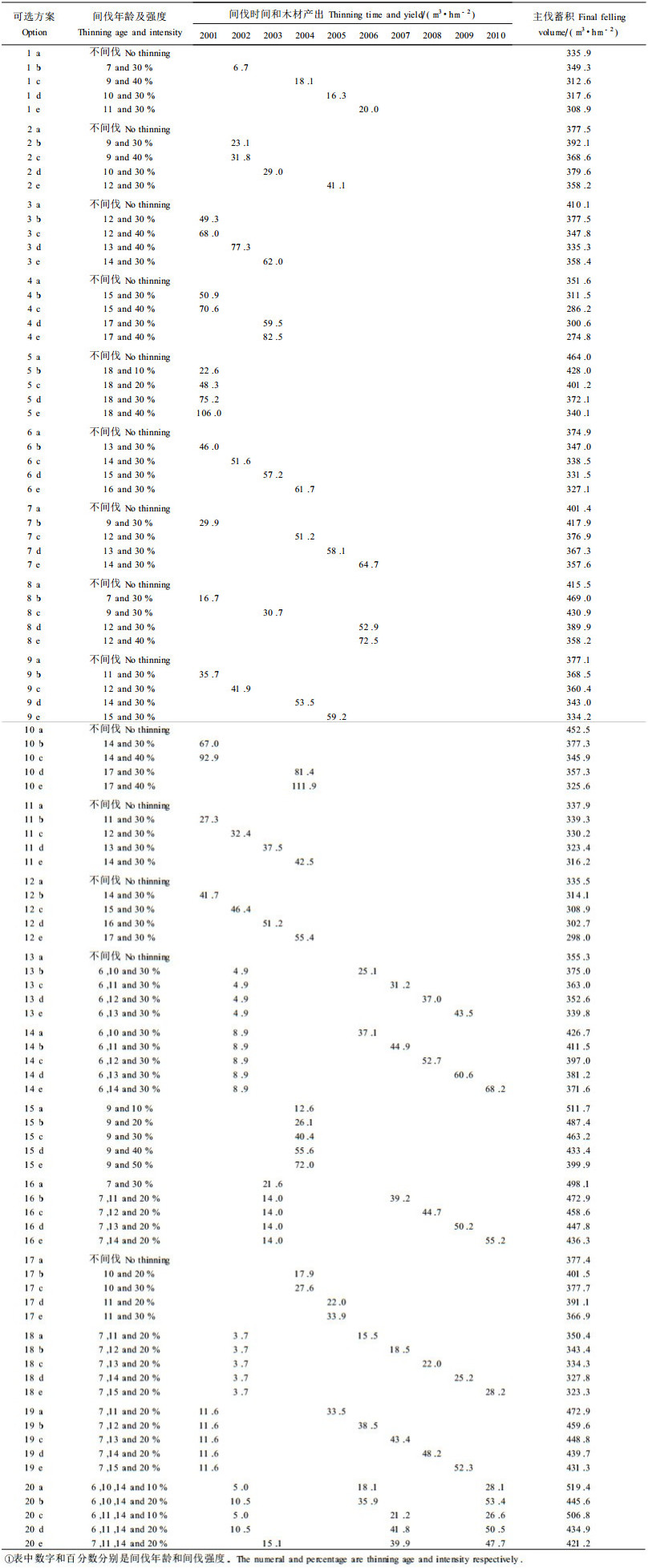
2 线性规划、模拟退火和遗传算法在杉木人工林可持续经营中的应用 2.1 杉木人工林的例子

假设有编号1~20的20个杉木林分，它们在2000年底的基本情况见表 1，轮伐期都是20 a。每个林分有5种可选的经营方案，分别用a、b、c、d、e表示，包括不间伐和不同的间伐次数及间伐强度的组合(表 2)。目标方程要求各林分的主伐木材产量总合达到最大值(各林分达到主伐年龄的时间不同)，同时要求在2001—2010年的10年里，每年的(间伐)木材产量不小于100 m³。

根据Hui(1997)的杉木人工林生长模型和间伐模型，可以估算出给定了间伐时间和强度的间伐木材产出量，并继续推导到下一次间伐时的林分状态，直到主伐的蓄积量。表 2包括了根据生长模型和间伐模型计算不间伐、1~3次间伐的林分发展过程。在表 2中的第2列是各个林分可选的经营方案，后面的11列是根据生长模型和间伐模型推算出来的间伐和主伐材积。如果只对某一具体的林分来考虑经营方案，从表 2就很容易找出来，而要使所有20个林分作为一个整体来满足可持续经营的要求，就需要在多达5²⁰=95 367 431 640 625种组合中找出最优或接近最优的组合，却不是轻而易举的事。实际生产过程中的问题比这个例子要大得多，枚举排序的方法是不现实的，必须采用优化的算法找出全局性的最优解。

2.2 一个通用的森林经营模型

模型元素

变量  X_ij=第i个林分采用第j个经营模式的面积(hm²)

常量  M_pt=在t时期p产品的产量

  A_j=第i个林分的总面积(hm²)

系数  u_ij=第i个林分采用第j个经营模式的每公顷产出价值

  v_ijpt＝如果第i个林分采用第j个经营模式，其在t时期p产品的每公顷产量

模式公式

目标方程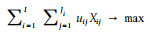      

约束条件      

           隐性约束条件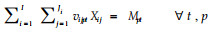

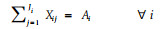
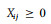
该模型的优点在于它几乎可以处理所有的森林经营问题(Gadow et al.1992)。对于本文的问题，只有一种产品，即木材。目标方程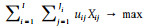就各林分主伐时的每公顷材积u_ij和林分面积的乘积之和。如果林分不允许分割，即一个林分只能采用5种方案中的1种，若第i个林分采用了第j种方案，则X_ij=A_i, 且X_ik=0(k=1…5, k≠j)。

这个模型的另一个优点在于它的数据结构可以同时用线性规划、模拟退火和遗传算法3种方法来求解，表 2右边的11列的转置矩阵就是线性规划的系数矩阵，与林分面积的矩阵相乘就构成了线性规划不等式矩阵的左边项，而其右边项就是各约束条件的值(每年的木材产出量)。

2.3 约束条件

线性规划是依赖于目标方程和约束条件来求解的，而模拟退火和遗传算法一般是不需要约束条件就可以根据目标方程来搜索最优的组合的。森林可持续经营的问题，经常是带有约束条件的，例如“平衡产出”就要求在计划期内每年的产量平衡(大于某个值)，或每年的用工投入在一定的范围(大于某个值)。

模拟退火在处理约束条件时，是对每次随机产生的新组合进行判断，只有符合所有约束条件的组合才能进行进一步的Metropolis选择判别。只要有一个约束条件未能满足，则这个新组合就被淘汰，重新产生一个新的组合，再做同样的约束条件判断，直到出现完全满足所有约束条件的新组合出现，再进行下一步的判别和选择。

对于遗传算法，要求在每一次迭代时群体中的每个个体都满足所有约束条件，这样可以保证群体的最优个体满足所有约束条件。但是这还不能保证这些个体之间的后代也都满足全部约束条件，所以在产生下一代群体时，需要对每个新的个体进行判断，使进入下一代的个体都满足全部约束条件。本例的约束条件是要求在2001—2010的10 a里，每年的(间伐)木材产量不小于100 m³，即：。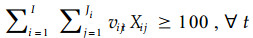

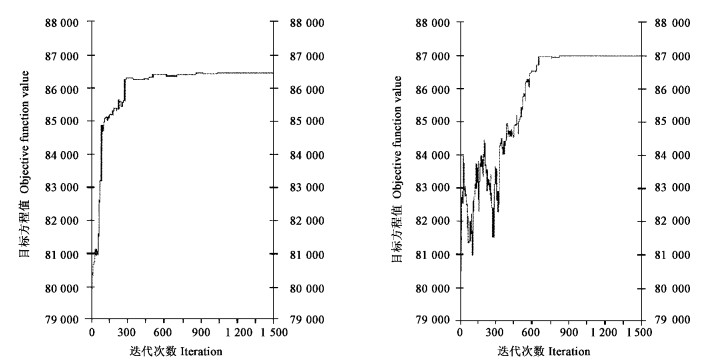
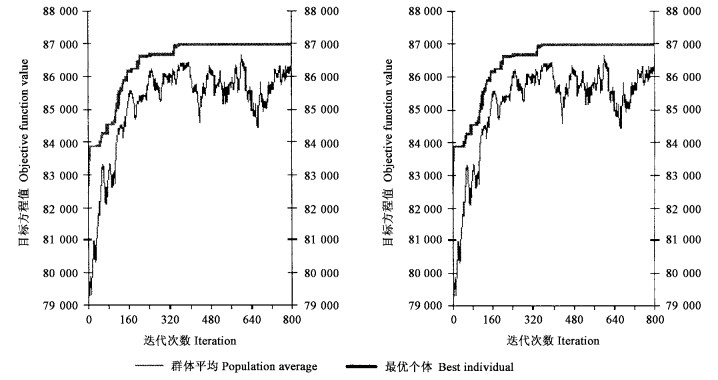
2.4 模拟退火和遗传算法的求解过程

选择和调整好各项合适的参数后，模拟退火和遗传算法都可以很快地把最优解收敛到相近的程度。图 1、2分别显示了不同参数的模拟退火和遗传算法的收敛过程。可以看出，不同的参数设置，可能会加快和降低收敛的速度，对运算时间和最优解的质量是有所影响的，限于篇幅，这个问题将另文讨论。

3 线性规划、模拟退火和遗传算法结果的比较

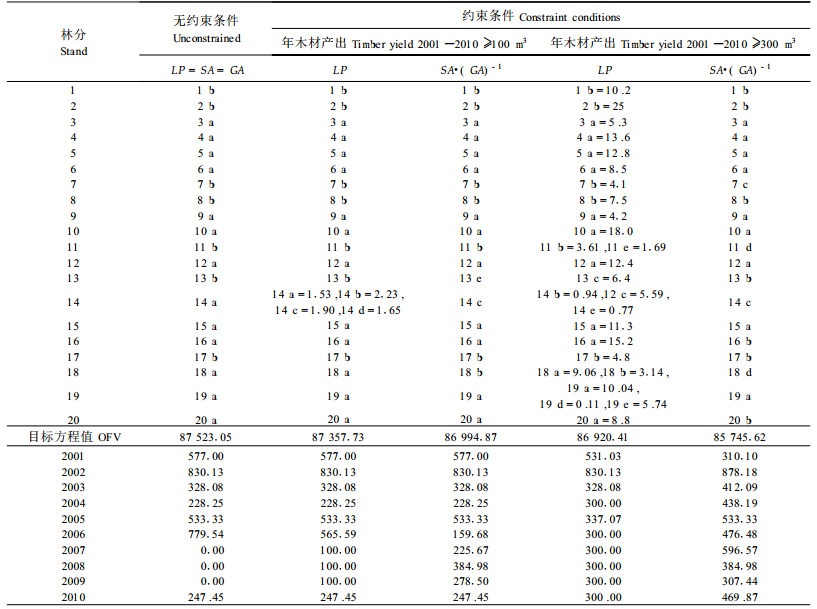
把3种方法的结果列在表 3，3种方法及相应的不同约束条件时的目标方程值(OFV，objective function value)列在表 3中间“目标方程值”一行。其中“无约束条件”是指不考虑每年的间伐材积，不是绝对的没有约束条件，其中还有隐性的约束条件，即各林分的面积。在“无约束条件”下，三者都可以求出最优解，而且线性规划求出的也是整数解。

当增加每年间伐材积大于100 m³这个约束条件时，线性规划的解出现了部分林分被“分割”的情况，其目标方程值高于模拟退火和遗传算法的整数方案，其原因是线性规划的解可以在约束条件的临界值附近满足它们，如2007—2008年的间伐材积正好是100 m³，而模拟退火和遗传算法由于它们的“整数性”而使得这个时期的产量不会正好是临界值。

进一步提高约束条件对每年间伐材积的要求，使之达到300 m³时，三者的目标方程值都有所下降，而模拟退火和遗传算法比线性规划的下降要大。一个重要的特点是线性规划使更多的林分出现“分割”以尽量提高目标方程值。线性规划的解在除2001和2002年以外的8个年份的间伐材积都在临界值300 m³附近，相比之下，模拟退火和遗传算法的解仍然波动较大。

4 讨论和结论

如果允许林分面积被分割成采用不同经营方案的若干部分，线性规划是完美的求解算法。而当约束条件都比较宽松时，线性规划也有可能得出整数解(即林分不分割)，但不是一定就能够得到整数解。要获得整数解，尤其是在林分数目很大的时候，可以采用模拟退火和遗传算法，它们可以在天文数字般的众多随机组合中搜索出全局性的最优解。对于可持续经营要求“稳定产出”的要求，在林分数目足够大的条件下，这种波动就会减小，同时，也可以采用增加约束条件的办法来求得更加平稳的解决方案。

在林分数目很大的时候，线性规划的算法由于变量数目很大而需要很大的计算机内存，而模拟退火和遗传算法对内存的需求增大不明显，增大的只是迭代的次数，而在合适的参数组合下。两者的收敛速度都很快，反之，不适合的参数设置，可能使迭代提早结束，未能获得满意的全局性最优解。关于模拟退火和遗传算法的参数设置，限于篇幅，将另文讨论。

模拟退火和遗传算法不单在森林可持续经营中有很大的用途(Wu et al., 1997;2000)，也已经广泛地应用到图像处理、电信水电工程布线等领域(Vidal, 1993)。可以预见，它们在与林业研究相关的生态保护区的选址等方面也将有广阔的应用前景。