文章信息
- 鲍甫成, 侯祝强.
- Bao Fucheng, Hou Zhuqiang.
- 针叶树材管胞气体渗透流阻及其渗透系数
- THE FLOW-RESISTOR AND GAS PERMEABILITY OF SOFTWOOD TRACHEID
- 林业科学, 2001, 37(4): 80-87.
- Scientia Silvae Sinicae, 2001, 37(4): 80-87.
-
文章历史
- 收稿日期:2000-03-23
-
作者相关文章
针叶树材管胞比量占针叶树材总体的90%以上(北京林学院, 1983; 何天相, 1985), 气体在针叶树材中渗透的通道几乎全都由管胞的孔隙所构成(Bolton et al., 1978; Siau, 1984), 所以针叶树材气体渗透性与气体在管胞中的流动特性和规律紧密相关。
本文将根据针叶树材管胞的解剖结构, 运用流体力学的理论, 导出管胞在3个纹理方向上关于气体渗透流阻(Flow-Resistor)的数学表达式, 并由此计算管胞的气体渗透系数, 试图在针叶树材结构单元—管胞的层次上揭示气体渗透性及其规律, 以获得对针叶树材气体渗透性更深入的认识。
1 木材气体渗透系数与流阻当木材中的渗透气体不存在非线性流分量时, 渗透气体流过的通道两端压强差ΔP与体积流率Q成正比, 可以使用Darcy定律或其修正形式——Adzumi方程来描述气体在木材中的渗透。Darcy定律与电阻的Ohm (欧姆)定律都属于线性唯象定律(林瑞泰, 1995), 如同由Ohm定律定义电压、电流和电阻一样, 在Darcy定律中以Q类比于电流而以ΔP类比于电压, 以R类比电阻, C类比电导, 则可定义气体在木材中渗透的气体流阻R (Gas Resistance) (Bramhall, 1971), 以及气体流导C (Gas Conductance) (Miyara, 1991),

|
(1) |
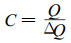
|
(2) |
同样, 气体流阻R与气体流导C之间也存在着类似于电阻与电导互为倒数的关系。考虑到渗透气体的可压缩性, 根据Siau的计算方法(Siau, 1984), 渗透气体经可压缩性修正后的流阻,
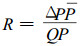
|
(3) |
根据渗透系数的定义, 气体渗透系数Kg与流阻的关系为:

|
(4) |
(4) 式中, L为渗透长度; A为渗透截面; η为气体动力粘滞系数。
在通常的木材气体渗透系数测量条件下, 木材中渗透气体的流速低于110 m s (侯祝强等, 1999), 即满足流体可作为不可压流的条件(周光坰等, 1992); 木材的气体渗透系数是在稳态流的条件下定义的, 因此, 本文在渗透气体为线性流的前提下, 运用定常流的条件, 推导针叶树材管胞3个纹理方向的气体流阻的数学表达式。为简单计, 以下使用“流阻”来替代“气体流阻”。
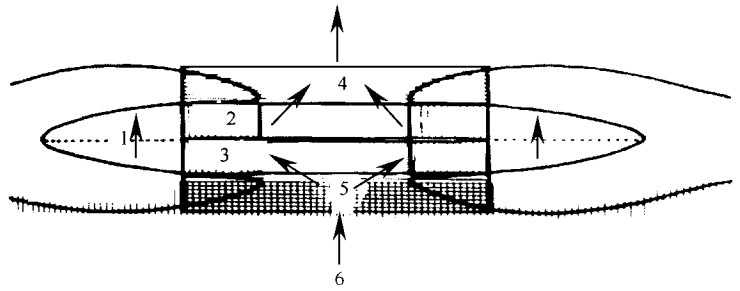
2 针叶树材管胞的流阻 2.1 针叶树材管胞的各流阻单元根据Bolton和Petty提出的关于气体渗透的针叶树材管胞结构(Bolton et al., 1978), 气体在管胞中渗透的路径可分为串接在一起的两部分:管胞腔和管胞纹孔系统。管胞腔提供气体在管胞内的渗透通道, 而纹孔系统提供气体在管胞间的渗透通道。后者也包括3个串接在一起的单元, 即纹孔口、纹孔缘与纹孔塞间通道、纹孔膜微孔(如图 1所示, 图中箭头显示气体渗透的路径)。
|
图 1 针叶树材管胞结构(引自Bolton, 1978) Fig. 1 The theoretical model for tracheid (from 1978, Bolton) 1.纹孔膜微孔Pit membrane openings; 2.纹孔缘与纹孔塞之间气体流出通道Border-torus annulus on the downstream (exit); 3.纹孔缘与纹孔塞之间气体流入通道Border-torus annulus on the upstream (entry); 4.气体流出端纹孔口Pit apertures on the downstream side; 5.气体流入端纹口Pit apertures on the upstream side; 6.管胞胞腔Tracheid lumen. |
设管胞(Tracheid)在某一纹理方向的流阻为Rg, 且管胞胞腔的流阻为RL、纹孔口(Pit Aperture)的流阻为RPA、纹孔缘与纹孔塞间的通道(Border-Tourus Annuli)的流阻为RBT、纹孔膜微孔(Pit Membrane Opening)的流阻为RMO (如图 2所示)。这样有,
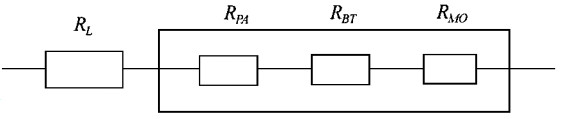
|
图 2 管胞流阻各分量串联示意图 Fig. 2 Schematic diagram of series components of flow resistor in tracheids |

|
(5) |
(5) 式代表着针叶树材管胞流阻的一般形式, 对气体沿管胞纵向、径向和弦向渗透的都适用。本文循Bolton、Petty和Comstock等(Bolton et al., 1978; Siau, 1984)处理的方法, 忽略针叶树材管胞不同纹孔类型的差异, 关于针叶树材管胞纹孔流阻的讨论只考虑具缘纹孔。
2.2 针叶树材管胞各单元流阻的表达式视针叶树材管胞为一个矩形体(Smith, 1965; Bolton et al., 1978), 且管胞的长轴沿树木轴向即纵向排列, 气体经由管胞沿纵向、径向和弦向流动的途径如图 3所示。由图 3可知, 渗透气体在胞腔内沿纵向、径向或者弦向流过时, 其渗透的路径和距离均不相同, 从而3个纹理方向的胞腔流阻不相同。管胞纵向搭接面、径面和弦面上导通纹孔的数目不相等, 从而管胞3个纹理方向的纹孔系统流阻也不同。
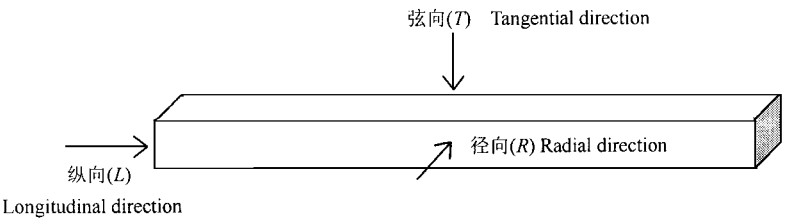
|
图 3 气体经由管胞沿纵向、径向和弦向渗透示意 Fig. 3 Schematic diagram of gases flow through tracheid in the longitudinal, radial and tangential directions |
视管胞腔与管胞一样也为矩形体(Siau, 1971), 渗透气体无论沿纵向还是沿径向或弦向, 其过流截面均为一矩形。管胞腔的几何线度比常温常压下空气分子平均自由程大很多, 所以渗透气体沿3个纹理方向在管胞腔内流动时, 都不会产生滑流(Comstock, 1967)。由矩形截面的边条件, 通过求解二维定常不可压流的动量方程及运用(4)式1), 可以得到针叶树材管胞腔渗透气体流阻:
1) 侯祝强. 针叶树材气体渗透的三维流阻网络理论. 北京: 中国林业科学研究院博士论文, 1999, 19~ 34

|
(6) |
(6) 式中L为渗透气体通过管胞腔流动的长度, S (a, b)为,

|
(7) |
(7) 式中, th ()为双曲正切函数符号; a和b分别为过流截面高度和宽度的一半; 流阻单位为Pa·s·/m-3。
2.2.2 管胞纹孔口流阻针叶树材具缘纹孔口半径在2×10-6m (2 μm) (Bolton et al., 1978)左右, 根据滑流产生的条件, 渗透气体流经纹孔口时无滑流出现。视纹孔口为圆形, 由圆形截面管道粘性流的Hagen-Poiseuille公式及(4)式, 便得到了一个管胞第i个纹孔口的流阻:

|
(8) |
(8) 式中, r为纹孔口半径; d为纹孔口厚度。纹孔口属短毛细管, 考虑关于Poiseuille (泊肃叶)方程的Couette修正时(Siau, 1984), (8)式中的d用下式中的d′代替,
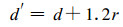
|
(9) |
根据Bolton和Petty关于流体渗透的针叶树材纹孔结构(Bolton et al., 1978), 渗透气体在纹孔缘与纹孔塞间通道(Border-Torus Annuli)的流动, 可视为气体在两平行圆环形板之间的流动, 纹孔口与纹孔塞之间的平均距离为4×10-6m (4 μm)左右, 则渗透气体在其间流过时, 不会出现滑流。根据Bolton和Petty引用Schiller圆环形通道中气体压强差和气体体积流率的关系(Bolton et al., 1978), 可以得到纹孔缘与纹孔塞之间通道的流阻:
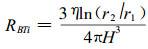
|
(10) |
(10)式中, r1、r2分别为纹孔口和纹孔塞的半径; H为纹孔缘与纹孔塞间距离的一半; 下标i与(8)式的意义相同。纹孔缘与纹孔塞之间通道虽为短毛细管, 但r1与r2除, 故不需计算r1、r2的有效长度(Effective Length) Couette修正(Siau, 1984)。
2.2.4 纹孔膜微孔流阻纹孔膜微孔形状多变无规, 鉴于其孔径线度极小, 按习惯的处理方法作为圆孔对待(Petty et al., 1969; Petty, 1973; Bolton et al., 1978)。纹孔膜微孔有效半径(Effective Radius)与常温常压下空气分子的平均自由程接近或一致(Siau, 1984), 气体流经纹孔膜微孔时将会出现滑流, 这时的渗透气体有粘性流和滑流两个线性流分量, 纹孔膜微孔流阻为粘性流流阻和滑流流阻的并联。纹孔膜微孔粘性流的流阻表达形式与(8)式相同, 而纹孔膜微孔滑流分量的流阻为,
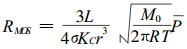
|
(11) |
这样, 第i个纹孔口的第j个纹孔膜微孔的流阻:
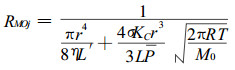
|
(12) |
(12)式中, L′表示经Couette修正后纹孔膜微孔的有效长度(Effective Length); r是微孔的半径; Kc是短毛细管中滑流的Clausing修正因子(Siau, 1984); σ=0.9为表面特性因子; Ρ为气体平均压强(Pa); R为气体普适常数; T为绝对温度, M0为气体摩尔质量。
3 针叶树材管胞流阻的3个纹理方向分量 3.1 管胞流阻纵向分量为最后结果表达式不至过于复杂, 设管胞腔纵向长度为2LL、径向直径2LR和弦向直径2LT, 参考图 3可知气体在管胞中的纵向渗透路径是:首先通过管胞纵向搭接面上的导通纹孔, 进入管胞腔并穿过由LR和LT所构成的平面, 然后再经过管胞另一纵向搭接面上的导通纹孔, 进入相邻的管胞。此时气体在管胞腔内纵向渗透截面高度的一半为LT, 而宽度的一半为LR, 渗透长度等于2LL, 这样管胞腔流阻的纵向分量,
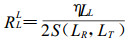
|
(13) |
(13)式中RLL的上标“L”表示纵向、下标“L”表示胞腔, S(LR, LT)为,
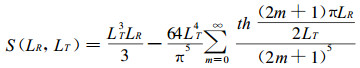
|
(14) |
如果管胞纵向的导通纹孔数目为NL, 则针叶树材管胞的一个纹孔(Pit)的流阻RPL(下标表示纹孔)为这NL个纹孔系统流阻的并联, 即,

|
(15) |
(15)式中, RPAiL、RBTiL为第i个纹孔的纹孔口流阻和纹孔塞缘间流阻。气体渗透通过纹孔膜时膜两侧各点的压强相同, 故各个微孔两端的压强差相等。同时, 通过纹孔膜时气体体积流率为通过各个微孔的气体体积流率之和, 若第i个纹孔的纹孔膜微孔数目为NLj, 则第i个纹孔的纹孔膜流阻RΜΟiL为这NLj个微孔流阻的并联, 即
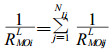
|
(16) |
(16)式中, 下标“j”表示NLj个微孔的序数。这样, 一个针叶树材管胞纵向流阻:

|
(17) |
(17)式中, L′Bi为第i个经Couette修正的纹孔的纹孔缘厚度; rTi为第i个纹孔口的半径; rBi为第i个纹孔的纹孔塞半径; Hi为第i个纹孔的纹孔缘与纹孔塞之间的距离。LMij和L′Mij分别为第i个纹孔的第j个纹孔膜微孔的厚度和经Couette修正后的有效厚度(Effective Thickness), rMij为第i个纹孔的第j个纹孔膜微孔的半径, 其余各量意义与(12)相同。
3.2 管胞流阻径向分量参考图 3可知当气体沿管胞径向渗透时, 气体在管胞中的径向渗透路径是:首先经过管胞径面壁的导通纹孔进入管胞腔, 并经过边长为2LL和2LT的矩形截面流过管胞腔, 然后再经过管胞另一端的径面壁导通纹孔进入相邻的管胞。此时气体在管胞腔内渗透截面高度的一半为LT, 宽度的一半为LL, 渗透长度等于2LR, 这样管胞腔流阻的径向分量为,

|
(18) |
根据Couette修正的条件(Siau, 1984), 气体沿管胞腔径向渗透时须按短毛细管对待。因此, (18)式中使用了短毛细管Couette修正的有效长度(Effective Length) L′R, 且式中的S (LL, LT)为,

|
(19) |
如果管胞沿径向导通纹孔数目为NR, 第i个纹孔的纹孔膜数目为NRj, 根据上节管胞的纵向流阻的讨论, 管胞径向流阻为,

|
(20) |
(20)式中, 各量的意义与前面所述相同。
3.3 管胞流阻弦向分量参考图 3可知当气体沿管胞弦向渗透时, 气体在管胞中的弦向渗透路径是:首先经由管胞弦面壁的导通纹孔进入管胞腔, 再由边长为2LL和2LR的矩形截面流过管胞腔, 然后再经过管胞另一端弦面壁的导通纹孔进入相邻的管胞。此时气体在管胞腔内渗透截面高度的一半为LR, 而宽度的一半为LL, 渗透长度等于2LT, 这样管胞腔流阻的弦向分量为,

|
(21) |
同理, 这里使用了经Couette修正的气体在胞腔内的有效渗透长度(Effective Length) L′T, (21)式中的S (LL, LR)为,
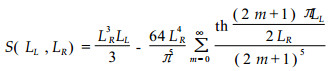
|
(22) |
如果管胞弦向的导通纹孔数目为NT, 第i个纹孔纹孔膜微孔数目为NTj, 那么一个针叶树材管胞的弦向流阻:

|
(23) |
(23)式中, 各量的意义与前面所述相同。
4 针叶树材管胞3个纹理方向的渗透系数 4.1 针叶树材管胞的结构参数根据上节讨论的结果, 使用管胞的结构参数可以计算得到管胞流阻。本文使用管胞结构参数的平均值来计算管胞流阻的平均值, 并采用两种方法选取试件管胞结构参数的平均值:一是通过抽样测量获得试件管胞一部分结构参数的平均值, 这主要针对测量较易进行, 可以进行足够数量抽样测量的结构参数, 如管胞和管胞腔有效长度、管胞和管胞腔径向与弦向直径、管胞径向和弦向壁厚、晚材率、搭接率、纹孔闭塞率等; 二是引用或部分引用已在针叶树材流体渗透性研究中成功应用的数据, 如管胞搭接面、径面、弦面壁上的纹孔数目, 以及纹孔膜微孔的大小与数目等。
试件管胞结构参数抽样测量的试材, 采自广西凭祥市中国林科院热带林实验中心大青山林场。在20a的马尾松人工林中, 选择6株正常生长的树, 从距地面2.3m处向上截取。各个测量试样均是从试材下端10 cm处开始, 按50 cm相等间隔在3个不同的高度截取, 加工制作成18个2 cm×2 cm×4 cm的样品。气干半年后, 按照管胞结构参数测量要求进行切片制样。
管胞长度系根据18个样品, 分早晚材各随机选取50根管胞进行测量得到; 管胞径向和弦向直径、管胞腔径向和弦向直径、管胞组织比量、木射线组织比量系根据18个样品, 在相应的纵向、径向、弦向切片上(均包含着40~50个管胞单元)测量得到; 晚材率系在18个样品横截面上测量得到; 搭接率系根据18个样品, 分早晚材随机选取50个管胞测量得到; 纹孔闭塞率系根据18个样品的切片, 分早晚材各随机选取50个管胞测量得到。表 1中所列的结果系由早、晚材测量结果的平均值, 以晚材率为权重加权平均后所得1)。
|
|
表 2和表 3列出了引用的管胞结构参数。表 2中纹孔膜微孔半径引自Petty (1970), 纹孔膜厚度引自Siau (1984)。纹孔口、纹孔塞、纹孔膜、纹孔膜上微孔半径、纹孔缘厚度、纹孔缘与纹孔塞之间的高度等参数引自Bolton和Petty (Bolton et al., 1978)。表 3中管胞搭接面以及径面壁、弦面壁的导通纹孔数目, 系根据Petty所引用Philips关于管胞纵向搭接面纹孔的数目(Petty, 1970), 以及Koran关于管胞径面壁与弦面壁纹孔的数目(Koran, 1974; 1977), 结合本文关于马尾松木材纹孔闭塞率、晚材率、木射线组织比量、管胞与木射线间纹孔数目的抽样测量结果计算所得, 表 2和表 3中所列数据计算与确定的方法参见侯祝强的相关工作1)。
|
|
|
|
若已知管胞纵向、径向、弦向的流阻, 根据(4)式管胞相应的3个纹理方向的渗透系数可分别写成为:
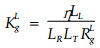
|
(24) |
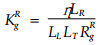
|
(25) |
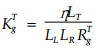
|
(26) |
(24)、(25)、(26)式中, 渗透系数和流阻的上标“L”、“R”、“T”分别表示纵向、径向、弦向。
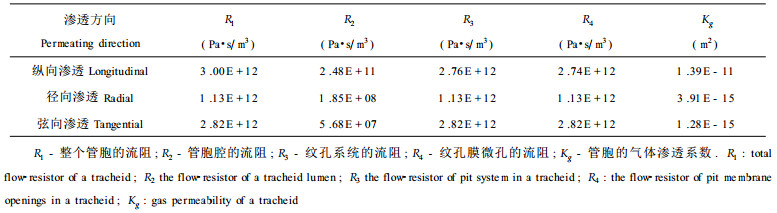
按照针叶树材气体渗透系数实际测量条件, 分别选取1.13×105Pa、1.17×105Pa和1.35×105Pa, 作为计算单个管胞纵向、径向和弦向流阻滑流项的气体平均压强; 取温度为20℃, 20℃时空气的动力粘滞系数η=1.81×10-5Pa·s。使用表 1、表 2、表 3所列的管胞结构参数, 根据(17)、(20)、(23)式及上述3式进行计算, 表中渗透系数使用国际单位m2 (1 m2=1.013×1012 Darcy), 结果(平均值)列在表 4中。
|
|
根据表 4中列出的结果, 纹孔系统纵向、径向和弦向流阻分别占管胞流阻的91.4%、99.8%和99.9%, 表明气体沿3个纹理方向流过管胞时, 渗透的阻力几乎全都集中在纹孔。本文这一结果与关于木材流体渗透的Petty模型、Sebastian模型和Comstock模型的有关结论一致(Siau, 1995)。另外, 管胞纹孔系统的流阻基本上来自于纹孔膜上的微孔, 对于3个纹理方向的渗透来说其占各纹孔系统流阻的比率都在99%以上(取3位有效数字时, 弦向已为100%)。参考图 3可知, 当气体沿径向和弦向流过管胞时, 气体在管胞腔内的过流截面较纵向流动时要大近两个数量级, 所以气体沿管胞径向和弦向渗透时, 相应的管胞腔流阻很小, 分别只占管胞流阻的0.02%和0.01%。
管胞流阻在3个纹理方向表现出明显的差异, 使管胞气体渗透性在纵向、径向和弦向也表现出明显的差异。如前所述, 针叶树材基本由管胞构成, 管胞气体渗透性在纵向、径向和弦向的差异, 直接导致了针叶树材气体渗透性在3个纹理方向的差异。
本文计算所得的管胞气体纵向渗透系数平均值为2.7×10-11m2, 鲍甫成等关于马尾松人工林木材纵向气体渗透系数平均测量结果为1.8×10-11m2 (鲍甫成等, 1994); 此外, 计算所得的管胞径向渗透系数和弦向渗透系数之比为3, Milota等关于美国南方黄松径向渗透系数和弦向渗透系数测量结果之比为2.7 (Milota et al., 1995), 通过这两个结果的比较可以证明本文关于管胞流阻与管胞气体渗透系数计算的合理性。
综上所述, 管胞流阻可以描述气体渗透阻力的分布情况, 反映气体在3个纹理方向的渗透性差异, 在木材细胞层次揭示出针叶树材气体渗透性的机制。
鲍甫成, 郝丙业, 杜浩, 等. 1994. 中国主要针叶树人工林与天然林及幼龄材与成熟材流体渗透性比较研究. 世界林业研究, 7(专集): 144-153. |
北京林学院主编. 木材学(木材机械加工专业用). 北京: 中国林业出版社, 1983: 66
|
何天相. 木材构造与识别. 见: 成俊卿主编. 木材学. 北京: 中国林业出版社, 1985: 87
|
侯祝强, 鲍甫成. 1999. 木材可压缩流体的流动型态分析. 林业科学, 35(3): 63-68. DOI:10.3321/j.issn:1001-7488.1999.03.012 |
林瑞泰. 1995. 多孔介质传热传质引论. 北京: 科学出版社, 17-21.
|
周光坰, 严宗毅, 许世雄等编. 流体力学(上册). 北京: 高等教育出版社, 1992: 191~ 194
|
Bolton A J, Petty J A. 1978. A model describing axial flow of liquids through conifer wood. Wood Sci. Technol., 12(1): 37-48. DOI:10.1007/BF00390009 |
Bramhall G. 1971. The validity of Darcy' s Law in the axial permeability of wood. Wood Sci. Technol., 5(2): 121-134. DOI:10.1007/BF01134223 |
Comstock G L. 1967. Longitudinal permeability of wood to gases and non-swelling liquids. For. Prod. J., 17(10): 41-46. |
Koran Z. 1974. Intertracheid pitting in the radial walls of Black spruce tracheids. Wood Sci., 7(2): 11-15. |
Koran K. 1977. Tangential pitting in black spruce tracheid. Wood. Sci. Technol., 11(2): 115-123. |
Kuroda N, Siau J F. 1988. Evidence of nonlinear flow in softwoods from wood permeability measurement. Wood Fiber Sci, 1977, 20(1): 162~ 169 https://wfs.swst.org/index.php/wfs/article/view/1908
|
Milota M R, Tschernitz J L, Verrill S P, et al. 1995. , Gas permeability of plantation loblolly pine. Wood and Fiber S cience, 27(1): 34-40. |
Miyara A J, Costanza V. 1991. Gas flow in hardwood. wood Sci. Technol., 25(4): 289-299. |
Petty A J, Preston R D. 1969. The dimension and number of pit membrane pores in conifer wood. Proc. Roy. Soc., B 172: 137-151. |
Petty J A. 1973. Diffusion of non-swelling gases through dry conifer wood. Wood Sci. Technol., 7(4): 297-307. DOI:10.1007/BF00351075 |
Petty J A. 1970. Permeability and structure of the wood of Sitka sprouce. Proc. Roy. Soc. Lond, B175: 149-166. |
Siau J F. 1971. Flow in wood. Syracuse, New York: Syracuse University Press, 9-10.
|
Siau J F. 1984. Transport Processes in Wood. Berlin Heidelberg, New York: Springer-Verlag, 73-95.
|
Smith D M. 1965. Rapid measurement of tracheid cross-section dimensions of conifers. For. Prod. J., 15(8): 325-334. |
 2001, Vol. 37
2001, Vol. 37