文章信息
- 刘晓丽, 殷亚方, 姜笑梅.
- Liu Xiaoli, Yin Yafang, Jiang Xiaomei
- 人工林尾巨桉原木内部轴向残余应变径向分布
- Radial Distribution of Internal Longitudinal Residual Strain in Eucalyptus urophylla × E. grandis Plantation Log
- 林业科学, 2009, 45(2): 105-110.
- Scientia Silvae Sinicae, 2009, 45(2): 105-110.
-
文章历史
- 收稿日期:2007-11-20
-
作者相关文章
2. 中国林业科学研究院林业研究所 北京 100091;
3. 中国林业科学研究院木材工业研究所 北京 100091
2. Research Institute of Forestry, CAF Beijing 100091;
3. Research Institute of Wood Industry, CAF Beijing 100091
由于树木形成层的分生活动,每年在树干外围都会产生一定厚度的生长鞘,在生长鞘内形成了一定大小的生长应力,而位于树干内部的树芯也会形成一种应力与此相平衡。随着生长鞘的逐年累加,树干外围的生长应力都会叠加在上一年形成的生长鞘上,这样循环往复的过程使得树芯处形成了具有一定规律的应力分布(Archer et al., 1974;Kubler,1959a;Okuyama et al., 1975a;1978)。这种应力与生长应力不同,它是生长应力逐年叠加而形成的一种内部应力,被称为残余应力(residual stress)。残余应力的测试是通过测量相应的残余应变来间接计算得到的。目前主要有2种方法用来测试原木的内部轴向残余应变(internal longitudinal residual strain,ILRS),一种是由Jacobs (1938)创立的“中心板锯割法"(diametrical planks),另一种为“薄层移去法"(thin layer removal methods),该方法日本学者使用较多(Okuyama et al., 1975b;Sasaki et al., 1981a;1981b)。残余应力的径向分布模式使锯解后的板材出现不同程度的弯曲和开裂现象,制约了板材的出材率。
目前对于树木内部轴向残余应变的研究较多地集中在径向分布的理论分析上,更为具体的研究,如内部轴向残余应变的径向分布在树干不同高度上的变异特点、原木直径对径向分布的影响以及内部轴向残余应变与木材性质径向变异间的关系等方面,所做研究还相当有限。本文利用“中心板锯割法"结合“应变片法"对尾巨桉(Eucalyptus urophylla × E. grandis)原木内部轴向残余应变进行了测试,着重分析了内部轴向残余应变径向分布特性,通过对树干不同高度间内部轴向残余应变径向分布的比较,强调了树干直径对内部轴向残余应变径向分布的影响。对人工林尾巨桉幼龄材内部残余应变径向分布的研究,是生长应力研究工作的拓展和深入,为人工林桉树幼龄材制订更合理下锯方式提供重要参考,为实现木材的高附加值利用,提高板材的出材率提供理论依据。
1 材料与方法 1.1 试验材料试验林位于广西扶绥县东门林场,在林内选取垂直、健康生长的人工林尾巨桉9株(平均树高29.7 m,平均胸径22.5 cm),在树基处伐倒。伐倒木从胸高处每隔2.2 m进行截断,共得36段原木,以每个原木段中点处的高度值和直径分别表示该原木的高度和直径,依次记为2.4,4.6,6.8及9.0 m(表 1)。原木端头用沥青涂刷,防止水分过多地散失。
|
|
采用“中心板锯割法",用手锯和凿子在每段原木的中部制备如图 1a所示的径切板(保留原木南北向部分,而将东西向部分去除),长度为300 mm,厚度为35 mm,宽度为直径。在板的两端仍保持原木状态,是为了抑制应力的释放。将径切板表面砂光,从靠近树皮向髓心方向,每15 mm粘贴一个应变片,如图 1b所示,每个板上粘贴11个应变片;将与应变片连接的导线全部接到应变仪的11个通道上,调零;将径切板从原木上锯下,再将径切板从一侧开始锯成木条,锯解时采用对称下锯,使得径切板的应力能够均匀释放,如图 1c所示;应变仪记录下整个测试过程中的残余应变的变化情况,待读数稳定后,记录读数。

|
图 1 内部轴向残余应变测试方法 Figure 1 Measurement of internal longitudinal residual strain a.切制中心板Removal of diametrical plank;b.中心板截断Cutting of diametrical plank;c.分层锯解成木条Stripping. |
每个原木段从南向至北向共测得11个点的内部轴向残余应变,对所有测试结果进行回归分析,得到一条回归曲线及回归方程(图 2)。

|
图 2 内部轴向残余应变径向分布回归曲线 Figure 2 Regression curve of radial distribution of internal longitudinal residual strain |
图 2中给出的内部轴向残余应变(以下简称残余应变),负值表示拉应变,正值表示压应变,横坐标正值部分表示树干北向。由图 2可见,在树干南、北向径向对应位置的残余应变大小相似,沿髓心呈现良好的对称性,径向分布表现为:在靠近树皮的位置为拉应变,向髓心方向拉应变呈下降趋势,至某个半径处残余应变达到零值,随即转变为压应变,向髓心处压应变呈明显的增加趋势,一般在髓心附近压应变达到最大值,与已有的研究结果一致(Okuyama et al., 1978;1979;Wilkins et al., 1991;Wahyudi et al., 1999;2001)。
Kubler(1959a;1959b)提出了内部轴向残余应力的轴对称分布模型,Boyd(1950)也曾提出相似的模型,其他学者(Gillis,1973;Archer et al., 1974;Beck,1974;Post,1979)进行了发展和完善,通过试验测试进行验证。而由于环境、气候和地形等对生长应力形成的影响,树干内部轴向残余应力也会形成非对称性分布,对其存在、成因和分布特性同样做了大量的研究工作(Wilson et al., 1977;Boyd et al., 1974;Nicholson,1973;Archer,1976;Vendhan et al., 1978;李静辉等,1994)。目前关于内部轴向残余应力在树干内的分布模式最具代表性的是Kubler(1959a;1959b)所给出的公式:

|
(1) |
式中:εl为在任意半径处的轴向残余应力(kg·cm-2);εlp为新形成生长鞘上的轴向生长应力(kg·cm-2);R为原木树干半径(cm);r为树干任意位置处半径(cm)。
式(1)一般遵循的假设是在树木生长的任何阶段,外层形成的生长应力是恒定的,这样的生长应力在无穷小的层内叠加为残余应力。由此得到的残余应力是r/R的函数,而且其分布模式在任何阶段内都是一致的。本文对尾巨桉的残余应变径向分布测试结果进行曲线拟合(图 2)得到回归方程:

|
(2) |
式中:y为内部轴向残余应变(×10-6);x为树干任意位置处半径(cm)。
式(2)所示的回归方程直接给出了残余应变和树干任意位置处半径间的关系,在0.01水平极显著相关(相关系数r=0.87),与Kubler(1959a;1959b)得到的式(1)相比,因为没有表面轴向生长应变和树干半径这2个参数的存在,因此在这2个参数未知的情况下也可以估算出某个半径处的残余应变值;但该模型还需要大量的试验来验证是否具有普遍适用性。
关于残余应变径向分布模式的研究,另一个值得关注的问题是残余应变为0时的树干半径问题,本研究尾巨桉残余应变为0时树干半径为0.681R(R为原木树干的半径)。已有研究表明,王桉的残余应变在0.7R处为0(Boyd,1950a),红栎(Quercus rubra)应变符号发生转变的点为0.6R(Wilhelmy et al., 1973),本研究得到的结果与此相似,但也有研究(Swaczyna,1979a;1979b)发现山毛榉(Fagus spp.)的内部残余应变转变点为0.45R,距离髓心较近。因此关于残余应变为0时树干半径大小的研究并没有统一的定论,与边材宽度和年轮宽度有一定的关系,还与树种、测试样本的多少及测试方法有直接的关系。
2.2 不同原木高度内部轴向残余应变径向分布特性对4个高度上的原木测量结果分别求得平均值(表 2)。表中S1~S5表示树干南向从树皮到髓心的5个位置;N1~N5表示树干北向从树皮到髓心的5个位置;Pith表示髓心部位。负值表示拉应变,正值表示压应变。
|
|
由表 2可见,在各个高度上树干南、北向径向对应位置的残余应变大小相似,沿髓心呈现良好的对称性,如2.4 m的N1位置残余应变为952×10-6,S1位置的残余应变为870×10-6,但9.0 m上的S1和N1位置残余应变相差较多。以北向为例,从树皮N1向髓心Pith处比较4个高度上的测试结果可以看出,靠近树皮拉应变最大为6.8 m上的S1位置,达到1 162×10-6,最小为4.6 m上的N1位置,为515×10-6。在Pith处的压应变最大达到1 021×10-6,最小751×10-6。
为了进一步对不同树干高度上残余应变径向分布的进行比较,将每个高度所得结果进行回归分析,得到4个高度上的回归方程(表 3)。
|
|
在4个高度上回归方程都为抛物线,4个高度上的曲线拟合效果都很好,相关系数表示出拟合效果的差异,从2.4到9.0 m,R呈明显的下降趋势,说明2.4 m高度处曲线拟合最好,而6.8和9.0 m上相对较差。残余应变的径向分布在4个高度上差异不显著,与Okuyama等(1978)对日本柳杉(Cryptomeria japonica)残余应变的研究结果一致。但残余应变径向变化梯度在各高度间有一定的差异,在6.8和9.0 m上变化梯度大于2.4和4.6 m的。根据表 3中的回归方程,计算出残余应变为零值时的树干半径,在4个高度上分布在0.588R(6.8 m)至0.728R(4.6 m)之间,表明原木半径不同使得残余应变为0时的树干半径大小不一。4个高度上的平均为0.668R,与通过公式(2)得到的结果相似。
2.3 原木直径对内部轴向残余应变径向分布的影响树木生长应力的影响因子有很多,既然生长应力是残余应力形成的最直接原因,那么影响生长应力的因素必然也会影响残余应力。在众多的影响因子中,值得一提的是树木的生长速度,它直接反映出原木的直径大小。观察发现,小径级原木伐倒后,相对于大径级原木而言,由于生长应力造成的心裂趋势更严重。研究表明,树木的生长速度对残余应变的大小和径向分布模式都没有显著的影响,但是生长速度慢的树木,其残余应变径向分布曲线较陡峭(Okuyama et al., 1979;Wilkins et al., 1991;Wahyudi et al., 1999;2001),所研究的树种包括巨桉(E. grandis)、柚木(Tectona grandis)和马占相思(Acacia mangium)等。Wahyudi等(1999)曾提出,既然生长速度对残余应力没有显著影响,那么产生作用的就应该是树干的直径。Fournier等(1990)发现,对阔叶树距离髓心较远的位置其轴向和横向应力与其他学者得到的应力分布是一致的,而径向应力变小。幼龄针叶材的应力分布是不同的,尤其是在髓心附近,轴向是拉应力而横向是压应力,可见原木直径对残余应变径向分布的重要作用。基于此,对本研究所测试的每个高度上原木直径进行了分类,分为最大、最小和中等直径。将每类直径所对应的残余应变径向分布绘制成图 3~6。
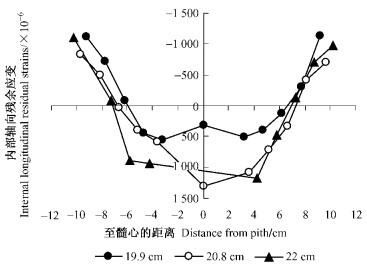
|
图 3 2.4 m内部轴向残余应变径向分布随树干直径变化曲线 Figure 3 Radial distribution of internal longitudinal residual strain with tree diameter changing at 2.4 m |

|
图 4 4.6 m内部轴向残余应变径向分布随树干直径变化曲线 Figure 4 Radial distribution of internal longitudinal residual strain with tree diameter changing at 4.6 m |

|
图 5 6.8 m内部轴向残余应变径向分布随树干直径变化曲线 Figure 5 Radial distribution of internal longitudinal residual strain with tree diameter changing at 6.8 m |

|
图 6 9.0 m内部轴向残余应变径向分布随树干直径变化曲线 Figure 6 Radial distribution of internal longitudinal residual strain with tree diameter changing at 9.0 m |
由图 3~6可以看出,从2.4到9.0 m,伴随树高增加原木直径的减小,残余应变分布曲线变得陡峭,即残余应变的变化梯度增大。同一高度上原木直径不同残余应变的变化梯度也有所不同。2.4和4.6 m其三类树干直径间(最大、最小和中等直径)残余应变变化梯度没有明显的差别和变化趋势,三类直径的残余应变分布曲线几乎重合。而6.8和9.0 m上,3条曲线明显分开,随着原木直径的减小,曲线的变化梯度呈增大趋势。而上文也曾提到,随着原木高度的增加曲线拟合后的相关性有下降的趋势。由此可以看出,原木直径存在某个临界值,当大于这个临界值时残余应变的变化梯度受直径影响较小,而小于这个临界值时,变化梯度会随着原木直径的减小而增大。在2.4和4.6 m处原木直径相对较大,直径的影响显现不出来,曲线的拟合也相对较好;而在6.8和9.0 m处,原木直径对残余应变的作用显现出来,造成曲线拟合的相关性降低。根据本研究结果,原木直径小于19.9 cm时,残余应变径向分布的变化梯度就随着直径的减小而变化愈加陡峭,当大于19.9 cm时,残余应变径向分布的变化梯度随着直径的增大而愈加平缓。由于测试的只是单一树种,测试样本较少,19.9 cm是否可以作为临界值,以及该结论能否适用于其他树种,还需做大量测试和研究来验证。但临界值存在的假设还是值得深入研究的。由此可见,树干内部残余应变受到树干直径的影响。在进行木材加工时,由于残余应力(应变)的径向分布模式使树干外部的板材处于收缩状态,而内部板材处于拉伸状态,这样的不平衡状态使板材出现弯曲和开裂等缺陷。直径越小的原木其板材的弯曲越严重(Okuyama et al., 1979)。可见原木直径是导致残余应变径向分布梯度变化进而影响板材出材率的重要原因;但原木直径究竟对残余应变径向变化梯度的影响有多大,还需做深入的研究。
当前为了提高原木锯解过程中板材的出材率,尽量使用大径级的原木是非常有效的方法,但鉴于当前大径级原木的短缺,如何有效利用小径级原木,实现小径积原木的高附加值利用就显得尤为重要。就人工林尾巨桉而言,根据本文得到的研究结果,在锯解直径小于19.9 cm原木段时,可选用对称下锯法,尽量锯解厚度较小的板材,这样可使得残余应力分布比较均匀,最大可能地减少开裂的产生。而进一步研究不同龄级、不同径级人工林尾巨桉内部残余应变径向分布模式与原木直径的关系,对于提高尾巨桉小径积原木的出材率和合理开发利用具有理论和现实意义。
3 结论本文采用“中心板锯割法"结合“应变片法"对人工林尾巨桉原木内部轴向残余应变径向分布进行了测试和研究,结果表明:
1) 原木内部轴向残余应变径向上分布沿髓心的对称性较好,在靠近树皮处为拉应变,向髓心方向拉应变逐渐减小,到某个树干半径后(0.681R)减为零值,随即转变为压应变,向髓心方向压应变逐渐增大;内部轴向残余应变径向分布的回归方程为:y=-21.075x2+4.529 7x+890.75(r=0.87),在0.01水平极显著相关;
2) 内部轴向残余应变在不同原木高度上的径向分布模式相似,均拟合为抛物线,回归曲线相关性均在0.01水平极显著,但相关性随着原木高度的增加而降低;
3) 原木直径影响内部轴向残余应变径向分布曲线的变化梯度,直径越小,曲线越陡峭。本研究首次提出原木直径对内部轴向残余应变径向变化梯度的影响具有一个临界值的观点,原木直径小于这个临界值时,随着直径的减小,内部轴向残余应变径向分布的变化梯度明显增大,对于本研究中的人工林尾巨桉木材,原木直径的可能临界值为19.9 cm。
李静辉, 关明星, 方广盛, 等. 1994. 树木生长应力与测试分析(Ⅱ)——非均质各向异性体. 东北林业大学学报, 22(1): 86-91. |
Archer R R, Byrnes F E. 1974. On the distribution of tree growth stresses. Part Ⅰ:An anisotropic plane strain theory. Wood Sci Technol, 8: 184-196. DOI:10.1007/BF00352022 |
Archer R R. 1976. On the distribution of tree growth stressesⅡ:Stresses due to asymmetric growth strains. Wood Sci Technol, 10: 293-309. |
Beck J L. 1974. Anisotropic theory of growth stresses. Phys and Engr Lab Dept Sci and Ind Res Lower Hutt New Zeal Rep, 452: 32. |
Boyd J D. 1950. Tree growth stresses Ⅰ. Growth stress evaluation. Australian Journal of Scientific Research, Series B, Biological Sciences, 3(3): 270-293. |
Boyd J D, Foster R C. 1974. Tracheid anatomy changes as responses to changing structural requirements of the tree. Wood Sci Technol, 8: 91-105. DOI:10.1007/BF00351365 |
Fournier M, Bordonne P A, Guitard D, et al. 1990. Growth stress patterns in tree stems. Wood Sci Technol, 24: 131-142. |
Gillis P P. 1973. Theory of growth stresses. Holzforschung, 27(6): 197-207. DOI:10.1515/hfsg.1973.27.6.197 |
Jacobs M R. 1938. The fibre tension of woody stems, with special reference to the genus Eucalyptus. Commonwealth Forestry Bureau, Australia, Bulletin, 22: 37. |
Kubler H. 1959a. Studies on growth stresses in trees. Part Ⅰ. The origin of growth stresses and the stresses in transverse direction. Holz als Roh-und Werkstoff, 17: 1-9. DOI:10.1007/BF02608827 |
Kubler H. 1959b. Studies on growth stresses in trees. Part Ⅱ. Longitudinal stresses. Holz als Roh-und Werkstoff, 17(2): 44-54. DOI:10.1007/BF02626321 |
Nicholson J E. 1973. Growth stress differences in Eucalyptus. Forest Science, 19(3): 169-174. |
Okuyama T, Kikata Y. 1975a. The residual stresses distribution in wood logs due to growth stresses. Mokuzai Gakkaishi, 21(5): 326-327. |
Okuyama T, Kikata Y. 1975b. The residual stresses distribution in wood logs measured by thin layer removal method. J Soc Mat Jap, 24: 845-848. DOI:10.2472/jsms.24.845 |
Okuyama T, Sasaki Y. 1978. The residual stresses in wood logs due to growth stresses(Ⅳ) The growth stresses piled in the trunk. Mokuzai Gakkaishi, 24(2): 77-84. |
Okuyama T, Sasaki Y. 1979. Crooking during lumbering due to residual stresses in the tree. Makuzai Gakkaishi, 25(11): 681-687. |
Post I L. 1979. An incremental longitudinal growth stress distribution model. Holzforschung, 33: 107-111. DOI:10.1515/hfsg.1979.33.4.107 |
Sasaki Y, Okuyama T, Kikata Y. 1981a. Determination of the residual stress in a cylinder of inhomogeneous anisotropic material Ⅱ. Mokuzai Gakkaishi, 27: 277-282. |
Sasaki Y, Okuyama T, Kikata Y. 1981b. Determination of the residual stress in a cylinder of inhomogeneous anisotropic material Ⅰ. Mokuzai Gakkaishi, 27(4): 270-276. |
Swaczyna I. 1979a. The effect of conversion and steaming on the deformation of green beech wood. Holztechnologie, 20(1): 17-22. |
Swaczyna I. 1979b. Influence of splitting on the degree and the position of linear deformations in swaing edge-grained boards. Holztechnologie, 20(3): 158-161. |
Vendhan C P, Archer R R. 1978. Relief of asymmetric growth stresses in logs. Holzforschung, 32(4): 123-127. DOI:10.1515/hfsg.1978.32.4.123 |
Wahyudi I, Okuyama T, Hadi Y S, et al. 1999. Growth stresses and strains in Acaia mangium. Forest Products Journal, 49(2): 77-81. |
Wahyudi I, Okuyama T, Hadi Y S, et al. 2001. Relationship between released strain and growth rate in 39 year-old Tectona grandis planted in Indonesia. Holzforschung, 55: 63-66. DOI:10.1515/HFSG.2001.63 |
Wilhelmy V, Kubler H. 1973. Probe for measurement of strain inside solid states. Exp Mech, 13: 142-144. DOI:10.1007/BF02323973 |
Wilkins A P, Kitahara R. 1991. Relationship between growth strain and rate of growth in 22 year-old Eucalyptus grandis. Australian Forestry, 54: 95-98. DOI:10.1080/00049158.1991.10674562 |
Wilson B F, Archer R R. 1977. Reaction wood:Induction and mechanical action. Ann Rev Plant Physial, 28: 23-43. DOI:10.1146/annurev.pp.28.060177.000323 |
 2009, Vol. 45
2009, Vol. 45



