2. 武汉理工大学自动化学院, 湖北 武汉 430070;
3. 深海技术科学太湖实验室, 江苏 无锡 214028
2. School of Automation, Wuhan University of Technology, Wuhan 430070, China;
3. Taihu Laboratory of Deepsea Technological Science, Wuxi 214028, China
遥控水下机器人(ROV)因其运动灵活、适应性好、作业能力强等优点,被广泛应用于海洋资源开发、深海打捞作业、核电检测等领域[1-2]。ROV通常配备有多台推进器,控制系统通过调节多台推进器转速实现多自由度的运动控制。
目前,ROV常用的推进方式有液压推进和电动推进2种。液压推进系统具有功率密度大、响应速度快等优点[3],但系统构成复杂,并且整体运行效率较低。与液压推进系统相比,电动推进系统的控制精度和运行效率都较高,其在ROV中的应用越来越广泛[4]。然而,许多电动推进的作业级ROV仍需要在其本体上搭载一套液压源和管路,为机械手、钻机等作业装置提供动力源。此时,液压源只有在作业情况下才会使用,而在其他情况下都处于停机状态,成为ROV的载荷负担。因此,有研究机构提出在这类ROV基础上增加液压推进器,构建新型的电动-液压混合推进系统,并分时利用液压源驱动液压推进器为ROV提供辅助推力,从而等效提高推进系统的功率密度,增强ROV的航行运动能力。通常,ROV被设计为过驱动系统,即推进器数量要多于其运动自由度[5],所以需要结合合适的推力分配算法才能发挥推进系统的作用。
经过多年发展,在水下机器人、水面动力定位平台、无人机、空间飞行器等装备领域[6-8],已经形成了多种技术成熟的推力分配策略。其中,伪逆法和直接分配法较早被应用于推力分配问题的求解,它们均是计算过程简单、实时性高的方法[9-10]。在配置固定方位推进器的ROV中,伪逆法的应用更加广泛。然而,基于伪逆法的推力分配未考虑推进器的物理约束,导致其计算结果可能超出推进器的推力限制,出现过饱和现象。因此,文[11]提出对输入量进行归一化处理以避免推力过饱和问题,该方式简单实用,但也在一定程度上降低了推进系统的推力利用率。相比于对输入量进行缩放处理,再分配伪逆法[12]、级联伪逆法[13]和多步分配法[14]等方法则利用数学规划模型对伪逆法的计算结果进行了二次分配优化,这种避免推力过饱和的解决方式更加优越。与伪逆法相比,二次规划(QP)和序列二次规划(SQP)方法的计算更复杂、适用范围更广,可用于求解含转速加速度限制、回转速率限制等约束的全回转推进系统的推力分配问题[15-16]。此外,许多智能优化算法,如遗传算法[17]、蜂群算法[18]、粒子群优化(PSO)算法[19]、和声搜索算法[20]、强化学习算法[21]等也被用于推力分配问题的求解。这些算法虽然能够高精度地求解各种复杂的线性/非线性推力分配问题,但普遍存在实现复杂、实时性差及对处理器性能要求高的缺陷。上述各种推力分配策略本质上是利用数学优化方法进行线性/非线性问题求解,需要建立推力分配问题的精确数学模型,并将推力分配过程中应该考虑的因素定量表达在数学模型中。对于新型的电动-液压混合推进系统,由于系统中2种推进器的特性及作用不同,因此在推力分配过程中应考虑期望推力变化快慢、当前电动-液压推进系统推力等状态,以发挥出电动推进系统效率高、功率配置大和液压推进系统响应速度快的组合优势,并在一定程度上实现对2种推进系统的均衡使用。这种复杂的使用需求所对应的推力分配目标函数,难以用精确的数学公式表达,且无法直接引用已有的推力分配策略。目前,尚未见到有关混合推进系统推力分配的研究文献。而在电池-超级电容复合电源储能领域,有非常成熟的能量管理策略[22-24],其设计思想可以为混合推进系统的推力分配提供参考。对复合电源的2种储能装置进行充放电管理时,应综合考虑总需求功率、2种储能装置的特性、剩余电量等因素进行决策。
针对电动-液压混合推进型ROV,为发挥液压推进系统和电动推进系统的组合优势,本文借鉴电动汽车的复合电源能量管理思想,结合2种推进系统的推力性能,提出了一种基于模糊逻辑的多级推力分配策略,并搭建了混合推进ROV仿真模型,对所提推力分配策略的可行性进行了测试验证。
2 混合推进系统推力分配问题(Thrust allocation problem of the hybrid propulsion system) 2.1 混合推进系统配置以某作业级ROV为研究对象,重点研究其水平面的推力分配问题。采用右手空间坐标系建立ROV的运动坐标系o-xyz,取ROV的重心作为坐标系的原点,并且假设ROV的几何中心位于坐标系的
|
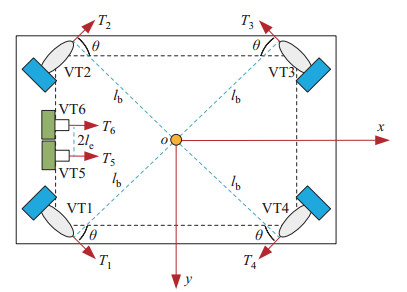
图 1 推进器布置俯视图 Fig.1 Arrangement of the thrusters (top view) |
图 1中,VT1~VT4为4台呈X型对推布置的电动推进器,电动推进器与ROV纵轴的夹角均为
| $ \begin{align} \begin{cases} \tau_{x} =T_{1} \cos \theta +T_{2} \cos \theta -T_{3} \cos \theta -\\ \phantom{\tau_{x} = } T_{4} \cos \theta +T_{5} +T_{6} \\ \tau_{y} =T_{1} \sin \theta -T_{2} \sin \theta -T_{3} \sin \theta +T_{4} \sin \theta \\ \tau_{n} =-T_{1} l_{\rm b} +T_{2} l_{\rm b} -T_{3} l_{\rm b} +T_{4} l_{\rm b}- \\ \phantom{\tau_{n} = } T_{5} l_{\rm e} +T_{6} l_{\rm e} \end{cases} \end{align} $ | (1) |
其中,
| $ \begin{align} \mathit{\boldsymbol{\tau}} =\mathit{\boldsymbol{BT}}= [\mathit{\boldsymbol{B}}_{1} \; \; \mathit{\boldsymbol{B}}_{2}]\mathit{\boldsymbol{T}} \end{align} $ | (2) |
其中,
| $ \begin{align} \mathit{\boldsymbol{B}}_{1} & =\begin{bmatrix} \cos \theta & \cos \theta & -\cos \theta & -\cos \theta \\ \sin \theta & -\sin \theta & -\sin \theta & \sin \theta \\ -l_{\rm b} & l_{\rm b} & -l_{\rm b} & l_{\rm b} \end{bmatrix} \end{align} $ | (3) |
| $ \begin{align} \mathit{\boldsymbol{B}}_{2} & =\begin{bmatrix} 1 & 1 \\ 0 & 0 \\ l_{\rm e} & -l_{\rm e} \end{bmatrix} \end{align} $ | (4) |
| $ \begin{align} \mathit{\boldsymbol{\tau}} & =[\tau_{x} \; \; \tau_{y} \; \; \tau_{n} ]^{\rm T} \end{align} $ | (5) |
| $ \begin{align} \mathit{\boldsymbol{T}} & =[T_{1} \; \; T_{2} \; \; T_{3} \; \; T_{4} \; \; T_{5} \; \; T_{6} ]^{\rm T} \end{align} $ | (6) |
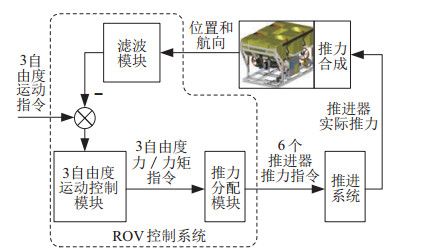
ROV通过控制系统调节6台推进器转速实现其水平面的运动控制,系统工作原理如图 2所示。
|
图 2 ROV控制系统工作原理 Fig.2 Working principle of the ROV control system |
图 2中,ROV控制系统主要由滤波模块、3自由度运动控制模块和推力分配模块组成。首先,滤波模块对传感器输出的位置、航向等数据进行预处理;然后,3自由度运动控制模块根据指令位置和航向,计算所需要的期望力及力矩;最后,推力分配模块依据期望力及力矩,结合一定的推力分配规则确定每台推进器需要产生的期望推力为
| $ \begin{align} [ T_{{\rm d}1} \; \; T_{{\rm d}2} \; \; T_{{\rm d}3} \; \; T_{{\rm d}4} \; \; T_{{\rm d}5} \; \; T_{{\rm d}6} ]^{\rm T}={\mathit{\boldsymbol{f}}}(\tau_{{\rm d}x}, \tau_{{\rm d}y}, \tau_{{\rm d}n}) \end{align} $ | (7) |
其中,
该ROV的电动推进系统是主运动驱动系统,能够提供较大的纵向力、横向力和转艏力矩,并且运行效率高,但受供电电流的限制,其响应速度较慢;液压推进系统产生转艏力矩的效果较差,主要用于提供一定的纵向力,其功率不大,但响应速度较快。如何通过推力分配策略发挥2种推进系统的组合优势是本文研究的核心。
3 基于模糊逻辑的多级推力分配策略(Multi-level thrust allocation method based on fuzzy logic) 3.1 主要思想依据电动推进系统和液压推进系统的功能及特性,结合ROV推力需求、当前2种推进系统的推力状态等因素,提出混合推进系统推力分配过程中应遵循如下思想原则:
(1) 当ROV期望纵向力的变化率较大时,尽量由液压推进系统提供较大比例的纵向力增量,以利用其快响应的特性。
(2) 当ROV期望纵向力的变化率较小时,主要从降低能耗的角度确定纵向力增量的分配比例。此时,若期望纵向力及其变化量方向相同,则优先采用电动推进系统提供较大比例的纵向力增量;反之,则尽量利用液压推进系统抵消反向的纵向力增量。
(3) 同时,应依据2种推进系统的当前状态,适当调整纵向力增量的分配比例,达到一定的负载均衡效果。
(4) 在推力分配过程中,还需考虑2个推进系统的极限能力,对期望纵向力在2个系统间的分配值进行修正,以充分利用2种推进系统的能力。
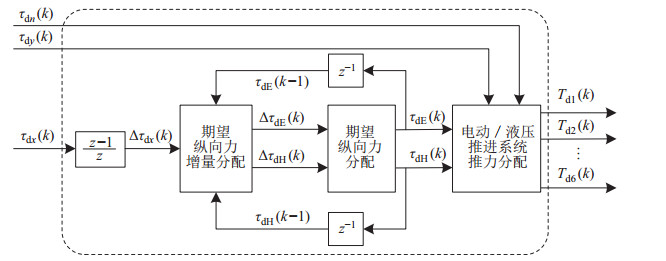
依据上述思想原则,设计一种包括期望纵向力增量分配、期望纵向力分配以及电动-液压推进系统推力分配的3级推力分配架构,如图 3所示。
|
图 3 多级推力分配框图 Fig.3 Block diagram of the multi-level thrust allocation |
图 3中,多级推力分配策略的实现流程为:首先,将
期望纵向力增量分配是多级推力分配策略的关键环节,需要依据期望纵向力增量、当前的电动推进系统推力及液压推进系统推力等参数,确定增量在2种推进系统之间的分配值。该分配过程是个3输入、2输出的决策问题,且很难用精确的数学关系描述输入输出关系。而由于模糊逻辑方法不依赖于研究过程的精确数学模型(通过规则表表达人类的知识经验),就能够基于当前状态进行模糊推理,达到模仿人脑的决策效果,非常适用于本文的应用场合,因此本文引入模糊理论,设计3维Mamdani型模糊控制器进行期望纵向力增量的分配。模糊控制器的输入为
| $ \begin{align} \begin{cases} \Delta \tau_{\rm dH} (k)=K_{\rm H} (k)\times \Delta \tau_{{\rm d}x} (k) \\ \Delta \tau_{\rm dE} (k)=(1-K_{\rm H} (k))\times \Delta \tau_{{\rm d}x} (k) \end{cases} \end{align} $ | (8) |
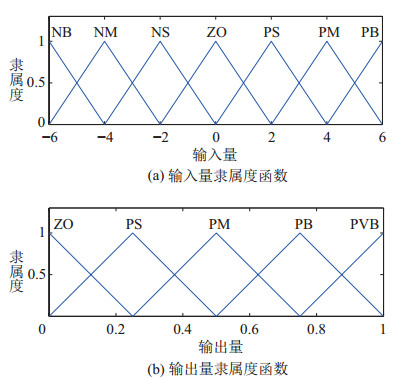
模糊控制器3个输入量的模糊论域均为
|
图 4 模糊隶属度函数 Fig.4 Fuzzy membership functions |
模糊控制规则表是模糊控制器的核心,本模糊控制器的规则表规模为7
|
|
表 1 当 |
由于
理论上,根据
| $ \begin{align} \begin{cases} \tau_{\rm dE} (k)=\tau_{\rm dE} (k-1)+\Delta \tau_{\rm dE} (k) \\ \tau_{\rm dH} (k)=\tau_{\rm dH} (k-1)+\Delta \tau_{\rm dH} (k) \end{cases} \end{align} $ | (9) |
然而,通过式(9) 计算的
| $ \begin{align} \tau_{\rm dE} (k)& = \begin{cases} 0, & |\tau_{\rm dH} (k)|>|\tau_{\rm dE} (k)| \\ \tau_{\rm dH} (k)+\tau_{\rm dE} (k), & \text{其他} \end{cases} \end{align} $ | (10) |
| $ \begin{align} \tau_{\rm dH} (k)& = \begin{cases} \tau_{\rm dH} (k)+\tau_{\rm dE} (k), & |\tau_{\rm dH} (k)|>|\tau_{\rm dE} (k)| \\ 0, & \text{其他} \end{cases} \end{align} $ | (11) |
由于推进系统的物理限制,式(9)~(11) 计算的期望值还可能超过对应推进系统的能力,因此需要进一步修正计算结果。记液压推进器和电动推进器的推力范围分别为
| $ \begin{align} \tau_{{\rm H}\max} =2\times T_{{\rm H}\max} \end{align} $ | (12) |
电动推进系统可以产生横向力、纵向力和转艏力矩,其产生纵向力的能力与期望产生的横向力及转艏力矩相关。由于考虑到液压推进系统也可以提供一定的纵向力,因此在计算电动推进系统产生纵向力的能力时,优先让电动推进系统产生期望的转艏力矩和横向力,并在所有推进器推进能力均未饱和的情况下才尽量产生满足需求的纵向力。记电动推进系统产生的实际纵向力与其期望纵向力的比例为
| $ \begin{align} \begin{bmatrix} T_{{\rm d}1} \\ T_{{\rm d}2} \\ T_{{\rm d}3} \\ T_{{\rm d}4} \end{bmatrix}=\mathit{\boldsymbol{B}}_{1}^{+} \begin{bmatrix} 0 \\ \tau_{{\rm d}y} (k) \\ \tau_{{\rm d}n} (k) \end{bmatrix}+p \mathit{\boldsymbol{B}}_{1}^{+} \begin{bmatrix} \tau_{{\rm d}x} (k) \\ 0 \\ 0 \end{bmatrix} \end{align} $ | (13) |
其中,
| $ \begin{align} \mathit{\boldsymbol{B}}_{1}^{+} =\mathit{\boldsymbol{B}}_{1}^{\rm T} (\mathit{\boldsymbol{B}}_{1} \mathit{\boldsymbol{B}}_{1}^{\rm T})^{-1} \end{align} $ | (14) |
采用线性规划方法可以求解
| $ \begin{align} \begin{cases} -T_{{\rm E}\max} \leqslant T_{{\rm d}1} \leqslant T_{{\rm E}\max}\\ -T_{{\rm E}\max} \leqslant T_{{\rm d}2} \leqslant T_{{\rm E}\max} \\ -T_{{\rm E}\max} \leqslant T_{{\rm d}3} \leqslant T_{{\rm E}\max}\\ -T_{{\rm E}\max} \leqslant T_{{\rm d}4} \leqslant T_{{\rm E}\max}\\ 0\leqslant p\leqslant 1 \end{cases} \end{align} $ | (15) |
此时,可以得到电动推进系统能够沿其期望纵向力方向产生的最大推力为
| $ \begin{align} \tau_{{\rm E}\max} (k)=p_{\max} \times \tau_{{\rm d}x} (k) \end{align} $ | (16) |
为充分利用混合推进系统的推力,当一种推进系统能够产生的最大纵向力不足其期望纵向力时,应对其分配的期望值进行修正,并尽量采用另一种推进系统进行补偿。因此,依据2种推进系统能够产生的最大纵向力,将期望纵向力的分配结果进一步修正为
| $ \begin{align} &\tau_{\rm dE} (k)= \begin{cases} {\rm{sgn}} \tau_{\rm dE} (k)\times \tau_{{\rm E}\max}, &\kern -28mm |\tau_{\rm dE} (k)|>|\tau_{{\rm E}\max} (k)| \\ \tau_{\rm dE} (k), &\kern -28mm |\tau_{\rm dE} (k)|\leqslant |\tau_{{\rm E}\max} (k)| \text{ 且 } |\tau_{\rm dH} (k)|\leqslant |\tau_{{\rm H}\max} | \\ {\rm{sgn}} \tau_{\rm dE} (k)\times \min ( | \tau_{{\rm E}\max} (k) | , | \tau_{\rm dH} (k) + \tau_{\rm dE} (k) -{\rm{sgn}} \tau_{\rm dH} (k)\times \tau_{{\rm H}\max} |), & \text{其他} \end{cases} \end{align} $ | (17) |
| $ \begin{align} &\tau_{\rm dH} (k)= \begin{cases} {\rm{sgn}} \tau_{\rm dH} (k)\times \tau_{{\rm H}\max}, &\kern -5mm |\tau_{\rm dH} (k)|>|\tau_{{\rm H}\max} | \\ \tau_{\rm dH} (k), &\kern -5mm |\tau_{\rm dH} (k)|\leqslant |\tau_{{\rm H}\max} | \text{ 且 } |\tau_{\rm dE} (k)|\leqslant |\tau_{{\rm E}\max} (k)| \\ {\rm{sgn}} \tau_{\rm dH} (k)\times \min (\tau_{{\rm H}\max}, |\tau_{\rm dH} (k) + \tau_{\rm dE} (k) -\tau_{{\rm E}\max} (k) | ), & \text{其他} \end{cases} \end{align} $ | (18) |
其中,
经过期望纵向力分配后,可分别得到电动推进系统和液压推进系统期望的力/力矩,从而将复杂的混合推进系统推力分配问题分解为2个单一推进系统的推力分配问题。对于电动推进系统,其期望的力及力矩分别为
| $ \begin{align} \begin{bmatrix} T_{{\rm d}1} (k) \\[-1pt] T_{{\rm d}2} (k) \\[-1pt] T_{{\rm d}3} (k) \\[-1pt] T_{{\rm d}4} (k) \end{bmatrix}=\mathit{\boldsymbol{B}}_{1}^{+} \begin{bmatrix} \tau_{\rm dE} (k) \\ \tau_{{\rm d}y} (k) \\ \tau_{{\rm d}n} (k) \end{bmatrix} \end{align} $ | (19) |
已知液压推进系统的期望力为
| $ \begin{align} \begin{bmatrix} T_{{\rm d}5} (k) \\[-1pt] T_{{\rm d}6} (k) \end{bmatrix}=\frac{1}{2}\times \begin{bmatrix} \tau_{\rm dH} (k) \\[-1pt] \tau_{\rm dH} (k) \end{bmatrix} \end{align} $ | (20) |
至此,得到每台推进器的指令推力,多级推力分配过程结束。
4 仿真实验(Simulation experiments)为验证所提多级推力分配策略的有效性,在Matlab/Simulink中搭建电动-液压混合推进的作业级ROV仿真模型,并分别采用本文策略和传统单一伪逆法进行ROV混合推进系统的推力分配,比较2种推力分配策略的ROV闭环控制仿真结果。
4.1 混合推进ROV仿真模型混合推进ROV仿真模型由ROV动力学模型、ROV运动学模型、海流扰动模型、电动推进系统模型、液压推进系统模型、运动控制模型、推力分配模型和推力合成模型组成。
依据ROV的设计参数及其水动力性能的CFD(computational fluid dynamics)评估结果,给出ROV尺寸、质量、转动惯量以及主要水动力系数,如表 2所示。水动力系数的数学意义请见文[25]。
|
|
表 2 ROV主要参数 Tab. 2 Main parameters of the ROV |
电动推进系统仿真模型中包含4台相同的电动推进器模型,电动推进器模型采用1阶惯性环节简化近似,其惯性时间常数取1.6 s,推力(单位N)范围为
| $ \begin{align} T_{i} (s)= \begin{cases} \dfrac{T_{{\rm d}i} (s)}{1.6 s+1}, & i=1, 2, 3, 4 \\[6pt] \dfrac{T_{{\rm d}i} (s)}{0.5 s+1} \left(1-\dfrac{T_{i} (s)}{10000}\right), & i=5, 6 \end{cases} \end{align} $ | (21) |
采用本文策略建立推力分配仿真模型,根据推进器的理论最大推力和布置方式,可以计算出液压推进系统和电动推进系统能够产生的纵向力范围分别为
| $ \begin{align} \begin{bmatrix} T_{{\rm d}1} \\[-2pt] T_{{\rm d}2} \\[-2pt] T_{{\rm d}3} \\[-2pt] T_{{\rm d}4} \\[-2pt] T_{{\rm d}5} \\[-2pt] T_{{\rm d}6} \end{bmatrix} =\begin{bmatrix} 0.3536 & 0.25 & 0.25 \\[-2pt] 0.3536 & -0.25 & -0.25 \\[-2pt] -0.3536 & -0.25 & 0.25 \\[-2pt] -0.3536 & 0.25 & -0.25 \\[-2pt] 0 & 0.147 & 0 \\[-2pt] 0 & 0.147 & 0 \end{bmatrix} \begin{bmatrix} \tau_{{\rm d}x} (k) \\[-2pt] \tau_{{\rm d}y} (k) \\[-2pt] \tau_{{\rm d}n} (k) \end{bmatrix} \end{align} $ | (22) |
ROV水平面控制模型中包含3个带输出限幅的PID(比例积分微分)调节器,分别用于实现纵向位置、横向位置和航向的控制。其中,纵向PID调节器的系数分别为1000、50和3000,输出范围为
仿真过程中,设置海流大小为0.2 kn,方向45
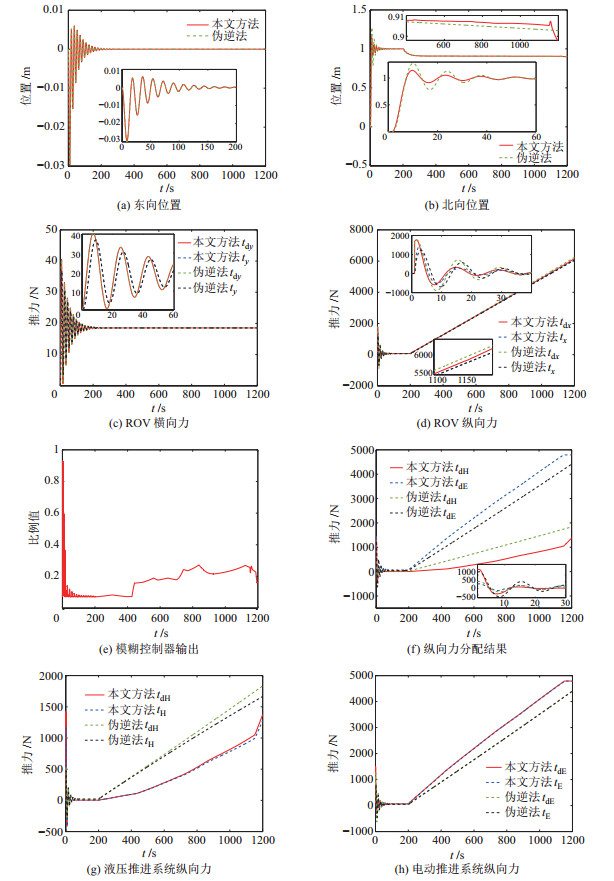
|
图 5 斜坡扰动下的仿真结果 Fig.5 Simulation results under slope disturbance |
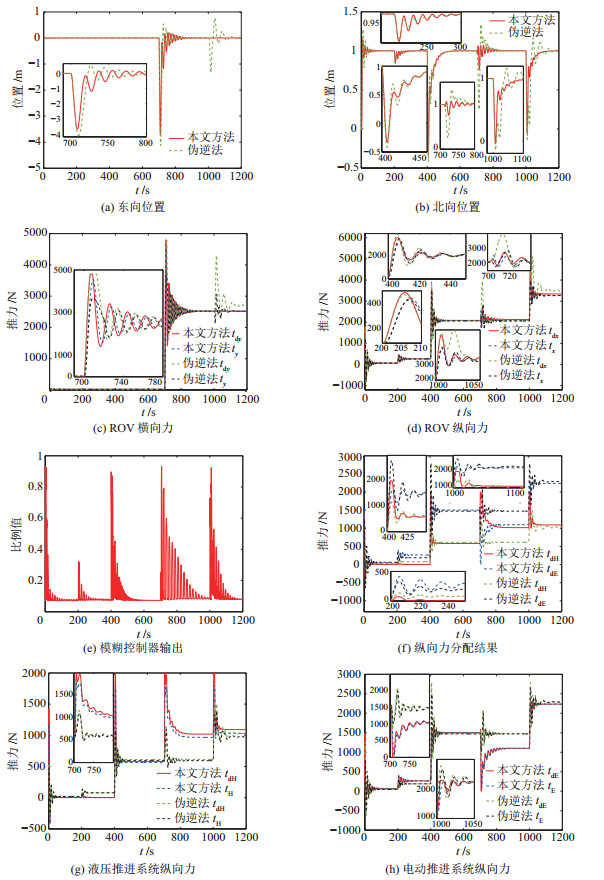
|
图 6 阶跃扰动下的仿真结果 Fig.6 Simulation results under step disturbances |
图 5(a)中,采用2种推力分配策略的ROV东向位置变化曲线完全一致,对应2种策略下的ROV期望横向力也完全吻合,如图 5(c)所示。图 5(c)还显示,推进系统产生的实际横向力滞后于其期望横向力,这主要是由电动推进器的惯性特性导致的。
图 5(b)的ROV阶跃响应仿真结果表明,采用本文策略的ROV阶跃响应的快速性和超调量都要优于采用伪逆法的ROV。结合图 5(d)可知,在给定阶跃位置指令时,ROV期望纵向力会快速增大至约1800 N,而此时采用本文策略的ROV产生的实际纵向力的增大速率更大,从而使ROV阶跃响应的快速性更好。同时,在阶跃响应上升期间,采用本文策略的ROV产生实际纵向力的滞后时间明显小于采用伪逆法的ROV,因而前者具有更小的超调。图 5(b)中,在第200 s施加斜坡扰动后,采用2种策略的ROV北向位置均会出现波动,并且稳态后的位置误差均缓慢增大。在斜坡扰动影响下,采用本文策略的ROV在大部分时间都更接近目标位置,然而其位置在第1170 s出现一定的波动,并且波动后的位置误差逐渐超过采用伪逆法的ROV位置误差。ROV出现位置误差的主要原因是PID调节器不能完全消除时变扰动导致的控制偏差。此外,推进系统惯性及液压推进系统推力损失等因素导致的推力偏差可等效为对ROV施加的扰动,从而引起ROV在斜坡扰动下的位置误差逐渐增大。结合图 5(d)可知,在斜坡扰动下,采用2种策略的ROV产生的实际纵向力非常接近,而采用伪逆法的ROV实际纵向力与期望纵向力之间的推力偏差大于采用本文策略的ROV,并且在前1170 s的推力偏差变化率也更大,因此采用伪逆法的ROV的位置误差也更大;在第1170 s时,采用本文策略的ROV产生的推力偏差变化率出现了一定的突变,引起其位置出现小幅度波动。
分析图 5(e)和图 5(f)可知,在整个仿真过程中,采用伪逆法分配给电动推进系统和液压推进系统的期望纵向力比例保持恒定,结合式(22) 不难得出该比例为0.294,而采用本文策略能够动态调节期望纵向力增量在2种推进系统之间的分配比例。在ROV阶跃响应初期,当ROV对纵向力有较大的突增需求时,本文策略能够迅速增大液压系统的分配比例,利用液压推进系统提供大部分的推力,发挥其快速响应的优势;随着ROV位置的收敛,期望纵向力的波动幅度也逐渐减小,本文策略分配给液压推进系统的期望纵向力迅速减小,主要利用电动推进系统提供绝大部分的推力,从而起到节能作用。图 5(e)和图 5(f)还表明,在ROV受斜坡扰动过程中,2种策略下的期望纵向力均主要由电动推进系统提供。在此过程中,本文策略将期望纵向力增量分配给液压推进系统的比例曲线整体上呈先增大、后略微降低的趋势,实现了一定负载均衡的效果,同时分配比例在大部分时间都小于0.294,有利于节省能源。此外,还可以发现,在电动推进系统达到输出极限后,本文策略能够直接将后续期望纵向力增量完全分配至液压推进系统,如图 5(f)中第1170 s时的仿真结果所示。
结合图 5(g)和图 5(h)可以进一步解释图 5(d)中推力偏差和图 5(b)中位置误差的原因。在斜坡扰动阶段,电动推进系统的实际纵向力与其期望纵向力保持极小的偏差,而液压推进系统产生实际推力的偏差与其推力大小正相关,意味着将期望纵向力增量分配给液压推进系统的比例越大,则引起ROV位置误差的变化率也越大。因此,在前1170 s,采用本文策略的ROV的位置误差更小且变化更缓慢,随着电动推进系统在1170 s达到输出饱和后,其位置误差变化率也同步增大。
图 6(a)和图 6(b)的仿真结果表明,在第200 s、400 s和1000 s施加纵向扰动时,采用本文策略的ROV北向位置出现短期波动,但东向位置保持不变;而采用伪逆法的ROV不仅北向位置出现波动,还会在第1000 s出现东向位置波动。在第700 s施加横向扰动时,采用2种策略均会出现ROV东向位置和北向位置曲线同时波动的现象。对比采用2种策略的ROV位置控制效果可知,采用本文策略的ROV在小扰动下的位置波动略大于采用伪逆法的,但在其他几组不同幅度扰动下它的位置波动均更小。
结合图 6(c)(d)进行分析,对于采用本文策略的ROV,在第700 s受到横向扰动时,ROV期望纵向力及实际纵向力会出现波动,进而导致ROV出现北向位置波动。进一步可以分析,采用本文策略的ROV在第700 s受到扰动后的短时动态调整流程如下:首先,施加横向扰动会导致其东向位置出现偏差;然后,在对应PID调节器的作用下,输出期望横向力快速达到4807 N,而图 6(d)表明此前电动推进系统需产生的纵向力已经达到2100 N左右,显然电动推进系统不能同时提供4807 N的横向力和2100 N的纵向力;此时,在本文分配策略的作用下,会优先利用电动推进系统提供4807 N的横向力,同时大幅度降低电动推进系统的期望纵向力,并提高分配给液压推进系统的期望力,以尽量使ROV实际纵向力满足期望值;但由于推进器的物理特性,因此在推进系统推力动态调整过程中的实际纵向力不能实时满足期望值,进而引起ROV北向位置出现波动;随后,又经过短暂的调节,采用本文策略的ROV逐渐恢复至目标位置,推力分配结果也达到新的稳态。对于采用伪逆法的ROV,在第700 s出现北向位置波动和第1000 s出现东向位置波动的主要原因是伪逆法没有考虑推进器的物理限制,导致混合推进系统沿纵向和横向产生的实际推力均达不到期望推力,进而引起位置波动,具体调节过程不再赘述。
图 6(e)和图 6(f)的仿真结果表明,在第400 s施加小扰动情况下,ROV期望纵向力变化缓慢,本文策略分配给液压推进系统的推力经过动态调整后保持在0附近,并通过电动推进器提供所需的纵向力,从而通过适当降低接近目标位置时的控制性能以达到节能目的,更符合实际ROV工程应用中的使用需求;当ROV期望纵向力出现快速变化时,本文策略会优先通过液压推进系统提供较大比例的增量,从而使整个ROV对大扰动有更强的抗干扰能力。图 6(f)的仿真结果还表明,在本文推力分配策略作用下,电动推进系统能够产生的纵向力的上限是动态变化的,例如在第700 s和第1000 s的最大纵向力分别约为0 N和2200 N。可见,在优先满足期望横向力和转艏力矩需求的条件下,通过评估电动推进系统产生纵向力的能力,再由液压推进系统来补充不足的纵向力,这样既可以实现整个混合推进系统的充分利用,又可以在一定程度上降低混合推进系统产生的不同方向力/力矩之间的耦合。
5 结论(Conclusion)针对某电动-液压混合推进ROV,依据混合推进系统的配置方案对2种推进系统的特点及使用原则进行了分析,并提出了一种基于模糊逻辑的多级推力分配策略。仿真结果表明本文策略针对大幅度突变期望纵向力,能够优先采用液压推进系统提供大比例的推力,以发挥其快速响应的优点,从而使ROV具有较好的快速性和抗干扰性;对变化率较小的期望纵向力,本文策略能够结合系统的状态进行决策,使ROV在接近目标位置的情况下尽量节能,满足实际工程使用需求;同时,该策略还在一定程度上降低了混合推进系统产生的不同方向力/力矩之间的耦合,有利于减弱由于推进系统产生预期之外的力/力矩给ROV运动造成的不良影响。采用本文策略的ROV在运动响应速度、运动耦合度、抗干扰能力、节能等方面具有良好的综合性能。
后续的研究工作主要有:(1) 结合混合推进ROV实物开展水池试验,进一步测试推力分配策略的综合性能;(2) 细化和改进混合推进系统的使用原则,并对推力分配策略中模糊控制规则表、比例因子等进行优化。
| [1] |
Dong M J, Chou W S, Yao G D. A new navigation strategy for underwater robot in reactor pool combined propeller speed detection and dynamics analysis with sonar data correction[J]. Journal of Nuclear Science and Technology, 2018, 55(1): 1-10. DOI:10.1080/00223131.2017.1372229 |
| [2] |
Zhao C Y, Thies P R, Johanning L. Investigating the winch performance in an ASV/ROV autonomous inspection system[J]. Applied Ocean Research, 2021, 115. DOI:10.1016/j.apor.2021.102827 |
| [3] |
田烈余, 周锋, 张培豪, 等. 液压推进型水下机器人的运动控制方法研究[J]. 机电工程, 2018, 35(7): 694-697. Tian L Y, Zhou F, Zhang P H, et al. Motion control method of underwater vehicle with hydraulic thrusters[J]. Journal of Mechanical & Electrical Engineering, 2018, 35(7): 694-697. |
| [4] |
Huo X X, Zhang C W, Ge T, et al. Nonlinear correction of a hydraulic propulsion system used in deep-sea work-class ROVs[J]. Journal of Ship Mechanics, 2019, 23(12): 1500-1515. |
| [5] |
Blond M, Simon D, Creuze V, et al. Optimal thrusters steering for dynamically reconfigurable underwater vehicles[J]. International Journal of Systems Science, 2019, 50(12): 2348-2361. DOI:10.1080/00207721.2019.1655603 |
| [6] |
Chen C, Zhang J Y, Wang N, et al. Conversion control of a tilt tri-rotor unmanned aerial vehicle with modeling uncertainty[J]. International Journal of Advanced Robotic Systems, 2021, 18(4). DOI:10.1177/17298814211027033 |
| [7] |
Yu P K, Su Y, Gerber M J, et al. An over-actuated multi-rotor aerial vehicle with unconstrained attitude angles and high thrust efficiencies[J]. IEEE Robotics and Automation Letters, 2021, 6(4): 6828-6835. DOI:10.1109/LRA.2021.3095035 |
| [8] |
Tsopelakos A, Papadopoulos E. Design and evaluation of dynamic positioning controllers with parasitic thrust reduction for an overactuated floating platform[J]. IEEE Transactions on Control Systems Technology, 2017, 25(1): 145-160. DOI:10.1109/TCST.2016.2554060 |
| [9] |
Johansen T A, Fossen T I. Control allocation -- A survey[J]. Automatica, 2013, 49(5): 1087-1103. DOI:10.1016/j.automatica.2013.01.035 |
| [10] |
Lang X Y, de Ruiter A. Distributed optimal control allocation for 6-dof spacecraft with redundant thrusters[J]. Aerospace Science and Technology, 2021, 118. DOI:10.1016/j.ast.2021.106971 |
| [11] |
李新飞, 马强, 袁利毫, 等. 矢量推进水下机器人的推力分配方法[J]. 哈尔滨工程大学学报, 2018, 39(10): 1605-1611. Li X F, Ma Q, Yuan L H, et al. Thrust allocation method of underwater robots with vector propulsion[J]. Journal of Harbin Engineering University, 2018, 39(10): 1605-1611. |
| [12] |
Bui P V, Kim Y B. Development of constrained control allocation for ship berthing by using autonomous tugboats[J]. International Journal of Control, Automation and Systems, 2011, 9: 1203-1208. DOI:10.1007/s12555-011-0622-4 |
| [13] |
Zhang Y K, Li Z, Cheng Z T, et al. Attitude tracking control reconfiguration for space launch vehicle with thrust loss fault[J]. IEEE Access, 2019, 7: 184353-184364. DOI:10.1109/ACCESS.2019.2959836 |
| [14] |
Sun G W, Xie J R, Qu J Q, et al. Multistep thrust allocation method based on priority idea for remotely operated vehicle with horizontal thrusters configured as X shape[J]. International Journal of Advanced Robotic Systems, 2022, 19(2). DOI:10.1177/17298806221090077 |
| [15] |
赵言锋, 林明星, 代成刚, 等. ROV水动力性能及推力控制分配研究与仿真[J]. 中国科学: 技术科学, 2020, 50(3): 287-298. Zhao Y F, Lin M X, Dai C G, et al. Research and simulation of ROV hydrodynamic performance and thrust control distribution[J]. Scientia Sinica Technologica, 2020, 50(3): 287-298. |
| [16] |
Witkowska A, Śmierzchalski R. Adaptive dynamic control allocation for dynamic positioning of marine vessel based on backstepping method and sequential quadratic programming[J]. Ocean Engineering, 2018, 163: 570-582. DOI:10.1016/j.oceaneng.2018.05.061 |
| [17] |
夏国清, 刘彩云, 陈兴华, 等. 基于NSGA-Ⅱ的DP船舶推力分配方法研究[J]. 华中科技大学学报(自然科学版), 2019, 47(5): 101-104. Xia G Q, Liu C Y, Chen X H, et al. Study on thrust allocation method based on NSGA-Ⅱ for DP ship[J]. Journal of Huazhong University of Science and Technology (Natural Science Edition), 2019, 47(5): 101-104. |
| [18] |
Wu D F, Ren F K, Zhang W D. An energy optimal thrust allocation method for the marine dynamic positioning system based on adaptive hybrid artificial bee colony algorithm[J]. Ocean Engineering, 2016, 118: 216-226. DOI:10.1016/j.oceaneng.2016.04.004 |
| [19] |
Zheng F Y, Liu L W, Chen Z M, et al. Hybrid multi-objective control allocation strategy for compound high-speed rotorcraft[J]. ISA Transactions, 2020, 98: 207-226. |
| [20] |
Yadav P, Kumar R, Panda S K, et al. Optimal thrust allocation for semisubmersible oil rig platforms using improved harmony search algorithm[J]. IEEE Journal of Oceanic Engineering, 2014, 39(3): 526-539. |
| [21] |
Kolaric P, Lopez V G, Lewis F L. Optimal dynamic control allocation with guaranteed constraints and online reinforcement learning[J]. Automatica, 2020, 122. DOI:10.1016/j.automatica.2020.109265 |
| [22] |
王琪, 孙玉坤, 罗印升. 混合动力电动汽车的复合电源功率分配控制策略[J]. 电工技术学报, 2017, 32(18): 143-151. Wang Q, Sun Y K, Luo Y S. A power distribution control strategy of hybrid energy storage system in hybrid electric vehicles[J]. Transactions of China Electrotechnical Society, 2017, 32(18): 143-151. |
| [23] |
Mamun A A, Liu Z F, Rizzo D M, et al. An integrated design and control optimization framework for hybrid military vehicle using lithium-ion battery and supercapacitor as energy storage devices[J]. IEEE Transactions on Transportation Electrification, 2019, 5(1): 239-251. |
| [24] |
Zhang Q, Cheng X L, Liao S Y. Implementation of a predictive energy management strategy for battery and supercapacitor hybrid energy storage systems of pure electric vehicles[J]. Journal of Intelligent & Fuzzy Systems, 2021, 41(2): 2539-2549. |
| [25] |
施生达. 潜艇操纵性[M]. 北京: 国防工业出版社, 2021. Shi S D. Maneuverability of submarine[M]. Beijing: National Defense Industry Press, 2021. |
 2023, Vol. 45
2023, Vol. 45


