2. 立命馆大学机器人系, 日本 滋贺 525-8577
2. Department of Robotics, Ritsumeikan University, Shiga 525-8577, Japan
随着陆地上可再生的资源逐渐减少,海洋中蕴含的大量资源成为人类竞相开发和研究的新对象。水下机器人能够在海洋开发中的探查、监控、搜救和维护等环节发挥重要作用,已成为海洋技术研究的热点。传统的水下机器人如自主水下航行器(AUV)和遥控无人潜水器(ROV)等已经获得了广泛的实际应用[1]。但运动效率问题一直是这类机器人实现在水下长期自主运行的主要挑战之一。仿生水下蛇形机器人由多个关节组成,具有非常灵活的身体,在运动效率、功能执行、环境适应、自主学习等方面相比AUV和ROV更具优势,因此具有巨大的潜在价值和广阔的应用前景[2-3]。
目前,国内外诸多研究机构开展了水下蛇形机器人的研究,其中包括中国科学院沈阳自动化研究所研发的水陆两栖蛇形机器人“探查者Ш”[4]、日本东京工业大学Hirose等[5]研制的水陆两栖蛇形机器人ACM-R5、瑞士洛桑联邦理工学院科研团队研发的水下蛇形机器人AmphiBot Ⅲ[6]、挪威科技大学Pettersen等[7]研发的Mamba等。这些水下蛇形机器人主要通过关节摆动模仿蛇的曲线运动来产生驱动力,这种仿生运动具有运动效率高、噪声小的优势,但是也存在如下缺点:1) 仿生运动模式下,水下蛇形机器人的移动速度较慢;2) 仿生运动依靠关节的摆动产生驱动力,当处于限制摆动的狭小空间时,机器人不能产生足够的驱动力使自身前进;3) 当关节损坏或是被物体缠绕时,机器人无法有效运动。
为解决上述问题、提升蛇形机器人的水下运动能力,本文将在水下领域广泛应用的推进器与蛇形机器人相结合,改进其推进方式:首先,在水下蛇形机器人的尾部安装推进器,产生沿机器人身体方向的线性力,这样能够显著提高水下蛇形机器人的前进速度[8-9];其次,当水下蛇形机器人进入狭窄空间或遭遇个别关节损坏时,机器人无法使用仿生运动方式前进,但可以通过尾部单独的推进器提供动力;再者,合理配置水下蛇形机器人上的推进器的位置和数量,不仅可以提高其前向速度,还可以提高其灵活性、机动性和操控性,以及提供悬停能力[10-11]。
为最大程度地提升带有推进器的水下蛇形机器人的运动效率,本文对带有推进器的水下蛇形机器人的高效运动模式展开研究。目前关于水下蛇形机器人的运动效率的研究主要涉及机器人结构设计和运动步态优化两方面。结构设计方面,文[12]在水下蛇形机器人尾部增加被动尾鳍可将航行速度提升1倍;文[13-14]通过实验证明背鳍、尾鳍可以显著提高水下蛇形机器人的航行速度和运动效率;文[15-16]设计了基于板簧的蛇形机器人关节架构,提高了蛇形机器人的运动效率。运动步态优化方面,韩国大邱庆北科学技术院学者提出一种步态分解方法,将蛇形机器人步态进行分类,从而调整参数至最优[17]。挪威科技大学团队则提出通过多目标优化问题来研究水下蛇形机器人的高效运动步态参数。以前向速度和功耗为优化目标,采用粒子群优化(PSO)算法实现多目标优化,从而获得水下蛇形机器人仿生步态(蜿蜒步态和仿鳗步态)的Pareto最优解集[18]。从中可以发现选定不同的步态参数对仿生运动的平均功耗和前进速度影响很大,但是文[18]研究对象并不包含推进器。另外,该团队也研究了带有推进器的水下蛇形机器人的运动情况,实验结果表明在同等速度下,仅靠推进器推进时的能量消耗小于仿生运动时的、以及仿生运动与推进器结合运动时的能量消耗[8]。但是该实验尚有一些不完善之处:首先,由于实验中的运动参数(包括仿生运动参数和推进器推力)为人工选取所得,因此选取的参数很有可能不是运动效率最优的组合,从而导致实验结果存在一定的片面性;此外,其实验平台采用的蛇形机器人不具有尾鳍,在仿生运动模式下的运动效率较低[12]。
针对上述研究存在的问题,本文提出基于优化算法,研究带有推进器的水下蛇形机器人的运动效率问题。首先通过迭代牛顿-欧拉法[19]对水下蛇形机器人进行动力学建模,然后考虑到步态参数和推进器推力对水下蛇形机器人的速度和能耗的影响,采用非支配排序遗传(NSGA-Ⅱ)算法[20]对运动参数进行仿真优化,最终获得不同能耗、切向速度下的最优运动参数组合。此外,还探究了不同性能的推进器对水下蛇形机器人运动效率的影响。
2 水下蛇形机器人建模(Modeling of underwater snake robot)对于关节具有多个自由度的水下蛇形机器人,采用迭代牛顿-欧拉法对其进行动力学建模。最早由Kelasidi等[21]将迭代牛顿-欧拉法应用在水下蛇形机器人建模中。迭代牛顿-欧拉法常用于解决给定操作臂末端运动轨迹求解关节力矩等问题,具有简洁、计算量小等优势。
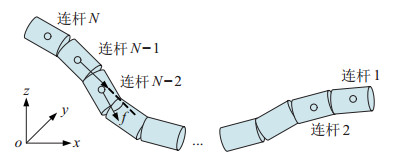
水下蛇形机器人模型如图 1所示,每个连杆长度为2
|
图 1 运动学相关参数 Fig.1 Kinematics parameters |
连杆
| $ \begin{align} {}^{j}\mathit{\boldsymbol{\beta}}_{j} ={}^{j}\mathit{\boldsymbol{f}}_{{\rm e}j} + \begin{bmatrix} {}^{j}\mathit{\boldsymbol{\omega}}_{j} \times \left({}^{j}\mathit{\boldsymbol{\omega}}_{j} \times {}^{j}{{M\mathit{\boldsymbol{}}}}\; {{S\mathit{\boldsymbol{}}}}_{j}\right) \\ {}^{j}\mathit{\boldsymbol{\omega}}_{j} \times \left({}^{j}\mathit{\boldsymbol{J}}_{j} \; {}^{j}\mathit{\boldsymbol{\omega}}_{j}\right) \end{bmatrix} \end{align} $ | (1) |
其中
从水下蛇形机器人的尾部到头部迭代计算,得到各连杆与科氏加速度和转动惯量有关的矩阵
| $ \begin{align} {}^{j}\mathit{\boldsymbol{J}}_{j}^{\rm c} ={}^{j}\mathit{\boldsymbol{J}}_{j} +{}^{j+1}\mathit{\boldsymbol{T}}_{j}^{\rm T} \; {}^{j+1}\mathit{\boldsymbol{J}}_{j+1}^{\rm c} {}^{j+1}\mathit{\boldsymbol{T}}_{j} \end{align} $ | (2) |
其中
根据空间惯量矩阵,逆向迭代可以求解出连杆
| $ \begin{align} {}^{j}\mathit{\boldsymbol{\beta}}_{j}^{\rm c} ={}^{j}\mathit{\boldsymbol{\beta}}_{j} +{}^{j+1}\mathit{\boldsymbol{T}}_{j}^{\rm T} \; {}^{j+1}\mathit{\boldsymbol{\beta}}_{j+1}^{\rm c} +{}^{j+1}\mathit{\boldsymbol{T}}_{j}\; {}^{j+1}\mathit{\boldsymbol{J}}_{j+1}^{\rm c} \; {}^{j+1}\mathit{\boldsymbol{r}}_{j} \end{align} $ | (3) |
其中
在逆向迭代的最后一步可以得出头部相对于全局参考系(标记为0)的加速度:
| $ \begin{align} {}^{0}\mathit{\boldsymbol{\dot{V}}}_{0} =-{}^{0}\mathit{\boldsymbol{J}}_{0}^{\rm c}\; {}^{0}\mathit{\boldsymbol{\beta}}_{0}^{\rm c} \end{align} $ | (4) |
然后对系统进行一次从头部至尾部的正向迭代,计算出水下蛇形机器人各关节的加速度旋量和关节力旋量:
| $ \begin{align} {}^{j}\mathit{\boldsymbol{\dot{V}}}_{j} & ={}^{j}\mathit{\boldsymbol{T}}_{j-1} \; {}^{j-1}\mathit{\boldsymbol{\dot{V}}}_{j-1} +{}^{j}\mathit{\boldsymbol{r}}_{j} \end{align} $ | (5) |
| $ \begin{align} {}^{j}\mathit{\boldsymbol{f}}_{j} & ={}^{j}\mathit{\boldsymbol{J}}_{j}^{\rm c} \; {}^{j}\mathit{\boldsymbol{\dot{V}}}_{j} +{}^{j}\mathit{\boldsymbol{\beta}}_{j}^{\rm c} \end{align} $ | (6) |
最终可以得到关节处的力矩:
| $ \begin{align} ^{j}{\mathit{\boldsymbol{\varGamma}}}_{j} ={}^{j}\mathit{\boldsymbol{g}}_{j}\; {}^{j}\mathit{\boldsymbol{f}}_{j} +\mathit{\boldsymbol{I}}_{{\rm a}j}\; {}^{j}\mathit{\boldsymbol{\dot{W}}}_{j} \end{align} $ | (7) |
其中
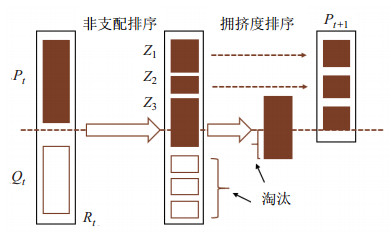
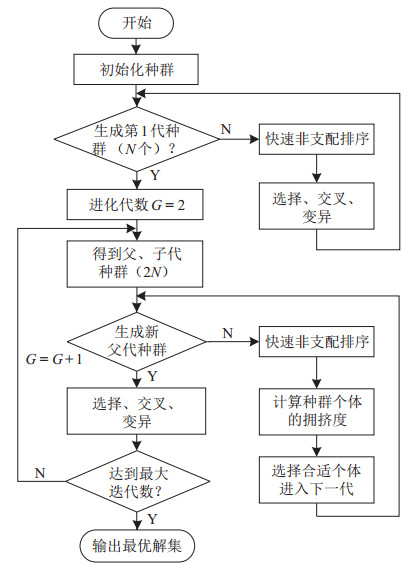
NSGA-Ⅱ算法是由Deb等[24]于2000年提出的基于快速非支配排序的遗传算法,相较于传统NSGA算法,其时间复杂度降低了1个量级,并加入精英策略确保最优秀的个体得到保存,同时提出拥挤度的概念,保证了种群多样性[25]。NSGA-Ⅱ算法求得的Pareto最优解分布均匀,具有良好的收敛性和鲁棒性,是求解多目标优化问题的一种常用方法[26-27]。非支配排序和拥挤度排序流程图如图 2所示,NSGA-Ⅱ算法流程图如图 3所示,具体流程描述如下:
|
图 2 非支配排序和拥挤度排序流程图 Fig.2 Flow chart of non-dominated sorting and congestion sorting |
|
图 3 NSGA-Ⅱ算法流程图 Fig.3 Flow chart of NSGA-Ⅱ algorithm |
步骤1:随机初始化父代种群
步骤2:对
步骤3:对
步骤4:对分好等级的非支配解集按拥挤距离进行排序,取拥挤度最高的前
步骤5:重复步骤2~4,直至满足结束条件。
3.2 高效运动评价指标采用运输经济度量法评价运动效率。此方法是将运输消耗能量与运动速度的比值作为评价标准,评价公式如式(8) 所示:
| $ \begin{align} \eta =\frac{P_{\rm av}} {v_{t}} \end{align} $ | (8) |
本文的研究对象为带有推进器的水下蛇形机器人,式(8) 中的平均能耗
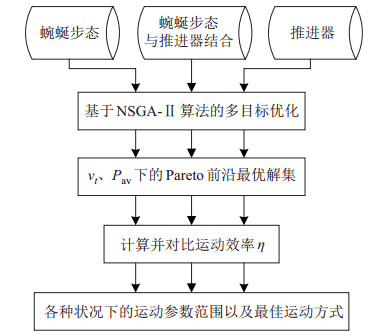
基于运输经济中的效率指标来衡量蛇形机器人的运动方式是否高效,这种评判方法将指标分解为2个部分,切向速度和总功率,能够有效地避免效率指标单一导致的数值发散问题,将效率优化问题转换为多目标优化——同时满足切向速度最大和总功率最小。此外,蛇形机器人动力学模型复杂,求解数值解对计算的硬件要求高并且耗费时间长。因此,本文采用NSGA-Ⅱ算法快速、高效地优化这两项指标。为了方便应用NSGA-Ⅱ算法,仿真中规定与蛇形机器人实际运动方向相反的方向为正方向,也就是当蛇形机器人达到运动速度数值的最小值时,实际运动速度为最大,这样可以通过NSGA-Ⅱ算法求解使切向速度和总功率同时最小的Pareto前沿最优解集。根据优化结果计算并分析各种情况下的运动效率
|
图 4 基于NSGA-Ⅱ算法的多目标优化流程图 Fig.4 Flow chart of multi-objective optimization based on NSGA-Ⅱ algorithm |
以典型的仿生运动步态——蜿蜒步态——为研究重点,对比分析水下蛇形机器人在结合推进器和不结合推进器时的运动性能。其中,蜿蜒步态的给定函数如下:
| $ \begin{align} \phi_{i} =\alpha \sin (\omega t+(i-1)\beta)+\gamma, \; \; \; i=1, 2, \cdots, N-1 \end{align} $ | (9) |
式中
由于蛇形机器人蜿蜒步态下各参数与运动速度的关系已经被广泛研究和探讨[28-31],因此本文不再关注各参数与速度的关系,而是将重点放在运动参数的最优分布上。研究中选取4个参数作为变量,即关节运动幅值
| $ \begin{equation} 0\leqslant \alpha \leqslant 1, \; \; \; 0\leqslant \omega \leqslant {\rm{ \mathsf{ π} }}, \; \; \; 0\leqslant \beta \leqslant {\rm{ \mathsf{ π} }} /2, \; \; \; 0 \leqslant F_{t} \leqslant 1 \end{equation} $ | (10) |
在Matlab 2019a中运行NSGA-Ⅱ多目标优化算法对带有推进器的水下蛇形机器人进行仿真实验。其中优化算法的交叉概率设为0.9,变异概率设为0.1。蛇形机器人运动仿真和实验的基本参数如表 1所示[19]。
|
|
表 1 蛇形机器人基本参数 Tab. 1 Basic parameters of the snake robot |
共分3种情况进行仿真。1) 蜿蜒模式:蛇形机器人只采用蜿蜒步态游动,这时前进的动力来自身体与水的相互作用;2) 推进器模式:仅由推进器推进前行,即蛇形机器人的关节不转动,前进的所有动力来自尾部的推进器;3) 混合模式:蜿蜒运动与推进器推进相结合的混合运动模式,这时二者共同为蛇形机器人提供前进的动力。
首先优化蜿蜒模式下的Pareto解集,部分参数值如表 2所示。可以看到,在蜿蜒模式下水下蛇形机器人的最快速度为
|
|
表 2 蜿蜒模式下的Pareto解集 Tab. 2 Pareto set of the lateral undulation mode |
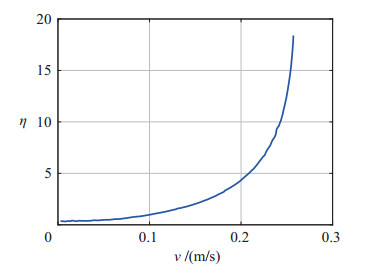
|
图 5 蜿蜒模式下的效率-速度关系 Fig.5 Efficiency-velocity relationship in the lateral undulation mode |
推进器模式(推力系数
|
|
表 3 推进器模式( |
混合模式下的Pareto解集如表 4所示,从中可以看出,混合运动模式下,最优相位偏差在0.65~0.7 rad之间,最优相位幅值在0.3~0.5 rad之间,且最优幅值随着推进器推力的增大而呈现减小的趋势。
|
|
表 4 混合模式( |
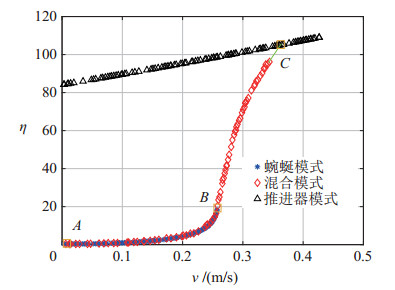
将3种运动情况下的最优效率-速度关系绘制于图 6。由于推力限定在1 N的范围内,在混合模式下,水下蛇形机器人的速度将无法达到推进器模式下的速度,因此人为延长趋势线(图中绿线部分)。
|
图 6 蜿蜒模式、混合模式( |
从图 6可以看出,蜿蜒模式下的运动效率最高,在同等速度下,蜿蜒模式的
为了探究不同性能的推进器对水下蛇形机器人运动效率的影响,在仿真中给定不同的
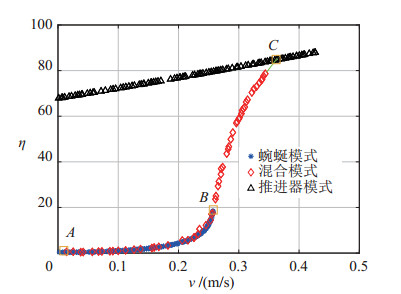
|
图 7 蜿蜒模式、混合模式( |
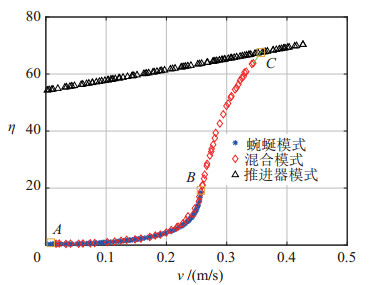
|
图 8 蜿蜒模式、混合模式( |
|
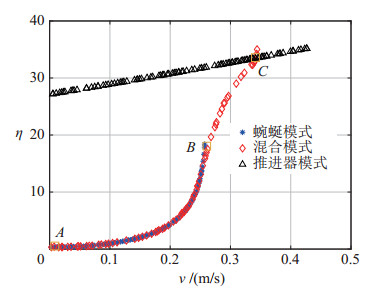
图 9 蜿蜒模式、混合模式( |
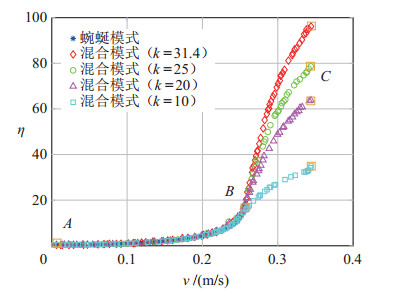
图 10为不同
|
图 10 不同推进器参数下混合模式的效率-速度关系 Fig.10 Efficiency-velocity relationship in the hybrid mode with different thruster parameters |
以提高带有推进器的水下蛇形机器人运动效率为目标,本文根据上述实现结果,首次提出了一种高效运动模式:低速阶段,蜿蜒运动具有最高的运动效率,因此宜采用蜿蜒步态;中速阶段,混合运动效率最高,应当采用蜿蜒运动与推进器相结合的运动方式;高速阶段,则由推进器直接推进。
5 实验分析(Experimental analysis)根据仿真优化的结果,搭建带有推进器的水下蛇形机器人(图 11)作为实验平台。其中为提高水下蛇形机器人蜿蜒运动效率,在蛇形机器人的尾部添加了柔性尾鳍[32]。实验验证之前,在水池中先后进行了机器人的防水测试和多次配重的调整,保证其入水后的安全性和浮力中性状态。

|
图 11 尾部带有推进器的水下蛇形机器人 Fig.11 Underwater snake robot with a rear thruster |
实验中采用数字式多功能功率计测量平台的整体输入功率。速度测量系统基于Open CV计算机视觉库,使用罗技C920 1080p摄像头作为视觉采集设备,摄像头与电脑上位机互传数据,能够实时显示当前画面,如图 12所示。此系统通过识别蛇形机器人的头部特征,在上位机上实时描绘跟踪物体的运动轨迹、计算跟踪物体的位移和速度。

|
图 12 视觉测量上位机界面 Fig.12 Interface of the host computer for visual measurement |
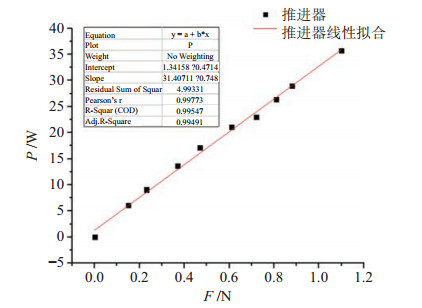
实验平台所选用的泵喷式推进器如图 13所示,为了精确计算推进器能耗,对所采用的推进器进行了水下实验,测试其功率与推力之间的关系,测试平台如图 14所示,测量结果如图 15所示。从中可以看出,推进器的功率与推力基本成线性关系,拟合数据得到推进器功率公式:
| $ \begin{align} P=31.4 \times F_{t} +1.34 \end{align} $ | (11) |

|
图 13 泵喷推进器实物图 Fig.13 Physical photo of the pump-jet thruster |

|
图 14 推力测试平台 Fig.14 Thrust testing platform |
|
图 15 推进器功率和推力曲线图 Fig.15 Curve of the power and the force of the thruster |
在初始状态为静水的水池环境中对3种运动模式分别进行实验,每组运动参数均测3次取其平均值作为实验结果。其中,每次通过摄像头测量蜿蜒运动最后1个周期内的平均速度,通过功率表测量运动过程的平均功率。实验给定参数及测量结果如表 5~7所示。
|
|
表 5 蜿蜒模式下给定参数及测量数值表 Tab. 5 Table of the given parameters and the measurements in the lateral undulation mode |
|
|
表 6 混合模式下给定参数及测量数值表 Tab. 6 Table of the given parameters and the measurements in the hybrid mode |
|
|
表 7 推进器模式下给定参数及测量数值表 Tab. 7 Table of the given parameters and the measurements in the thruster mode |
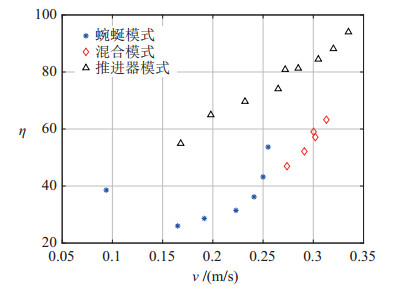
为了实现蛇形机器人的防水,在转动关节处采用动轴密封技术,具体为使用O圈和油封圈挤压转动轴,这会极大增大转动轴的摩擦力,带来较多的无用功。此外,线路损耗和关节内部齿轮加工精度不足也会造成功率的损失。经过与无动轴密封的蛇形机器人损耗进行对比,从电机到蛇形机器人关节的传动效率约为70%,采用有效做功作为新的功率计量值,绘制速度-功率关系图,如图 16所示。
|
图 16 蜿蜒模式、混合模式以及推进器模式下的效率-速度关系 Fig.16 Efficiency-velocity relationship in the lateral undulation mode, hybrid mode and thruster mode |
对比图 16中蜿蜒模式和混合模式两种运动方式的效率-速度曲线,可以看出混合模式下的水下蛇形机器人可以实现比蜿蜒模式下更快的速度。对比混合模式和推进器模式下的运动曲线,可以发现同一速度下,蛇形机器人采用混合模式比推进器模式具有更高的运动效率。实验结果与仿真结果吻合。
实验结果与仿真结果均证实了本文所提运动模式的有效性。在低速运动阶段,蜿蜒模式运动效率最高;中速阶段,蜿蜒运动与推进器推进相结合的混合运动模式更为高效;高速阶段,推进器直接推进运动效率更高。而文[8]通过仿真和实验得到如下2个结论:1) 推进器对水下蛇形机器人的速度提升起到关键作用;2) 相比仿生运动和混合运动,水下蛇形机器人仅使用尾部推进器可以实现更快的运动速度和更低的能耗。本文认同其结论1) 中推进器对速度提升起到至关重要的作用,但认为结论2) 具有两方面的局限性。首先,文[8]在实验中人为给定了水下蛇形机器人的运动参数,没有对运动参数进行优化;其次,该实验平台采用的无尾鳍水下蛇形机器人在仿生运动模式下的运动效率较低。本文针对这两点局限,采用NSGA-Ⅱ算法优化水下蛇形机器人的运动参数,并在实验样机的尾部添加尾鳍,使样机具有更高的运动效率。此外,本文选用的推进器为泵喷式推进器,与文[8]选用的螺旋式推进器相比,泵喷式推进器可以与尾部关节融合设计,所以不会带来额外的阻力,具有更高的推进效率。实验结果证明,相较于推进器模式,水下蛇形机器人在中低速下蜿蜒模式和混合模式的能耗更低。
6 结论(Conclusion)基于优化算法研究尾部带有推进器的水下蛇形机器人的高效运动模式,并设计了带有尾鳍的高效样机进行实验验证。首先考虑仿生步态参数和推进器对水下蛇形机器人的平均功耗、前进速度的影响,通过NSGA-Ⅱ算法对上述运动参数进行优化,获得不同能耗和切向速度下的最优参数组合;还通过仿真给出了不同性能的推进器对水下蛇形机器人运动效率的影响。最终,仿真和实验结果均表明,带有推进器的水下蛇形机器人在蜿蜒运动和推进器直接推进时具有不同的运动效率,且这两种运动方式的运动速度区间也不相同。因此,为了最大程度地发挥带有推进器的水下蛇形机器人的运动能力,提高运动效率,首次提出了一种高效运动模式,即:低速运动阶段,采用蜿蜒模式;中速阶段,采用蜿蜒运动与推进器推进相结合的混合运动模式;高速阶段,采用推进器直接推进的方式。
为提高实验所用蛇形机器人样机的运动效率,在样机上添加了柔性尾鳍,因此实验结果能够更好地体现所提出的高效运动模式的有效性。除增加柔性尾鳍以外,未来还将从如下方面提升运动效率:提高蛇形机器人整体外形的水动力效率;改进驱动器到转动轴扭矩的传输效率,如取消齿轮减速驱动,采用直接驱动,提高驱动器的运行效率;改进控制策略,以实现对关节运动轨迹的精准控制,从而生成更好的仿生步态,如基于端到端位置前馈控制的方法[33];以及改进防水方案、减小转动轴摩擦力,也能减少部分不必要的损耗,从而提升整体的运动效率。
| [1] |
Wiens A J. Gait optimization for a multilink anguilliform swimmer[D]. Montreal, Canada: McGill University, 2013.
|
| [2] |
Pettersen K Y. Snake robots[J]. Annual Reviews in Control, 2017(44): 19-44. |
| [3] |
张安翻. 仿鳗鱼机器人运动控制方法与高效率步态研究[D]. 北京: 中国科学院大学, 2018. Zhang A F. Modeling and control of an eel robot and its high efficiency gait[D]. Beijing: University of Chinese Academy of Sciences, 2018. |
| [4] |
Li B, Ma S G, Ye C L, et al. Development of an amphibious snake-like robot[C]//8th World Congress on Intelligent Control and Automation. Piscataway, USA: IEEE, 2010: 613-618.
|
| [5] |
Hirose S, Yamada H. Snake-like robots: Machine design of biologically inspired robots[J]. IEEE Robotics and Automation Magazine, 2009, 16(1): 88-98. DOI:10.1109/MRA.2009.932130 |
| [6] |
Porez M, Boyer F, Ijspeert A J. Improved lighthill fish swimming model for bio-inspired robots: Modelling, computational aspects and experimental comparisons[J]. International Journal of Robotics Research, 2014, 33(10): 1322-1341. DOI:10.1177/0278364914525811 |
| [7] |
Liljebäck P, Stavdahl O, Pettersen K Y, et al. Mamba -- A waterproof snake robot with tactile sensing[C]//IEEE/RSJ International Conference on Intelligent Robots and Systems. Piscataway, USA: IEEE, 2014: 294-301.
|
| [8] |
Kelasidi E, Pettersen K Y, Liljebäck P, et al. Locomotion efficiency of underwater snake robots with thrusters[C]//IEEE International Symposium on Safety, Security, and Rescue Robotics. Piscataway, USA: IEEE, 2016: 174-181.
|
| [9] |
Kelasidi E, Moe S, Pettersen K Y, et al. Path following, obstacle detection and obstacle avoidance for thrusted underwater snake robots[J]. Frontiers in Robotics and AI, 2019, 6(57). DOI:10.3389/frobt.2019.00057 |
| [10] |
Sverdrup-Thygeson J, Kelasidi E, Pettersen K Y, et al. Modeling of underwater swimming manipulators[C]//10th IFAC Conference on Control Applications in Marine Systems. Laxenburg, Austria: IFAC, 2016: 81-88.
|
| [11] |
Liljeback P, Mills R. Eelume: A flexible and subsea resident IMR vehicle[C]//OCEANS. Piscataway, USA: IEEE, 2017. DOI: 10.1109/OCEANSE.2017.8084826.
|
| [12] |
Kelasidi E, Kohl A M, Pettersen K Y, et al. Experimental investigation of locomotion efficiency and path-following for underwater snake robots with and without a caudal fin[J]. Annual Reviews in Control, 2018, 46: 281-294. DOI:10.1016/j.arcontrol.2018.10.001 |
| [13] |
Huang Z, Ma S G, Lin Z M, et al. Impact of caudal fin geometry on the swimming performance of a snake-like robot[J]. Ocean Engineering, 2022, 245. DOI:10.1016/j.oceaneng.2021.110372 |
| [14] |
Huang Z, Ma S G, Bagheri H, et al. The impact of dorsal fin design on the swimming performance of a snake-like robot[J]. IEEE Robotics and Automation Letters, 2022, 7(2): 4939-4944. DOI:10.1109/LRA.2022.3153903 |
| [15] |
Kakogawa A, Kawabata T, Ma S G. Plate-springed parallel elastic actuators for efficient movement of a planar snake robot[C]//IEEE/ASME International Conference on Advanced Intelligent Mechatronics. Piscataway, USA: IEEE, 2019: 235-240.
|
| [16] |
Kakogawa A, Kawabata T, Ma S G. Plate-springed parallel elastic actuator for efficient snake robot movement[J]. IEEE/ASME Transactions on Mechatronics, 2021, 26(6): 3051-3063. DOI:10.1109/TMECH.2021.3052037 |
| [17] |
Song B, Ju S, Yun D. Snake robot gait decomposition and gait parameter optimization[DB/OL]. (2021-12-03)[2022-02-22]. https://arxiv.org/abs/2112.02057v1.
|
| [18] |
Kelasidi E, Jesmani M, Pettersen K Y, et al. Multi-objective optimization for efficient motion of underwater snake robots[J]. Artificial Life and Robotics, 2016, 21(4): 411-422. DOI:10.1007/s10015-016-0332-3 |
| [19] |
Khalil W, Gallot G, Boyer F. Dynamic modeling and simulation of a 3-D serial eel-like robot[J]. IEEE Transactions on Systems, Man, and Cybernetics, Part C, 2007, 37(6): 1259-1268. DOI:10.1109/TSMCC.2007.905831 |
| [20] |
郑强. 带精英策略的非支配排序遗传算法的研究与应用[D]. 杭州: 浙江大学, 2006. Zheng Q. Elitist non-dominated sorting genetic algorithm and its application[D]. Hangzhou: Zhejiang University, 2006. |
| [21] |
Kelasidi E, Pettersen K Y, Gravdahl J T, et al. Modeling of underwater snake robots[C]//IEEE International Conference on Robotics and Automation. Piscataway, USA: IEEE, 2014: 30-37.
|
| [22] |
Morison J R, Johnson J W, Schaaf S A. The force exerted by surface waves on piles[J]. Journal of Petroleum Technology, 1950, 2(5): 149-154. DOI:10.2118/950149-G |
| [23] |
李立, 王明辉, 李斌, 等. 蛇形机器人水下3D运动建模与仿真[J]. 机器人, 2015, 37(3): 336-342. Li L, Wang M H, Li B, et al. Modeling and simulation of snake robot in 3D underwater locomotion[J]. Robot, 2015, 37(3): 336-342. |
| [24] |
Deb K, Pratap A, Agarwal S, et al. A fast and elitist multi-objective genetic algorithm: NSGA-Ⅱ[J]. IEEE Transactions on Evolutionary Computation, 2002, 6(2): 182-197. DOI:10.1109/4235.996017 |
| [25] |
李莉. 基于遗传算法的多目标寻优策略的应用研究[D]. 苏州: 江南大学, 2008. Li L. Application research on multi-objectives optimization based on the genetic algorithm[D]. Suzhou: Jiangnan University, 2008. |
| [26] |
Deb K, Thiele L, Laumanns M, et al. Scalable test problems for evolutionary multi-objective optimization[M]. Berlin, Germany: Springer, 2002.
|
| [27] |
Deb K, Sundar J. Reference point based multi-objective optimization using evolutionary algorithms[C]//Genetic and Evolutionary Computation Conference. New York, USA: ACM, 2006: 635-642.
|
| [28] |
McIsaac K A, Ostrowski J P. Motion planning for anguilliform locomotion[J]. IEEE Transactions on Robotics and Automation, 2003, 19(4): 637-652. DOI:10.1109/TRA.2003.814495 |
| [29] |
Vela P A, Morgansen K A, Burdick J W. Second order averaging methods for oscillatory control of underactuated mechanical systems[C]//American Control Conference. Piscataway, USA: IEEE, 2002: 4672-4677.
|
| [30] |
Melli J B, Rowley C W, Rufat D S. Motion planning for an articulated body in a perfect planar fluid[J]. SIAM Journal on Applied Dynamical Systems, 2006, 5(4): 650-669. DOI:10.1137/060649884 |
| [31] |
Yu J Z, Wang L, Shao J Y, et al. Control and coordination of multiple biomimetic robotic fish[J]. IEEE Transactions on Control Systems Technology, 2006, 15(1): 176-183. |
| [32] |
Kelasidi E, Pettersen K Y, Gravdahl J T, et al. Modeling and propulsion methods of underwater snake robots[C]//IEEE Conference on Control Technology and Applications. Piscataway, USA: IEEE, 2017: 819-826.
|
| [33] |
Yang X, Zhu W L, Zhu Z W, et al. Design, assessment, and trajectory control of a novel decoupled robotic nanomanipulator[J]. IEEE/ASME Transactions on Mechatronics. DOI: 10.1109/TMECH.2022.3147767.
|
 2023, Vol. 45
2023, Vol. 45


