1 引言（Introduction）

经肛内镜微创手术（TEM）与经括约肌径路手术（York-Mason术）、经骶尾径路手术（Kraske术）和黏膜剥离切除手术（EMR）相比，具有无需外部切口、切除效率高、术后患者恢复快，能切除直肠较深部位肿瘤等优点^[1]。但是手术工具特殊的细长形状增加了手术的难度，医生难以进行缝合、打结等复杂操作。使用高灵活度的手术机器人代替刚性工具可以有效降低手术的操作难度并提高操作精度、稳定性。TEM手术作为一种单孔手术，要求手术器械的体积小、灵活度高，同时具有一定的负载能力。经肛直肠镜是在该手术中创造工作空间的主要工具，所有手术工具都通过经肛直肠镜进入人体，因此柔性机器人的结构设计需要遵循一定的尺寸指标。直肠镜的最大内径为40 mm，在双臂操作的情况下，单个柔性机器人弯曲时偏离轴线不得超过20 mm，直肠镜尾部的操作孔直径为15 mm，为了方便前后进给操作，要求单个柔性臂的最大直径不得超过13 mm，经肛直肠镜的内部长度为120 mm，手术器械的动作区段长度不可超过此长度限制。此外，为了避免手术器械遮挡内窥镜视野，需要以弯曲状态进行手术操作，要求单个柔性臂的末端可实现60$ ^{\circ} $的弯曲。

目前，国内外许多研究机构都在进行柔性手术器械的研究，并且大多采用了柔性体与线传动模式结合的结构。Berthet-Rayne等^[2]提出了一种带有轮齿的滚动接触式关节机器人，以横向和纵向关节相互穿插连接的方式实现正交方向的弯折动作；哈尔滨工业大学的Wang等^[3]针对鼻腔手术提出了一种以镍钛合金丝驱动，并用离散的刚性杆件加以约束的结构；Hu等^[4]提出了一种螺旋弹簧状结构的柔性机器人，并施加滚动约束以限制弹簧的轴向形变，通过2段独立的柔性区段实现高灵活度，可以完成复杂的手术缝合操作；上海交通大学的徐凯等^[5]提出了一种无铰链关节、以镍钛骨架为主体的蛇形柔性臂，采用被离散刚性圆盘约束的镍钛合金丝驱动，单个柔性臂具有2段独立的弯折区段；哈尔滨工业大学的杨文龙等^[6-7]设计了一种带有柔性骨架的切口式杆件连续性机械臂，并基于此结构建立了柔性连续性机器人的力感知模型；Leibrandt等^[8]设计了一种滚动接触式关节柔性臂结构，并提出了一种非线性校准模型用于将关节映射到执行器空间提高控制性能；天津大学的王建辰^[9]提出了变刚度单孔手术机器人的理念，能够通过交换装置改变温度从而切换柔性臂的刚柔特性；沈阳理工大学纪竹青等^[10]设计了一种基于相变合金的刚度可调控柔性机器人，采用镍钛合金片驱动2个独立的弯折关节；新加坡国立大学的Li等^[11]提出了一种基于三棱柱万向节并联机构的可变刚度经口手术器械，刚度可实时连续调整；Li等^[12]设计了一种蛇形柔性内窥镜，由一个主动蛇形机器人和一个被动柔性体组成，主动段由金属印刷弹簧式接头组成并以特殊排列的肌腱进行驱动；Zhang等^[13]设计了一种以离散盘体约束合金丝的连续体机器人结构，并提出了一种形态感知算法实时估计机器人的末端位姿。

综上所述，当前的柔性连续体机器人为了在体积尺寸的限制之下实现高灵活度，通常都采用体外多线并联驱动的方式，线驱动模式具有传动距离长的特点，同时将动力元件（电机与传动结构）置于手术执行部分的外部，可以在最大程度上缩小手术器械的入体体积，是当前广泛应用的驱动模式。上文所述的柔性连续体机器人，无论是否存在显式的动作关节，都通过使机构获得冗余自由度的方式来提高柔性操作臂的灵活性。对于不存在显式动作关节的机器人，如以离散刚性杆约束的镍钛合金丝机器人、切口式杆件柔性机器人，虽然具有力感知的能力和高灵活性，但是刚度难调控。而对于存在显式动作关节的机器人，如滚动关节柔性臂结构，其灵活度受到关节活动范围和动作方向的限制。因此，本文提出了一种基于万向轴关节的串联杆件式柔性机器人结构，万向轴关节相较于常用的球铰关节和球面接触滑动式关节，不存在绕轴线方向的转动自由度，避免了因为该冗余自由度而产生的运动误差，同时降低了结构的复杂度。此外，基于万向轴关节的串联杆式柔性机器人系统研究较少。金星泽^[14]研究了万向轴关节柔性机器人的构形。本文面向TEM单孔手术，设计并实现了一种基于万向轴关节的主从遥操作型串联杆件式柔性机器人系统，提出了一种基于柔性体变形恒曲率模型的运动学建模优化方法，实现了机器人系统的人机协同控制并对机器人的定位精度和负载能力进行了实验验证。

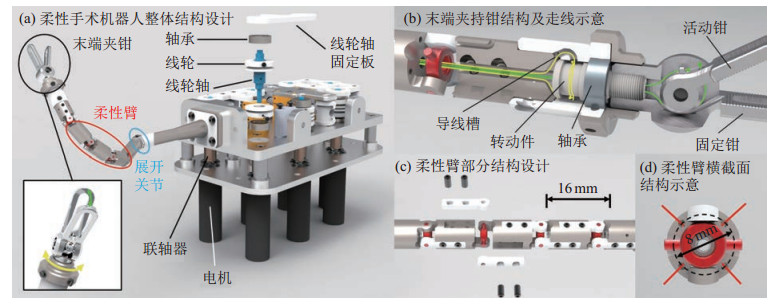
2 机器人设计（Design of the robot）

柔性机器人主要由3个部分构成：1) 具有高灵活度的万向轴关节柔性臂，该部分由直径为10 mm的刚性杆件与万向轴关节串联组成，具有冗余自由度；2) 搭载在柔性臂末端的夹持钳，此部分具有开合和腕部扭转2个自由度，在手术时与组织直接接触；3) 驱动箱，驱动箱将电机的转动动作转化为丝线的牵拉动作，从而驱动柔性臂与末端夹持钳进行手术操作。下面介绍各部位的细节设计。

2.1 万向轴关节柔性臂设计

柔性末端部分主要由多个刚性连杆与万向轴关节穿插连接组成，如图 1(c)所示，每个万向轴关节具有2个轴线互相垂直的旋转自由度，整个柔性操作臂总共具有4个万向轴关节，末端柔性操作臂的俯仰和横摆运动由4根开环丝线控制，如图 1(d)中的4根红色线段所示，4根控制线分别从4个线孔中穿出，线孔均匀分布在刚性杆中央通孔的周围，为了与TEM手术常用的经肛直肠镜配合使用，柔性手术器械的直径不得大于15 mm，在综合考虑负载能力、结构稳定性、加工以及装配难度等问题后，将机器人直径设计为10 mm。为了最小化手术器械的体积，在保证灵活度和负载能力的前提下，将2个万向轴关节之间的距离设置为16 mm。每个万向轴关节的其中一个轴可沿正向或负向旋转最多20$ ^{\circ} $，单个万向轴关节的极限转角为27.99$ ^{\circ} $，可以保证手术器械在产生弯折动作时，偏离轴线的距离小于15 mm，允许双臂在直肠镜内部同时操作。

2.2 末端执行机构设计

手术器械的末端执行部分有2个自由度，分别为腕部扭转自由度和夹持钳开合自由度。如图 1(b)所示，丝线通过柔性臂内部的通孔到达末端夹钳处，并从活动钳转轴的两侧绕过并固定形成闭环，2根丝线分别控制夹持钳的张开动作与闭合动作。

为了使柔性手术器械在手术环境中具有更高的灵活度，在夹钳处设计有一个腕关节扭转自由度。如图 1(b)所示，2根丝线由中央通孔进入末端的导线槽中，导线槽将丝线的方向由沿柔性臂轴线方向转为沿横截面圆周方向，再分别沿顺时针和逆时针方向缠绕在转动件上并固定形成闭环，转动件与轴承装配在柔性段末端并与固定钳相连。

2.3 传动机构设计

本文的柔性机器人采用体外线传动模式，所有的线轮、电机以及传动结构等均置于柔性臂的外部。图 1(a)给出了线轮的结构与装配方式，线轮固连在线轮轴上，线轮轴穿过底板与位于底板下方的电机通过联轴器相连。

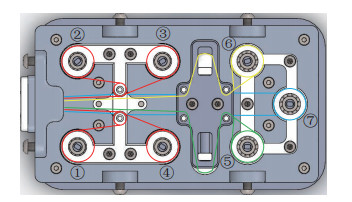
传动机构的内部绕线结构如图 2所示，①~④号线轮缠绕控制柔性臂动作的开环丝线，⑤⑥号线轮均为闭环线传动模式线轮，经过一个丝线张力调整模块（弹簧滑块机构，在丝线有效长度缩短时，丝线带动滑块压缩弹簧；在丝线有效长度拉长时，弹簧推出滑块从而张紧丝线）与末端执行器相连，分别控制夹持钳的开合和腕部自由度的扭转，⑦号线轮控制展开关节的左右横摆展开动作。

3 运动学分析（Kinematic analysis）

柔性体恒曲率模型目前被广泛应用在柔性连续体的运动学建模和控制方法分析中，该方法具有解算复杂度低并且精度较高的特点。本文首先分析万向轴关节的构形特点，得出了万向轴关节使用恒曲率模型进行建模的理论基础，最后建立了串联杆件式万向轴关节机器人的运动学模型。

3.1 万向轴关节构形基础

首先引入柔性体恒曲率模型的概念，该模型具有3个理论前提：1) 弹性圆柱体的变形为等曲率变形，即发生变形时任一段圆柱体轴线的曲率相等；2) 不考虑弹性圆柱体沿轴线方向的伸缩变形和绕轴线方向的扭转变形，只考虑其弯曲变形；3) 传动线与穿线孔之间的摩擦作用忽略不计，在柔性体发生弯曲时，其中轴线的形状为恒曲率圆弧。

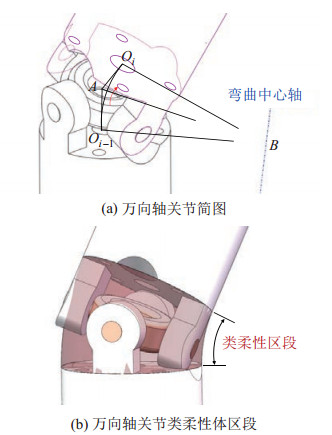
对万向轴关节的构形进行分析，如图 3(a)所示，点$ A $为万向轴关节2个旋转轴的中心交点，$ O_{i} $为此关节下一杆件起始端面的中心点，$ O_{i-1} $为此关节上一杆件末尾端面的中心点，弯曲中心轴为$ O_{i} $所在端面与$ O_{i-1} $所在端面的交线，点$ B $为弯曲中心轴与平面$ AO_{i}O_{i-1} $的交点。经过简单的几何关系推导可以证明$ \triangle ABO_{i} $与$ \triangle ABO_{i-1} $全等，即可证得$ BO_{i} = BO_{i-1} $，进而可以证明，$ O_{i-1} $所在端面以$ BO_{i-1} $为半径绕弯曲中心轴转动一定角度后，可以与$ O_{i} $所在的端面重合，符合柔性体恒曲率模型的变形特点。根据以上证明，可以得知万向轴关节在产生动作时具有类似柔性体变形的特性。

万向轴关节发生动作的整个过程，并不是与纯柔性体变形过程完全一致，其中轴线的长度会发生变化，最大变化量为0.12 mm。因此，若要符合柔性体恒曲率模型的条件，需要将某个动作下的万向轴关节视为一个独立的类柔性区段，如图 3(b)所示，对其运动学模型进行分析。此外，本文的柔性臂结构为刚性杆件串联而成，在轴向方向的形变量极小，可以忽略不计。

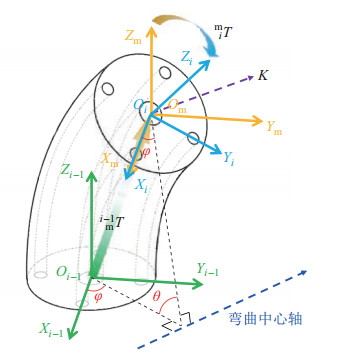
3.2 柔性机器人运动学

柔性体恒曲率模型的正运动学可以用一个坐标变换表示，如图 4所示，在此段柔性体起始面建立坐标系$ O_{i-1} $-$ X_{i-1}Y_{i-1}Z_{i-1} $，在终止面建立坐标系$ O_{i} $-$ X_{i}Y_{i}Z_{i} $，从坐标系$ O_{i-1} $-$ X_{i-1}Y_{i-1}Z_{i-1} $到$ O_{i} $-$ X_{i}Y_{i}Z_{i} $的坐标变换即为该段柔性体恒曲率模型的齐次变换，将这一变换记为$ {}_{\; \; \; \, i}^{i-1} \mathit{\boldsymbol{T}} $，而$ {}_{\; \; \; \, i}^{i-1} \mathit{\boldsymbol{T}} $可以分解为从坐标系$ O_{i-1} $-$ X_{i-1}Y_{i-1}Z_{i-1} $到坐标系$ O_{\rm m} $-$ X_{\rm m}Y_{\rm m}Z_{\rm m} $（记为$ {}_{\; \; \, \rm m}^{i-1} \mathit{\boldsymbol{T}} $），再从坐标系$ O_{\rm m} $-$ X_{\rm m}Y_{\rm m}Z_{\rm m} $到坐标系$ O_{i} $-$ X_{i}Y_{i}Z_{i} $的变换（记为$ {}_{\; i}^{\rm m} \mathit{\boldsymbol{T}} $）。$ {}_{\; \; \, \rm m}^{i-1} \mathit{\boldsymbol{T}} $为平移变换，$ {}_{\; i}^{\rm m} \mathit{\boldsymbol{T}} $为绕$ K $轴的旋转变换，$ K $轴与恒曲率模型的弯曲中心轴平行，并经过终止面的原点$ O_{i} $。这里，$ i $为第$ i $段类柔性区段的代号，$ \rm m $则为坐标齐次变换的中间坐标系代号。

平移变换的移动向量由式(1) 给出，其中$ \varphi $为柔性体的弯曲方向角，$ \theta $为柔性体的弯曲角，中间参数$ r $可由参数$ a $和$ \theta $求得，$ a $为万向轴中心点到杆件端面的距离（如$ AO_{i-1} $或$ AO_{i} $），为已知参数。

$ \begin{align} \begin{cases} {}_{\; \; \; \, i}^{i-1} \mathit{\boldsymbol{P}}= \begin{bmatrix} r\cdot (1-\cos \theta)\cdot \cos \varphi \\ r\cdot (1-\cos \theta)\cdot \sin \varphi \\ r\cdot \sin \theta \end{bmatrix} \\ r=a/\tan \dfrac{\theta} {2} \end{cases} \end{align} $

(1)

旋转变换的转轴为$ K $轴，$ K $轴的方向可以由弯曲方向角$ \varphi $求出，用式(2) 表示：

$ \begin{align} \mathit{\boldsymbol{K}}=\begin{bmatrix} k_{x} \\ k_{y} \\ k_{z} \end{bmatrix} =\begin{bmatrix} -\sin \varphi \\ \cos \varphi \\ 0 \end{bmatrix} \end{align} $

(2)

根据转轴$ K $的方向以及弯曲角$ \theta $，即可求取旋转矩阵$ \mathit{\boldsymbol{R}}_{K}(\theta) $，由式(3) 给出，其中$ \rm c $为$ \cos $的缩写，$ \rm s $为$ \sin $的缩写（此后的公式均以此法表示）。

$ \begin{align} \mathit{\boldsymbol{R}}_{K} (\theta) =\begin{bmatrix} \rm c^{2}\varphi \cdot c\theta +s^{2}\varphi & \rm c\varphi \cdot s\varphi \cdot c\theta & \rm c\varphi \cdot s\theta \\ \rm c\varphi \cdot s\varphi \cdot c\theta & \rm s^{2}\varphi \cdot c\theta +c^{2}\varphi & \rm s\varphi \cdot s\theta \\ \rm -c\varphi \cdot s\theta & \rm -s\varphi \cdot s\theta & \rm c\theta \end{bmatrix} \end{align} $

(3)

由上述分析可以推得万向轴关节类柔性区段的正运动学齐次变换矩阵为

$ \begin{align} & {}_{\; \; \; \, i}^{i-1} \mathit{\boldsymbol{T}} \\ =& \begin{bmatrix} \begin{array}{c}\rm c^{2}\varphi \cdot c\theta +\\[-5pt]s^{2}\varphi\end{array} & \rm c\varphi \cdot s\varphi \cdot c\theta & \rm c\varphi \cdot s\theta & \begin{array}{c}r\cdot (1-\rm c\theta)\cdot\\[-5pt] \rm c\varphi\end{array} \\ \rm c\varphi \cdot s\varphi \cdot c\theta & \begin{array}{c}\rm s^{2}\varphi \cdot c\theta +\\[-5pt]c^{2}\varphi\end{array} & \rm s\varphi \cdot s\theta & \begin{array}{c}r\cdot (1-\rm c\theta)\cdot\\[-5pt] \rm s\varphi\end{array} \\ -\rm c\varphi \cdot s\theta & -\rm s\varphi \cdot s\theta & \rm c\theta & r\cdot \rm s\theta \\ 0 & 0 & 0 & 1 \end{bmatrix} \end{align} $

(4)

除了万向轴类柔性区段外，还需计算刚性杆件的正运动学变换，该变换为简单平移变换，如式(5) 所示，其中$ d_{i} $为第$ i $段刚性杆件的长度。

$ \begin{align} \mathit{\boldsymbol{T}}_{ri} = \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & d_{i} \\ 0 & 0 & 0 & 1 \end{bmatrix} \end{align} $

(5)

则整个柔性机器人的整体运动学为类柔性段和刚性段按照一定的顺序连乘，从柔性臂起始到末端的齐次变换矩阵为

$ \begin{align} \mathit{\boldsymbol{T}}=\prod\limits_{i=1}^n \mathit{\boldsymbol{T}}_{ri} \; {}_{\; \; \; \, i}^{i-1} \mathit{\boldsymbol{T}} \end{align} $

(6)

3.3 万向轴关节运动学优化方法

上文介绍的运动学模型基于万向轴关节的虚拟关节$ \theta $、$ \varphi $给出，根据万向轴的真实关节构形，万向轴的运动关节实际为2个相互正交的旋转轴，可以使用绕动轴的真实关节角度$ \alpha $、$ \beta $描述其姿态。万向轴关节的真实关节转角动作旋转矩阵为

$ \begin{align} & {}_{\; \; \; \, i}^{i-1} \mathit{\boldsymbol{R}}_{YXZ} \\ =& \rm \begin{bmatrix} {\rm c}\beta & 0 & {\rm s}\beta \\ 0 & 1 & 0 \\ -{\rm s}\beta & 0 & {\rm c}\beta \end{bmatrix}\cdot \begin{bmatrix} 1 & 0 & 0 \\ 0 & {\rm c}\alpha & -{\rm s}\alpha \\ 0 & {\rm s}\alpha & {\rm c}\alpha \end{bmatrix}\cdot \begin{bmatrix} \rm c\gamma & -\rm s\gamma & 0 \\ \rm s\gamma & \rm c\gamma & 0 \\ 0 & 0 & 1 \end{bmatrix} \\ =&\begin{bmatrix} {\rm c}\beta c\gamma +{\rm s}\beta {\rm s}\alpha s\gamma & -{\rm c}\beta {\rm s}\alpha +{\rm s}\beta {\rm s}\alpha s\gamma & {\rm s}\beta {\rm c}\alpha \\ {\rm c}\alpha s\gamma & {\rm c}\alpha c\gamma & -{\rm s}\alpha \\ -{\rm s}\beta c\gamma +{\rm c}\beta {\rm s}\alpha s\gamma & {\rm s}\beta s\gamma +{\rm c}\beta {\rm s}\alpha c\gamma & {\rm c}\beta {\rm c}\alpha \end{bmatrix} \end{align} $

(7)

与式(3) 中的对应元素联立，可得如下方程组：

$ \begin{align} \begin{cases} -\sin \alpha =\sin \varphi \cdot \sin \theta \\ \sin \beta \cdot \cos \alpha =\cos \varphi \cdot \sin \theta \\ \cos \alpha \cdot \sin \gamma =\cos \varphi \cdot \sin \varphi \cdot \cos \theta \end{cases} \end{align} $

(8)

求解以上方程组可以解得万向轴关节的真实关节角度，当类柔性体模型的弯曲方向角$ \varphi $不属于集合$ = \{0, {\rm{ \mathsf{ π} }} /2, {\rm{ \mathsf{ π} }} , 3 {\rm{ \mathsf{ π} }} /2\} $时，$ \gamma $角不为0，由于万向轴关节仅存在绕动轴的转动$ \alpha $、$ \beta $，无法绕杆件的轴线方向转动，因此$ \gamma $角会成为累积偏差，影响下一万向轴关节的姿态方向。以下提出一种优化方法。

在计算出偏差角$ \gamma $之后，在下一个万向轴关节处对此偏差进行补偿。由于偏差角$ \gamma $是沿杆件轴线的旋转角度，可以通过修正下一万向轴关节的恒曲率模型弯曲方向角$ \varphi $，来补偿前一关节的偏差对下一个关节的影响。对于第1个万向轴关节，其恒曲率模型齐次变换为$ \mathit{\boldsymbol{R}}_{1}= \mathit{\boldsymbol{R}}_{\varphi \theta} $，真实关节的变换矩阵记为$ {}_{\; \; \; \, i}^{i-1} \mathit{\boldsymbol{R}}_{YXZ} $，通过联立式(3) 和式(7) 计算出偏差角$ \gamma_{1} $，将该偏差角转换为绕动系$ {Z} $轴的旋转矩阵形式$ \mathit{\boldsymbol{R}}_{\gamma_{1}} $，将其下一万向轴关节的恒曲率模型齐次变换矩阵左乘$ \mathit{\boldsymbol{R}}_{\gamma_{1}} $，即可获得修正矩阵$ \mathit{\boldsymbol{R}}_{2} =\mathit{\boldsymbol{R}}_{\gamma_{1}} \mathit{\boldsymbol{R}}_{\varphi \theta} $，将其与真实关节变换矩阵$ {}_{i+1}^{\; \; \; i} \mathit{\boldsymbol{R}}_{YXZ} $联立即可求得第2个万向轴关节的偏差角$ \gamma_{2} $，以此类推到末端，如式(9)所示：

$ \begin{align} \mathit{\boldsymbol{R}}_{2} =&\; \mathit{\boldsymbol{R}}_{\gamma_{1}} \mathit{\boldsymbol{R}}_{\varphi \theta}\\ =&\begin{bmatrix} {\rm c}\gamma_{1} & -{\rm s}\gamma_{1} & 0 \\ {\rm s}\gamma_{1} & {\rm c}\gamma_{1} & 0 \\ 0 & 0 & 1 \end{bmatrix}\times \\ & \begin{bmatrix} {\rm c}^{2}\varphi \cdot {\rm c}\theta +{\rm s}^{2}\varphi & \begin{array}{c}{\rm c}\varphi \cdot {\rm s}\varphi \cdot {\rm c}\theta -\\[-5pt]{\rm c}\varphi \cdot {\rm s}\varphi\end{array} & {\rm c}\varphi \cdot {\rm s}\theta \\ \begin{array}{c}{\rm c}\varphi \cdot {\rm s}\varphi \cdot {\rm c}\theta -\\[-5pt]{\rm c}\varphi \cdot {\rm s}\varphi\end{array} & {\rm s}^{2}\varphi \cdot {\rm c}\theta +{\rm c}^{2}\varphi & {\rm s}\varphi \cdot {\rm s}\theta \\ -{\rm c}\varphi \cdot {\rm s}\theta & -{\rm s}\varphi \cdot {\rm s}\theta & {\rm c}\theta \end{bmatrix} \end{align} $

(9)

以优化后的变换矩阵代替恒曲率模型齐次变换矩阵进行正运动学分析，可以有效补偿万向轴关节产生的偏差$ \gamma $。

3.4 机器人运动学仿真分析与验证

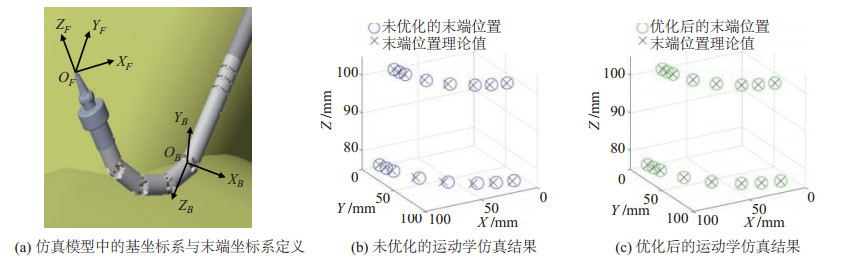
通过Matlab仿真验证运动学模型以及运动学优化方法的正确性。在机器人的末端分别建立基坐标系和从坐标系，坐标系的定义如图 5(a)所示，在Simscape仿真环境中测定多个位姿下的变换矩阵$ {}_{F}^{B} \mathit{\boldsymbol{T}} $（从坐标系$ \{ F\} $相对于基坐标系$ \{B\} $的变换矩阵），作为仿真实验的测量值。

在仿真模块中测定16组末端位置的坐标，分别记录无优化的正运动学和优化后的正运动学仿真结果，比较两者在3维空间中的位置偏差，如表 1所示，实验点可视化结果如图 5(b)(c)所示。

图 5(b)为未优化的运动学仿真结果，显然未优化的运动学计算方法所得出的末端点位置与其理论值存在偏差，尤其在弯曲方向角接近45$ ^{\circ} $时偏差最为明显。如图 5(c)所示，基于优化后的运动学得出的末端点位置，与理论末端点位置一致，由此验证了万向轴关节运动学建模优化方法的正确性。

3.5 机器人驱动空间映射

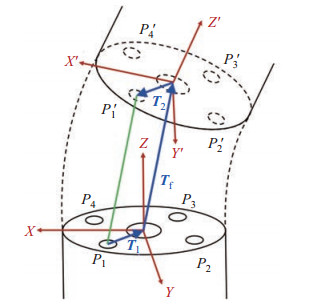
以万向轴关节4根驱动丝线的有效长度作为参数构建机器人的驱动空间，驱动丝线有效长度指万向轴关节中的丝线长度，如图 6中的绿色线段所示。根据万向轴关节的正运动学模型，可以得到上一杆件终止面的中心点到下一杆件起始面中心点的齐次坐标变换，由此，可以推导出上一杆件导线孔到下一杆件对应导线孔的齐次坐标变换，变换过程如图 6中蓝色箭头所指路径所示。

首先由导线孔出口$ P_{1} $变换至该杆件终止面的中心点，变换矩阵为$ \mathit{\boldsymbol{T}}_{1} $，再经过万向轴关节的正运动学齐次变换矩阵$ \mathit{\boldsymbol{T}}_{\rm f} $，最后经过下一杆件起始面中心变换至对应的导线孔入口$ P_{1}' $，变换矩阵为$ \mathit{\boldsymbol{T}}_{2} $。故由导线孔$ P_{1} $到$ P_{1}' $的齐次变换矩阵为

$ \begin{align} \mathit{\boldsymbol{T}}_{i1} &=\mathit{\boldsymbol{T}}_{1} \mathit{\boldsymbol{T}}_{\rm f} \mathit{\boldsymbol{T}}_{2} \\ & =\begin{bmatrix} 1 & 0 & 0 & -4 \\[-1.5pt] 0 & 1 & 0 & -4 \\[-1.5pt] 0 & 0 & 1 & 3 \\[-1.5pt] 0 & 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} {\rm c}\beta_{i} & 0 & {\rm s}\beta_{i} & 0 \\[-1.5pt] 0 & 1 & 0 & 0 \\[-1.5pt] -{\rm s}\beta_{i} & 0 & {\rm c}\beta_{i} & 0 \\[-1.5pt] 0 & 0 & 0 & 1 \end{bmatrix}\times \\[-1.5pt] & \quad\, \begin{bmatrix} 1 & 0 & 0 & 0 \\[-1.5pt] 0 & {\rm c}\alpha_{i} & -{\rm s}\alpha_{i} & 0 \\[-1.5pt] 0 & {\rm s}\alpha_{i} & {\rm c}\alpha_{i} & 0 \\[-1.5pt] 0 & 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} 1 & 0 & 0 & 4 \\[-1.5pt] 0 & 1 & 0 & 4 \\[-1.5pt] 0 & 0 & 1 & 3 \\[-1.5pt] 0 & 0 & 0 & 1 \end{bmatrix} \\ & = \begin{bmatrix} {\rm c}\beta_{i} & {\rm s}\beta_{i} \cdot {\rm s}\alpha_{i} & {\rm s}\beta_{i} \cdot {\rm c}\alpha_{i} & \begin{array}{c}4({\rm c}\beta_{i} +{\rm s}\beta_{i} \cdot {\rm s}\alpha_{i})+\\[-5pt]3\rm s\beta_{i} \cdot {\rm c}\alpha_{i} -4\end{array} \\ 0 & {\rm c}\alpha_{i} & -{\rm s}\alpha_{i} & 4\rm c\alpha_{i} -3\rm s\alpha_{i} -4 \\ -{\rm s}\beta_{i} & {\rm c}\beta_{i} \cdot {\rm s}\alpha_{i} & {\rm c}\beta_{i} \cdot {\rm c}\alpha_{i} & \begin{array}{c}4(-{\rm s}\beta_{i} +{\rm c}\beta_{i} \cdot {\rm s}\alpha_{i})+\\[-5pt]3\rm c\beta_{i} \cdot {\rm c}\alpha_{i} +3 \end{array}\\ 0 & 0 & 0 & 1 \end{bmatrix} \end{align} $

(10)

其中$ \beta_{i} $、$ \alpha_{i} $表示第$ i $个关节的真实转角，矩阵$ \mathit{\boldsymbol{T}}_{1} $与$ \mathit{\boldsymbol{T}}_{2} $由杆件的实际几何参数确定。在确定了齐次变换矩阵之后，即可通过其中的平移变换信息计算出丝线有效长度，计算公式由式(11)(12) 给出：

$ \begin{align} & \begin{cases} l_{i1x} =4({\rm c}\beta_{i} +{\rm s}\beta_{i} \cdot {\rm s}\alpha_{i})+3{\rm s}\beta_{i} \cdot {\rm c}\alpha_{i} -4 \\ l_{i1y} =4{\rm c}\alpha_{i} -3{\rm s}\alpha_{i} -4 \\ l_{i1z} =4(-{\rm s}\beta_{i} +{\rm c}\beta_{i} \cdot {\rm s}\alpha_{i})+3{\rm c}\beta_{i} \cdot {\rm c}\alpha_{i} +3 \end{cases} \end{align} $

(11)

$ \begin{align} & l_{i1} =\sqrt{l_{i1_x}^{2} +l_{i1_y}^{2} +l_{i1_z}^{2}} \end{align} $

(12)

根据以上方法可以类推出其他3条开环控制丝线的有效长度，则4条驱动丝线的有效长度如下：

$ \begin{align} \begin{cases} l_{1} = \sum\limits_{i=1}^4 \sqrt{l_{i1_x}^{2} +l_{i1_y}^{2} +l_{i1_z}^{2}} \\ l_{2} = \sum\limits_{i=1}^4 \sqrt{l_{i2_x}^{2} +l_{i2_y}^{2} +l_{i2_z}^{2}} \\ l_{3} = \sum\limits_{i=1}^4 \sqrt{l_{i3_x}^{2} +l_{i3_y}^{2} +l_{i3_z}^{2}} \\ l_{4} = \sum\limits_{i=1}^4 \sqrt{l_{i4_x}^{2} +l_{i4_y}^{2} +l_{i4_z}^{2}} \end{cases}\kern-10pt, \qquad i=1, 2, 3, 4 \end{align} $

(13)

当4条丝线的有效长度发生变化时，记变化量为$ \Delta l_{1}, \Delta l_{2}, \Delta l_{3}, \Delta l_{4} $，则驱动电机的位置控制量为

$ \begin{align} \Delta P_{j} =\frac{\Delta l_{j}} {D/2}, \quad j=1, 2, 3, 4 \end{align} $

(14)

解算出电机控制量$ \Delta P_{j} $与万向轴关节角$ \beta_{i} $、$ \alpha_{i} $（其中$ D $为绕线轮直径），即可根据驱动空间到关节空间、和关节空间到工作空间的映射控制柔性机器人末端的位姿。

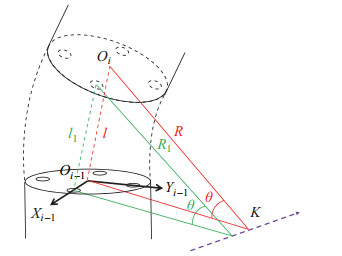
根据万向轴关节的几何结构特性，可以建立驱动空间$ ( l_{1}, l_{2}, l_{3}, l_{4}) $到虚拟关节空间$ (\theta , \varphi) $的映射关系，根据图 7中所示的几何关系（途中略去了丝线$ l_{2}, l_{3}, l_{4} $），可以列出如下关系，图中所标注的弯曲中心轴到$ O $点的距离为$ R=a/\tan ( \theta /2 $)，其中$ a $为已知量，将式(15) 中的所有子式联立求解，即可解算出4根驱动丝线$ l_{1}, l_{2}, l_{3}, l_{4} $有效长度与万向轴类柔性体角度参数$ \theta $、$ \varphi $之间的关系，由此可以得到从驱动空间到虚拟关节空间的映射。

$ \begin{align} \begin{cases} \dfrac{\dfrac{l_{3} -l_{1}} {2}}{2R\cdot \cos \varphi} =\sin \dfrac{\theta} {2} \\ \dfrac{\dfrac{l_{4} -l_{2}} {2}}{2R\cdot \sin \varphi} =\sin \dfrac{\theta} {2} \\ l_{1} +l_{3} =l_{2} +l_{4} =2l \\ l=2R\cdot \sin \dfrac{\theta} {2} \end{cases} \end{align} $

(15)

3.6 机器人主从映射

首先，从主手工作空间开始，在主手控制器的$ YOZ $平面内划定一个矩形区域，在此区域内读取位置坐标$ ( y, z) $，同时将关节空间的$ \beta $、$ \alpha $角度值作为参数，建立一个矩形区域（此区域不是实际存在的、具有物理意义的区域，只是用于与主手工作空间产生映射），建立上述2个矩形区域之间的映射，在确定了参数$ \beta $、$ \alpha $之后，即可确定此刻类柔性体的形状，此时根据已经确立的真实关节参数$ \beta $、$ \alpha $可以解算出4根驱动丝线的有效长度（关节空间到驱动空间的映射），再根据驱动空间到虚拟关节空间的映射，即可解算出虚拟关节空间参数值$ \theta $、$ \varphi $，最终通过关节空间到工作空间的映射可以解算出机器人的末端位置。上述提到的映射均为一一映射。

4 系统设计与实验（System design and experiment） 4.1 柔性机器人系统设计与实现

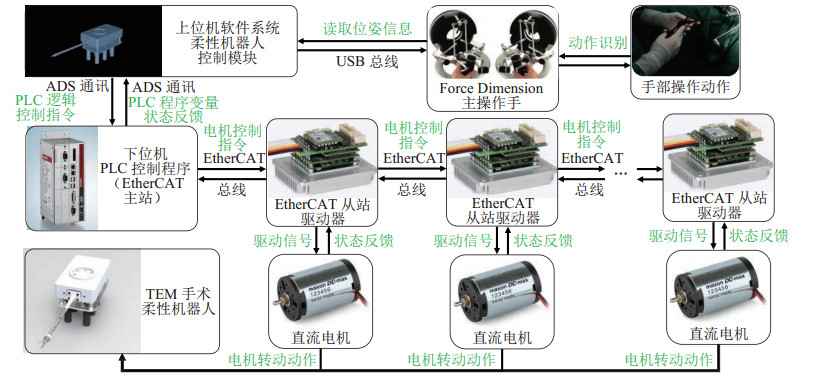
面向TEM手术的柔性机器人系统整体架构如图 8所示，其中核心信息处理部分为上位机软件控制系统，它读取主手位姿信息并将其处理为下位机逻辑控制指令输出。下位机接到上位机的逻辑控制指令之后根据控制指令生成电机的控制信号，将此信号转译为EtherCAT报文从下位机（EtherCAT主站）发出，传输到各个驱动器（EtherCAT从站）进行处理，生成驱动电机的动作信号，其中的上位机为装有TwinCAT实时内核的PC，下位机为运行PLC程序的工业PC，主手控制器采用Force Dimension公司的Omega7，驱动系统硬件部分主要由2个24 V直流电源与7组驱动器和电机组成，驱动器型号为Elmo Gold Solo Twitter，电机型号为Maxon DCX 22直流电机。实验平台整体如图 9所示。机器人在确定了由驱动空间到关节空间、由关节空间到工作空间的映射之后，可以根据以上映射的结果进行控制，机器人的动作演示如图 9所示。

4.2 机器人绝对定位精度与重复定位精度实验

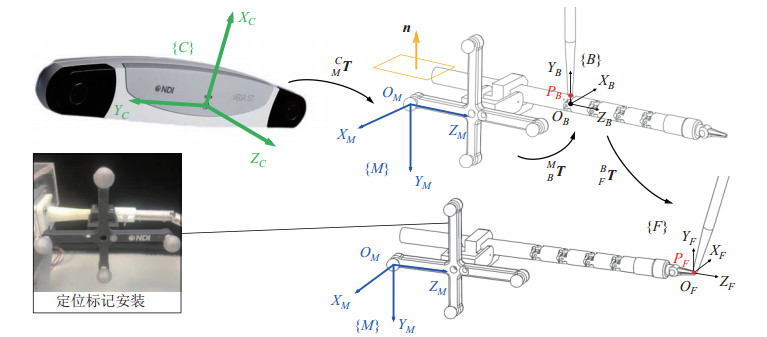
使用光学定位系统对柔性机器人的末端位置进行检测并测定其定位精度，在柔性机器人静态部分按照图 10所示的方式安装定位标记，可以保证定位标记的$ {Z}_{M} $轴方向与柔性机器人的轴线方向一致，但是存在绕此轴旋转方向的安装偏差，测定底板法向量$ \mathit{\boldsymbol{n}} $（图 10中黄色箭头所示）与$ {Y}_{M} $轴的方向之后即可根据这2个方向向量计算出定位标记的安装偏差，进而可以得到标定矩阵$ \mathit{\boldsymbol{T}}_{\rm c} $（$ \mathit{\boldsymbol{T}}_{\rm c} $为一个绕$ {Z}_{M} $轴的旋转矩阵，用于描述安装偏差，将其右乘变换矩阵$ {}_{M}^{\;C} \mathit{\boldsymbol{T}} $时，得到新的变换矩阵$ {}_{M}^{\;C} \mathit{\boldsymbol{T}}' $，由该矩阵确定的空间坐标系$ M ' $的$ Y_M' $轴与底板法向量$ \mathit{\boldsymbol{n}} $平行）。

由于无法将标志坐标系与基坐标系直接重合固连，需要间接求取基坐标系。基坐标系的原点为第1个万向轴关节的中心点，探针难以直接检测该点，因此在检测到标志坐标系相对于相机坐标系$ \{ C\} $的变换矩阵$ {}_{M}^{\;C} \mathit{\boldsymbol{T}} $之后，再检测第1个万向轴关节的轴外侧，即$ {Y}_{B} $轴与柔性臂外表面的交点$ P_{B} $，其在相机坐标系下的表示$ ^{C}P_{B} $点坐标由式(16) 给出：

$ \begin{align} {}^{C}\mathit{\boldsymbol{P}}_{B} ={}_{M}^{\;C} \mathit{\boldsymbol{T}}{}^{M}\mathit{\boldsymbol{P}}_{B} \end{align} $

(16)

可以推得$ ^{M}\mathit{\boldsymbol{P}}_{B} ={}_{M}^{\;C} \mathit{\boldsymbol{T}}^{-1} {}^{C}\mathit{\boldsymbol{P}}_{B} $，利用此式即可以推得$ P_{B} $点在$ \{M\} $系下的表示，进而将此点向底板法向量$ \mathit{\boldsymbol{n}} $负向偏移5 mm即可以得到$ \{B\} $系原点在$ \{M\} $系下的表示$ ^{M}O_{B} $。矩阵之间的变换关系如图 10所示。而$ \{B\} $系的$ Z_B $轴方向与$ \{M\} $系的$ Z_M $轴方向相同，将$ \{M\} $系绕轴$ Z_M $旋转180$ ^{\circ} $即可以得到$ \{B\} $系的姿态矩阵，由此可以得到由$ \{M\} $到$ \{ B\} $的变换矩阵$ {}_{B}^{M} \mathit{\boldsymbol{T}} $。

通过检测$ P_{B} $点并进行矩阵变换得到了变换矩阵$ {}_{B}^{M} \mathit{\boldsymbol{T}} $之后，对柔性机器人末端夹钳的尖端位置点$ P_{F} $进行检测，得到该点在$ \{C\} $系下的表示$ ^{C}{P\mathit{\boldsymbol{}}}_{F} $，进而得到尖端点在$ \{B\} $系下的坐标表示：

$ \begin{align} {}^{C}\mathit{\boldsymbol{P}}_{F} ={}_{M}^{\;C} \mathit{\boldsymbol{TT}}_{\rm c} {}_{B}^{M} \mathit{\boldsymbol{T}} {}^{B}\mathit{\boldsymbol{P}}_{F} \Rightarrow {}^{B}\mathit{\boldsymbol{P}}_{F} ={}_{B}^{M} \mathit{\boldsymbol{T}}^{-1}\mathit{\boldsymbol{T}}_{\rm c}^{-1} {}_{M}^{\;C} \mathit{\boldsymbol{T}}^{-1} {}^{C}\mathit{\boldsymbol{P}}_{F} \end{align} $

(17)

使用光学定位系统检测末端位置，通过以上方法计算末端位置在基坐标系下的表示，以此结果作为实验的测量值。在检测末端位置时，每次采点时持续采集3 s，每秒60帧，使用总计180帧数据求取平均值作为一组测量值。实验时设定4个实验点以及坐标，4个实验点为事先设定的随机点，实验点的理论位置见表 2，分别记为点1、点2、点3、点4，4个点的坐标值表示其在主手操作平面（3.6节中提到的$ YOZ $平面）内的位置，每个目标点分别测定30组数据。测定每组数据时，在主从控制模式下使机器人末端由初始位置运动到目标点位置，使用探针对末端点位置进行检测，重复此操作检测末端位置。

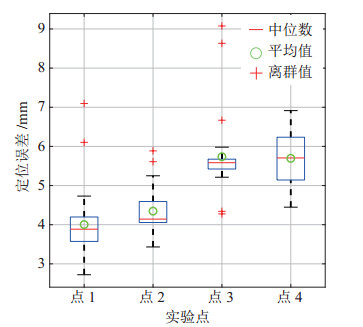
对每个目标点测量30组数据并求其平均值，最终求得主从映射实验结果的位置，如表 3所示，通过计算得到绝对定位误差$ E $。对比实验结果可以发现，当机器人末端靠近$ \{B\} $系的坐标轴$ X_B $时误差有增大的趋势，最大误差为5.57 mm。将各个测量点的绝对定位误差值绘制成箱型分布图，结果如图 11所示。

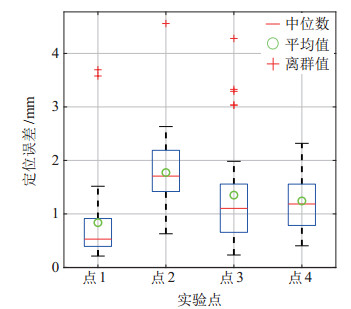
根据以上实验数据，可以检测机器人的末端重复定位精度，每个目标点的30组数据分析如图 12所示。在4个目标点位置，机器人的重复定位误差最大不超过2.70 mm，并且在点1、点3处的重复定位误差不超过2.00 mm。整体来看，机器人末端的重复定位精度远优于需求的指标5.00 mm，满足手术要求。

4.3 机器人带载定位精度实验

选取3个目标实验点，在末端分别施加0 g、10 g、20 g、30 g、40 g的负载，使用光学定位系统测定末端位置。在每组负载下记录坐标点30次，并取平均值，测量结果如表 4所示。实验发现，当负载小于40 g时，柔性臂形状基本不受影响，表现出了足够的刚性，但是当负载超过40 g时，虽然能将重物举起，但是柔性臂的末端偏离了预设位置，在实际手术过程中需要夹持的缝合针质量为15 g左右，在机器人的负载能力范围之内。实验场景如图 13所示。

4.4 机器人定位实验误差分析

对于本文提出的面向TEM手术的柔性机器人，为了验证其性能，进行了定位精度实验，经过对结构以及运动控制算法的分析，机器人定位误差的来源主要有以下几个：

1) 本文的驱动丝线选用直径为0.80 mm的尼龙丝线，为了保证丝线在通线孔中可以自由滑动，通线孔的直径被设计得略大于丝线线径。此间隙的存在会降低关节运动的精确度。

2) 万向轴关节的轴与轴孔之间是滑动接触，因此轴孔的直径在制造时略微大于转轴的直径，存在间隙，在运动时会产生误差。

3) 柔性机器人在初始零位下应为笔直状态，但是由于机器人自重的影响，在横置状态下，柔性臂无法在初始位置下保持完美的笔直状态，会对后续的动作产生影响，降低位置精度。

4) 除了上述主要误差来源之外，还存在其他的误差，例如驱动丝线在牵拉时存在细微的弹性形变，影响定位精度。

5 结论（Conclusion）

提出一种基于万向轴关节的串联杆件式柔性机器人结构，能够配合TEM手术常用的经肛直肠镜进行手术操作。基于柔性体恒曲率模型，建立了万向轴关节的运动学模型，并提出了一种优化方法，有效地避免了将柔性体恒曲率模型用于万向轴关节时产生的偏差，建立了机器人从驱动空间到关节空间、关节空间到工作空间的映射关系，以此为基础实现了对机器人的主从控制，并进行了相关实验。使用光学定位系统检测柔性机器人的末端重复定位精度和绝对定位精度。机器人能够稳定可靠地到达设定的目标点，绝对定位精度误差最大不超过6.00 mm，同时测得机器人的重复定位精度在2.70 mm以内，最后测定了机器人的带载定位精度，当负载不超过40 g时，机器人的末端偏离理论位置最大不超过5.00 mm，具有足够进行手术操作的负载能力。