2. 中国科学院大学, 北京 100049
2. University of Chinese Academy of Sciences, Beijing 100049, China
500 m口径球面射电望远镜[1](以下简称FAST)是目前世界上最大最灵敏的单口径球面射电望远镜,如图 1所示。FAST工程于2011年正式开工建设,2016年9月建设完成后进入调试及试观测阶段,并于2020年1月通过国家验收,投入正式运行[2]。FAST与目前国际上的单口径射电望远镜相比,具有3项自主创新:利用天然的喀斯特地貌作为台址、实现可实时变形的主动反射面系统以及实现光机电一体化的轻型馈源索支撑系统。全新的设计思路使望远镜突破了在地面建造全可动天线的百米工程极限,开创了建造巨型射电望远镜的新模式。FAST三项自主创新之一的馈源支撑系统由多级机构组成,该系统将馈源精准定位于瞬时焦点,实现对天体的高精度指向跟踪观测。FAST馈源支撑系统中的第1级控制主要由6座支撑塔、6根钢索和馈源舱(舱体包括结构框架、AB轴、Stewart平台、馈源接收机)组成,是一种典型的索牵引并联机构。钢索一端固定于馈源舱的铰接点上,另一端通过支撑塔顶端和底部的转向定滑轮与卷扬机相连,卷扬机带动6根钢索拖动质量达30 t的馈源舱在开口直径约为207 m的球冠面上运动,使馈源舱到达目标点。馈源接收机位姿的精准调整和补偿则由安装在馈源舱内的AB轴转向机构和Stewart平台来共同完成。

|
图 1 500 m口径球面射电望远镜 Fig.1 FAST |
索牵引并联机构具有大负载和大工作空间等特点,对钢索理论模型的研究决定了整个系统的力学特性。许多学者对FAST馈源支撑系统进行了研究分析。姚蕊等[3]对考虑钢索自重的悬链线模型进行简化,通过抛物线模型对索牵引并联机构的尺度参数进行了优化。黄亮等[4]基于静力学分析对不考虑弹性变形的钢索建立了悬链线模型,并对其进行简化,提出了赝曲线模型,以提高其求解效率。殷家宁等[5]同时考虑钢索的自重和弹性变形,通过重新构造悬链线模型中变量的关系,提出了一种高速的近似求解算法。李辉等[6]使用张力均衡分配的优化原则对FAST馈源支撑系统中柔性钢索牵引并联机构进行了静力学分析,并对馈源支撑系统进行了
对于空间中运动的具有大变形大位移的梁单元,Shabana[10]提出了基于有限元和连续介质力学的绝对节点坐标法,该方法使用节点的位移和梯度矢量作为广义坐标来描述空间梁单元的位移和变形。沈剑等[11]基于绝对节点坐标法对柔性绳索进行了动力学分析;吴懋琦等[12]采用绝对节点坐标法对柔性结构大变形下非线性的平面梁应变-位移关系进行精确描述。对于变质量的柔性体,同样可以使用绝对节点坐标法进行分析。Luo等[13]利用绝对节点坐标法对大位移和大变形的变长度系绳进行了描述,研究了绳系卫星编队的动力学问题;王忠民等[14]基于绝对节点坐标法,建立了一种变长度的Euler-Bernoulli梁单元模型,分析了材料参数和伸展规律对悬臂梁系统的末端非线性挠度响应的影响;Bulín等[15]利用绝对节点坐标法对滑轮绳索系统进行动力学分析,并将模拟数据与实验数据进行对比,验证了该方法的有效性。由于柔性系统的动力学方程刚性问题突出,目前多采用刚性求解器进行解算,如隐式龙格-库塔法、向后差分公式方法等。
FAST使用六索牵引并联机构作为馈源支撑平台的粗调系统,目前该系统的控制器是按直线模型设计的;该控制器在加速度或速度比较大的工况条件下,对系统的抑制振动效果较弱,有必要对其动力学性能进行深入的研究。
本文基于FAST馈源支撑系统中所使用的六索牵引并联机构,考虑钢索的自重和弹性变形建立了钢索在静力平衡状态下的悬链线模型;提出一种六索牵引并联机构的动力学建模方法:该方法应用绝对节点坐标法描述具有时变性的钢索单元,根据虚功原理对钢索的动态特性进行分析,结合钢索和馈源舱间的约束、钢索出索点的约束得到六索牵引并联机构整体的动力学方程组。该动力学模型不仅考虑了馈源舱的动态特性,而且包括了大跨度柔性钢索的振动,该模型更接近于FAST实际的运行状态。使用Matlab进行计算仿真,将仿真数据与实际观测数据进行对比,验证了所建立模型的有效性。
2 钢索的悬链线模型(Catenary model of the cable)FAST馈源支撑系统索牵引并联机构通过6座支撑塔牵引6根钢索控制馈源舱的位姿,整个系统的力学特性主要取决于单根钢索的模型。
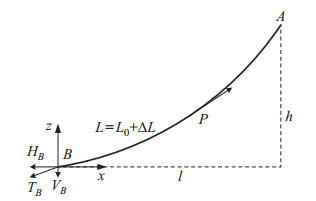
当钢索处于静态平衡状态时,考虑钢索的自重和弹性变形,建立悬链线模型。单根钢索的悬链线模型如图 2所示,钢索两端为连接点
|
图 2 钢索的悬链线模型 Fig.2 Catenary model of the cable |
钢索上任意一点
| $ \begin{gather} \left(\frac{{\rm d} x}{{\rm d} p}\right)^{2}+\left(\frac{{\rm d} z}{{\rm d} p}\right)^{2} =1 \end{gather} $ | (1) |
| $ \begin{gather} T_{P} \frac{{\rm d} x}{{\rm d} p} =H_{P} =H_{B} \end{gather} $ | (2) |
| $ \begin{gather} T_{P} \frac{{\rm d} z}{{\rm d} p} =V_{P} =V_{B} +\rho gs \end{gather} $ | (3) |
其中,
| $ \begin{align} T_{P} =EA_{0} \left(\frac{{\rm d} p}{{\rm d} s}-1\right) \end{align} $ | (4) |
由式(1)~(3)可得:
| $ \begin{align} T_{P} =\sqrt{H_{B}^{2} +\left(V_{B} +\rho gs\right)^{2}} \end{align} $ | (5) |
整理式(1)~(5)得到:
| $ \begin{align} \frac{{\rm d} x}{{\rm d} s} & =\frac{H_{B}} {EA_{0}} +\frac{H_{B}} {\sqrt{H_{B}^{2} + \left({V_{B} +\rho gs}\right)^{2}}} \end{align} $ | (6) |
| $ \begin{align} \frac{{\rm d} z}{{\rm d} s} & =\frac{V_{B} +\rho gs}{EA_{0}} +\frac{V_{B} +\rho gs}{\sqrt{H_{B}^{2} + \left({V_{B} +\rho gs}\right)^{2}}} \end{align} $ | (7) |
式(6)(7)的边界条件为
| $ \begin{align} z| _{x=0} & =0 \end{align} $ | (8) |
| $ \begin{align} z| _{x=l} & =h \end{align} $ | (9) |
对式(6)(7)进行积分,并根据边界条件式(8),得到关于
| $ \begin{align} x =&\frac{H_{B}} {EA_{0}} s+\frac{H_{B}} {\rho g} \begin{bmatrix} \dfrac{s}{h}\dfrac{V_{B} +\rho gs}{H_{B}} \\ -\dfrac{s}{h}\dfrac{V_{B}} {H_{B}} \end{bmatrix} \end{align} $ | (10) |
| $ \begin{align} z =&\frac{V_{B}} {EA_{0}} s+\frac{\rho g}{2EA_{0}} s^{2}+ \\ &\frac{1}{\rho g}\left({\sqrt{H_{B}^{2} +\left({V_{B} +\rho gs}\right)^{2}}-\sqrt{H_{B}^{2} +V_{B}^{2}}}\right) \end{align} $ | (11) |
式(10)(11)即为单根钢索悬链线模型的表达式,根据另一边界条件式(9)进行数值迭代计算可以求出
假设钢索在运动过程中只受拉力而不受压力,钢索单元的材料均匀、各向同性,忽略剪切和扭转变形。在全局坐标系
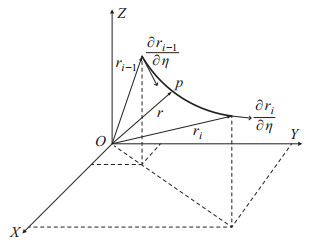
将钢索单元视为1维的2节点单元,在3维空间坐标系中每个节点的坐标由该点的位置和梯度矢量6个广义位移分量组成,每个单元包含2个节点,即有12个广义位移坐标,如图 3所示。
|
图 3 钢索单元 Fig.3 A single cable element |
| $ \begin{align} \mathit{\boldsymbol{u}}_{i}& =\left[\mathit{\boldsymbol{e}}_{i-1} , \mathit{\boldsymbol{e}}_{i} \right]^{\rm T}, \quad i=1, \cdots , n \end{align} $ | (12) |
| $ \begin{align} \mathit{\boldsymbol{e}}_{i}& =[e_{1}, e_{2}, e_{3}, e_{4}, e_{5}, e_{6}] \\ & =\left[r_{iX}, r_{iY}, r_{iZ}, \frac{\partial r_{iX}} {\partial \eta}, \frac{\partial r_{iY}} {\partial \eta}, \frac{\partial r_{iZ}} {\partial \eta}\right] \end{align} $ | (13) |
其中
| $ \begin{align} \mathit{\boldsymbol{r}}& =\mathit{\boldsymbol{Su}} \end{align} $ | (14) |
| $ \begin{align} \mathit{\boldsymbol{S}}& = \begin{bmatrix} (1-3\xi^{2}+2\xi^{3})\mathit{\boldsymbol{I}} \\ l_{\rm e} (\xi -2\xi^{2}+\xi^{3})\mathit{\boldsymbol{I}} \\ (3\xi^{2}-2\xi^{3})\mathit{\boldsymbol{I}} \\ l_{\rm e} (\xi^{3}-\xi^{2})\mathit{\boldsymbol{I}} \end{bmatrix}^{\rm T} \end{align} $ | (15) |
其中,
| $ \begin{align} \mathit{\boldsymbol{\dot{r}}} & ={\dot{{\mathit{\boldsymbol{S}}}}{\mathit{\boldsymbol{u}}}}+{{\mathit{\boldsymbol{S}}}\dot{{\mathit{\boldsymbol{u}}}}} \end{align} $ | (16) |
| $ \begin{align} \mathit{\boldsymbol{\ddot{{\mathit{\boldsymbol{r}}}}}} & ={\ddot{{\mathit{\boldsymbol{S}}}}{\mathit{\boldsymbol{u}}}}+ 2{\dot{{\mathit{\boldsymbol{S}}}}\dot{{\mathit{\boldsymbol{u}}}}}+{{\mathit{\boldsymbol{S}}}\ddot{{\mathit{\boldsymbol{u}}}}} \end{align} $ | (17) |
对于
| $ \begin{align} \mathit{\boldsymbol{\dot{S}}} & =\frac{\partial \mathit{\boldsymbol{S}}}{\partial \xi} \dot{\xi}+\frac{\partial \mathit{\boldsymbol{S}}}{\partial t} \end{align} $ | (18) |
| $ \begin{align} \mathit{\boldsymbol{\ddot{S}}} & =\frac{\partial^{2}\mathit{\boldsymbol{S}}}{\partial \xi^{2}}\dot{\xi}^{2}+\frac{\partial \mathit{\boldsymbol{S}}}{\partial \xi} \ddot{\xi}+2\frac{\partial^{2}\mathit{\boldsymbol{S}}}{\partial t\partial \xi} \dot{\xi}+\frac{\partial^{2}\mathit{\boldsymbol{S}}}{\partial t^{2}} \end{align} $ | (19) |
在得到钢索单元上任意一点的位置、速度和加速度的情况下,根据虚功原理可以得到钢索单元的动力学方程。钢索单元惯性力的虚功为
| $ \begin{align} \mathtt{δ} W_{\rm eI} & =-\int_0^{l_{\rm e}} \rho \mathtt{δ} {{\mathit{\boldsymbol{r}}}}^{\rm T}\ddot{{\mathit{\boldsymbol{r}}}} {\rm d}\eta \\ & =-\int_0^{l_{\rm e}} \rho \mathtt{δ} {{\mathit{\boldsymbol{r}}}}^{\rm T}\ddot{{\mathit{\boldsymbol{r}}}} \frac{{\rm d}\eta} {{\rm d}\xi} {\rm d}\xi \\ & =-\mathtt{δ} {{\mathit{\boldsymbol{u}}}}^{\rm T}l_{\rm e} \int_0^1 \rho \ddot{{\mathit{\boldsymbol{r}}}} {\rm d}\xi \\ & =-\mathtt{δ} {{\mathit{\boldsymbol{u}}}}^{\rm T} \left({{\mathit{\boldsymbol{M}}}}_{\rm eI} \ddot{{\mathit{\boldsymbol{u}}}}+{{\mathit{\boldsymbol{C}}}}_{\rm eI} \dot{{\mathit{\boldsymbol{u}}}}+{{\mathit{\boldsymbol{K}}}}_{\rm eI} {{\mathit{\boldsymbol{u}}}}\right) \end{align} $ | (20) |
式中,
| $ \begin{align} \mathit{\boldsymbol{M}}_{\rm eI} & =l_{\rm e} \int_0^1 \rho \mathit{\boldsymbol{S}}^{\rm T}\mathit{\boldsymbol{S}} {\rm d}\xi \end{align} $ | (21) |
| $ \begin{align} \mathit{\boldsymbol{C}}_{\rm eI} & =l_{\rm e} \int_0^1 \rho \mathit{\boldsymbol{S}}^{\rm T}\mathit{\boldsymbol{\dot{S}}} {\rm d}\xi \end{align} $ | (22) |
| $ \begin{align} \mathit{\boldsymbol{K}}_{\rm eI} & =l_{\rm e} \int_0^1 \rho \mathit{\boldsymbol{S}}^{\rm T}\mathit{\boldsymbol{\ddot{S}}} {\rm d}\xi \end{align} $ | (23) |
钢索单元弹性力的虚功
| $ \begin{align} \mathtt{δ} W_{\rm eE} & =\int_0^{l_{\rm e}} EA_{0} \mathtt{δ} {\varepsilon} {\varepsilon} {\rm d}\eta \\ & =\mathtt{δ} {{\mathit{\boldsymbol{u}}}}^{\rm T}l_{\rm e} \int_0^1 \frac{\partial {\varepsilon}} {\partial {{\mathit{\boldsymbol{u}}}}}EA_{0} {\varepsilon} {\rm d}\xi \\ & =\mathtt{δ} {{\mathit{\boldsymbol{u}}}}^{\rm T}l_{\rm e} \int_0^1 EA_{0} {\varepsilon} ({{\mathit{\boldsymbol{S}}}}_{\eta}^{\rm T}{{\mathit{\boldsymbol{S}}}}_{\eta}) {\rm d}\xi {{\mathit{\boldsymbol{u}}}} \\ & =\mathtt{δ} {{\mathit{\boldsymbol{u}}}}^{\rm T}{{\mathit{\boldsymbol{Q}}}}_{\rm eE} \end{align} $ | (24) |
式中,
| $ \begin{align} {\varepsilon} =\sqrt{\mathit{\boldsymbol{r}}_{\eta}^{\rm T}\mathit{\boldsymbol{r}}_{\eta}} -1 \end{align} $ | (25) |
其中
| $ \begin{align} {\varepsilon} =\frac{l_{\rm es} -l_{\rm e}} {l_{\rm e}} \end{align} $ | (26) |
| $ \begin{align} l_{\rm es} & =\int_0^{l_{\rm e}} \sqrt{{{\mathit{\boldsymbol{u}}}}^{\rm T}{{\mathit{\boldsymbol{S}}}}_{\eta}^{\rm T}{{\mathit{\boldsymbol{S}}}}_{\eta} {{\mathit{\boldsymbol{u}}}}} {\rm d}\eta \\ & = \int_0^{l_{\rm e}} \sqrt{{{\mathit{\boldsymbol{u}}}}^{\rm T}{{\mathit{\boldsymbol{S}}}}_{\eta}^{\rm T}{{\mathit{\boldsymbol{S}}}}_{\eta} {{\mathit{\boldsymbol{u}}}}-1+1} {\rm d}\eta \\ & \approx \int_0^{l_{\rm e}} \big(1+\frac{{{\mathit{\boldsymbol{u}}}}^{\rm T}{{\mathit{\boldsymbol{S}}}}_{\eta}^{\rm T}{{\mathit{\boldsymbol{S}}}}_{\eta} {{\mathit{\boldsymbol{u}}}}-1}{2}\big) {\rm d}\eta \\ & =\frac{1}{2} \int_0^{l_{\rm e}} \left(1+{{\mathit{\boldsymbol{u}}}}^{\rm T}{{\mathit{\boldsymbol{S}}}}_{\eta}^{\rm T}{{\mathit{\boldsymbol{S}}}}_{\eta} {{\mathit{\boldsymbol{u}}}}\right){\rm d}\eta \end{align} $ | (27) |
将式(27)代入式(24)(26)即可求得钢索单元弹性力的虚功。
在忽略外界干扰的情况下,钢索所受外力仅为重力,
| $ \begin{align} \mathtt{δ} W_{\rm eG} & =\int_0^{l_{\rm e}} \mathtt{δ} {{\mathit{\boldsymbol{r}}}}^{\rm T}{{\mathit{\boldsymbol{f}}}} {\rm d}\eta \\ & =l_{\rm e} \mathtt{δ} {{\mathit{\boldsymbol{u}}}}^{\rm T}\int_0^1 {{{\mathit{\boldsymbol{S}}}}^{\rm T}{{\mathit{\boldsymbol{f}}}}} {\rm d}\xi =\mathtt{δ} {{\mathit{\boldsymbol{u}}}}^{\rm T}{{\mathit{\boldsymbol{Q}}}}_{\rm eG} \end{align} $ | (28) |
根据虚功原理可知,钢索单元的惯性力虚功、弹性力虚功、广义外力虚功之和为0:
| $ \begin{align} \mathtt{δ} W_{\rm eI} -\mathtt{δ} W_{\rm eE} +\mathtt{δ} W_{\rm eG} =0 \end{align} $ | (29) |
则钢索单元的动力学方程为
| $ \begin{align} \mathit{\boldsymbol{M}}_{\rm eI} \mathit{\boldsymbol{\ddot{{\mathit{\boldsymbol{u}}}}}}+\mathit{\boldsymbol{C}}_{\rm eI} \mathit{\boldsymbol{\dot{{\mathit{\boldsymbol{u}}}}}}+\mathit{\boldsymbol{K}}_{\rm eI} \mathit{\boldsymbol{u}}+\mathit{\boldsymbol{Q}}_{\rm eE} -\mathit{\boldsymbol{Q}}_{\rm eG} =\mathit{\boldsymbol{0}} \end{align} $ | (30) |
当钢索单元长度不变时,式(30)中质量矩阵
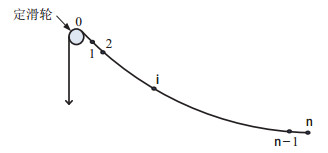
钢索单元由对图 4所示的单根钢索进行离散化处理得到,钢索的初始长度为
|
图 4 单根钢索的离散化处理 Fig.4 Discretization of a single cable |
| $ \begin{align} L_{\rm d} (t)=L_{\rm d0} +\Delta L_{\rm d} (t) \end{align} $ | (31) |
将整根钢索的长度变化视为第1个钢索单元的长度变化,其余
| $ \begin{align} l_{\rm e}^{(1)}(t)=l_{\rm e0}^{(1)}+\Delta l_{\rm e}^{(1)}=l_{\rm e0}^{(1)}+\Delta L_{\rm d} \end{align} $ | (32) |
设置长度阈值
| $ \begin{align} \dot{\xi} & =\frac{\Delta \dot{L}_{\rm d}} {l_{\rm e}^{(1)}}(1-\xi) \end{align} $ | (33) |
| $ \begin{align} \ddot{\xi} & =\frac{\Delta \ddot{L}_{\rm d}} {l_{\rm e}^{(1)}} (1-\xi)-2\frac{\Delta \dot{L}_{\rm d}^{2}}{ \left(l_{\rm e}^{(1)}\right)^{2}}(1-\xi) \end{align} $ | (34) |
对钢索单元进行组装,即可得到整根钢索的动力学方程。将钢索划分为
| $ \begin{align} \mathit{\boldsymbol{q}}=\left[{\mathit{\boldsymbol{e}}_{0}} \; \; \cdots \; \; {\mathit{\boldsymbol{e}}_{i}} \; \; \cdots \; \; {\mathit{\boldsymbol{e}}_{n}} \right]^{\rm T} \end{align} $ | (35) |
引入只包含0和1元素的布尔矩阵
| $ \begin{align} \mathit{\boldsymbol{u}}_{i} & =\mathit{\boldsymbol{B}}_{i} \mathit{\boldsymbol{q}} \end{align} $ | (36) |
| $ \begin{align} \mathit{\boldsymbol{B}}_{i} & =[\mathit{\boldsymbol{0}}_{12\times 6} \cdots \mathit{\boldsymbol{I}}_{12\times 12} \cdots \mathit{\boldsymbol{0}}_{12\times 6}] \end{align} $ | (37) |
整根钢索惯性力虚功为
| $ \begin{align} \mathtt{δ} W_{\rm I} & =\sum\limits_{i=1}^n \mathtt{δ} W_{\rm I}^{(i)} =\sum\limits_{i=1}^n \mathtt{δ} {{\mathit{\boldsymbol{e}}}}_{i}^{\rm T}l_{\rm e}^{(i)}\int_0^1 \rho {{\mathit{\boldsymbol{S}}}}^{\rm T}\ddot{{\mathit{\boldsymbol{r}}}} {\rm d}\xi \\ & =\mathtt{δ} {{\mathit{\boldsymbol{q}}}}^{\rm T} \left({{\mathit{\boldsymbol{M}}}}_{\rm I} \ddot{{{\mathit{\boldsymbol{q}}}}}+{{\mathit{\boldsymbol{C}}}}_{\rm I} \dot{{{\mathit{\boldsymbol{q}}}}}+{{\mathit{\boldsymbol{K}}}}_{\rm I} {{\mathit{\boldsymbol{q}}}}\right) \end{align} $ | (38) |
其中,
| $ \begin{align} \mathit{\boldsymbol{M}}_{\rm I} & =\sum\limits_{i=1}^n \mathit{\boldsymbol{B}}_{i}^{\rm T} \mathit{\boldsymbol{M}}_{\rm eI}^{(i)}\mathit{\boldsymbol{B}}_{i} \end{align} $ | (39) |
| $ \begin{align} \mathit{\boldsymbol{C}}_{\rm I} & =\sum\limits_{i=1}^n \mathit{\boldsymbol{B}}_{i}^{\rm T} \mathit{\boldsymbol{C}}_{\rm eI}^{(i)}\mathit{\boldsymbol{B}}_{i} \end{align} $ | (40) |
| $ \begin{align} \mathit{\boldsymbol{K}}_{\rm I} & =\sum\limits_{i=1}^n \mathit{\boldsymbol{B}}_{i}^{\rm T} \mathit{\boldsymbol{K}}_{\rm eI}^{(i)}\mathit{\boldsymbol{B}}_{i} \end{align} $ | (41) |
同理得到广义弹性力和外力为
| $ \begin{align} \mathit{\boldsymbol{Q}}_{\rm E} & =\sum\limits_{i=1}^n \mathit{\boldsymbol{B}}_{i}^{\rm T}\mathit{\boldsymbol{Q}}_{\rm eE}^{(i)} \end{align} $ | (42) |
| $ \begin{align} \mathit{\boldsymbol{Q}}_{\rm G} & =\sum\limits_{i=1}^n \mathit{\boldsymbol{B}}_{i}^{\rm T}\mathit{\boldsymbol{Q}}_{\rm eG}^{(i)} \end{align} $ | (43) |
得到整根钢索的动力学方程为
| $ \begin{align} \mathit{\boldsymbol{M}}_{\rm I} \mathit{\boldsymbol{\ddot{q}}}+\mathit{\boldsymbol{C}}_{\rm I} \mathit{\boldsymbol{\dot{q}}}+\mathit{\boldsymbol{K}}_{\rm I} \mathit{\boldsymbol{q}}+\mathit{\boldsymbol{Q}}_{\rm E} -\mathit{\boldsymbol{Q}}_{\rm G} =\mathit{\boldsymbol{0}} \end{align} $ | (44) |
FAST馈源支撑系统中索牵引并联机构的平面示意图如图 5所示。钢索与支撑塔的连接点为
| $ \begin{align} \mathit{\boldsymbol{x}}_{\rm e} =[x \; \; y \; \; z \; \; \alpha \; \; \beta \; \; \gamma ]^{\rm T}=[\mathit{\boldsymbol{x}}_{\rm e1} \; \; {\mathit{\boldsymbol{x}}_{\rm e2}} ]^{\rm T} \end{align} $ | (45) |

|
图 5 六索牵引并联机构平面示意图 Fig.5 The schematic of cable-driven parallel manipulator |
在忽略外界干扰的情况下刚性动平台的动力学方程可表示为
| $ \begin{align} \mathit{\boldsymbol{M}}_{\rm p} \mathit{\boldsymbol{\ddot{x}}}_{\rm e} +\mathit{\boldsymbol{C}}_{\rm p} \mathit{\boldsymbol{\dot{x}}}_{\rm e} =\mathit{\boldsymbol{F}}_{\rm pg} +{\tau} \end{align} $ | (46) |
其中
| $ \begin{align} \mathit{\boldsymbol{\tau}} =-\mathit{\boldsymbol{\varLambda T}}_{n} \end{align} $ | (47) |
| $ \begin{align} \mathit{\boldsymbol{\varLambda}} & = \begin{bmatrix} {\mathit{\boldsymbol{u}}_{P_1}} & {\mathit{\boldsymbol{u}}_{P_2}} & \cdots & {\mathit{\boldsymbol{u}}_{P_6}} \\ {\mathit{\boldsymbol{Rb}}_{1} \times \mathit{\boldsymbol{u}}_{P_1}} & {\mathit{\boldsymbol{Rb}}_{2} \times \mathit{\boldsymbol{u}}_{P_2}} & \cdots & {\mathit{\boldsymbol{Rb}}_{6} \times \mathit{\boldsymbol{u}}_{P_6}} \end{bmatrix} \end{align} $ | (48) |
| $ \begin{align} \mathit{\boldsymbol{T}}_{n} & =[{t_{1}} \; \; {t_{2}} \; \; {t_{3}} \; \; {t_{4}} \; \; {t_{5}} \; \; {t_{6}} ]^{\rm T} \end{align} $ | (49) |
其中
| $ \begin{align} \begin{cases} \mathit{\boldsymbol{e}}_{j, n_j} =\mathit{\boldsymbol{x}}_{\rm e1} +\mathit{\boldsymbol{R}}(\mathit{\boldsymbol{x}}_{\rm e2})\mathit{\boldsymbol{b}}_{j} \\ \mathit{\boldsymbol{\dot{e}}}_{j, n_j} =\mathit{\boldsymbol{\dot{x}}}_{\rm e1} +\mathit{\boldsymbol{\dot{R}}}(\mathit{\boldsymbol{x}}_{\rm e2})\mathit{\boldsymbol{b}}_{j} \\ \mathit{\boldsymbol{\ddot{e}}}_{j, n_j} =\mathit{\boldsymbol{\ddot{x}}}_{\rm e1} +\mathit{\boldsymbol{\ddot{R}}}(\mathit{\boldsymbol{x}}_{\rm e2})\mathit{\boldsymbol{b}}_{j} \end{cases}\kern -10pt, \quad j=1, \cdots , 6 \end{align} $ | (50) |
根据钢索与馈源舱之间的约束,可以得到六索牵引并联机构的动力学模型,其整体的广义位移表示为
| $ \begin{align} \mathit{\boldsymbol{q}}_{\rm{com}} =\, [& \mathit{\boldsymbol{e}}_{1, 0}, \cdots, \mathit{\boldsymbol{e}}_{1, i_1}, \cdots, \mathit{\boldsymbol{e}}_{1, n_1-1}, \cdots, \mathit{\boldsymbol{e}}_{j, i_j} \cdots, \\ & \mathit{\boldsymbol{e}}_{6, 0}, \cdots, \mathit{\boldsymbol{e}}_{6, n_6 -1}, \mathit{\boldsymbol{x}}_{\rm e}]^{\rm T} \end{align} $ | (51) |
每根钢索的第0个节点与塔顶定滑轮接触,定滑轮直径与钢索长度相比可忽略不计,即将
| $ \begin{align} \mathit{\boldsymbol{T}}=\left[{e}_{j, 0} (1), \; \; {e}_{j, 0} (2), \; \; {e}_{j, 0} (3) \right]-\mathit{\boldsymbol{P}}_{A_j} =\mathit{\boldsymbol{0}} \end{align} $ | (52) |
| $ \begin{align} \begin{cases} \mathit{\boldsymbol{M\ddot{q}_{\rm{com}}}}+\mathit{\boldsymbol{C\dot{q}_{\rm{com}}}}+\mathit{\boldsymbol{Kq}}_{\rm{com}}+\mathit{\boldsymbol{T}}_{{{\mathit{\boldsymbol{q}}}}_{\rm com}}^{\rm T}\mathit{\boldsymbol{\lambda}} =\mathit{\boldsymbol{Q}} \\ \mathit{\boldsymbol{T}}=\mathit{\boldsymbol{0}} \end{cases} \end{align} $ | (53) |
式中
以FAST馈源支撑系统中的六索牵引并联机器人为研究对象,分别建立钢索的动力学方程和馈源舱的刚性动力学方程,并基于钢索末端与馈源舱的约束建立了六索牵引并联机器人的动力学方程组,如式(53)所示。本文中使用Matlab软件中求解刚性微分方程的ode23tb算法进行计算。
5 数值算例(Numerical example)结合FAST馈源支撑系统的主要参数建立索牵引并联机构的动力学方程组,并进行仿真计算。钢索和馈源舱主要参数如表 1所示;塔顶出索点在全局坐标系中的位置和铰接点在动平台局部坐标系中的位置如表 2所示。
|
|
表 1 FAST钢索和馈源舱主要参数 Tab. 1 Main parameters of the FAST cable and the feed cabin |
|
|
表 2 出索点和铰接点位置坐标(单位:m) Tab. 2 Position coordinates of the cable outlet points and the cable attachment points (unit: m) |
馈源舱在全局坐标系

|
图 6 静力学和动力学模型馈源舱位置及位置误差 Fig.6 Position and position error of the feed cabin in static and dynamic models |
由图 6可以看出,考虑了钢索的动态特性后,馈源舱位置在其静力平衡位置附近振动,该结果体现了钢索动态特性对馈源舱位置精度的影响。
5.2 算例2馈源舱在FAST换源过程中进行加减速运动,馈源舱的初始点为

|
图 7 钢索的速度 Fig.7 Speed of the cables |
|
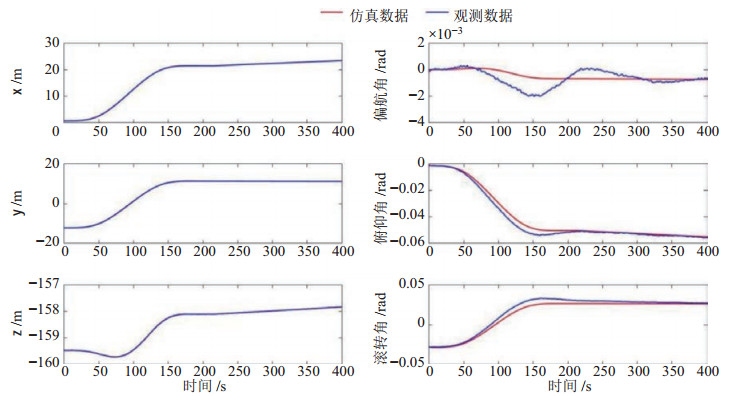
图 8 馈源舱位姿仿真数据与观测数据对比 Fig.8 Comparison between the simulation and observation data of the feed-cabin pose |

|
图 9 钢索拉力的仿真数据与观测数据对比 Fig.9 Comparison between the simulation and observation data of the cable force |
由于测量设备自身的误差,以及在建立模型时进行的简化(例如将钢索上不均匀分布的传输光缆质量均匀分摊到钢索上,将塔顶定滑轮与钢索的接触点视为定点等),使得馈源舱位姿和钢索拉力的仿真数据和观测数据存在一定的误差。但是仿真数据和观测数据的趋势相同,最大相对误差不超过20%,证明了本文模型的有效性。六索牵引并联机构的动力学数值仿真模型是基于柔性多体系统建立的,仿真结果体现出钢索的时变性对馈源舱位姿的影响。与文[6]中在静力平衡位置进行线性简化得到的动力学模型相比,当馈源舱在馈源焦面上的运动超过一定距离时,本文所建立的动力学模型不需要重新计算。
6 结论(Conclusion)针对FAST馈源支撑系统中的六索牵引并联机构进行了力学分析。在初始时刻使用悬链线模型计算6根钢索的长度,对钢索进行离散化处理并采用绝对节点坐标法对钢索单元进行动力学分析,建立了六索牵引并联机构的动力学模型。由仿真结果可知,馈源舱位姿在其静力平衡位置附近振动,证明了钢索动态特性对馈源舱位姿的影响。
将FAST实际运行中钢索的长度变化的速度和加速度代入所建立的动力学方程组中,证明了所建立动力学模型的有效性。在建立模型的过程中对索牵引并联机构进行了简化,导致所建立动力学模型与实际模型存在一定的误差。但将动力学方程组计算得到馈源舱位姿和钢索拉力与观测数据进行对比,结果仍然呈现出较好的吻合性,说明了该建模方法的有效性,对该类索牵引并联机构的动力学建模具有参考意义。
后续将对文中建立的微分-代数动力学方程组计算精度及效率问题、初始位姿等误差源的辨识问题以及动力学抑振控制问题,进行进一步的探讨。
| [1] |
Nan R D. Five hundred meter aperture spherical radio telescope (FAST)[J]. Science China: Physics, Mechanics & Astronomy, 2006, 49(2): 129-148. |
| [2] |
Jiang P, Yue Y L, Gan H Q, et al. Commissioning progress of the FAST[J]. Science China: Physics, Mechanics & Astronomy, 2019, 62(5). DOI:10.1007/s11433-018-9376-1 |
| [3] |
姚蕊, 唐晓强, 李铁民, 等. 大型射电望远镜馈源定位3T索牵引并联机构分析与设计[J]. 机械工程学报, 2007, 43(11): 105-109. Yao R, Tang X Q, Li T M, et al. Analysis and design of 3T cable-driven parallel manipulator for the feedback's orientation of the large radio telescope[J]. Chinese Journal of Mechanical Engineering, 2007, 43(11): 105-109. |
| [4] |
黄亮, 朱文白, 唐晓强. 大射电望远镜巨型柔性并联机构悬索分析及简化[J]. 天文研究与技术, 2013, 10(1): 77-84. Huang L, Zhu W B, Tang X Q. Analysis and a simplified model of the cable of a large-scale flexible parallel manipulator for a large radio telescope[J]. Astronomical Research and Technology, 2013, 10(1): 77-84. |
| [5] |
Yin J N, Jiang P, Yao R. An approximately analytical solution method for the cable-driven parallel robot in FAST[J]. Research in Astronomy and Astrophysics, 2021, 21(2): 46-57. DOI:10.1088/1674-4527/21/2/46 |
| [6] |
李辉, 孙京海, 朱文白, 等. 500 m口径球面射电望远镜柔性馈源支撑系统仿真[J]. 计算机辅助工程, 2011, 20(1): 106-112. Li H, Sun J H, Zhu W B, et al. Simulation on flexible feed support system of five-hundred-meter aperture spherical radio telescope[J]. Computer Aided Engineering, 2011, 20(1): 106-112. |
| [7] |
Du J L, Hong B, Cui C Z, et al. Dynamic analysis of cabledriven parallel manipulators with time-varying cable lengths[J]. Finite Elements in Analysis & Design, 2012, 48(1): 1392-1399. |
| [8] |
金小琳. 四索牵引并联机器人的动力学分析与振动控制[D]. 西安: 西安电子科技大学, 2018. Jin X L. Dynamic analysis and vibration control of four-cabledriven parallel manipulators vibration attenuation control[D]. Xi'an: XiDian University, 2018. |
| [9] |
赵雅聪, 王启明. 柔索并联机构的动力学建模与仿真[C]//第28届全国结构工程学术会议论文集. 北京: 工程力学杂志社, 2019: 351-355. Zhao Y C, Wang Q M. The dynamic modeling and simulation of flexible cable parallel manipulator[C]//Proceedings of the 28th National Conference on Structural Engineering. Beijing: Editorial Board of Engineering Mechanics, 2019: 351-355. |
| [10] |
Shabana A A. Flexible multibody dynamics: Review of past and recent developments[J]. Multibody System Dynamics, 1997, 1: 189-222. DOI:10.1023/A:1009773505418 |
| [11] |
沈剑, 韩峰, 陈放, 等. 基于绝对节点坐标法柔性绳索体建模仿真研究[J]. 科学技术与工程, 2016, 16(31): 1-7. Shen J, Han F, Chen F, et al. Modeling and simulation of flexible cable-body by absolute nodal coordinate formulation[J]. Science Technology and Engineering, 2016, 16(31): 1-7. |
| [12] |
吴懋琦, 谭述君, 高飞雄. 基于绝对节点坐标法的平面梁有限变形下变形重构[J]. 力学学报, 2021, 53(10): 2776-2789. Wu M Q, Tan S J, Gao F X. Shape reconstruction of plane beam with finite deformation based on absolute nodal coordinate formulation[J]. Chinese Journal of Theoretical and Applied Mechanics, 2021, 53(10): 2776-2789. |
| [13] |
Luo C Q, Sun J L, Wen H, et al. Dynamics of a tethered satellite formation for space exploration modeled via ANCF[J]. Acta Astronautica, 2020, 177: 882-890. |
| [14] |
王忠民, 吴力国. 基于变长度单元ANCF的轴向伸展悬臂梁振动分析[J]. 振动与冲击, 2019, 38(3): 186-191. Wang Z M, Wu L G. Vibration analysis of axially deploying cantilever beam based on ANCF with length-varying beam element[J]. Journal of Vibration and Shock, 2019, 38(3): 186-191. |
| [15] |
Bulín R, Hajzman M, Polach P. Nonlinear dynamics of a cablepulley system using the absolute nodal coordinate formulation[J]. Mechanics Research Communications, 2017, 82: 21-28. |
| [16] |
Wago T, Kobayashi N, Sugawara Y. Improvement on evaluating axial elastic force in Bernoulli-Euler beam based on the absolute nodal coordinate formulation by accurate mean axial strain measure[C]//ASME 2011 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference. New York, USA: ASME, 2011: 963-970.
|
 2023, Vol. 45
2023, Vol. 45


