2. 复杂工程系统测量与控制教育部重点实验室, 江苏 南京 210096
2. Key Laboratory of Measurement and Control of Complex Systems of Engineering, Ministry of Education, Nanjing 210096, China
人机协作类任务要求机器人基于人体状态观测结果推理出满足任务要求的机器人协作轨迹[1]。例如图 1所示的人机交递任务,机器人需要通过观测人机协作运动中人手的位置,根据其与机械臂末端位置的非线性映射来推理出机械臂响应的运动轨迹,从而完成交递任务[2]。然而,这种非线性关系难以通过手动编程的方式赋予机器人,因此采用模仿学习[3]的方法,即通过示教者示教人手轨迹与机器人轨迹获取示教样本,机器人从示教样本中学习这种非线性关系,并将该关系泛化到新的环境与任务下,这是提高人机协作类任务学习与泛化适应性的关键[4-5]。
|
图 1 人机交递运动的模仿学习 Fig.1 Imitation learning of human-robot handover motion |
近年来,模仿学习因其高可用的优势,在赋予机器人特定技能的任务中得到了广泛的应用。Silvério等[6]提出一种基于四元数的动态模仿学习系统,基于模仿学习算法编码与复现出满足正交矩阵约束的姿态运动轨迹。针对机器人与环境高度交互的任务场景,Abu-Dakka等[7-8]基于经典模仿学习算法,通过迁移函数使得刚度矩阵与其切空间之间互相映射,实现了柔性控制中刚度矩阵的学习与泛化。Kramberger等[9]引入环境变量,利用LWR(局部加权回归)法对模仿学习模型的参数进行预测,通过考虑环境变量,提高了模仿学习的学习能力。Manschitz等[10]通过对一个完整待学习序列任务轨迹进行分割,将任务轨迹划分为不同的运动基元,通过构建不同运动基元间的概率转移,将运动基元进行合理串联组合,实现机器人对任务动作序列的学习与泛化。人机协作的任务场景要求模仿学习算法基于人的状态(如人手的位置)及时合理地推理出机器人运动轨迹,在完成任务的基础上机器人轨迹还要具有满足人类偏好的轨迹特征,从而构建友好的人机协作环境[2]。
已有的面向人机协作类任务的模仿学习算法主要包含2类,时间驱动的模仿学习算法与人手位置驱动的模仿学习算法[11]。时间驱动的模仿学习算法例如动态运动基元(DMP)[12]和概率运动基元(ProMP)[13-14]以时间为输入编码人手与机械臂的末端轨迹。然而时间驱动的方法需要处理时间规整的问题[15],对于新场景中人手轨迹速度的变化,往往需要严苛的场景假设条件才能实现观测轨迹与示教轨迹之间的时间规整[1]。
人手位置驱动的模仿学习算法直接预测对应机械臂末端的位置,避免了时间规整的问题,克服了时间驱动模仿学习算法对环境具有严苛假设的缺点,具有更强的应用性[11]。经典的高斯过程(GP)[16-17]和高斯混合模型(GMM)[18-19]虽然可以直接编码人手位置和机械臂末端位置间的非线性关系,但算法不具备外插能力,难以直接调整已有的模型以满足新的任务需要[20]。任务参数化高斯混合模型(TP-GMM)[21]采用对局部轨迹特征建模的方法提高了高斯混合模型的外插特性,但是依然难以实现任意轨迹点的调整[5]。核化运动基元(KMP)算法[22]以人手位置为输入,采用核函数度量输入数据之间的特征距离,可以学习具有高维输入的轨迹的特征,可以适应轨迹任意点的调整。
然而将经典KMP用于人机协作任务中的人手轨迹模仿学习,存在2个主要难点。一是远离示范空间的轨迹泛化问题:当任务中人手位置可能出现的空间区域较大时,需要示教轨迹覆盖这些区域,并对人手位置可能出现的完整空间区域进行充分采样。大量的空间区域采样会增加算法的计算量,降低推理的实时性;若人手运动出现在未示教过的新空间区域,则无法泛化生成新的机器人轨迹。二是轨迹长度自适应问题:已有的人手位置驱动的模仿学习算法无法实现对机械臂末端响应轨迹长度变化的适应与泛化。
针对上述问题,本文提出一种基于KMP的人机交递轨迹模仿学习算法。当人手位置出现在未采样过的新空间区域时,第2级KMP模型利用参数调制方法生成适应新空间区域中人手位置的推理模型,而第1级KMP模型学习人机交递轨迹中人手位置与机械臂末端位置之间的非线性关系。进一步,第3级KMP模型对人机交递中机械臂末端轨迹的长度进行建模与调制,从而实现对机械臂末端响应轨迹长度的自适应调整。
该方法避免了在完整空间区域进行大量示范与采样。对于新任务中出现未训练过的人手位置空间的情况,可以仅利用单例任务示范轨迹样本,将已学习到的人手位置与机械臂末端位置间的非线性关系迁移至新任务中的人手位置空间区域,从而实现了人机交递轨迹的单例迁移(one shot transfer)。
2 问题描述与方法概述(Problem statement and method overview)在图 1所示的人机交递任务中,图(a)(b)中人处于机器人不同方向相同距离处,人机动作轨迹方位不同,长度相近;图(b)(c)示教中含有不同尺度的联合轨迹。本文假设:1)人的自然伸手动作起始状态不同,但轨迹长度近似相等,机器人需要适应人手位置的变化并响应出满足交递任务需要的不同方向、不同长度的末端轨迹以满足任务需要;2)当人手动作轨迹泛化到不同子区域时,机械臂末端响应轨迹应保持相似的轨迹形状。
图 2(a)是示教样本联合轨迹簇说明图,图 2(c)是示教样本轨迹簇
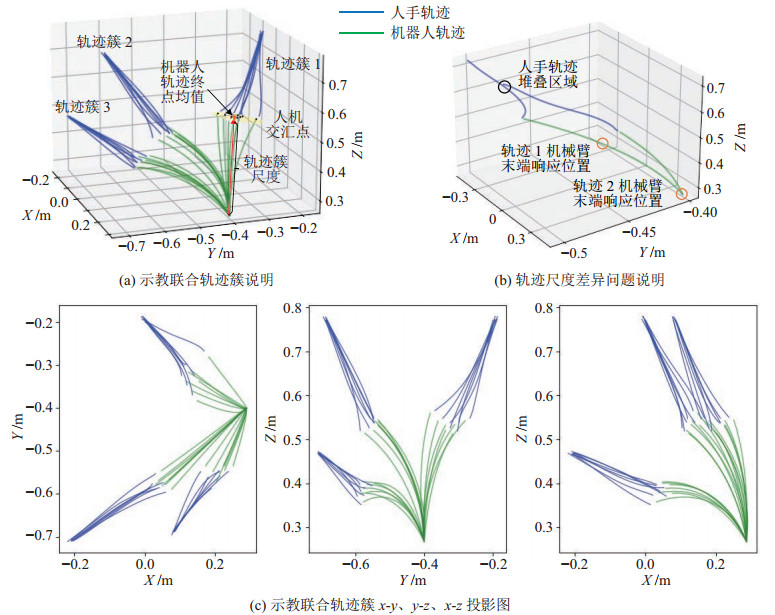
|
图 2 示教样本说明 Fig.2 Illustration of demonstration samples |
图 1(b)(c)反映了示教轨迹存在不同尺度的联合轨迹的情况,图 2(b)说明了这种情况下示教样本中的轨迹尺度差异问题,尺度较大的联合轨迹(轨迹1)中间位置会与尺度较小的联合轨迹(轨迹2)人手起始位置重叠。人机协作中一个人手位置需要对应一个机械臂末端位置,但即便轨迹1与轨迹2重叠点处的人手位置相近,它们所对应的机械臂末端响应位置也存在较大的差异。经典的KMP算法对于联合轨迹尺度变化没有适应性,根据堆叠的人手位置无法推理出正确的机械臂末端位置,因此需要对联合轨迹尺度进行缩放。
方法总体原理如图 3所示。在学习阶段,选择一组轨迹簇,定义该轨迹簇所在空间区域为基准子区域。基准子区域提供后续相关空间与尺度变换的基准,其选择对算法没有影响,建议基准子区域选择于各子区域中心位置。一级KMP模型负责学习基准子区域中人手位置与机械臂末端位置间的非线性关系。由于一级KMP模型对人手位置的采样仅仅存在于基准子区域内,所以若人手当前位于基准子区域外,则仅靠一级KMP模型无法推理出合理的机械臂末端位置。
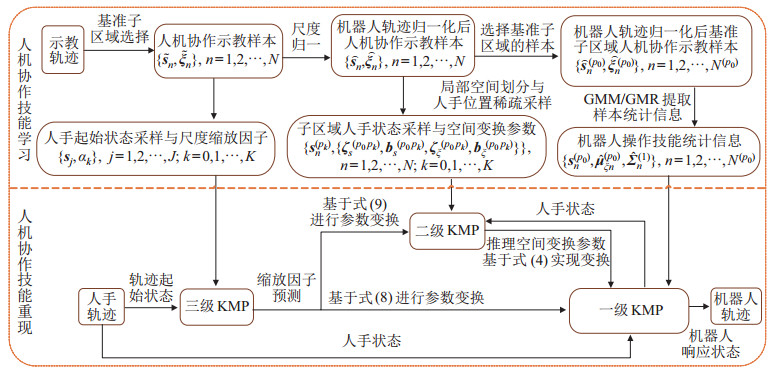
|
图 3 多级核化运动基元系统框图 Fig.3 Block diagram of the multi-level KMP system |
基于假设2),在获取必要调制参数的基础上二级KMP模型对推理模型进行调制,生成适应当前人手位置的推理模型,从而采用参数调制的方法将学习到的非线性关系推广至不同子区域,实现对整个人手位置空间的覆盖,详见3.2节。
针对人机交递任务,人手轨迹的起始位置往往决定了人手轨迹的相对位置,从而确定了联合轨迹的尺度,定义基准子区域中的联合轨迹簇尺度为基准尺度,定义不同子区域中联合轨迹簇尺度与基准尺度比例为尺度缩放因子。设计三级KMP模型学习人手轨迹起始位置与尺度缩放因子间的映射关系,详见3.3节。
3 基于多级核化运动基元的人机协作运动轨迹模仿学习(Imitation learning of human-robot collaborative movement trajectories based on multi-level KMPs) 3.1 数据预处理针对示教出的多组轨迹簇,首先需要对轨迹簇进行尺度归一化。不失一般性,假设机械臂末端轨迹起始位置位于坐标系原点。如图 3所示,在训练过程中,针对含有不同尺度的联合轨迹簇的原始示教样本
| $ \begin{equation} \begin{aligned} l_{k}^{(\rm c)} & =\| \mathit{\boldsymbol{x}}_{k} \|, \; k=1, 2, \cdots \\ \alpha_{k} & =\frac{l_{k}^{(\rm c)}} {l_{0}^{(\rm c)}} \\ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\boldsymbol{\xi}}_{i} & =\tilde{\mathit{\boldsymbol{\xi}}}_{i} \mathit{\boldsymbol{R}}_{k} \text{diag} \left(\frac{1}{\alpha_{k}}, 1, 1\right)\mathit{\boldsymbol{R}}_{k}^{-1} \\ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\boldsymbol{s}}_{i} & =\tilde{\mathit{\boldsymbol{s}}}_{i} +\mathit{\boldsymbol{x}}_{k} \mathit{\boldsymbol{R}}_{k} \text{diag} \left(\frac{1}{\alpha_{k}}, 1, 1\right)\mathit{\boldsymbol{R}}_{k}^{-1} -\mathit{\boldsymbol{x}}_{k} \end{aligned} \end{equation} $ | (1) |
其中,
定义人机交递任务中人手位置潜在空间区域为人手位置全空间
一级KMP模型从基准子区域
| $ \begin{equation} \begin{aligned} E(\mathit{\boldsymbol{\xi}} (\mathit{\boldsymbol{s}}^{* (p_{0})}) )& = \mathit{\boldsymbol{k}}^{(p_{0})*} (\mathit{\boldsymbol{K}}+\lambda \mathit{\boldsymbol{\varSigma}}^{(1)})^{-1}\mathit{\boldsymbol{\mu}}_{\mathit{\boldsymbol{\xi}}}^{(p_{0})} \\ \mathit{\boldsymbol{k}}^{(p_{0})*} & = \left[ k \left(s^{* (p_{0})}, s_{1}^{(p_{0} ) }\right), \cdots, k \left(s^{* (p_{0})}, s_{N^{(p_{0})}}^{(p_{0})}\right) \right] \\ \mathit{\boldsymbol{\mu}} _{\mathit{\boldsymbol{\xi}}}^{(p_{0})} & =\left[\hat{\mathit{\boldsymbol{\mu}}}_{\mathit{\boldsymbol{\xi}} 1}^{(p_{0}){\rm T}}, \hat{\mathit{\boldsymbol{\mu}}}_{\mathit{\boldsymbol{\xi}} 2}^{(p_{0}){\rm T}}, \cdots, \hat{\mathit{\boldsymbol{\mu}}}_{\mathit{\boldsymbol{\xi}} N^{(p_{0})}}^{(p_{0}){\rm T}}\right]^{\rm T} \end{aligned} \end{equation} $ | (2) |
式中,
然而,一级KMP模型学习所得的推理模型无法处理基准子区域外的人手状态查询
| $ \begin{align} \begin{bmatrix} \mathit{\boldsymbol{s}}_{n}^{(p_{k})} \\ \mathit{\boldsymbol{\xi}}_{n}^{(p_{k})} \end{bmatrix}\approx \begin{bmatrix} \mathit{\boldsymbol{A}}_{\mathit{\boldsymbol{s}}}^{(p_{0} p_{k})} & 0 \\ 0 & \mathit{\boldsymbol{A}}_{\mathit{\boldsymbol{\xi}}}^{(p_{0} p_{k})} \end{bmatrix}\left(\begin{bmatrix} \mathit{\boldsymbol{s}}_{n}^{(p_{0})} \\ \mathit{\boldsymbol{\xi}}_{n}^{(p_{0})} \end{bmatrix}- \begin{bmatrix} \mathit{\boldsymbol{b}}_{\mathit{\boldsymbol{s}}}^{(p_{0} p_{k})} \\ \mathit{\boldsymbol{b}}_{\mathit{\boldsymbol{\xi}}}^{(p_{0} p_{k})} \end{bmatrix}\right) \end{align} $ | (3) |
其中,
在基准子区域
| $ \begin{equation} \begin{aligned} \mathit{\boldsymbol{s}}_{n}^{(p_{k})} & = \mathit{\boldsymbol{A}}_{\mathit{\boldsymbol{s}}}^{( p_{0} p_{k} )} \left( \mathit{\boldsymbol{s}}_{n}^{( p_{0} )} -\mathit{\boldsymbol{b}}_{\mathit{\boldsymbol{s}}}^{( p_{0} p_{k} )} \right) \\ \hat{\boldsymbol \mu}_{\mathit{\boldsymbol{\xi}} n}^{(p_{k})} & = \mathit{\boldsymbol{A}}_{\mathit{\boldsymbol{\xi}}}^{( p_{0} p_{k} )} \left( \hat{\boldsymbol \mu}_{ \mathit{\boldsymbol{\xi}} n}^{( p_{0} )} - \mathit{\boldsymbol{b}} _{\mathit{\boldsymbol{\xi}}}^{( p_{0} p_{k} )} \right) \\ \hat{\mathit{\boldsymbol{\varSigma}}}_{n}^{(p_{k})} & = \mathit{\boldsymbol{A}}_{\mathit{\boldsymbol{\xi}}}^{( p_{0} p_{k} )} \hat{\mathit{\boldsymbol{\varSigma}}}_{n}^{(p_{0})} \mathit{\boldsymbol{A}}_{\mathit{\boldsymbol{\xi}}}^{( p_{0} p_{k} )-1} \\ \mathit{\boldsymbol{K}}^{(p_{k})} & = \mathit{\boldsymbol{K}}^{(p_{0})} \end{aligned} \end{equation} $ | (4) |
其中
设计二级KMP模型,对于非基准子区域中的人手查询状态,实时推理式(3)中的变换参数
对于二级KMP模型的学习,在子区域
| $ \begin{align} &\begin{aligned} & (\mathit{\boldsymbol{A}}_{\mathit{\boldsymbol{s}}}^{(p_{0} p_{k})}, \mathit{\boldsymbol{b}}_{\mathit{\boldsymbol{s}}}^{(p_{0} p_{k})}) \\ =\; & \min\limits_{(\mathit{\boldsymbol{A}}_{\mathit{\boldsymbol{s}}}^{(p_{0} p_{k})}, \mathit{\boldsymbol{b}}_{\mathit{\boldsymbol{s}}}^{(p_{0} p_{k})})} \sum\limits_{n=1}^N \left\| \mathit{\boldsymbol{s}}_{n}^{(p_{k})} \!-\! \mathit{\boldsymbol{A}}_{\mathit{\boldsymbol{s}}}^{(p_{0} p_{k})} \left(\mathit{\boldsymbol{s}}_{n}^{(p_{0})} \!-\! \mathit{\boldsymbol{b}}_{\mathit{\boldsymbol{s}}}^{(p_{0} p_{k})}\right) \right\| \\ & (\mathit{\boldsymbol{A}}_{\mathit{\boldsymbol{\xi}}}^{(p_{0} p_{k})}, \mathit{\boldsymbol{b}}_{\mathit{\boldsymbol{\xi}}}^{(p_{0} p_{k})}) \\ =\; & \min\limits_{(\mathit{\boldsymbol{A}}_{\mathit{\boldsymbol{\xi}}}^{(p_{0} p_{k})}, \mathit{\boldsymbol{b}}_{\mathit{\boldsymbol{\xi}}}^{(p_{0} p_{k})})} \sum\limits_{n=1}^N \left\| \mathit{\boldsymbol{\xi}}_{n}^{(p_{k})} -\mathit{\boldsymbol{A}}_{\mathit{\boldsymbol{\xi}}}^{(p_{0} p_{k})} \left(\mathit{\boldsymbol{\xi}}_{n}^{(p_{0})} - \mathit{\boldsymbol{b}}_{\mathit{\boldsymbol{\xi}}}^{(p_{0} p_{k})}\right) \right\| \end{aligned} \end{align} $ | (5) |
| $ \begin{align} & D_{\mathit{\boldsymbol{\zeta}}} = \left\{ \mathit{\boldsymbol{s}}_{n}^{(p_{k})}, \left\{ \mathit{\boldsymbol{\zeta}}_{\mathit{\boldsymbol{s}}}^{(p_{0} p_{k})}, \mathit{\boldsymbol{b}}_{\mathit{\boldsymbol{s}}}^{(p_{0} p_{k})}, \mathit{\boldsymbol{\zeta}}_{\mathit{\boldsymbol{\xi}}}^{(p_{0} p_{k})}, \mathit{\boldsymbol{b}}_{\mathit{\boldsymbol{\xi}}}^{(p_{0} p_{k})} \right\} \right\} \end{align} $ | (6) |
最终学习所得的二级KMP模型推理公式如式(7)所示,针对人手查询状态
| $ \begin{equation} \begin{aligned} E(\mathit{\boldsymbol{\eta}} (\mathit{\boldsymbol{s}}^{*}) )& = \mathit{\boldsymbol{k}}^{*} (\mathit{\boldsymbol{K}}+\lambda \mathit{\boldsymbol{\varSigma}}^{(2)})^{-1} \mathit{\boldsymbol{\mu}}_{\mathit{\boldsymbol{\eta}}} \\ \mathit{\boldsymbol{\eta}} & = \left( \mathit{\boldsymbol{\zeta}}_{\mathit{\boldsymbol{s}}}^{(p_{0} p_{k})}, \mathit{\boldsymbol{b}}_{\mathit{\boldsymbol{s}}}^{(p_{0} p_{k})}, \mathit{\boldsymbol{\zeta}}_{\mathit{\boldsymbol{\xi}}}^{(p_{0} p_{k})}, \mathit{\boldsymbol{b}}_{\mathit{\boldsymbol{\xi}}}^{(p_{0} p_{k})} \right), \\ &\qquad k=0, 1, \cdots, K \\ \mathit{\boldsymbol{k}}^{*} & =\left[ k(\mathit{\boldsymbol{s}}^{*}, \mathit{\boldsymbol{s}}_{1}), \cdots, k(\mathit{\boldsymbol{s}}^{*}, \mathit{\boldsymbol{s}}_{N}) \right] \\ \mathit{\boldsymbol{\mu}}_{\mathit{\boldsymbol{\eta}}} & =\left[ \mathit{\boldsymbol{\eta}}_{1}^{\rm T}, \mathit{\boldsymbol{\eta}}_{2}^{\rm T}, \cdots, \mathit{\boldsymbol{\eta}}_{N}^{\rm T} \right]^{\rm T} \end{aligned} \end{equation} $ | (7) |
三级KMP模型需要利用尺度归一化之前的示教轨迹的人手样本状态与尺度归一化产生的缩放因子完成训练。在推理过程中调制一、二级KMP模型,从而推理出满足具体任务下联合轨迹尺度要求的机械臂末端轨迹。
基于三级KMP模型,在如图 3所示的人机协作技能复现阶段,对于一条人手轨迹,三级KMP模型基于人手轨迹起始位置
| $ \begin{equation} \begin{aligned} \hat{\mathit{\boldsymbol{\mu}}}_{\mathit{\boldsymbol{\xi}} n}^{p_{0}} & \leftarrow \hat{\mathit{\boldsymbol{\mu}}}_{\mathit{\boldsymbol{\xi}} n}^{p_{0}} \mathit{\boldsymbol{R}}_{0} \text{diag} (\alpha^{*}, 1, 1) \mathit{\boldsymbol{R}}_{0}^{-1} \\ \mathit{\boldsymbol{s}}_{n}^{p_{0}} & \leftarrow \mathit{\boldsymbol{s}}_{n}^{p_{0}} +\mathit{\boldsymbol{x}}_{0} \mathit{\boldsymbol{R}}_{0} \text{diag} (\alpha^{*}, 1, 1) \mathit{\boldsymbol{R}}_{0}^{-1} -\mathit{\boldsymbol{x}}_{0} \end{aligned} \end{equation} $ | (8) |
针对二级KMP模型,采用式(9)实现对二级KMP模型在联合轨迹尺度层面的调制。不同于一级KMP模型,二级KMP模型采样状态包含所有子区域中的轨迹簇,不同轨迹簇具有不同的延伸向量,需要针对不同轨迹簇中的人手采样状态在相应延伸向量的方向上进行调整。由于二级KMP模型负责学习与预测人手采样状态与方向调整所需变换参数之间的非线性关系,而旋转调整关系并不因为尺度变化而改变,所以仅仅需要调整人手的采样状态。值得一提的是,二级KMP模型下不同轨迹簇的延伸向量的指向往往不同,所以人手采样状态之间的相对关系会随着尺度调制过程而发生改变,在参数调制之后需要重新计算
| $ \begin{equation} \begin{aligned} \mathit{\boldsymbol{s}}_{n} & \leftarrow \mathit{\boldsymbol{s}}_{n} +\mathit{\boldsymbol{x}}_{k} \mathit{\boldsymbol{R}}_{k} \text{diag} (\alpha^{*}, 1, 1)\mathit{\boldsymbol{R}}_{k}^{-1} -\mathit{\boldsymbol{x}}_{k} \\ \mathit{\boldsymbol{\eta}}_{n} & \leftarrow \mathit{\boldsymbol{\eta}}_{n}, \; \; \; n=1, 2, \cdots, N;\; \; k=0, 1, \cdots, K \end{aligned} \end{equation} $ | (9) |
对于三级KMP模型的训练,为了学习得出人手起始位置与对应轨迹缩放因子之间的非线性关系,从式(1)未归一化的原始示教轨迹
| $ \begin{equation} \begin{aligned} E(\alpha ( \mathit{\boldsymbol{s}}^{*}) )& = \mathit{\boldsymbol{k}}^{*} \left( \mathit{\boldsymbol{K}}+\lambda \mathit{\boldsymbol{\varSigma}}^{(3)}\right)^{-1} \mathit{\boldsymbol{\mu}}_{\alpha} \\ \mathit{\boldsymbol{\mu}}_{\alpha} & =[\alpha_{1}, \alpha_{2}, \cdots, \alpha_{J} ]^{\rm T} \end{aligned} \end{equation} $ | (10) |
面向人机交递类任务,使用UR5机器人作为实验平台。利用Kinect相机采集人手位置轨迹,采用核相关滤波法(KCF)跟踪人手矩形框中心在3D空间中的位置,从而获取人手位置轨迹。使用直接示教法采集机械臂末端的示教轨迹,在“重力补偿”模式下示教者拖拽机器人,同时采集机械臂末端的位置轨迹。针对一次交递过程,分别采集交递动作的人手位置轨迹与机械臂末端位置轨迹,构成一次交递动作的联合轨迹。在人机交递场景下,通过在人手位置可能出现的空间区域采集多条联合轨迹构成示教样本数据集。
从以下3个角度评估多级KMP算法的性能:1)针对人机交递任务下的联合示教轨迹,测试算法对人手位置与机械臂末端位置之间非线性关系的学习与泛化能力,测试算法推理过程的实时性;2)测试算法对于联合轨迹尺度的适应与泛化性;3)验证算法的单例迁移能力。
4.1 基于多级KMP的人机交递轨迹学习与重现实验联合轨迹示教样本如图 4(a)所示,图 4(b)是不同轨迹簇中联合轨迹的均值轨迹。联合轨迹根据人手位置轨迹的分布不同可划分为7组轨迹簇,每组轨迹簇含有5条联合轨迹,构成含有35条轨迹的示教样本。考虑到在工程中,交递任务执行前需要机器人回归至约定状态,故实验采集示教样本时机械臂轨迹的起始位置均相同。值得一提的是,所提出的二级KMP模型能够预测得出待推理机械臂轨迹相对于基准子区域机械臂轨迹的平移量,因而算法对不同轨迹簇的机械臂轨迹起始位置无严格要求。采用留一交叉验证法(LOOCV)[23]进行测试。从多条演示轨迹中选取一条轨迹作为测试轨迹,其余轨迹均作为训练轨迹,从而共进行35组LOOCV测试。
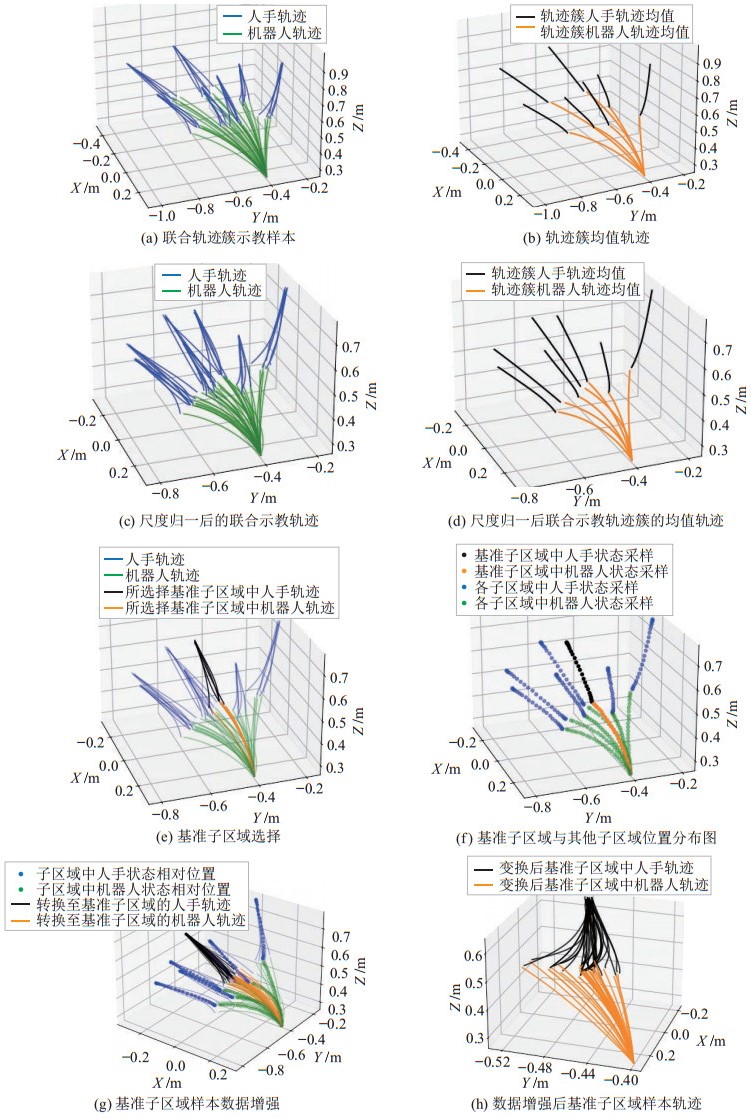
|
图 4 多级KMP系统数据预处理过程 Fig.4 Data preprocessing process of the multi-level KMP system |
针对传统KMP算法和提出的多级KMP算法,分别采用LOOCV进行性能验证。采用式(11)度量人机交递任务下的机械臂末端轨迹推理精度。
| $ \begin{align} e=\bigg\| \left\| \mathit{\boldsymbol{\xi}}_{\text{predict}}^{\text{end}} - \mathit{\boldsymbol{s}}_{\text{test}}^{\text{end}} \right\|_{{\rm L}2} - \left\| \mathit{\boldsymbol{\xi}}_{\text{test}}^{\text{end}} - \mathit{\boldsymbol{s}}_{\text{test}}^{\text{end}} \right\|_{\text{L2}} \bigg\|_{{\rm L}1} \end{align} $ | (11) |
其中
传统KMP算法对每一组轨迹簇进行等密度采样,一组轨迹簇采样状态个数为500个,7组轨迹簇共3500个采样状态。算法的核函数为式(12)的高斯核函数,针对算法超参数,通过手动调优,选择
| $ \begin{align} k( \mathit{\boldsymbol{s}}_{i}, \mathit{\boldsymbol{s}}_{j})=\sigma_{\rm f}^{2} \exp\left(-h\| \mathit{\boldsymbol{s}}_{i} - \mathit{\boldsymbol{s}}_{j} \|^{2} \right) \end{align} $ | (12) |
针对多级KMP模型,一级KMP模型对基准空间子区域采样500个采样状态,二级KMP模型对每个人手空间子区域采样30个采样状态,三级KMP模型对每条轨迹采样其人手轨迹起始位置。针对超参数,每一级KMP模型的
模型训练中,首先选择基准子区域,并计算基准子区域中的轨迹簇尺度,进一步将图 4(a)中尺度不同的轨迹簇进行尺度归一化,使得所有子区域中的轨迹簇尺度与基准子区域中的轨迹尺度相同,生成如图 4(c)所示的尺度归一化后的联合轨迹,并记录缩放因子,联合人手轨迹起始位置构成三级KMP模型的训练样本,图 4(d)是尺度归一化后不同轨迹簇的均值轨迹。基准子区域是一级KMP模型的训练子区域,如图 4(e)所示选择黑色与橙色轨迹所在空间为基准子区域,图 4(f)是基准子区域与其他子区域的位置分布图。计算各个子区域至基准子区域的变换关系,与各个子区域中的采样状态构成二级KMP模型的训练参数。如图 4(g)所示,将各个子区域中的轨迹变换至基准子区域以增加一级KMP模型的训练集,增强对人手位置与机械臂末端位置非线性关系的学习效果。数据增强后的基准子区域中的联合轨迹数据集如图 4(h)所示。
图 5所示是多级KMP算法的部分测试效果图,图 5(a)~(d)分别为以第2、14、26、31号轨迹作为测试轨迹的预测效果图。表 1为35次LOOCV测试误差统计。由表 1可以看出,多级KMP算法的平均误差与最大误差小于经典KMP算法,整体精度优于经典KMP算法。两种算法的中位误差与平均误差相近,没有出现大量远高于平均值的误差量,实验可以反映出算法的真实性能。多级KMP算法的均方根误差小于经典KMP算法,误差分布更加集中,算法稳定性优于经典KMP算法。多级KMP算法在处理人机交递任务时交递精度优于传统KMP算法,其原因主要在于传统KMP算法需要对每个人手空间子区域进行等密度采样,才能学习得到人手位置与机械臂末端位置之间的非线性关系,从而实现人机交递动作的学习与复现。针对一个人手位置进行推理所需的特征信息仅仅包含在该位置所处子区域的采样状态中,然而传统KMP算法在推理的过程中需要参考所有子区域内的采样状态,这就导致推理会受到其他子区域采样状态的干扰,精度降低,经典KMP算法的均方根误差较大,不同轨迹簇中的测试集误差差距大,轨迹推理稳定性受轨迹簇位置分布的影响大。另一方面,多级KMP算法仅仅在一个空间子区域内提取人手位置与机械臂末端位置之间的非线性关系,并将该非线性关系迁移至其他子区域,在推理过程中仅仅参考人手所处子区域的采样状态,避免了其他子区域采样状态的干扰,具有更高的推理精度。从表 1可以看出,多级KMP算法的误差总体较小,最大误差为8.09 cm,出现在对第26条轨迹的预测中,即图 5(c)。由图可知,产生误差的主要原因是人手轨迹的终止位置并非人手位置采样点(蓝色采样点)与机械臂末端位置采样点(绿色采样点)的交界处,这是由于文中假设同一轨迹簇下人手与机械臂的动作是交汇于同一平面的,但实际示教过程中同一轨迹簇人机交递动作交汇点与假设交汇平面存在一定误差。
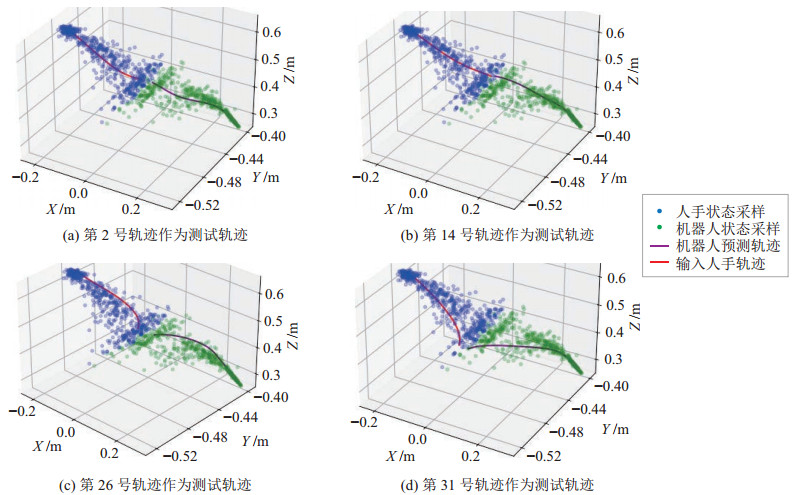
|
图 5 多级KMP算法的部分测试效果 Fig.5 Partial test results of the multi-level KMP algorithm |
|
|
表 1 人机交递任务LOOCV误差 Tab. 1 LOOCV error of the human-robot handover task |
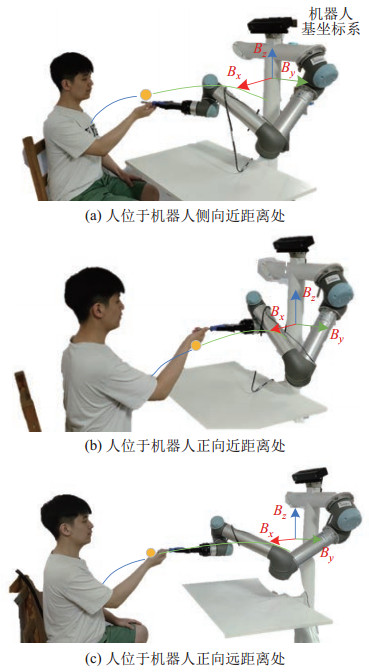
图 6是人机交递实物实验图。在协作运动中,通过实时检测人手在世界坐标系中的3维位置,并利用本文算法实时推理其对应的机械臂位置,进一步控制机械臂运动,以实现人手与机械臂同时运动的实验效果。图 6(a)是人位于机器人正向近距离时产生的交递动作,图 6(b)是人位于机器人侧向近距离时产生的交递动作,图 6(c)是人位于机器人正向远距离时产生的交递动作。本文方法对人手交递动作的方位差异具有很强的适应性,对人位于机器人正向近距离位置、侧向近距离位置、正向远距离位置时的交递动作均能推理出满足任务要求的机械臂末端响应轨迹。

|
图 6 人机交递实验 Fig.6 Human-robot handover experiment |
算法实时性分析如表 2所示,其中总推理时间是对一条包含100个人手位置的人手轨迹进行完整推理所需的时间。经典KMP算法完成一次人机交递过程可以分为2个阶段,首先需要检测人手并确定其初始位置,第2阶段对一条人手轨迹上的每个位置实时推理其机械臂末端响应位置。人机交递任务往往对第2阶段的推理具有较高的实时性要求,而对第1阶段无严苛的实时性要求。
|
|
表 2 算法推理时长对比 Tab. 2 Comparison of algorithm inference duration |
本文的多级KMP算法将轨迹尺度预测归为第1阶段,从而定义对实时性要求较高的第2阶段的推理时间为实时响应部分的总推理时间。定义实时响应部分的平均推理时间为对单个人手位置推理其机械臂末端响应位置所需的时间,定义参数变换时间为利用二级KMP模型对一级KMP模型进行参数调制所需的时间。从表 2可以看出,本文的多级KMP算法的一级KMP模型仅仅在基准子区域进行人手位置采样,避免了一级KMP模型对整个人手位置空间区域进行采样而导致采样状态过多的问题,实时性更高。
4.2 尺度适应与泛化性能分析当示教轨迹中存在尺度不同但人手位置轨迹堆叠的联合轨迹时,本文的多级KMP算法比传统KMP算法在轨迹尺度适应性与泛化性方面更优。
如图 7所示,采集3组不同联合轨迹簇,每组轨迹簇具有10条轨迹,轨迹簇间联合轨迹尺度不同,利用LOOCV法验证传统KMP算法与多级KMP算法对轨迹尺度的适应性。
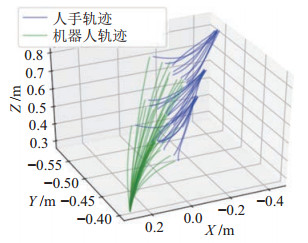
|
图 7 具有不同尺度的联合示教轨迹簇 Fig.7 Demonstrated joint trajectory clusters with remarkable scale difference |
如表 3所示,多级KMP算法针对具有尺度差异的示教轨迹,仍然能够学习得出满足任务需要的人手位置与机械臂末端位置的映射关系,具有很强的轨迹复现与泛化能力。而经典KMP算法由于缺少轨迹尺度适应性,机械臂末端响应轨迹交递成功率较低。
|
|
表 3 多级KMP算法与经典KMP算法的轨迹尺度适应性对比 Tab. 3 Comparison of trajectory scale adaptability between multi-level KMP and classical KMP algorithms |
图 8是经典KMP算法与多级KMP算法的联合轨迹尺度适应性对比图,图 8(a)(c)(e)是以第2、12、22条轨迹作为测试轨迹时多级KMP算法的预测效果,图 8(b)(d)(f)是以第2、12、22条轨迹作为测试轨迹时传统KMP算法的预测效果。表 4针对图 8中的轨迹给出了轨迹加速度数据与终点误差数据,以度量轨迹的平滑度与精度性能。第2、22条测试轨迹是传统KMP算法成功推理的轨迹,第12条测试轨迹为传统KMP算法推理失败的示例。从图中可以看出,第12条预测轨迹与示教轨迹的形状差异过大,且不平滑;从表 4可看出,经典KMP算法在推理第12条轨迹时,平均加速度大于多级KMP算法,且最大加速度较大,存在加速度突变轨迹点,平滑性差。而针对第2、22条轨迹,经典KMP算法虽然成功完成推理,但是机械臂末端轨迹终点与人手轨迹末端终点的距离较远,如表 4所示,经典KMP算法的终点误差远大于多级KMP算法。与经典KMP算法相比,本文的多级KMP算法推理出的机械臂末端轨迹具有平滑且轨迹终点距离小的特点,轨迹尺度适应性更好。
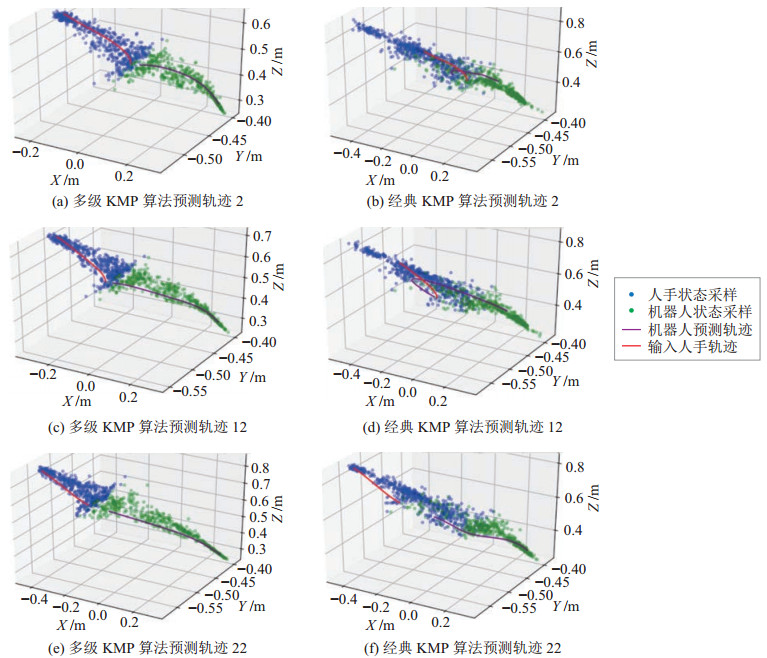
|
图 8 经典KMP与多级KMP算法的联合轨迹尺度适应性对比 Fig.8 Comparison of joint trajectory scale adaptability between multi-level KMP and classical KMP algorithms |
针对新的人手轨迹可能出现的工作区间,多级KMP算法仅仅需要一条示教联合轨迹便可以将已学习到的人手位置与机械臂末端位置间的非线性关系迁移至目标空间,可以有效提高算法的迁移能力。如图 9所示,其中蓝色、绿色轨迹是4.1节中的示教轨迹,黑色、橙色轨迹是新的人手空间区域中的示教轨迹。从新的轨迹簇中选择一条轨迹作为训练集,其余4条轨迹作为验证集。
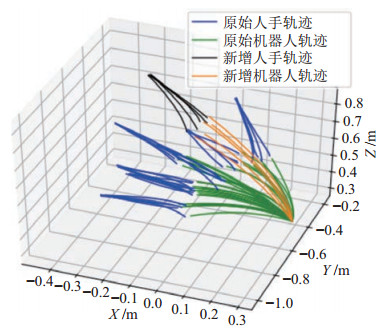
|
图 9 联合轨迹分布图 Fig.9 Joint trajectory distribution |
利用3.2节、3.3节中的方法提取目标迁移空间中的训练示教轨迹的尺度变换信息与空间变换信息,利用KMP算法的外插功能将变换信息外插至二级KMP模型与三级KMP模型中,从而生成适应新的人手空间区域的预测模型。
图 10针对4条轨迹验证多级KMP算法的单例迁移性能,图 10(a)(c)(e)(g)分别是以第2~5条轨迹作为测试轨迹时,测试轨迹与二级KMP模型的空间稀疏采样状态的分布示意图,图 10(b)(d)(f)(h)是以第2~5条轨迹作为测试轨迹时机器人轨迹的预测效果图。由图 10可以看出,针对新的人手空间区域的测试轨迹,算法可以推理出满足任务要求的机械臂末端响应轨迹。
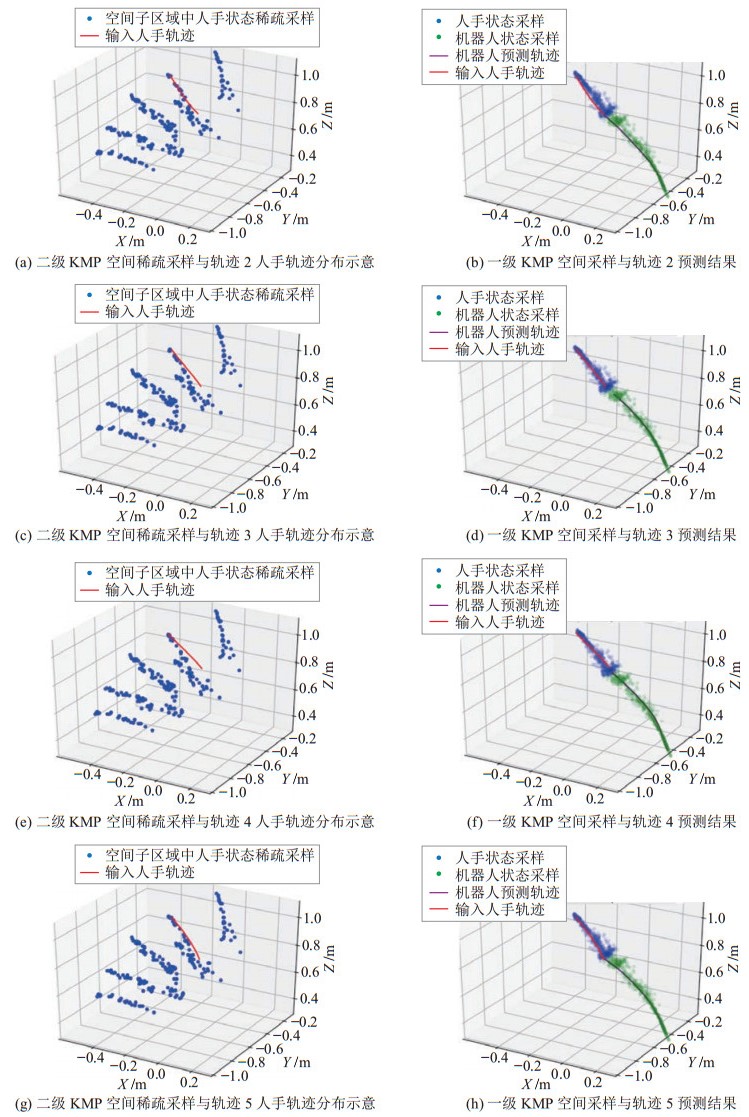
|
图 10 单例迁移性能测试 Fig.10 Test of the one-shot transfer ability |
针对人机物品交递任务中的人机动作轨迹模仿学习与泛化问题,提出一种多级KMP算法,相比经典KMP算法有以下3方面的改进:首先,在基准子区域中学习人手位置与机械臂末端位置之间的非线性映射关系并将其迁移至全空间中,避免了在完整的人手空间区域中进行大密度采样,消除了在对某一子区域内人手位置进行推理时其他区域采样状态的干扰,具有更高的预测精度与实时性。其次,考虑了尺度缩放问题,因此对于具有不同尺度的联合轨迹示教样本具有更强的学习能力。此外,支持单例模仿学习,即对于新的给定任务仅需要单例任务示范,可将已学习到的人手位置与机械臂末端位置之间的非线性关系迁移至新的任务中的人手位置空间区域。
本文的多级KMP算法在经典KMP算法的基础上提高了算法的尺度适应性与泛化性,增强了算法的迁移能力,降低了算法对大量示教样本的依赖,提高了算法的实时性,在机器人仓采(bin-picking)等难以完全使用示教样本覆盖工作空间、对算法泛化性要求高的工作场景中具有很强的推广性。
| [1] |
Maeda G, Ewerton M, Neumann G, et al. Phase estimation for fast action recognition and trajectory generation in human-robot collaboration[J]. International Journal of Robotics Research, 2017, 36(13-14): 1579-1594. DOI:10.1177/0278364917693927 |
| [2] |
Maeda G J, Neumann G, Ewerton M, et al. Probabilistic movement primitives for coordination of multiple human-robot collaborative tasks[J]. Autonomous Robots, 2017, 41(3): 593-612. DOI:10.1007/s10514-016-9556-2 |
| [3] |
Schaal S. Is imitation learning the route to humanoid robots?[J]. Trends in Cognitive Sciences, 1999, 3(6): 233-242. DOI:10.1016/S1364-6613(99)01327-3 |
| [4] |
Huang Y L, Silvério J, Rozo L, et al. Generalized task-parameterized skill learning[C]//IEEE International Conference on Robotics and Automation. Piscataway, USA: IEEE, 2018: 5667-5474
|
| [5] |
黄艳龙, 徐德, 谭民. 机器人运动轨迹的模仿学习综述[J]. 自动化学报, 2022, 48(2): 315-334. Huang Y L, Xu D, Tan M. On imitation learning of robot movement trajectories: A survey[J]. Acta Automatica Sinica, 2022, 48(2): 315-334. |
| [6] |
Silvério J, Rozo L, Calinon S, et al. Learning bimanual end-effector poses from demonstrations using task-parameterized dynamical systems[C]//IEEE International Conference on Intelligent Robots and Systems. Piscataway, USA: IEEE, 2015: 464-470.
|
| [7] |
Abu-Dakka F J, Kyrki V. Geometry-aware dynamic movement primitives[C]//IEEE International Conference on Robotics and Automation. Piscataway, USA: IEEE, 2020: 4421-4426.
|
| [8] |
Abu-Dakka F J, Huang Y L, Silvério J, et al. A probabilistic framework for learning geometry-based robot manipulation skills[J]. Robotics and Autonomous Systems, 2021, 141. DOI:10.1016/j.robot.2021.103761 |
| [9] |
Kramberger A, Gams A, Nemec B, et al. Generalization of orientation trajectories and force-torque profiles for robotic assembly[J]. Robotics and Autonomous Systems, 2017, 98: 333-346. DOI:10.1016/j.robot.2017.09.019 |
| [10] |
Manschitz S, Gienger M, Kober J, et al. Learning sequential force interaction skills[J]. Robotics, 2020, 9(2). DOI:10.3390/robotics9020045 |
| [11] |
Huang Y L, Abu-Dakka F J, Silvério J, et al. Toward orientation learning and adaptation in Cartesian space[J]. IEEE Transactions on Robotics, 2021, 37(1): 82-98. DOI:10.1109/TRO.2020.3010633 |
| [12] |
Ijspeert A J, Nakanishi J, Hoffmann H, et al. Dynamical movement primitives: Learning attractor models for motor behaviors[J]. Neural Computation, 2013, 25(2): 328-373. DOI:10.1162/NECO_a_00393 |
| [13] |
Paraschos A, Daniel C, Peters J R, et al. Probabilistic movement primitives[C]//Advances in Neural Information Processing Systems 26. Red Hook, USA: Curran Associates Inc., 2013.
|
| [14] |
Dermy O, Paraschos A, Ewerton M, et al. Prediction of intention during interaction with iCub with probabilistic movement primitives[J]. Frontiers in Robotics and AI, 2017, 4. DOI:10.3389/frobt.2017.00045 |
| [15] |
Amor H B, Neumann G, Kamthe S, et al. Interaction primitives for human-robot cooperation tasks[C]//IEEE International Conference on Robotics and Automation. Piscataway, USA: IEEE, 2014: 2831-2837.
|
| [16] |
Seeger M. Gaussian processes for machine learning[J]. International Journal of Neural Systems, 2004, 14(2): 69-106. DOI:10.1142/S0129065704001899 |
| [17] |
Silvério J, Huang Y L, Rozo L. An uncertainty-aware minimal intervention control strategy learned from demonstrations[C]//IEEE/RSJ International Conference on Intelligent Robots and Systems. Piscataway, USA: IEEE, 2018: 6065-6071.
|
| [18] |
Ghahramani Z, Jordan M. Supervised learning from incomplete data via an EM approach[C]//Advances in Neural Information Processing Systems 6. Red Hook, USA: Curran Associates Inc., 1993.
|
| [19] |
Mainprice J, Berenson D. Human-robot collaborative manipulation planning using early prediction of human motion[C]// IEEE/RSJ International Conference on Intelligent Robots and Systems. Piscataway, USA: IEEE, 2013: 299-306.
|
| [20] |
Luo R C, Mai L C. Human intention inference and on-line human hand motion prediction for human-robot collaboration[C]//IEEE/RSJ International Conference on Intelligent Robots and Systems. Piscataway, USA: IEEE, 2019: 5958-5964.
|
| [21] |
Calinon S, Bruno D, Caldwell D G. A task-parameterized probabilistic model with minimal intervention control[C]//IEEE International Conference on Robotics and Automation. Piscataway, USA: IEEE, 2014: 3339-3344.
|
| [22] |
Huang Y L, Rozo L, Silvério J, et al. Kernelized movement primitives[J]. International Journal of Robotics Research, 2019, 38(7): 833-852. DOI:10.1177/0278364919846363 |
| [23] |
杉山将. 图解机器学习[M]. 北京: 人民邮电出版社, 2015: 34-42. Sugiyama M. Illustration of machine learning[M]. Beijing: Posts and Telecom Press, 2015: 34-42. |
 2023, Vol. 45
2023, Vol. 45


