2. 河南科技大学信息工程学院, 河南 洛阳 471023
2. College of Information Engineering, Henan University of Science and Technology, Luoyang 471023, China
与载人飞行器相比,无人机作为一类不载操作人员,并能利用机载传感器和飞行控制系统自主执行预设任务或通过无线电遥控设备发送指令执行任务的飞行器[1],具有对作业环境要求低、无人员伤亡风险、飞行灵活、任务完成高效等特点。在20世纪中期以后,无人机开始逐步脱离其早期作为靶机的功能,投身于更为广阔且更为重要的军事领域,其在执行战场侦测、火力支援、情报收集、攻防博弈等危险性任务时有着载人飞行器无法比拟的优势[2]。根据其结构与飞行动力学形式的不同,可将无人机分为固定翼无人机、旋翼无人机、无人飞艇与扑翼无人机等。
近年来,无人机在军事和民用领域扮演着重要角色,其相关技术正在飞速发展。美国国防部办公室在《2005-2030年无人机系统路线图》[3]中表示:“提高无人机的安全及可靠性是确保其成功的最直接和最长远的需要”,这一点表明了无人机安全及可靠性的重要性,也预示无人机的安全飞行控制系统相关技术研究具有巨大发展空间[4]。目前,导致无人机在飞行过程中出现安全控制问题的原因有很多,如复杂动态干扰环境下无人机飞行超出自身结构确定的安全边界、输入/输出和状态约束下的飞行控制能力下降、系统故障与外部攻击下的控制可靠性降低,以及无人机集群系统内部碰撞等。以上因素都是导致无人机失控、出现安全问题的主要诱因,需在设计飞行控制器时加以明确考虑。
由于无人机在军事和民用领域具有极高的应用价值,所以研发无人机高性能安全飞行控制技术直接决定了无人机完成任务的效能[5]。但是无人机自身具有高度非线性、强耦合、快时变、强不确定、静不稳定等特性,从而导致其高性能飞行控制器难以有效设计[6]。同时,无人机在特定的任务环境下,常常受到外部环境以及内部自身物理条件的限制,其各个状态、控制输入均会受到各式各样的约束或控制性能指标受到严格限制,通常表现为地形位置限制、姿态角约束、饱和约束、指定性能指标约束以及控制输入饱和等。值得一提的是,其中有些约束是无法提前预知的,因此预设的期望信号很有可能与实时约束发生冲突。如果在有限的控制周期内不能有效检测这些约束并加以及时规避,就有可能造成无人机失控或坠机等不可逆的飞行事故,导致重大损失。
另一方面,无人机长期运行在强腐蚀、大温差、多扰动和恶意攻击的极端环境中,这会导致系统的损伤、设备和元器件的老化,进而导致无人机产生传感器故障和执行器故障等。同时,为了完成单个无人机无法完成的任务,可以构建无人机集群系统来执行复杂任务。在集群无人机系统中,单个无人机可能存在故障使得队形切换,各个无人机之间通过网络进行信息交互时可能会出现网络攻击,或者在强动态干扰作用下各无人机之间会发生碰撞等。以上问题都会造成无人机或无人机集群系统飞行控制系统性能降低,甚至导致无人机或无人机集群系统不能完成预定的任务,出现坠机等严重事故。因此,提高复杂、恶劣环境下的无人机安全飞行控制能力是未来航空技术领域发展的重要方向之一,对提高国家战略地位也具有重要意义。
本文以近年来国内外无人机安全飞行控制领域的研究成果为基础,分别对安全边界保护控制、不同约束下的安全控制、系统故障与攻击下的安全控制,以及无人机集群系统安全控制方法与研究成果进行了分析与综述。最后,给出了该领域未来具有发展潜力的研究方向。
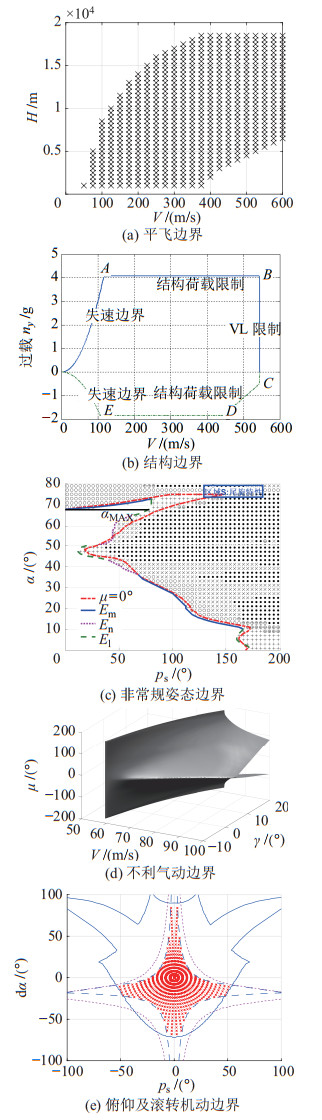
2 气动/结构边界限制下的无人机安全飞行控制(Safety flight control for UAV under constraints of aerodynamics and structure envelopes)随着无人机的气动外形越来越复杂,以及各种型号无人机的不断投入使用,失控与坠机事件也常有发生,进而导致任务失败、装备损毁甚至技术泄密等严重后果,这是制约无人机发展的重要因素。在有人飞行器领域,早在2000年美国商业航空安全组织就曾依据气动特性与动力学机理定义出5类失控边界,如图 1所示[7-8],供驾驶员判定飞行器状态。但是,对于无人机来说,经验丰富的驾驶员完成的职责将完全交由机载飞行控制系统来承担,飞行控制策略在兼顾任务完成能力的同时,还需要保证无人机的飞行安全。
|
图 1 5类失控边界 Fig.1 5 types of loss-of-control envelopes |
固定翼无人机对机动能力要求较高,关于其气动机理的研究相对透彻,其在非定常气动条件下的机动安全飞行边界广受关注。而旋翼无人机的空气动力学更为复杂,涡流、激振问题更为突出,所以其安全边界确定问题同样受到广泛关注。无人飞艇具有优异的悬空能力,无需进行大范围机动,因此,更多情况下关注外界扰动下的安全飞行边界。扑翼无人机的位置与姿态运动耦合更加紧密,其气动与安全边界研究尚处在起步阶段。
从控制科学的视角出发,无人机失控事故都是飞行状态超过特定约束的表现。为了阐明无人机的失控边界,先给出一般意义下的飞行器失控边界的定义与分析方法。在航空领域,飞行状态进入不满足可控性指标的区域统称为“失控”[9],而预判失控的集合分析技术称为“边界判定”。相应的失控边界是指由飞行状态描述的超曲面,它能为飞行器判断当前状态是否必然导致失控提供依据,而边界判定技术则专注于获取更加精准的失控边界,进而生成用于控制的安全约束。
飞行边界主要分为固定边界与动态边界两种。令
| $ \begin{align} \mathit{\boldsymbol{\dot{x}}}=\mathit{\boldsymbol{f}}(\mathit{\boldsymbol{x}}, \mathit{\boldsymbol{u}}) \end{align} $ | (1) |
其中
| $ \begin{align} \underline{\mathit{\boldsymbol{x}}}\leqslant \mathit{\boldsymbol{x}}\leqslant \overline{\mathit{\boldsymbol{x}}} \end{align} $ | (2) |
其中,
伴随着对飞行器气动机理理解的不断深入与计算机仿真技术的发展,原先依赖试飞实验的边界判定方式逐步被数字分析技术取代,以非线性吸引域方法[11]、可达集[12]、可达配平集[13]以及分支分析方法[14]最具代表性。文[15] 基于蒙特卡洛模拟法提出了一种随机边界判定方法,极大地降低了求解边界时的计算负载。文[16] 考虑控制约束的影响,利用可达集方法对某客机纵向含舵机特性的增广系统进行了边界的解算。文[7-8] 针对歼击机过失速机动的边界判定问题展开了研究,深入探讨了多种不同类边界之间的内在联系与耦合关系。Chu教授团队以垂尾缺失后飞行边界的变化为切入点,深入探讨了结构损伤后边界的变化机理[17],并借助数值方法构建了在线全状态边界判定方法[18]。在此基础上,该团队又提出了一种基于蒙特卡洛模拟的概率边界判定方法,进一步降低了全状态边界计算的复杂度[19]。
相较载人飞行器,无人机的体积更小、质量更轻、飞行速度相对较慢,基于无人机自身气动特性与结构的飞行边界存在适应性差的缺点,难以有效应对如恶劣环境或系统故障等特殊场景。因此,采用动态飞行边界进行描述的可靠性更高[10]。具体可描述为如下形式:
| $ \begin{align} \mathit{\boldsymbol{x}}_{\rm l} (t)\leqslant \mathit{\boldsymbol{x}}(t)\leqslant \mathit{\boldsymbol{x}}_{\rm u} (t), \forall t\in [ 0, T ) \end{align} $ | (3) |
此刻,
虽然无人机飞行边界的相关研究仍处在探索阶段,但已有不少有价值的研究成果。比如,文[20] 引入了一种微分涡格算法,结合卡尔曼滤波方法在线学习逼近无人机边界。文[21] 在配平飞行边界判定过程中引入了自适应机制,实现了在配载变化或发生故障的情况下边界的自动调节。
考虑生成边界的约束和飞行器自身特性约束的飞行控制技术被称为“安全边界保护控制”,它通过主动限制飞行器机动能力,迫使飞行状态处在安全区域范围内,进而确保其不会进入失控区域,是保证飞行安全的一种重要手段,主要包括控制指令限幅、模型预测控制与参考指令管理3种方法[22],下面将逐次进行介绍。
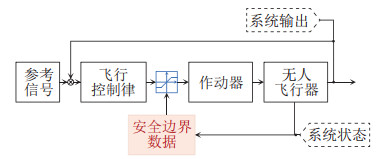
2.1 基于控制指令限幅的安全边界保护控制对无人机的边界保护与安全控制早期分属于2个不同的模块,多采用限制控制指令的架构[22]。控制限幅架构保证飞行安全的核心在于:根据飞行边界,建立系统状态与作动器限幅之间的映射关系,进而根据映射关系限制作动器指令信号,系统控制框图如图 2所示。
|
图 2 基于控制指令限幅的安全控制系统框图 Fig.2 Diagram of control command limiting-based |
在有人机方面,基于控制指令限幅的安全边界保护控制已有不少研究成果。考虑到限幅映射的解算对有人飞行器的气动参数有着较大的依赖,Yavrucuk等[23]借助神经网络在线逼近飞行器模型,实现了限幅映射的在线解算。进而,文[24] 引入动态配平思想,借助自适应神经网络提出了一种在线限幅映射学习方法。该方法通过在线估计局部动态配平条件,有效地降低了飞行器先验信息条件。该方法已成功应用于XV-15倾转旋翼机的快速俯仰机动。在此基础上,文[25] 在自适应神经网络的训练过程中,引入历史数据回溯机制,实现了更加精确的动态配平条件与限幅映射的估计。
另一方面,基于控制指令限幅的安全控制方法对飞行器静稳定性具有严苛要求,难以满足先进无人机特殊构形的需求,因而其在无人机层面产生的成果较少。文[26] 针对空中机器人提出了力矩限幅方案,并在UH-60无人直升机上进行了仿真验证。借助指数势函数,文[27] 针对无人机姿态回路提出了一种速率受限控制方法。
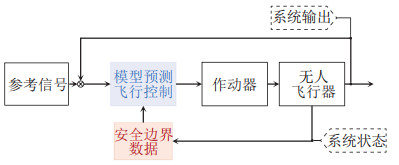
2.2 基于模型预测的安全边界保护控制基于模型预测的安全边界保护控制,旨在借助具有约束处理能力的模型预测控制(MPC)方法,处理无人机的安全飞行边界约束,控制系统框图如图 3所示。
|
图 3 基于模型预测的安全控制框图 Fig.3 Diagram of model prediction-based safety control |
MPC作为一种高性能控制算法,通过建立精确数学模型来预测控制系统的未来状态,在考虑相关约束的条件下根据最优化的方式来确定控制输出量,确保控制性能达到优化指标,并在随后的采样周期中循环重复整个控制优化过程,具有结构简单、能同时处理高维飞行边界等特点[28]。
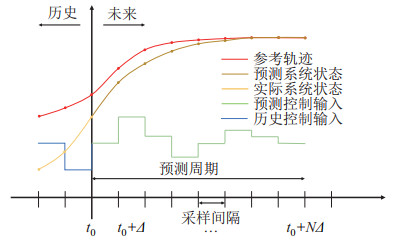
模型预测控制主要可以分为预测模型、滚动优化、反馈校正3个要素[29]。1) 预测模型:根据无人机动力学特性,针对未来时刻的状态响应所建立的系统模型。2) 滚动优化:在每一个采样时刻,通过预测无人机状态响应,最优化有限时域性能指标,实现滚动求解未来有限时间内的最优控制律[30]。3) 反馈校正:在每一采样时刻采集无人机的状态信息,将状态信息与模型预测值进行比较,从而得到模型预测误差,再利用误差校正下一步的预测值来获取更为精准的将来时刻控制序列,从而避免如模型失配、外界干扰等因素带来的不利影响,控制过程如图 4所示。
|
图 4 时序下的模型预测控制过程 Fig.4 Model predictive control process in time series |
以如下无人机平衡点线性化的一般离散系统为例[28]:
| $ \begin{align} \mathit{\boldsymbol{x}}_{k+1} =\mathit{\boldsymbol{Ax}}_{k} +\mathit{\boldsymbol{Bu}}_{k} \end{align} $ | (4) |
其中,
| $ \begin{align} \begin{bmatrix} \hat{\mathit{\boldsymbol{x}}}_{k+1|k} \\ \vdots \\ \hat{\mathit{\boldsymbol{x}}}_{k+H_{\rm p} |k} \end{bmatrix}=\mathit{\boldsymbol{\varPsi x}}_{k} +\mathit{\boldsymbol{\varTheta U}}_{k} \end{align} $ | (5) |
其中,
| $ \begin{align*} \mathit{\boldsymbol{\varPsi}} = \begin{bmatrix} \mathit{\boldsymbol{A}} \\ \vdots \\ \mathit{\boldsymbol{A}}^{H_{\rm p}} \end{bmatrix}, \; \; \mathit{\boldsymbol{\varTheta}} =\begin{bmatrix} \mathit{\boldsymbol{B}} & \cdots &{\mathit{\boldsymbol{0}}}&{\mathit{\boldsymbol{0}}} \\ \mathit{\boldsymbol{AB}}& {\mathit{\boldsymbol{B}}} &\cdots&{\mathit{\boldsymbol{0}}}\\ \vdots & \vdots&\ddots & \vdots \\ {\mathit{\boldsymbol{A}}}^{H_{\rm p} -1}{\mathit{\boldsymbol{B}}} & {\mathit{\boldsymbol{A}}}^{H_{\rm p} -2}{\mathit{\boldsymbol{B}}} & \cdots & {\mathit{\boldsymbol{B}}} \end{bmatrix} \end{align*} $ |
则可求解如下优化问题获取最优控制序列
| $ \begin{align} & \min _{\mathit{\boldsymbol{U}}_{k}} \sum\limits_{j=1}^{H_{\rm{p}}} \hat{\mathit{\boldsymbol{x}}}_{k+j | k}^{\rm{T}} \mathit{\boldsymbol{Q}} \hat{\mathit{\boldsymbol{x}}}_{k+j | k}+\mathit{\boldsymbol{U}}_{k}^{\rm{T}} \mathit{\boldsymbol{R}} \mathit{\boldsymbol{U}}_{k} \\ & \text{s.t. } \begin{cases} \mathit{\boldsymbol{x}}_{k+1}=\mathit{\boldsymbol{A}}\mathit{\boldsymbol{x}}_{k}+\mathit{\boldsymbol{B}} \mathit{\boldsymbol{u}}_{k} \\ \mathit{\boldsymbol{F}}_{\rm{u}}\left(\mathit{\boldsymbol{u}}_{k}\right) \leq \mathit{\boldsymbol{c}}_{\rm{u}} \\ \mathit{\boldsymbol{F}}_{\rm{x}}\left(\hat{\mathit{\boldsymbol{x}}}_{k+1|k}\right) \leq \mathit{\boldsymbol{c}}_{\rm{x}} \end{cases} \end{align} $ | (6) |
其中,
针对安全边界约束下的有人飞行器模型预测安全控制问题,目前已有一些研究成果。文[31] 使用模型预测控制对F-16战斗机进行边界保护,为了解决MPC控制在线计算量巨大的问题,设计了准线性控制环结构对受控的非线性模型进行拟合,并进行了阵风干扰下的仿真验证以证明设计的可行性。
考虑到无人机动力学的非线性特性,基于线性化模型的模型预测控制的可靠性难以得到保证。在缺乏高性能计算元件辅助的条件下,工业界与学界提出了结合MPC与反馈线性化的复合边界保护控制策略[32-33]。比如,通过多平衡点线性化,文[34] 提出了一种模型预测飞行控制方法,实现了输入输出同时约束下无人直升机机动过程的边界保护。文[35] 充分考虑了飞行边界范围内飞行器的动力学特性,提出了一种基于主动模型的平稳增量模型预测飞行控制方法,实现了无人直升机的边界保护。文[36] 针对多种约束下的无人机4维轨迹跟踪问题,提出了一种模型预测飞行控制策略。在反馈线性化的基础上,文[37] 结合滑模控制与MPC方法,针对四旋翼无人机提出了一种鲁棒飞行控制策略,有效地处理了输入约束。
与此同时,随着无人机机载计算能力的不断提升,直接依据非线性模型进行状态预测的MPC策略也得到了广泛研究。通过对闭环无人机模型进行泰勒展开,文[38] 提出一种非线性MPC方法,并实现了无人机的工程应用。文[39] 结合非线性MPC与隶属估计方法,提出一种基于输出反馈的MPC策略,进一步提高了飞行控制的鲁棒性与时效性,并且实现了避障过程中对无人机滚转角的安全保护。针对倾转旋翼无人机的切换过程,文[40] 提出一种模型预测飞行控制方法,在实现模态切换的同时,保证了飞行状态满足特定约束。同样借助非线性MPC方法,文[41] 研究了一种更具针对性的边界保护控制策略,实现了空速与姿态同时受限情况下对倾转旋翼无人机的安全边界保护。
2.3 基于参考指令管理的安全边界保护控制基于参考指令管理的安全控制的初衷与控制限幅架构类似,均是构建限幅映射以达到保护飞行安全的目的,区别在于前者限制控制系统输入,后者限制输出。随着机载计算能力的不断提升与规划技术的快速发展,指令限幅的方式逐渐被在线重规划技术所取代,其中以参考指令管理器(RG)最具代表性。
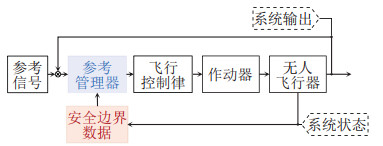
RG是结合规划与控制分层思想衍生而出的一种边界保护控制方法。相较MPC方法,RG额外考虑了预稳定过程与辅助控制器,系统控制框图如图 5所示。具体而言,RG通过先设计一个不考虑约束的预稳定闭环系统,在不改变该预稳定闭环系统结构的情况下,通过调节某些瞬态大幅度变化的参考信号,保证闭环系统的状态和输入满足约束,同时保持原有的良好控制性能。
|
图 5 基于参考指令管理器的安全控制系统框图 Fig.5 Diagram of reference governor-based safety control |
应用于非线性系统的RG方法有许多种,包括基于线性化模型的RG、基于非线性模型的RG、鲁棒RG以及基于牛顿迭代的RG等[42]。文[43] 基于预测控制的概念,通过在原有的预稳定非线性系统中添加RG控制器,以满足系统约束,解决了非线性控制系统需要满足时间点输入和状态硬约束的问题。文[44] 研究了一种增量式步长RG,该RG每个时间步长都对参考量有一个固定幅度的更新。文[45] 提出了一种鲁棒的非线性RG方法,解决了带有不确定参数的非线性系统约束问题。文[46] 针对隐式的RG框架,提出了一种基于牛顿迭代的RG方法,通过对原预稳定系统额外增加一个辅助RG控制器,使得系统满足安全约束,扩展了RG的应用范围。
在基于参考指令管理的有人飞行器安全飞行控制方面,文[47] 是最早引入连续时间RG进行飞行控制系统设计的论文,有效解决了输入约束下喷气式战斗机的安全保护控制问题。文[48] 进一步研究了在输入约束下有人飞行器基于离散时间RG的边界保护控制问题。文[49] 针对存在输入约束与姿态约束的有人飞行器,提出了一种基于RG的边界保护控制策略,并以战斗机为例进行了边界保护控制的验证。文[50] 应用RG实现了对战斗机过失速机动的边界保护,主要借助线性参变建模方法,通过引入一种增量模型进一步提高了边界保护控制的可靠性。
与此同时,针对无人机基于参考指令管理的安全边界保护控制研究则更加关注其面临的突发状况与特殊应用场景。文[51] 结合MPC提出了一种复合RG边界保护飞行控制方法,并赋予了无人机容错飞行的能力。文[52] 针对无人机提出了一种显式RG飞行控制策略,实现了状态与输入同时受限。文[53] 利用RG实现了系留无人机在绳索紧拉约束下的非线性控制。文[54] 针对非凸约束提出了一种混合RG方法,实现了旋翼无人机的避障控制。
3 不同约束下的无人机安全飞行控制(Safety flight control for UAV with different constraints)由于受到物理硬件和工作环境等的限制,实际无人机系统中广泛存在着不同约束。舵面偏转角、发动机最大转速等系统物理特性限制通常会表现为输入约束[55];针对特定的任务环境[56]或狭小空间[57],无人机常常受到外部地理环境的限制,这类限制会表现为航迹约束[58];考虑到无人机在实际控制中会对飞行姿态有较高的要求以保证飞行安全性,这类限制会表现为姿态角约束[59],等等。
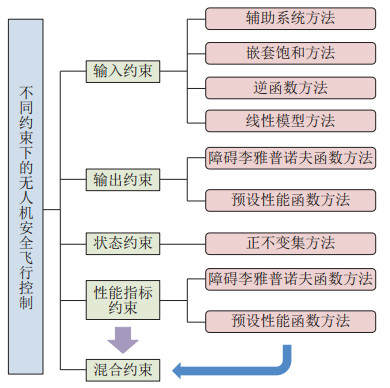
近几年来,因未考虑各种约束而导致的无人机坠机事件在军事与民用领域中均有发生。如2020年8月14日,美国加州文图拉县海军基地中,MQ-8B“火力侦察兵”无人机在进行例行训练时,主旋翼撞到基地内的建筑物,当场坠毁,并造成建筑表面受损。2021年1月23日,一架DJI Mavic Air 2无人机因未准确监测周围实时环境,与一架智利海军直升机相撞,造成直升机上的一名乘客受伤,无人机坠毁。因此,随着飞行控制性能要求不断提高,如何在保证稳态性能的前提下尽可能地追求控制系统的瞬态性能,以便在保证飞行器安全的同时完成预设任务,成为近年来无人机飞行控制领域的重要研究课题之一。针对约束类型的不同,可将其分为输入约束、输出约束、状态约束与混合约束等。不同约束下的无人机安全飞行控制方法概览如图 6所示。
|
图 6 不同约束下的无人机安全飞行控制方法概览 Fig.6 Overview of safety flight control for UAV with different constraints |
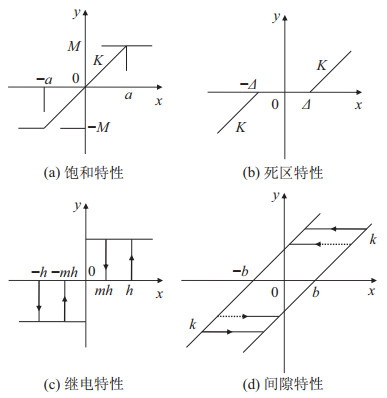
输入约束主要是由系统硬件的物理限制引起的,包括饱和、继电、死区以及间隙特性等[60-62],具体形式如图 7所示。
|
图 7 典型输入非线性环节 Fig.7 Typical input nonlinear elements |
图 7中
饱和特性是无人机执行器最为常见的输入非线性环节,如图 7(a)所示。例如:对于固定翼无人机系统,其可通过改变自身执行机构,如副翼、升降舵和方向舵,来调整作用在机身上的气动力或力矩,实现对固定翼无人机的控制。但在某些特定条件下,所需要的舵面偏转超过无人机所能提供的最大偏转角,导致出现输入饱和;旋翼无人机系统通过改变旋翼的周期变距、转速与挥舞角进行控制,同样可能在某些特定条件下出现输入饱和。总的来说,无人机能够提供的控制能量是有限的,存在执行器输入饱和限制,它会严重影响闭环控制系统的性能,极端情况下会导致整个系统的不稳定。从系统安全性的角度出发,输入饱和是控制系统中最普遍也最需要解决的一类约束问题。
针对输入饱和问题,早期学者们提出了一种抗积分饱和补偿器控制方法[63],主要思想为先设计标称系统控制器,然后以执行机构的输入输出差值作为输入设计补偿器来抑制饱和特性的影响。但该方法主要适用于线性系统,在非线性系统中缺乏严格理论证明。在此基础上,Jagannathan[64]在2004年提出了一种辅助系统方法,其核心思想在于通过设计标称稳定的辅助系统,将实际控制输入与饱和控制输入之间的差值作为辅助系统的输入,并将有界的辅助系统状态变量引入控制器设计中以实现动态补偿调节,来消除或减少控制输入饱和对系统带来的不利影响。在采用辅助系统方法处理跟踪控制问题时,通常需要构建包含辅助系统变量与跟踪误差的新变量,并通过调节控制器参数保证新变量的有界性,从而进一步证明输入饱和限制下跟踪误差的有界性。近年来,国内外学者陆续开展了一些关于辅助系统方法的研究工作,例如文[65] 针对一类具有输入饱和的非线性不确定系统,通过构建辅助系统来处理饱和问题,在此基础上设计了鲁棒控制器,并将其应用于无人机飞行控制系统中进行仿真验证。文[66] 通过双曲正切函数近似代替输入饱和函数,并通过设计飞行控制器来保证饱和约束下的四旋翼无人机系统跟踪性能。文[67] 针对固定翼无人机系统,结合Nussbaum函数设计了一类新的辅助系统,用以解决输入饱和下的容错控制问题。
嵌套饱和方法由Tee1教授[68]于1992年提出,实现了具有输入饱和的高阶积分系统在全局范围内的渐近稳定。为了避免由于系统阶数过高和初始条件较大导致的瞬态性能恶化这一问题[69],Marchand教授提出了两种非线性控制方法,第一种是文[70] 中方法的扩展,第二种是文[71] 中提出的可以改善性能的可变饱和水平方法。基于此种嵌套饱和方法,文[72] 提出了一种用于无人机路径跟踪的综合制导与控制方案。利用浸入不变性的概念,分析了系统在时间坐标和路径坐标上的稳定性,从而保证了无人机系统的渐近稳定性。文[73] 针对尾座式垂直起降无人机采用嵌套饱和函数方法对控制输入进行限制,解决了推力限幅控制问题。
为保证无人机系统在输入饱和条件下的控制性能与安全性,控制学界相继提出多种饱和处理方法。文[74] 提出了一种多约束协调控制方法,并将其应用于输入受限飞行控制,提高了输入饱和条件下飞行器的安全性。文[75] 通过将滤波误差补偿机制和辅助系统方法集成到动态面控制框架中,解决了四旋翼无人机输入饱和下的跟踪控制问题。文[76] 通过一类Sigmoid函数去估计输入饱和特性,并对估计误差采用模糊逻辑系统进行补偿,实现了四旋翼无人机离散闭环系统的稳定性。文[77] 结合自适应方法对无人直升机系统中的饱和项与执行器故障进行了处理,并设计了跟踪控制器。除此之外,文[78] 针对输入饱和条件下的无人机系统,通过双曲正切函数结合一类有限时间收敛的辅助系统处理输入饱和问题,并设计了有限时间跟踪飞行控制器。
3.1.2 输入死区下的安全飞行控制无人机系统内部的作动器不可避免地对接收到的小幅信号反应不够灵敏,呈现输入死区特性,如图 7(b)所示,死区区间
针对输入死区现象,早期学者们通过直接求解输入死区模型的逆函数来补偿死区特性带来的不利影响。但由于逆函数求解的局限性,研究人员基于另一种思路,即对输入死区模型进行简化,构建线性输入与未知干扰的组合,并基于简化后的模型设计控制器。结合有限时间稳定理论,文[80-81] 分别针对对称输入死区非线性与非对称输入死区非线性,提出了有限时间条件下的自适应跟踪控制策略。
关于具有输入死区的无人机系统的飞行控制方法设计,目前也有一些研究成果。文[82] 针对具有输入死区与干扰的四旋翼无人机姿态系统,将死区模型简化后的误差项与外部干扰相结合,设计了一种自抗扰动态面控制器,保证了无人机姿态的稳定性。文[83] 考虑具有输入死区的无人机系统,基于死区斜率的有界性补偿了控制输入的死区非线性,并设计了一种基于自适应神经网络的有限时间控制器,保障了无人机的姿态稳定性。文[84] 针对输入输出死区下的多无人机系统设计了基于反步法的跟踪飞行控制器,并利用自适应律补偿输入死区和外部干扰的影响。
3.2 输出约束下的无人机安全控制无人机在执行任务时,其输出必然面临着相应约束要求,如无人机在狭小空间环境下的作业、指定高度下的侦察打击等。以无人机迎角为例,若迎角达到其失速迎角值,则无人机可能会因失速而威胁飞行安全。在飞行过程中,如果受限问题不能及时解决,系统控制性能会退化甚至致使无人机失控。为了完成预先给定的任务,无人机的输出约束应该在飞行控制器设计时加以明确考虑。
3.2.1 障碍李雅普诺夫函数方法针对输出约束问题,Tee等[85]提出了一类障碍李雅普诺夫函数(BLF)方法,通过在李雅普诺夫函数中引入非线性映射,使得当状态趋近给定约束时,BLF将趋向于无穷。因此,当能保证BLF有界时,即可实现对系统输出的约束。BLF方法的优势在于将复杂的控制约束问题转化为常规不受约束的李雅普诺夫稳定问题,在实现约束的同时也为与其他控制方法的融合设计提供了便利。常用的BLF可分为tan型[86]与log型[87]。针对无人机系统的任意输出
| $ \begin{align} V=\frac{k_{\rm b}^{2}} {\rm{\mathit{π}}} \tan \frac{{\rm{\mathit{π}}} e ^{2}}{2k_{\rm b}^{2}} \end{align} $ | (7) |
与
| $ \begin{align} V=\frac{1}{2}\log \frac{k_{\rm b}^{2}} {k_{\rm b}^{2} - e ^{2}} \end{align} $ | (8) |
式中:
鉴于两类函数的特性,它们都能通过保证跟踪误差的有界性从而有效地处理系统输出约束问题,并广泛应用于输出约束下的无人机安全控制系统设计。针对多旋翼无人机系统,文[88] 采用一种对称BLF处理输出受限问题,并达到了期望的安全跟踪效果;文[89] 则针对时变输出约束下的无人机系统,通过设计一种对称时变BLF实现了姿态的鲁棒控制。文[90] 提出了一类积分型BLF,结合动态面控制方法设计了一类自抗扰受限控制器,实现了对姿态约束下的无人机群姿态调整。
3.2.2 基于预设性能的安全控制与BLF方法的思想类似,Bechlioulis等[91]提出了一类基于预设性能的控制(PPC)方法,其核心思想是在控制器设计中引入预设性能函数(PPF)。该方法通过构造一类非线性映射,使得当系统输出趋于预设的约束时,映射后的变量将趋于无穷。由此可知,通过保证转换后的变量有界,可实现对系统输出的性能约束。PPC方法的优势在于它能通过简单的非线性映射,将一个受限的变化量转化为一个非受限变量,可以在性能约束下实现更加灵活的控制[92]。
基于PPC控制思想,对无人机系统的输出跟踪误差设计预设性能函数,通过跟踪误差和期望跟踪信号的有界性来保证无人机系统输出满足约束条件,这方面也获得了许多研究成果。文[93] 通过设计一种基于预设性能的自适应控制器,实现了期望性能指标约束下的舰载无人机跟踪控制。为了保证3自由度直升机系统在预设姿态角约束下的瞬态与稳态性能,文[94] 设计了一种有限时间保性能控制器。文[95] 将预设性能函数与容错控制方法相结合,针对输出受限下的无人直升机姿态与高度系统,提出了一种自适应容错控制方法。文[96] 针对无人机编队目标跟踪中的输出受限控制问题,提出了一种基于预设性能的分布式多机编队目标跟踪控制方法。
3.3 状态约束下的无人机安全控制在无人机的实际飞行过程中,为了保证任务的精准执行、满足自身安全性要求,需要对无人机状态进行约束。因此,状态约束条件下的安全控制问题也是无人机安全飞行控制的重要研究方向之一。无人机在飞行过程中不满足状态约束条件,必然会导致控制目标未达成,可能造成不可逆的严重后果。以固定翼无人机为例,空速不可过大或过小:过大会引起机翼震颤,过小则会导致飞机失速。而对无人直升机来说,旋翼的挥舞角与机体的姿态角均不能过大而超出约束条件,否则容易导致失控。因此,状态约束下的无人机安全飞行控制技术研究具有重要的实际应用价值。
目前状态约束下的主流控制方法是正不变集(PIS)方法,其主要利用PIS的性质,构造和寻找系统状态的PIS。如系统初始状态处于给定集合内,则在控制器作用下可保证系统的最终状态也将位于集合内,该方法对解决无人机状态约束下的控制问题具有重要意义。文[97] 针对一类具有有界干扰的离散线性系统状态受限问题,设计了一种具有鲁棒特性的PIS。文[98] 针对非线性连续系统,通过寻找最大的正不变圆设计了一种控制方法,以有效处理系统状态受限问题。
正不变集理论作为一套较为成熟的理论,在无人机飞行控制方面也有具体的应用。文[99] 针对具有状态约束的无人直升机系统,结合PIS方法设计了一类特殊的滑模控制器,并通过硬件平台验证了其有效性。文[100] 将PIS方法与分布式优化方法相结合,针对状态约束下无人机群的避碰问题规划了安全的飞行路径。文[101] 基于线性矩阵不等式构造了鲁棒PIS,进而使得无人机在所设计控制律下实现状态受限条件下的安全飞行控制。此外,如果无人机系统的受限状态都为系统输出,则也可利用输出约束下的BLF方法和基于预设性能的安全控制方法进行状态约束下的无人机安全控制器设计。
3.4 性能指标约束下的无人机优化安全控制无人机在执行任务时,其飞行控制系统性能必然面临着各类性能指标要求,如跟踪精度、收敛速度和超调量等,以满足精准作业需求。随着飞行控制的高精度化,如何在保证稳态性能的前提下尽可能地追求闭环飞控系统的瞬态性能,从而保证无人机在安全的同时还能完成预设任务,成为近年来飞行控制领域的重要研究方向之一。
3.4.11976年,Davison[102]提出了鲁棒控制方法,其目的在于处理系统中存在的未建模误差、参数摄动和外部干扰等。1981年,
近年来,以线性矩阵不等式方法代替哈密顿-雅可比不等式求解方法,已成为当今有效解决系统不确定性问题的鲁棒控制方法之一,且已在飞行控制领域取得了不少显著成果。文[107] 利用
相比其他最优控制方法,如动态规划(DP)算法以及伪谱法等,自适应动态规划(ADP)算法由于其独特的结构,在解决具有强耦合以及强非线性的复杂系统最优控制问题方面,表现出很大的潜力和优势。ADP算法于1992年提出[110],该算法的基本思想是利用神经网络方法对代价函数进行估计,并按照时间正向求解DP问题。对于ADP算法的研究,前期大多是关于算法结构方面的,较少涉及到稳定性分析或者收敛性证明[111]。随后,关于ADP的理论研究与应用逐步成为优化控制领域的研究热点问题之一。文[112] 针对具有控制输入饱和约束的非线性连续系统,提出了一类基于策略迭代的ADP算法,通过结合最小二乘算法求得HJB(Hamilton-Jacobi-Bellman)方程的解,进而获得近似的最优控制输入。
对于具有强耦合、强非线性、快时变特性的无人机飞行控制系统而言,ADP算法的性能指标不但包括无人机的状态与跟踪误差指标,亦含有控制能量指标。目前虽然其应用研究相对较少,不过也取得了一些成果。文[113] 提出了一种基于自适应评价算法的优化飞行控制器,采用全新的离线与在线相结合的神经网络训练方法,在保证控制器可靠性的同时还能提高控制器的实际控制性能,并成功应用于商务喷气式客机的全状态飞行控制器设计中,取得了较好的控制效果。文[114] 针对近空间飞行器,结合ADP算法与积分滑模方法,设计了一种鲁棒优化跟踪控制器。
而针对无人机而言,由于缺少了飞行员的直接操纵,飞行控制器的优化设计更显重要,但ADP算法的使用对无人机机载计算机要求更高。文[115] 针对具有气动参数不确定性以及舵面部分失效的无人机系统,提出了一种基于约束ADP算法的自适应神经网络飞行控制器,在保证系统稳定的同时,还能保持良好的飞行性能。文[116] 针对旋翼无人机轨迹跟踪控制问题,结合反步法与基于单神经网络的ADP算法,设计了一种最优跟踪控制器,实现了无人直升机的盘旋与跟随优化控制。
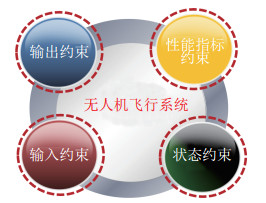
3.5 混合约束下的无人机安全控制前面分别讨论了无人机在输入、输出、状态和性能约束下的安全飞行控制问题。然而在无人机实际飞行中这些约束往往不是单独出现的,因而设计飞行控制器时需要同时考虑2种或2种以上的约束,如图 8所示。因此,如何在多种约束同时存在即存在混合约束的情况下,实现对无人机系统的安全飞行控制是一个重要且具有实际工程意义的问题。
|
图 8 无人机系统的混合约束 Fig.8 Multiple constraints of the UAV system |
近年来,愈来愈多的学者将目光聚焦于混合约束下的无人机安全控制问题,并取得了一些研究成果。文[117] 针对多无人机系统,在同时考虑输入饱和与输出约束的条件下,设计了自适应抗饱和控制器,保证了无人机集群的安全跟踪。对于固定翼无人机的纵向系统,文[118] 提出了一类自适应容错控制策略,保证了无人机在故障、状态约束以及输入饱和同时存在时的闭环稳定性。文[119] 则针对无人直升机在狭小环境中飞行时存在的实时航迹约束、姿态性能约束问题,在考虑多约束、外部干扰及建模不确定性的前提下,提出了一种基于干扰观测器的自适应模糊优化安全跟踪控制器。通过将预设性能函数与辅助系统方法相结合,文[120] 给出了多无人机在全状态约束下的协同控制策略。文[121] 通过设计一类基于学习的模型预测控制策略,实现了对无人机编队的安全跟踪控制。文[122] 针对管道上的轮式无人机,考虑管道约束与输出约束,设计了一种非线性模型预测控制策略并分析了闭环系统稳定性。
4 故障与网络攻击下的无人机安全飞行控制(Safety flight control for UAV with faults and cyber-attacks)尽管无人机在军事和民用领域发挥着重要的作用,并带来了巨大的便利和收益,但同时也存在一些威胁和挑战。比如,随着无人机应用领域的不断扩展以及作业环境越来越复杂,其控制系统也会变得更加复杂,这些不利因素将会大大增加无人机发生故障的概率,严重影响其飞行安全。因此,迫切需要对无人机在不同故障类型下的容错控制方法进行深入研究。此外,无人机一般都需要通过有线或无线的方式与地面站进行通信,攻击者可以利用网络攻击对无人机系统的信息传输进行通信干扰或注入虚假数据,这样的入侵行为会影响无人机所获取信息的正确性,甚至破坏整个控制系统的性能和服务,这样的攻击行为已成为无人机系统的主要安全威胁之一。
4.1 各种故障下的无人机安全控制随着现代科学技术如航空航天、人工智能、计算机、复合材料等技术的迅速发展,无人机的研发也相应进入了快车道,其结构与气动布局也随着任务的多样化而变得越来越精细和复杂。众所周知,对于特定系统,故障概率和系统结构的复杂度有一定的正相关性。相比于其他机械,无人机所执行的很多军事和民用任务都决定了其飞行区域大多是在复杂多变的近地环境。同时,如果无人机发生故障,由于没有驾驶员的操控和及时处理,无人机飞行变得非常危险,最终很可能出现无人机失控、坠毁,从而造成财产的巨大损失,甚至导致灾难性后果[123]。
近年来,无人机在研发测试和实际飞行中突发故障导致飞行事故的事件时有发生。如2016年,在美国亚利桑那州,一架无人机由于遭遇湍流而引发结构性故障最终导致坠毁。2018年,美国的一架全球鹰无人机也发生了坠毁,原因是发动机出现故障后没有得到及时有效的处理。2022年,日本自主研发的无人机“苍天”发生了一起因飞机故障而引发的坠机事故。因此,在无人机飞行过程中,研究有效的容错控制技术以保证无人机的安全可靠性具有重要的理论与实际意义。
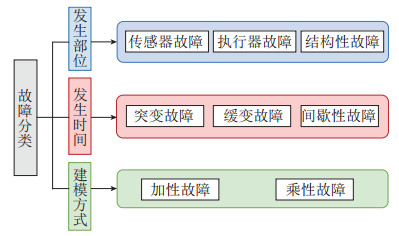
无人机故障分类的方法有很多种[123],如图 9所示,主要可以从3方面进行分类:
|
图 9 故障分类 Fig.9 Classification of the faults |
(1) 按照故障发生的部位分类
从此方面进行分类,故障可分为:传感器、执行器以及结构性故障等。
传感器故障是因无人机传感器测量值和实际值不相等而产生的零点漂移、精度下降、固定偏差以及完全失效等故障。对于传感器的实际值
| $ \begin{align} \hat{y}_i(t) = \tau_i y_i + \mu_i \end{align} $ | (9) |
其中,
针对传感器故障影响下的无人机系统,学者们在安全容错飞行控制方面已取得了很多的研究结果。例如:文[126] 研究了受外部干扰和传感器故障影响的无人机的鲁棒故障检测与跟踪容错控制系统设计方法。针对四旋翼无人机姿态动力学系统,文[127] 提出了一种模糊自适应容错控制方案以解决系统中存在的4种传感器故障,即零点漂移、精度下降、固定偏差以及完全失效故障。
执行器故障是指无人机执行机构如气动舵面等发生的部分失效或全部失效的故障,该故障是所有故障中最直接也是后果最严重的一种故障。对于执行器的输入信号
| $ \begin{align} u_i^{\rm f}(t) = (1-s_i) u_i+w_i \end{align} $ | (10) |
其中
考虑无人机系统发生执行器故障的情况,文[129-130] 分别提出了一种故障检测方法和一种基于暂态性能指标的主动容错控制方法,均解决了无人机系统中存在的执行器故障问题。
结构性故障[131]是指除传感器和执行器以外无人机系统零部件发生的故障,这类故障是由于疲劳、腐蚀或外力撞击等原因产生的,会导致系统质量、质心位置、转动惯量等物理参数发生变化,与控制系统的参数不一致,从而影响控制性能。结构性故障不容易被系统检测和定位,因此也难以用控制的方法处理。关于结构性故障,文[132] 测试了结构性故障下六旋翼无人机的复合材料螺旋桨的几种失效情况,包括人为诱导在内。
(2) 根据故障发生的时间性质分类
从此方面进行分类,故障可分为:突变、缓变以及间歇性故障[133-134]。
突变故障是指无人机系统突然发生的故障,如机体断裂、执行器卡死等故障。例如:文[135] 针对突变故障设计了一种新的实时检测的故障容错机制,该机制能保证在采用神经网络容错策略导致自适应速度较慢的情况下,仍能使无人机系统具有较好的控制性能。
缓变故障是指无人机系统随时间缓慢产生或加重的故障,如电机效率降低或由老化、磨损造成的零部件性能下降等故障。文[136] 设计了一种完整的主动容错控制方案,通过故障估计来适应缓变故障,实验验证证明了所提出方法的有效性。
间歇性故障是指无人机系统在不同时间段发生的故障,如传感器产生的浮动偏差等。文[137] 针对无人机系统间歇性故障等,采用扩展卡尔曼滤波器更新神经网络的加权参数,进而准确地检测间歇性故障。
(3) 根据建模方式分类
从此方面进行分类,故障可分为:加性和乘性故障[138]。加性故障是与无人机系统的输出及控制输入的变化或消失无关的故障,常用于描述突变故障。乘性故障是指系统的输出随系统控制输入的变化而变化的故障,常用于描述缓变或间歇性故障。对于受乘性执行器故障影响的无人机编队系统,文[139] 提出了一种鲁棒自适应非线性容错控制方案。
当无人机遭受任何一种故障时,面向无故障情况设计的飞行控制方法可能无法保证无人机正常飞行。为了保证无人机继续安全飞行以完成预定的任务,容错控制是不可或缺的技术手段。容错控制的思想最早由Niederlinski[140]提出。文[141] 在1980年首次给出了容错控制的概念。在此研究的基础上,文[142] 对容错控制的相关知识进行了更加精细的划分,全面阐述了容错控制的基本问题。容错控制方法是指在发生故障的情况下仍能保持控制性能的一种方法,主要可分为2类:被动容错控制和主动容错控制[143]。被动容错控制主要受鲁棒控制的启发,不需要进行故障检测和诊断,也不需要在线获取故障信息,在故障发生前就已经设计好固定控制策略。相较于被动容错控制,主动容错控制是利用故障信息,结合故障特点进行主动性故障估计并且实施控制补偿,以抵消故障的影响,从而达到容错目的。
随着航空航天技术的快速发展,无人机控制系统越来越复杂,而且无人机由于没有驾驶员的干预和实时判断,对于容错控制技术的需求更加迫切。因此,为提高飞行控制系统的安全性,如何将更加可靠先进的容错控制方法运用到无人机飞行控制系统的设计中,受到了研究者们的广泛关注,并取得了大量创新性的成果。由于传感器和执行器故障是无人机最常见的故障,并且均威胁着无人机的安全,因此,文[144] 利用自适应因子来适应传感器/执行器等故障,进而提高无人机飞行控制系统的容错能力。在不增加传感器或执行器的情况下,文[145] 提出了一种基于观测器的自适应容错控制方法,对故障进行估计并抵消故障带来的不利影响,进而解决了四旋翼无人机的传感器和执行器故障诊断与补偿控制问题。基于无人机系统的简化耦合动力学模型,文[146] 设计了一种滑模容错控制方法来解决传感器/执行器故障问题,进而提高了无人机系统的容错能力。
4.2 受到攻击时无人机的安全控制随着无人机技术的迅速发展,网络攻击形式呈现不断更新的趋势,并且具有隐蔽性、复杂性以及多样性等特点。有针对性地解决网络攻击给无人机飞行控制带来的不利影响,可以提升无人机在飞行过程中的安全性。针对无人机系统,现有的鲁棒控制方法以及容错控制方法重点在于考虑系统遭受干扰与故障时,能提供一定的可恢复能力。而对于无人机系统在遭受外部源侵入攻击等恶意攻击的情况,以上两种方法可能不再适用。因此,针对无人机遭受各种攻击的情形,研究其安全飞行控制策略是十分必要的。
当下应对各种攻击的安全飞行控制方法主要分为弹性控制方法和主动防御控制方法。前者主要基于攻击模型来分析飞行控制系统性能与攻击参数之间的量化关系,具体包括:随机系统方法[147-148]、李雅普诺夫泛函方法[149]、切换系统理论[150-151]以及上述方法的有机结合。后者基于系统冗余通信、计算和控制资源,采用主动补偿机制应对网络攻击造成的信息不可用和不完整,以保证飞行控制系统性能。常见的主动防御控制方法包括:预测控制方法[152]、多通道网络化控制方法[153]、基于冗余通道的网络化控制方法[154]。一般来说,为研究攻击对无人机系统的影响,首先需要分析确定出攻击类型再构建恰当的动态数学模型,然后基于所构建的数学模型设计相应的弹性控制方法。由此可见,攻击的分类和建模对无人机安全飞行控制问题的研究以及攻击问题的解决至关重要。目前,对于单个无人机来讲,主流的攻击类型可归为两类:拒绝服务(DoS)攻击和欺骗攻击。下面分别针对这两类攻击下的无人机安全控制进行相应的描述。
4.2.1 DoS攻击下的无人机安全控制DoS攻击作用于无人机系统,会影响其正常的工作,造成地面对无人机的指挥瘫痪、远程控制失控,甚至坠毁。其主要的攻击方式分为2种,即漏洞型攻击和耗费型攻击[155]。其中,漏洞型攻击是指攻击方利用无人机系统通信协议或者程序出现的漏洞,对无人机控制系统进行入侵和控制。而耗费型攻击是通过长时间发送无效数据包来耗尽有限的通信资源,进而影响无人机系统与指挥中心的正常通信。针对网络出现漏洞的无人机系统,文[156] 提供了不同级别的漏洞以及每个级别所需的预防措施,分析了可以在无人机上执行的一些主要攻击方法,如漏洞型DoS攻击等。对于遭受耗费型DoS攻击影响的无人机系统,文[157] 提出了一个能实时为无人机系统提供DoS攻击弹性控制的软件框架,该框架为无人机中央处理器、内存和通讯信道3类关键系统资源提供了防御机制。
4.2.2 欺骗攻击下的无人机安全控制相比于DoS攻击,欺骗攻击的攻击过程更为隐蔽和复杂。针对无人机系统,欺骗攻击主要是入侵无人机系统中的信息传输网络,比如无人机与地面站的通信,该攻击方式主要影响信息的完整性和真实性,进而影响无人机的飞行控制性能。欺骗攻击可进一步细分为2类:虚假数据注入(FDI)攻击和重放攻击。对于欺骗攻击,文[158] 分析了一种基于惯性导航-系统组合导航的无人机隐蔽欺骗算法,但为了避免无人机在遭受欺骗攻击过程中飞行轨迹频繁变化造成的不良后果,所提出的算法要求欺骗器规划的欺骗轨迹相对于无人机预先设定的参考轨迹缓慢变化。文[159] 从防御者的角度,研究了一类具有白噪声的信息物理系统中FDI攻击下的检测问题,并将设计的方法应用于无人机系统进行仿真验证,证实了攻击检测器的有效性。
5 集群无人机安全编队控制(Safety formation control for swam UAVs)受动物集群特性启发,可充分利用不同的无人机个体各自拥有的优势进行协同作业,来完成复杂的任务。通过对不同类型无人机的组合进行区分,集群无人机系统主要可以分为2类:同构集群和异构集群。近年来,关于无人机集群的报道屡见不鲜,如2020年,哈尔滨工业大学为庆祝建校一百周年放飞了千架无人机进行灯光秀表演,造型炫技,震撼全场。在这之前,英特尔公司于2018年在美国加利福尼亚州福尔瑟姆放飞2018架无人机,庆祝其公司50周年诞辰,并绘制了“intel 50”字样。该项目也创造了吉尼斯纪录。然而无人机集群控制系统也时常发生意外事件,比如2021年国庆期间,河南郑州市高新区万达广场,多架无人机在飞行过程中突然失去控制,直接从高空坠落。另外,2022年福建省福州市在元宵节期间举办无人机花式表演,然而无人机刚升空十几秒就出现故障进而导致“炸机”,最终坠入闽江。因此,为了保证集群无人机系统工作时的安全性,有必要进一步深入研究编队协同下的集群无人机安全飞行控制技术。
5.1 防碰撞前提下的集群无人机安全控制编队协同控制作为集群无人机系统飞行控制中的重要研究问题之一,其主要思想是保证无人机在执行大型复杂任务时进行时间、空间和任务之间的有机协调,分散搭载设备,这样可以在面临复杂任务时使得不同无人机分别执行相对较为简单的任务,从而大大提高任务效率。编队控制的主要方法包括基于一致性的编队控制方法、领航-跟随编队法、人工势场法、虚拟结构法、基于行为的方法以及预测控制法等。其中,基于一致性的编队控制算法由于仅需对邻近的无人机进行感知,无需集中协同就可以完成分布式的编队控制,因而相对于其他算法而言其研究更为广泛[160-162]。另外,即使其中几个无人机出现了一些意外,也不会影响到整个集群系统的稳定性。
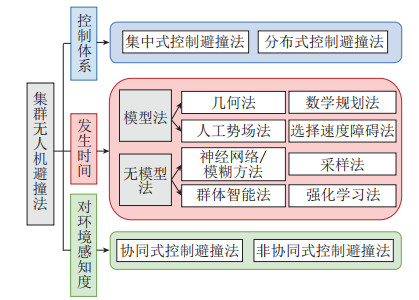
防碰撞是无人机集群系统安全飞行控制需要重点考虑的方面之一,主要在编队飞行过程中保证各个无人机之间避免相互碰撞,进而提高无人机编队系统的安全控制性能。在无人机集群编队防碰撞过程中,各个无人机需要获得其相邻无人机的位置信息且可能需要将自己的位置信息发送给其邻居无人机。为了避免无人机运动过程中发生碰撞,从20世纪90年代开始,就有专家开始研究相对简单的碰撞预测系统。到目前为止,集群无人机系统的防碰撞控制方法主要可以分为3大类,如图 10所示。其中,常用的是模型法和无模型法。下面将针对集群无人机防碰撞情况下的安全控制方法展开介绍。
|
图 10 集群无人机避撞法分类 Fig.10 Classification of swam UAVs collision avoidance methods |
模型法是指基于精确模型的防碰撞处理法,如几何法、人工势场法、选择速度障碍法以及数学规划法等。其中几何法是一种较为常用的防碰撞方法,如文[163] 基于几何法解决了2个恒速无人机在飞行过程中的碰撞问题。人工势场法主要思想是将配置空间抽象化,将每个无人机的邻居无人机或者障碍物等的分布情况一一反映在虚拟势场值中,从而可以根据势场值的大小决定各个无人机的运动方向以及速度。文[164] 基于3维空间人工势场方法建立了多无人机协同编队动力学模型,研究了包含障碍物的避碰人工势场方法,保证了多无人机协同编队系统的安全控制。文[165] 针对无人机集群系统,提出了一种基于人工势场法的协同编队安全控制方法,并设计了无人机集群防碰撞体系。然而在实际飞行过程中,无人机不可避免地遇到复杂地形以及多威胁的环境。在此情况下,人工势场法容易陷入局部极小[166],使得其无法适应当前复杂环境而产生局部停滞,甚至使各无人机之间的信息交互受到阻碍。因此,出现了大量对人工势场法的改进算法,如文[167] 基于一致性理论中的有向图概念,设计了一种改进的无人机与无人机之间的人工势场函数,可以有效地处理无人机编队防碰撞问题。文[168] 提出了一种选择速度避障新方法,解决了多无人机之间的防碰撞问题。数学规划法主要思想是采用优化控制方法,试图以最低成本找到一条最优的无障碍路径。文[169] 将防撞约束和最短时间限制指标相结合,利用基于混合整数的线性规划方法解决了障碍约束问题。
5.1.2 无模型法无模型法是指集群无人机系统在决策过程中基于大量数据或专家知识通过学习、训练来生成所需的协同控制器,如神经网络避碰法、模糊控制避碰法、采样避碰法、群体智能避碰法、强化学习避碰法等。其中神经网络避碰法[170]主要思想是将神经网络的强非线性映射能力与先进控制方法相结合。模糊控制避碰法同神经网络法类似,主要适用于含有不确定性以及需要推理的场景。其优势是一旦控制器设计完成,就能高效快速地生成避碰动作。例如:为解决单超声传感器检测障碍物时所产生的幻影现象,文[171] 提出了一种采用分组循环发射的多超声传感器设计方法,并利用模糊控制算法对四旋翼飞行器实现避障,使其能在未知环境中安全飞行。采样法是比较经典的一种运动规划方法,常见的采样避碰法有随机路标图法和快速搜索树法。其主要思想不是直接探测障碍物的存在,而是将碰撞看作一个“黑盒”来处理。如文[172] 针对2个无人机对大载荷进行协同运输的问题,采用基于采样的运动规划算法和模型预测控制方法实现无人机协调控制,旨在实现无人机在有障碍物环境下的平稳安全飞行。群体智能避碰法[173]包括蚁群优化算法、粒子群优化算法、进化算法以及模拟退火算法等,主要利用群体行为针对给定的优化目标进行启发式搜索。然而该类方法存在一些局限性,如计算量大且容易陷入局部最优等。强化学习避碰法的主要思想是通过不断试错进行寻优避碰。如文[174] 提出了一个集成自主障碍物检测模块和强化学习模块的通用避碰框架,以实现对障碍物的有效回避。在障碍物检测模块中,设计了一种基于深度卷积神经网络的单目视觉显著性检测算法,能够准确地估计出障碍物在视场中的位置以实现安全避碰。
多无人机编队防碰撞[175]还可以从以下2个角度进行分类:1) 从控制体系角度分析,可分为集中式控制和分布式控制方法;2) 从无人机对环境的感知程度角度出发,可分为协同式控制和非协同式控制方法。
5.2 故障条件下集群无人机的安全控制集群无人机系统是由多个无人机子系统组成的复杂互联系统。因此,要想实现协同控制,集群无人机系统中的各个子系统的可靠性和安全性都需要满足较高的要求。当集群无人机系统中的一个或多个无人机子系统出现故障时,有可能影响到邻近无人机和整个集群无人机系统的安全性和稳定性,这也会导致集群无人机系统的通信受到影响,甚至将影响整个集群无人机系统的飞行安全。因此,如何确保集群无人机系统在发生故障时有一定的容错能力是无人机飞行控制领域中一个非常重要的问题。集群无人机系统的故障主要可分为2类:一类是单无人机系统自身出现故障导致整个集群无人机系统出现问题,另一类是多无人机互联耦合过程中产生的故障,如网络通信故障等。下面分别针对集群无人机这2类故障进行详细的描述。
5.2.1 单个无人机发生故障时集群无人机的安全控制集群无人机系统中单个无人机的自身故障类型和上一节介绍的故障类型相同。当单个无人机存在故障时,并不是集群无人机系统所有的无人机内部均发生故障,而是其中一个或者几个发生故障,使得无人机控制性能下降,进而导致集群无人机系统难以有效协同控制,甚至发生碰撞。到目前为止,针对集群无人机系统的容错控制研究已经有一些初步的成果。文[176] 研究了无人机子系统存在永久故障和间歇性故障时的编队控制问题,并提出了一种容错控制方案以保证在单无人机系统发生故障后仍能保持编队的控制性能。文[177] 针对一类集群无人机系统,研究了执行器故障条件下的协同容错控制问题。文[178] 针对执行器故障影响下的多无人机姿态一致性控制难题,将神经网络、干扰观测器和高阶滑模微分器等进行集成,提出了一种复合分散分数阶反步自适应神经网络容错控制方法,解决了执行器故障条件下受风力影响的姿态同步跟踪控制问题。
5.2.2 网络通信故障条件下的集群无人机安全控制网络通信故障主要指的是集群无人机系统中各个无人机在进行信息交互过程中发生的故障。多架无人机之间的通信故障是一种重要的故障源,由于信号发射机和接收机设备的故障等原因引起的通信故障造成单个无人机不能接收到邻居节点无人机的有用信息,进而对编队协同控制性能产生巨大影响。针对此类故障,文[179] 开发了基于行为的协调控制算法,该算法适用于因接收器或传输器故障而导致部分通信失效的无人机,以及接收器和传输器都发生故障导致通信完全失效的无人机。同时,该算法能够根据故障的类型修订故障无人机和非故障无人机的行为。文[180] 提出了一种新的领航-跟随编队容错通信拓扑管理方法,该方法在保持编队队形的同时,即使在编队飞行过程中出现通信故障,也能使编队通信成本最小化。
5.3 网络攻击下集群无人机的安全控制集群无人机系统要想实现期望的编队控制性能,就需要通过网络在各个无人机之间进行信息交互,在信息传输的过程中无人机极易受到攻击的影响,导致集群无人机系统存在安全问题。
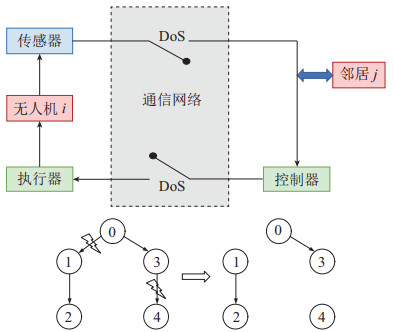
5.3.1 DoS攻击下集群无人机的安全控制DoS攻击是恶意攻击者通过干扰集群无人机系统的通信网络或占用网络资源来影响各个无人机的信息实时获取与交互(如信息延迟或丢包),主要影响信息的可用性。对于集群无人机系统,有2种DoS攻击发起方式,如图 11所示。一种是攻击者对其中一个无人机发起DoS攻击,导致该无人机与其他无人机之间的信息不能互相传输,失去通信能力。另一种是攻击者直接在无人机信息交互网络通道发起攻击,同样会导致无人机系统失去通信能力。
|
图 11 对集群无人机系统的DoS攻击 Fig.11 DoS attacks on swarm UAVs |
集群无人机系统通信网络具有高机动性和分布式特点,是一种易受攻击的网络。到目前为止,关于DoS攻击的研究成果颇多。如文[181] 研究了遭受DoS攻击的线性多智能体系统基于事件触发的安全协同控制问题,并将该方法运用于多无人机系统进行验证。文[182] 考虑每个通道的攻击相互独立的情况,设计了基于状态反馈方法和基于观测器方法的两种分布式协同控制器,使得多个子系统在遭受DoS攻击的情况下仍能达成一致性控制性能。现有的大多数关于DoS攻击的方法侧重于预防,而不是分析安全漏洞。为了进行有效的分析,文[183] 提出了一种基于生成树的多无人机网络安全分析攻防模型,设计了一个攻击防御树,并利用这种攻击防御树,建立了一种基于风险评估的博弈方案。高机动多集群无人机在动态环境中工作时,通信信道存在许多安全问题,如:劫持攻击、GPS欺骗攻击、DDoS/DoS和干扰攻击等。为此,文[184] 研究了多集群无人机的安全控制问题。
5.3.2 欺骗攻击下集群无人机的安全控制欺骗攻击,主要通过入侵集群无人机系统中的通信网络,对通信通道中的传输信息进行篡改,进而使得所传输的信息具有非完备和非真实等特性。与DoS攻击导致数据丢包与延迟相比,欺骗攻击是对真实数据的篡改,集群无人机系统根据错误的信息实现对单个无人机的监测、制定错误的决策或发布相应的错误控制信息,从而对无人机集群系统的破坏性会更强。下面分别针对FDI攻击和重放攻击进行分析。
1) FDI攻击下的集群无人机安全控制
针对FDI攻击,第一种方法是构建基于各个无人机及其邻居之间差异的监测、检测和识别算法,然后对集群无人机受到的攻击进行分离[185-186]。尽管通过这种方法可以抵消各种攻击,包括传感器和执行器攻击以及对通信链路的攻击,但通常需要对图的连通性等进行额外的假设。此外,拒绝邻居的信息可能会损害网络连通性。第二种方法是设计有弹性的分布式控制协议[187-189],以减轻攻击的影响。到目前为止,关于FDI攻击下的集群无人机系统协同控制也有一些成果。如文[190] 研究了FDI检测策略及其在量化无人机系统编队控制中的应用问题,并针对量化过程对编码矩阵的设计的不同要求,给出了有效编码矩阵设计的充分条件。
2) 重放攻击下的集群无人机安全控制
重放攻击可以看成一种特殊的FDI攻击[191],其攻击过程主要分为两步:一是记录正常集群无人机系统通信信道中传输的数据,二是在发起攻击时重放这些记录的数据来代替通信信道中正在传输的数据。由于重放攻击的数据源自于集群无人机系统正常运行的数据,因此其天生具有隐蔽性。同时,重放攻击不需要详细的系统模型知识,是一种基于数据的攻击策略,对集群无人机系统安全飞行控制有较大影响。文[192] 提出了一种基于椭圆曲线密码体制的轻量级身份认证方法,并将该方法应用于无人机网络,对其抗攻击性能进行了相应评估。
6 挑战与展望(Challenges and prospects)从控制学科的视角出发,结合无人机的发展趋势,初步探讨了无人机安全飞行控制系统的概念以及国内外研究现状。基于归纳的国内外现有研究成果,对无人机安全控制的未来发展需解决的关键技术及难题进行如下展望。
1) 复杂环境与特殊情况下的无人机安全边界智能判定:对于特种构形的无人机,其机理模型必然存在气动参数不准确的情况,尤其在复杂环境(如多源干扰、突发障碍等)与特殊情况(如大机动飞行、机构故障、网络攻击等)下,外源输入将极大地改变无人机系统特性,可能导致现有的飞行边界判定方法难以实用。因此,有必要研究复杂环境与特殊情况的表征与建模,明晰其对无人机机理模型的作用机制,实现复杂环境与特殊情况的自主感知,并突破安全边界的智能、高可靠判定技术,这是提高无人机安全飞行控制能力的必然途径。
2) 多约束耦合下的无人机边界保护控制:对于无人机的安全约束,必然涵盖无人机的不同方面,例如状态约束、输入约束、输出约束等。然而,无人机作为典型的快动态运动体,具有明确的层级系统特征,控制输入需要驱动受控状态才能逐级实现对非受控状态的控制。当多个状态同时接近约束时,约束间的耦合作用将会凸显,甚至出现矛盾对立的情况。因此,研究如何有机协调多约束间的耦合关系,进而实现无人机在多约束条件下的安全飞行控制,有着极大的研究价值。
3) 非线性受扰无人机基于正不变集方法的安全飞行控制:基于不变集的特性,在受限区域对最大不变子集的估计严重依赖于对李雅普诺夫函数的选取,但目前仍未有对应李雅普诺夫函数的明确解析形式。另外,最大不变子集的计算十分复杂,且受到系统不确定和外部干扰的影响,对系统的计算能力有着较高的要求。因此,面向无人机系统的复杂性与高度耦合性,基于正不变集方法的无人机安全控制技术仍需进一步探索。
4) 智能任务重规划与安全控制综合:当无人机遭遇大变化干扰、极端环境变化、大系统故障、恶意攻击时,无人机的控制能力将出现急剧衰退,原定的任务方案将可能不能完全执行或执行存在严重的偏差,甚至导致无人机系统崩溃。因此,研究集“感知-规划-控制”于一体的智能任务重规划与安全控制综合框架,可赋予无人机更高层次的自主能力和安全性。
5) 故障条件下的无人机集群系统安全控制:集群无人机系统是由多个独立的无人机无线互联组成,当其中的一个或多个无人机出现故障时,会通过连接而影响到邻近无人机和整个集群无人机系统的安全性,如导致无人机间的碰撞。考虑故障情况下,无人机集群系统具有耦合性、传递性和涌发性等特征,将单个无人机出现执行器故障、传感器故障以及结构性故障等的容错控制研究结果推广应用到集群无人机的协同控制还存在技术挑战。因此,设计高质量的容错控制器来保证集群无人机系统在发生故障时的性能,是一个非常值得研究的课题。
6) 复杂动态条件下集群无人机系统的防碰撞安全控制:当集群无人机系统在协同飞行模式下遭遇动态障碍物时,其安全避障问题尤显重要,仍需进一步深入研究。在目前的集群无人机编队控制研究中,大多数的安全飞行控制方式都是以2维编队为基础进行的,还需进一步研究3维编队的防碰撞控制。在复杂的环境和突发事件中,充分发挥编队控制的优势,实现编队的自组、保持和重构,也是安全飞行控制的重点研究方向之一。同时,还需建立与现有移动自组网技术相结合的通讯标准,从而实现无人机与其他平台之间的互联。另一方面,集群无人机编队的避障安全飞行控制试验还比较少,需要在物理和虚拟软件上进行技术综合,以满足安全飞行控制的发展需求。
7) 各种外部攻击下的无人机安全控制:目前无人机正朝着大规模集群无人机系统的方向发展,因而实现不同外部攻击下无人机安全控制的相关技术亟需发展。当集群无人机系统通信网络和传感器网络等都受到攻击时,多无人机协同控制的一致性和闭环稳定性分析具有挑战性。为了保证高阶非线性集群无人机系统的可靠性和安全性,针对未知界信号的数据注入攻击,研究一致性控制策略也是有必要的。同时,实际集群无人机控制系统通常具有非线性和不确定性,线性集群无人机系统的安全控制方法无法直接应用于非线性集群无人机系统。因此,如何设计有效的控制器使得不确定非线性集群无人机系统在DoS攻击下实现一致性控制,也是目前亟需解决的难题之一。
| [1] |
Valavanis K P. Advances in unmanned aerial vehicles: State of the art and the road to autonomy[M]. Dordrecht, Netherlands: Springer, 2007.
|
| [2] |
李大光. 机器人与未来战争[J]. 领导科学论坛, 2016(12): 77-96. Li D G. Robots and the future war[J]. The Science of Leadership Forum, 2016(12): 77-96. DOI:10.3969/j.issn.2095-5103.2016.12.006 |
| [3] |
US Department of Defense. Unmanned aircraft systems roadmap 2005-2030[DB/OL]. [2022-10-01]. https://rosap.ntl.bts.gov/view/dot/18248.
|
| [4] |
郭雷, 余翔, 张霄, 等. 无人机安全控制系统技术: 进展与展望[J]. 中国科学: 信息科学, 2020, 50(2): 184-194. Guo L, Yu X, Zhang X, et al. Safety control system technologies for UAVs: Review and prospect[J]. Scientia Sinica Informationis, 2020, 50(2): 184-194. |
| [5] |
Yu X, Guo L, Zhang Y M, et al. Autonomous safety control of flight vehicles[M]. Boca Raton, USA: CRC Press, 2021.
|
| [6] |
Mettler B. Identification modeling and characteristics of miniature rotorcraft[M]. New York, USA: Springer, 2013.
|
| [7] |
雍可南. 歼击机过失速机动边界判定与保护控制[D]. 南京: 南京航空航天大学, 2015. Yong K N. Envelope predicating and protecting control for the post-stall maneuver of fighters[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2015. |
| [8] |
叶辉, 陈谋, 吴庆宪. 基于多滑模调节器切换的机动飞行边界保护控制[J]. 航空学报, 2014, 35(12): 3358-3370. Ye H, Chen M, Wu Q X. Envelope protection control for maneuver flight based on multi-regulator sliding mode control switch approach[J]. Acta Aeronautica et Astronautica Sinica, 2014, 35(12): 3358-3370. |
| [9] |
Kwatny H G, Dongmo J E T, Chang B C. Nonlinear analysis of aircraft loss of control[J]. Journal of Guidance, Control, and Dynamics, 2013, 36(1): 149-162. DOI:10.2514/1.56948 |
| [10] |
Tang L, Roemer M, Ge J H, et al. Methodologies for adaptive flight envelope estimation and protection[C]//AIAA Guidance, Navigation, and Control Conference. Reston, USA: AIAA, 2009. DOI: 10.2514/6.2009-6260.
|
| [11] |
Chakraborty A, Seiler P, Balas G J. Nonlinear region of attraction analysis for flight control verification and validation[J]. Control Engineering Practice, 2011, 19(4): 335-345. DOI:10.1016/j.conengprac.2010.12.001 |
| [12] |
Mitchell I, Bayen A M, Tomlin C J. A time-dependent Hamilton-Jacobi formulation of reachable sets for continuous dynamic games[J]. IEEE Transactions on Automatic Control, 2005, 50(7): 947-957. DOI:10.1109/TAC.2005.851439 |
| [13] |
Goman M G, Khramtsovsky A V, Kolesnikov E N. Evaluation of aircraft performance and maneuverability by computation of attainable equilibrium sets[J]. Journal of Guidance, Control, and Dynamics, 2008, 31(2): 329-339. DOI:10.2514/1.29336 |
| [14] |
Wu D W, Chen M, Ye H. Analysis and recovery of aircraft deep-stall phenomena using bifurcation analysis[J]. IEEE Access, 2020, 8: 29319-29333. DOI:10.1109/ACCESS.2020.2972570 |
| [15] |
Yin M Z, Chu Q P, Zhang Y, et al. Probabilistic flight envelope estimation with application to unstable overactuated aircraft[J]. Journal of Guidance, Control, and Dynamics, 2019, 42(12): 2650-2663. DOI:10.2514/1.G004193 |
| [16] |
王爽, 詹浩. 飞行最大可控边界集及其机动边界保护控制[J]. 西北工业大学学报, 2014, 32(4): 523-528. Wang S, Zhan H. The safe-set of aircraft and maneuverability envelope protection[J]. Journal of Northwestern Polytechnical University, 2014, 32(4): 523-528. DOI:10.3969/j.issn.1000-2758.2014.04.009 |
| [17] |
Nabi H N, Lombaerts T, Zhang Y, et al. Effects of structural failure on the safe flight envelope of aircraft[J]. Journal of Guidance, Control, and Dynamics, 2018, 41(6): 1257-1275. DOI:10.2514/1.G003184 |
| [18] |
Zhang Y, de Visser C C, Chu Q P. Database building and interpolation for an online safe flight envelope prediction system[J]. Journal of Guidance, Control, and Dynamics, 2019, 42(5): 1166-1174. DOI:10.2514/1.G003834 |
| [19] |
Zhang Y, Huang Y Z, Chu Q P, et al. Database-driven safe flight-envelope protection for impaired aircraft[J]. Journal of Aerospace Information Systems, 2021, 18(1): 14-25. DOI:10.2514/1.I010846 |
| [20] |
Menon P K, Sengupta P, Vaddi S, et al. Impaired aircraft performance envelope estimation[J]. Journal of Aircraft, 2013, 50(2): 410-424. DOI:10.2514/1.C031847 |
| [21] |
Lombaerts T, Looye G, Ellerbroek J, et al. Design and piloted simulator evaluation of adaptive safe flight envelope protection algorithm[J]. Journal of Guidance, Control, and Dynamics, 2017, 40(8): 1902-1924. DOI:10.2514/1.G002525 |
| [22] |
Falkena W, Borst C, Chu Q P, et al. Investigation of practical flight envelope protection systems for small aircraft[J]. Journal of Guidance, Control, and Dynamics, 2011, 34(4): 976-988. DOI:10.2514/1.53000 |
| [23] |
Yavrucuk I, Prasad J V R, Unnikrishnan S. Envelope protection for autonomous unmanned aerial vehicles[J]. Journal of Guidance, Control, and Dynamics, 2012, 32(1): 248-261. |
| [24] |
Yavrucuk I, Prasad J V R. Online dynamic trim and control limit estimation[J]. Journal of Guidance, Control, and Dynamics, 2012, 35(5): 1647-1656. DOI:10.2514/1.53116 |
| [25] |
Gursoy G, Yavrucuk I. Direct adaptive limit and control margin estimation with concurrent learning[J]. Journal of Guidance, Control, and Dynamics, 2016, 39(6): 1356-1373. DOI:10.2514/1.G001515 |
| [26] |
Sahani N, Horn J. Command limiting for full-envelope guidance and control of rotorcraft[C]//AIAA Guidance, Navigation, and Control Conference. Reston, USA: AIAA, 2005. DOI: 10.2514/6.2005-6348.
|
| [27] |
Sun D L, Jafarnejadsani H, Hovakimyan N. Command limiting for aerial vehicles with rate control augmentation systems[J]. IEEE Transactions on Aerospace and Electronic Systems, 2021, 57(3): 1702-1712. DOI:10.1109/TAES.2021.3050674 |
| [28] |
Heise S, Maciejowski J. Model predictive control of a supermaneuverable aircraft[C]//AIAA Guidance, Navigation, and Control Conference. Reston, USA: AIAA, 1996. DOI: 10.2514/6.1996-3768.
|
| [29] |
Falcone P, Tufo M, Borrelli F, et al. A linear time varying model predictive control approach to the integrated vehicle dynamics control problem in autonomous systems[C]//IEEE Conference on Decision and Control. Piscataway, USA: IEEE, 2007: 2980-2985.
|
| [30] |
钱积新, 赵均, 徐祖华. 预测控制[M]. 北京: 化学工业出版社, 2007. Qian J X, Zhao J, Xu Z H. Predictive control[M]. Beijing: Chemical Industry Press, 2007. |
| [31] |
van Oort E, Chu Q P, Mulder J A. Robust model predictive control of a feedback linearized F-16/MATV aircraft model[C]//AIAA Guidance, Navigation, and Control Conference. Reston, USA: AIAA, 2006. DOI: 10.2514/6.2006-6318.
|
| [32] |
Henson M. Nonlinear model predictive control: Current status and future directions[J]. Computers & Chemical Engineering, 1998, 23(2): 187-202. |
| [33] |
Allgöwer F, Zheng A. Nonlinear model predictive control[M]. Basel, Switzerland: Springer, 2000.
|
| [34] |
Oktay T, Sultan C. Model predictive control of maneuvering helicopters[C]//AIAA Guidance, Navigation, and Control Conference. Reston, USA: AIAA, 2012. DOI: 10.2514/6.2012-4530.
|
| [35] |
Song D L, Han J D, Liu G J. Active model-based predictive control and experimental investigation on unmanned helicopters in full flight envelope[J]. IEEE Transactions on Control Systems Technology, 2013, 21(4): 1502-1509. DOI:10.1109/TCST.2012.2208968 |
| [36] |
Deori L, Garatti S, Prandini M. 4-D flight trajectory tracking: A receding horizon approach integrating feedback linearization and scenario optimization[J]. IEEE Transactions on Control Systems Technology, 2019, 27(3): 981-996. DOI:10.1109/TCST.2018.2810201 |
| [37] |
Bhattacharjee D, Subbarao K. Robust control strategy for quadcopters using sliding mode control and model predictive control[C]//AIAA Scitech 2020 Forum. Reston, UAS: AIAA, 2020. DOI: 10.2514/6.2020-2071.
|
| [38] |
Slegers N, Kyle J, Costello M. Nonlinear model predictive control technique for unmanned air vehicles[J]. Journal of Guidance, Control, and Dynamics, 2006, 29(5): 1179-1188. DOI:10.2514/1.21531 |
| [39] |
Scholte E, Campbell M E. Robust nonlinear model predictive control with partial state information[J]. IEEE Transactions on Control Systems Technology, 2008, 16(4): 636-651. DOI:10.1109/TCST.2007.912120 |
| [40] |
Bauersfeld L, Spannagl L, Ducard G J J, et al. MPC flight control for a tilt-rotor VTOL aircraft[J]. IEEE Transactions on Aerospace and Electronic Systems, 2021, 57(4): 2395-2409. DOI:10.1109/TAES.2021.3061819 |
| [41] |
Rohr D, Studiger M, Stastny T, et al. Nonlinear model predictive velocity control of a VTOL tiltwing UAV[J]. IEEE Robotics and Automation Letters, 2021, 6(3): 5776-5783. DOI:10.1109/LRA.2021.3084888 |
| [42] |
Kolmanovsky I, Garone E, di Cairano S. Reference and command governors: A tutorial on their theory and automotive applications[C]//American Control Conference. Piscataway, USA: IEEE, 2014: 226-241.
|
| [43] |
Bemporad A. Reference governor for constrained nonlinear systems[J]. IEEE Transactions on Automatic Control, 1998, 43(3): 415-419. DOI:10.1109/9.661611 |
| [44] |
Tsourapas V, Sun J, Stefanopoulou A. Incremental step reference governor for load conditioning of hybrid fuel cell and gas turbine power plants[J]. IEEE Transactions on Control Systems Technology, 2009, 17(4): 756-767. DOI:10.1109/TCST.2008.2010554 |
| [45] |
Sun J, Kolmanovsky I V. Load governor for fuel cell oxygen starvation protection: A robust nonlinear reference governor approach[J]. IEEE Transactions on Control Systems Technology, 2005, 13(6): 911-920. DOI:10.1109/TCST.2005.854323 |
| [46] |
宫洵, 胡云峰, 杨荣彬, 等. 基于迭代Reference Governor的自由活塞发动机活塞运动控制[J]. 控制理论与应用, 2017, 34(2): 188-196. Gong X, Hu Y F, Yang R B, et al. Piston motion control of free piston engine based on iterative reference governor[J]. Control Theory & Applications, 2017, 34(2): 188-196. |
| [47] |
Kapasouris P, Athans M, Stein G. Design of feedback control systems for stable plants with saturating actuators[C]//27th IEEE Conference on Decision and Control. Piscataway, USA: IEEE, 1988: 469-479.
|
| [48] |
Pachter M, Miller R B. Manual flight control with saturating actuators[J]. IEEE Control Systems Magazine, 1998, 18(1): 10-20. DOI:10.1109/37.648622 |
| [49] |
Famularo D, Martino D, Mattei M. Constrained control strategies to improve safety and comfort on aircraft[J]. Journal of Guidance, Control, and Dynamics, 2008, 31(6): 1782-1792. DOI:10.2514/1.34426 |
| [50] |
Ye H, Chen M, Wu Q X. Flight envelope protection control based on reference governor method in high angle of attack maneuver[J]. Mathematical Problems in Engineering, 2015. DOI:10.1155/2015/254975 |
| [51] |
de Almeida F A. Reference management for fault-tolerant model predictive control[J]. Journal of Guidance, Control, and Dynamics, 2011, 34(1): 44-56. DOI:10.2514/1.50938 |
| [52] |
Nicotra M M, Naldi R, Garone E. A robust explicit reference governor for constrained control of unmanned aerial vehicles[C]//American Control Conference. Piscataway, USA: IEEE, 2016: 6284-6289.
|
| [53] |
Nicotra M M, Naldi R, Garone E. Nonlinear control of a tethered UAV: The taut cable case[J]. Automatica, 2017, 78: 174-184. DOI:10.1016/j.automatica.2016.12.018 |
| [54] |
Lucia W, Franzè G, Sznaier M. A hybrid command governor scheme for rotary wings unmanned aerial vehicles[J]. IEEE Transactions on Control Systems Technology, 2018, 28(2): 361-375. |
| [55] |
Chen M, Ge S S, Ren B B. Adaptive tracking control of uncertain MIMO nonlinear systems with input constraints[J]. Automatica, 2011, 47(3): 452-465. DOI:10.1016/j.automatica.2011.01.025 |
| [56] |
Sudhakar S, Vijayakumar V, Kumar C S, et al. Unmanned aerial vehicle (UAV) based forest fire detection and monitoring for reducing false alarms in forest-fires[J]. Computer Communications, 2020, 149: 1-16. DOI:10.1016/j.comcom.2019.10.007 |
| [57] |
Saska M, Hert D, Baca T, et al. Formation control of unmanned micro aerial vehicles for straitened environments[J]. Autonomous Robots, 2020, 44(6): 991-1008. DOI:10.1007/s10514-020-09913-0 |
| [58] |
周洪波, 裴海龙, 贺跃帮, 等. 状态受限的小型无人直升机轨迹跟踪控制[J]. 控制理论与应用, 2012, 29(6): 778-784. Zhou H B, Pei H L, He Y B, et al. Trajectory-tracking control for small unmanned helicopter with state constraints[J]. Control Theory & Applications, 2012, 29(6): 778-784. |
| [59] |
杨成顺, 杨忠, 葛乐. 飞行状态受限的多旋翼无人直升机姿态控制[J]. 电光与控制, 2015, 22(9): 37-41. Yang C S, Yang Z, Ge L. Attitude control for multi rotor unmanned helicopter with flight state constraints[J]. Electronics Optics and Control, 2015, 22(9): 37-41. |
| [60] |
Zhou B, Duan G-R. Global stabilization of linear systems via bounded controls[J]. Systems and Control Letters, 2009, 58(1): 54-61. DOI:10.1016/j.sysconle.2008.08.002 |
| [61] |
Guan W, Yang G H. Adaptive fault-tolerant control of linear time-invariant systems in the presence of actuator saturation[J]. Journal of Control Theory and Applications, 2009, 7(3): 321-327. DOI:10.1007/s11768-009-8067-5 |
| [62] |
Hu Q L, Ma G F, Xie L H. Robust and adaptive variable structure output feedback control of uncertain systems with input nonlinearity[J]. Automatica, 2008, 44(2): 552-559. DOI:10.1016/j.automatica.2007.06.024 |
| [63] |
Tyan F, Bernstein D S. Anti-windup compensator synthesis for systems with saturation actuators[J]. International Journal of Robust and Nonlinear Control, 1995, 5(5): 521-537. DOI:10.1002/rnc.4590050510 |
| [64] |
Jagannathan S, Hameed M. Adaptive force-banlancing control of mems gyroscope with actuator limits[C]//American Control Conference. Piscataway, USA: IEEE, 2004: 1862-1867.
|
| [65] |
Zhou Y L, Chen M, Jiang C S. Robust tracking control of uncertain MIMO nonlinear systems with application to UAVs[J]. IEEE/CAA Journal of Automatica Sinica, 2015, 2(1): 25-32. DOI:10.1109/JAS.2015.7032903 |
| [66] |
Wang R, Liu J K. Trajectory tracking control of a 6-DOF quadrotor UAV with input saturation via backstepping[J]. Journal of the Franklin Institute, 2018, 355(7): 3288-3309. DOI:10.1016/j.jfranklin.2018.01.039 |
| [67] |
Yu Z Q, Zhang Y M, Jiang B, et al. Nussbaum-based finitetime fractional-order backstepping fault-tolerant flight control of fixed-wing UAV against input saturation with hardware-inthe-loop validation[J]. Mechanical Systems and Signal Processing, 2021, 153. DOI:10.1016/j.ymssp.2020.107406 |
| [68] |
Teel A R. Global stabilization and restricted tracking for multiple integrators with bounded controls[J]. Systems & Control Letters, 1992, 18(3): 165-171. |
| [69] |
Marchand N. Further results on global stabilization for multiple integrators with bounded controls[C]//IEEE International Conference on Decision and Control. Piscataway, USA: IEEE, 2003: 4440-4444.
|
| [70] |
Sussmann H J, Sontag E D, Yang Y. A general result on the stabilization of linear systems using bounded controls[J]. IEEE Transactions on Automatic Control, 1994, 39(12): 2411-2425. DOI:10.1109/9.362853 |
| [71] |
Marchand N, Hably A. Global stabilization of multiple integrators with bounded controls[J]. Automatica, 2005, 41(12): 2147-2152. DOI:10.1016/j.automatica.2005.07.004 |
| [72] |
Yong K N, Chen M, Wu Q X. Immersion and invariance-based integrated guidance and control for unmanned aerial vehicle path following[J]. International Journal of Systems Science, 2019, 50(5): 1052-1068. DOI:10.1080/00207721.2019.1587544 |
| [73] |
吴林峰, 李春文. 尾座式垂直起降无人机在时变侧风干扰下的轨迹跟踪控制[J]. 清华大学学报(自然科学版), 2022, 62(1): 179-188. Wu L F, Li C W. Position tracking control for a tailsitter VTOL UAV experiencing time-varying crosswind disturbances[J]. Journal of Tsinghua University (Science and Technology), 2022, 62(1): 179-188. |
| [74] |
Yong K N, Chen M, Shi Y, et al. Flexible performance-based robust control for a class of nonlinear systems with input saturation[J]. Automatica, 2020, 122. DOI:10.1016/j.automatica.2020.109268 |
| [75] |
Liu K, Wang R J. Antisaturation command filtered backstepping control-based disturbance rejection for a quadarotor UAV[J]. IEEE Transactions on Circuits and Systems Ⅱ: Express Briefs, 2021, 68(12): 3577-3581. DOI:10.1109/TCSII.2021.3069967 |
| [76] |
Shao S Y, Chen M, Hou J, et al. Event-triggered-based discrete-time neural control for a quadrotor UAV using disturbance observer[J]. IEEE/ASME Transactions on Mechatronics, 2021, 26(2): 689-699. DOI:10.1109/TMECH.2021.3051835 |
| [77] |
Yan K, Chen M, Wu Q X, et al. Robust adaptive compensation control for unmanned autonomous helicopter with input saturation and actuator faults[J]. Chinese Journal of Aeronautics, 2019, 32(10): 2299-2310. DOI:10.1016/j.cja.2019.06.001 |
| [78] |
Fu C Y, Tian Y T, Huang H Y, et al. Finite-time trajectory tracking control for a 12-rotor unmanned aerial vehicle with input saturation[J]. ISA Transactions, 2018, 81: 52-62. DOI:10.1016/j.isatra.2018.08.005 |
| [79] |
Xu B, Wang X, Sun F C, et al. Intelligent control of flexible hypersonic flight dynamics with input dead zone using singular perturbation decomposition[J]. IEEE Transactions onNeural Networks and Learning Systems, 2021. DOI:10.1109/TNNLS.2021.3131578 |
| [80] |
Li H Y, Zhao S Y, He W, et al. Adaptive finite-time tracking control of full state constrained nonlinear systems with deadzone[J]. Automatica, 2019, 100: 99-107. DOI:10.1016/j.automatica.2018.10.030 |
| [81] |
Zhao N N, Wu L B, Ouyang X Y, et al. Finite-time adaptive fuzzy tracking control for nonlinear systems with disturbances and dead-zone nonlinearities[J]. Applied Mathematics and Computation, 2019, 362. DOI:10.1016/j.amc.2019.06.008 |
| [82] |
陈超, 段纳, 徐止政. 具有输入死区与扰动的四旋翼无人机自抗扰控制[J]. 信息与控制, 2022. Chen C, Duan N, Xu Z Z. ADRC control of the quadrotor UAV with input dead zone and disturbances[J]. Information and Control, 2022. |
| [83] |
Lin G H, Cheng Z J, Ren H R, et al. Command-filter-based finite-time control for human-in-the-loop UAVs with deadzone inputs[C]//8th International Conference on Information, Cybernetics, and Computational Social Systems. Piscataway, USA: IEEE, 2021: 338-343.
|
| [84] |
Dong G W, Cao L, Yao D Y, et al. Adaptive attitude control for multi-MUAV systems with output dead-zone and actuator fault[J]. IEEE/CAA Journal of Automatica Sinica, 2021, 8(9): 1567-1575. DOI:10.1109/JAS.2020.1003605 |
| [85] |
Tee K P, Ge S S, Tay E H. Barrier Lyapunov functions for the control of output-constrained nonlinear systems[J]. Automatica, 2009, 45(4): 918-927. DOI:10.1016/j.automatica.2008.11.017 |
| [86] |
Jin X, Xu J X. Iterative learning control for output-constrained systems with both parametric and nonparametric uncertainties[J]. Automatica, 2013, 49(8): 2508-2516. DOI:10.1016/j.automatica.2013.04.039 |
| [87] |
Gao T T, Liu Y J, Liu L, et al. Adaptive neural network-based control for a class of nonlinear pure-feedback systems with time-varying full state constraints[J]. IEEE/CAA Journal of Automatica Sinica, 2018, 5(5): 923-933. DOI:10.1109/JAS.2018.7511195 |
| [88] |
Zuo Z Y, Wang C L. Adaptive trajectory tracking control of output constrained multi-rotors systems[J]. IET Control Theory and Applications, 2014, 8(13): 1163-1174. DOI:10.1049/iet-cta.2013.0949 |
| [89] |
Fu C Y, Hong W, Lu H Q, et al. Adaptive robust backstepping attitude control for a multi-rotor unmanned aerial vehicle with time-varying output constraints[J]. Aerospace Science and Technology, 2018, 78: 593-603. DOI:10.1016/j.ast.2018.05.021 |
| [90] |
Su Z K, Li C T, Zhen Z Y. Anti-disturbance constrained control of the air recovery carrier via an integral barrier Lyapunov function[J]. Aerospace Science and Technology, 2020, 106. DOI:10.1016/j.ast.2020.106157 |
| [91] |
Bechlioulis C P, Rovithakis G A. Robust adaptive control of feedback linearizable MIMO nonlinear systems with prescribed performance[J]. IEEE Transactions on Automatic Control, 2008, 53(9): 2090-2099. DOI:10.1109/TAC.2008.929402 |
| [92] |
Shao S Y, Chen M. Adaptive neural discrete-time fractionalorder control for a UAV system with prescribed performance using disturbance observer[J]. IEEE Transactions on Systems, Man, and Cybernetics: Systems, 2021, 51(2): 742-754. DOI:10.1109/TSMC.2018.2882153 |
| [93] |
Zhang Y, Wang S H, Chang B, et al. Adaptive constrained backstepping controller with prescribed performance methodology for carrier-based UAV[J]. Aerospace Science and Technology, 2019, 92: 55-65. DOI:10.1016/j.ast.2019.05.032 |
| [94] |
Wang X D. Smooth attitude tracking control of a 3-DOF helicopter with guaranteed performance[DB/OL]. (2021-01-27)[2022-10-01]. https://arxiv.org/abs/2101.11241.
|
| [95] |
Yan K, Chen M, Wu Q X. Neural network-based adaptive fault tolerant tracking control for unmanned autonomous helicopters with prescribed performance[J]. Proceedings of the Institution of Mechanical Engineers, Part G: Journal of Aerospace Engineering, 2019, 233(12): 4350-4362. DOI:10.1177/0954410018823364 |
| [96] |
张毅, 方国伟, 杨秀霞. 具有性能预设的多机编队目标跟踪控制[J]. 系统工程与电子技术, 2021, 43(4): 1069-1079. Zhang Y, Fang G W, Yang X X. Target tracking control of multi-UAV formation with prescribed performance guarantees[J]. Systems Engineering and Electronics, 2021, 43(4): 1069-1079. |
| [97] |
Raković S V, Kerrigan E C, Kouramas K I, et al. Invariant approximations of robustly positively invariant sets for constrained linear discrete-time systems subject to bounded disturbances[R]. Cambridge, UK: University of Cambridge, 2004.
|
| [98] |
Tarbouriech S, Burgat C. Positively invariant sets for constrained continuous-time systems with cone properties[J]. IEEE Transactions on Automatic Control, 1994, 39(2): 401-405. DOI:10.1109/9.272344 |
| [99] |
Chen Z, Tu X W, Xing L, et al. A special kind of sliding mode control for nonlinear system with state constraints[J]. IEEE Access, 2019, 7: 69998-70010. DOI:10.1109/ACCESS.2019.2918786 |
| [100] |
Borrelli F, Keviczky T, Balas G J. Collision-free UAV formation flight using decentralized optimization and invariant sets[C]//43rd IEEE Conference on Decision and Control. Piscataway, USA: IEEE, 2004: 1099-1104.
|
| [101] |
李志南, 李卫华, 王鹏, 等. 输入受限的多旋翼无人机轨迹跟踪鲁棒正定不变集设计[J]. 控制与决策, 2021, 36(4): 857-866. Li Z N, Li W H, Wang P, et al. Design of robust positively invariant set for trajectory tracking of multi rotor UAV with input saturation[J]. Control and Decision, 2021, 36(4): 857-866. |
| [102] |
Davison E. The robust control of a servomechanism problem for linear time-invariant multivariable systems[J]. IEEE Transactions on Automatic Control, 1976, 21(1): 25-34. DOI:10.1109/TAC.1976.1101137 |
| [103] |
Zames G. Feedback and optimal sensitivity: Model reference transformations, multiplicative seminorms, and approximate inverses[J]. IEEE Transactions on Automatic Control, 1981, 26(2): 301-320. DOI:10.1109/TAC.1981.1102603 |
| [104] |
Doyle J C, Glover K, Khargonekar P P. State-space solutions to standard H2 and H∞ control problems[J]. IEEE Transactions on Automatic control, 1989, 34(8): 831-847. DOI:10.1109/9.29425 |
| [105] |
Dym H, Gohberg I. A maximum entropy principle for contractive interpolants[J]. Journal of Functional Analysis, 1986, 65(1): 83-125. DOI:10.1016/0022-1236(86)90018-2 |
| [106] |
Georgiou T T. On the computation of the gap metric[C]//27th IEEE Conference on Decision and Control. Piscataway, USA: IEEE, 1988: 1360-1361.
|
| [107] |
Gadewadikar J. H∞ output feedback control: Application to unmanned aerial vehicle[D]. Arlington, USA: University of Texas, 2007.
|
| [108] |
Gadewadikar J, Lewis F L, Subbarao K, et al. Structured H∞ command and control-loop design for unmanned helicopters[J]. Journal of Guidance, Control, and Dynamics, 2008, 31(4): 1093-1102. DOI:10.2514/1.31377 |
| [109] |
Kim H S, Park J B, Joo Y H. A systematic approach to fuzzymodel-based robust H∞ control design for a quadrotor UAV under imperfect premise matching[J]. International Journal of Fuzzy Systems, 2017, 19(4): 1227-1237. DOI:10.1007/s40815-016-0233-6 |
| [110] |
Werbos P J. Approximate dynamic programming for realtime control and neural modeling[M]//Handbook of Intelligent Control: Neural, Fuzzy, and Adaptive Approaches. New York, USA: Van Nostrand Reinhold, 1992: 493-526.
|
| [111] |
Padhi R, Unnikrishnan N, Wang X H, et al. A single network adaptive critic (SNAC) architecture for optimal control synthesis for a class of nonlinear systems[J]. Neural Networks, 2006, 19(10): 1648-1660. DOI:10.1016/j.neunet.2006.08.010 |
| [112] |
Abu-Khalaf M, Lewis F L. Nearly optimal control laws for nonlinear systems with saturating actuators using a neural network HJB approach[J]. Automatica, 2005, 41(5): 779-791. DOI:10.1016/j.automatica.2004.11.034 |
| [113] |
Ferrari S, Stengel R F. Online adaptive critic flight control[J]. Journal of Guidance, Control, and Dynamics, 2004, 27(5): 777-786. DOI:10.2514/1.12597 |
| [114] |
Xia R S, Chen M, Wu Q X, et al. Neural network based integral sliding mode optimal flight control of near space hypersonic vehicle[J]. Neurocomputing, 2020, 379: 41-52. DOI:10.1016/j.neucom.2019.10.038 |
| [115] |
Ferrari S, Steck J E, Chandramohan R. Adaptive feedback control by constrained approximate dynamic programming[J]. IEEE Transactions on Systems, Man, and Cybernetics, Part B: Cybernetics, 2008, 38(4): 982-987. DOI:10.1109/TSMCB.2008.924140 |
| [116] |
Nodland D, Zargarzadeh H, Jagannathan S. Neural networkbased optimal adaptive output feedback control of a helicopter UAV[J]. IEEE Transactions on Neural Networks and Learning Systems, 2013, 24(7): 1061-1073. DOI:10.1109/TNNLS.2013.2251747 |
| [117] |
Yu Z Q, Zhang Y M, Qu Y H. Prescribed performance-based distributed fault-tolerant cooperative control for multi-UAVs[J]. Transactions of the Institute of Measurement and Control, 2019, 41(4): 975-989. DOI:10.1177/0142331218809006 |
| [118] |
Zhang Q, Chen X, Xu D Z. Adaptive neural fault-tolerant control for the yaw control of UAV helicopters with input saturation and full-state constraints[J]. Applied Sciences, 2020, 10(4). DOI:10.3390/app10041404 |
| [119] |
Ma H X, Chen M, Feng G, et al. Disturbance-observer-based adaptive fuzzy tracking control for unmanned autonomous helicopter with flight boundary constraints[J]. IEEE Transactions on Fuzzy Systems, 2023, 31(1): 184-198. DOI:10.1109/TFUZZ.2022.3184386 |
| [120] |
Yong K N, Chen M, Wu Q X. Constrained adaptive neural control for a class of nonstrict-feedback nonlinear systems with disturbances[J]. Neurocomputing, 2018, 272: 405-415. DOI:10.1016/j.neucom.2017.07.015 |
| [121] |
Hafez A T, Givigi S N, Yousefi S. Unmanned aerial vehicles formation using learning based model predictive control[J]. Asian Journal of Control, 2018, 20(3): 1014-1026. DOI:10.1002/asjc.1774 |
| [122] |
Zhao S P, Ruggiero F, Fontanelli G A, et al. Nonlinear model predictive control for the stabilization of a wheeled unmanned aerial vehicle on a pipe[J]. IEEE Robotics and Automation Letters, 2019, 4(4): 4314-4321. DOI:10.1109/LRA.2019.2931821 |
| [123] |
姜斌, 杨浩. 飞控系统主动容错控制技术综述[J]. 系统工程与电子技术, 2007, 29(12): 2106-2110. Jiang B, Yang H. Survey of the active fault-tolerant control for flight control system[J]. Systems Engineering and Electronics, 2007, 29(12): 2106-2110. DOI:10.3321/j.issn:1001-506x.2007.12.026 |
| [124] |
Bounemeur A, Chemachema M, Essounbouli N. Indirect adaptive fuzzy fault-tolerant tracking control for MIMO nonlinear systems with actuator and sensor failures[J]. ISA Transactions, 2018, 79: 45-61. DOI:10.1016/j.isatra.2018.04.014 |
| [125] |
Cao L, Li H Y, Dong G W, et al. Event-triggered control for multiagent systems with sensor faults and input saturation[J]. IEEE Transactions on Systems, Man, and Cybernetics: Systems, 2021, 51(6): 3855-3866. DOI:10.1109/TSMC.2019.2938216 |
| [126] |
López-Estrada F R, Ponsart J C, Theilliol D, et al. LPV modelbased tracking control and robust sensor fault diagnosis for a quadrotor UAV[J]. Journal of Intelligent & Robotic Systems, 2016, 84(1): 163-177. |
| [127] |
Hu C F, Cao L, Zhou X P, et al. Fuzzy adaptive nonlinear sensor-fault tolerant control for a quadrotor unmanned aerial vehicle[J]. Asian Journal of Control, 2020, 22(3): 1163-1176. DOI:10.1002/asjc.1981 |
| [128] |
Li Y M, Tong S C. Adaptive neural networks decentralized FTC design for nonstrict-feedback nonlinear interconnected large-scale systems against actuator faults[J]. IEEE Transactions on Neural Networks and Learning Systems, 2017, 28(11): 2541-2554. DOI:10.1109/TNNLS.2016.2598580 |
| [129] |
Liu Z B, Wang L N, Song Y C, et al. Fault diagnosis and accommodation for multi-actuator faults of a fixed-wing unmanned aerial vehicle[J]. Measurement Science and Technology, 2022, 33(7). DOI:10.1088/1361-6501/ac6146 |
| [130] |
Qian M S, Jiang B, Liu H H T. Dynamic surface active fault tolerant control design for the attitude control systems of UAV with actuator fault[J]. International Journal of Control, Automation and Systems, 2016, 14(3): 723-732. DOI:10.1007/s12555-015-0020-4 |
| [131] |
周来宏. 四旋翼无人机抗干扰与容错控制方法研究[D]. 沈阳: 东北大学, 2019. Zhou L H. Anti-disturbance and fault-tolerant control for the quadrotor UAV[D]. Shenyang: Northeastern University, 2019. |
| [132] |
Gururajan S, Mitchell K, Ebel W. Flights of a multirotor UAS with structural faults: Failures on composite propeller(s)[J]. Data, 2019, 4(3). DOI:10.3390/data4030128 |
| [133] |
杨新哲. 基于观测器的四旋翼直升机姿态系统主动容错控制研究[D]. 南京: 南京航空航天大学, 2012. Yang X Z. Research about observer based active fault tolerant control for quad-rotor helicopters[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2012. |
| [134] |
赵璟. 带有约束的飞控系统的容错保性能控制[D]. 南京: 南京航空航天大学, 2016. Zhao J. Fault-tolerant guaranteed cost control for flight control system subject to constraints[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2016. |
| [135] |
Mokhtari S, Abbaspour A, Yen K K, et al. Neural networkbased active fault-tolerant control design for unmanned helicopter with additive faults[J]. Remote Sensing, 2021, 13(12). DOI:10.3390/rs13122396 |
| [136] |
Ortiz-Torres G, Castillo P, Sorcia-Vázquez F D J, et al. Fault estimation and fault tolerant control strategies applied to VTOL aerial vehicles with soft and aggressive actuator faults[J]. IEEE Access, 2020, 8: 10649-10661. DOI:10.1109/ACCESS.2019.2963693 |
| [137] |
Abbaspour A, Aboutalebi P, Yen K K, et al. Neural adaptive observer-based sensor and actuator fault detection in nonlinear systems: Application in UAV[J]. ISA Transactions, 2017, 67: 317-329. DOI:10.1016/j.isatra.2016.11.005 |
| [138] |
范佳明. 四旋翼飞行器容错控制研究[D]. 天津: 天津工业大学, 2017. Fan J M. Resaerch on fault-tolerant control of quadrotor UAV[D]. Tianjin: Tiangong University, 2017. |
| [139] |
Yang H L, Jiang B, Liu H H T, et al. Attitude synchronization for multiple 3-DOF helicopters with actuator faults[J]. IEEE/ASME Transactions on Mechatronics, 2019, 24(2): 597-608. DOI:10.1109/TMECH.2019.2895222 |
| [140] |
Niederlinski A. A heuristic approach to the design of linear multivariable interacting control systems[J]. Automatica, 1971, 7(6): 691-701. DOI:10.1016/0005-1098(71)90007-0 |
| [141] |
Šiljak D D. Reliable control using multiple control systems[J]. International Journal of Control, 1980, 31(2): 303-329. DOI:10.1080/00207178008961043 |
| [142] |
Patton R. Robustness issues in fault-tolerant control[C]//IEE Colloquium on Fault Diagnosis and Control System Reconfiguration. Stevenage, UK: IET, 1993.
|
| [143] |
Shen Q K, Jiang B, Shi P. Fault diagnosis and faulttolerant control based on adaptive control approach[M]. Cham, Switzerland: Springer, 2017.
|
| [144] |
Hajiyev C, Soken H E. Robust adaptive Kalman filter for estimation of UAV dynamics in the presence of sensor/actuator faults[J]. Aerospace Science and Technology, 2013, 28(1): 376-383. DOI:10.1016/j.ast.2012.12.003 |
| [145] |
Ma H J, Liu Y L, Li T B, et al. Nonlinear high-gain observerbased diagnosis and compensation for actuator and sensor faults in a quadrotor unmanned aerial vehicle[J]. IEEE Transactions on Industrial Informatics, 2019, 15(1): 550-562. DOI:10.1109/TII.2018.2865522 |
| [146] |
Tan J, Fan Y H, Yan P P, et al. Sliding mode fault tolerant control for unmanned aerial vehicle with sensor and actuator faults[J]. Sensors, 2019, 19(3). DOI:10.3390/s19030643 |
| [147] |
Zhang D, Shen Y P, Zhou S Q, et al. Distributed secure platoon control of connected vehicles subject to DoS attack: Theory and application[J]. IEEE Transactions on Systems, Man, and Cybernetics: Systems, 2021, 51(11): 7269-7278. DOI:10.1109/TSMC.2020.2968606 |
| [148] |
Gu Z, Ahn C K, Yue D, et al. Event-triggered H∞ filtering for T-S fuzzy-model-based nonlinear networked systems with multisensors against DoS attacks[J]. IEEE Transactions on Cybernetics, 2022, 52(6): 5311-5321. DOI:10.1109/TCYB.2020.3030028 |
| [149] |
Chen X L, Hu S L, Yue D, et al. Attack-tolerant switched fault detection filter for networked stochastic systems under resilient event-triggered scheme[J]. IEEE Transactions on Systems, Man, and Cybernetics: Systems, 2022, 52(3): 1984-1996. DOI:10.1109/TSMC.2020.3035768 |
| [150] |
Yuan Y, Sun F C, Zhu Q Y. Resilient control in the presence of DoS attack: Switched system approach[J]. International Journal of Control, Automation and Systems, 2015, 13(6): 1423-1435. DOI:10.1007/s12555-014-0261-7 |
| [151] |
Lian J, Huang X. Resilient control of networked switched systems against DoS attack[J]. IEEE Transactions on Industrial Informatics, 2022, 18(4): 2354-2363. DOI:10.1109/TII.2021.3097722 |
| [152] |
Pang Z H, Liu G P, Zhou D H, et al. Secure networked predictive control under DoS attacks[M]//Networked Predictive Control of Systems with Communication Constraints and Cyber Attacks. Singapore: Springer, 2019: 205-219.
|
| [153] |
Yuan H H, Xia Y Q. Resilient strategy design for cyberphysical system under DoS attack over a multi-channel framework[J]. Information Sciences, 2018, 454-455: 312-327. DOI:10.1016/j.ins.2018.04.082 |
| [154] |
Zhu Y Z, Zhang L X, Zheng W X. Distributed H∞ filtering for a class of discrete-time Markov jump Lur'e systems with redundant channels[J]. IEEE Transactions on Industrial Electronics, 2016, 63(3): 1876-1885. DOI:10.1109/TIE.2015.2499169 |
| [155] |
李晓孟. 多重攻击下信息物理系统的安全控制研究[D]. 广州: 广东工业大学, 2021. Li X M. Research on the security control for cyber physical systems under multiple attacks[D]. Guangzhou: Guangdong University of Technology, 2021. |
| [156] |
Dahiya S, Garg M. Unmanned aerial vehicles: Vulnerability to cyber attacks[C]//International Conference on Unmanned Aerial System in Geomatics. Cham, Switzerland: Springer, 2019: 201-211.
|
| [157] |
Chen J Y, Feng Z W, Wen J Y, et al. A container-based DoS attack-resilient control framework for real-time UAV systems [C]//Design, Automation & Test in Europe Conference & Exhibition. Piscataway, USA: IEEE, 2019: 1222-1227.
|
| [158] |
Guo Y, Wu M P, Tang K H, et al. Covert spoofing algorithm of UAV based on GPS/INS-integrated navigation[J]. IEEE Transactions on Vehicular Technology, 2019, 68(7): 6557-6564. DOI:10.1109/TVT.2019.2914477 |
| [159] |
Ye D, Zhang T Y. Summation detector for false data-injection attack in cyber-physical systems[J]. IEEE Transactions on Cybernetics, 2020, 50(6): 2338-2345. DOI:10.1109/TCYB.2019.2915124 |
| [160] |
Gong J Y, Ma Y J, Jiang B, et al. Fault-tolerant formation tracking control for heterogeneous multiagent systems with directed topology[J]. Guidance, Navigation and Control, 2021, 1(1). DOI:10.1142/S2737480721500011 |
| [161] |
Wu Y, Gou J Z, Hu X T, et al. A new consensus theorybased method for formation control and obstacle avoidance of UAVs[J]. Aerospace Science and Technology, 2020, 107. DOI:10.1016/j.ast.2020.106332 |
| [162] |
Wang X Y, Xi L L, Chen Y Z, et al. Decentralized MPC-based trajectory generation for multiple quadrotors in cluttered environments[J]. Guidance, Navigation and Control, 2021, 1(2). DOI:10.1142/S2737480721500072 |
| [163] |
Park J W, Oh H D, Tahk M J. UAV collision avoidance based on geometric approach[C]//SICE Annual Conference. Piscataway, USA: IEEE, 2008: 2122-2126.
|
| [164] |
Paul T, Krogstad T R, Gravdahl J T. Modelling of UAV formation flight using 3D potential field[J]. Simulation Modelling Practice and Theory, 2008, 16(9): 1453-1462. DOI:10.1016/j.simpat.2008.08.005 |
| [165] |
Kuriki Y, Namerikawa T. Consensus-based cooperative formation control with collision avoidance for a multi-UAV system [C]//American Control Conference. Piscataway, USA: IEEE, 2014: 2077-2082.
|
| [166] |
Tumova J, Dimarogonas D V. Multi-agent planning under local LTL specifications and event-based synchronization[J]. Automatica, 2016, 70: 239-248. DOI:10.1016/j.automatica.2016.04.006 |
| [167] |
朱旭, 闫茂德, 张昌利, 等. 基于改进人工势场的无人机编队防碰撞控制方法[J]. 哈尔滨工程大学学报, 2017, 38(6): 961-968. Zhu X, Yan M D, Zhang C L, et al. UAV formation collision avoidance control method based on improved artificial potential field[J]. Journal of Harbin Engineering University, 2017, 38(6): 961-968. |
| [168] |
Jenie Y I, van Kampen E J, Remes B. Cooperative autonomous collision avoidance system for unmanned aerial vehicle[M]//Advances in Aerospace Guidance, Navigation and Control. Berlin, Germany: Springer, 2013: 387-405.
|
| [169] |
李大东, 孙秀霞, 孙彪, 等. 基于混合整数线性规划的无人机任务规划[J]. 飞行力学, 2010, 28(5): 88-91. Li D D, Sun X X, Sun B, et al. Mission planning for UAVs based on MILP[J]. Flight Dynamics, 2010, 28(5): 88-91. |
| [170] |
Yang S, Bai W W, Li T S, et al. Neural-network-based formation control with collision, obstacle avoidance and connectivity maintenance for a class of second-order nonlinear multi-agent systems[J]. Neurocomputing, 2021, 439: 243-255. DOI:10.1016/j.neucom.2020.12.106 |
| [171] |
Wen Z M, Zhou S D, Wang M. Fuzzy control for the obstacle avoidance of a quadrotor UAV[J]. Applied Mechanics and Materials, 2015, 4058(1550): 314-320. |
| [172] |
Spurny V, Petrlik M, Vonasek V, et al. Cooperative transport of large objects by a pair of unmanned aerial systems using sampling-based motion planning[C]//24th IEEE International Conference on Emerging Technologies and Factory Automation. Piscataway, USA: IEEE, 2019: 955-962.
|
| [173] |
Guo Y, Parker L E. A distributed and optimal motion planning approach for multiple mobile robots[C]//IEEE International Conference on Robotics and Automation. Piscataway, USA: IEEE, 2002: 2612-2619.
|
| [174] |
Ma Z W, Wang C, Niu Y F, et al. A saliency-based reinforcement learning approach for a UAV to avoid flying obstacles[J]. Robotics and Autonomous Systems, 2018, 100: 108-118. DOI:10.1016/j.robot.2017.10.009 |
| [175] |
唐文兵. 多无人机协同防碰撞方法研究[D]. 杭州: 浙江理工大学, 2020. Tang W B. Cooperative collision avoidance method for multiUAV systems[D]. Hangzhou: Zhejiang Sci-Tech University, 2020. |
| [176] |
Xu Q, Yang H, Jiang B, et al. Fault tolerant formations control of UAVs subject to permanent and intermittent faults[J]. Journal of Intelligent & Robotic Systems, 2014, 73(1): 589-602. |
| [177] |
史建涛, 何潇, 周东华. 多机编队系统的协同容错控制[J]. 上海交通大学学报, 2015, 49(6): 819-824. Shi J T, He X, Zhou D H. Cooperative fault tolerant control for multi-vehicle systems[J]. Journal of Shanghai Jiao Tong University, 2015, 49(6): 819-824. |
| [178] |
Yu Z Q, Zhang Y M, Jiang B, et al. Decentralized fractionalorder backstepping fault-tolerant control of multi-UAVs against actuator faults and wind effects[J]. Aerospace Science and Technology, 2020, 104. DOI:10.1016/j.ast.2020.105939 |
| [179] |
Sujit P B, Sousa J B. Multi-UAV task allocation with communication faults[C]//American Control Conference. Piscataway, USA: IEEE, 2012: 3724-3729.
|
| [180] |
Wang G Q, Luo H, Hu X X, et al. Fault-tolerant communication topology management based on minimum cost arborescence for leader-follower UAV formation under communication faults[J]. International Journal of Advanced Robotic Systems, 2017, 14(2). DOI:10.1177/1729881417693965 |
| [181] |
Ma Y S, Che W W, Deng C, et al. Observer-based eventtriggered containment control for MASs under DoS attacks[J]. IEEE Transactions on Cybernetics, 2022, 52(12): 13156-13167. DOI:10.1109/TCYB.2021.3104178 |
| [182] |
Lu A Y, Yang G H. Distributed consensus control for multiagent systems under denial-of-service[J]. Information Sciences, 2018, 439-440: 95-107. DOI:10.1016/j.ins.2018.02.008 |
| [183] |
Garg S, Aujla G S, Kumar N, et al. Tree-based attack-defense model for risk assessment in multi-UAV networks[J]. IEEE Consumer Electronics Magazine, 2019, 8(6): 35-41. DOI:10.1109/MCE.2019.2941345 |
| [184] |
Gupta R, Kumari A, Tanwar S, et al. Blockchain-envisioned softwarized multi-swarming UAVs to tackle COVID-I9 situations[J]. IEEE Network, 2021, 35(2): 160-167. DOI:10.1109/MNET.011.2000439 |
| [185] |
Sundaram S, Hadjicostis C N. Distributed function calculation via linear iterative strategies in the presence of malicious agents[J]. IEEE Transactions on Automatic Control, 2010, 56(7): 1495-1508. |
| [186] |
Pasqualetti F, Bicchi A, Bullo F. Consensus computation in unreliable networks: A system theoretic approach[J]. IEEE Transactions on Automatic Control, 2012, 57(1): 90-104. DOI:10.1109/TAC.2011.2158130 |
| [187] |
Zeng W, Chow M Y. Resilient distributed control in the presence of misbehaving agents in networked control systems[J]. IEEE Transactions on Cybernetics, 2014, 44(11): 2038-2049. DOI:10.1109/TCYB.2014.2301434 |
| [188] |
Zhang T Y, Ye D. False data injection attacks with complete stealthiness in cyber-physical systems: A self-generated approach[J]. Automatica, 2020, 120. DOI:10.1016/j.automatica.2020.109117 |
| [189] |
Ruan M H, Gao H, Wang Y Q. Secure and privacy-preserving consensus[J]. IEEE Transactions on Automatic Control, 2019, 64(10): 4035-4049. DOI:10.1109/TAC.2019.2890887 |
| [190] |
Liu L, Wu H Y, Xi Z Y, et al. FDI attack detection for formation control of quantized UAV systems by coding sensor outputs [C]//International Conference on Unmanned Aircraft Systems. Piscataway, USA: IEEE, 2020: 1278-1285.
|
| [191] |
Zhu M, Martínez S. On distributed constrained formation control in operator-vehicle adversarial networks[J]. Automatica, 2013, 49(12): 3571-3582. DOI:10.1016/j.automatica.2013.09.031 |
| [192] |
Li T, Ma J F, Feng P B, et al. Lightweight security authentication mechanism towards UAV networks[C]//International Conference on Networking and Network Applications. Piscataway, USA: IEEE, 2019: 379-384.
|
 2023, Vol. 45
2023, Vol. 45


