2. 西北工业大学航天飞行动力学技术国家级重点实验室, 陕西 西安 710072
2. National Key Laboratory of Aerospace Flight Dynamics, Northwestern Polytechnical University, Xi'an 710072, China
随着空间技术的快速发展,通过多次发射并在轨道上装配组件来建造大型空间设施(如空间站、大型通讯卫星等)的需求日益迫切[1-2]。其中运动规划技术作为利用空间机械臂进行在轨装配的关键技术在近十年受到国内外学者的广泛研究[3-4]。
运动规划算法通常可以分为局部算法和全局算法。局部规划算法,如人工势场法[5],利用传感器实时获取机器人周边环境信息,动态调整运动轨迹,可灵活应对突发情况。但是此类算法不是完备的,在拥挤杂乱的环境下容易陷入局部极值。相对应地,全局规划算法,尤其是基于采样的方法,利用事先获取的完整环境信息,可以在复杂环境下高效求解高自由度机器人的运动规划问题[6]。其中,RRT(快速扩展随机树)及其改进算法[7]通过随机采样逐步构造一棵随机树,寻找连接初始和目标构形的运动轨迹。此类算法可以较为方便地处理机器人运动学甚至动力学约束,已得到了广泛应用[8]。
然而,基于采样的规划算法在处理狭窄通道问题时性能急剧下降,但此类问题在装配中却很常见。窄通道是指占整个构形空间比重很小但包含部分解的无碰撞区域,因此难以通过常规方式对其进行采样以及拓展。目前常见的解决方法主要包括改进采样策略和改进拓展方式两种。其中,文[9] 利用高斯采样增加示教区域的样本点密度,从而在一定程度上增加窄通道中的样本点。文[10] 则利用桥测试方法更为高效地对窄通道直接进行采样。但是这两种算法都需要额外的碰撞检测,耗费大量时间,且在高维环境下效率降低。而ADD-RRT(adaptive dynamic domain RRT)[11]根据节点的可拓展能力,即动态域,对随机采样点进行筛选,只对有潜力的样本点进行拓展。另一方面,文[12] 利用回撤技术,将发生碰撞的构形沿着障碍物边界回撤到无碰撞区域,但是需要进行耗时的穿透深度计算。文[13] 提出RRV算法,通过额外的随机采样和主成分分析(PCA),随机树可以像藤蔓一样攀附着障碍物生长,以快速通过复杂区域。此外,多棵树同时生长也能在一定程度上提高复杂环境下的规划效率[14-15]。
运动规划一般都是在构形空间中进行,但是机械臂在执行装配操作时任务指令通常在工作空间中下达,且通常工作空间中同一个目标末端状态可能对应多种不同的机械臂构形。如果采取“先求逆运动学,再规划运动”的框架,则可能导致初始和目标构形不在同一连通域内[8]。为此,文[16] 直接在工作空间中采样,同时考虑了任务对末端施加的约束,再利用雅可比矩阵的伪逆进行拓展。考虑到在整个工作空间中采样会产生大量无用节点,文[17] 提出EET(exploring/exploiting tree)算法,以牺牲算法完备性为代价,平衡算法对工作空间信息的利用和探索行为,减小工作空间采样范围,提高规划效率和路径质量。文[18] 结合EET算法进一步考虑了机械臂运动学约束和末端任务约束,同时并行搜索不同拓扑特性的工作空间路径以提升路径最优性。然而,单纯基于工作空间采样的规划算法是不完备的,并且算法所利用的工作空间信息通常只包含位置信息而缺乏姿态信息,因此在杂乱的环境下算法可能会因陷入局部极值而依然难以求解。文[19] 提出根据算法进程动态切换采样、拓展策略,能够在保证算法完备性的同时提高算法效率和路径质量。
在之前的工作[10]中,提出了用于复杂环境尤其是窄通道环境的基于构形空间采样的运动规划算法,利用桥测试以及PCA等技术分析局部空间类型,提高了算法在复杂环境下的规划效率和成功率。本文拓展了此算法,用于解决工作空间中的装配运动规划问题。新算法结合混合采样方法,既充分利用工作空间信息进一步提高算法效率,又保证了算法的完备性。此外,在局部拓展中充分考虑了机械臂的运动学与动力学特性,增强了所规划的运动轨迹的可执行性,也提高了整体规划效率。
2 问题描述(Problem description)本节将对3维工作空间中串联机械臂的运动规划问题与其所涉及的符号作相关定义。
将机械臂所在的工作空间表示为
本文主要研究面向在轨装配的点到点运动规划问题。对于给定的机械臂几何与运动学模型、工作空间障碍物
为了进一步提高空间机械臂在拥挤、狭小环境下进行装配运动规划的效率,结合EET算法[17]和ADD-RRV算法[10]的优势,提出基于混合采样的RRV算法(HS-RRV),其流程框架如算法1所示。
与经典RRT算法的基本流程类似,本算法通过随机采样(Rand_Sample函数)寻找最近的节点(Nearest_Node函数),利用局部规划器连接相邻节点(Extend函数),从而逐渐在构形空间构造一棵随机树(Tree_Grow函数)。但是,不同于经典RRT算法,本算法不仅在构形空间中进行搜索,还利用了工作空间中的信息,并且根据随机树的拓展进程对两者的偏向进行动态调节。因此,本算法中随机树的每一个节点都包含2种子节点,即机械臂的关节构形子节点
算法1 HS-RRV
1:
2:
3:
4:
5: repeat
6:
7:
8:
9:
10:
11:
12: until
13: return
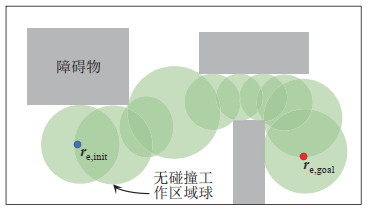
为了有效利用工作空间信息引导随机树的拓展,在算法初始化后,首先利用基于圆球的Wavefront算法[17]捕获工作空间的连通性特征。如图 1所示,圆球的直径表明了无碰撞工作空间区域的几何特征,一系列相互交叠的圆球构成了连接初始和目标末端位置的无碰撞通道,可用于引导机械臂末端在工作空间中的拓展。Wavefront算法的工作流程如下:
|
图 1 算法工作原理示意图 Fig.1 Schematic diagram of the Wavefront algorithm |
(1) 将初始末端位置作为圆心,将其与最近障碍物之间的距离作为半径,构造第1个圆球;
(2) 在第1个圆球的表面随机均匀采样
(3) 重复上述过程,直到目标点被圆球覆盖。
3.2 平衡工作/构形空间拓展在算法1中,随机采样同时在工作空间和构形空间中进行,利用采样权重
混合采样过程如算法2所示,算法以概率
算法2
1: if
2:
3:
4: else
5: if
6:
7:
8:
9: else
10:
11: end if
12:
13: end if
14: return
工作空间中的采样利用Sample_WS函数在Wavefront算法生成的末端无碰撞圆球中进行(算法2的第2行)。具体而言,以当前圆球的中心位置为采样均值,以
上述工作空间采样中利用工作空间连通性信息引导随机树在构形空间探索拓展,排除了与当前规划问题无关的部分构形空间,避免随机树在整个构形空间中盲目地拓展,缩小了采样、搜索范围,提高了规划效率。但是,搜索区域的减小将导致算法不完备。当工作空间信息不准确(如被排除的构形空间也包含部分解)或不能提供有效拓展方向(如机械臂因几何或者运动学等约束而陷入局部极值)时,单一的工作空间采样则因无法搜索整个构形空间而导致规划失败。
因此,当工作空间中的样本点难以被有效拓展时,采样逐渐偏向整个构形空间。为了跳出局部极值,首先以前文描述的方式利用Sample_WS函数获取工作空间中的随机样本点
在获取随机样本点后,需要利用Nearest_Node函数分别为不同类型(关节构形或末端位姿)的样本点依据各自的距离度量搜索最近节点进行拓展(算法1的第7行)。尽管随机树中的每个节点均包含关节构形和末端位姿2种子节点,但搜索仅利用与随机样本点类型相同的子节点。通常,合适的度量需要反映连接2个样本点的代价。考虑到工作空间度量难以精确获取,因此,对于工作空间中的任意2个样本点
| $ \begin{align} {\rm Dist}(\mathit{\boldsymbol{x}}_{i}, \mathit{\boldsymbol{x}}_{j})=k_{1} \| \mathit{\boldsymbol{r}}_{i} -\mathit{\boldsymbol{r}}_{j} \|+k_{2} \| \mathit{\boldsymbol{\psi}}_{i} -\mathit{\boldsymbol{\psi}}_{j} \| \end{align} $ | (1) |
其中
局部规划器的工作流程如算法3所示。
对于工作空间中的采样,在利用Nearest_Node函数获取最近的末端位姿节点
| $ \begin{align} \min \mathit{\boldsymbol{\dot{q}}} \frac{1}{2}\| \mathit{\boldsymbol{w}}_{1} \|^{2}, \; \; \; \text{ s.t. } \mathit{\boldsymbol{J}}(\mathit{\boldsymbol{q}}_{\text{near}})\mathit{\boldsymbol{\dot{q}}}-\alpha_{1} \cdot \Delta \mathit{\boldsymbol{x}}=\mathit{\boldsymbol{w}}_{1} \end{align} $ | (2) |
算法3
1:
2:
3:
4: if
5: return
6: else
7: return
8: end if
其中
| $ \begin{align} \min _{\mathit{\boldsymbol{\dot{q}}}} \frac{1}{2}\| \mathit{\boldsymbol{w}}_{2} \|^{2}, \; \; \; \text{ s.t. } \mathit{\boldsymbol{\dot{q}}}-\mathit{\boldsymbol{\xi}}_{\rm a} =\mathit{\boldsymbol{w}}_{2} \end{align} $ | (3) |
其中
| $ \begin{align} \min _{\mathit{\boldsymbol{\dot{q}}}} \frac{1}{2}\| \mathit{\boldsymbol{w}}_{\mathit{\boldsymbol{J}}} \|^{2}, \; \; \; \text{ s.t. } \begin{bmatrix} -\mathit{\boldsymbol{E}} \\ \mathit{\boldsymbol{E}} \end{bmatrix} \mathit{\boldsymbol{\dot{q}}}-\begin{bmatrix} -\mathit{\boldsymbol{\dot{Q}}}_{\min} \\ \mathit{\boldsymbol{\dot{Q}}}_{\max} \end{bmatrix}\leqslant \mathit{\boldsymbol{w}}_{\mathit{\boldsymbol{J}}} \end{align} $ | (4) |
最终,任务空间中的局部规划可以描述为考虑任务优先级的分层二次最小二乘规划(HQLP)问题:
| $ \begin{align} \text{lex min} \left\{ \frac{1}{2}\| \mathit{\boldsymbol{w}}_{J} \|^{2}, \; \frac{1}{2}\| \mathit{\boldsymbol{w}}_{1} \|^{2}, \; \frac{1}{2}\| \mathit{\boldsymbol{w}}_{2} \|^{2} \right\} \end{align} $ | (5) |
对于构形空间中的采样,获取最近的构形节点
| $ \begin{align} \min _{\mathit{\boldsymbol{\dot{q}}}} \frac{1}{2}\| \mathit{\boldsymbol{w}}_{3} \|^{2}, \; \; \text{ s.t. } \mathit{\boldsymbol{\dot{q}}}-\alpha_{2} \cdot \Delta \mathit{\boldsymbol{q}}=\mathit{\boldsymbol{w}}_{3} \end{align} $ | (6) |
其中
| $ \begin{align} \text{lex min} \left\{\frac{1}{2}\| \mathit{\boldsymbol{w}}_{J} \|^{2}, \; \frac{1}{2}\| {\mathit{\boldsymbol{w}}_{3}} \|^{2} \right\} \end{align} $ | (7) |
上述2类规划问题可以用文[20] 所提出的求解器求解,得到满足多优先级任务要求的参考速度
如果在新构形
此外,需要注意,参数
正如前文所述,算法中部分参数可自主调节,调节流程如算法4所示。
算法4
1: if l='W' then
2: if
3:
4: if
5:
6:
7: end if
8: else
9:
10: if {
11:
12:
13: end if
14: end if
15:
16: end if
17: return
如果随机采样与拓展在工作空间中进行,那么采样所在的圆球
此外,算法还根据工作空间中的拓展是否有进展来调节采样概率
对于装配问题,构形空间中通常会存在诸多拥挤复杂的区域(例如窄通道),导致随机拓展更容易因为发生碰撞而失败。因此,当初次拓展失败后,需要对局部构形空间进行分析,以获取更加高效的拓展方向,从而使随机树能够快速穿越复杂区域,到达目标点。在前期工作[10]基础上,为降低应用复杂度,修改并简化了再次拓展的Extend_further算法,其流程如算法5所示。
算法5
1:
2: if
3:
4: else
5:
6: end if
7:
8:
9: return
为了分析局部空间,首先利用Near_Constrained _Config函数搜集以邻近节点
| $ \begin{align} \mathit{\boldsymbol{q}}'_{\text{rand}} =\mathit{\boldsymbol{q}}_{\text{near}} +\sum _{k=1}^n \left( \frac{\lambda_{\text{const}}^{i}} {\lambda_{\text{const}}^{1}} \left(\mathit{\boldsymbol{q}}_{\text{obs}} -\mathit{\boldsymbol{q}}_{\text{near}}\right)\cdot \mathit{\boldsymbol{v}}_{\text{const}}^{i} \right) \mathit{\boldsymbol{v}}_{\text{const}}^{i} \end{align} $ | (8) |

|
图 2 桥测试法和局部空间PCA法获取的2种再次拓展方向的示意图 Fig.2 Schematic diagram of two directions of further extension obtained by bridge test and PCA on local space respectively |
其中
注意到本文并没有像文[10] 那样严格区分局部空间是窄通道环境还是位于凸障碍物边界。但是考虑到受限节点已经位于障碍物附近,能够反映出部分障碍物边界特征,因此简化后的算法在2种情形下均有良好性能。
此外,当节点数量不足以进行主成分分析时(需要节点数至少大于
(1) 将
(2) 沿方向
(3) 如果
(4) 如果中点是无碰撞构形,则可以作为再次拓展的方向
考虑到随机树在复杂区域内拓展效率低的特点,当获取到更高效的拓展方向后,可采取多次连续拓展的策略,以更快速地通过复杂区域。
4 仿真与分析(Simulation and analysis)为了验证算法的有效性与优越性,将HS-RRV算法和经典RRT[6]、ADD-RRT[11]、Bi-RRT[14]、EET[17]以及HS-RRT算法进行对比。其中HS-RRT算法是HS-RRV算法的简化版本,即未考虑局部空间辨识后再拓展(算法5)部分。所有仿真均利用Matlab软件在内存为16GB,CPU为2.60GHz、I7-9750的笔记本电脑中进行。
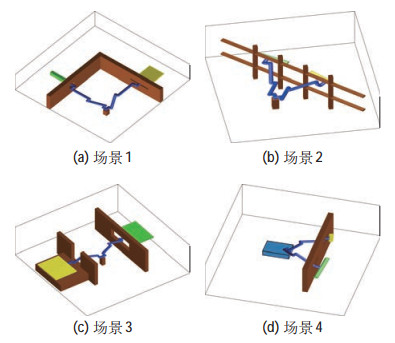
如图 3所示,仿真包含4个空间大小均为8m
|
图 3 仿真场景示意图 Fig.3 Schematic diagram of simulation scenarios |
|
|
表 1 机械臂D-H参数和惯性参数 Tab. 1 D-H parameters and inertial parameters of the manipulator |
仿真中,所有机械臂的关节角运动范围为
|
|
表 2 4种场景下使用不同规划器的平均规划结果 Tab. 2 Average planning results of different planners in 4 scenarios |
此场景下,机械臂需要将1.2m
| $ \begin{align*} \mathit{\boldsymbol{q}}_{\text{init}} =[ 0 , \pi /3, \pi /4, -\pi /4, -\pi /2, -\pi /2, -\pi /3 ]^{\rm T} \end{align*} $ |
对应初始末端位姿(位置单位m,姿态单位rad)为
| $ \begin{align*} \mathit{\boldsymbol{x}}_{\rm e, \text{init}} =[ 4.011, -0.210, 1.267, \pi /2, 0, \pi /2 ]^{\rm T} \end{align*} $ |
部件目标位姿为
| $ \begin{align*} \mathit{\boldsymbol{x}}_{\rm e, \text{goal}} =[ 0.210, 4.011, 1.267, -\pi /2, -\pi / 2, 0 ]^{\rm T} \end{align*} $ |
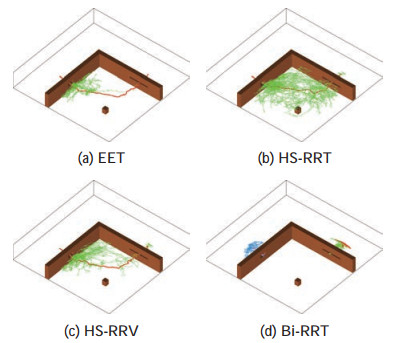
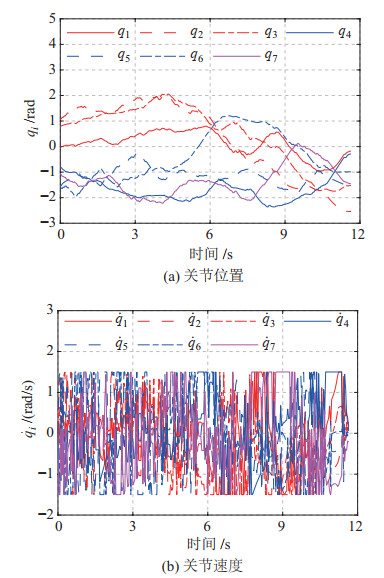
4种算法的单次规划结果如图 4所示,为清晰起见,图中仅保留了工作空间中的障碍物以及末端位置的随机拓展轨迹(绿色和蓝色)与最终轨迹(红色和紫色)。其中,HS-RRV算法所规划出的关节轨迹如图 5所示,可见关节运动始终满足关节位置和关节速度约束。
|
图 4 场景1下使用不同规划器的规划结果 Fig.4 Planning results of different planners in scenario 1 |
|
图 5 场景1下HS-RRV算法规划所得关节轨迹 Fig.5 Joint trajectories planned with HS-RRV algorithm in scenario 1 |
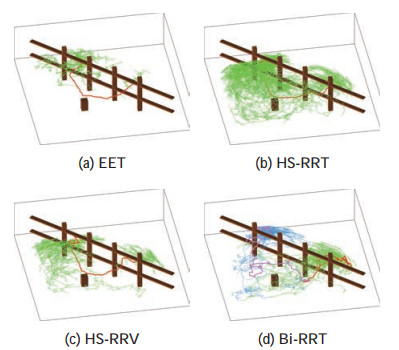
由于部件最初已经在狭缝中,EET、HS-RRT和HS-RRV算法利用工作空间信息,均能够较快找到从狭缝中取出部件的轨迹。此后,部件需要经过旋转、对准才能被安装到另一侧狭缝,但上述算法均没有有效的姿态信息可以利用。由于EET算法限制了采样与搜索范围导致算法不完备,因而搜索容易陷在第2个狭缝前,难以找到解,算法成功率较低。与此相对应地,HS-RRT算法相较于EET算法仅增加了在整个构形空间中进行采样与拓展的环节,保证了算法的完备性,从而在同样的运行时间下显著提升了算法的成功率。HS-RRV算法结合了对局部复杂区域的分析,进一步提高了算法的成功率,其成功率约是EET算法的1.7倍,是HS-RRT算法的1.2倍。与此同时,Bi-RRT算法没有利用工作空间信息缩小采样搜索范围,而是始终在整个构形空间中随机均匀采样,尽管从初始和目标状态同时构造了2棵随机树,但在大部分情况下均难以在狭缝中拓展,如图 4(d)所示。Bi-RRT算法在极少数情况下其中一棵随机树能够穿越部分狭缝,但在给定时间内的整体求解成功率为0。注意到,由于HS-RRT、HS-RRV以及Bi-RRT等算法是完备的,因此在足够长的运行时间下,算法总能够找到解,这是EET算法所不能保证的。
从表 2也可以看出,HS-RRV算法能够以更少的迭代次数找到解,相应地,生成的节点也更少,从而所需的存储空间更小。此外,节点数的减少也会提高算法寻找相邻节点的效率,从而提高算法整体效率。碰撞检测次数是另一个影响规划效率的重要因素,在HS-RRV算法中,随机树的拓展、桥测试均需要进行碰撞检测,但在较少的迭代次数下所需的总碰撞检测次数也较少。综合而言,HS-RRV算法的规划效率更高,约是EET算法的2.4倍,是HS-RRT算法的1.6倍。需要注意的是,算法的成功率越低,其统计的规划时间越是低估其实际所需时间。
注意到,此场景下利用工作空间信息进行拓展的3种算法的轨迹长度相当。
4.2 仿真场景2此场景下,需要将2m
| $ \begin{align*} \mathit{\boldsymbol{q}}_{\text{init}} & =[ 0 , 5\pi /12, 5\pi /12, -\pi /4, -\pi /2, \\ &\quad -2\pi /3, -\pi /3]^{\rm T} \end{align*} $ |
对应的初始末端位姿为
| $ \begin{align*} \mathit{\boldsymbol{x}}_{\rm e, \text{init}} =[2.937, 0.625, 2.453, 2.25, -0.02, -1.28]^{\rm T} \end{align*} $ |
杆件目标位姿为
| $ \begin{align*} \mathit{\boldsymbol{x}}_{\rm e, \text{goal}} =[0.625, 2.937, 2.4530, -0.66, -0.02, -1.28]^{\rm T} \end{align*} $ |
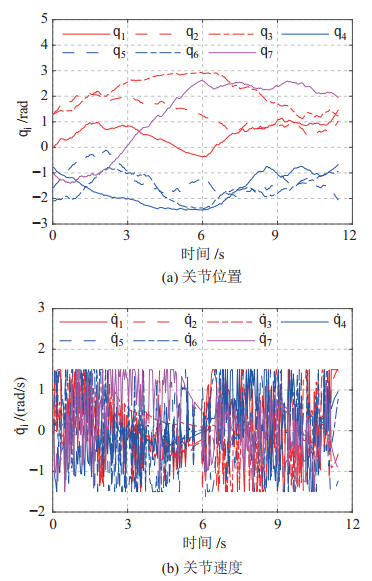
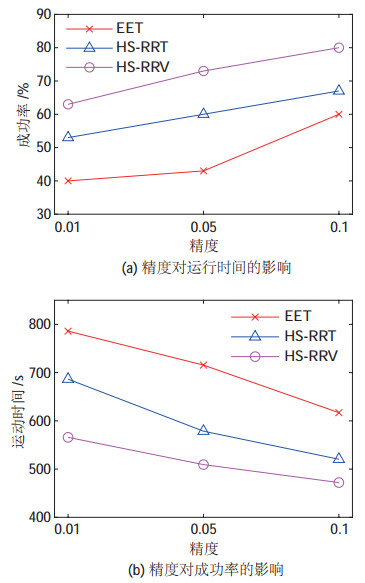
4种算法的单次规划结果如图 6所示,其中HS-RRV算法规划出的关节轨迹如图 7所示。此时,利用工作空间信息的单树算法可以较为轻松地将杆件搬运至目标区域附近,但是难以精确到达目标点。这是由于较大的杆件、目标区域较为复杂的环境以及机械臂几何构形与运动极限等约束,使得算法需要花费更大的计算代价才能精确到达目标点。如图 8所示,随着规划精度
|
图 6 场景2下使用不同规划器的规划结果 Fig.6 Planning results of different planners in scenario 2 |
|
图 7 场景2下HS-RRV算法规划所得关节轨迹 Fig.7 Joint trajectories planned with HS-RRV algorithm in scenario 2 |
|
图 8 规划精度对算法运行时间和成功率的影响 Fig.8 Influence of the planning accuracy on the running time and success rate of algorithms |
除此以外,HS-RRV算法的成功率始终高于EET和HS-RRT算法,如表 2所示(对应0.05精度),分别是它们的1.7倍和1.2倍。此时,HS-RRV算法在迭代次数和节点数上相对于前2种算法同样具有明显优势。但是,为了能够以更高的精度接近目标点,HS-RRV算法需要更多的局部空间分析以及再拓展,因此碰撞检测次数有所上升。综合而言,HS-RRV算法的规划效率依然优于EET算法,是其1.4倍;但是仅稍优于HS-RRT算法。
然而,值得关注的是,Bi-RRT算法在此场景下有着令人瞩目的表现,算法成功率达到100%,且规划效率也明显高于其他3种单树算法。但是,Bi-RRT算法需要预先获取末端目标状态下对应的机械臂构形,其本身也是一个复杂的逆运动学求解问题,需要耗费较大的计算代价,本文并没有重点研究此问题。同时,利用Bi-RRT算法得到的关节和末端轨迹都是最长的,其中末端轨迹长度更是其他3种算法的2倍多。但这也为规划算法提供了可参考的改进方向:如果有高效的逆运动学求解方法,则可将HS-RRV与Bi-RRT算法相结合,在保证轨迹质量的同时提高算法的效率和规划精度。
4.3 仿真场景3此场景下,机械臂需要将2m
| $ \begin{align*} \mathit{\boldsymbol{q}}_{\text{init}} =[\pi /2, \pi /2, \pi /4, -\pi /2, -\pi /4, -\pi /2, \pi /2 ]^{\rm T} \end{align*} $ |
对应的初始末端位姿为
| $ \begin{align*} \mathit{\boldsymbol{x}}_{\rm e, \text{init}} =[-3.771, 0.710, -0.040, \pi /2, 0, -\pi /2 ]^{\rm T} \end{align*} $ |
杆件目标位姿为
| $ \begin{align*} \mathit{\boldsymbol{x}}_{\rm e, \text{goal}} =[3.700, 0.7101, 0.509, -\pi /2, 0, -\pi /2]^{\rm T} \end{align*} $ |
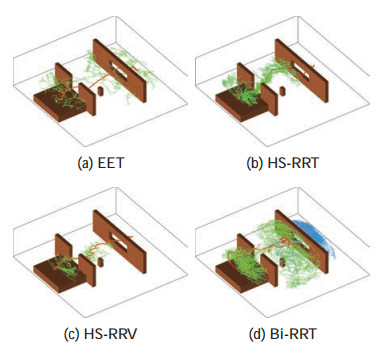
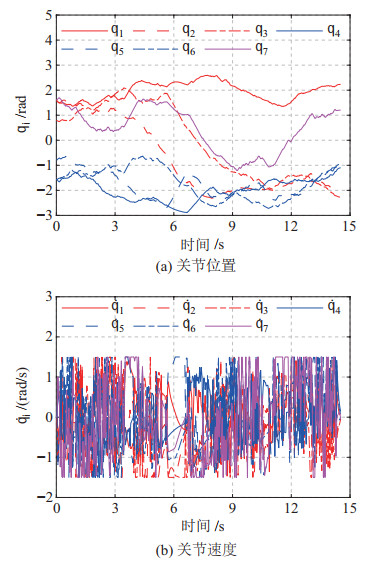
4种算法的单次规划结果如图 9所示,HS-RRV算法规划出的关节轨迹如图 10所示。此时,由于板件初始状态靠近障碍物,且窗口可行空间有限,EET算法很难成功。Bi-RRT算法虽然有较高的成功率,但是为了寻找穿越窗口的轨迹而耗费了大量时间。然而,同时搜索工作空间和构形空间的HS-RRT算法因为具有完备性,因而既保证了一定的成功率,又提高了规划效率。HS-RRV算法进一步提升了性能,如表 2所示,其成功率约是EET算法的5.3倍,HS-RRT算法的1.7倍,Bi-RRT算法的1.3倍;其规划效率分别是上述3种算法的2.7倍、1.6倍和2.5倍;其轨迹长度也是远小于EET和Bi-RRT算法,与HS-RRT算法相当。
|
图 9 场景3下使用不同规划器的规划结果 Fig.9 Planning results of different planners in scenario 3 |
|
图 10 场景3下HS-RRV算法规划所得关节轨迹 Fig.10 Joint trajectories planned with HS-RRV algorithm in scenario 3 |
此场景下,利用自由漂浮基座空间机械臂系统将2m
| $ \begin{align*} \mathit{\boldsymbol{q}}_{\text{init}} =[ \pi /6, \pi /3, 0, \pi /2, 0, -\pi /6, 0 ]^{\rm T} \end{align*} $ |
对应的初始末端位姿为
| $ \begin{align*} \mathit{\boldsymbol{x}}_{\rm e, \text{init}} =[ 2.658, 1.948, 1.249, -\pi /3, -\pi /2, -\pi /2 ]^{\rm T} \end{align*} $ |
杆件目标位姿为
| $ \begin{align*} \mathit{\boldsymbol{x}}_{\rm e, \text{goal}} &=[ 2.856, -0.562, 1.222, -\pi /2, \\ &\quad -\pi /12, -7\pi /12]^{\rm T} \end{align*} $ |
此时,规划不仅需要考虑系统运动学,还需要考虑其动力学特性。假设基座不受控且不考虑重力以及其他外力的影响,机械臂和基座之间存在动力学耦合,机械臂运动会对基座位姿产生干扰,同时基座位姿扰动又会影响机械臂运动(其动力学建模可参考文[8])。此场景下,基座位姿也作为子节点被添加到随机树中。值得关注的是,单一的工作空间中的采样可能会因机械臂与基座运动的相互干扰而使拓展陷入局部极值,导致拓展难以进行。但本文算法结合了工作空间-构形空间混合采样,使得当工作空间中的样本点难以被有效拓展时,算法尝试在整个构形空间随机采样,并根据度量选取关节构形距离最近且基座姿态相对于初始姿态扰动最小的节点作为最近节点进行拓展,选取度量如下:
| $ \begin{align} {\rm Dist} \left(\mathit{\boldsymbol{q}}_{i}, \mathit{\boldsymbol{\psi}}_{i}, \mathit{\boldsymbol{q}}_{\text{rand}}, \mathit{\boldsymbol{\psi}}_{\rm b, \text{init}}\right) = \left\| \mathit{\boldsymbol{q}}_{i} -\mathit{\boldsymbol{q}}_{\text{rand}} \right\|+\left\| \mathit{\boldsymbol{\psi}}_{i} -\mathit{\boldsymbol{\psi}}_{\rm b, \text{init}} \right\| \end{align} $ | (9) |
从而尽可能减小基座姿态扰动带来的不利影响。
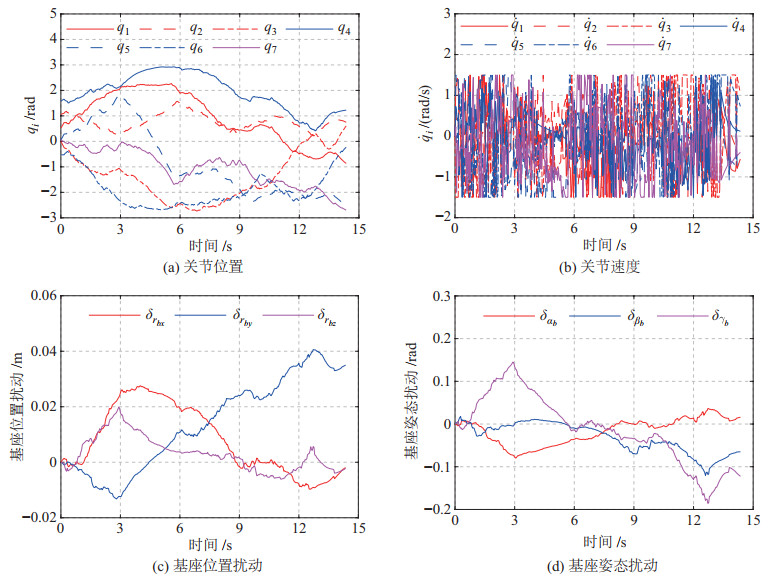
4种算法的单次规划结果如图 11所示。其中,HS-RRV算法规划所得关节轨迹以及机械臂运动导致的基座扰动如图 12所示。
|
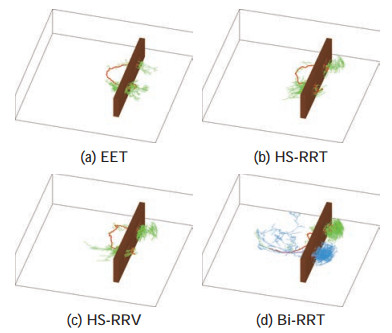
图 11 场景4下使用不同规划器的规划结果 Fig.11 Planning results of different planners in scenario 4 |
|
图 12 场景4下HS-RRV算法规划所得关节轨迹与相应的基座扰动 Fig.12 Joint trajectories planned with HS-RRV algorithm and the resulting base disturbances in scenario 4 |
如表 2所示,此场景下HS-RRV和HS-RRT算法两者性能相当,但HS-RRV算法在规划成功率、效率等方面略优。同时,HS-RRV算法相对于EET算法极大地提升了成功率(约是其2.4倍),但HS-RRV算法所需规划时间却不足EET算法的一半。此外,Bi-RRT算法虽然也有着较高的成功率,但是规划耗时约是HS-RRV算法的2倍。可见,HS-RRV算法在处理复杂非线性动力学系统的规划问题时依然有优异的表现,表明算法具有广泛的适用性。
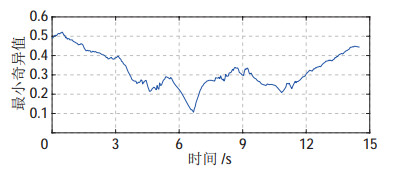
4.5 局部规划器性能分析正如3.2.2节中所提,当利用局部规划器在工作空间中拓展时,对于冗余机械臂,除了可以完成末端拓展这一主要任务外,还可以利用剩余自由度使机械臂关节向随机方向拓展,以尽可能避开运动学奇异构形,也能降低机械臂陷入几何结构局部极值的可能性。以场景3为例,与HS-RRV算法规划结果相对应的雅可比矩阵
|
图 13 场景3下HS-RRV规划结果对应J的最小奇异值变化 Fig.13 Changes of minimum singular value of J corresponding to the planning result of HS-RRV algorithm in scenario 3 |
为进一步凸显3.2.2节所提局部规划器的优势,还以4种场景下不包含关节随机拓展次要任务的HS-RRV算法(记作HS-RRV-1)作为对比,每个场景均运行了30次,统计结果如表 3所示。此时,HS-RRV-1算法需要经历更多随机采样和碰撞检测才能找到解,因此所需规划时间也更长,平均规划时间至少增加了10%,最多可达70%;相应地,规划成功率降低了至少10%。此外,虽然HS-RRV-1算法在工作空间拓展时由于没有次要任务的干扰,规划所得的关节轨迹长度更短,但为了绕开奇异点和局部极值,末端轨迹长度增加。
|
|
表 3 不包含随机拓展次要任务的HS-RRV算法的规划结果 Tab. 3 Planning results of HS-RRV algorithm without considering the secondary task of random extension |
另一方面,3.2.2节所提的局部规划器可以直接考虑机械臂关节位置、速度甚至加速度等运动学限制,并整合为统一的速度约束,使得规划出的参考速度在主动满足运动学限制的前提下尽可能减小与局部规划目标的误差。然而,传统算法通常没有直接考虑关节约束,而是先根据局部目标规划出参考速度,再对超出限制的参考速度进行饱和处理以满足约束,此时得到的运动速度可能会偏离期望拓展方向。此后,传统算法还需对积分得到的新关节构形进行筛选,舍去不满足关节位置限制的构形,但这将降低样本点的利用率。4种场景下未直接考虑关节约束的HS-RRV算法的规划结果如表 4所示,可见其运行效率、规划成功率相对于3.2.2节所提算法下降约10%。除此以外,传统局部规划器还难以考虑加速度限制以及其他不等式约束。
|
|
表 4 不直接考虑关节约束的HS-RRV算法的规划结果 Tab. 4 Planning results of HS-RRV algorithm without considering joint constraints directly |
综上,本文所提出的局部规划器,相对于不考虑随机拓展次要任务、不直接考虑关节限制的传统算法,运行效率、规划成功率更高,有更广泛的适用性。
5 结论(Conclusion)为应对利用空间机械臂进行在轨装配时因工作空间狭小、复杂而导致运动规划效率低下的问题,提出了HS-RRV规划算法。该算法结合了工作空间和构形空间混合采样的策略,采样权重随算法进程自主调节,既利用工作空间信息提高规划效率,又保证了算法的完备性,防止陷入局部极值。此外,在局部规划器设计中,充分利用了机械臂的冗余性,以同时完成多种不同优先级的任务;还考虑了机械臂的运动学与动力学约束,以提高所规划轨迹的可执行性。当算法随机拓展陷入复杂区域而难以推进时,利用桥测试和PCA方法对局部空间进行分析,以获取更加高效的拓展方向。仿真结果表明,HS-RRV算法相比其他测试算法在迭代次数、生成的节点数、规划效率以及规划成功率等方面均有明显优势,且对多种复杂系统与工作环境有广泛的适用性。未来,将考虑测量的不确定性、装配时的接触力约束等因素,对机械臂运动规划算法作进一步研究。
| [1] |
Rognant M, Cumer C, Biannic J M, et al. Autonomous assembly of large structures in space: A technology review[C]//8th European Conference for Aeronautics and Aerospace Science. 2019. DOI: 10.13009/EUCASS2019-685.
|
| [2] |
孟光, 韩亮亮, 张崇峰. 空间机器人研究进展及技术挑战[J]. 航空学报, 2021, 42(1): 8-32. Meng G, Han L L, Zhang C F. Research progress and technical challenges of space robot[J]. Acta Aeronautica et Astronautica Sinica, 2021, 42(1): 8-32. |
| [3] |
余敏, 罗建军, 王明明, 等. 一种改进RRT* 结合四次样条的协调路径规划方法[J]. 力学学报, 2020, 52(4): 1024-1034. Yu M, Luo J J, Wang M M, et al. Coordinated path planning by integrating improved RRT* and quartic spline[J]. Chinese Journal of Theoretical and Applied Mechanics, 2020, 52(4): 1024-1034. |
| [4] |
Misra G, Bai X. Task-constrained trajectory planning of free-floating space-robotic systems using convex optimization[J]. Journal of Guidance, Control, and Dynamics, 2017, 40(11): 2857-2870. DOI:10.2514/1.G002405 |
| [5] |
Khatib M, Al Khudir K, de Luca A. Task priority matrix at the acceleration level: Collision avoidance under relaxed constraints[J]. IEEE Robotics and Automation Letters, 2020, 5(3): 4970-4977. DOI:10.1109/LRA.2020.3004771 |
| [6] |
LaValle S M. Planning algorithms[M]. Cambridge, UK: Cambridge University Press, 2006.
|
| [7] |
李洋, 徐达. 基于引力自适应步长RRT的双臂机器人协同路径规划[J]. 机器人, 2020, 42(5): 606-616. Li Y, Xu D. Cooperative path planning of dual-arm robot based on attractive force self-adaptive step size RRT[J]. Robot, 2020, 42(5): 606-616. |
| [8] |
张红文, 朱战霞, 袁建平. 自由漂浮空间机器人无逆运动学基于采样的运动规划[J]. 西北工业大学学报, 2021, 39(5): 1005-1011. Zhang H W, Zhu Z X, Yuan J P. Non-inverse kinematics of free-floating space robot based on motion planning of sampling[J]. Journal of Northwestern Polytechnical University, 2021, 39(5): 1005-1011. DOI:10.3969/j.issn.1000-2758.2021.05.009 |
| [9] |
孙明镜, 曹其新, 黄修长, 等. 面向机械臂狭窄空间的快速稳定规划算法[J]. 机械设计与研究, 2019, 35(6): 67-71. Sun M J, Cao Q X, Huang X C, et al. A fast and stable planning algorithm for narrow space of manipulator[J]. Machine Design and Research, 2019, 35(6): 67-71. |
| [10] |
Cai P, Yue X K, Zhang H W. ADD-RRV for motion planning in complex environments[J]. Robotica, 2022, 40(1): 136-153. DOI:10.1017/S0263574721000436 |
| [11] |
Jaillet L, Yershova A, LaValle S M, et al. Adaptive tuning of the sampling domain for dynamic-domain RRTs[C]//IEEE/RSJ International Conference on Intelligent Robots and Systems. Piscataway, USA: IEEE, 2005: 2851-2856.
|
| [12] |
Lee J, Kwon O, Zhang L J, et al. A selective retraction-based RRT planner for various environments[J]. IEEE Transactions on Robotics, 2014, 30(4): 1002-1011. DOI:10.1109/TRO.2014.2309836 |
| [13] |
Tahirovic A, Ferizbegovic M. Rapidly-exploring random vines (RRV) for motion planning in configuration spaces with narrow passages[C]//IEEE International Conference on Robotics and Automation. Piscataway, USA: IEEE, 2018: 7055-7062.
|
| [14] |
Kuffner J J, LaValle S M. RRT-connect: An efficient approach to single-query path planning[C]//IEEE International Conference on Robotics and Automation. Piscataway, USA: IEEE, 2000: 995-1001.
|
| [15] |
Thakar S, Rajendran P, Kim H, et al. Accelerating bi-directional sampling-based search for motion planning of non-holonomic mobile manipulators[C]//IEEE/RSJ International Conference on Intelligent Robots and Systems. Piscataway, USA: IEEE, 2020: 6711-6717.
|
| [16] |
陈伟, 白克强, 李孚洋, 等. 渐进式约束扩展的机械臂运动规划算法[J]. 计算机应用研究, 2020, 37(9): 2754-2757, 2761. Chen W, Bai K Q, Li F Y, et al. Progressive constrained extended manipulator motion planning algorithm[J]. Application Research of Computers, 2020, 37(9): 2754-2757, 2761. |
| [17] |
Rickert M, Sieverling A, Brock O. Balancing exploration and exploitation in sampling-based motion planning[J]. IEEE Transactions on Robotics, 2014, 30(6): 1305-1317. DOI:10.1109/TRO.2014.2340191 |
| [18] |
Liu B, Scheurer C, Janschek K. Motion planning with Cartesian workspace information[J]. IFAC-PapersOnLine, 2020, 53(2): 9826-9833. |
| [19] |
Rajendran P, Thakar S, Bhatt P M, et al. Strategies for speeding up manipulator path planning to find high quality paths in cluttered environments[J]. Journal of Computing and Information Science in Engineering, 2021, 21(1). DOI:10.1115/1.4048619 |
| [20] |
Cai P, Yue X K, Wang M M, et al. Hierarchical motion planning at the acceleration level based on task priority matrix for space robot[J]. Nonlinear Dynamics, 2022, 107: 2309-2326. |
| [21] |
van den Bergen G. A fast and robust GJK implementation for collision detection of convex objects[J]. Journal of Graphics Tools, 1999, 4(2): 7-25. |
 2023, Vol. 45
2023, Vol. 45


