数码迷彩伪装是军事装备应对高空侦察的主要技术手段之一,通过在装备表面涂装数码迷彩涂层,有效提高其野外生存能力。目前数码迷彩涂装多采用人工喷涂,需要手动对军事装备进行遮蔽,效率低、涂装质量不稳定,无法在战时实现快速的迷彩换装。
喷涂机器人能够高度集成于智能生产线中,具有自动化程度高、喷涂效率高、涂装质量稳定、经济和环保等诸多优点。目前的机器人喷涂技术多为单色喷涂。为实现多种颜色、复杂数码迷彩图案的精细化喷涂,国内外学者针对机器人喷涂开展了大量的研究[1-5]。
不同作业场景下,喷距、喷幅和喷枪移动速度等喷涂工艺参数对机器人精细化喷涂影响较大。为实现融合喷涂工艺参数的机器人喷涂,首先需要建立喷枪的涂料沉积模型。根据雾化类型,现有的传统空气喷枪分为圆形和扇形喷枪。圆形空气喷枪的涂料沉积率可以近似为抛物线方程[6-7],以此为基础,国外学者结合待喷工件的CAD(计算机辅助设计)模型实现了自由曲面上的喷涂机器人自动轨迹规划[8]。国内学者根据射流连续性假设,在喷枪锥形空间分布的基础上提出了釉料涂层厚度分布曲线[9],为机器人喷涂离线示教系统的建立奠定了数学基础。以上研究对象均为圆形空气喷枪,针对扇形空气喷枪,西安理工大学的学者提出了漆膜厚度的椭圆双
涂料沉积模型和涂层分布函数揭示了喷涂工艺参数的数学表达,并为机器人喷涂路径规划提供了工艺输入。针对单一颜色的机器人喷涂路径生成方法,国内外学者开展了大量研究。国内学者融合喷涂工艺及工件表面参数,提出了一种基于工件CAD模型的工具路径规划通用框架,实现了机器人单色喷涂轨迹自动生成[12]。此外,有学者类比数控刀位轨迹,提出了基于速度优化的喷涂路径生成方法[13]。鉴于迷彩图案混有多种颜色,且不同色块之间相互交错,单色喷涂路径规划方法无法满足以上任务需求。为此,结合平面迷彩喷涂工艺特性,西北工业大学的学者设计了一种直角坐标机器人[14-15]。该设备采用多喷枪系统,基于待喷涂图案的分布特点,生成简单迷彩色块的喷枪运动轨迹,但仍需对边界圆弧过渡进行优化。近年来,有学者将图像处理[16]和智能算法[17]应用于机器人迷彩喷涂轨迹规划中,完成了融合迷彩图案与待喷工件特点的喷涂路径生成,但仍需进一步考虑油漆过喷和圆弧过渡的问题。
数码迷彩图案具有网格化和色域交叉的特点,且喷涂过程要求路径无重复、全覆盖,非常适合采用基于栅格的生物激励神经网络路径规划方法[18]进行喷涂路径规划。Yang在合作与竞争共存的分流反馈网络(shunting cooperative competitive feedback network)模型[19]基础上提出了生物激励神经网络(BINN)[20]用于解决动态环境下平面中机器人避障路径的生成问题,其改进方法实现了机器人全覆盖路径规划(CCPP)[21-22]。该算法适用于静态和动态变化的工作环境,且不会造成路径局部锁死。之后有学者基于启发式搜索算法,引入滚动窗口概念对BINN算法进行改进,在确保规划的路径安全可靠的同时,提高了规划效率[23]。以上方法虽然可实现机器人的全覆盖路径规划,但仍需进一步解决斜向路径造成的局部重复问题。
为解决传统空气喷枪圆弧过渡和过喷、数码迷彩喷涂路径难以规划的问题,本文对传统喷枪进行结构优化设计,并提出融合矩形喷枪喷涂工艺和改进生物激励神经网络的迷彩喷涂路径规划方法。首先,设计引流式梯形台喷嘴板,并将其装配于空气喷枪末端,同时基于圆形空气喷枪涂料沉积模型[6-7],进一步分析矩形喷枪的喷涂工艺特性。然后,采用Shi-Tomasi角点检测算法[24]提取待喷涂数码迷彩色块的顶点坐标,并将非喷涂区域设置为障碍物,建立迷彩图案的栅格地图。引入融合数码迷彩喷涂工艺的机器人移动规则,将传统BINN算法中神经元活性传播方向限定为互相正交的4个方向,缩小神经元动态活性域范围[21],同时采用分流方程[25]更新神经元活性值,降低了计算复杂度。最终,运用矩阵变换的方法,将2维路径映射至车辆模型表面,生成3维迷彩喷涂路径。所提数码迷彩喷涂路径生成方法的原理框架如图 1所示。
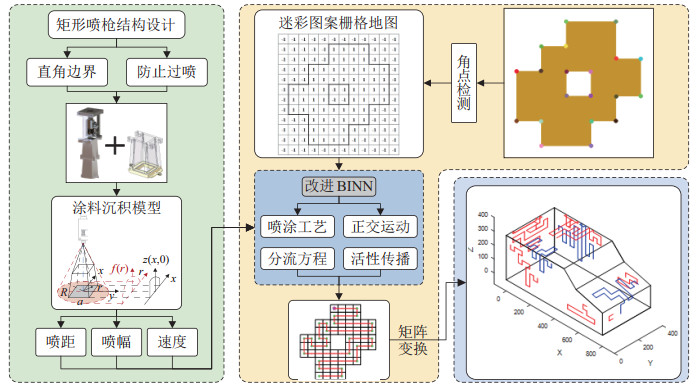
|
图 1 数码迷彩喷涂路径生成原理框架图 Fig.1 The framework of spraying path generation for digital camouflage |
传统空气喷枪喷幅多在100 mm以上,涂料得以充分雾化,因此能完成无需考虑工件边界影响的单色喷涂。当面对具有特定轮廓的多色喷涂工况时,需提前制作喷绘模板,或采用胶带遮蔽工件,按先后顺序完成多色图案喷涂。这种喷涂方式工序复杂、费时费力,且易造成涂料浪费。本文针对传统空气喷枪边缘混色和圆弧过渡的问题,设计一种具有直角边界和防过喷的矩形喷枪,并分析其涂料沉积模型。
2.1 矩形喷枪结构设计以传统空气喷枪为基础,设计矩形喷枪,如图 2所示。底部为引流式梯形台喷嘴板,通过C型连接件与机器人连接,中间安装空气喷枪。
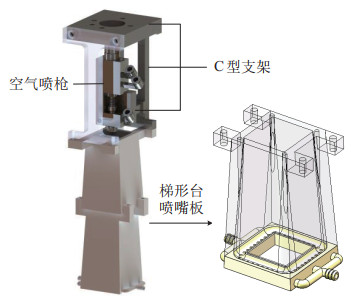
|
图 2 矩形喷枪 Fig.2 Rectangular gun |
梯形台喷嘴板内部中空,内腔侧壁用于限定涂料喷雾形状,其作用是将喷出的锥状漆雾限定为方形漆雾,因此在梯形台内部开有环形内孔,并通过直径为2 mm的槽孔与梯形台内侧壁连通,用于回收被限定的漆雾。如图 2所示,漆雾通过撞击侧壁汇流到底部槽孔,并通过负压泵回收至涂料搅拌器,便于重复利用。
根据GJB 7929标准[26],数码迷彩图案的基本单元边长应不大于50 mm。同时,为确保低空侦察时数码迷彩的伪装效果,根据以下公式[27-28]确定数码迷彩的基本单元尺寸:
| $ \begin{align} a\leqslant D\times \tan \partial \end{align} $ | (1) |
其中,
传统圆形空气喷枪的漆雾空间分布可以近似为锥状体[4, 6-9, 29],涂料以一定的扇角
| $ \begin{align} f(r)=C({R^{2}-r^{2}}), \quad 0\leqslant r\leqslant R \end{align} $ | (2) |
其中,
| $ \begin{align} Z(x, y)=C(R^{2}-x^{2}-y^{2}), \quad 0\leqslant x^{2}+y^{2}\leqslant R^{2} \end{align} $ | (3) |
锥状体喷炬在通过梯形台喷嘴板后,喷雾空间分布被重新限定,红色区域为圆形喷枪喷涂区域,灰色区域为矩形喷枪喷涂区域,如图 3所示。涂料由圆形喷枪喷出,经梯形台喷嘴板后,在平面上形成边长为
| $ \begin{align} Z({x, y})=C(R^{2}-x^{2}-y^{2}), \quad 0\leqslant x\leqslant \frac{a}{2}, \; \; 0\leqslant y\leqslant \frac{a}{2} \end{align} $ | (4) |
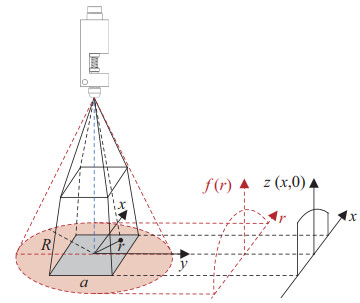
|
图 3 矩形喷枪涂料沉积模型 Fig.3 The paint deposition model of rectangular gun |
其中,
使用矩形喷枪开展迷彩喷涂作业时,喷枪沿正方形边线方向以速度
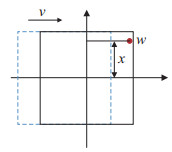
|
图 4 平面喷涂 Fig.4 Spraying on a plane |
| $ \begin{align} q_{0} =2\int_0^{t_{0}} z(x, y){\rm d}t, \quad 0\leqslant x\leqslant \frac{a}{2}, \; 0\leqslant y\leqslant \frac{a}{2} \end{align} $ | (5) |
其中,
| $ \begin{align} q_{0} =2\int_0^{ \frac{a}{2v}} C(R^{2}-x^{2}-\frac{a^{2}}{4}+avt-v^{2}t^{2}){\rm d}t \end{align} $ | (6) |
进一步求解式(6) 可得:
| $ \begin{align} q_{0} =\frac{Ca({12R^{2}-12x^{2}-a^{2}})}{12v} \end{align} $ | (7) |
分析式(7) 可知,涂层累积厚度
为了验证矩形喷枪涂料沉积模型的正确性,搭建实验平台进行喷漆实验,平台由矩形喷枪、机械臂和供漆系统组成,如图 5所示。

|
图 5 喷漆系统 Fig.5 The spray painting system |
首先进行圆形喷枪静态喷涂实验(实验1)。将杜尔EcoGun Mini RS(0.8 mm)圆形喷枪固定于机械臂末端,移动机器人令喷枪与待喷平面工件(厚度为1.5 mm的钢板)垂直且相距200 mm,喷枪开关由电磁阀控制。设定喷漆工艺参数,雾化压力为0.2 MPa,供料压力为0.15 MPa,通过喷枪顶部旋钮控制流量,确保充分雾化、无液滴,静态喷涂时间
|
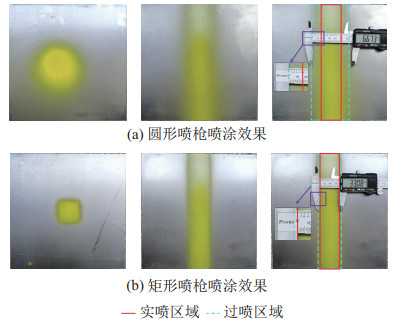
图 6 喷涂效果对比 Fig.6 Comparison of the spraying effect |
|
|
表 1 有效喷幅D(节选) Tab. 1 Effective spraying range D |
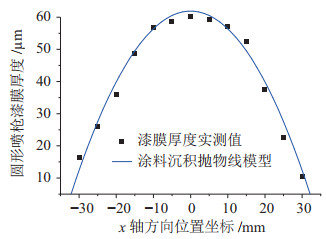
采用德力西DTG D1涂层测厚仪测定漆膜厚度,以标记点为原点,测量与原点距离为
|
|
表 2 圆形喷枪静态喷涂漆膜厚度(节选) Tab. 2 The paint film thickness under static spraying by a circular gun |
|
图 7 圆形喷枪实测漆膜厚度与仿真厚度对比结果 Fig.7 Comparison between the measured and simulated paint film thickness obtained with a circular spray gun |
然后,在实验1条件下进行矩形喷枪匀速喷涂实验(实验2)。将梯形台喷嘴板装于圆形喷枪正下方,喷涂工艺参数同实验1。喷枪沿水平方向以0.1 m/s的速度匀速直线运动,水平扫过平面工件(厚度为1.5 mm的钢板),往复完成8次喷涂后,标记喷绘图案中心点为原点,喷枪移动中心线为水平轴线,与水平轴线垂直且通过原点的线为垂直轴线。分析图 6(b)可知,优化后的矩形喷枪虚边约为1.5 mm,有效限制了过喷现象。采用游标卡尺测量喷幅宽度,记为
|
|
表 3 矩形喷枪匀速喷涂漆膜厚度(节选) Tab. 3 The paint film thickness under uniform spraying by a rectangular gun |
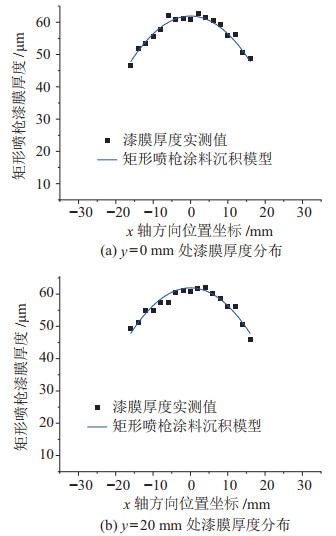
将
|
图 8 矩形喷枪实测漆膜厚度与仿真厚度对比结果 Fig.8 Comparison between the measured and simulated paint film thickness obtained with a rectangular gun |
对比分析实验1和2可知,圆形喷枪所喷绘的图案为平均喷幅
结合矩形喷枪的喷涂工艺特性,提出一种基于改进BINN的数码迷彩图案喷涂路径规划方法。该方法采用图像处理方法建立数码迷彩图案喷涂环境,以迷彩喷涂工艺为输入,结合改进的BINN规划算法和矩阵变换,实现了3维空间的迷彩喷涂路径规划。具体实施步骤归纳如下:
1) 提取车辆表面的几何特征,建立车辆简化3维模型;
2) 根据GJB 7929标准要求,设计包含中绿、深绿和褐土3种颜色的林地型数码迷彩;
3) 运用角点检测算法提取数码迷彩色块的角点坐标;
4) 建立数码迷彩图案的栅格环境地图;
5) 采用改进的生物激励神经网络方法对平面迷彩色块进行全覆盖路径规划;
6) 通过矩阵变换将规划好的平面路径转换成空间路径。
3.1 迷彩图像预处理由于实验室条件限制,不便于开展真实车辆的迷彩喷涂实验,为方便后续算法的验证,以某车展公开展出的装甲车为例,提取车辆表面的主要几何特征,包含平面、立面、斜面、垂直相交面和倾斜相交面等几何元素,如图 9所示。

|
图 9 某装甲车主要几何特征 Fig.9 Main geometric features of an armoured car |
以提取的5种几何特征为基础,建立如图 10所示的车辆简化3维模型,确保模型具备装甲车的主要表面几何特征。将车辆的简化3维模型在俯视、左视、右视、前视和后视5个方向上进行平面展开。根据GJB 7929标准[26],在平面展开图上设计林地型数码迷彩图案,整体包含中绿、深绿和褐土3种颜色,数码迷彩斑点包含交错、并置、外围和内包4种位置关系,如图 10所示。
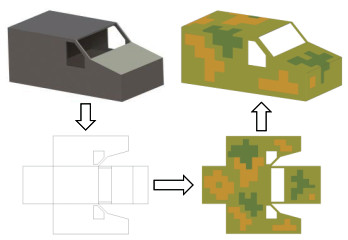
|
图 10 车辆简化3维模型与林地型数码迷彩图案 Fig.10 The simplified 3D model of vehicle and the woodland digital camouflage pattern |
迷彩图案以32个像素为一个单元,对应实际喷涂环境的32 mm。采用Shi-Tomasi角点检测算法[22]确定迷彩图案的强角点,并提取像素坐标。其原理是建立图像中

|
图 11 角点检测输出结果 Fig.11 Results of corner detection |
在前人研究基础上,融合数码迷彩喷涂工艺,限定机器人运动方向为正交的4个方向,缩小了神经元动态活性域范围,实现了数码迷彩图案的无重复全覆盖路径规划。
3.2.1 迷彩图案栅格环境建模以矩形喷枪边长
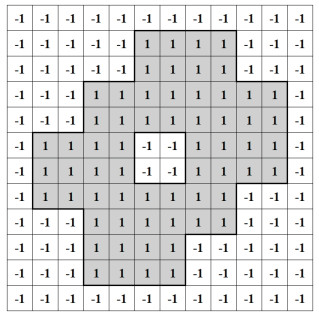
|
图 12 数码迷彩色块栅格地图 Fig.12 Grid map of the digital camouflage block |
所建数码迷彩图案的栅格地图中,每个栅格代表一个神经元,根据工作环境设置神经元的活性值,且每个神经元与相邻的神经元之间产生关联,依次构成网状的拓扑状态空间。
3.2.2 融合迷彩喷涂工艺的算法原理与改进改进BINN全覆盖路径规划算法的基本思想是:用神经网络拓扑状态空间表示机器人工作环境,每个神经元的动态神经活性值表示其动态环境的变化;根据工作要求定义工作环境初始活性值,并通过实时更新外部激励输入和神经元活性值,确保未工作区域和障碍物的神经元活性值分别保持在峰值和谷值;通过全局峰值吸引和局部障碍物峰谷排斥作用引导机器人运动,最终遍历所有工作区域内的神经元。
(1) 喷涂环境的神经元活性值更新
初始化神经元活性值均为0,每一个栅格点的神经元活性值的变化可由式(8) 决定,即分流方程(shunting equation):
| $ \begin{align} \frac{{\rm d}x_{i, j}} {{\rm d}t}=\, & -Ax_{i, j} \!+\!(B\!-\!x_{i, j}) \left( [I_{i, j} ]^{+}+\sum _{n=1}^k {W_{n} [x_{i_{n}, j_{n}}]^{+}} \right) - \\ & (D+x_{i, j})[I_{i, j}]^{-} \end{align} $ | (8) |
式中:
| $ \begin{align} I_{i, j} =\begin{cases} E, & \text{待喷涂区域} \\ -E, & \text{非喷涂区域} \\ 0, & \text{已喷涂区域} \end{cases} \end{align} $ | (9) |
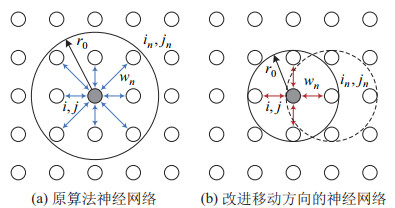
|
图 13 基于中央神经元(i, j) 的带约束神经网络结构 Fig.13 Architecture of the constrained neural network based on the central neuron (i, j) |
式中:
(2) 神经元活性判断域的修正策略
神经元之间仅在较小区域
| $ \begin{align} f(a)= \begin{cases} \dfrac{u} {a}, & 0<a<r_{0} \\ 0, & a\geqslant r_{0} \end{cases} \end{align} $ | (10) |
式中:
数码迷彩图案喷涂过程中,若喷枪斜向移动,则在转角喷涂时会出现斜向图案,见图 14中区域1,且斜向喷涂过的区域会出现局部厚度突增的现象,见图 14中深色区域2。因此,为满足数码迷彩喷涂工艺需求,限定矩形喷枪仅在横向和纵向移动;同时,缩小神经元动态活性判断域
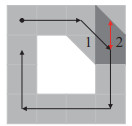
|
图 14 斜向喷涂 Fig.14 Oblique spraying |
BINN网络中的任意一个神经元均与相邻神经元产生侧向连接,这种连接关系在神经网络状态空间中组成一个子空间,被称为
| $ \begin{align} p_{n} \Leftarrow x_{p_{n}} =\max \{{x_{n} +cy_{n}, \; n=1, 2, \cdots, k} \} \end{align} $ | (11) |
式中,
| $ \begin{align} \Delta \theta_{n} & =| {\theta_{n} -\theta_{i, j}} | \\ & = \left| \arctan 2\frac{y_{p_{n}} -y_{p_{i, j}}} {x_{p_{n}} -x_{p_{i, j}}} -\arctan 2\frac{y_{p_{i, j}} -y_{p_{p}}} {x_{p_{i, j}} -x_{p_{p}}} \right| \end{align} $ | (12) |
(3) 路径生成步骤与算法流程图
算法流程如图 15所示,具体步骤为:读取数码迷彩图案的拐点坐标,建立栅格环境地图;初始化后,将待喷涂区域目标点的外部输入置为
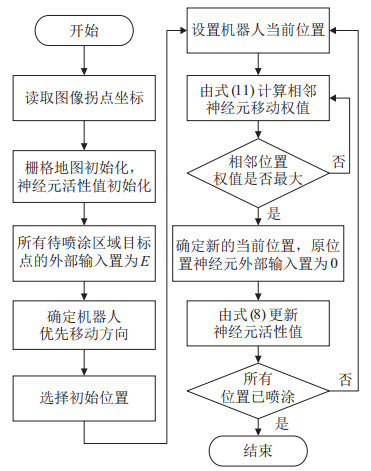
|
图 15 基于改进BINN的数码迷彩喷涂路径规划流程 Fig.15 Flowchart of the spraying path planning for digital camouflage pattern based on the improved BINN |
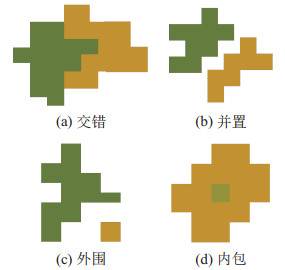
如3.1节所述,GJB 7929标准[26]规定,迷彩斑点包含交错、并置、外围和内包4种位置关系,如图 16所示。本文在小车简化模型的平面展开图上绘制如图 10所示的迷彩图案。
|
图 16 数码迷彩斑点位置关系 Fig.16 Position relationship of the digital camouflage spots |
由于较多的转折会导致机器人频繁加速和减速,造成能耗增加,并且重复路径会造成漆膜厚度不均匀。因此,面向机器人迷彩喷涂的路径规划要求尽量降低路径转折,减少重复路径,且完全遍历待喷涂区域。为满足以上要求,本文融合数码迷彩喷涂工艺,对传统BINN算法进行改进,并在Matlab 2018b环境下对迷彩色块进行全覆盖的喷枪喷涂路径规划,与BINN算法进行对比分析,验证所述改进算法的有效性。
结合喷涂工艺的特殊性,路径起始点必须为图案的边界位置,并且尽量满足由上到下的整体路线。因此,根据不同的图案,手动确定起始栅格。以带内部障碍的内包型迷彩图案为例,建立如图 12所示的栅格地图,工作环境由
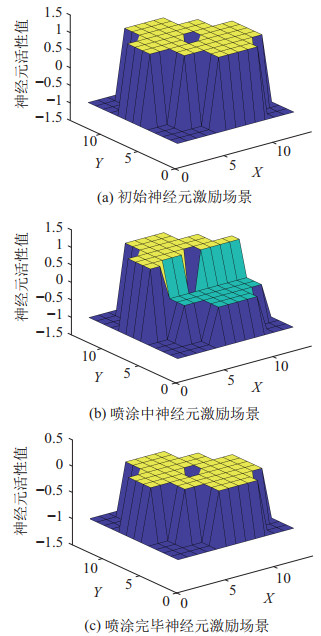
|
图 17 BINN激励场景图 Fig.17 Activity landscape of the biologically inspired neural network |
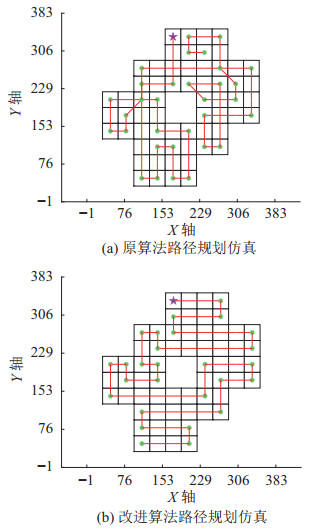
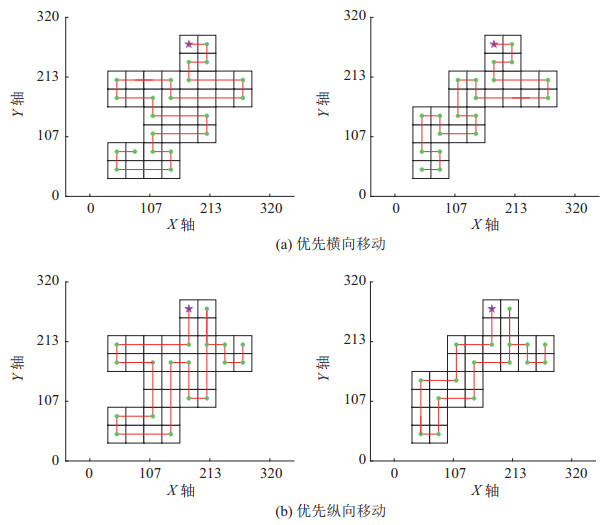
仿真1:设置改进的BINN环境模型的参数,
|
图 18 内包型迷彩图案路径规划 Fig.18 Path planning of the built-in type camouflage pattern |
图 18中红色星号表示起始位置,绿色圆点表示路径转折点,红线表示所规划的路径。图 18中算法所规划的路径均能满足全覆盖的要求。但是图 18(a)中路径包含斜向路径,且有多处重复,会造成实际喷涂中涂层厚度的突变和拐角处过喷问题。
表 4为2种方法的运行结果对比,分别从路径长度、转折次数、重复率、覆盖率和运行时长5个方面进行比较。选定合适的起点时,2种方法均能实现全覆盖路径规划,但是融合喷涂工艺的改进BINN算法降低了路径总长度和转折次数,且效率提升了16.4%,同时避免了不必要的重复路径,确保了涂层厚度的均匀性。
|
|
表 4 相同起点和工作环境下2种方法性能对比 Tab. 4 Performances of the two methods under the same starting point and working environment |
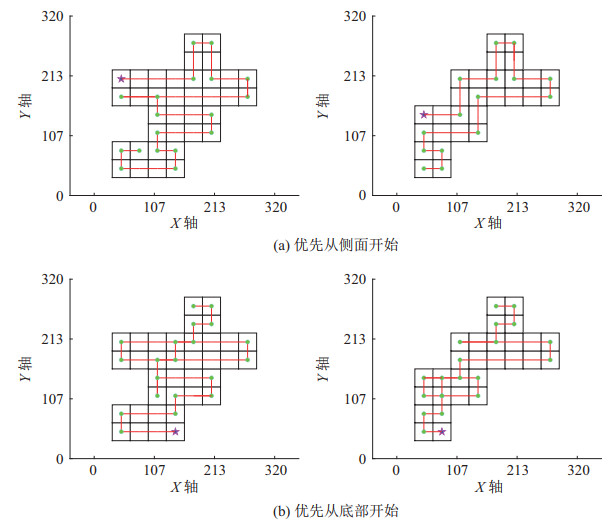
仿真2:保持环境参数与实验1相同,分别选择不同边界位置为路径起点进行路径规划。由于初始工作环境给定了待喷涂区域的外部激励,除了障碍物栅格的活性值处于波谷外,所有待喷涂栅格具有相同的活性值且均处于波峰,因此机器人初始运动方向可以为纵向也可以为横向。本文遵循一般的喷涂顺序,规定机器人的初始运动方向为横向。以内部带障碍的内包型迷彩图案为例,路径规划仿真结果如图 19所示。
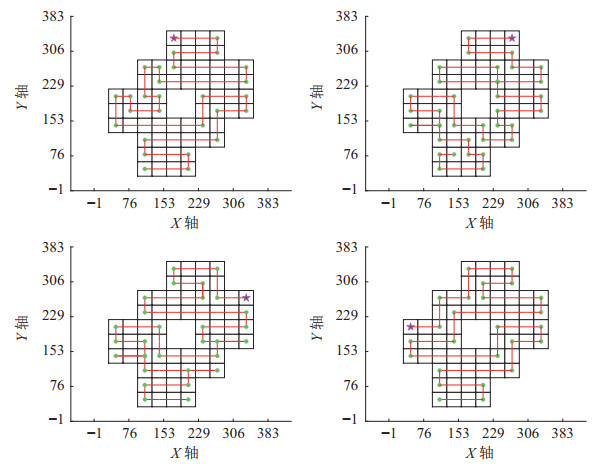
|
图 19 不同初始位置的路径规划 Fig.19 Path planning in different initial positions |
分析图 19结果可知,采用本文算法进行路径规划时,选择不同的初始位置虽然都能完成全覆盖路径规划,但是会造成不同程度的重复和路径长度、转折点的增加。因此,在整体自上而下和横向喷涂的前提下,需选择合适的初始位置,以确保无重复路径出现。
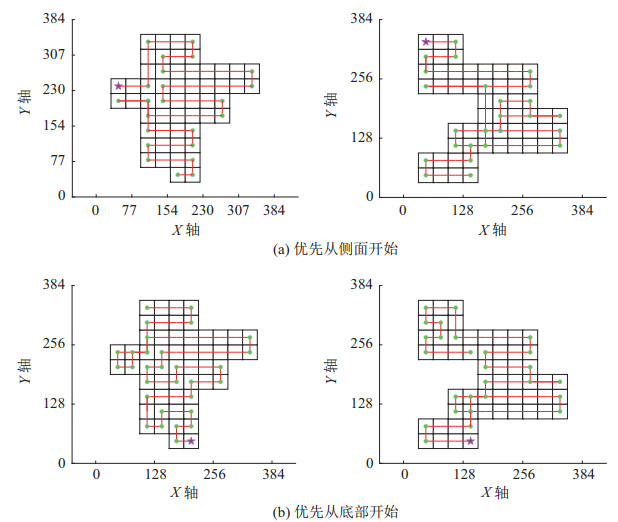
仿真3:保持环境参数与实验1、实验2相同,分别对图 16所示的交错、并置和外围3种位置关系的迷彩图案进行路径规划。规划时分别选择不同的移动方向和不同的初始位置。路径规划仿真结果如图 20~25所示。
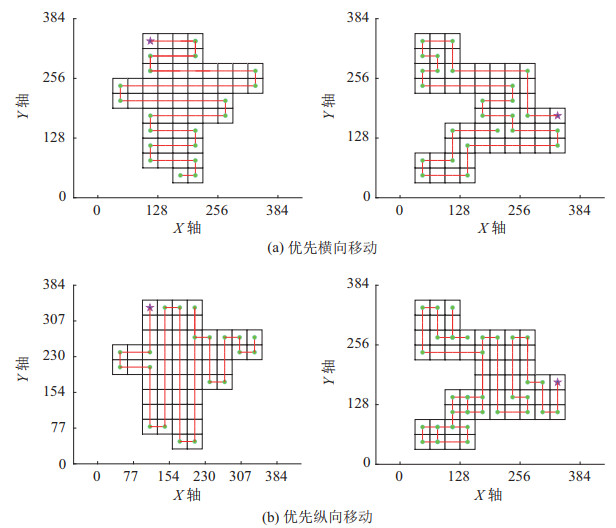
|
图 20 交错位置图案的路径规划(不同移动方向) Fig.20 Path planning for staggered patterns (in different movement directions) |
|
图 21 交错位置图案的路径规划(不同初始位置) Fig.21 Path planning for staggered patterns (in different initial positions) |
|
图 22 并置位置图案的路径规划(不同移动方向) Fig.22 Path planning for parallel patterns (in different movement directions) |
|
图 23 并置位置图案的路径规划(不同初始位置) Fig.23 Path planning for parallel patterns (in different initial positions) |
|
图 24 外围位置图案的路径规划(不同移动方向) Fig.24 Path planning for peripheral patterns (in different movement directions) |
|
图 25 外围位置图案的路径规划(不同初始位置) Fig.25 Path planning for peripheral patterns (in different initial positions) |
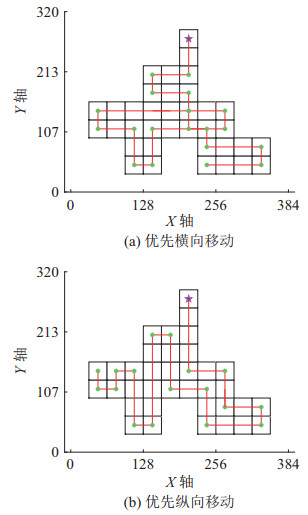
分析图 20和21交错位置图案的路径规划仿真图可知,横向喷涂的方式能够生成无重复的全覆盖路径,而纵向喷涂的方式会造成路径的重复和拐点的增加。不同的初始位置也会产生不同的仿真结果,从其余侧面和从底面开始喷涂,均会产生重复路径。结合由上到下、由左到右的喷涂原则,对于交错位置图案,选择图 20(a)所示的路径为最终的喷涂路径。
与交错位置图案的情形类似,分析图 22和23可知,横向喷涂的方式能够生成无重复的全覆盖路径,而纵向喷涂会产生重复路径。优先从侧面和从底面开始喷涂,均会产生重复路径。结合由上到下、由左到右的喷涂原则,对于并置位置图案,选择图 22(a)所示的路径为最终的喷涂路径。
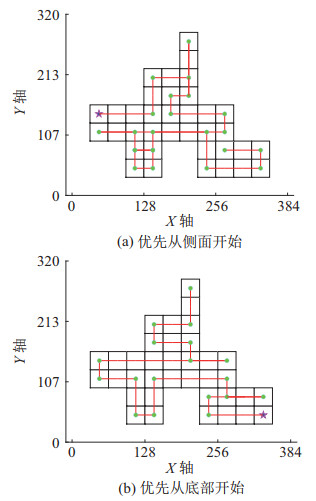
不同于交错和并置位置,外围位置关系的迷彩图案存在一个单向喷涂的路线,因此该路线处的栅格要么作为起始位置,要么作为终点位置。对于这一特殊图案,规定初始位置位于此处栅格,以免造成不必要的路径重复。分析图 24和25的仿真结果可知,纵向喷涂的方式能够生成无重复的全覆盖路径。优先从侧面和从底面开始喷涂,均会产生重复路径。对于外围位置图案,选择图 24(b)所示的路径为最终的喷涂路径。
通过仿真结果可知,本文方法在选择合适的初始位置和喷涂方向的前提下,能够实现迷彩图案的全覆盖无重复路径规划。在相同的初始条件和工作环境下,相较于文[21]方法,降低了路径长度和转折次数,效率提高了16.4%。
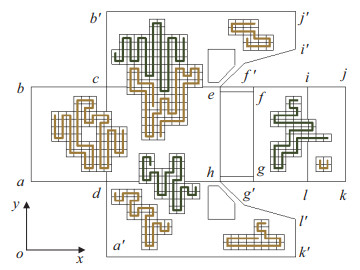
3.3 空间路径的矩阵变换由3.2节算法生成迷彩图案喷涂路径,见图 26。参考机器人运动学中的刚体位姿变换方法[30],运用矩阵变换实现平面路径向3维空间的转换。
|
图 26 迷彩图案喷涂路径平面展开图 Fig.26 Spraying path of camouflage pattern on the plane |
笛卡儿空间坐标系中点的位置向量可表示为
| $ \begin{align} {\mathit{\boldsymbol{P}}}'=&{R\mathit{\boldsymbol{}}}_{z, \phi} {R\mathit{\boldsymbol{}}}_{y, \theta} {R\mathit{\boldsymbol{}}}_{x, \varphi} {\mathit{\boldsymbol{P}}}+{\mathit{\boldsymbol{P}}}_{\Delta} \\ =&\begin{pmatrix} {c_{\phi}} & {-s_{\phi}} & 0 \\ {s_{\phi}} & {c_{\phi}} & 0 \\ 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} {c_{\theta}} & 0 & {s_{\theta}} \\ 0 & 1 & 0 \\ {-s_{\theta}} & 0 & {c_{\theta}} \end{pmatrix}\times\\ & \begin{pmatrix} 1 & 0 & 0 \\ 0 & {c_{\varphi}} & {-s_{\varphi}} \\ 0 & {s_{\varphi}} & {c_{\varphi}} \end{pmatrix}\begin{pmatrix} x \\ y \\ z \end{pmatrix}+\begin{pmatrix} {x_{\Delta}} \\ {y_{\Delta}} \\ {z_{\Delta}} \end{pmatrix} \\ =&\begin{pmatrix} {c_{\phi} c_{\theta}} & {-s_{\phi} c_{\varphi} +c_{\phi} s_{\theta} s_{\varphi}} & {s_{\phi} s_{\varphi} +c_{\phi} s_{\theta} c_{\varphi}} \\ {s_{\phi} c_{\theta}} & {c_{\phi} c_{\varphi} +s_{\phi} s_{\theta} s_{\varphi}} & {-c_{\phi} s_{\varphi} +s_{\phi} s_{\theta} c_{\varphi}} \\ {-s_{\theta}} & {c_{\theta} s_{\varphi}} & {c_{\theta} c_{\varphi}} \end{pmatrix}\times\\ &\begin{pmatrix} x \\[-1pt] y \\[-1pt] z \end{pmatrix} +\begin{pmatrix} {x_{\Delta}} \\[-1pt] {y_{\Delta}} \\[-1pt] {z_{\Delta}} \end{pmatrix} \end{align} $ | (13) |
式中,
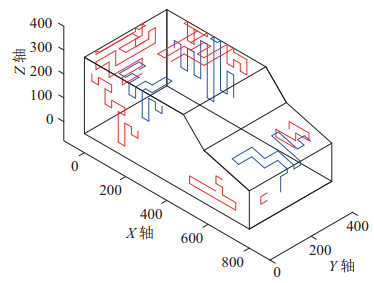
图 26平面展开图中的2维路径也可经式(13) 处理得到3维路径。具体计算过程如下:面
|
图 27 迷彩图案3维喷涂路径图 Fig.27 3D spraying path of camouflage pattern |
为进一步验证矩形喷枪的喷涂性能与数码迷彩图案全覆盖路径规划方法的有效性,搭建如图 28所示的由喷涂机器人和供漆系统组成的喷涂实验平台,进行迷彩喷漆实验。

|
图 28 迷彩喷涂实验平台 Fig.28 Experimental platform for camouflage spray painting |
供漆系统具备两色一清洗的功能,即不停机工况下实现两种颜色的更换,如图 29所示。整个供漆系统通过压缩空气提供动力,隔膜泵将不同涂料桶中的液体泵入换色阀。机器人控制柜控制电磁阀的通断实现2种颜色的切换和喷枪的开关操作。矩形喷枪固定于喷涂机器人末端法兰,连接供漆系统,设置与2.3节实验相同的喷涂工艺参数。使用KAIRO语言将规划好的迷彩喷涂路径点编写成机器人运动程序。
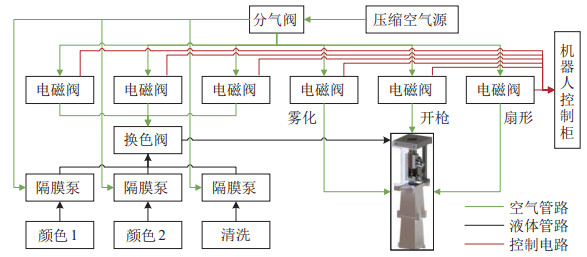
|
图 29 两色一清洗供漆系统 Fig.29 The paint-supply system with two kinds of colours and a set of cleaning lines |
1) 迷彩喷涂工艺流程
由于喷涂机器人工作范围有限,因此本实验仅对靠近机器人的侧面、顶面、前面和后面进行喷涂。具体喷涂工艺流程如下:
(1) 工件预处理:打磨工件表面,去除浮锈;采用压缩空气吹扫工件表面。
(2) 喷涂底色:按照2:1:1的比例将油漆、稀释剂和固化剂混合搅拌均匀;使用圆形空气喷枪按照预先规划好的路径进行喷涂,对工件整体喷涂中绿色底漆。
(3) 换色:执行自动换色程序,将供漆系统中的中绿色油漆替换为褐土色油漆。
(4) 喷涂褐土色迷彩斑点:执行褐土色迷彩图案喷涂程序,使用矩形喷枪喷涂褐土色迷彩色块。
(5) 换色:完成褐土色迷彩图案喷涂后,执行自动换色程序,将供漆系统中的褐土色油漆替换为深绿色油漆。
(6) 喷涂深绿色迷彩斑点:执行深绿色迷彩图案喷涂程序,使用矩形喷枪喷涂深绿色迷彩色块。
(7) 清洗:完成所有数码迷彩图案的喷涂工作后,执行自动清洗程序,将供漆系统中的油漆清洗、吹扫干净。
以上步骤中,除了预处理和调漆工作需要人工完成,第(2)~(7) 步均由机器人迷彩喷涂系统自动完成。
2) 拐角处喷涂轨迹的处理
在喷涂迷彩色块拐角处时,机器人末端运动方向会发生90°的偏转,如图 30所示。因此,机器人在拐点附近的运动轨迹是从匀速运动状态减速,至拐点处速度降为0;转变运动方向后,加速运动至匀速状态。匀速运动可以保证漆膜厚度均匀,减速—静止—加速这一运动过程会造成漆膜变厚。
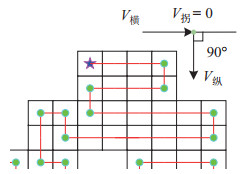
|
图 30 拐点处运动变化 Fig.30 Variation of motion at the inflection point |
为保证涂层厚度的均一性,在喷涂实验中对拐点附近的运动轨迹作如下处理:如图 31所示,机器人在
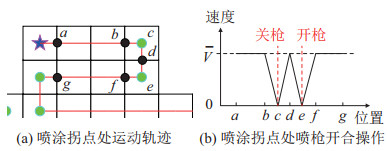
|
图 31 拐点附近的速度变化与开关喷枪操作 Fig.31 The velocity curve and the switch of the spray gun near the inflection point |
3) 迷彩喷涂实验结果与分析
完成上述迷彩喷涂实验后,等待油漆完全固化。实际喷涂效果和设计的迷彩图案对比如图 32所示。效果图中产生的色差是由于现场选用的喷漆颜色和实际调漆造成的,不影响实验结果分析。分析图 32可知,实际迷彩喷涂的图案与设计的迷彩图案保持一致,整体涂装色彩均匀,边界处无明显过喷现象,且拐角处无明显圆弧过渡。

|
图 32 实际喷涂效果对比图 Fig.32 Comparison of the actual spraying effect |
如图 33所示,测量并置型图案中褐土色的迷彩斑点,可以看到,测量得到的实际喷涂宽度为130 mm,设计的迷彩图案宽度为128 mm,误差为2 mm,满足国标要求的误差间隙不大于5 mm。

|
图 33 迷彩图案宽度对比图 Fig.33 Width comparison of camouflage pattern |
使用本节第2) 部分介绍的拐点处理方式进行喷涂,能够尽量降低拐角区域漆膜厚度的突变,但是匀速运动状态和减速运动状态所产生的漆膜厚度会有不同。因此,为了验证该喷涂方法产生的漆膜厚度的均匀性,使用德力西DTG D1涂层测厚仪对图 34所示2种迷彩图案的

|
图 34 漆膜厚度测定区域示意图 Fig.34 The measurement area of the thickness of the paint film |
图 34(a)中
|
|
表 5 a'b'c'd'区域测点厚度值q0(单位:µm。节选) Tab. 5 Thickness value q0 at the measurement points in area a'b'c'd' (unit: µm) |
由图 31(a)可知,整个喷涂阶段只进行了一次加速和一次减速。分析表 5实测漆膜厚度值可知:在加速和减速阶段,油漆整体厚度相对匀速运动阶段会有所增加,最大厚度值为123.5 µm;边界位置的油漆最薄,最小厚度值为87.5 µm;匀速运动阶段,漆膜厚度最均匀,靠近运动轴心处较厚,远离运动轴心处变薄。针对加速和减速阶段的开关枪处理,保证了这2个阶段只完成单次喷涂,有效抑制变速运动阶段漆膜厚度的增大,整体漆膜厚度较为均匀。
图 34(b)中
|
|
表 6 d'f'g'h区域测点厚度值q0(单位:µm。节选) Tab. 6 Thickness value q0 at the measurement points in area d'f'g'h (unit: µm) |
由图 22(a)可知,整个喷涂过程包含1个匀速运动阶段、3个减速运动阶段和2个加速运动阶段。对于频繁的加减速喷涂,分析表 6实测漆膜厚度值可知:在加速和减速阶段,油漆整体厚度同样会有所增加,最大厚度值为123.1 µm;边界位置的漆膜厚度较薄,最小厚度值为88.3 µm;整体呈现靠近运动轴心较厚、远离运动轴心变薄的厚度分布状态。针对频繁加减速的喷涂区域,开关枪的作用尤为突出,
综上,工件表面迷彩图案的漆膜厚度较为均匀,针对拐角喷涂做的处理有效抑制了加减速运动造成的油漆厚度突变。实验证明,本文方法能够实现工件表面数码迷彩图案的自动喷涂,迷彩斑点边界清晰,涂层厚度较为均匀,能够满足迷彩涂装作业的需求。
5 结论(Conclusion)对喷涂机器人末端喷涂机构进行结构优化,结合数码迷彩色块基本单元的尺寸约束,设计了一种用于数码迷彩涂装作业的矩形喷枪。该喷枪能够喷出方形漆雾,并对过量油漆进行回收利用。然后,在抛物线模型基础上,深入分析了矩形喷枪的涂料沉积模型。矩形喷枪的静态和动态喷涂性能实验结果表明,所建立的涂料沉积模型符合实际喷涂情况,优化后的矩形喷枪漆膜厚度范围在45~63 µm之间,具有较好的涂层均一性,并且过喷区域小于1.5 mm,有效解决了机器人喷涂过程中边界混色和圆弧过渡的问题。
针对喷涂机器人的喷枪路径规划中,斜向路径和局部重复路径易造成喷涂图案异常和漆膜厚度突变的问题,提出了融合矩形喷枪喷涂工艺的改进BINN全覆盖路径规划方法。所提方法缩小了神经元动态活性判断域范围,将机器人移动方向限定为正交的4个方向。然后,以角点检测算法提取的迷彩图像坐标为输入建立栅格环境地图,完成路径规划任务。最后,运用矩阵变换实现平面路径向空间路径的映射。分析内包型迷彩图案的路径规划仿真及数码迷彩喷涂机器人喷涂实验可知,所提方法能够完成迷彩图案的无重复全覆盖路径规划,路径生成效率提高了16.4%,降低了路径长度和拐点数量,实现了3维数码迷彩图案的精细化喷涂。该方法可以进一步拓展应用到机器人涂胶和喷釉等行业。
| [1] |
Liu Z L, Wu J, Wang D. An engineering-oriented motion accuracy fluctuation suppression method of a hybrid spray-painting robot considering dynamics[J]. Mechanism and Machine Theory, 2019, 131: 62-74. DOI:10.1016/j.mechmachtheory.2018.09.015 |
| [2] |
Ge J H, Li J X, Peng Y P, et al. Online 3-D modeling of complex workpieces for the robotic spray painting with low-cost RGB-D cameras[J]. IEEE Transactions on Instrumentation and Measurement, 2021, 70. DOI:10.1109/TIM.2021.3083425 |
| [3] |
华霄桐, 王国磊, 张思敏, 等. 用于复杂管道内表面喷涂的冗余机器人轨迹避障规划[J]. 机器人, 2019, 41(5): 690-696. Hua X T, Wang G L, Zhang S M, et al. Trajectory planning of redundant robot for painting inner surface of complex duct considering obstacle avoidance[J]. Robot, 2019, 41(5): 690-696. |
| [4] |
Song Y Y, Wu J, Liu Z L, et al. Similitude analysis method of the dynamics of a hybrid spray-painting robot considering electro-mechanical coupling effect[J]. IEEE/ASME Transactions on Mechatronics, 2021, 26(6): 2986-2997. DOI:10.1109/TMECH.2021.3049388 |
| [5] |
潘敬锋, 訾斌, 王正雨, 等. 基于试验与仿真联合分析的喷涂机器人轨迹精度可靠性研究[J]. 机械工程学报, 2020, 56(19): 210-220. Pan J F, Zi B, Wang Z Y, et al. Research on reliability of spray robot trajectory accuracy based on conjoint analysis of experiment and simulation[J]. Journal of Mechanical Engineering, 2020, 56(19): 210-220. |
| [6] |
Andulkar M V, Chiddarwar S S. Incremental approach for trajectory generation of spray painting robot[J]. Industrial Robot, 2015, 42(3): 228-241. DOI:10.1108/IR-10-2014-0405 |
| [7] |
Zeng Y, Yu Y Q, Zhao X Y, et al. Trajectory planning of spray gun with variable posture for irregular plane based on boundary constraint[J]. IEEE Access, 2021, 9: 52902-52912. DOI:10.1109/ACCESS.2021.3070566 |
| [8] |
Andulkar M V, Chiddarwar S S, Marathe A S. Novel integrated offline trajectory generation approach for robot assisted spray painting operation[J]. Journal of Manufacturing Systems, 2015, 37(1): 201-216. |
| [9] |
冯川, 孙增圻. 机器人喷涂过程中的喷炬建模及仿真研究[J]. 机器人, 2003, 25(4): 353-358. Feng C, Sun Z Q. Models of spray gun and simulation in robotics spray painting[J]. Robot, 2003, 25(4): 353-358. DOI:10.3321/j.issn:1002-0446.2003.04.015 |
| [10] |
张永贵, 黄玉美, 高峰, 等. 喷漆机器人空气喷枪的新模型[J]. 机械工程学报, 2006, 42(11): 226-233. Zhang Y G, Huang Y M, Gao F, et al. New model for air spray gun of robotic spray-painting[J]. Journal of Mechanical Engineering, 2006, 42(11): 226-233. DOI:10.3321/j.issn:0577-6686.2006.11.037 |
| [11] |
华霄桐, 张思敏, 刘兴杰, 等. 基于椭圆双β喷枪模型的喷涂轨迹优化[J]. 清华大学学报(自然科学版), 2020, 60(12): 985-992. Hua X T, Zhang S M, Liu X J, et al. Optimization of spraying trajectory based on elliptical double β spraying gun model[J]. Journal of Tsinghua University (Science and Technology), 2020, 60(12): 985-992. |
| [12] |
Tang Y, Chen W. Surface modeling of workpiece and tool trajectory planning for spray painting robot[J]. PLOS ONE, 2015, 10(5). DOI:10.1371/journal.pone.0127139 |
| [13] |
缪东晶, 王国磊, 吴聊, 等. 自由曲面均匀喷涂的机器人轨迹规划方法[J]. 清华大学学报(自然科学版), 2013, 53(10): 1418-1423. Liao D J, Wang G L, Wu L, et al. Trajectory planning for freeform surface uniform spraying[J]. Journal of Tsinghua University (Science and Technology), 2013, 53(10): 1418-1423. |
| [14] |
Chu M, Tian S H, Pan X C. A new design of digital camouflage spray device[J]. Applied Mechanics and Materials, 2013, 442: 332-337. DOI:10.4028/www.scientific.net/AMM.442.332 |
| [15] |
初苗, 田少辉, 周宪. 一种新型数码迷彩喷涂装置的设计和试验[J]. 机械设计与研究, 2014, 30(1): 111-114. Chu M, Tian S H, Zhou X. Design and test research of a new digital camouflage spraying device[J]. Machine Design and Research, 2014, 30(1): 111-114. |
| [16] |
Zhang X T, Shi W, Wang B H, et al. Trajectory planning for digital camouflage spray painting robot based on projection method[C]//International Conference on Intelligent Robotics and Applications. Cham, Switzerland: Springer, 2019: 221-230.
|
| [17] |
Zhang G T, Sha J J, Wang X W, et al. A robot spraying path planning method for the digital camouflage pattern[C]//Chinese Automation Congress. Piscataway, USA: IEEE, 2020: 3470-3475.
|
| [18] |
徐博, 徐旻, 陈立平, 等. 智能机械全覆盖路径规划算法综述[J]. 计算机测量与控制, 2016, 24(10): 1-5, 53. Xu B, Xu M, Chen L P, et al. Review on coverage path planning algorithm for intelligent machinery[J]. Computer Measurement & Control, 2016, 24(10): 1-5, 53. |
| [19] |
Grossberg S. Nonlinear neural networks: Principles, mechanisms, and architectures[J]. Neural Networks, 1988, 1(1): 17-61. |
| [20] |
Yang S X, Meng M. Neural network approaches to dynamic collision-free trajectory generation[J]. IEEE Transactions on Systems, Man, and Cybernetics, Part B: Cybernetics, 2001, 31(3): 302-318. |
| [21] |
Luo C M, Yang S X, Stacey D A, et al. A solution to vicinity problem of obstacles in complete coverage path planning[C]//IEEE International Conference on Robotics and Automation. Piscataway, USA: IEEE, 2002: 612-617.
|
| [22] |
Yang S X, Luo C. A neural network approach to complete coverage path planning[J]. IEEE Transactions on Systems, Man, and Cybernetics, Part B: Cybernetics, 2004, 34(1): 718-724. |
| [23] |
邱雪娜, 刘士荣, 宋加涛, 等. 不确定动态环境下移动机器人的完全遍历路径规划[J]. 机器人, 2006, 28(6): 586-592. Qiu X N, Liu S R, Song J T, et al. A complete coverage path planning method for mobile robots in uncertain dynamic environments[J]. Robot, 2006, 28(6): 586-592. |
| [24] |
Shi J. Good features to track[C]//IEEE Conference on Computer Vision and Pattern Recognition. Piscataway, USA: IEEE, 1994: 593-600.
|
| [25] |
Ögmen H, Gagné S. Neural network architectures for motion perception and elementary motion detection in the fly visual system[J]. Neural Networks, 1990, 3(5): 487-505. |
| [26] |
中国人民解放军总装备部. 陆军武器装备数码迷彩通用要求: GJB 7929-2012[S]. 北京: 总装备部军标出版发行部, 2012. General Armament Department of the Chinese People's Liberation Army. General requirements for digital pattern painting of army equipment[S]. Beijing: Military Standard Publishing and Distribution Department of General Armament Department, 2012. |
| [27] |
贾其, 吕绪良, 李磊, 等. 迷彩斑点单元形状和尺寸研究[J]. 光电技术应用, 2008, 23(1): 21-23, 41. Jia Q, Lv X L, Li L, et al. Research on the shape and size of cell in pattern painting camouflage using electrochromic materials[J]. Electro-optic Technology Application, 2008, 23(1): 21-23, 41. |
| [28] |
吴凡. 基于背景分割和斑点优化的数码迷彩设计[D]. 合肥: 合肥工业大学, 2017. Wu F. Digital camouflage design based on background segmentation and spot optimization[D]. Hefei: Hefei University of Technology, 2017. |
| [29] |
Chen H P, Xi N. Automated tool trajectory planning of industrial robots for painting composite surfaces[J]. The International Journal of Advanced Manufacturing Technology, 2008, 35(7): 680-696. |
| [30] |
Spong M W, Hutchinson S, Vidyasagar M. Robot modeling and control[M]. New York, USA: Wiley, 2005.
|
 2023, Vol. 45
2023, Vol. 45


