1   Introduction

With the development of autonomous surface ships, manoeuvring simulation and prediction are becoming more and more important, since unmanned operation or automatic decision-making of autonomous surface ships require the accurate prediction of the ship's motions and better knowledge of the ship's manoeuvrability capabilities. Numerical ship simulators based on high-fidelity manoeuvring models can be used to simulate and predict the dynamic motion of autonomous surface ships travelling with complicated environmental disturbances, and the results can be used to train decision-making systems, reducing the navigational risks of autonomous surface ships.

The ship manoeuvring models are the key parts of vessel simulators, and they started to be studied at the beginning of the 20th century. However, it wasn't until the sixties that the studies achieved the desired progress in the field. Nevertheless, only with the development of computers, the domain was fully able to evolve fast enough and even to have simulators based on powerful desktop computers. For example, Varela and Guedes Soares (2015a, 2015b) presented an interactive 3D desktop ship simulator that simulated an LNG ship approaching or departing from a floating LNG production platform. The simulator can be used to train the operation planners and ship masters for offloading and approaching manoeuvres. Fang et al. (2018) proposed a real-time simulator based on the Manoeuvring Modelling Group (MMG) model, and simulator was used to provide decision support for the safety of ship navigation in heavy traffic areas. Yin et al. (2021) developed a whole ship simulator for the teaching and training of navigation, where the 6DOF nonlinear manoeuvring model was used. In addition to the above applications, ship manoeuvring models are also widely used for testing and verification of other complex systems, for instance, dynamic positioning (DP) ships (Sørensen, 2011) and control systems (Ridao et al., 2015). Li et al. (2024) carried out the formation control simulation tests using a nonlinear manoeuvring model and an adaptive event-triggered control strategy, where the communication burden can save 53% and 24%.

The methods to obtain the mathematical model of surface ships were recommended by the Manoeuvring Committee of the 25th ITTC (Hochbaum et al., 2008). Figure 1 presents the overview of manoeuvring prediction methods where three classifications are defined: no simulation, system-based manoeuvring simulation and CFD-based manoeuvring simulation. In the classification of system-based manoeuvring simulation, manoeuvring tests, system identification methods and manoeuvring mathematical models are three key parts for obtaining the equation of motion and for the manoeuvring prediction in the next step.

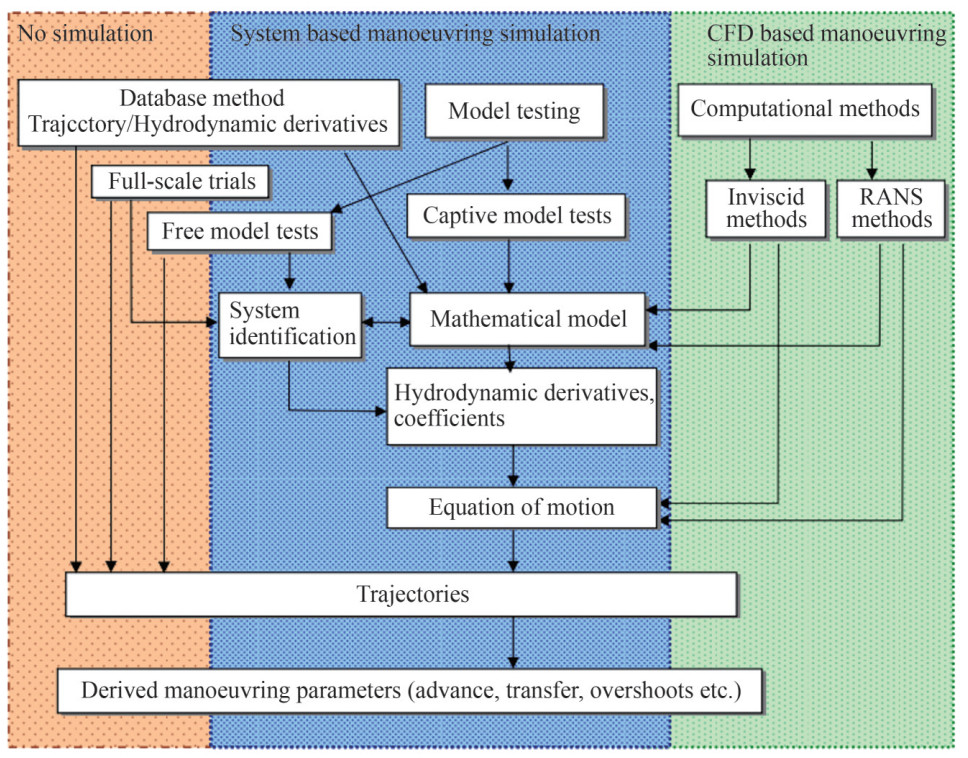Figure  1  Overview of manoeuvring prediction methods (ITTC, 2005)

Download: Full-Size Img

Therefore, this paper gives a review of the system identification methods for the manoeuvring modelling of surface ships. Particular attention is placed on the manoeuvring models, manoeuvring tests, and system identification methods, as indicated in Figure 1.

The classical manoeuvring models, such as the Abkowitz model, MMG and Nomoto model, are briefly revisited and the typical mathematical model structures with hydrodynamic coefficients are presented here. The manoeuvring tests, such as full-scale sea trials, free model tests and captive model tests, are also introduced and some test results are presented for illustration. In the last part, the system identification methods used in the selected papers will be analysed and the statistical distributions of the manoeuvring models, manoeuvring test data, and environmental disturbances will be given.

This paper is organized as follows. In Section 2, classical manoeuvring mathematical models are revisited and briefly introduced. Section 3 introduces the manoeuvring tests for system identification. In section 4, the system identification method for manoeuvring modelling of marine surface ships is summarised. The conclusion is given in the last section.

2   Manoeuvring mathematical models

The ship moving in the ocean is typically considered a rigid body and its motion can be described in 6 degrees of freedom, as shown in Figure 2. For manoeuvrability, the surge, sway and yaw motions are typically studied based on the assumption that the hydrodynamic forces and moments can be approximated at one frequency of oscillation and the fluid memory effects can be neglected (Fossen, 2011; Sutulo and Guedes Soares, 2011). Therefore, to describe the dynamic motion of the ship, many manoeuvring models were proposed considering the actual application. In the following sections, the widely used manoeuvring models will be briefly introduced.

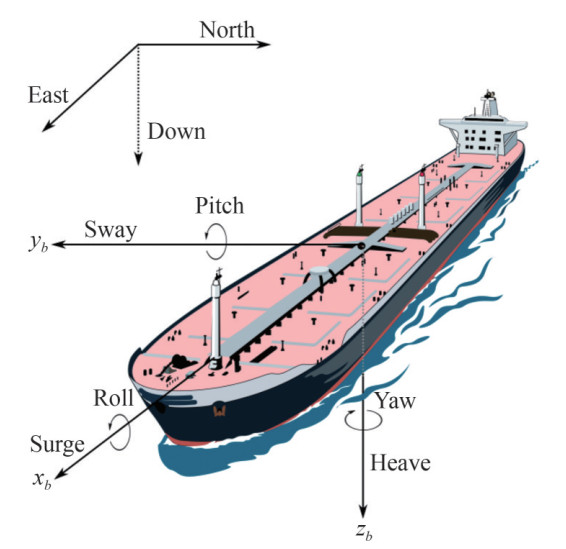Figure  2  The motions of the marine surface ship moving in the ocean (Fossen, 2011)

Download: Full-Size Img

The Euler equations of arbitrary motion in the horizontal plane are given:

where m and I_zz are the mass and the moment of inertia, respectively. x_G is the position of centre-of-mass in the x-direction. μ₁₁, μ₂₂ and μ₂₆ are the added masses and moments, respectively. X, Y and N are the hydrodynamic forces and moments described using different mathematical models, which results in the widely used manoeuvring models.

2.1   Abkowitz model

Abkowitz model (Abkowitz, 1980) as well as its revised versions were proposed under the assumption that the hydrodynamic forces of the whole ship are a function of the various variables, such as acceleration, velocity (or r/min) and rudder angle. Taylor's expansion was used to approximate the nonlinear hydrodynamic forces of the surge, sway and yaw motions, where the terms of order higher than three were neglected considering the trade-off between the complexity and accuracy of the manoeuvring models. The nonlinear Abkowitz model is defined as:

where $ X_{\dot{u}}, Y_{\dot{v}}, \cdots, N_{\dot{r}}$ are the added masses and moments, respectively and f₁(·), f₂(·), f₃(·) are the hydrodynamic forces and moments, which are defined as

The above equations are based on the assumption that the ship geometry is symmetrical about the centre plane. Meanwhile, it is assumed that the accelerations are linearly related to the hydrodynamic force and moment. Therefore, there are 60 hydrodynamic coefficients in the above equations (Abkowitz, 1980). This nonlinear manoeuvring model was validated with the Mariner ship, and the results were compared with sea trials.

Chislett and Strom-Tejsen (1965) estimated the hydrodynamic coefficients of the classical Abkowitz model based on the planar motion mechanism, and the obtained manoeuvring models were used to predict the turning manoeuvres, which agree well with full-scale trials. Luo and Zou (2009) employed the least square support vector machine method (LS-SVM) to estimate the hydrodynamic coefficients of the classical Abkowitz model based on the simulated manoeuvring tests. An additional ramp signal was introduced to diminish the multicollinearity. The results show the good predictive ability of the trained SVM. Further works can be found in Luo (2016), Luo et al. (2016), Luo and Li (2017). Other versions of SVM, ε-Support Vector Regression (ε-SVR) (Liu et al., 2019; Zhang and Zou, 2011) and nu-SVM (Wang et al., 2019a), were used to estimate the hydrodynamic coefficients of the Abkowitz model.

From the published papers, it can be concluded that the classical Abkowitz model has a good performance for the prediction of manoeuvring motion. The truly challenging part is how to get the accuracy values of the 60 hydrodynamic coefficients based on manoeuvring test data. There are some methods proposed to diminish the parameter uncertainty, for example, additional ramp signal (Luo and Zou, 2009), parallel processing, exaggerated over- and under-estimation and parameter transformation (Luo and Li, 2017). Recently, the truncated LS-SVM was proposed to diminish the parameter uncertainty (Xu et al., 2020a, 2020b; Xu and Guedes Soares, 2020, 2019), and it can significantly diminish the parameter uncertainty due to the illconditioned problem of the classical Abkowitz model.

2.2   Modified Abkowitz model

In practical applications, the classical Abkowitz model is still too complex and difficult to estimate the hydrodynamic coefficients. One of the important reasons is that the higher-order hydrodynamic terms lack physical interpretation and are hardly measured in the towing tank tests. Hwang (1980), proposed the modified nonlinear Abkowitz model based on the sea trials of the Esso OSAKA ship. The nondimensional hydrodynamic forces and moments in Eq. (2) were defined as:

The modified version is more concise and there are only 21 hydrodynamic parameters to be determined, which significantly reduces the complexity of the original mathematical model. More details of the modification can be found in (Hwang, 1980). The comparison with the sea trials was also conducted and showed good agreement.

Yoon and Rhee (2003) identified the hydrodynamic coefficients described in Eqs. (4)‒(6) based on the sea trials of the 113 K tanker, they concluded that the hydrodynamic coefficients are difficult to identify based on the standard manoeuvring trials due to the strong multicollinearity in the regression model. Xu et al. (2018c) employed a genetic algorithm (GA) based least square method to estimate the hydrodynamic coefficients of the modified Abkowitz model, and the results were validated with the free-running ship model tests (Hinostroza et al., 2017). It is important to point out that although the modified Abkowitz model is significantly simplified compared with the classical one, it requires more information on ship geometry and propeller, for example, resistance coefficient, wet surface area, diameter and area of the propeller, wake fraction, and thrust coefficient just to name a few. It to some extent limit its application due to the incomplete information.

2.3   Manoeuvring modelling group (MMG) model

The MMG model is another version of manoeuvring models for the description of ship motion, which was proposed by the Manoeuvring Modelling Group (MMG) at the Japanese Towing Tank Conference (JTTC) (Yasukawa and Yoshimura, 2015). The basic idea is to describe the hydrodynamic forces and moment of the ship hull, propeller and rudder separately. The right-hand side of Eq. (1) can be described as:

where the subscript, (H, P, R) represents the ship hull, propeller and rudder. The hydrodynamic forces on the ship hull can be described using the Inoue method (Inoue et al., 1981; Inoue and Murayama, 1969):

and Kijima method (Kijima and Nakiri, 2003):

The forces of the ship propeller are described as:

The forces of the rudder are described as:

The definition of variables in Eqs. (8)‒(11) will not be repeated, since the details can be found in Inoue et al. (1981), Inoue and Murayama (1969), Kijima and Nakiri (2003). In addition to the Inoue method and Kijima method, there are also some useful manoeuvring models, such as the Ogawa model (Ogawa and Kasai, 1978), Matsunaga model (Matsunaga, 1993), Yasukawa model (Yasukawa and Yoshimura, 2015), just to name a few. A comparative study of the various empirical manoeuvring models and associated uncertainties can be found in Sutulo and Guedes Soares (2019). MMG model can also be extended for ships with multi-propeller and multi-rudder, such as Okuda et al. (2022) proposed an equivalent single rudder (ESR) model for the manoeuvring simulations of twin-propeller and twin-rudder ships within the framework of MMG method. It eliminates the modelling complexity by treating the two rudders of the port and starboard as one rudder on the centre of the hull.

2.4   Other nonlinear manoeuvring models

Besides the above classical Abkowitz model and MMG model, there are still many modified nonlinear manoeuvring models, which were proposed for specific applications. They are typically modifications from the classical Abkowitz model or MMG models by neglecting or including new high-order hydrodynamic terms. For example, Sutulo and Guedes Soares (2014) proposed a nonlinear manoeuvring model based on the Inoue model by including higher-order nonlinear hydrodynamic terms, as presented in Eq. (12). The parameter identification of this nonlinear model can be found in (Costa et al., 2021)

Another popular nonlinear manoeuvring model is the vectorial model, which was proposed in Fossen (2011).

The vectorial models for the description of the ship motion in waves and wind are defined as:

where v =[u, v, w, p, q, r]^T and η =[x, y, z, ϕ, θ, ψ]^T are the generalized velocities and positions. The matrix M, C(v) and D(v) denote the system inertia, Coriolis and damping, respectively. g(η) is a vector of generalized gravitational and buoyancy forces. τ, τ_wind, τ_wave are the vector of forces and moments due to actuators and environmental disturbances.

The vectorial models have some clear advantages for marine control systems design. The properties such as symmetry, skew-symmetry and positiveness of matrices can be incorporated into the stability analysis of the control system (Fossen, 2011). Golding et al. (2006) presented an online estimation method for nonlinear viscous damping forces for a surface vessel at low speed. Ross (2008) developed a much more complex manoeuvring model in the vectorial presentation based on the Lagrangian approach, the identification of the parameters using Planar Motion Mechanism Tests can be found in Ross et al. (2015).

Delefortrie and Vantorre (2021) proposed a novel mathematical model formulation to account for the effect of heeling of the ship while manoeuvring in calm water, harbour conditions. The performance of the new model was compared against free running model tests in the ship manoeuvring simulator.

It is worth noting that there is no unique manoeuvring model, which can be used to describe the motions of all surface ships, since the hydrodynamic coefficients are largely related to the ship's geometry, propeller, rudder and environmental disturbances, such as shallow water. Therefore it is recommended to modify the classical manoeuvring models based on the practical application by neglecting the unimportant hydrodynamic terms. The sensitivity analysis of the hydrodynamic coefficient should be carried out before parameter identification.

2.5   Implicit model

The implicit model, also well-known as the black box model, is another important method to predict the manoeuvring motion of marine surface ships, where the heavy burden of hydrodynamic coefficient determination is avoided. Moreira and Guedes Soares (2003b) presented a Recursive Neural Network (RNN) manoeuvring simulation model for surface ships, where the simulated manoeuvres were carried out using the Mariner hull form. This method was later used to predict the manoeuvres based on the sea trial data (Moreira and Guedes Soares, 2012, 2003a). Luo et al. (2014) proposed implicit models of manoeuvring motion using the SVM regression with the Gauss kernel function, the full-scale trials of a catamaran were used as the training data and the disturbances induced by current and the wind were also considered in the paper. Chen et al. (2023a, b) applied a reduced-order dynamic mode decomposition (DMD) algorithm to predict zig-zag and turning circle manoeuvring motions. of KVLCC2 tanker. Diez et al. (2022) proposed a data-driven approach to forecast the response of ship (KRISO Container Ship) manoeuvring in waves based on the dynamic mode decomposition (DMD).

The multi-output Gaussian processes were used to model the dynamic system of a container ship with the simulated manoeuvring test data (Ariza Ramirez et al., 2018). Other works on Gaussian processes can be found in (Ouyang and Zou, 2021; Xue et al., 2021). From the published papers, the performance of the implicit model highly depends on the chosen algorithm, such as Neural Network, SVM, and Gaussian processes, just to name a few, and it is hard to draw conclusions about which algorithm has a better performance for the prediction of ship manoeuvring motion since it largely depends on the quality of the training data and the parameters of the chosen algorithm. In general, the implicit models have a better performance compared with the classical manoeuvring models.

2.6   Nomoto model

The Nomoto model (Nomoto et al., 1956) or steering model is a simplified model that typically focuses on the yaw motion. Here, the ship is considered as a single-input and single-output (SISO) system with one rudder input and yaw angle as the output. The Nomoto model is defined as

The parameters T and K are well-known Nomoto parameters. The 2nd order Nomoto model (Nomoto et al., 1956), is a generalised version that is widely used for autopilot design. The above equation can be further simplified as

The Nomoto model is widely used for the heading controller design for marine surface ships. Since it is over-simplified and neglects the sway dynamic, therefore the ship trajectory can never be reproduced correctly based on any of these Nomoto models (Sutulo and Guedes Soares, 2011).

3   Manoeuvring tests

With the mathematical manoeuvring models mentioned above, the next important step is to carry out the experiments and collect the data for the hydrodynamic parameter estimation. In this section, the typical manoeuvring tests will be briefly introduced and discussed.

3.1   Captive model test

In the long period, the captive model tests were the main tools to determine the hydrodynamic coefficients for the mathematical models of ship manoeuvring motion. One of the advantages of the captive model tests is that the values of some hydrodynamic coefficients can be measured directly, for example, linear hydrodynamic coefficients. Meanwhile, the coupled hydrodynamic parameters can be eliminated by imposing restrictions on the ship's motion in the lab. Another important advantage is that environmental disturbances can be controlled.

Captive model tests are usually carried out in the towing tank with a carriage, where a horizontal planar motion mechanism (PMM) is installed (ITTC, 2017a). The ship can be attached to the towing tank to perform the prescribed motions and the force gauges are used to measure the hydrodynamic forces during the tests. In the Figure 3, the scaled ship model was attached to the carriage and PMM tests were carried out in the towing tank.

Figure  3  PMM tests of DTC ship model. cf. Ref. (Papanikolaou et al., 2016; Xu and Guedes Soares, 2020, 2019)

Download: Full-Size Img

As recommended by ITTC (2002a), there are three types of model tests, that can be executed in the towing tank to study the manoeuvrability of marine surface ships. As presented in Figure 4, they are steady straight-line tests, harmonic tests and steady circular motion tests. For the harmonic tests, as presented in Figures 4(c)‒(d), an important factor that needs to be considered in the PMM test is to vary the oscillation frequency and amplitude. According to (ITTC, 2017a), a single frequency is a dominant choice, but 3 and 5 frequencies are also common choices, however, they are usually subject to restrictions of the facilities in the towing tanks. For example, the amplitude of sway motion is restricted due to limitations of the horizontal planar motion mechanism, meanwhile, the interaction with the towing tank wall is also needed to avoid during the tests. The restrictions of the oscillation frequency are usually expressed as:

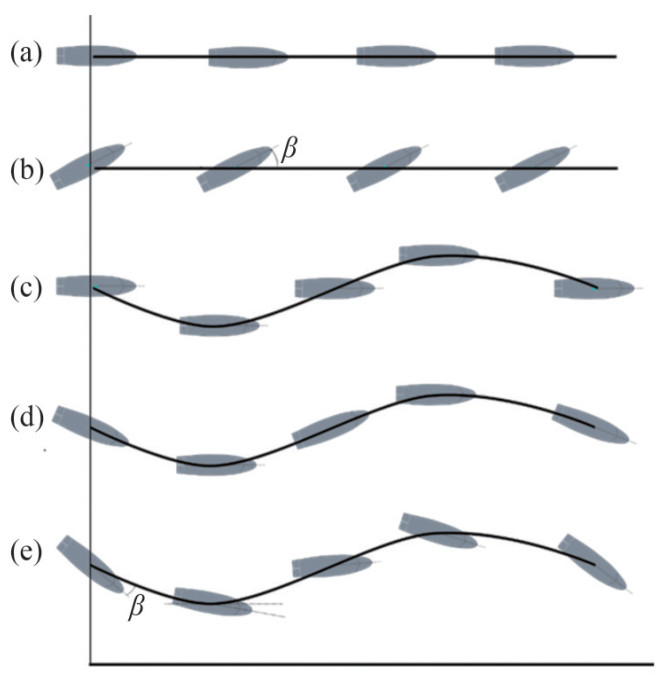Figure  4  PMM test of ship model travelling along the pathline: (a) straight line (pure surge or surge acceleration); (b) pure drift; (c) pure sway; (d) pure yaw; (e) pure yaw + drift. (Xu et al., 2020a)

Download: Full-Size Img

where ω₁′ denotes the restrictions due to tank length, and it is limited by (ω₁′ ≥ c2πL/l). l is the length of the tank, c is the constant values, and typically 1 ‒ 2 for sway and 2 ‒ 3 for yaw tests (Eloot, 2006). ω₂′ represented the restriction for avoiding the towing tank resonance, which occurs in $\omega _{2}^{\prime }=\sqrt{{}^{{\rm{ \mathsf{ π}}} L}\!\!\diagup\!\!{}_{b}\;}$ for depth water and $ \omega_2^{\prime}=\frac{{\rm{ \mathsf{ π}}}}{b} \sqrt{L h}$ for shallow water. b is the tank width and h is the water depth. The restrictions on ω₃′ are defined to avoid unrealistic combinations of pulsation and translation, and it is recommended less than 0.25 during PMM tests (ITTC, 2017a).

An important problem in the design of captive tests is the decision on the number of tests to be performed and the values of the governing parameters in the tests. As a full variation of all parameters would lead to an exceedingly large number of tests, the use of techniques for the design of experiments is advised (Sutulo and Guedes Soares, 2002). An approach to synthesizing D-optimized experimental design for an arbitrary number of factors was developed and tested on a third-order polynomial regression model with 5 through 8 factors in Sutulo and Guedes Soares (2004), while a Multifactor Regression Model was adopted in Sutulo and Guedes Soares (2006).

During PMM tests, it is possible to control the variable (surge, sway speed and yaw rate) of ship dynamic motion, therefore, the nonlinear coupled hydrodynamic terms of yaw and sway motion can be decoupled using pure sway tests. Meanwhile, the environmental disturbance (wave, wind and current) can also be controlled and measured in the lab, therefore, it is also convenient to evaluate the effect of environmental disturbance on obtained hydrodynamic coefficients, which is almost not possible for the free-running model tests and sea trials. Therefore, the captive tests, where circular motion tests and oblique towing tests are at least as important, are still the most reliable way to estimate the hydrodynamic coefficients of the manoeuvring models. But, of course, the disadvantage of the PMM test is expensive and time-consuming.

3.2   Free-running ship test

The captive model test can provide rich information for the estimation of the hydrodynamic coefficients; however, the test cost is also significantly high and time-consuming. Free-running ship model tests are a credible alternative since they are cheaper and easier to carry out the predefined trajectory and measure the motion of the ship in a real environmental disturbance. It is also worth indicating that the free-running ship model tests can also be carried out in large model test basins, where the quality of indoor measurements is significantly higher than the outdoor swimming pools. Right now, the sensors with high accuracy, such as inertial measurement unit (IMU), real-time kinematic positioning (RTK) system, and anemometer, make the test results more reliable and convincing. Figure 5 shows the basic hardware structure for the free-running ship tests, where the IMU, GPS, control unit, battery, Wifi, motor and thruster are installed on the ship model.

Figure  5  The basic hardware structure of a free-running ship model (Xu and Guedes Soares, 2022)

Download: Full-Size Img

As recommended by ITTC (2002b), there are three types of model tests (turning test, zigzag test and spiral test), which are widely used for the manoeuvring tests of marine surface ships. For example, in Xu et al. (2020c), the turning tests in shallow water were carried out using the free-running ship model, and the trajectories with the different water depths. It can be observed that shallow water has an important effect on the maneuverability of marine surface ships. More details can be found in Xu et al. (2020c). In Figure 6, the zigzag 30° ‒ 30° was carried out in the outdoor swimming pool, where the trajectory and yaw angle are also measured and presented in this figure.

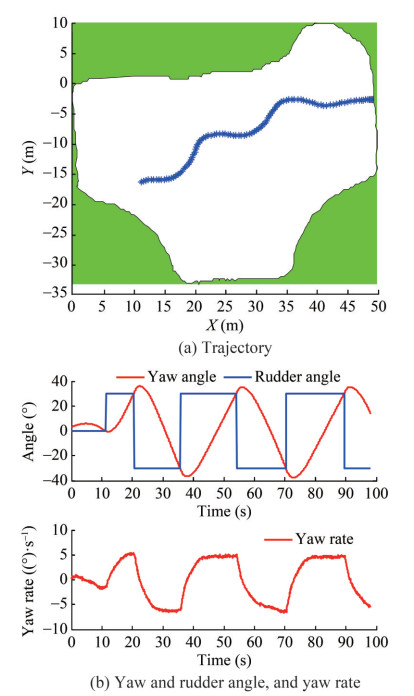Figure  6  The zigzag 30°‒30° using the free-running ship (Xu and Guedes Soares, 2022)

Download: Full-Size Img

Although the data quality has been improved a lot with the novel sensor technology, it is still low accuracy compared with the sensors in towing tank. The adverse effect on the tested result from the reduced-scale ship model is also a challenge since the environmental disturbance is time-varying and cannot be scaled using the scale ratio.

3.3   Full-scale sea trials

Full-scale sea trials are the best way to evaluate the manoeuvrability of marine surface ships, since the fully dynamic motion of ships can be measured directly without the scale effect in the ocean environment, such as waves, currents and wind. As suggested by ITTC (2017b), there are 14 different recommended tests, such as turning circles, zigzag manoeuvres, modified zigzag manoeuvres, spiral manoeuvres, pullout tests, and stopping tests, just to name a few.

The turning circles, zigzag manoeuvre, and spiral manoeuvre are the three most popular tests for manoeuvring tests. For example, in the turning circles, the essential information of the marine surface ships can be measured, such as tactical diameter, advance distance, maximum transfer, and speed loss. From the zigzag manoeuvre, the following manoeuvring characteristics can be obtained, such as initial turning time, execute heading angle and overshoot angle. The spiral manoeuvring tests can be used to evaluate the course stability of the ship.

One of the well-known full-scale sea trials was carried out using the ESSO OSAKA tanker, where the manoeuvring tests were carried out in two shallow water depths and deep water in the Gulf of Mexico (Crane Jr, 1979). The turning circles, zigzag manoeuvres, stopping, coasting turns, coasting Z-manoeuvres, and accelerating turns were carried out with current, wave and wind. The tests were used to study the effects of the water depth, speed and propeller rpm, and the final objective was to improve the quality of simulations of manoeuvring behaviour. Guedes Soares et al. (1999) carried out full-scale manoeuvring trials of a fast catamaran of 45m in length with waterjet propellers. The full-scale sea trials of two fast patrol ships were carried out (Guedes Soares et al., 2004), and the results were used to identify the manoeuvring characteristics of the patrol ships. Selvik et al. (2015) discussed the validation process for the simulation models based on the sea trials of the research vessel "R/V Gunnerus", which is owned by the Norwegian University of Science and Technology.

The uncertainty of trial results due to environmental effects was presented in Gavrilin and Steen (2015). A sea trial of the training ship Hanbada was performed by Kim et al. (2017), and the results were used to estimate the hydrodynamic coefficients of the nonlinear manoeuvring model. The full-scale sea trial of the research vessel YUKUN was performed by Dalian Maritime University and the results were used to build the nonlinear whole-ship mathematical model (Meng et al., 2022; Zhang et al., 2015). Pires da Silva et al. (2021), carried out sea trials of naval ships in the Atlantic Ocean, to develop and test the fast combined mathematical models for seakeeping and manoeuvring in waves. Pires da Silva et al. (2023) studied the sensitivity of the model to the variability of environmental factors.

4   Parameter estimation methods for manoeuvring models

As presented in Figure 1, with the manoeuvring models and the test data, the next step is to estimate the hydrodynamic parameters. The system identification method is a mature technology for data-driven modelling. It can be used to get the mathematical models of one dynamic system based on the measured input and output (Ljung, 1999). Right now, system identification methods have been widely used for manoeuvring modelling for surface ships in the academia area.

4.1   Least squares (LS) method

The LS method is one of the popular methods for parameter estimation. For example, The LS has been used to identify the nonlinear viscous damping matrix of a surface ship (Golding et al., 2006). Sutulo and Guedes Soares (2014) used one offline optimized least square method to estimate the parameter of the nonlinear manoeuvring model, where the different cost functions were defined. Bai et al. (2019a, 2019b) proposed a modified GA to search the optimal distance metric defined based on the least square method, and full-scale trials were applied to identify the system. Ross et al. (2015) identified the parameters of a nonlinear manoeuvring model for marine vessels based on Planar Motion Mechanism Tests. Kim et al. (2017) used the LS method to estimate the linear coefficients and nonlinear coefficients using sea trial measurement data. Xu et al. (2018c), used the optimised least square method to estimate the hydrodynamic coefficients of the modified Abkowitz model based on the free-running ship model tests.

Although the least square method can provide good results in most cases, it still has some issues when dealing with noisy data. It is sensitive to outliers and leads to inconsistent estimates, as described by Golub and Reinsch (1970). As discussed in Hansen (1998), the least square method with large-scale test data is usually ill-conditioned.

The singular value decomposition (SVD) was introduced to lighten the ill-conditioned problem of the least square method (Bell et al., 1978; Chan and Hansen, 1990). Another method to diminish the ill-posed problem is the Tikhonov regularization method (Golub et al., 1999) since it can significantly reduce the effect of the smaller singular values. Xu et al. (2019a) employed the truncated SVD and Tikhonov regularization method for the hydrodynamic parameter estimation based on the PMM test data. Xu and Guedes Soares (2022) presented the convergence analysis of the Tikhonov regularization method for the parameter estimation based on free-running ship model tests with noise.

4.2   Kalman filters

Kalman filter is a widely used technique in modern control theory, and it can provide the optimal estimation of the system based on the model structure and the measurement. It is also one of the popular methods for the estimation of hydrodynamic coefficients based on experimental tests.

Hwang (1980) used the Extended Kalman Filter (EKF) to estimate the hydrodynamic coefficient of the modified Abkowitz model, based on the sea trials of "ESSO OSAKA", and the obtained manoeuvring models provided a good prediction of the ship's manoeuvre. Fossen et al. (1996) discussed the convergence and robustness of an off-line parallel EKF algorithm for the parameter estimation based on the full-scaled experiments of DP ship model. Yoon and Rhee (2003) applied the EKF for the identification of the dynamics models when a combatant is in intact and damaged condition. The EKF was further extended for the identification of 4-DoF manoeuvring mathematical models by including roll motion (Jeon et al., 2022). An unscented Kalman filter was used to estimate the parameters of non-linear manoeuvring models of a modern high-speed trimaran ferry using a full-scale trial (Revestido Herrero and Velasco González, 2012). Perera et al. (2015) identified the nonlinear vessel steering model using an EKF, and later it was extended to identify the vessel steering model with unstructured uncertainties by persistent excitation manoeuvres (Perera et al., 2016).

Based on the above papers, The modified version of Kalman filters, such as the extended Kalman filter, Unscented Kalman filter, are typically used for the parameters estimation of manoeuvering models, since the classical Kalman filters can only be used for linear systems and the nonlinear terms in manoeuvring models play important roles. Typically, the EKF can be used for nonlinear systems with 1st order approximation and the Unscented Kalman filter (UKF) is more robust for highly nonlinear systems.

4.3   Neural networks

Considering the structure of Neural Networks (Bishop, 1998), they are usually used for implicit models of surface ships. Rajesh and Bhattacharyya (2008) discussed the application of nonparametric system identification to a nonlinear manoeuvring model for large tankers using the artificial neural network method. Moreira and Guedes Soares (2003a) applied the Recursive Neural Network (RNN) to predict the manoeuvring motion of ships based on the simulations of the Mariner, and later this method was further used for the sea trials of a catamaran (Moreira and Guedes Soares, 2012) and free-running ship model tests (Moreira and Guedes Soares, 2022) Wang et al. (2015) used the generalized ellipsoidal function-based fuzzy neural network (GEBF-FNN) to describe the dynamic motion of a tanker using zig-zag manoeuvres. A self-designed fully connected neural network with Bayesian optimization was proposed for the nonparametric modelling of ship manoeuvring models based on free-running model tests of the KVLCC2 ship model (He et al., 2022). Wakita et al. (2022) employed the recurrent neural networks (RNNs) to identify a low-speed manoeuvring model using free-running model tests.

4.4   Support vector machines (SVM)

In recent years, kernel-based support vector machines (SVM) have been widely used for parameter estimation. It was proposed by Vapnik (1998, 1995) and initially used for the classifications, and later extended for the regression analysis (Cortes and Vapnik, 1995; Suykens et al., 2002). Luo and Zou (2009), and Luo et al. (2016) used the least square SVM (LS-SVM) to identify the hydrodynamic parameters of the Abkowitz model based on simulation data. For LS-SVM, the two important parameters, the regularization factor and kernel parameters, are important and closely related to the performance.

Global optimization algorithms can be used to search the optimal values, for instance, Genetic Algorithm (GA) (Xu and Guedes Soares, 2020), Particle Swarm Optimization (PSO) (Luo et al., 2016), Beetle Antennae Search (BAS) (Chen et al., 2019b), Artificial Bee Colony (ABC) (Zhu et al., 2017a), quantum-inspired evolutionary algorithm (Xu and Guedes Soares, 2020), just to name a few.

Meanwhile, the LS-SVM can also be used to estimate the parameters of the roll motion of marine ships (Chen et al., 2019a). There are also different versions of SVM used for the manoeuvring modelling of marine surface ships, such as nu-SVM (Wang et al., 2019a, 2019b), ε-SVM (Liu et al., 2019), Truncated LS-SVM (Xu et al., 2020c; Xu and Guedes Soares, 2020, 2019), online SVM (Hao et al., 2004; Tatinati et al., 2013; Xu et al., 2019b), just to name a few.

4.5   Gaussian processes (GP)

Gaussian Processes (GP) are generic supervised machine learning methods that are used to solve regression and probabilistic classification problems. GP is used to build the dynamic model based on input-output data, and its advantage is the ability to work with the problem with small quantities of data or data with noise. In Ariza Ramirez et al. (2018), the multi-output Gaussian processes were used for dynamic system identification of ships, and the results show that multi-output Gaussian processes can be accurately applied for non-parametric dynamic system identification in ships. Xue et al. (2020b) proposed an input noisy Gaussian Process (NIGP) model for the nonparametric system identification of ships and it can automatically propagate the input uncertainty to the output using the Taylor approximation. Further work can be found in Xue et al. (2022, 2021); Ouyang and Zou (2021) proposed the Gaussian process regression optimized by GA for nonparametric modelling of ship manoeuvring, and case studies were carried out with training datasets from simulations and experiments of KCS ship.

Besides the above methods, there are still other technologies, used to estimate the hydrodynamic coefficients of the manoeuvring models, for instance, the maximum likelihood method (MLE) (Åström and Källström, 1976; Hassani et al., 2013), Bayesian regression (Xue et al., 2020a), and online adaptive methods (Casado and Ferreiro, 2005; Yue et al., 2022), just to name a few. The algorithms for estimating parameter values are many. Each one has its advantages and disadvantages. The choice of parameter estimation methods not only depends on the hypothesized structure of the manoeuvring models but is also affected by the special considerations of each problem.

5   Discussion

This section presents a summary of the parameter estimation methods for the manoeuvring models of surface ships. A total of 68 published papers are selected and analysed, with particular concerns placed on the manoeuvring models, manoeuvring tests, system identification methods and environmental disturbance in the selected papers.

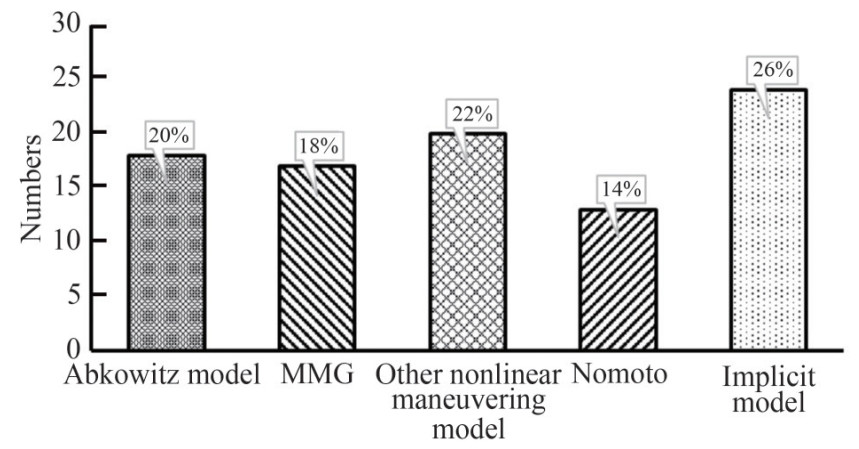
Table A1 in Appendix A presents selected 92 published scientific papers on the system identification for manoeuvring models of marine surface ships. The manoeuvring models used in the selected papers are given in Table A1 and the distribution is presented in Figure 7. There are 5 typical manoeuvring models, the Abkowitz model, MMG, Nomoto model, implicit model, and nonlinear manoeuvring model. The nonlinear manoeuvring model cannot be classified into the other 4 typical classes. They are usually defined based on the classical manoeuvring models by adding customized terms according to the specified applications.

Figure  7  The distribution of the manoeuvring models in the recent publications

Download: Full-Size Img

From Figure 7, the nonlinear manoeuvring models take the big proportion (22%) in the selected papers, because most authors proposed their nonlinear manoeuvring models based on the actual application, for example, shallow water (Delefortrie et al., 2016; Lataire et al., 2012) and hull damaged condition (Jeon et al., 2022). Those models are usually revised based on the nonlinear Abokwitz model and MMG model by adding or neglecting some nonlinear terms considering their contribution to the hydrodynamic forces.

The Abokwitz and its revised version (20%) are still the most popular models compared with MMG and Nomoto models. One of the important reasons is that it can provide a good prediction of the manoeuvring motion of surface ships, however, it is necessary to point out that the complexity of the model structure makes it challenging to obtain the parameters from the PMM test or use system identification methods. Therefore, it is necessary to simplify the model under the premise that the revised version can still provide a good prediction.

The Nomoto models (14%) were typically used for the control or autopilot design, and they are not recommended for the manoeuvring simulation of the marine surface ship since they are oversimplified and only describe the yaw motion (Sutulo and Guedes Soares, 2011). The MMG model (18%) has fewer hydrodynamic coefficients and is suitable for parameter estimations using system identification methods. It is necessary to point out that the performance of MMG model is highly related to the specified application. A good performance of the MMG model for one ship cannot guarantee the same accuracy for other ships. Therefore, it is recommended to do the sensitivity analysis of the hydrodynamic coefficients based on the sea trials (Gavrilin and Steen, 2018; Pires da Silva et al., 2023). Sensitivity analysis is a means of dealing with model uncertainties and often leads to model simplifications.

If the manoeuvring prediction is primary and the hydrodynamic coefficients are not required, the data-driven implicit model (26%) usually can provide a good performance. The drawback is that the prediction of the obtained implicit model highly depends on the training set. If only small-scale data are available, the obtained implicit model usually cannot fully describe the dynamic of the ships in the complex ocean environment. Therefore, the large-scale training data plays a key role in the implicit model. Meanwhile, large-scale training data also provides a challenge for the current machine learning methods, such as NN, SVM and Dynamic Mode Decomposition (DMD) (Diez et al., 2022). The implicit model is also suitable for complex conditions, where the principle of kinematic motion is not clear, such as manoeuvring in shallow water (Xu and Guedes Soares, 2020).

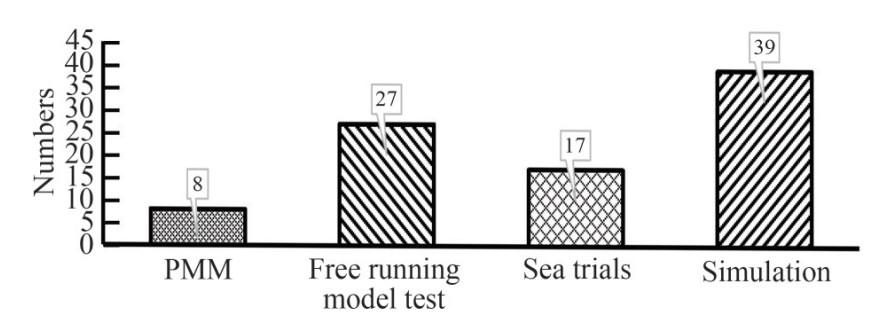
Figure 8 shows the distributions of the tests used in the selected papers. They are PMM tests (9%), free-running ship model tests (30%), sea trials (19%) and simulations (43%). Right now, simulation tests, such as turning circles, and zigzag manoeuvring tests, are still the main means for parameter estimations. This is mainly because they are simple to carry out and easy to control the noise in the data. The captive model test, more specifically, the PMM test is the least used test for system identification, because the PMM test is very expensive and few people can obtain the test data from towing tanks. However, the PMM tests are still the most reliable way to estimate the hydrodynamic coefficients of the manoeuvring models.

Figure  8  The distribution of the manoeuvring tests in the recent publications

Download: Full-Size Img

Recently, the rising tendency to use the free-running ship model for the evaluation of manoeuvrability can be observed, especially motivated by the development of machine learning methods. The free-running ship model test can be easily carried out in the ocean basin laboratory as well as the outdoor lake. The results are more accurate and reliable with the novel technology and sensors, such as the real-time kinematic positioning (RTK) system, fibre optic gyrocompass, and inertial measurement unit (IMU). However, it should be pointed out that the free-running ship model can not replace the laboratory test considering the data accuracy and environmental disturbances. The sea trial is one direct and long-historical method for evaluation of the manoeuvrability of marine surface ships, the true motions of the ship with full-scale environmental disturbance can be directly measured without considering the scaled effect.

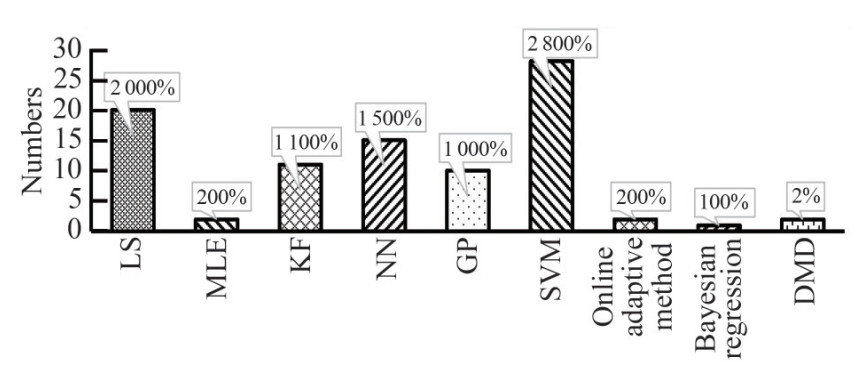
Figure 9 shows the distributions of the system identification methods used in the selected papers. They are the least square method (LS) (22%), Kalman filter (EKF) (12%), neural network (NN) (16%) and SVM (31%), Gaussian Processes (GP) (11%), and other methods, such as. maximum likelihood estimation (MLE), Bayesian regression, and DMD. The system identification methods are usually divided into two groups, white box modelling and black box modelling. For white-box modelling, typically, the mathematical model needs to be defined first and then the parameters or hydrodynamic coefficients can be estimated based on the above methods. Some typical methods are LS, KF, and SVM. For black-box modelling, it is a typical data-driven method, where the manoeuvring models do not need to be defined. The methods, such as NN, SVM, and Gaussian process are typically used for black box modelling.

Figure  9  The distribution of the system identification methods in the recent publications

Download: Full-Size Img

The least square method and revised version is another important method for the parameter estimation of the hydrodynamic coefficients, it is simple and easy to implement, but it is sensitive to noise and outliers.

The idea is to find the best-fitting curve for the given data set by minimising the L2 norm, which is usually defined as the offsets of the points from the curve. Therefore, the solution is usually theoretically optimal for the given data points. Meanwhile, the solution is sensitive to noise, especially the outlier. Some technologies were proposed to improve this condition, such as Principal component analysis (PCA), singular value decomposition (SVD), and Weighted least squares (WLS). Therefore, when using the least square method and the revised version, it is highly recommended to minimise the noise in the data, especially the outliers. From Table 1, the least square methods are usually used for hydrodynamic parameter estimation, therefore, the mathematical manoeuvering model needs to be selected or defined. It will inevitably induce model uncertainty in the prediction since there are no mathematical models that can fully describe the motion of the ship.

SVM is the most popular method for manoeuvering modelling of marine surface ships in the last 20 years. SVM was initlly proposed for the classification problem, and the objective is to find a hyperplane in a high-dimensional space that distinctly classifies the data points. The main advantage is that it can transfer the nonlinear classification problem into the linear problem in high dimension using the kernel function. There are many different versions of SVM, such as LS-SVM (Suykens et al., 2002), ε-SVM (Zhang and Zou, 2011), nu-SVM (Wang et al., 2019a), and truncated LS-SVM (Xu and Guedes Soares, 2020), just to name a few. Currently, there are no clues indicating which version has a better performance. Typically, for ε-SVM, the ε-insensitive hinge loss needs to be pre-defined, and it indicates that there is no penalty for errors within the ε margin. The advantage is that the kernel matrix is sparse and the disadvantage is that a convex quadratic programming (QP) problem will need to be solved for the solutions. nu-SVM has the advantage of using a parameter nu for controlling the number of support vectors, it represents the lower and upper bound on the number of examples that are support vectors and that lie on the wrong side of the hyperplane, respectively. For LS-SVM, it can find the solution by solving a set of linear equations instead of a convex quadratic programming (QP) problem for classical SVMs. Since the hinge loss was neglected, the kernel matrix lost the sparsity, and it cannot be used for large-scale problems (Suykens et al., 2002). Truncated LS-SVM was proposed to solve this problem by employing the SVD technology on the kernel matrix, it can reduce the parameter uncertainty due to the noise and have a good performance for the large scaled regression problem. Meanwhile, It is necessary to note that the different kernel functions and parameters can also significantly affect the performance of the SVM. From the published papers, the SVM can be used for both hydrodynamic coefficient estimation and data driven implicit model.

Neural networks are also widely used for the manoeuvring modelling of marine surface ships, such as the Feed Forward Neural Network (Luo and Zhang, 2016), Recursive neural network (Moreira and Guedes Soares, 2003a; Perera et al., 2012), Deep Learning (Woo et al., 2018), just to name a few. Neural networks are a set of powerful bio-inspired algorithms for machine learning and can be used to solve complex problems that are difficult to describe using mathematical models. Neural networks are composed of interconnected nodes that process information and can learn from data. It usually includes the input layer, output layer and hidden layers, where the layers are made of nodes. The nodes combine input from the data with a set of weights, and the output of nodes is summed and then filtered with the activation function. The neural networks' performance highly depends on the number of layers and nodes in each layer. However, using a large number of layers and nodes is not recommended, since the complex structure usually will result in overfitting. From the published papers, Neural Networks are typically used for the data-driven implicit model or black box modelling.

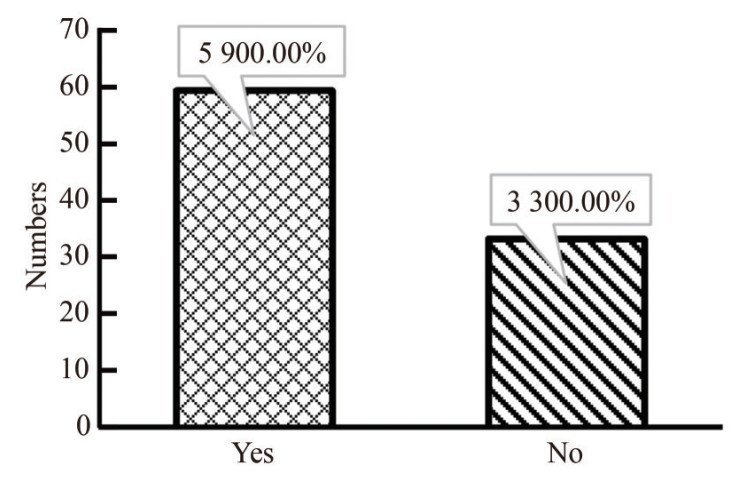
In Figure 10, the distribution of the environmental disturbance considered in the selected papers is summarized. As can be concluded, most papers (64%) considered the effect of environmental disturbances. The environmental disturbances are necessary to be considered for the manoeuvring modelling of surface ships, but, it is important to point out that the regularization factor of the system identification should be carefully chosen because the noise level of the measured outputs has a significant effect on the selection of the regularization factors (Xu and Guedes Soares, 2022). Yang et al. (2024) proposed an interesting work on the manoeuvring simulation of full-scale ships in broken ice regions. The ship-ice interaction was solved through the non-smooth discrete element method (NDEM), while the 3-DOF MMG model was utilized to simulate the autonomous navigation movement of ships.

Figure  10  The distribution of the environmental disturbance in the recent publications

Download: Full-Size Img

6   Conclusions

The system identification method is one of the mature technologies for the manoeuvring modelling of marine surface ships based on experimental data. This article provides an overview of the system identification methods used to build the manoeuvring models of marine surface ships. The classical manoeuvring models, manoeuvring tests and system identification methods are briefly introduced. The 92 papers published in journals and international conferences have been carefully selected and the statistical analysis of the manoeuvring models, manoeuvring test data, system identification method and environmental disturbance used in the paper is presented. The conclusion can be summarized:

1) The manoeuvring models are usually generalised from the nonlinear Abokwitz model and the MMG model by adding or neglecting some nonlinear terms considering the application.

2) The Abkowitz model is still popular due to the good performance of the manoeuvring prediction, but it is necessary to simplify the structure according to the practical applications without reducing the accuracy. The Nomoto models are typically used for the control or autopilot design. The implicit model can be used for manoeuvring simulation in a complex application, for example in shallow water.

3) Most of the papers still use simulation tests as the training set. It is worth noting that this is not the correct way to do it, except to demonstrate that the technique works, such as evaluation of parameter identification methods. It is not a good way to make manoeuvring predictions. The captive tests are still the most reliable way to estimate the hydrodynamic coefficients of the manoeuvring models considering the quality of the data.

4) The rising tendency of using the free-running ship model for the manoeuvring predictions can be observed, especially motivated by the development of machine learning methods. The results are more accurate and reliable with the novel technology and sensors.

5) The SVM, LS and NN are three popular methods (69%) for the manoeuvering modelling of marine surface ships. The choice of parameters can significantly improve the performance of the system identification methods.

It should be noted that the papers in Table 1 were seleted carefully based on the publication source. Most of them were published in well-recognized journals in the field of Ocean Engineering. Therefore, the paper is a review that describes the current status in the field of system identification for manoeuvring modelling of marine surface ships.

Appendix A